Molecular dynamics simulations unveil the aggregation patterns and salting out of polyarginines at zwitterionic POPC bilayers in solutions of various ionic strengths

Abstract

This study employs molecular dynamics (MD) simulations to investigate the adsorption and aggregation behavior of simple polyarginine cell-penetrating peptides (CPPs), specifically modeled as R₉ peptides, at zwitterionic phosphocholine POPC membranes under varying ionic strengths of two peptide concentrations and two concentrations of NaCl and CaCl₂. The results reveal an intriguing phenomenon of R₉ aggregation at the membrane, which is dependent on the ionic strength, indicating a salting-out effect. As the peptide concentration and ionic strength increase, peptide aggregation also increases, with aggregate lifetimes and sizes showing a corresponding rise, accompanied by the total decrease of adsorbed peptides at the membrane surface. Notably, in high ionic strength environments, large R₉ aggregates, such as octamers, are also observed occasionally. The salting-out, typically uncommon for short positively charged peptides, is attributed to the unique properties of arginine amino acid, specifically by its side chain containing amphiphilic guanidinium (Gdm⁺) ion which makes both intermolecular hydrophobic like-charge Gdm⁺ – Gdm⁺ and salt-bridge Gdm⁺ – C-terminus interactions, where the former are increased with the ionic strength, and the latter decreased due to electrostatic screening. The aggregation behavior of R₉ peptides at membranes can also be linked to their CPP translocation properties, suggesting that aggregation may aid in translocation across cellular membranes.

Graphical Abstract

1. Introduction

Peptide adsorption at the cellular membrane is a first and critical prerequisite for their successful subsequent translocation to the cell [1]. Cellular membranes are highly complex and composed of many different lipids, forming two separate leaflets together with embedded or associated proteins. Thus, they make a very heterogeneous medium with a strongly hydrophobic interior originating from hydrocarbon lipid tails [2], [3]. This makes it difficult for charged species to be efficiently translocated due to the huge energy penalty of carrying charged ions across a hydrophobic interior [4], [5]. Therefore, in normal, active, cellular-controlled processes, endocytosis (or exocytosis), driven by ATP and catalyzed by the membrane protein machinery, represents the main pathway to the cellular interior of any cargo to the cells but is often not very cargo-specific [6], [7].

Remarkably, it has been shown in the past that some charged peptides, often rich in positively charged residues, translocate the cellular membranes as efficiently and do not need ATP as an energy source. In particular, so-called cell-penetrating peptides (CPPs) with a typical length of 5 – 30 amino acids are often composed of a large ratio of arginine (Arg) and lysine (Lys) [8], [9], [10]. Interestingly, Arg is more often found in the CPP sequences than Lys, but both residues are found to be in contact with the negatively charged lipid headgroups [11], [12]. However, homo-oligomers of Arg peptides in the length of 5 – 15 units show superior translocation compared to their equally charged Lys counterparts, often referred to as arginine “magic” [13]. The reason behind their larger propensity is not completely clear from the molecular point of view, and the translocation mechanism details are not understood quantitatively. This stems from the fact that the typical procedures for the determination of free energy of translocation along the z-axis of the membrane bilayer are not optimal and result in too high translocation barriers [14], suggesting that another more efficient translocation pathway is operative instead. Recently, new reaction coordinate protocols coupled with transient pore formation, have been suggested to obtain the energetics of the process [15], [16], [17], [18]. However, the energetic estimation of charged peptide translocation is still far from being reliably quantified.

In our previous work, we established by molecular dynamics (MD) simulations that oligoarginines (such as nona-arginines, R₉) efficiently adsorb to zwitterionic phosphocholine (PC) membranes, with a free energy of adsorption of about −5 kcal mol^-1, in contrast to nona-lysines (K₉), which are not adsorbed to PC membranes at all [19], [20], [21], [22], [23]. Even though both R₉ and K₉ have the same positive charge, we have shown by MD simulations that R₉ can interact with the PC phosphate group in the membrane interior more efficiently than K₉. Additionally, in the case of R₉ adsorption, a stronger hydrophobic effect also contributes to the free energy of peptide adsorption [23]. Moreover, several experimental works from our groups have shown that the adsorption of oligoarginines at PC bilayers is not a computational artifact and is indeed occurring using various experimental techniques, such as lipid/polydiacetylene colorimetric assays [24] or fluorescence assays on supported lipid bilayers [21]. It is important to note that zwitterionic but overall neutral PC bilayers have been chosen as a model lipid membrane since they constitute a majority of lipids in the outer cellular leaflet, where peptide adsorption occurs upon translocation to the cell from the outside [25]. Through MD simulations and fluorescence experiments, we have also shown that ionic strength is an important factor in peptide adsorption strength [22]. Specifically, we have computationally predicted and experimentally shown that the degree of R₉ adsorption decreases upon the addition of NaCl or CaCl₂ salt. This decrease is due to an increasing ionic strength, which screens electrostatic interactions between the charged peptides and lipid species. The interaction between salt cations and lipids also results in a net positive charge at the interfacial membrane, further reducing peptide adsorption [11].

However, another interesting phenomenon observed in MD simulations is the attraction and aggregation of like-charged R₁₀ and R₉ (vs K₁₀ and K₉) peptides in water and at membranes, respectively, which is counterintuitive from the electrostatic point of view. In addition to MD simulations, which robustly show the Arg aggregation in both media, the aggregation of R₁₀ (and lack of K₁₀ aggregation) in aqueous solutions has been experimentally suggested by SAXS measurements [26]. Similarly, fluorescence assay experiments have indicated the aggregation of R₉ (but not K₉) at membranes at supported lipid PC bilayers [21]. The reasons behind the “magical” pairing of Arg-rich peptides can be attributed to the chemical nature of the guanidinium cation (Gdm⁺), found in the side chain of Arg amino acid. Our previous findings by extensive MD simulations at both classical [27], [28] and the ab initio level [27], [29], [30], indicate an unexpected counterintuitive self-aggregation tendency of Gdm⁺ cations in water, despite their positive charge due to attractive van der Waals interaction originating from specific Gdm⁺ geometry and charge distribution, which overcome repulsive electrostatic interaction between positively charged cations. This behavior is not observed in equally charged spherical ammonium (NH₄⁺) ions, which hints at why Lys-rich peptides do not show aggregation ability.

The tight adsorption of Arg-rich peptides to PC bilayers has been quantified in our previous simulations and experiments, [21], [23] but the aggregation propensity of Arg-rich peptides at the membrane surface remains enigmatic. To resolve this puzzle, in this work, we focus on the detailed molecular view of the R₉ aggregation propensity at 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) using available unbiased microsecond MD simulations and try to assess it in a more detailed and quantifiable way. As our workhorse system, we analyzed simulations of aggregation of R₉ at POPC bilayers in solutions of different ionic strengths of NaCl and CaCl₂ using the scaled-charge approach using the ProsECCo75 force field, which corrects for the overstabilization of electrostatic interactions in non-polarizable simulations [31], [32], [33], [34]. This force field has been successfully applied in many systems, ranging from ions in aqueous solutions to the adsorption of ions at phospholipid membranes [35], [36], [37], [38], [39], [40]. Specifically, we concentrate on the quantification of aggregation propensity and aggregation patterns of R₉ peptides at membranes in different peptide and salt concentration conditions in molecular detail, which is relevant for further studies of the CPP penetration mechanism, which has still not been connected to their increased translocation ability [19].

2. Computational methods

In our previous work, all-atom molecular dynamics (MD) simulations were conducted to systematically examine the interactions of nona-arginines (R₉) in aqueous solutions of either NaCl or CaCl₂ with POPC bilayers [22]. Whereas the former analysis focused on assessing the adsorption energetics, here we focused on the aggregation properties of R₉ at membranes. In this work, we analyzed ten simulations performed for two concentrations of R₉ peptides (0.021 and 0.056 m) at two concentrations of NaCl or CaCl₂ salt (0.133 m and 1.065 m) and the reference simulation with counterions only, respectively. In the first set of simulations, the total number of peptides (6 or 16 R₉ molecules corresponding to the concentrations above) were equally placed in the bulk phase on both sides of the POPC bilayer in random initial configurations. To further prove the convergence of the MD simulations, we performed an additional set of 2 μs MD simulations of the same systems (replicas). However, in this case, the initial setup was different, and we placed 50 % of peptides adsorbed on the POPC surface while the others were in the bulk. In our previous work, it was shown that 2 and 4 peptides bind too strongly at POPC, while 6 peptides are optimal for aggregation analysis due to better sampling during adsorption/desorption from POPC. On the other hand, we chose the maximum concentration of peptides (16) to study the effect of high peptide concentration, and we omitted the intermediate peptide concentrations (10 and 13 peptides). In all systems, chloride counterions are used to neutralize the systems, and the simulation boxes for all studied systems contained 15,856 water molecules within a box size of 8 × 8 x 12 nm. To achieve the above-specified concentrations, 38 and 304 salt molecules (NaCl or CaCl₂) were added to the systems, respectively. The membrane bilayer comprised 100 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipids in each leaflet, resulting in a total of 200 lipids.

This study employed CHARMM36-based ProsECCo75 models for lipids and peptides [31], [34], [41], [42], [43], along with an electronic continuum correction (ECC) approach for ion parameters to address the overbinding issue of charged molecules to zwitterionic bilayers [32], [33], [44]. Specifically, partial charges in the ProsECCo75 models, including those of the phosphate and choline groups of POPC, peptide termini, and the charged groups of Arg, were adjusted to scale down the total charge of each group from + 1 to + 0.75 (Table S1). No other modifications were made to the CHARMM36 lipid or peptide parameters [45]. NBFIX was disabled, as the ECC approach achieved a similar effect without the need for an additional ad hoc correction [31], [34]. All used topologies are available in GitLab at https://gitlab.com/sparkly/prosecco/prosECCo75. The systems were solvated with CHARMM-specific TIP3P ("TIPS3P") water [46], and buffered Verlet lists were employed for tracking atomic neighbors with a 1.2 nm cut-off for the Lennard-Jones potential. Van der Waals interactions were treated using a cut-off of 1.2 nm, with the forces smoothly attenuated to zero between 1.0 and 1.2 nm. Long-range electrostatics were treated using the smooth particle mesh Ewald method [47]. After the steepest descent minimization of all systems, for the equilibration, we used the Berendsen thermostat and barostat [48], while the production runs utilized the Parrinello–Rahman barostat [49] with a semi-isotropic pressure coupling and a 1 bar reference pressure. The Nosé –Hoover thermostat [50] was applied with a target temperature of 310 K. Covalent bonds involving hydrogens in peptides and lipids were constrained using the P-LINCS algorithm [51], and the SETTLE algorithm was used for constraints in water molecules [52]. MD simulations were conducted for 2 μs with a time step of 2 fs using the GROMACS package [53]. Analysis of production trajectories was performed using in-house Python scripts in conjunction with the MDAnalysis library [54], The analyses omitted the first 500 ns of simulation times, while VMD was used to generate MD simulation figures [55].

3. Results and discussion

3.1. Number density profiles and R₉ aggregation propensity at POPC bilayer

First, we summarize the analysis of the peptide adsorption reported previously [22]. The symmetrized number density profiles of R₉ adsorption to the POPC membrane for two different peptide concentrations, i.e., low (0.021 m) and high (0.056 m) in different salt concentrations (Fig. 1, top and bottom panels). The non-symmetrized number density profiles are shown in Fig. S1, indicating a good qualitative agreement with symmetrized ones (apart from inevitable quantitative differences due to thermal equilibrium and periodic boundary conditions). To prove that simulation time is sufficient for proper sampling, we plotted the z-distances between the centers of mass of each peptide and the center of mass of the POPC bilayer during the simulation time. First, we show the profiles for the system with the strongest peptide binding at low peptide concentration where almost no aggregation occurs (system with counterions only, Table 1), and the result is displayed in Fig. S2. We see that the peptides are very quickly adsorbed at POPC, and during simulation time, several exchange events between bound and unbound states of individual peptides are observed. Second, in other systems, where the adsorption is not as strong but aggregation is more present (for example, a system with high peptide concentration and counterions, Table 1), the exchange is even more pronounced (Fig. S3), thus ensuring sufficient sampling for the analysis of the aggregates. The number of adsorbed peptides decreases with both peptide and salt concentration, which is more pronounced in the case of CaCl₂ due to the higher ionic strength of the solution. Interestingly, in the case of the high peptide concentration and the highest CaCl₂ concentration (Table 2), the adsorption of R₉ is quite weak (but still existing), which can be explained by the decrease of the electrostatic interactions between positively charged peptides and negatively charged POPC phosphate groups due to high ionic strength [22].

Fig. 1.

Symmetrized number density profiles for peptide center of mass for low R₉ concentration (upper panel) and high R₉ concentrations (bottom panel) in different systems with respect to the distance from the POPC bilayer center. The number density of POPC phosphorus atoms is shown as the dashed line for the reference system without added salt for low and high peptide concentrations.

Table 1.

The probabilities of the R₉ peptides adsorption at POPC, n(R₉)_ad, and of R₉ aggregation occurring at POPC. The contributions of three different interactions between specific groups in R₉ peptides are given in percentages in systems with low peptide concentration. Error bars were estimated by the standard deviation of three individual 500 ns MD simulation blocks.

System	n (R9)ad / %	Aggregation / %	Gdm+ – Gdm+ / %	Gdm+ – COO- / %	NH3+ – COO- / %
Water	61.7 ± 1.7	2.2 ± 0.3	41.0 ± 3.3	53.7 ± 2.3	5.3 ± 3.5
0.133 m NaCl	61.7 ± 1.7	3.9 ± 0.7	36.7 ± 3.6	57.6 ± 3.6	5.8 ± 2.4
1.036 m NaCl	53.3 ± 6.7	31.4 ± 6.3	49.3 ± 2.0	46.7 ± 1.4	4.0 ± 0.8
0.133 m CaCl2	55.0 ± 1.7	11.4 ± 6.2	42.4 ± 1.2	50.4 ± 1.7	7.2 ± 1.9
1.036 m CaCl2	36.7 ± 6.7	43.3 ± 5.8	50.9 ± 2.6	42.7 ± 1.9	6.5 ± 1.8

Table 2.

The probabilities of the R₉ peptides adsorption at POPC, n(R₉)_ad, and of R₉ aggregation occurring at POPC. The contributions of three different interactions between specific groups in R₉ peptides are given in percentages in systems with high peptide concentration. Error bars were estimated by the standard deviation of three individual 500 ns MD simulation blocks.

System	n (R9)ad / %	Aggregation / %	Gdm+ – Gdm+ / %	Gdm+ – COO- / %	NH3+ – COO- / %
Water	45.6 ± 0.6	68.1 ± 3.7	42.3 ± 0.9	51.3 ± 0.7	6.4 ± 0.8
0.133 m NaCl	44.4 ± 0.6	76.9 ± 10.6	44.6 ± 0.5	49.7 ± 0.6	5.6 ± 0.7
1.065 m NaCl	38.1 ± 2.5	87.8 ± 0.9	50.7 ± 0.6	45.5 ± 0.6	3.8 ± 0.4
0.133 m CaCl2	41.9 ± 1.3	68.3 ± 1.1	45.3 ± 0.5	48.5 ± 0.5	6.2 ± 0.5
1.065 m CaCl2	16.9 ± 1.9	76.5 ± 2.3	53.9 ± 1.3	42.5 ± 1.6	3.6 ± 0.7

Additionally, we performed the second set of MD simulations with different initial conditions, where half of the peptides were bound to the surface (see Computational Methods). The density profiles for low peptide and high peptide concentrations, both symmetric and asymmetric, are shown in Figs. S4 and S5, respectively. The results look qualitatively very similar, showing the desorption of peptides at higher ionic strengths, thus confirming the convergence of MD simulations. Here, we also plotted the z-distances between the centers of mass of each peptide and the center of mass of the POPC bilayer during the simulation time (Figs. S6 and S7), which again show a similar number of exchange events between bound and unbound states, thus confirming the original findings. The number of exchanges is smaller in the case of 6 peptides for both sets of simulations due to lower ionic strength and increased electrostatic interactions compared to simulations with 16 peptides, identical to the original set of MD simulations.

Using only number density profiles, assessing the degree of peptide aggregation is impossible since the profiles are time-averaged in the analysis and mask possible aggregation events. Here, we assessed the aggregation propensity by analyzing the individual MD simulation frames and checking whether, in the vicinity of adsorbed peptides at POPC, other peptides are found (not necessarily bound to POPC), using a cut-off of 0.6 nm between any atoms of the peptide in contact. If the criterion is fulfilled, we denote the associated peptides as an aggregate. Table 1, Table 2 show the calculated total degree of aggregation (i.e., the number of frames with some aggregate form of any size divided by the total analyzed frames) for low and high peptide concentrations. In addition, for each of the aggregates (regardless of its degree of oligomerization which is discussed later), we analyzed the contribution of different interactions between selected groups in R₉ (Gdm⁺ – Gdm⁺, Gdm⁺ – COO^- and NH₃⁺ – COO^-) that is given as a ratio of a number of contacts between two given groups (also with a cut-off of 0.6 nm) vs. the total number of three selected contact types within this threshold distance.

The analysis of the aggregation data shows several interesting facts. The number of adsorbed R₉ peptides decreases with the salt concentrations, which is more pronounced in the case of CaCl₂ than NaCl due to the higher ionic strength of solutions, as shown in our previous work [22], and agrees with the number density profiles shown in Fig. 1. However, the peptide aggregation propensity is reversed – the higher the ionic strength is, the peptide aggregation increases, ranging from a negligible propensity in neat water solutions at low peptide concentrations (2.2 %, system without added ions, Table 1) up to a significant aggregation (87.8 %, 1.065 m NaCl, Table 2) in high peptide concentration systems with high NaCl concentration. Similarly, the aggregation propensity is high in all systems with high peptide concentrations, above 65 %. Tables S2 and S3 show the same analysis for the MD simulations of replicas, and the results are very similar qualitatively and within reasonable numerical agreement.

This resembles a biologically very important phenomenon in protein chemistry, where the solubility of a protein decreases in the presence of high concentrations of salts, known as salting-out [56], [57]. However, it is interesting that salting-out occurs here for highly positively charged Arg oligomers at membranes, which are charged and relatively short. The detailed analysis shows that the amount of like-charge Gdm⁺ – Gdm⁺ interactions, which are mostly hydrophobic [30], increase with the salt concentration, thus contributing mostly to the increase in peptide aggregation. This is slightly more pronounced for high peptide concentrations where the aggregation is more pronounced too (Table 1, Table 2). On the other hand, the electrostatic interactions between Gdm⁺ – COO^- and NH₃⁺ – COO^- decrease with the addition of salt due to charge screening.

3.2. The diversity and lifetime of adsorbed R₉ aggregates at POPC

As the next step, we analyzed the distribution of aggregates depending on their size. Fig. 2 shows the aggregate distribution for two R₉ peptide concentrations in different salt solutions. The upper panel shows the distribution for lower peptide concentrations. We see that the amount of dimers dominates in all systems, being in the 80 – 100 % range. Only in systems with higher ionic strength (especially in CaCl₂ solutions), a significant percentage of trimers (∼ 20 %), a small number of tetramers (∼ 5 %), and a very small number of pentamers (∼ 0.5 %, not shown in the Figure) are also present.

Fig. 2.

The percentage of different-sized aggregates in systems with low peptide concentration (upper panel) and high peptide concentrations (bottom panel) in systems with different ionic strengths.

A more interesting picture occurs in systems with higher peptide concentrations (bottom panel). Although the dimers are still dominant in all systems, the distribution of trimers and higher aggregates is qualitatively different than in the low peptide concentration regime. In particular, large aggregates also occur in non-negligible amounts in the systems with high ionic strength with 1.065 m NaCl or CaCl₂. Even more interestingly, in the system with 1.065 m CaCl₂, the percentage of larger aggregates than heptamers is almost 20 %. Although this indicates that the aggregation is sensitive to the ionic strength, we should also remember that, in this case, the number of peptides that are indeed adsorbed at the POPC interface is the smallest (Table 2). We repeated the same analysis for the second set of MD simulations. The results are shown in Fig. S8, where we see a qualitatively identical trend to the original set of simulations, i.e., in the system with high peptide concentrations and ionic strengths, the diversity of observed aggregates is larger.

In general, we can see the following trends in our MD simulations. First, in the systems with low peptide concentration, the maximum size of aggregates is much smaller than higher peptide concentrations, reaching the maximum size of pentamer in the system with 1.065 m NaCl and CaCl₂. This is not surprising since the higher concentration of peptides can form not only a larger number of aggregates but also larger aggregates (for example, in a low peptide concentration regime, the maximum size of aggregate is a hexamer, which was not observed in the simulations). Second, the diversity of differently-sized aggregates is much more pronounced for higher peptide concentrations, where heptamers and even higher aggregates are present, especially at higher salt concentrations and, in turn, higher ionic strengths.

In Table 3, we analyzed the average lifetime of R₉ aggregates formed at the membrane, depending on their size. Overall, the lifetime of same-sized aggregates increases upon increasing the peptide and salt concentration, which is most notable for the dimers. In the systems where many different-sized aggregates are present, the lifetime of larger aggregates is generally decreasing compared to dimers, reaching minimum lifetimes of ca. 100 ps for very large aggregates. Therefore, despite the lower number of adsorbed R₉ peptides upon the increase of peptide and salt concentrations, the aggregated peptides that are adsorbed at the POPC interface have an overall larger adsorption lifetime when all aggregate sizes are considered. A similar analysis was performed for the second set of MD simulations, and the results are presented in Table S4. Here again, the results are very similar, with a single exception: the dimer in the reference water system has a significantly longer lifetime, which is a single consequence of different initial conditions where salts are not present.

Table 3.

The average lifetime of R₉ aggregates (in ps) of different sizes (dimer–heptamer and higher aggregates) at the POPC bilayer for low and high peptide concentrations in systems with different salt compositions and concentrations. The error bar is the standard deviation of the mean value when multiple aggregation events occur. The range of aggregate lifetimes is presented for larger aggregates (> heptamer).

system	dimer	trimer	tetramer	pentamer	hexamer	heptamer	> heptamer
Water	a 297 ± 38 b 799 ± 50	– 335 ± 20	– 270 ± 32	– 207 ± 43	– 150 ± 29	– –	– –
0.133 m NaCl	492 ± 88 857 ± 60	– 360 ± 22	– 287 ± 25	– 218 ± 23	– 140 ± 21	– 220 ± 58	– –
1.065 m NaCl	928 ± 103 638 ± 26	652 ± 141 425 ± 18	380 ± 77 352 ± 18	c∼300 241 ± 17	– 258 ± 21	– 159 ± 13	– 150 – 200
0.133 m CaCl2	760 ± 119 561 ± 31	231 ± 55 337 ± 19	c∼100 254 ± 20	– 159 ± 71	– 129 ± 14	– 217 ± 48	– c∼100
1.065 m CaCl2	1030 ± 144 659 ± 48	493 ± 53 443 ± 31	366 ± 65 321 ± 23	138 ± 18 273 ± 20	– 237 ± 20	– 244 ± 19	– 150 – 250

^aThe upper row shows data for low peptide concentration.

^bThe lower row shows data for high peptide concentration.

^cA single continuous aggregation event.

Finally, we show in Fig. 3 how the size of R₉ aggregates changes over time. It is visible that by increasing ionic concentration, the amount of aggregates and their lifetime increases with the ionic strength and peptide concentration, which agrees with the results shown in Table 3 and Fig. 2. Interestingly, some of the values in the graph are equal to zero (especially at higher ionic strengths), which indicates that none of the peptides are bound at POPC, in agreement with our previous study where we have shown that R₉ peptides can desorb from POPC in these conditions. The results for the second set of MD simulations are shown in Fig. S9, where high agreement is visible, again reiterating the convergence of the original set of MD simulations.

Fig. 3.

The maximum size of aggregates formed at the POPC membrane during simulation time. The first 500 ns were discarded from the analysis.

3.3. Visualization of different aggregates at the POPC interface

Finally, despite the quantitative analysis of the distribution of R₉ aggregates at POPC, it is instructive to visualize the aggregates at the membrane surface. In Fig. 4, we show a typical snapshot from the MD simulation of the reference system, where no additional salt is added to the system. According to Table 1, we see that in the system with low peptide concentration, the aggregation of R₉ is rare, being observed only in less than 1 % of the simulation time.

Fig. 4.

A selected snapshot from MD simulations showing the lack of aggregation of R₉ peptides in the reference system without added salt at low peptide concentration. In panel a), we observe four adsorbed R₉ peptides (opaque representation) and two non-adsorbed R₉ peptides (ghost representation). Panel b) shows the magnified region where one of the R₉ peptides is adsorbed at the POPC interface with indicated intramolecular Gdm⁺ – Gdm⁺ interaction and deep penetration of R₉ sidechains and interaction of its Gdm⁺ groups with POPC phosphate groups.

A detailed analysis of the MD snapshot shows a typical situation when peptides do not aggregate at the POPC surface (Fig. 4a). When no aggregation is present, peptides lie almost parallel to the membrane surface, and sidechains are inserted in the membrane interior where Gdm⁺ cations interact strongly with the POPC phosphate groups (Fig. 4b). This has been observed in many simulation studies so far, and the detailed analysis of the energetics of this particular interaction is presented in Ref [23]. Notably, we also observe the intramolecular like-charge Gdm⁺ – Gdm⁺ interaction (Fig. 4b), which is typical for arginine-rich peptides, as suggested previously by MD simulations [21], [24], [26].

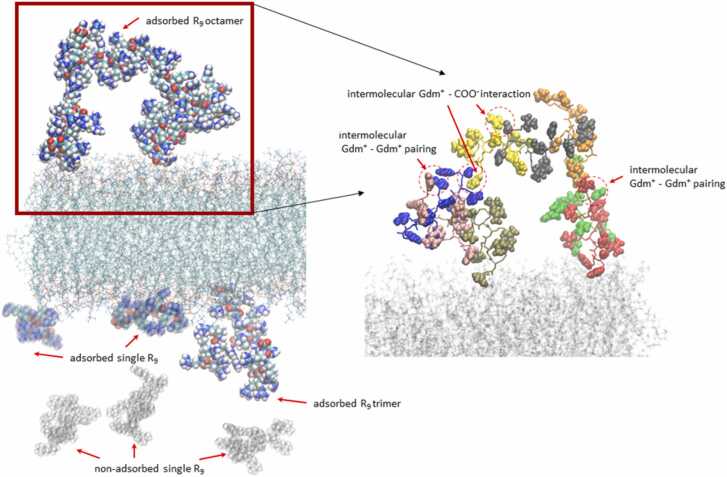
In the case when the concentration of R₉ peptides is high, together with high CaCl₂ concentration, the probability of aggregation of R₉ increases, as suggested in Table 1, Table 2. We see that R₉ aggregates can be formed in different sizes, as illustrated in Fig. 5 (left panel), where we see an R₉ octamer and R₉ trimer, which are bound to the POPC interface but do not lie perpendicularly to the membrane surface, like in the case when single R₉ molecules are adsorbed. Instead, they form a cluster where one peptide (in the case of a trimer) or two peptides (in the case of an octamer) are adsorbed to the interface, and other peptides are aggregated on top of them. For this particular system, this is also reflected in the reduced R₉ number density (Fig. 1) in the vicinity of the membrane together with the calculated number of adsorbed peptides (Table 2), which is significantly lowered compared to systems with lower peptide concentration and lower ionic strength. Nevertheless, the peptides that are adsorbed (although in a smaller quantity), are in a large ratio adsorbed as aggregates (> 50 %, Table 2). The weaker adsorption of the aggregate is not unexpected, since the Gdm⁺ groups, responsible for tight adsorption of single R₉ to POPC phosphate group, are consumed in the intermolecular interactions between R₉ peptides in the aggregate and are not available for interaction with POPC membrane (see below) (Fig. 5).

Fig. 5.

Left panel: A selected snapshot from MD simulations showing the aggregation of R₉ peptides in the system with 1.065 m CaCl₂ at high peptide concentration. The R₉ octamer and R₉ trimer are shown in the opaque representation. Two single-adsorbed R₉ peptides are shown in the transparent representation, whereas non-adsorbed R₉ peptides in the bulk are shown in the ghost representation. Right panel: The selected intermolecular interactions in the adsorbed R₉ octamer. Individual R₉ peptides are shown in the licorice representation with different colors, while the corresponding Gdm⁺ and COO^- groups are shown in the vdW representation. Gdm⁺ - Gdm⁺ like-charge pairing and salt-bridge-like Gdm⁺ - COO^- interactions are indicated with red arrows and in red dashed circles.

Finally, let’s take a look at one of the aggregates and describe in more detail the interactions, which are quantified in Table 1, Table 2. The intermolecular interactions in the R₉ octamer are presented in the right panel of Fig. 5. We see that the intermolecular aggregate has many contacts between Gdm⁺ groups with either Gdm⁺ groups of another peptide in the aggregate (like-charge pairing) or with carboxylic COO^- group (salt-bridges). This is at odds with our previous studies of polyarginine R₁₀ aggregate in water, where energetically favored salt-bridge interactions between the negatively charged C-terminus and adjacent Gdm⁺ groups dominate compared to like-charge Gdm⁺ – Gdm⁺ interactions, which are hydrophobic and weaker due to the missing attractive electrostatic contribution [26]. However, upon the interaction of R₉ with POPC, the ratio of intermolecular Gdm⁺ – Gdm⁺ interactions is either similar or larger vs. Gdm⁺ – COO^- interactions (Table 1, Table 2). This effect is due to the peptide interaction with the membrane, which limits its conformational freedom compared to the aqueous solution, where polyarginine is more flexible and more easily adopts conformations that enable more favored salt-bridge interactions. More interestingly, the ratio of Gdm⁺ – Gdm⁺ interactions increase with the increase of ionic strength, which is another manifestation of the salting-out effect at higher salt concentrations where Gdm⁺ – COO^- electrostatic interactions are being effectively screened out and hydrophobic Gdm⁺ – Gdm⁺ interactions are unaffected or even increased as computationally predicted for model hydrophobic systems in water [58].

3.4. Implications to the cell-penetration peptides (CPPs) translocation mechanism

As mentioned in the Introduction, CPPs, such as nona-arginine R₉, passively translocate across cellular membranes without the need for ATP. [8], [9], [10] This property is especially interesting in light of controlled drug delivery since it enables the delivery of active compounds to the cells without modifying innate translocation cellular mechanisms, such as endocytosis [59], [60]. The details of the translocation mechanism are not currently known at the molecular level, predominantly due to the inability of current computational techniques to properly evaluate the energy barrier for the translocation of CPPs across the hydrophobic lipid bilayer interior, which is almost impermeable for charged species, such as polyarginines used in this work. However, the calculated barriers for arginine/polyarginine translocation using the simple z-coordinate are similar to the barriers for lysine/polylysine translocation [61], [62]. Therefore, a question arises: Why do polylysines not penetrate across the bilayers? For neutral membranes, the reason is clear since it has been shown both computationally and experimentally that K₉ does not adsorb to the neutral POPC bilayers (which serve as a mimic of the neutral outer cellular leaflet [3]), in contrast to R₉, it cannot translocate across bilayers if there is no peptide adsorption [21], [23]. This results from the fact that the interaction of Arg side chain – Gdm⁺ ions with the POPC phosphate groups is stronger compared to the analogous Lys side chain –NH₃⁺ ions interaction due to the planarity of the Gdm⁺ ion, which more easily interacts with the buried POPC phosphate group [23]. MD simulations have suggested an alternative idea: octa-arginine (R₈) can stabilize the artificially created pore in the neutral DPPC or negatively charged DOPE/DOPS lipid bilayers, in contrast to octa-lysine (K₈), thus facilitating R₈ translocation of the bilayer [62], [63].

However, the arguments above are not fully sufficient for the understanding of the molecular view of the translocation mechanism. Namely, when lipid bilayers are negatively charged, like, for example, during the endosomal escape [64], [65], then both polyarginine and polylysine, which are positively charged, can adsorb at the membrane due to attractive electrostatic forces potentially enabling polylysine to cross the bilayer, which has not been confirmed experimentally [65]. Also, the energy for the spontaneous pore opening is quite high (around 20 kcal mol^-1 for DPPC) [66], similar to energy barriers like those for single arginine/lysine translocation [61], thus again not explaining how the adsorption of octa-arginine can initiate the opening of the pore in the membrane.

Still, in MD simulations, the polyarginine aggregates are always present at the membranes, while polylysines are mutually repelled at the membrane surface, regardless of their respective membrane binding affinity. This has also been experimentally confirmed by fluorescence measurements at supporting lipid bilayers [21]. As previously computationally suggested, the transfer of single Arg [67], (or Gdm⁺ cation) [29] into lipid bilayers is nonadditive. The same energy penalty for crossing the barrier is paid for transferring a single Arg or multiple Arg amino acids. Intuitively, we would expect that the same energy barrier would also be present for a single polyarginine peptide or several polyarginine peptides (that do not repel each other), which might follow the first peptide across the membrane in a concerted manner once the membrane pore is spontaneously created. Therefore, the existence of polyarginine aggregates adsorbed at the lipid membranes can serve in two ways. First, they can destabilize the membrane due to a high positive charge catalyzing the spontaneous transient pore formation in the membrane, similar to the electroporation effect [68]; second, the aggregates can also serve as a reservoir for additional polyarginine peptides once the membrane translocation process of polyarginine has started. Unfortunately, the computational estimates of the barriers for single vs. aggregated polyarginine translocation and the energetics for peptide aggregate-induced pore formation are still missing due to inadequate computational techniques and the possible involvement of another additional translocation pathway [14], [15], [16], [17], [18]. Nevertheless, we believe that the fact that polyarginines indeed aggregate at model membranes, as shown in this work, and are sensitive to ionic strength is interesting enough to be considered as one of the possible ways how to understand the arginine “magic” [19] and the fact why polyarginine acts as an efficient CPP.

4. Conclusions

In this work, we showed by MD simulations that simple polyarginine CPP (modeled as R₉ peptide) adsorbs and aggregates at the zwitterionic POPC membrane in an ionic strength-dependent manner. In our previous work, we showed that the increase in R₉ concentration and ionic strength (modeled as 0.133 and 1.065 m NaCl and CaCl₂ solutions, respectively) decreased the total number of adsorbed peptides [22].

We performed a detailed analysis of the adsorbed peptides at the POPC bilayer, revealing an interesting phenomenon of R₉ aggregation, which is also dependent on the ionic strength. We analyzed in detail how peptide concentration and ionic strength influence peptide aggregation and showed that by the increase of ionic strength, either by the increase of peptide concentration or the presence of Na⁺ and Ca²⁺ salts, aggregation of peptides is also significantly increased. In particular, we show that the diversity of aggregates and the aggregate size also increase with the ionic strength. The majority of aggregates at the POPC bilayer are present in the form of dimers, but large R₉ aggregates (heptamers and larger) can be sporadically found at the POPC bilayer in systems with high ionic strength, which is a clear indication of the salting-out effect, i. e. the loss of peptide solubility with the addition of salt, which is unusual for short positively charged peptides. However, since arginine contains amphiphilic Gdm⁺ ion in the side chain with counterintuitive properties, from like-charge pairing and anisotropic solvation, the salting-out effect is a consequence of its hydrophobic properties and screening of electrostatic interactions in high ionic strength solution. We also analyzed the aggregate lifetimes at the membrane, which generally increase with the peptide concentration and ionic strength for the same-sized aggregates.

Finally, the aggregation of R₉ peptides at membranes can potentially be connected to the CPP translocation properties of polyarginines. Since the R₉ peptides are aggregated (or, at worst, non-repelled) at the POPC membrane, during the transfer across spontaneously created transient pores in the bilayers, they might translocate in a concerted manner without additional energy penalty, where arginine aggregates serve as a peptide reservoir. This is contrasted to the transfer of the non-CPPs, such as polylysine peptides, which do not aggregate and do not translocate cellular membranes. Still, the molecular details and energetics of the translocation process are not currently available due to high computational demands and improper reaction coordinates for peptide translocation, which is planned to be addressed in future work.

CRediT authorship contribution statement

Mario Vazdar: Writing – review & editing, Writing – original draft, Visualization, Supervision, Resources, Project administration, Methodology, Investigation, Funding acquisition, Formal analysis, Conceptualization. Man Thi Hong Nguyen: Writing – original draft, Visualization, Methodology, Investigation, Formal analysis.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. none.

Appendix A. Supplementary material

Supplementary material

.