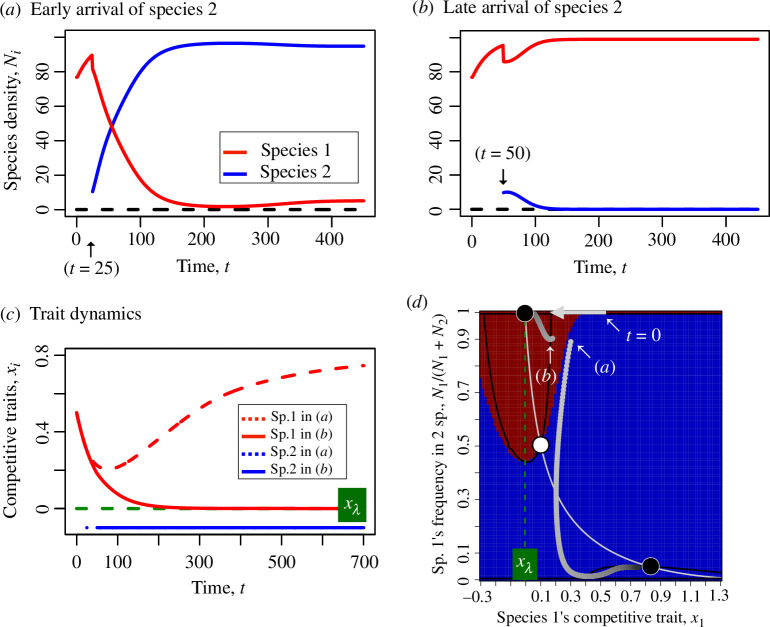
Figure 2.

Population and trait dynamics of two species and a nullcline plot. (a) When the difference in immigration timing is small, ecological character displacement (ECD) occurs and an early-arriving species 1 stably coexists with a late-arriving species 2. The population density of species 1 is low owing to maladaptation to a local habitat. (b) When the difference is large, the early-arriving species 1 is locally adapted and prevents establishment of the late-arriving species 2 by driving extinction of species 2 (i.e. evolution-mediated priority effect, EPE). (c) When the difference in immigration timing is small, colonization of species 2 prevents a competitive trait of species 1, x₁, to approach the optimum trait maximizing the per capita fecundity, x_λ, and causes x₁ to diverge from species 2’s trait, x₂, to avoid interspecific competition (i.e. ECD) (red dashed line). On the other hand, when the difference is large, x₁ approaches x_λ, which promotes extinction of species 2 (i.e. EPE) (red solid line). (d) The nullclines show alternative stable states including two locally stable equilibria (black points): one where species 2 goes extinct when x₁ reaches x_λ and the other where species 1 and 2 stably coexist owing to trait divergence. A white circle represents a locally unstable equilibrium. Black and grey lines are nullclines of species 1’s frequency and trait evolution, respectively. Grey points are results of numerical iterations of the recursion equations shown in (a), (b), and (c), and the arrow ‘t = 0’ indicates the initial condition. The red and blue regions indicate the basins of attraction towards the extinction and coexistence equilibria, respectively. Parameter values are ${\alpha }_{ii}=s_i=1$, ${\alpha }_{12,\mathrm{m}\mathrm{a}\mathrm{x}}={\alpha }_{21,\mathrm{m}\mathrm{a}\mathrm{x}}=1.1$, $x_2=-0.1$, $x_{\lambda }=0$, ${\lambda }_{i,\mathrm{m}\mathrm{a}\mathrm{x}}=100$ (i = 1, 2) and G_x = 0.01, and initial conditions are $x_{\mathrm{1,0}}=0.5$, $N_{\mathrm{1,0}}=({\lambda }_1-1)/{\alpha }_{11}$ and N_2,0 = 0 until the immigration timing of species 2, t_i, and $N_{2,t_i}=N_{\mathrm{1,0}}/10$ where t_i = 25 or 50.