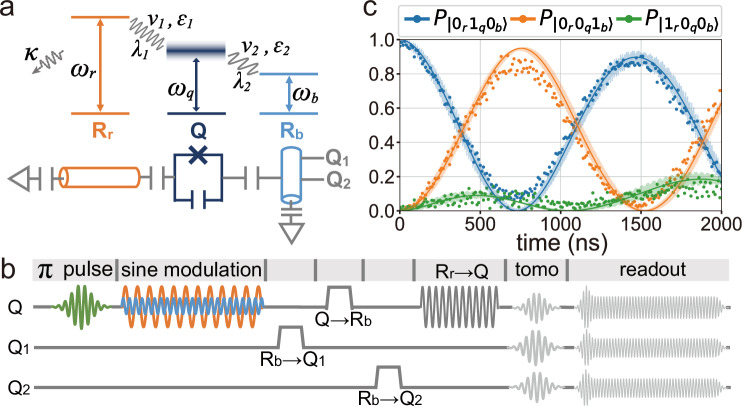
Fig. 2. Experimental implementation.

a Synthesis of the NH three-mode system. The NH Hamiltonian is realized in a circuit, where a Josephson-junction-based qubit (Q), together with a bus resonator (R_b) and a readout resonator (R_r), comprises an effective three-mode system in the single-excitation subspace. The decaying rates of Q and R_b are respectively 0.06 MHz and 0.08 MHz, both of which can be neglected compared to that of R_r, κ = 5 MHz. Q is coupled to R_r (R_b) at the first upper (lower) sideband with respect to the first (second) parametric modulation. b Pulse sequence. The qubit Q is first prepared in the excited state at its idle frequency, followed by the application of two sine modulations. The modulation frequencies (ν₁, ν₂) and amplitudes are tunable for controlling λ₁ and λ₂. After the modulating pulse, the evolved R_r-Q-R_b output state is mapped to the Q-Q₂-Q₁ system for readout, where Q₁ and Q₂ are two ancilla qubits, each of which can be controllably coupled to the bus resonator. c Observed evolutions of the populations. All data are measured for the initial state $\mid 0_r{1}_q{0}_b⟩$ at the point λ₁ = 2π × 0.21 MHz and λ₂ = 2π × 0.31 MHz. The results are obtained by discarding the measurement outcome $\mid 0_r{0}_q{0}_b⟩$ and renormalizing the remaining populations of $\mid 0_r{0}_q{1}_b⟩,\mid 0_r{1}_q{0}_b⟩$, and $\mid 1_r{0}_q{0}_b⟩$ in the single-excitation subspace. The solid curves are theoretical predictions using the NH Hamiltonian (1), while the fast oscillating curves are numerical simulation results using the original Hamiltonian (given in Section S3 of the Supplementary material) with frequency modulations included.