Biomarker Panel Development Using Logic Regression in the Presence of Missing Data

Abstract

We consider the problem of developing flexible and parsimonious biomarker combinations for cancer early detection in the presence of variable missingness at random. Motivated by the need to develop biomarker panels in a cross-institute pancreatic cyst biomarker validation study, we propose logic-regression based methods for feature selection and construction of logic rules under a multiple imputation framework. We generate ensemble trees for classification decision, and further select a single decision tree for simplicity and interpretability. We demonstrate superior performance of the proposed methods compared to alternative methods based on complete-case data or single imputation. The methods are applied to the pancreatic cyst data to estimate biomarker panels for pancreatic cysts subtype classification and malignant potential prediction.

1. INTRODUCTION

Biomarkers that can help detect cancers in early stage hold great potential to enhance the practice of precision medicine. The vast number of candidate biomarkers discovered nowadays and the close collaboration between labs provide rich opportunities for researchers to combine multiple markers across laboratories for improved diagnostic performance compared to the use of a single marker. The research in this paper is motivated by such a cross-lab collaborative study: the Pancreatic Cyst Biomarker Validation (PCBV) study. It is a collaborative effort among six research institutes that aims to validate biomarkers measured from cystic fluid for pancreatic cysts subtype classification and malignant potential prediction [16].

The task of developing biomarker panels for cancer early detection is often complicated by missing data that might arise due to study design or random mechanisms. As will be described below, in the PCBV study there exists a non-monotone missingness [15] with respect to the multiple biomarkers, caused by the limited specimen available from study participants. There is a critical need for efficient methods to handle such a complex missingness in biomarker panel development.

1.1. Motivating study

Pancreatic ductal adenocarcinoma (PDAC) occurs through a progression of histologic precursor lesions that can be microscopic (pancreatic intraepithelial neoplasia) or macroscopic (mucinous pancreatic cysts), culminating in invasive adenocarcinoma. Treatments against PDAC are more effective when the disease is localized to the pancreas, and therefore, resectable. This progression happens gradually over time, spanning a period of 10 years in some cases. However, a large proportion of patients (~85%) discover the disease only after it has spread outside of the pancreas, which makes treatment options difficult.

The late detection of PDACs is due to a lack of effective detection methods. Most current diagnostic evaluation for PDAC occurs at the onset of symptoms suggestive of the disease, a point at which the cancer has typically progressed. Screening for PDAC among individuals without symptoms is not a viable strategy because of the high false-positivity rate, and the potential for administering treatments that are not necessary.

Current efforts have thus focused on identifying a subset of the population at an increased risk for preinvasive disease using a low-cost test using biomarkers. Thus, molecular biomarkers with high specificity and sensitivity can be used for early-stage pancreatic cancer detection, which can be followed by a confirmation test using a (higher-cost) imaging test in a two-stage strategy. The overall strategy would be to use a combination of clinical, laboratory, and molecular factors to select individuals that are eligible for surveillance, and then to assay biomarker(s) at relatively low cost that can be easily acquired from blood, saliva, or urine. Aside from assessing individual biomarkers, it is also crucial to assess the complementarity of disparate biomarkers. Two or more biomarkers might work well together in combination, but to find such a relationship, the markers must be run together on the same sample set.

While many cyst-fluid biomarkers have been retrospectively evaluated on various patient cohorts, a comprehensive and rigorous comparison of the top candidates has not been performed. Hence, the Early Detection Research Network (EDRN) has sponsored a large validation study with the intention to advance pancreatic cyst biomarker development to clinically available assays. This study makes use of a reference set of cyst-fluid specimens that was assembled using specimens from four different centers. All centers had followed an EDRN SOP and contributed the samples to a central site, from which aliquots were distributed blinded to six laboratories that each ran their own biomarker assays. This study can provide invaluable information about the performance of the various cyst-fluid biomarkers that have shown promise in previous studies.

Patients with mucinous pancreatic cysts are considered separately because they have an identified precursor lesion, and because mucinous pancreatic cysts are genetically distinct from the solid precursor lesions of pancreatic intraepithelial neoplasia. Thus, we are interested in two different analyses, analysis 1, which focuses on separating mucinous from non-mucinous cysts, and analysis 2, which focuses on separating cysts with advanced neoplasia from those without.

The six laboratory centers, and the respective biomarkers measured at each laboratory are given below:

1. John Hopkins University (JHU): Telomerase and Methylated DNA

2. Stanford: Glucose and Amphiregulin

3. University of California at San Francisco (UCSF): Mean Fluorescence Ratio GA Test

4. University of Pittsburgh Medical Center (UPMC): Mucinous call, DNA sequencing assay (for example, PancreaSeqV1, PancreaSeqV2)

5. Van Andel Institute: MUC3AC:WGA, MUC5AC:WGA

6. Washington University at St. Louis (WashU): mAb Das-1

Measuring all biomarkers would require 1.1 ml cystic fluid per person, but only 0.35 to 1.1 ml is available from each participant in PCBV. Volume of cystic fluid available from 60% study participants is less than 1.1 ml. To accommodate this limited specimen volume issue, statisticians from the EDRN Data Management and Coordinating Center designed a random sample allocation scheme to randomly select a subset of labs to receive the participant’s specimen for each participant with less than 1.1 ml cystic fluid. This random specimen allocation algorithm results in missingness in biomarker measurement among labs selected to not receive the specimen. The resulting biomarker data has a non-monotone missingness pattern (i.e. there is no “nested pattern of missingness” — meaning observing a variable $X_k$ implies observing $X_j$ for any $j<k$) [15]; Among the 321 study participants, only ~18% of participants have all markers measured. A naive panel development using the subset with complete data would have substantial information loss and potential bias by discarding samples with partial measurements. Non-monotone missingness also creates a unique challenge in developing coherent models and practical estimation procedures for the missingness mechanism.

While missing data has long plagued association studies, research is fairly limited for evaluating a biomarker or panel’s classification performance. We consider a missingness at random (MAR) [15] mechanism in this paper that requires the missingness depends only on observed data. MAR in cancer early detection setting can happen due to sampling scheme (e.g. case/control sampling to save cost) and specimen allocation scheme to handle limited specimen volume. Missingness in the motivating PCBV application falls into the latter category; MAR is a reasonable assumption in PCBV since the probability of measuring a biomarker from an individual depends on that individual’s specimen volume. Most existing research addresses the evaluation of a single biomarker when missingness occurs for only one variable. Weighting and multiple imputation are common strategies for handling MAR. In the weighting paradigm, the inverse probability weighted (IPW) [12] and the augmented IPW (AIPW) [22] estimators have been proposed for biomarkers obtained in two-phase sampling designs [3, 21, 13, 26] and for handling verification bias [11, 29, 19, 23]. However, IPW (AIPW) weighting based on participants with complete information is not efficient for handling general missingness, especially non-monotone missingess, by discarding information from participants with partially measured data.

We therefore in this paper propose methods for biomarker panel development based on the multiple imputation (MI) framework [28, 10]. In MI, multiple complete datasets are imputed based on modeling of the missing data conditional on observed variables; parameter estimates are obtained from each imputed dataset and then combined. MI has been utilized in many existing works on evaluating classification performance of a biomarker when a univariate variable (marker or disease status) is missing (e.g. [18, 9, 5]). For panel development based on features selected from multiple biomarkers with missing data, MI has been used for development of linear marker combinations utilizing stepwise [27] or penalized [4, 25, 17, 30] approaches. However, most cancers (including pancreatic cancer) are heterogeneous: The increased variability in cases vs. controls cannot be accounted for by simple linear marker combinations. An alternative framework often considered in the applied literature for combining biomarkers in a binary test is the use of logic rules [1, 6, 14], e.g. the “OR/AND” rules that consider the combination to be the set of “or-and” combinations of positivity of each marker [7]. In particular, to declare an individual as disease positive, the OR combination of two markers requires either marker test to be positive whereas the AND combination of two markers requires both marker tests to be positive.

In the PCBV application, a set of binary tests based on individual biomarker values have been provided by each lab based on pre-specified threshold values. One question the team wanted to address is whether these cross-lab binary tests interact and complement each other in differentiating mucinous from non-mucinous cysts and in determining malignant potential of cysts. In particular, it is of interest to develop parsimonious logic rules based on the multiple binary markers/tests from PCBV study. To achieve this objective, we propose new methods for feature selection and construction of logic rules with many candidate binary markers in the presence of general missingness. Built on the MI framework for dealing with missing data, our methods use the logic regression [24] as the building block for combining binary markers. Logic regression is an adaptive regression methodology that attempts to construct predictors as Boolean combinations of binary covariates in the entire space of such combinations in order to optimize a performance measure such as minimizing the misclassification rate. To estimate a parsimonious model, we propose feature selection extending a bootstrap imputation and stability selection [17] idea that was proposed earlier for deriving linear marker combinations. Next we present details of the propose methods. We then evaluate and compare the methods through simulation studies and apply the proposed methods to developing logic biomarker panels using the PCBV data.

2. METHODS

We consider a binary disease outcome $D$, with values 1 and 0 standing for diseased and non-diseased, respectively. Let $\mathbf{X}=\left(X_1,\dots ,X_p\right)$ indicate biomarkers of dimension $p$. In this paper, we consider $\mathbf{X}$ to be binary biomarkers as measured in the PCBV application. But the methods can be straightforwardly extended to handle continuous biomarkers. We refer to $Z=\{D,\mathbf{X}\}$ as the complete-data unit. Suppose there is missingness in the data with respect to $Z$ and let $\mathrm{\Delta }=\left({\mathrm{\Delta }}_0,\dots ,{\mathrm{\Delta }}_p\right)\in \{0,1{\}}^{p+1}$ be the missing data indicator with ${\mathrm{\Delta }}_0=1$ implying outcome is observed and ${\mathrm{\Delta }}_j=1$ implying biomarker $X_j$ is observed. Suppose a missingness at random (MAR) assumption [15] holds such that the missingness depends only on observed data, i.e. $P(\mathrm{\Delta }\mid Z)=P\left(\mathrm{\Delta }\mid Z_{obs}\right)$, where $Z_{obs}=\left({\mathrm{\Delta }}_{0}D,{\mathrm{\Delta }}_1{X}_1,\dots ,{\mathrm{\Delta }}_p{X}_p\right)$. Our goal is to develop logic-rule based biomarker panels conditional on $\mathbf{X}$ to predict outcome $D$.

We adopt a logic regression model [24] for risk of $D$ conditional on $\mathbf{X}$.

$$\mathrm{logit}P\left(D=1∣\mathbf{X}\right)={\alpha }_0+{\beta }_1{L}_1\left(\mathbf{X}\right)+\cdots +{\beta }_q{L}_q\left(\mathbf{X}\right),$$ (2.1)

which can be represented as the combination of $q$ trees, each corresponding to a Boolean function $L_k\left(\mathbf{X}\right)$, $k=1\dots ,q$ of $\mathbf{X}$. This model allows interactions between biomarkers to impact the risk of outcome. Boolean expression $L$ combines the values and variables through operations $\bigwedge \left(\mathrm{A}\mathrm{N}\mathrm{D}\right)$, $\bigvee \left(\mathrm{O}\mathrm{R}\right)$, and ${}^c(\text{NOT})$, e.g. $L=\left(X_1\bigwedge X_2\right)\bigvee \left(X_3\bigwedge X_4\right)\bigvee \left(X_5^c\bigwedge X_6\right)$. As presented in [24], the fitting algorithm of logic regression requires prespecifying the number of trees (i.e. $q$), and more generally one can select the number of trees with the data using techniques such as cross-validation or randomization tests. In this paper, we consider a single logic tree (i.e. $q=1$) for interpretability as investigators in PCBV study are interested in learning simple mechanisms about the interactions between biomarkers on pancreatic cancer risk.

2.1. Bootstrap imputation and stability selection

The process of measuring biomarker can be costly and/or invasive, making it desirable to have a parsimonious set of biomarkers with satisfactory performance. When a large of candidate markers are present, we propose to first conduct a bootstrap imputation and stability selection procedure to pre-select a set of biomarkers from the candidates for constructing the logic rule.

Given a training data, our proposed procedure for selecting variables and constructing the logic tree is described as following:

1. Generate $M$ bootstrap datasets $\{Z_{obs}^{\left(b\right)},b=1,\dots ,M\}$ based on the observed data $Z_{\text{obs}}$, using nonparametric bootstrap that samples each participant’s data with replacement stratified on case control status.

2. Conduct imputation for each bootstrap dataset $Z_{obs}^{\left(b\right)}$ using the Multiple Imputation by Chained Equations (MICE) algorithm [10]. This leads to $M$ bootstrap-imputed dataset $\{Z^{\left(b\right)}=(D^{\left(b\right)},{\mathbf{X}}^{\left(b\right)}),b=1,\dots ,M\}$.

3. Using the $b$^th bootstrap imputed dataset $Z^{\left(b\right)},b=1,\dots ,M$, we apply the logic regression ($R$ package LogicReg) based on (2.1) with $q=1$ and $\lambda \in \mathrm{\Lambda }$ to construct a logic tree, with $\lambda$ a tuning parameter indicating the maximum number of leaves in a tree. This step is repeated for all $b=1,...,M$ bootstrap imputed datasets and a grid of $\lambda \in \mathrm{\Lambda }$. In our numerical studies, we specify the range $\mathrm{\Lambda }$ so as to allow for 1–9 tree leaves when $p=10$, and around 1–12 tree leaves for p larger than 10.

4. For each marker, we compute the probability the marker was selected across the $M$ bootstrap-imputed dataset, for each $\lambda \in \mathrm{\Lambda }$ separately; those biomarkers with maximum selection probability (across all $\lambda \in \mathrm{\Lambda }$) exceeding a threshold $\pi \in (0,1)$ would be included in the final selected set. That is, let $S_{\lambda }^{\left(b\right)}$ be the set of markers included in the tree. We select the set of biomarkers with selection probability exceeding $\pi :\{j:{\mathrm{m}\mathrm{a}\mathrm{x}}_{\lambda \in \mathrm{\Lambda }} {\sum }_{b=1}^M I(j\in S_{\lambda }^{\left(b\right)})/M\ge \pi \}$ out of the $M$ bootstrap-imputed data. Let’s denote the final selected set of markers as ${\mathbf{X}}_{\pi }$.

5. Using the set of biomarkers selected in Step 4 and the $M$ bootstrap imputed datasets $\{Z_{\pi }^{\left(b\right)}=(D^{\left(b\right)},{\mathbf{X}}_{\pi }^{\left(b\right)}),b=1,\dots ,M\}$, we re-estimate a logic tree from each of these bootstrap imputed datasets with default pruning.

6. The final classification is based on the classification from the $M$ new trees using the majority rule.

We call this method ‘MI w VS’.

Later in the simulation study, we will also consider a comparative method based on bootstrap imputed data without prior stability selection, which we refer to as ‘MI w/o VS’. In this comparative method, we generate $M$ bootstrap imputed datasets and then fit a logic regression to each dataset with default pruning. Final classification is then based on the $M$ estimated logic trees using the majority rule.

Note that Step 4 of the proposed ‘MI w VS’ procedure requires specification of a threshold parameter $\pi$ for selection probability. In a linear regression setting for stability selection, [20] showed that stability selection results are very similar for $\pi \in (0.6,0.9)$. In this work, we adopt a 5-fold cross-validation procedure to select the optimal π from the interval (0.4,0.9). For a grid of values across this interval, the following steps are repeated:

1. Data are randomly split into 5 groups stratified by case/control status, 4 fold for training and the remaining fold for testing.

2. The ‘MI w VS’ procedure is applied to the training subset, and its performance is estimated in an imputed version of the test subset.

3. Step 2 is then repeated over the different splits (5 in total) of training and test data.

After repeating the above steps for all values of $\pi$ in the grid, the value $\pi ={\pi }_{\text{opt}}$ that obtains the best average performance (based on Youden’s index) is chosen as the threshold for applying the ‘MI w VS’ procedure to the full data.

2.2. Selecting a single representative logic tree

The ‘MI w VS’ method proposed above leads to a biomarker panel based on ensemble trees. While ensemble trees are generally expected to have better accuracy compared to a single tree, the latter can be particularly appealing to lab researchers for its simplicity and interpretability. We thus propose a further step at the end of the ‘MI w VS’ procedure to select a single logic tree from the $M$ estimated logic trees. In particular, for each of the estimated logic tree, we compute its distance from the other $M-1$ logic trees, and we select the tree that has the smallest average distance from other trees as the “center” or representative of the $M$ trees. Classification result can then be directly obtained from this selected tree.

One natural way to estimate the distance between two logic trees is by calculating the Hamming distance [8] between their binary predictions for a given biomarker combination (restricted to the features chosen as leaves in the two trees), and then averaging over different combinations of those biomarkers. In our case, we can use different combinations of the selected biomarker measures, ${\mathbf{X}}_{{\pi }_{\mathrm{o}\mathrm{p}\mathrm{t}}}$, to calculate the average distance. We consider two ways to average the distance across various biomarker combinations: (i) For the first method, we calculate the average across all possible combinations of the final biomarker measures ${\mathbf{X}}_{{\pi }_{\mathrm{o}\mathrm{p}\mathrm{t}}}$, giving equal weight to each biomarker combination. This procedure does not require the use of observed data to characterize the biomarker distribution, and we call this method ‘MI w VS-Exhaustive’. (ii) For the second method, we compute the average across observations of ${\mathbf{X}}_{{\pi }_{\mathrm{o}\mathrm{p}\mathrm{t}}}$ in the actual data (after performing a single imputation step). Thus, it targets weighting the distance according to the observed biomarker distributions in the data, and we call this method ‘MI w VS-Datadep’. In simulation studies, we have studied both approaches for deriving the single logic tree.

This selected single logic tree will be useful to lab researchers for understanding the interaction between different biomarkers in affecting the risk of the outcome. Like in Section 2.1, a 5-fold cross-validation procedure is first implemented to identify the threshold $\pi ={\pi }_{\text{opt}}$ for optimal prediction performance of ‘MI w VS-Exhaustive’ and ‘MI w VS-Datadep’, and then we can apply these algorithms with the chosen threshold ${\pi }_{\text{opt}}$ on the full data for constructing a single logic tree.

3. SIMULATION STUDY

We consider a simulation study here that mimics the PCBV study. We generate $p\in \{10,20,30\}$ variables (biomarkers), $X_1,X_2,\dots ,X_p~Ber\left(0.5\right)$, and we let $L=\left(X_1\bigwedge X_2\right)\bigvee \left(X_3\bigwedge X_4\right)$. The response $D$ is generated as $D~Ber\left({\mu }_1\right)$ if $L=1$ and $D~Ber\left({\mu }_0\right)$ if $L=0$. We consider two scenarios:

1. High sensitivity scenario: with ${\mu }_1=0.35$ and ${\mu }_0=0.01$.

2. High specificity scenario with ${\mu }_1=0.98$ and ${\mu }_0=0.4$

The prevalence rate of disease in the population is 0.66 when ${\mu }_1=0.98$ and ${\mu }_0=0.4$, and is 0.16 when ${\mu }_1=0.35$ and ${\mu }_0=0.01$. If the classification rule was based directly on the knowledge of the oracle $L$, that is, predicting $D=1$ when $L=1$ and $D=0$ when $L=0$, we would have been able to achieve a sensitivity of 96% and specificity of 66% in Setting 1, and a sensitivity of 65% and specificity of 97% in setting 2. Note that in the PCBV data (Section 1.1), groups of biomarkers are evaluated together in a single laboratory on a subset of trial participants, however, this subset of evaluated participants differs between laboratories. Thus, when considering biomarker data from different laboratories together, we see that in the combined data, groups of biomarkers are either available or missing jointly.

We consider a two phase study design in simulation, where in phase 1, the response $D$ is measured in everyone in the trial consisting of 5000 participants, and then in phase 2, equal number $N$ of cases ($D=1$) and controls ($D=0$) are randomly sampled for biomarker measurement. Here, for phase 2 sampling of biomarker data, we consider different scenarios of case-control sampling, such that $N$ varies between $\{50,100,...,250,300\}$.

In our setup, biomarkers are evaluated at five different laboratories, such that 20% of total biomarkers evaluated are measured at a given laboratory (so 2 biomarkers measured together at each of the five laboratories when $p=10$, and 6 biomarkers measured together at each laboratory when $p=30$). In each of the first two labs, the biomarkers measured at that lab are evaluated in 75% of total participants in phase two, and in each of the next three labs, they are measured in 70% of total participants. Thus, as mentioned before, biomarker data measured in a given lab are available together. We simulate in a way that on average, the phase two data will contain 20% complete records, similar to the PCBV data. The above constitutes our training data. For evaluation of classification performance of our models, we additionally simulate a test data with 5000 participants.

In this simulation study, we compared six different approaches for constructing the logic tree based panels. In particular, we investigated the proposed multiple imputation based methods with feature selection, i.e. ‘MI w VS’, ‘MI w VS-Exhaustive’, and ‘MI w VS-Datadep’ methods for $\pi ={\pi }_{\mathrm{o}\mathrm{p}\mathrm{t}}$, as has been described in Section 2.

We also evaluated the comparative multiple imputation based method without prior feature selection, i.e. ‘MI w/o VS’. In addition, we applied logic regression (with default tuning) to the data after a single imputation (called the ‘Single imputation’ method) or to the complete data only (called the ‘Complete Case’ analysis). We conducted 500 Monte-Carlo simulations for each scenario, and recorded the classification performance of each method on the test dataset as well as the feature selection performance of each method.

3.1. Results

In this section, we compare performance of the different methods for the two settings, (i) Setting 1: high sensitivity with ${\mu }_1/{\mu }_0=0.35/0.01$, (ii) Setting 2: high specificity with ${\mu }_1/{\mu }_0=0.98/0.4$.

Classification performance results are presented in Figure 1 (for Setting 1) and Figure 3 (for Setting 2). We quantify this performance in terms of (i) sensitivity (the top panel), or probability of a positive prediction, conditioned on truly being positive, and (ii) specificity (the bottom panel), or probability of a negative prediction, conditioned on truly being negative. Additionally, we present results for feature selection performance of these methods in Figure 2 (for Setting 1) and Figure 4 (for Setting 2). We quantify this performance also in terms of (i) sensitivity in feature selection (top panel), probability that a variable (biomarker) with true association with the outcome ($X_1$, $X_2$, $X_3$ or $X_4$ in our simulation example) is correctly selected in the model, and (ii) specificity in feature selection (bottom panel), probability that a variable (biomarker) with no association with outcome ($X_5,\dots ,X_p$ in our simulation example) is correctly discarded from the model. We present these metrics as varying functions of $N:N\in \{50,100,...,250,300\}$, the total number of case-control units, separately for different values of the covariate dimension $p:p\in \{10,20,30\}$. In all figures (Figures 1–4), we present error bars representing 95% Confidence Intervals for the mean estimate of the respective performance metric, assuming normal quantiles.

Figure 1: High sensitivity setting, ${\mu }_1/{\mu }_0=0.35/0.01$ (Setting 1):

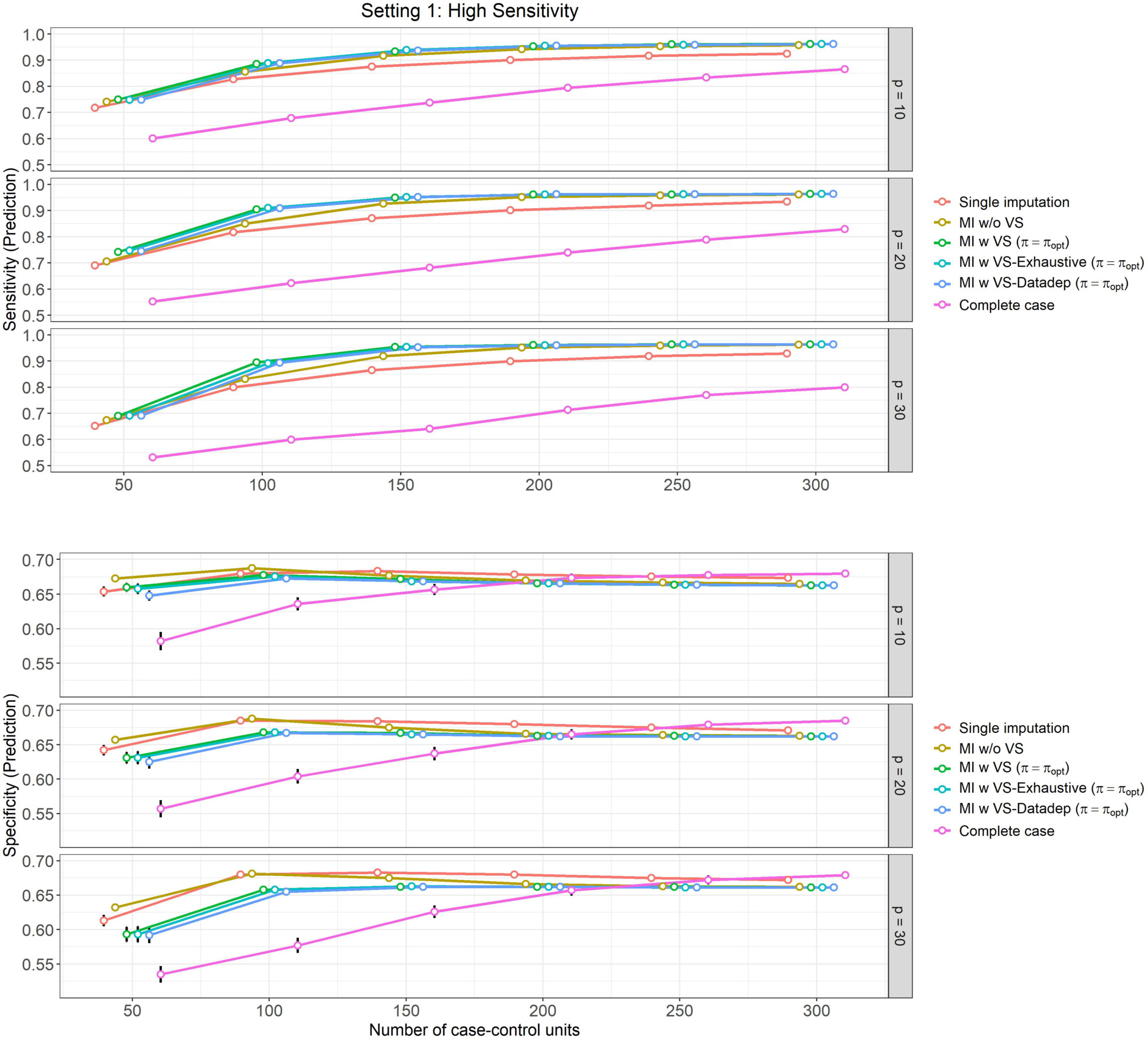
Mean prediction performance and their 95% Confidence Intervals (based on 500 Monte Carlo simulations) varying over different size of case-control sampling and dimension of the Covariate space.

Figure 3: High specificity setting, ${\mu }_1/{\mu }_0=0.98/0.4$ (Setting 2):

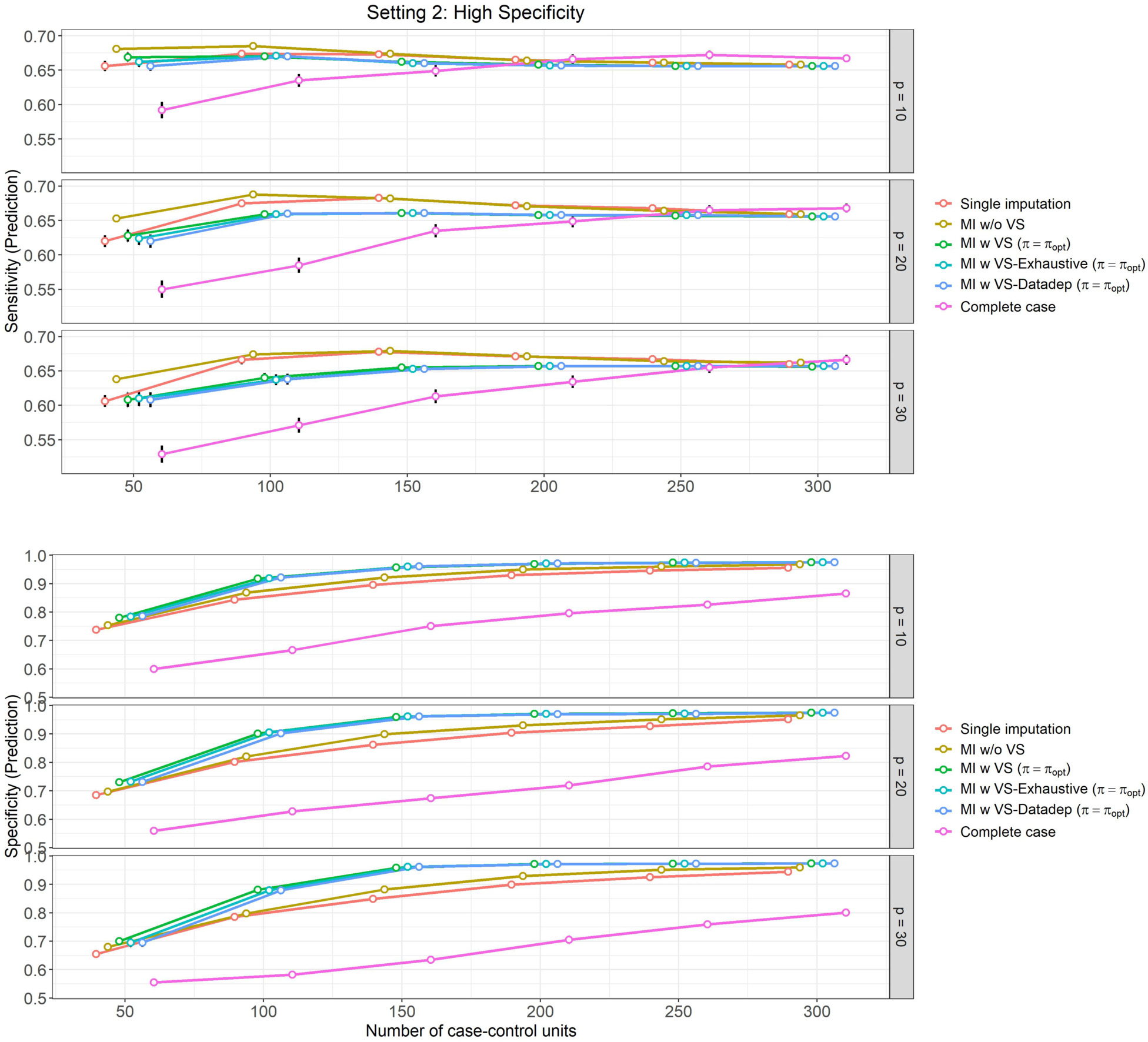
Mean prediction performance and their 95% Confidence Intervals (based on 500 Monte Carlo simulations) varying over different size of case-control sampling and dimension of the Covariate space.

Figure 2: High sensitivity setting, ${\mu }_1/{\mu }_0=0.35/0.01$ (Setting 1):

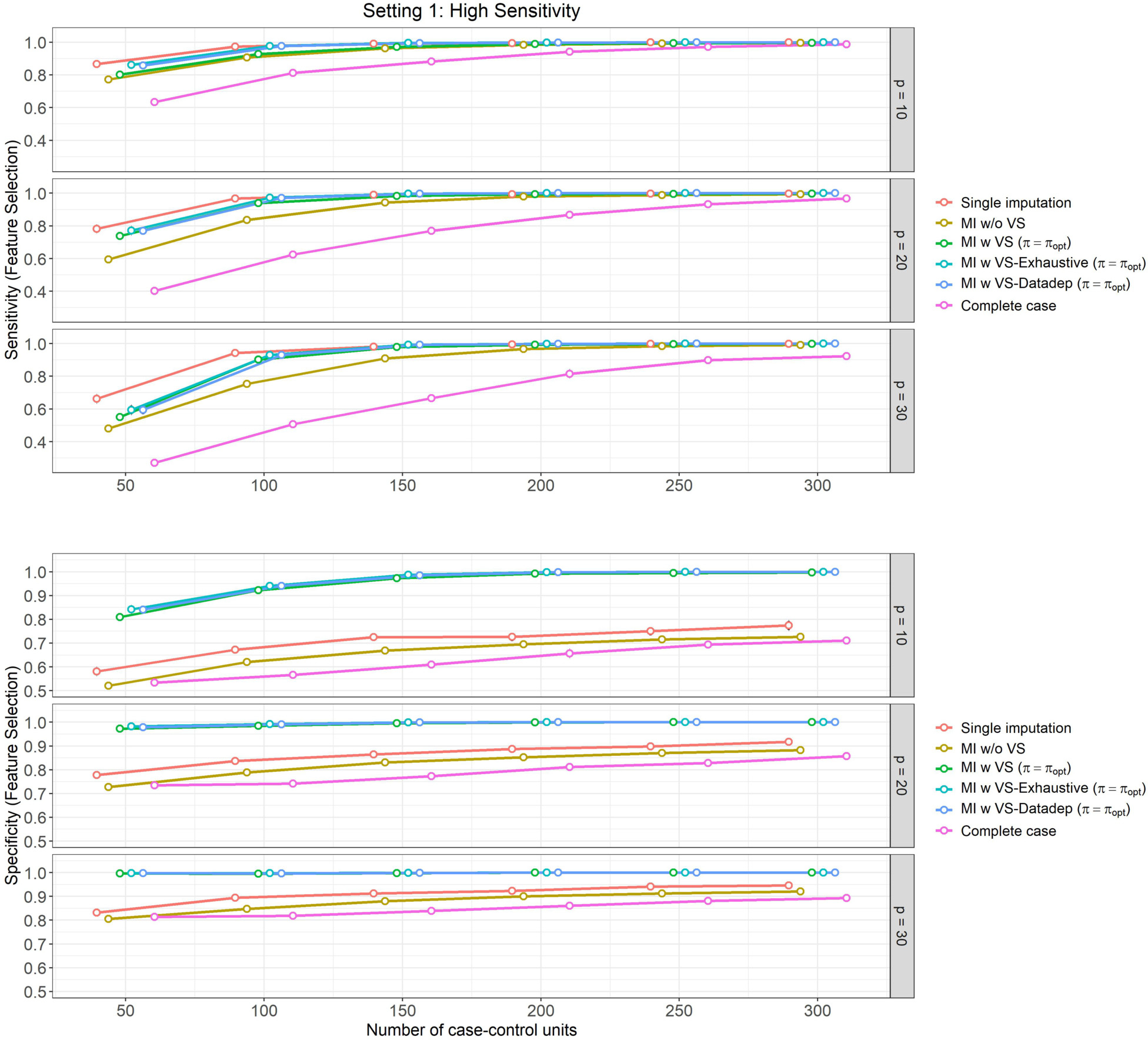
Mean feature selection performance and their 95% Confidence Intervals (based on 500 Monte Carlo simulations) varying over different size of case-control sampling and dimension of the Covariate space.

Figure 4: High specificity setting, ${\mu }_1/{\mu }_0=0.98/0.4$ (Setting 2):

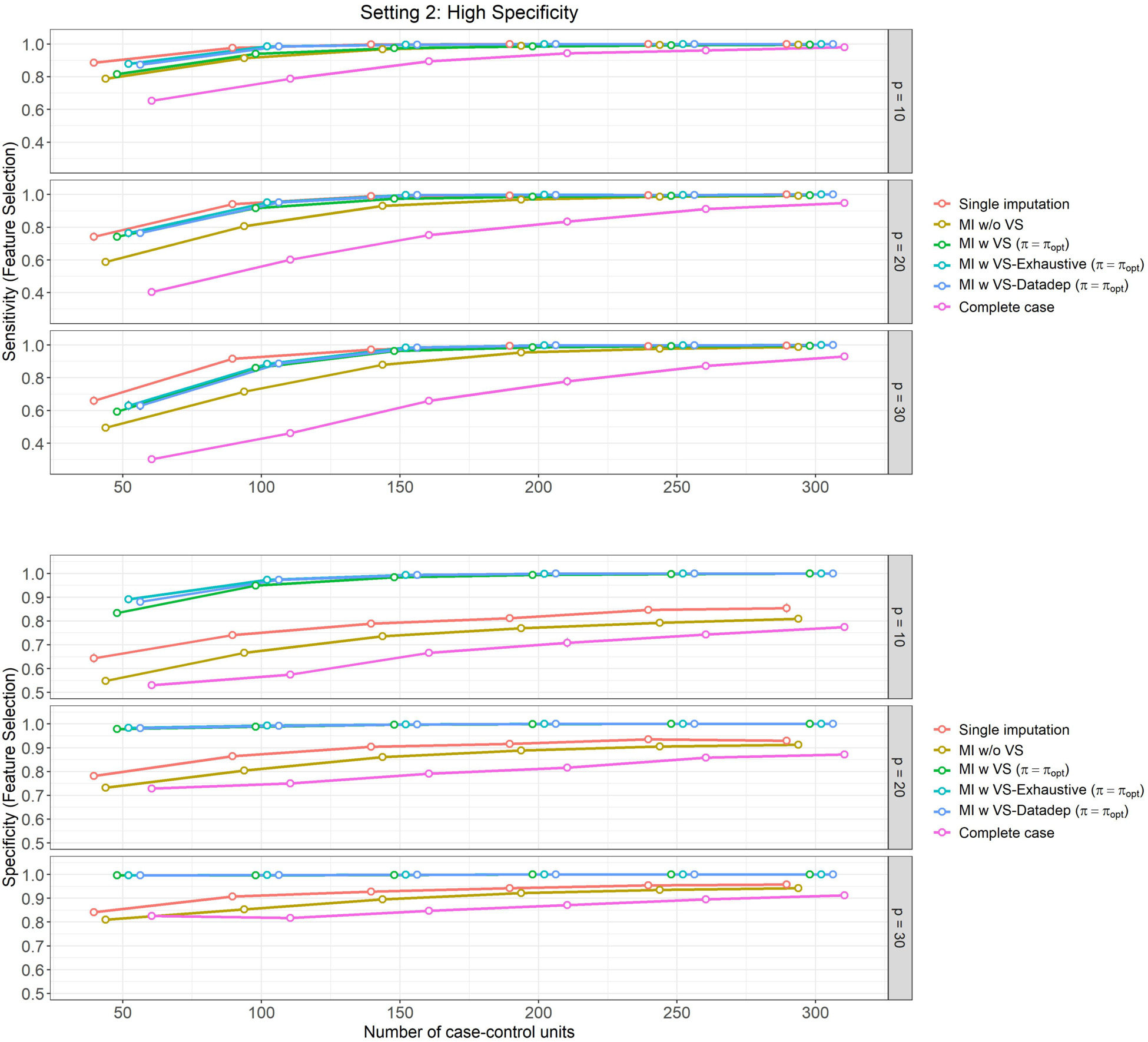
Mean feature selection performance and their 95% Confidence Intervals (based on 500 Monte Carlo simulations) varying over different size of case-control sampling and dimension of the Covariate space.

Our observations from Figure 1 (Classification performance for Setting 1) are as follows:

1. In Setting 1, which is curated so that the models show high sensitivity and relatively lower specificity, we can see that sensitivity of the methods (probability of predicting a positive response among those who are truly positive – shown in top panel in Figure 1) is highest (and nearly similar) for ‘MI w VS’, ‘MI w VS-Exhaustive’ and ‘MI w VS-Datadep’ (between 69%–96%), followed by ‘MI w/o VS’ (between 67%–96%), ‘Single imputation’ (between 65%–93%) and ‘Complete case’ (between 53%–87%) respectively. These differences are maintained for all values of $p$ and $N$, with the ‘Complete case’ analysis lagging behind others quite considerably.

2. Prediction sensitivity of all methods increase with $N$ from 53%–75% for $N=50$ to 80%–96% for $N=300$.

3. The difference in sensitivity between the methods are more pronounced for lower values of $N$, and slightly more so for higher values of covariate dimension $p$, suggesting that using multiple imputation with variable selection is more effective when sample size is limited.

4. In Setting 1, specificity (probability of predicting a negative response among those who are truly negative – shown in bottom panel of Figure 1) is lower than the estimated sensitivity for this setting for all methods and all values of $N$ and $p$ (ranging between 54% to 69% across methods and simulation scenarios).

5. For all methods except the ‘Complete case’ analysis, specificity increases only slightly with $N$, but this increase is slightly more pronounced for higher values of $p$. At lower values of $N$ (say $N=50$), specificity is lower for higher values of $p$ (ranging from 65%–67% for $N=50,p=10$, 60%–63% for $N=50,p=30$). At higher values of $N$, variation is lower, and all four methods perform similarly (around 66%–68%).

6. Specificity is particularly low for ‘Complete case’ analysis for lower values of $N$, but it increases gradually with $N$, and performs similar to (and even slightly better than) other methods for higher values of $N$, ranging from 54%–58% at $N=50$ to 68%–69% at $N=300$.

In Setting 2, which is curated so that the models show high specificity and lower sensitivity, the results are similar as in Setting 1, however, for specificity instead of sensitivity. In particular, we can observe the following from Figure 3 (Classification performance for Setting 2),

1. Performance (sensitivity and specificity) is similar for ‘MI w VS’ and ‘MI w VS-Exhaustive’, and ‘MI w VS-Datadep’.

2. Specificity (shown in bottom panel of Figure 3) is consistently higher for ‘MI w VS’, ‘MI w VS-Exhaustive’, and ‘MI w VS-Datadep’ (ranging from around 70% for $N=50,p=30$ to 78%–79% for $N=50,p=10$, to around 97%–98% for $N=300$ and all values of p) followed by methods ‘MI w/o VS’ (68%–75% for $N=50$ to 96%–97% for $N=300$), ‘Single imputation’ (66%–74% for $N=50$ to 94%–96% for $N=300$), and finally ‘Complete case’ analysis (56%–60% for $N=50$ to 80%–87% for $N=300$).

3. The difference in specificity between MI with variable selection methods (‘MI w VS’, ‘MI w VS-Exhaustive’, and ‘MI w VS-Datadep’) and the rest is more pronounced for moderate sizes of $N\in \{100,250\}$, and less so for lower values and higher values of $N(N=50$ and $N=300$).

4. The complete case analysis yields the worst specificity performance, which is more visible for smaller sample size, but even persists for higher values of $N$.

5. Sensitivity of the methods (top panel of Figure 3) is lower than the estimated specificity for this setting for all methods and all values of $N$ and $p$ (ranging between 53% to 67% across methods and simulation scenarios).

6. For all methods except the ‘Complete case’ analysis, no increase in sensitivity occurs with $N$ for $p=10$ (around 66%), and only slight increase is noted from $N=50$ to $N=100$ for $p=20,30$ (ranging from 61%–64% for $N=50$ to 66%–67% for $N=100$).

7. Methods ‘MI w/o VS’ and ‘Single imputation’ slightly dominates the variable selection methods (‘MI w VS’, ‘MI w VS-Exhaustive’, and ‘MI w VS-Datadep’) in sensitivity performance for $p=20,30$, but this difference disappears for $N>200$.

8. Sensitivity is particularly low for ‘Complete case’ analysis for lower values of $N$, but it increases gradually with $N$, and performs similar to the other methods for higher values of $N$, ranging from 53%–59% at $N=50$ to 67% at $N=300$.

In Figures 2 and 4, we present the results of feature selection performance of these methods for the aforementioned settings. The observations are similar for both settings, which we summarize below:

1. In terms of sensitivity in feature selection (top panels of Figures 2 and 4), ‘Single imputation’, ‘MI w VS-Exhaustive’ and ‘MI w VS-Datadep’ are the best performing methods overall. These methods perform equally well in most settings, except for $N=50$ for $p=30$, when ‘Single imputation’ slightly dominates the other two, but the difference is negligible.

2. ‘MI w VS’ is the next best performing method with respect to sensitivity, and performs similar to the aforementioned three (‘Single imputation’, ‘MI w VS-Exhaustive’, and ‘MI w VS-Datadep’) for $N\ge 150$. All four methods attain near perfect score of 1 for $N\ge 200$.

3. Finally, the ‘Complete case’ analysis is the worst performer overall, although performance gets better with increasing $N$.

4. In terms of feature selection specificity (bottom panel of Figures 2 and 4), ‘MI w VS-Exhaustive’ and ‘MI w VS-Datadep’ are the best performing methods, considering all scenarios of $N$ and $p$, followed closely by ‘MI w VS’, which slowly slightly lower specificity than the other two for $N\le 150$ and $p=10$. All these three methods achieve near perfect score of 1 for $N>150$ for $p=10$, and for all $N$ when $p=20,30$.

5. Single imputation is the next best performing method with respect to specificity, followed by ‘MI w/o VS’. Complete case analysis is again the worst performing method overall, with regards to this metric.

Overall, across all simulation scenarios that we have explored in our simulation exercise, $\pi ={\pi }_{\text{opt}}$ (optimized by 5 fold cross validation) was used when considering both classification performance and feature selection performance for ‘MI w VS’, ‘MI w VS-Exhaustive’, and ‘MI w VS-Datadep’. Thus, in our real data example that we present below, we have also evaluated $\pi ={\pi }_{\text{opt}}$ using a 10-fold cross-validation and used that as the threshold metric for methods ‘MI w VS’, ‘MI w VS-Exhaustive’, and ‘MI w VS-Datadep’.

4. REAL DATA ANALYSIS

In this section, we present results from our analysis of PCBV data using logic regression. The candidate biomarkers include 13 binary tests measured from the six research labs. For analysis 1 of differentiating mucinous from non-mucinous cysts, there are 209 cases and 95 controls, with 35 cases and 20 controls having full biomarker information. For analysis 2 of detecting mucinous cysts with advanced neoplasia, there are 62 cases and 239 controls, with 12 cases and 42 controls having full biomarker information.

As in the simulation example, we quantify the classification performance of each method in terms of (i) sensitivity, or probability of a positive prediction, conditioned on truly being positive, and (ii) specificity, or probability of a negative prediction, conditioned on truly being negative. We compute the classification performance of the 6 different methods using 10-fold cross-validation. Cross-validation helps to reduce overfitting assess how the results of the analysis generalizes to an independent data set. Particularly, in 10-fold cross validation, we divide the available data into 10 near-equal parts (or folds), stratified by case/control status, and then in each iteration, 9 out of 10 folds are used to train the model, and the 10th fold is used as the test subset to compute the model’s classification performance. The cross-validated (CV) performance is then computed as the average of the 10 performance estimates. We also construct a bootstrap confidence interval for the CV performance estimate by enforcing an outer layer bootstrap stratified on case/control status and repeat the process of CV performance estimate for 500 times. We computed the bootstrap standard error based on those 500 runs, and then construct 95% Wald Confidence Intervals.

The results are presented in Table 1. We summarize our observations below:

1. ‘MI w VS’ is the best performing method overall for both sensitivity and specificity across both analyses (analysis 1 and 2).

2. ‘MI w VS-Exhaustive’ and ‘MI w VS-Datadep’ perform similarly, but has slightly smaller sensitivity compared to ‘MI w/o VS’ and ‘MI w VS’ for Analysis 1, and slightly smaller specificity compared to ‘MI w/o VS’ and ‘MI w VS’ for Analysis 2. However, specificity for these methods is considerably higher than ‘MI w/o VS’ for Analysis 1 (although slightly lower than ‘MI w VS’), and similarly sensitivity for these methods is considerably higher than ‘MI w/o VS’ for Analysis 2 (although slightly lower than ‘MI w VS’).

3. Single imputation is the fifth best performing method, with its classification performance slightly worse compared to all the multiple imputation methods.

4. Complete case analysis had worse sensitivity compared to other methods for both Analysis 1 and 2; it also had worse specificity compared to the multiple imputation based methods for Analysis 2, and worse performance than ‘MI w VS’ methods (‘MI w VS’, ‘MI w VS-Exhaustive’, and ‘MI w VS-Datadep’) for Analysis 1.

Table 1.

10-fold cross-validated classification performance estimate and the corresponding 95% Wald Confidence Intervals based on bootstrap standard errors (in parentheses) for the PCBV analysis, (i) Analysis 1: mucinous vs non-mucinous cysts, (ii) Analysis 2: cysts with advanced neoplasia vs those without.

Method	Analysis 1		Analysis 2
	Sens.	Spec.	Sens.	Spec.
Single imputation	0.904 (0.858, 0.949)	0.817 (0.715, 0.92)	0.477 (0.32, 0.633)	0.921 (0.886, 0.956)
MI w/o VS	0.937 (0.901, 0.972)	0.889 (0.809, 0.97)	0.476 (0.304, 0.647)	0.949 (0.928, 0.97)
MI w VS ($\pi ={\pi }_{\text{opt}}$)	0.941 (0.901, 0.98)	0.952 (0.865, 1)	0.576 (0.393, 0.758)	0.961 (0.941, 0.981)
MI w VS-Exhaustive ($\pi ={\pi }_{\text{opt}}$)	0.922 (0.874, 0.97)	0.944 (0.828, 1)	0.576 (0.403, 0.75)	0.954 (0.929, 0.98)
MI w VS-Datadep ($\pi ={\pi }_{\text{opt}}$)	0.921 (0.872, 0.97)	0.944 (0.832, 1)	0.576 (0.406, 0.747)	0.955 (0.929, 0.981)
Complete Case analysis	0.89 (0.81, 0.97)	0.924 (0.817, 1)	0.455 (0.175, 0.735)	0.929 (0.846, 1)

In each of Figures 5 and 6, we present the logic tree that was fitted using ‘MI w VS-Exhaustive’ on the observed PCBV data, as the single representative tree for the two classification analyses: (i) Figure 5 showing the tree fitted for classifying mucinous vs non-mucinous cysts, and (ii) Figure 6 showing the tree fitted for classifying cysts with advanced neoplasia from those without.

Figure 5:

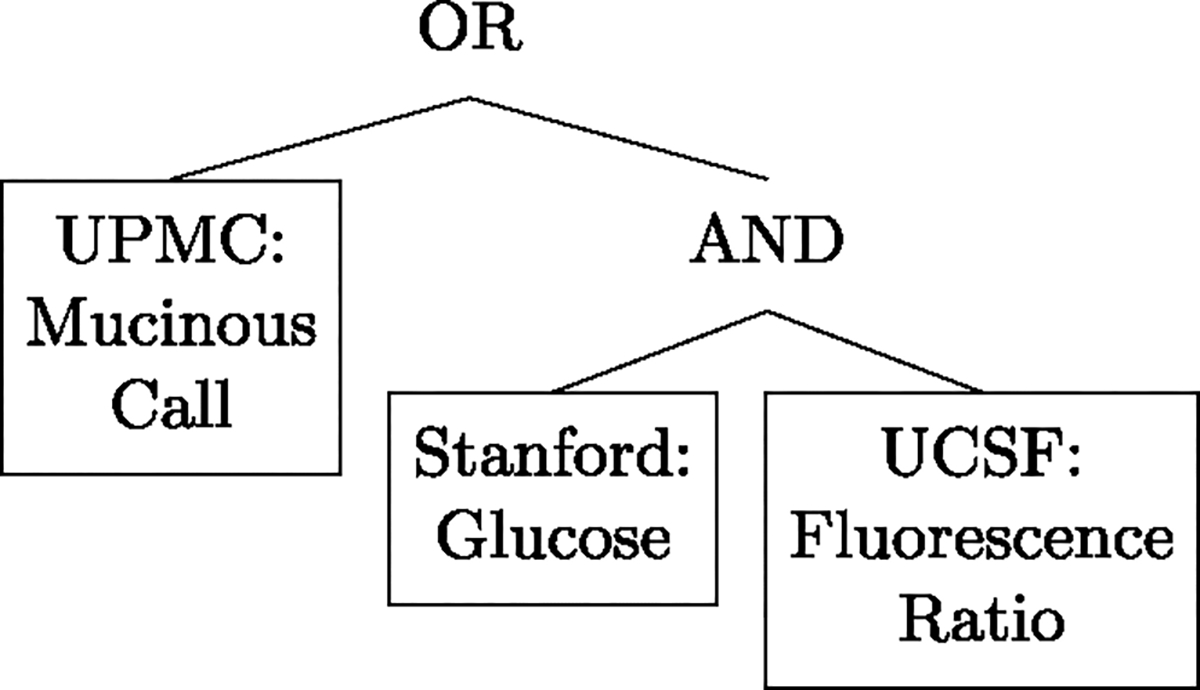
Logic Tree fitted to classify mucinous vs non-mucinous cysts using Method 4 (MI w VS-Exhaustive) on observed PCBV data.

Figure 6:

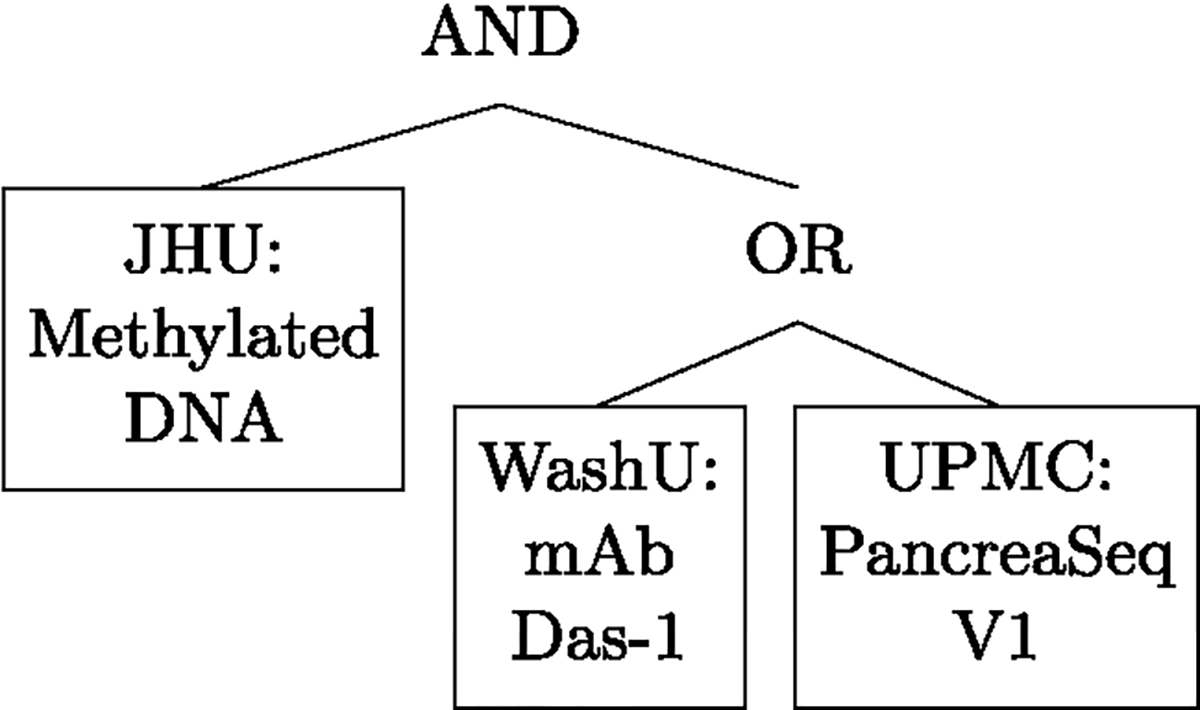
Logic Tree fitted to classify cysts with advanced neoplasia from those without using Method 4 (MI w VS-Exhaustive) on observed PCBV data.

5. DISCUSSION

We have proposed new procedures for developing parsimonious logic-tree based nonlinear biomarker panels in the presence of missing data under the MAR mechanism. Panels developed using MI have better performance compared to using complete cases or single imputation; more importantly, while trees have an inherent feature selection ability with pruning, an extra bootstrap imputation and stability selection step can further improve performance with a more parsimonious model. Moreover, we proposed two Hamming-distance based procedures to select a single tree that best represents the multiple trees based on the multiple imputed dataset. The single tree selected has comparable classification performance but greater interpretability, which can help lab researchers to better understand the interactions between different biomarkers as well as the mechanism of their associations with the disease outcome, and thus help guide the biomarkers’ further development.

Our methods in this paper utilize logic regression as building block for handling binary tests and binary outcome as needed in the motivating application. The proposed framework can be extended to deal with continuous biomarkers for either binary or linear outcome using other tree-building algorithms such as the classification and regression tree (CART) [2].