An effective and open source interactive 3D medical image segmentation solution

Abstract

3D medical image segmentation is a key step in numerous clinical applications. Even though many automatic segmentation solutions have been proposed, it is arguably that medical image segmentation is more of a preference than a reference as inter- and intra-variability are widely observed in final segmentation output. Therefore, designing a user oriented and open-source solution for interactive annotation is of great value for the community. In this paper, we present an effective interactive segmentation method that employs an adaptive dynamic programming approach to incorporates users’ interactions efficiently. The method first initializes an segmentation through a feature-based geodesic computation. Then, the segmentation is further refined by using an efficient updating scheme requiring only local computations when new user inputs are available, making it applicable to high resolution images and very complex structures. The proposed method is implemented as a user-oriented software module in 3D Slicer. Our approach demonstrates several strengths and contributions. First, we proposed an efficient and effective 3D interactive algorithm with the adaptive dynamic programming method. Second, this is not just a presented algorithm, but also a software with well-designed GUI for users. Third, its open-source nature allows users to make customized modifications according to their specific requirements.

Introduction

Background

Segmentation has long been one of the most important tasks in medical image analysis¹. Image segmentation methods can be roughly categorized as fully-automatic, manual, and semi-automatic (interactive) depending on how much user efforts are involved.

Fully-automatic segmentation does not require human input. It directly returns final segmentation results for new images. It has long been the goal of the image segmentation community. Some of the classical segmentation techniques include thresholding and atlas-based methods^2,3. However, it is challenging to segment to complex images/targets for this type of methods. More recently, deep learning-based segmentation have demonstrated state-of-the-art performances on a wide range of tasks^4,5. However, user interventions are still often needed to refine the automatic segmentation result. Unfortunately, performing volumetric correction of the automatic segmentation in many cases is as laborious as manual contouring from scratch.

On the other end of the spectrum, manual segmentation approaches are tedious, time consuming and can be affected by inter- and intra-observer variability. Indeed, regions delineated by experienced physicians may often have an overlapping ratio of around 90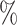, and less than that for small and low contrast targets. In some other cases, such as contouring post-operative clinical target volume and organs at risk, the mean conformity level between inter-observer could be as low as 65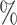⁶.

Given such an inter-observer matching, even if certain fully-automatic algorithm reaches a high agreement, say 95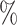, with respect to some manual annotation, it may merely be learning the specific preference of the person who contoured the training images. Such a preference may be determined by the disease, organ, history of the patient, protocols at certain medical site, etc., and is very hard to be generalized. Therefore, the interactive segmentation is an indispensable tool for individual physicians to reflect their specific needs^7–10.

One thing to note about manual segmentation is that the segmentation of each slice has long been considered as the reference standard for 3D volumetric segmentation, and automatic or semi-automatic algorithms typically compare their results against the manual contours to demonstrate their accuracy. However, it has several issues. For example, the relations and continuity along slices are largely ignored through this slice-by-slice contouring process. In addition, due to the unregulated nature of pure human operation, the manual contouring may induce severe inter-rater variability, some of which may be far beyond the difference between the algorithm output and one particular human annotation. As a result, the jagged reconstruction of the target will inevitably affect the subsequent shape and feature computation¹¹. Thus, a well-curated 3D semi-automatic algorithm with certain controllable regularization and robust propagation dynamics may be suitable for a wide range of scenarios.

While there exist far more algorithm/software solutions for 2D image segmentation^12,13, working in 3D is almost a completely different scenario. Although mathematically many algorithms could be generalized from 2D to 3D without too much changes in their formulation, the geometric and topological characteristics make 3D interactions difficult. For example, the ways how leakage may occur, how to incorporate the user interactions, all of which vary significantly between 2D and 3D. Therefore, in this work we only discuss those algorithms and tools that explicitly deal with 3D image data.

Recently, several interactive segmentation algorithms with outstanding performance have been conducted, such as SAM. SAM is a revolutionary large model for segmentation¹⁴. However, a notable limitation is its reliance on substantial training datasets and its primary focus on natural images but not medical images. Although several large segmentation models were designed and adapted for medical images, they mainly focus on two-dimensional images slices^4,15,16, with only a minority of research endeavors addressing the requirements of three-dimensional medical image processing¹⁷. While there have been efforts to extend SAM for segmentation of 3D data, most of these endeavors lack comprehensive interactive interfaces and platforms for users. Hence, this underscores the imperative necessity for the establishment of a user-oriented interactive 3D segmentation platform, further emphasizing the significance of our study.

Many interactive segmentation methods have been introduced for 3D medical image segmentation.

In early 2000’s, active contours models have been widely used in interactive segmentation, and the software implementing this trend of algorithms are still among the most widely used ones. In the active contour models, the initial boundary gradually evolves by optimizing certain energy function which fuses the image information with certain geometric and/or topologic regularization. According to image information used in the energy function, they can be roughly divided into two classes: edge-^18–20 and region-based^21–24 models.

Edge-based active contour models usually assumes high intensity gradients along the target boundaries. Based on such an assumption, the segmentation result is easily affected not only by image noise, but also by initial contour placement. The region-based models, on the other hand, utilize statistics of image features, such as pixel intensities, shape and texture features in global or local regions, to make contours converge to the target boundaries of interest. In this regards, the advantage of region-based models is that it is capable of handling weak boundaries and generally it is more robust to the noise. Among global region-based models, one of the most popular region-based models is the Chan-Vese (CV) model²¹. It assumes that the intensity of each region of the image is homogeneous. However, this method does not hold for images with intensity inhomogeneity. To overcome this limitation, the local region-based active contour models are proposed where local regional pixel information has been incorporated into the energy function^23,25,26.

Software programs implementing the active contour method include the ITK-SNAP⁸, RSS⁹, and Seg3D¹⁰. See details in the following section.

Apart from active contours models, the graph-based model is also a very popular family of segmentation methods^27–34. In these models, the segmentation problem is converted into a graph partition problem, and are solved by using maximum flow/minimum cut algorithms. Li et al.²⁷ proposed a graph optimization approach for obtaining optimal surfaces for medical volumes. However, although the graph cut algorithms give the global optimal solution, performing the graph cut algorithm over the entire volumetric data is quite time consuming. Towards alleviating the computation cost, Lombaert et al.³⁵ proposed a multi-band heuristic algorithm inspired by the narrow band level-set algorithm³⁶. Delong et al.³⁷ proposed a region push-relabel technique and Lermé et al.³⁸ accelerated the flow computation by first checking whether each node is helpful for max-flow computation before creating it. In addition to its computation cost, a multiple-region graph cut algorithm is NP-hard and this limits its application in the multiple target segmentation.

A classic interactive segmentation paradigm of region growing is GrowCut³⁹. The GrowCut algorithm is a widely used interactive tool for segmentation because of several key features: 1) natural handling of N-D images, 2) support for multi-label segmentation, 3) on-the-fly incorporation of user input, and 4) easy implementation. Starting from manually drawn seed and background pixels, GrowCut propagates these input labels based on principles derived from cellular automata in order to classify all of the pixels. Since all pixels must be visited during each iteration, the computational complexity grows quickly, as image size increases.

Related 3D interactive segmentation software

In general, the process of interactive segmentation can generally be divided into three steps. First, a user provides initial seeds in either the target region, the background region, or both. Second, the segmentation algorithm utilizes the user’s input seeds to produce the segmentation result. Finally, if the segmentation result is satisfactory, the segmentation process is finished. Otherwise, the user will continuously provide additional seeds to further refine the segmentation result.

Apparently, for better user experiences, it is necessary to have an integrated environment with graphical, intuitive, flexible and effective interactions. This includes 1) image IO, 2) results visualization, and 3) tools such as paint brush and eraser so that end user can conveniently interact with segmentation output.

To date, though there are many interactive segmentation algorithms proposed in the literature, there are few interactive segmentation programs fulfilling the above requirements, even fewer are open-sourced. Among them, ITK-SNAP⁸ is a free, open-source, and multi-platform interactive segmentation software for 3D medical images and ships with two well-known 3D active contour segmentation methods: Geodesic Active Contours^18,40 and Region Competition⁴¹. Gao et al.⁹ designed a local robust statistics-based active contour segmentation method and implemented on the 3D Slicer platform with the module named “Robust Statistics Segmenter (RSS)”. Moreover, Seg3D¹⁰ is an open-source image viewing and segmentation platform utilizing the sparse field level set as the main model. SmartPaint⁴² is a freely available software tool for interactive segmentation of medical 3D images. However, it only supports Windows platform. MITK⁴³ is an cross-platform interactive segmentation software integrated with 3D region growing, watershed and Otsu algorithm.

More recently, deep learning based interactive segmentation methods have also been studied. Notably, MONAI Label⁴⁴ is an open-source interactive medical image learning and labeling tool using the deep learning as its backend. The MONAI Label contains several pre-trained models. Given a new image to be segmented, the user select the trained model for target and provide some positive and negative clicks. The algorithm then uses the selected trained model and clicks to extract the target. But it can not be readily applied on the targets that are not in its trained list.

In this work, we reformulate the GrowCut as a clustering problem based on finding the shortest path that can be solved efficiently with the Dijkstra algorithm⁴⁵.

The motivation of adopting the GrowCut algorithm is stems from the historical development of interactive medical image segmentation processes. Back to around 2005, the ITK-SNAP⁸ standing as one of the few prominent options available to researchers and developers, relying on the level set methods. However, despite its many advantages, the level set method had its limitations, particularly when it came to dealing with touching boundaries. Later, the GrowCut algorithm based on cellular automata framework was developed and served as an alternative approach. Indeed, the GrowCut algorithm, was one of the first, if not the first, open-sourced 3D medical image segmentation software in the community which is able to simultaneously extract multiple touching targets with weak boundaries. As a result, the GrouCut was the state-of-the-art and the benchmark to be compared with and was therefore given a significant position. However, Growcut algorithm needs many epochs iterations, resulting in a slow convergence.

In the effort of improving the GrowCut algorithm, we end-up designing a new algorithm named ShortCut, which computes the image content modulated geodesic for segmentation. However, the realization of computing the geodesic is not trivial.

Moreover, the direct reformulation results in a static problem, changing the “dynamic” property of GrowCut. That is, editing is not allowed while running the Dijkstra algorithm. As an alternative, an efficient method we call the adaptive Dijkstra algorithm is proposed to incorporate user inputs. It updates only those local regions affected by the new input. This formulation and its implementation are described in Method Section. It is noted that a preliminary version of this work appeared in⁴⁶.

These improvements have greatly increased the speed of the subsequent modification process. It is through these innovative adjustments that the algorithm and software have been widely used in the field of 3D medical image processing, proving its ability to effectively address complex computational needs.

The following of this manuscript is organized as follows: The Method Section provides the details of the techniques, software design, and implementation on an open-source software platform. In the Results Section, we present the outcomes and discuss the reproducibility of both the methodology and software of the proposed work. Moreover, we not only performed a quantitative comparison with the other existing interactive segmentation software, but also we provided our insights on how to use them to get the better performance from them. Following that, in the Discussion and Conclusion Section, we summarize the advantages and challenges encountered during the practical application of our research. Additionally, the potential directions for future research and possible improvements are also outlined in this section.

Algorithm 1.

GrowCut

Methods

The GrowCut algorithm

The traditional GrowCut is a cellular automata (CA) based interactive image segmentation algorithm. It is summarized in Algorithm 1. The P denote the image domain. Specifically, the label 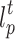and strength 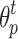of cell p in current round are copied to update the label 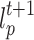and strength 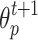in next round (line 4). The 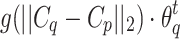is defined by the strength of cell q in current round, and the distance (in feature space) between feature vectors 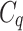and 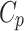. The label 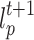and strength 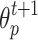of cell p in next round is determined by the cell q in current round (lines 5–6). Finally, the GrowCut algorithm terminates after a fixed number of iterations K or when no pixels change state. Convergence is guaranteed when K is sufficiently large because the updating process is monotonic and bounded⁴⁷.

GrowCut as clustering

From Algorithm 1, it is seen that 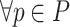, 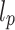in the steady state is determined by :

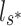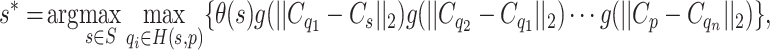1

where S is the set of seed pixels, and H(s, p) is any path connecting pixel p and seed s. This observation may be reached via proof by contradiction as was done in ⁴⁷.

It is known that the GrowCut algorithm converges slowly, especially when applied to 3D medical images because it traces through the entire image domain at each iteration⁴⁸. The speed of GrowCut can be significantly increased if the updating process is organized in a more structured manner. This goal can be achieved by approximating the product defined Eq. (1) as discussed below.

Suppose 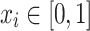, , 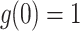and 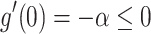. Define 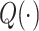as:

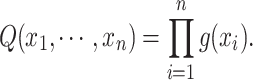2

Applying the Taylor expansion and Weierstrass product inequality⁴⁹ to Eq. (2), we have:

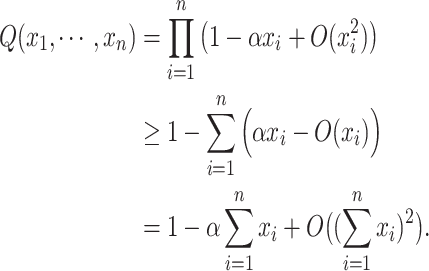3

Thus, 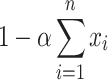gives an approximation to the lower bound of 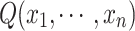. Normalizing 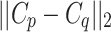to lie in [0, 1] and applying the result of Eq. (3) to Eq. (1), an approximate solution to the GrowCut algorithm is given as:

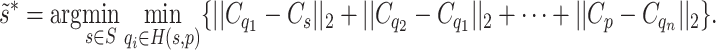4

Note that the inner part of Eq. (4) can be considered as the shortest weighted distance from p to s, and the outer part as the clustering based on this distance. One advantage of this formulation is that Eq. (4) can be solved very efficiently with the Dijkstra algorithm⁴⁵. The fastest implementation employs a Fibonacci heap⁵⁰ and has a time complexity of 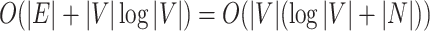where are the edges and vertices in the graph, respectively. The computational complexity of GrowCut is 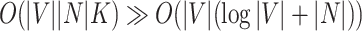, where K is the number of iterations. As a special case, when 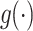is an exponential function, maximizing Eq. (2) is equivalent to minimizing its argument⁴⁷.

Algorithm 2.

Adaptive Dijkstra

Adaptive Dijkstra algorithm

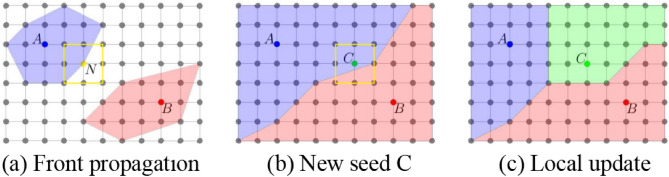
If we employ the standard Dijkstra algorithm to solve Eq. (4), we lose the “dynamic” property of GrowCut, which is crucial for a fully interactive system. Thus, we propose an adaptive Dijkstra algorithm that allows real-time interaction. The algorithm is summarized in Algorithm 2 and illustrated in Fig. 1.

Fig. 1.

The adaptive Dijkstra algorithm. (a) Expansion of the front by updating the neighbors (yellow square) of each point N on the front. (b) Addition of a new seed C to the final segmentation from seeds A and B (blue and red). (c) Pixels updated (green area) after adding seed C

Initially, when starting a new segmentation, labels of the seed image are assigned to the current label image labCrt. It is assumed that the target labels are positive integers. The current distance map distCrt is generated by setting its values to 0 at label points and 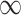at all other points. distCrt is used to initialize the Fibonacci heap fibHeap. Then, the algorithm always chooses the point with the smallest distance in the heap to update its neighbors’ distance and label information (lines 29–35), illustrated by Fig. 1(a). Once a point is removed from the heap, its state is fixed. New neighbors are updated while they are in the heap. This process continues until the heap is empty and the final segmentation is reached; see Fig. 1(b). Finally, distCrt and labCrt are stored (line 45) to be used in the next round of segmentation.

When updating the current segmentation, the new seeds added during the latest user editing stage are compared to labPre, and only those points whose labels are changed are selected as new seeds to update the previous segmentation (lines 11–15). The distance distCrt from these new seeds is propagated if its value is smaller than distPre, which may reassign labels based on the shortest-path clustering rule. Otherwise, the algorithm either keeps the previous state or terminates (lines 22–26). Finally, if distCrt equals to 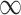, the current distance and label information are the same as the previous one. It means the distance and label information are updated where distCrt is not equal to 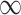(lines39–41), see Fig. 1(c), which significantly reduces the refinement time.

Implementation as a 3D slicer module

For an interactive segmentation algorithm to be fully utilized by the community especially the clinical end users, it must be incorporated in an easily used graphical user interface (GUI) software. Fortunately, 3D Slicer is a free, open-source and cross platform software for medical image processing and 3D visualization. Moreover, it is an open source software with a very permissive license allowing developers to plug their algorithms into 3D Slicer as modules, extending the capabilities of 3D Slicer into specific areas.

3D Slicer was selected as the development platform. The Python scripted module is used to implement the proposed method due to its flexibility and effectiveness. In particular, there is a special scripted module in 3D Slicer called the “Segment editor”⁵¹. It provides basic editing operations such as paint, draw and erase with real-time 3D visualization of the current segmentation. In addition, it also supports other scripted module as sub-module, called “Effect”, to be used along with the existing ones.

Therefore, it is appropriate to implement the proposed algorithm as an Effect of the Segment Editor module. It is officially referred to as “Grow from seeds” on 3D Slicer release⁵².

Results

Experiments were performed on a Linux computer with Intel Core i7-8700k CPU @ 3.70GHz and 32GB memory. The following commonly used metrics were used to validate the proposed solution: Dice similarity coefficient (Dice)⁵³, and the average symmetric surface distance (ASSD)⁵³.

Guidelines for using the proposed tool

This section is intentionally a rather detailed usage guidelines of the proposed algorithm/software. The purpose is therefore not only to evaluate the effectiveness of the proposed algorithm, but make it a useful tool for the community.

The workflow of the proposed ShortCut method has three components: 1) annotate few seed points in the target and background regions, 2) invoke the algorithm and initialize the 3D segmentation, and 3) interactively improve the segmentation results by placing/erasing seeds and algorithm fine-tuning.

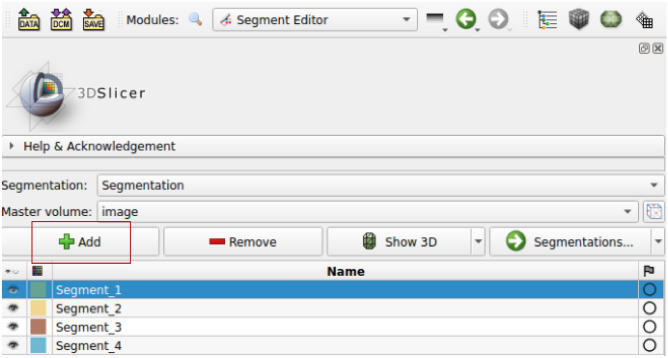
First, we use the “Paint” effect to draw seed points. Generally, in order to segment N targets, we need to draw 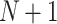strokes by clicking “Add” in the interface, as shown in Fig. 2.

Fig. 2.

Add segment by clicking “Add”

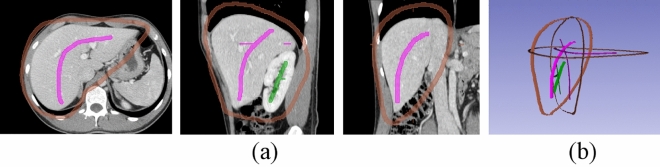
Different colored segments represent different segmentation targets. For the example as shown in Fig. 3, we added three regions (the third is for background) to segment liver and right kidney simultaneously. For better segmentation outcome, we recommend to draw the target seed points on each of the coronal, sagittal and coronal planes, respectively. Moreover, the target strokes should be drawn in roughly the central part of the target to be segmented. A good rule of thumb is that one could draw in central part of the “skeleton” in each 2D view. Correspondingly, in each 2D view, the background strokes should be outside of, but not too far from, the intended target. For example, the stroke pattern could look like Fig. 3. As shown in the three orthogonal 2D views and the right-most 3D view.

Fig. 3.

Drawing initial strokes. (a) The initial strokes on axial, sagittal and coronal planes, respectively. (b) The initial strokes in 3D view

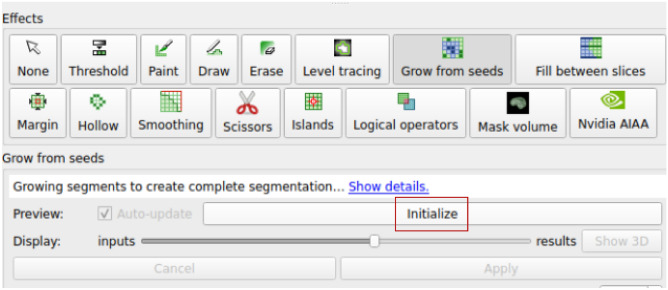
As shown in Fig. 3(b), the current seeds are sparse strokes, not a dense/complete 3D segmentation. Next, we run the proposed algorithm to obtain the dense 3D segmentation. To that end, we invoke the “Grow from seeds” in Slicer’s segmentation editor panel, and click the “Initialize” button, as shown in Fig. 4. The algorithm then takes over and obtains the 3D segmentation. For some larger volumes, this step may take half a minute or more to complete (for specific running time, please refer to Results Section). After this, we will get an initial segmentation result, as shown in Fig. 5.

Fig. 4.

Initialize 3D segmentation by clicking “Initialize”

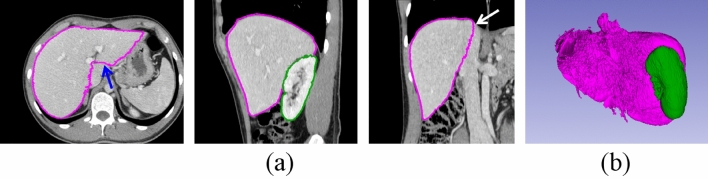
Fig. 5.

The initial (first) round segmentation result. (a) Segmentation result on axial, sagittal and coronal plane, respectively. There are under-segmentation (blue arrows) on the axial plane and leakage (white arrows) on coronal plane. (b) Initial result in 3D

As shown in Fig. 5, there exist both under- and over-segmentation. This is rather common in the first run of the interactive segmentation. To correct the over-segmentation (leakage), there are two possible approaches: adding more background seed point in the leaked area or erasing the target seed point near the leaked area inside the target area. To cure the under-segmentation, the target seed point can be added to the under-segmentation area. An example of adding strokes in the misclassified region is shown in Fig. 6. Adding or erasing seeds operations could be done by switching back to the “Paint” or “Erase” effect. Once the seed point is updated, “Grow from seeds” will automatically be triggered to update the 3D segmentation based on the newly added/removed seeds. Since the update is performed only on the possibly changed pixels by design, it is therefore very efficient once the initialization is finished and can achieve near real-time interactive update. In contrast, other interactive segmentation software mostly re-performs the complete computation after updating the seed points, resulting in a quite long update time (please refer to Results Section for comparison details).

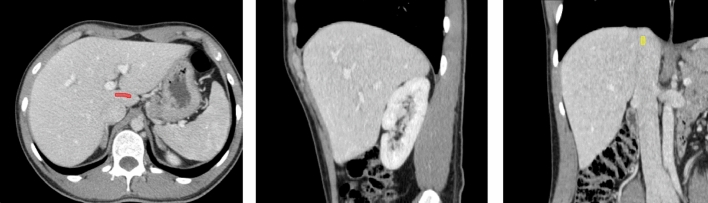
Fig. 6.

Adding more strokes in the misclassified region (second round). Adding target stroke in axial slice (in red color), to prevent under-segmentation. Adding background stroke in coronal slice (at the top of the inferior vena cava, in yellow color), to prevent leakage

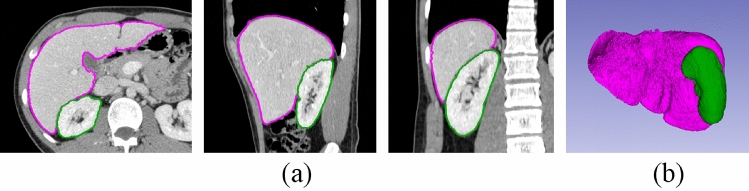
Finally, as shown in Fig. 7, both the liver and the kidney are segmented correctly after three rounds of interactions. By clicking the “Apply” button in the panel, the process is completed and the final segmentation results are saved.

Fig. 7.

The final segmentation result. (a) Segmentation result on axial, sagittal and coronal plane, respectively. (b) The 3D segmentation result. Significant improvement can be observed in the left lateral section

Comparison with the original GrowCut algorithm

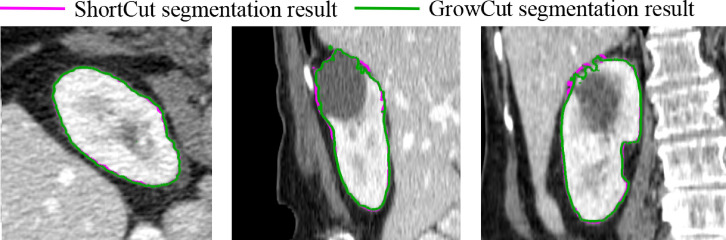
We compared the proposed ShortCut method with a publicly available GrowCut implementation⁴⁸. To illustrate the efficiency of the proposed method, three rounds of editing were used to segment the right kidney from BTCV abdomen dataset⁵⁴. After each round of editing, the adaptive Dijkstra algorithm was performed. As shown in Fig. 8, the update only happens locally, around new user inputs. The quantitative comparison of final segmentation results is summarized in Table 1. It shows that the proposed method is significantly faster than the original GrowCut implementation, while maintaining a high approximation accuracy (Dice:98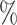). The segmentation results from GrowCut and proposed ShortCut are shown in Fig. 9.

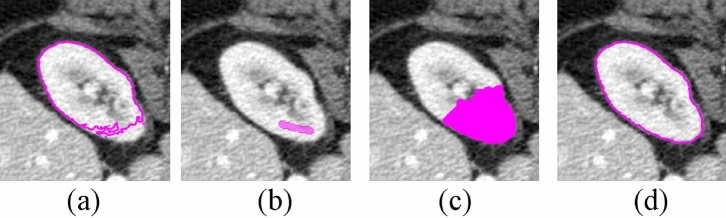
Fig. 8.

Effect of user interaction on kidney segmentation: (a) previous segmentation, (b) new seeds, (c) region updated by adaptive Dijkstra, and (d) new segmentation

Table 1.

Original GrowCut vs. the proposed implementation for right kidney segmentation

Method	Time (seconds)			Similarity
	1st round	2nd round	3rd round	Dice
GrowCut48	20.9	21.3	20.8	98%
Proposed	6.8	0.2	0.4

Fig. 9.

Segmentation results from GrowCut⁴⁸ (green) and the proposed method (magenta) in axial, sagittal and coronal views, respectively. It can be seen that they are almost identical

Comparisons with other interactive approaches

In this section, we evaluate the proposed algorithm on five diffferent targets: liver (MICCAI SLiver07⁵⁵), spleen (Segmentation Decathlon Task 09⁵⁶), aorta (multi-organ BTCV dataset⁵⁴), stomach (multi-organ BTCV dataset⁵⁴) and kidney (KiTS19⁵⁷). For each organ, three samples were randomly selected from a dataset for this comparison study.

The following segmentation approaches were used for comparsion: ITK-SNAP⁸, RSS⁹, DeepGrow⁵⁸ in MONAI Label ⁴⁴, SAM-2D ¹⁴, MedSAM  ¹⁷. In addition, we also provided experiences and recommendations for some “best practices” for using these interactive segmentation tools.

Comparison of segmentation accuracy

In this test, we performed a total of three rounds of interactions for each tool. In each round, a user was asked to draw/edit up to six strokes/clicks to initialize/improve the segmentation.

Under such testing conditions, Table 2 shows the comparison of the segmentation accuracy after each round for the different interactive methods/tools. Since the SAM-based methods only support labeling on 2D slices, annotating each slice is a very tedious process: First, we slice the 3D image in cross section and obtain the corresponding 2D images. Second, we place the labeled delineation point layer by layer and then utilize the SAM framework to segment the image slices with delineation. Finally, the obtained 2D annotations output from SAM are stacked to get the segmentation result of 3D volume. Lots of time was spent on such logistical overheads. Indeed, this again shows the necessity of a well designed GUI-based software for the interactive segmentation algorithm to be really helpful for the community. As can be seen from Table 2, when segmenting the liver, spleen, stomach and kidney, the proposed method achieves the highest accuracy. For the task of segmenting aorta, RSS method is better than the rest.

Table 2.

Comparison of interactive segmentation methods with three epochs with up to six strokes/clicks/interaction per epoch. (Average dice score and average ASSD distance in mm.) Due to operational limitations of MedSAM, we have retained only the most satisfactory segmentation result from interaction. The best results are marked in bold

Method	ShortCut		RSS		ITK-SNAP		DeepGrow		SAM-2D		MedSAM
	Dice	ASSD	Dice	ASSD	Dice	ASSD	Dice	ASSD	Dice	ASSD	Dice	ASSD
liver	0.92	3.15	0.89	4.56	0.91	4.48	0.85	5.72	0.86	3.91	0.94	1.34
	0.93	2.15	0.90	3.68	0.91	4.17	0.91	2.89	0.91	4.06	-	-
	0.94	1.92	0.91	3.28	0.91	3.86	0.92	2.70	0.91	3.65	-	-
spleen	0.91	1.34	0.86	2.76	0.92	1.23	0.88	2.30	0.84	7.41	0.96	0.30
	0.93	1.08	0.87	2.51	0.92	1.16	0.89	2.11	0.88	6.01	-	-
	0.93	0.99	0.88	2.22	0.92	1.11	0.90	2.00	0.91	2.16	-	-
aorta	0.84	2.68	0.88	1.52	0.73	3.35	0.76	1.88	0.92	0.66	0.94	0.50
	0.89	0.87	0.90	1.00	0.76	1.87	0.81	1.47	0.92	0.67	-	-
	0.90	0.63	0.91	0.90	0.77	1.84	0.82	9.64	0.92	0.67	-	-
stomach	0.84	2.19	0.75	3.90	0.64	6.74	0.58	9.64	0.74	3.27	0.91	1.18
	0.86	2.02	0.76	3.94	0.64	6.57	0.65	8.56	0.77	3.48	-	-
	0.86	1.80	0.75	4.25	0.64	6.56	0.67	8.16	0.78	3.74	-	-
right kidney	0.91	2.30	0.81	3.80	0.57	5.18	0.75	8.93	0.78	3.99	0.96	0.67
	0.93	1.10	0.84	2.87	0.61	4.65	0.81	8.68	0.84	3.85	-	-
	0.94	0.91	0.88	2.24	0.62	4.36	0.85	5.64	0.87	3.49	-	-

Though no algorithm achieves the best for all the tasks, which is natural due to the vast variations among their appearances and shapes, the proposed method gets the first place for the most of the times. Moreover, it can be observed that for challenging cases, such as the stomach (with air) and the kidney (with tumor), since the intensity has quite high variations, it is difficult for ITK-SNAP and RSS method to get the correct results. That being said, finding the right tool for a specific task is an art for the interactive segmentation. In the following Section, we provide some insights and experiences for such a task.

Running time comparison

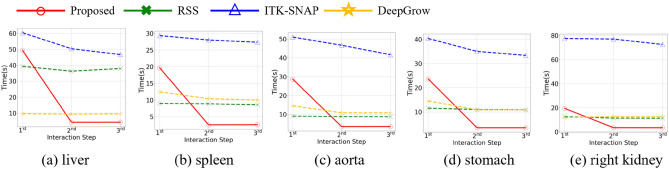
Fig. 10 shows the running time for various organs using different methods. For a consistent comparison, we still fixed the number of rounds to three and enforced a limit of six strokes/clicks per round. As the SAM-based method consumes significantly more time in layer-by-layer stroke drawing compared to other methods, we did not include it in the comparison in Fig. 10. As shown in Fig. 10, in the first round, for spleen, aorta and stomach, the running time of RSS is the shortest. Then, for liver and right kidney, the running time of DeepGrow is the shortest, possibly due to the fast feature extraction on GPUs. However, in the subsequent rounds of interaction, the proposed method is 2.2x to 22x faster than the other methods being compared (see Fig. 10 for detail).

Fig. 10.

Comparison of interactive segmentation methods on running time with three rounds with up to six strokes/clicks/interaction per round

It is noted that the updated running time includes both the time of drawing strokes and running the algorithm update. For ShortCut, after the first round, the running time of the subsequent algorithm update is generally within a few seconds even for large volumes. Thus, users can receive immediate feedback on their actions.

User effort comparison

To evaluate the effort required to achieve a pre-set performance threshold, we recorded the number of strokes required. Specifically, we used 0.92, 0.92, 0.84, 0.84, 0.90 for liver, spleen, aorta, stomach and right kidney, respectively, due to the different image characteristics and target volumes.

As shown in Table 3, the proposed ShortCut required fewer number of strokes compared with other methods in liver, spleen and stomach. However, for homogeneous organs with high contrast boundaries such as the spleen, the ITK-SNAP achieved the accuracy with just one stroke, since it does not require the rejection seeds. Moreover, for tubular structures, the RSS can achieve both smooth and accurate segmentation given few strokes along the axis of the tube.

Table 3.

Comparison of average number of strokes and total time (seconds) required to achieve a pre-set Dice accuracy for different interactive segmentation methods. “-” denotes that no matter how many strokes are drawn, the pre-set dice cannot be achieved. Note that for the proposed method, in the first round, we often use two strokes for each of the three anatomical views. Therefore, for the proposed method, the first round has already consumed six strokes. “S” and “T” represent the strokes and total time, respectively

Method	ShortCut	RSS	ITK-SNAP	DeepGrow	SAM-2D	MedSAM
DSC (Thr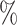)	S (T)	S (T)	S (T)	S (T)	S (T)	S (T)
liver(>92)	6.6 (55.3)	13 (458.9)	-	16.7 (156.9)	-	85.8(358.8)
spleen(>92)	8.3 (23.2)	-	1 (28.4)	-	-	82.9(346.5)
aorta(>84)	6 (27.6)	2.3 (29.5)	-	-	159.6 (243.2)	83.6(349.6)
stomach(>84)	6.3 (25.4)	-	-	-	-	102.6(429.3)
right kidney(>90)	6 (22.7)	-	-	-	-	116.8(488.5)

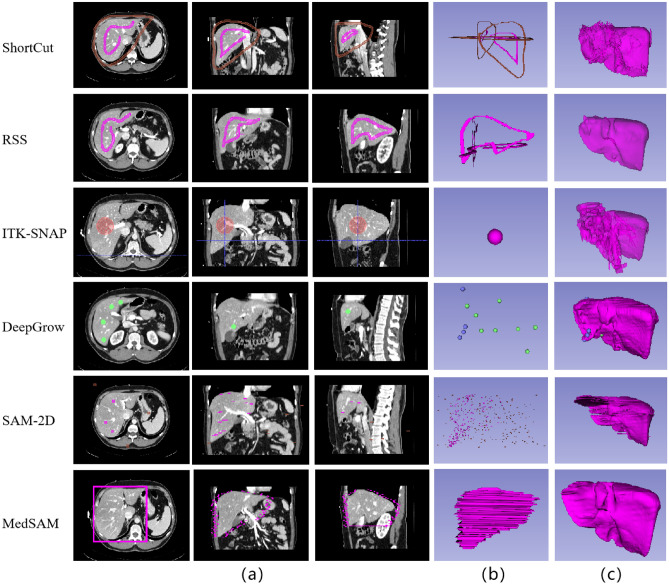
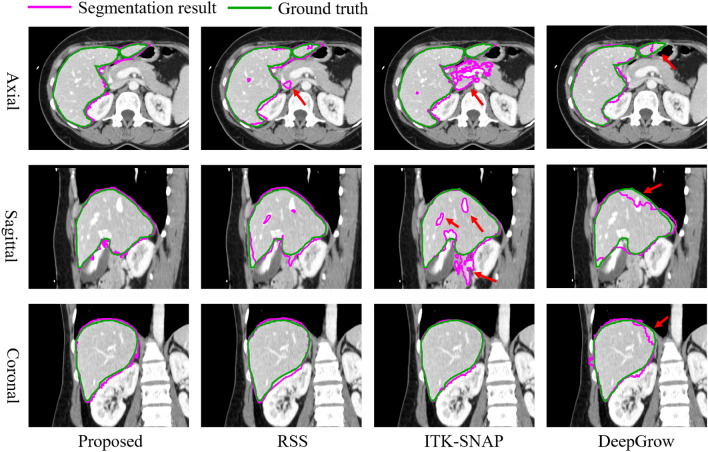
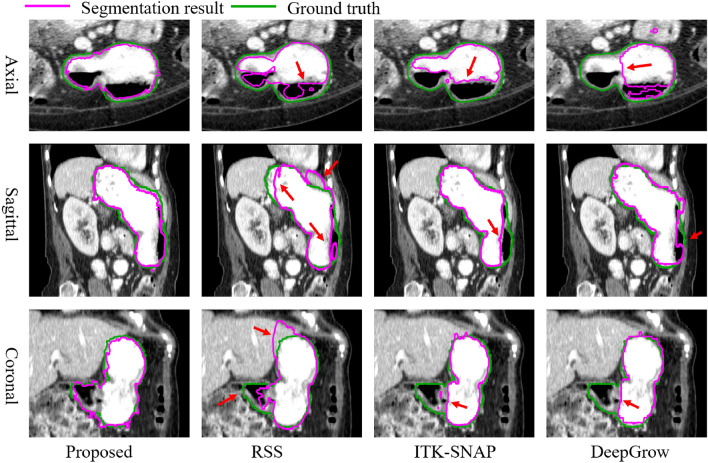
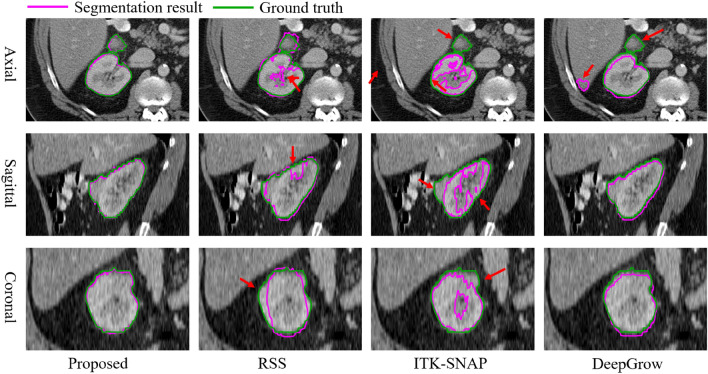
For visual comparison, we have depicted the 3D image delineations and segmentation results of various methods on the liver in Fig. 11. In Fig. 11, the number of strokes required by DeepGrow is more than placed in ShortCut as it requires multiple adjustments to the segmentation result. SAM-2D and MedSAM require even more strokes to segment 3D objects as it requires layer-by-layer labeling. ITK-SANP uses the least number of strokes, but it doesn’t segment well and has a lot of over-segmented areas. In contrast, RSS provides smoother segmentation results, although the precision is slightly lower than that of ShortCut. The segmentation results of the proposed method and other methods on liver, stomach and kidney are shown in Fig. 12, Fig. 13 and Fig. 14, respectively.

Fig. 11.

Delineated Stroke and segmentation results of different methods. (a) and (b) are the required drawing strokes of different methods in 2D and 3D views, respectively. (c) is the final obtained segmentation result from different methods. Although the obtained Dice score of RSS segmentation results isn’t the highest, its segmented surfaces appear relatively smooth

Fig. 12.

Visual comparison of liver segmentation from different methods. Since the liver has rich bordering structures, the rejection seeding mechanism of the ShortCut algorithm is very helpful

Fig. 13.

Visual comparison of stomach segmentation by different methods. With air, food content/water, and parenchyma possessing different intensity, the proposed method performs well in handling such internal heterogeneity

Fig. 14.

Visual comparison of right kidney segmentation by different methods. With tumor possessing different intensity, the proposed method performs well handling such internal heterogeneity

Experiences and recommendations for these tools

We can see from our empirical studies that there is no silver bullet for medical image segmentation tasks: different algorithms may have their own advantages in segmenting certain organs and lesions. In Table 2, we give an illustration of several different organs with different characteristics: intensity, texture, as well as geometry. It shows that for structures with smooth/well-defined boundaries, such as the spleen, the level set based methods performed quite well.

However, in cases where the target of interest is not only in close contact with other organs or tissues but with poor contrast. In this scenario, methods that provide mechanisms of rejecting certain region, such as the proposed ShortCut, may give a better result. Algorithms without such a mechanism may inevitably have leakages in final segmentation.

Although the accuracy metrics indicate good performance, the 3D visualizations of the ShortCut results seem to indicate a tendency for slightly noisy region boundaries. The noisy surface stems from the fact that we don’t have smooth constraint in the surface evolution when computing the geodesic. And this primary stems from the fact that the method operates similar to a first-order partial differential equation (modified Eikonal equation), which does not inherently guarantee computational smoothness. However, this characteristic allows the algorithm to utilize rapid computing methods such as Dijkstra algorithm, which is essential for interaction operations within 3D volumes. In contrast, if the smoothness is directly incorporated into the surface evolution, the second order curvature information may prevent the usage of fast algorithm. Moreover, incorporating curvature make the multi-surface evolution difficult to handle. This can be seen in most previous level-set based algorithms.

Such a dilemma could be solved by post-processing of the surface. And the proposed method has been in 3D Slicer, which has several choices for smoothing. This will solve the noisy surface problem in cases where smoothness is desired.

For tubular structures, the RSS algorithm provides a good framework where we only have to draw a few seeds along the center line of the tubular structure. If the target organ as well as the corresponding image modality exist in the learning-based tools, such as the DeepGrow, one could first try such learning based tools. However, additional re-training is required to generalize to unseen objects. As a result, we do not claim the proposed algorithm to be superior than the others in all the situations. Just that its algorithmic advantages may be helpful for certain challenging cases, and being an open GUI based program would be beneficial for the community.

Multiple object extraction

Compared to segmenting individual objects separately, multi-object segmentation has the following advantages: 1). efficiency, potentially reducing the overhead of sequential single object segmentation. 2). reliability, properties such as mutual repulsion between the boundary surfaces of different objects can be utilized. This can prevent leakage in low contrast situations and obtain correct overlapping and/or non-overlapping relationships between multiple objects.

Although the advantages of multi-object segmentation techniques are widely recognized, there are relatively limited number of articles on 3D interactive multi-object segmentation. Furthermore, the work that integrate the algorithms into software and make them open-source is very rare. Unfortunately, as an interactive algorithm, a user-friendly software is indispensable. We only find that CRF⁵⁹ fall into this open-source multi-object 3D segmentation software category. Indeed, software such as ITK-SNAP can extract multiple targets. However, each target can only be extracted independently and therefore it is not counted here. Moreover, in⁹, the algorithm described was a multi-target one, however, the open-source implementation in 3D Slicer is a single-target only. So, it is excluded from our comparison study.

In what follows, in order to demonstrate the performance of the proposed method, we conducted comparisons with CRF⁵⁹. Two examples were selected for this experiment: the first one involves segmenting the liver, kidneys, and spleen (from the Chaos dataset⁶⁰), and the second one is segmenting kidney and kidney tumor (from the KiTS19 dataset⁵⁷).

For a fair comparison, in the test, we performed a total of two rounds of interactions. In each round, the user draws/edits up to three strokes on each target or background to initialize/improve the segmentation. The experimental results for segmentation accuracy are presented in Table 4 and Table 5. The results demonstrate that our method outperforms the final interaction results of CRF⁵⁹ in the first round interaction.

Table 4.

Comparison segmentation accuracy (average dice score) of different methods for organs from the Chaos dataset. “F” and “S” represent the First and second round interaction, respectively

		Liver		Right kidney		Left kidney		Spleen
		F	S	F	S	F	S	F	S
ID0	ShortCut	0.88	0.90	0.90	0.91	0.88	0.91	0.88	0.91
	CRF59	0.68	0.77	0.69	0.78	0.62	0.80	0.74	0.78
ID1	ShortCut	0.80	0.90	0.79	0.90	0.79	0.90	0.80	0.91
	CRF59	0.63	0.68	0.64	0.71	0.66	0.72	0.67	0.74
ID2	ShortCut	0.83	0.87	0.84	0.88	0.84	0.88	0.85	0.89
	CRF59	0.73	0.83	0.76	0.83	0.77	0.80	0.79	0.84
ID3	ShortCut	0.87	0.90	0.87	0.90	0.88	0.90	0.85	0.91
	CRF59	0.74	0.80	0.74	0.82	0.76	0.81	0.77	0.82
ID4	ShortCut	0.84	0.89	0.86	0.90	0.86	0.90	0.88	0.91
	CRF59	0.64	0.74	0.66	0.73	0.69	0.79	0.72	0.82
Mean	ShortCut	0.84	0.89	0.85	0.90	0.85	0.90	0.85	0.90
	CRF59	0.68	0.77	0.70	0.77	0.70	0.78	0.74	0.80

Table 5.

Comparison segmentation accuracy (average dice score) of different methods for organs a from the Chaos dataset. “F” and “S” represent the First and second round interaction, respectively

		kidney		kidney tumor
		F	S	F	S
ID0	ShortCut	0.92	0.95	0.94	0.96
	CRF59	0.55	0.66	0.56	0.67
ID1	ShortCut	0.90	0.91	0.93	0.93
	CRF59	0.55	0.62	0.58	0.61
ID2	ShortCut	0.90	0.92	0.93	0.93
	CRF59	0.61	0.74	0.63	0.76
ID3	ShortCut	0.91	0.93	0.94	0.95
	CRF59	0.63	0.74	0.64	0.75
ID4	ShortCut	0.89	0.91	0.95	0.95
	CRF59	0.65	0.71	0.67	0.75
Mean	ShortCut	0.90	0.92	0.94	0.95
	CRF59	0.60	0.70	0.62	0.71

In addition to the accuracy, the segmentation time is also a crucial factor for interactive segmentation. To evaluate that, we also recorded the average runtime required for each round of interaction. The results are shown in Table 6 and Table 7, it can be seen that our algorithm requires much less time in the first round compared to CRF⁵⁹. Moreover, after the first round, our algorithm’s runtime is far lower than that of CRF⁵⁹, meaning that users can see real-time update results within 2 seconds instead of waiting for more than half a minute to see segmentation results. The fast runtime of our algorithm after the first round is attributed to the design of the adaptive Dijkstra algorithm in Method Section.

Table 6.

Average running time (seconds) of different methods on Chaos dataset. “F” and “S” represent the First and second round interaction, respectively

	F	S
ShortCut	0.98	0.20
CRF59	52.82	51.64

Table 7.

Average running time (seconds) of different methods on KiTS19 dataset. “F” and “S” represent the First and second round interaction, respectively

	F	S
ShortCut	2.72	0.24
CRF59	56.28	56.12

Disccusion and conclusions

In this paper, we presented an effective and efficient 3D medical image segmentation method. It provides a fast approximation to the GrowCut approach by reformulating the original problem of maximizing of a product as the minimization of a summation, which allows for a very efficient implementation using the Dijkstra algorithm. Furthermore, for better fitting the interactive scenario where the seeds are actively updated, we proposed an adaptive Dijkstra method which only updates the values for the affected nodes, making the subsequent adjustment very efficient for large volumetric data.

Moreover and importantly, for an interactive segmentation algorithm to be widely used, a well curated GUI and software platform is essential. We therefore implemented the algorithm in the 3D Slicer platform and open-sourced the entire project⁵².

This work represents a significant extension of a previous conference paper, primarily reflected in two key aspects. First, the innovations of this current work compared to the previous conference paper are primarily in algorithm efficiency and user interaction experience. The previous study enhanced the segmentation efficiency of the GrowCut algorithm through the Fast GrowCut algorithm. This current study further optimizes the algorithm by adopting an adaptive dynamic programming approach to handle more complex 3D images. By integrating into the 3D Slicer platform, it provides a user-friendly interactive interface and open-source implementation, supporting customizable modifications. This significantly enhances the flexibility and efficiency in practical applications. Second, although a vast array of excellent interactive image segmentation tools is available, and numerous interactive image segmentation algorithms have been proposed, it is also true that there is no silver bullet in the interactive image segmentation. Different algorithms have their unique advantages when segmenting specific organs and lesions. How to choose them correctly and use them well is also important for the algorithm-users. Therefore, in addition to algorithm development, to better bridge the gap between the algorithm developers and users, we have conducted quantitative analysis of the comparative advantages of different algorithms.

Experiments are conducted and the effectiveness as well as the efficiency of the algorithm has been demonstrated on a set of organs selected from various datasets. Moreover, we provide a brief guideline on how to achieve the best performance with different interactive segmentation tools.

Beyond using certain metrics such as the Dice value, the segmentation result is more of a preference than a reference. In this regards, various interactive segmentation tools should be used jointly to take advantage of their characteristics.

As for our software, it exhibits the following strengths which enhance its utility and application. First, we proposed an efficient and effective 3D interactive algorithm with the adaptive dynamic programming method. The method could handle the segmentation of a very large volumetric dataset. Moreover, as the comparison also showed, the algorithm performed better in the situation when there are multiple targets touching each other with weak boundaries.

Second, in contrast to non-interactive segmentation algorithms, the value of an interactive segmentation algorithm for 3D volumetric images would be very limited if it was only presented as an algorithm. This, however, is the unfortunate fact for most published algorithms presented to date. Furthermore, even if some researches have graphical user interface, the GUI is quite cumbersome and can only be used for very limited preprocessed data types. Arguably, implementing an interactive 3D volume segmentation algorithm into an end-user operable software may be as important as the algorithm itself. With such requirement in mind, the proposed method takes advantage of the robust and full-fledged 3D Slicer as its foundation and enables the user to directly utilize the convenient operations in 3D Slicer in the operations of the proposed algorithm. Only by doing this, can an algorithm really benefit both the algorithm research and clinical communities.

Thirdly, though there are well-designed GUI-based commercial interactive segmentation software solutions exist, they are not customizable. Therefore, the third advantage of the software is its open-source nature, the ability of users to make customized modifications according to their specific requirements, is of great importance.

The above is a summary of the advantages of the algorithm, but there are still some specific and different problems faced during the practical application of the segmentation algorithm. We partially addressed the segmentation issues, but we also believe that it is unlikely that there will be a single solution to solve all the problems as explained below:

Firstly, based on the extensive comparison experiment presented in this paper, the proposed method achieves excellent results in a very wide range of experiments and tasks. This excellent performance are shown in two aspects: accuracy and efficiency. Moreover, this article not only proposes an algorithm but also provides an open-source graphical user interface-based software. We believe that these contributions will be valuable to the community.

Secondly, the algorithm and its implementation in this paper have been utilized in the community for several years, demonstrating excellent performance in various situation. Therefore, the second significance of this paper is to summarize this method and propose ways to further optimize its utilization, aiming to achieve better results for more algorithm developers and clinical researchers. Having been in use for several years, we have accumulated various “best practice” for this and other algorithms.

Third, as mentioned above, although we achieved good results in different tasks, we do not claim that this paper is the silver bullet that solves the entire interactive segmentation problem. Indeed, in our experience with further research, we have found that different clinical users may have different segmentation preferences even for the same target in the same image, depending on their clinical purposes. Therefore, an interactive segmentation solution should not pursue a single “gold standard” but rather provide a great tool that achieves the preferences of each user with their own purpose.

Finally, we are also actively exploring solutions related to deep learning techniques in the context of interactive segmentation, which we hope to benefit the open-source medical image computing community.

Author contributions

Y.G., L.Z. and A.T. conceived the experiments, X.C. and Q.Y. conducted the experiments, X.C. and Y.G. analyzed the results. X.C., Q.Y. and Y.G. contributed to the writing of the manuscript. A.L, I.K., S.P. and R.K. contributed to the design and implementation of the research. All authors reviewed the manuscript.

Data availibility

The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.

Declarations

Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.