Figure 5.

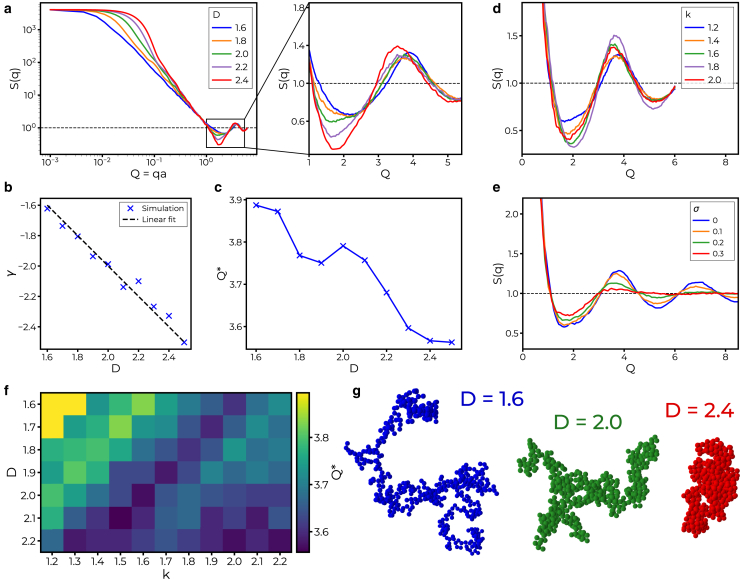
Simulation of fractal clusters using the approach from Tomchuk et al. (25). (a) Structure factors are shown from clusters with fixed $k=1.2$ and different values of the fractal dimension D. Curves are plotted on the scale $Q=qa$ which is independent of the mean particle radius a. The decay of the SF in the Guinier regime changes with D. Zooming into the region of the first correlation shell reveals a change of shape and position of the local maxima. (b) By linear fitting the slopes of the SF in the Guinier regime from $Q\approx 0.1$ to $Q\approx 0.6$ and plotting against D, it can be seen that the slope in this regime is correlated to the fractal dimension by the relation $\gamma \approx -D$. (c) Plotting the peak position of the first correlation shell $Q^{\ast }$ against D reveals a negative correlation. The observed values of $Q^{\ast }$ does not coincide with the classical peak position for a dense hard core fluid of $Q^{\ast }=\pi$. However, for high D, which represent the clusters with compact structures, $Q^{\ast }$ seems to converge to this value. (d) SF of simulated clusters at fixed $D=2$ for varying k. (e) The simulation can be extended by introducing polydisperse particles, wherein particle radii are randomly generated following a log-normal distribution. The parameter σ approximately gives the standard deviation of the distribution and controls the level of polydispersity. SF values of polydisperse cluster are shown for fixed $k=1.2,D=2$ and different σ. With increasing σ, that is with higher polydispersity, the amplitude of the extrema decreases. (f) First peak position $Q^{\ast }$ in dependence of both fractal parameters D and k. A pattern combining an oscillation with a linear decay is obtained. For compact clusters (high D and k), the peak position decreases. (g) Visual representation of three clusters created at different values of the fractal dimension D (monodisperse, $k=1.2$). By tuning D, either elongated and fractal or dense and compact clusters can be generated.