Using paired-end read orientations to assess technical biases in capture Hi-C

Abstract

Hi-C and capture Hi-C (CHi-C) both leverage paired-end sequencing of chimeric fragments to gauge the strength of interactions based on the total number of paired-end reads mapped to a common pair of restriction fragments. Mapped paired-end reads can have four relative orientations, depending on the genomic positions and strands of the two reads. We assigned one paired-end read orientation to each of the four possible re-ligations that can occur between two given restriction fragments. In a large hematopoietic cell dataset, we determined the read pair counts of interactions separately for each orientation. Interactions with imbalances in the counts occur much more often than expected by chance for both Hi-C and CHi-C. Based on such imbalances, we identified target restriction fragments enriched at only one instead of both ends. By matching them to the baits used for the experiments, we confirmed our assignment of paired-end read orientations and gained insights that can inform bait design. An analysis of unbaited fragments shows that, beyond bait effects, other known types of technical biases are reflected in count imbalances. Taking advantage of distance-dependent contact frequencies, we assessed the impact of such biases. Our results have the potential to improve the design and interpretation of CHi-C experiments.

Introduction

The Hi-C method has been used to define higher-order structural features such as topologically associating domains (1). Capture-C (2–4) and CHi-C (5–7) additionally employ a hybridization technology to enrich interactions at selected target regions, achieving a resolution that allows interactions between specific gene promoters and their distal regulatory elements to be identified.

Hi-C involves digestion of a formaldehyde cross-linked genome with restriction enzymes, and subsequent fill in and repair of the digested ends, thereby incorporating biotin-linked nucleotides. The repaired ends are then re-ligated, the cross-links reversed and associated proteins degraded, after which the DNA is sheared by sonication or other methods (8). This results in chimeric fragments that are composed of DNA from different regions of the genome. The premise in Hi-C is that intra-molecular re-ligations in cross-linked protein–DNA complexes are favored over inter-molecular random re-ligations (9). Therefore, a relatively high proportion of chimeric fragments represent pairwise DNA–DNA contacts. In Hi-C, chimeric fragments are enriched using the previously incorporated biotin-linked nucleotides. In Capture-C and CHi-C, additional enrichment of chimeric fragments associated with target regions is performed using complementary RNA (cRNA) probes, also referred to as baits. Baits are targeted to the two ends of restriction fragments that contain regions of interest. Certain bait selection criteria regarding the distance to the restriction sites as well as GC content and mappability are used to ensure the effectiveness of baits and to avoid off-target pull-downs, as those may complicate the interpretation of the data (10–13). Enriched sequencing libraries are subjected to paired-end sequencing and the reads are mapped to the corresponding reference genome. Read pairs that map to different strands and have a small distance to each other are considered artifacts resulting from un- or self-ligated restriction fragments and are therefore discarded (14,15). The remaining mapped read pairs are referred to as valid and those that map to a common pair of restriction fragments are combined into interactions with corresponding read pair counts.

In the subsequent data analysis, the task is to mitigate technical biases arising from the protocol and to distinguish relevant interactions from noise. Besides distance-dependent random contacts, random re-ligations are a significant source of noise in Hi-C (15). Technical biases arise from various limitations of the Hi-C assay, including incomplete restriction digestion, varying restriction fragment lengths as well as differing GC content, and mappability of restriction fragment ends. A number of methods have been developed to mitigate technical biases in Hi-C data (16–19). The additional target enrichment in CHi-C results in an asymmetric nature of the data (20). Furthermore, uneven capture efficiency represents an additional source of technical bias. cRNA baits have variable efficiencies that are difficult to predict. Moreover, due to bait selection criteria, for some target restriction fragments a bait can only be selected for one of the two ends, resulting in uneven enrichment of unilaterally and bilaterally baited fragments. Finally, interactions between two enriched restriction fragments (baited-baited) are more enriched than those between one enriched and any other restriction fragment (baited-other). A number of methods have been developed to address the specific requirements in CHi-C data analysis, some of which have recently been systematically compared (21). For example, the interaction caller CHiCAGO (22) considers distance-dependent random contacts and technical variability as two distinct count-generating processes that are modeled as a convolution of negative binomial and Poisson random variables, with the random variable for technical variability intended to represent multiple bias components, including those resulting from the Hi-C assay, target enrichment, and sequencing. CHiCANE (23) follows a similar approach but uses a regression model, which allows user-specified covariates such as GC content to be incorporated (20). Other methods use generalized linear models (24), background contact frequencies generated from negative control probe sets (10), integration of information from biological replicates (25), as well as maximum likelihood (26) or machine learning approaches (27) in order to mitigate technical bias in CHi-C data.

We noticed that relative paired-end read orientations have so far only been used to remove artifacts resulting from un- or self-ligated restriction fragments. In this work, we investigated whether the frequencies of different paired-end orientations of interactions contain information that could be used to improve the performance and interpretation of CHi-C experiments. In total, there are four different paired-end orientations and the sum of supporting read pairs of interactions across all orientations is typically interpreted as contact frequency or interaction strength. Here, we count supporting read pairs of interactions separately by paired-end orientation and interpret the four counts as observed re-ligation frequencies. We found substantial imbalances in the read pair counts of interactions for a large proportion of interactions in numerous human and mouse datasets. We attribute such imbalances to a number of known sources of technical bias, including bait effects, varying restriction fragment lengths, GC content, and mappability. We present a framework to detect such unbalanced interactions and analyze them with respect to various technical biases.

Materials and methods

Assignment of paired-end reads to chimeric fragments

Due to restriction digestion and subsequent re-ligation, paired-end reads from Hi-C experiments can have four different relative orientations to each other. On the other hand, there are four possible re-ligations between the ends of two given restriction fragments, resulting in four classes of chimeric fragments (Supplementary Figure S1). For cis-chromosomal interactions, i.e. both restriction fragments come from the same chromosome, we assign each relative paired-end read orientation to one of these chimeric fragment classes, which we label ‘0’, ‘1’, ‘2’ and ‘3’ (Table 1).

Table 1.

Assignment of paired-end reads to chimeric fragments. To each of the four possible relative orientations of mapped paired-end reads, we assigned a chimeric fragment class that results from which ends of a given pair of restriction fragments re-ligate with each other

Paired-end orientation		Chimeric fragment class
Inwards		3′–5′ re-ligation	‘0’
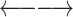
Outwards		5′–3′ re-ligation	‘1’
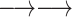
Both forward		3′–3′ re-ligation	‘2’
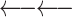
Both reverse		5′–5′ re-ligation	‘3’

Counting reads pairs separately by fragment class

In a previous work we developed Diachromatic, a tool for preprocessing and quality control of Hi-C and CHi-C data (15). In the original version of Diachromatic, only a single count was reported for each interaction, which is the sum of the supporting read pair counts across all four orientations of mapped paired-end reads. For this work, we extended Diachromatic to report the counts separately for each orientation to each of which we assigned one of the four chimeric fragment classes (Table 1).

In Diachromatic’s interaction format (Supplementary Table S1), each line represents an interaction and contains the coordinates and enrichment states of the two associated restriction fragments, as well as the counts of supporting read pairs. The fragment with the smaller coordinates (5′) always precedes the fragment with the larger coordinates (3′). Fragments selected for enrichment are marked with an E and all others with an N. This results in four enrichment states of interactions: NE, EN, EE, NN. For instance, NE means that only the 3′ fragment was selected for enrichment. The counts for the four orientations of mapped paired-end reads are reported separated by colons and in the following order: <Class 0>:<Class 1>:<Class 2>:<Class 3>.

In Diachromatic, an interaction is defined as any pair of restriction fragments with at least one supporting read pair. We restricted our analysis to interactions that occur within the same chromosome (cis-chromosomal) and have a distance of at least 20 000 bp. We pool the read pair counts of interactions that occur in more than one biological replicate by adding them up separately for the four orientations of mapped paired-end reads. We discarded all interactions that occur only in one replicate. Due to the low sequencing depth of Hi-C datasets, we also pooled interactions across eight different cell types. In this case, we pooled the already pooled biological replicates, requiring that pooled interactions must occur for at least two cell types. In other words, a pooled interaction must occur for at least two cell types and for each cell type in two biological replicates.

Unbalanced interaction calling

Classification

Within individual interactions reported by Diachromatic, we often observed strong imbalances in the four read pair counts. To classify an interaction as balanced or unbalanced, we use the P-value from a one-sided binomial test with a probability of success p = 0.5, taking the sum of all four counts as the number of trials (n) and the sum of the two highest counts as the number of successes (k). If the P-value from such a test is smaller than a given threshold t, we classify the interaction as unbalanced (U); otherwise, it is balanced (B).

Note that, depending on the chosen threshold t, a certain minimum number of read pairs is required for the binomial test to produce P-values below the threshold. For instance, an interaction with a total of n = 4 read pairs cannot be significant at a threshold of t = 0.05 because the smallest possible P-value of 0.0625 is already above the threshold. We refer to interactions that have fewer than the minimum number as ‘unclassifiable’; all other transactions are ‘classifiable’.

We point out that this classification procedure is not a valid binomial test because the two highest counts are chosen prior to performing the test. Here, we use the P-values only as a heuristic score for classification. This heuristic score is nonetheless adequate for the statistical analysis of the counts of balanced and unbalanced interactions introduced below.

Selection at a chosen FDR threshold

We developed a randomization procedure that allows us both to decide whether unbalanced interactions occur more often than expected by chance and to select them at a chosen false discovery rate (FDR) threshold (Supplementary Figure S2). In each iteration, we randomize the four counts of each interaction according to our null model (25% for each paired-end read orientation) and then determine the number of interactions that are still classified as unbalanced at a predetermined P-value threshold t. We use the originally observed number of unbalanced interactions n_o(t) and the mean μ_p(t) of the numbers of permuted unbalanced interactions from all iterations to estimate the FDR (28).

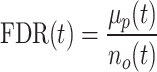(1)

To select unbalanced interactions at a chosen FDR threshold q, we use the same randomization procedure to estimate the FDR for each P-value threshold from a given range R = [t_min, (t_min + x), ..., (t_max − x), t_max], where x is a step size parameter. To classify interactions as unbalanced or balanced, we then use the largest P-value threshold for which the estimated FDR is still below q.

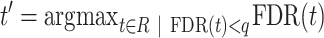(2)

For the analyses presented in this work, we determined a t′ for q = 0.05 for each dataset and used this as the P-value threshold for the binomial test to classify interactions as unbalanced or balanced. In addition to the FDR, we calculate Z-scores using 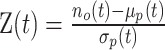, where σ_p(t) is the standard deviation of the numbers of permuted unbalanced interactions from all iterations.

Configurations of unbalanced interactions

We defined ten configurations of unbalanced interactions that differ in which two of the four counts are the highest (Table 2). For example, we assign configuration 13 to an interaction with counts 2:7:4:10 because the counts for classes 1 and 3 are highest. If 75% or more of the read pairs of an interaction are of the same class, we assign the interaction one of the configurations 0X, 1X, 2X or 3X, whichever count is highest. For visual representation, we assigned different colors to configurations. To distinguish interactions going from baited fragments towards 5′ or 3′, we used Diachromatic’s enrichment state tags, where NE corresponds to 5′ and EN to 3′.

Table 2.

Configurations of unbalanced interactions. Examples of unbalanced read pair counts for each configuration. According to our assignment of relative paired-end read orientations to chimeric fragment classes, the configurations differ in how many chimeric fragment classes are predominantly observed and how many restriction fragment ends are involved in re-ligations (see also Supplementary Figure S3). We assigned a label and color to each configuration

Example	Class	Ends involved	Label	Color
100:10:10:10	1	2	0X	–
10:100:10:10	1	2	1X	–
10:10:100:10	1	2	2X	–
10:10:10:100	1	2	3X	–
50:15:50:15	2	3	02	Red
50:15:15:50	2	3	03	Green
15:50:50:15	2	3	12	Magenta
15:50:15:50	2	3	13	Blue
50:50:15:15	2	4	02	Pink
15:15:50:50	2	4	23	Turquoise

Classification of baited fragments

We use our assignment of paired-end read orientations to chimeric fragment classes (Table 1) to detect baited restriction fragments that are either evenly enriched at both ends (BCF0), or predominantly at the 5′ end (BFC1) or 3′ end ( BFC2). To divide baited fragments into the classes BFC0, BFC1, and BFC2, we assume—based on our assignment—that class 2 read pairs result from re-ligations between two 3′ ends of fragments, while class 3 read pairs result from re-ligations between two 5′ ends of fragments. For a given baited fragment, we first determine the sums of the counts for read pairs of class 2 (s₂) and 3 (s₃) across all associated interactions. From this we calculate a score as follows.

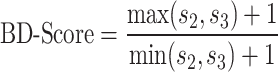(3)

1 is added to each quantity to avoid division by zero errors. If the score is greater than a specified threshold t, then we assign the baited fragment to BFC1 or BFC2 and otherwise to BFC0. If sum s₃ is greater than sum s₂, we assign the baited fragment to BFC1 and otherwise to BFC2.

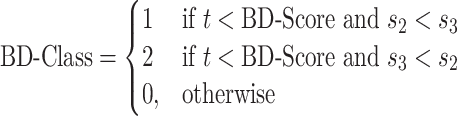(4)

We used a threshold of t = 2 to classify baited fragments. Baited fragments without interactions are not classified.

Calculation of repeat and GC content

We calculate the repeat content of a given sequence by determining the number of bases masked by RepeatMasker and dividing it by the total number of bases. We take advantage of the fact that reference genomes are typically available in soft-masked form, in which all bases masked by RepeatMasker are in lowercase (acgt) and all others in uppercase (ACGT). Similarly, we determine the GC content of a given sequence by dividing the number of all guanine (G) and cytosine (C) bases by the total number of bases.

Selection of interaction sets for comparisons

We selected comparison sets of balanced and unbalanced interactions that are almost identical in terms of the number of interactions and the distribution of total read pair counts per interaction. For such pairs of comparison sets, we then compared the distribution of the interaction distances. To select two comparison sets of balanced and unbalanced interactions for a given dataset, we first determine how many unbalanced interactions there are for each total read pair count. For instance, there might be 100 unbalanced interactions with a read pair count of 67. We then go through the interactions in random order and try to select the same number of balanced interactions for each read pair count, where we relabel selected interactions from B to BR and unselected interactions from B to BX. Furthermore, we relabel unbalanced interactions for which a balanced reference interaction could be selected from U to UR. If there are more unbalanced than balanced interactions for a given read pair count, we subsequently relabel the corresponding unbalanced interactions without reference from U to UX. For example, there could be only 90 balanced interactions with a read pair count of 67. In this case, we would relabel ten unbalanced interactions with a read pair count of 67. This selection procedure ensures that the total number of interactions and the distribution of read pair counts per interaction are identical for UR and BR interactions. For CHi-C data, we additionally take into account whether the 5′ or the 3′ restriction fragment of an interaction was selected for enrichment (Dichromatic interaction format) by performing the procedure separately for the different enrichment states (NN, NE merged with EN and EE). Within the enrichment states EE and NN, there are exactly the same number of interactions in the categories UR and BR. Within the enrichment states NE and EN, the interaction numbers may differ slightly, since our selection procedure for the comparison sets of unbalanced and balanced reference interactions does not differentiate between NE and EN. For the alternative selection of the two comparison sets, we use the same procedure, but instead of the total read pair counts (sum of the four counts), we use the maximum of the four counts as the selection criterion.

CHiCAGO interaction calling

We have developed the script dif2chicago.py, which converts Diachromatic interaction files into input files for the interaction caller CHiCAGO (.chinput). This script can optionally generate files that include either the total of the four read pair counts of interactions or only the maximum count. In addition, CHiCAGO requires a set of design files providing details about restriction fragments and their selection for enrichment. We converted the coordinates in the .baitmap file of Javierre et al., 2016 (29) from hg19 to hg38 using UCSC’s LiftOver tool (30). From the resulting file and the DigestMap we used for our interaction calling with Diachromatic, we then created a pair of .baitmap and .rmap files with consistent fragment IDs. Finally, we used the CHiCAGO tools script makeDesignFiles_py3.py to create the remaining hg38 design files from these two files. For a given dataset, we create .chinput files for each biological replicate from the unfiltered Diachromatic interaction files, i.e. including short and trans interactions, and place them in a directory. For interaction calling, we pass the path to this directory to CHiCAGO (1.32.0) and use default settings.

Enrichment of regulatory elements within other-ends

We assessed the enrichment of unbaited interacting restriction fragments (other-ends) for ENCODE’s Candidate Cis-Regulatory Elements (cCREs) (31) and enhancers from the Enhancer Atlas 2.0 (ENA2) (32). We used UCSC’s LiftOver tool to convert the coordinates of ENA2 enhancers from hg19 to hg38. For each of the five cCRE categories and ENA2 enhancers (prom, enhP, enhD, K4me3, CTCF, ENA2), we used BEDTools (33) to determine the number of interactions where the other-end contains at least one regulatory element. To assess whether the number of such other-ends is larger than expected by chance, we randomize the other-ends of all interactions. To randomize the other-end fragment of an interaction, we first randomly select one from all baited fragments and then define the genomic region at the same interaction distance and with the length of the original other-end as the random other-end. We performed 100 iterations of this randomization procedure and determined for each iteration and each category of regulatory element the number of randomized other-ends with at least one regulatory element. Afterwards, we calculated corresponding means and standard deviations. We consider the enrichment of the other-ends of interactions to be significant for a given regulatory element category if the observed count is more than three standard deviations above or below the mean. To compare the enrichments of a given regulatory element category across different interaction sets, we calculate a Regulatory Element Enrichment (REE) score by dividing the number of interactions whose other-end contains at least one regulatory element by the total length of all other-end fragments and multiplying the result by 10⁶. The REE score is independent of the number of interactions and the length of their other-end fragments. To validate our randomization procedure, we randomly selected genomic regions with a length between 50 and 1500 bp. If we apply our procedure using these elements, the REE scores within categories are approximately equal and our randomization procedure does not detect any significant enrichment (Supplementary Figure S4).

Software

Preprocessing of Hi-C and CHI-C data

We used Diachromatic (0.6.1_dev) to process Hi-C and CHI-C data from the raw FASTQ files to the interactions with the four counts for the different paired-end orientations. This includes the steps of truncation, mapping and counting supporting read pairs of interactions. Diachromatic uses bowtie2 (version 2.3.4.1) for mapping. Diachromatic expects the following input: (i) two paired-end FASTQ files, (ii) a bowtie2 index for the genomic reference sequence, (iii) information about the restriction enzyme used and whether overhanging cutting sites have been filled in, and (iv) a file with a genome-wide list of all restriction fragments, with fragments selected for enrichment marked accordingly (DigestMap). We used pre-computed bowtie2 indices for hg38 or mm10 as input for Diachromatic. For the restriction enzyme used, we selected HindIII and specified that overhanging cutting sites have been filled in. With our bait design tool GOPHER (11), we introduced the DigestMap format (Supplementary Table S1), which contains largely the same information as CHICAGO’s bait map file. We created a Python script that uses the information from the bait map file for the study on the hematopoietic cells to mark the corresponding restriction fragments in the DigestMap as baited.

Software developed for this work

We provide a collection of Python scripts, modules, Jupyter notebooks, and related documentation that can be used to reproduce any of the analyses presented here (https://github.com/TheJacksonLaboratory/diachrscripts). The scripts and notebooks were tested on the macOS and Linux platforms with Python versions 3.7 to 3.10. We implemented pooling interactions from different replicates in the script pooler.py. This script expects a path to a directory with Dichromatic interaction files as input. By default, all interactions that occur in fewer than two replicates are discarded. For the remaining interactions, the read pair counts of interactions that occur in multiple replicates are pooled by adding them up separately for the four orientations of mapped paired-end reads. The output file is in Diachromatic interaction format. We implemented the classification of interactions at a given FDR threshold into unbalanced (U) and balanced interactions (B) as well as the procedure for selecting two corresponding comparison sets in the script UICer.py. By default, the randomization procedure is used to determine a classification threshold that corresponds to an FDR of 5%. The output file is in Diachromatic interaction format, with the addition of two columns for interaction categories (Table 3) and (base 10) binomial P-value scores (logarithm to base 10). We implemented all further analyzes of unbalanced interactions presented in this paper in corresponding Python modules and Jupyter notebooks in which each analysis can be reproduced step by step. Scripts and documentation for analyzing Diachromatic interaction files using CHiCAGO are available on Zenodo (DOI: 10.5281/zenodo.13837266).

Table 3.

Interaction category labels. The output files of our unbalanced interaction caller (UICer.py) contain four categories of interactions. Labels of unbalanced interactions begin with a U and those of balanced interactions with a B. The ending R stands for ‘reference’ and means that an interaction belongs to one of the comparison sets of unbalanced and balanced interactions. Labels of interactions that do not belong to any comparison set end in X

Interaction category	Label
Unbalanced without reference	UX
Unbalanced with reference	UR
Balanced with reference	BR
Balanced without reference	BX

Data

Hi-C and CHi-C sequencing data from the hematopoietic cell study (29) were downloaded from EGA and prepared as recommended except that some chunks were omitted from the neutrophil and fetal thymus data to limit the memory footprint to <100 GB (Supplementary Table S2).

Additional data are available from the Open Science Framework platform (https://osf.io/u8tzp/). From this repository, we used CHICAGO’s baitmap file (22), which contains the coordinates of all fragments selected for enrichment. The bait coordinates for the experiment were taken from (7). We used UCSC’s LiftOver tool to convert the genomic coordinates from hg19 to hg38. We used BEDTools’ intersect command with the arguments F=1.00, -wa and -wb to assign baits to enriched fragments, where baits must overlap completely with fragments. Out of 37 602 baits, 37 572 could be assigned to one fragment and conversely, 22 055 out of 22 056 baited fragments were assigned one or two baits. The 30 cases in which the assignment failed are due to the conversion from hg19 to hg38 coordinates. If the same procedure is performed with the original hg19 coordinates, all baits are assigned to a fragment and at least one bait is assigned to each fragment. We assign a bait to the 5′ end of a fragment, if the center position of the bait is in the 5′ direction from the center position of the fragment, otherwise we assign the bait to the 3′ end of the fragment. For 56 fragments, two baits are assigned to either the 5′ or 3′ end. Most of these cases can be attributed to particularly short fragments. Since this analysis was concerned with whether the 5′ or the 3′ end of fragments are predominantly enriched, we treated these fragments like those with a bait at only one end.

Results

Assignment of paired-end reads to chimeric fragments

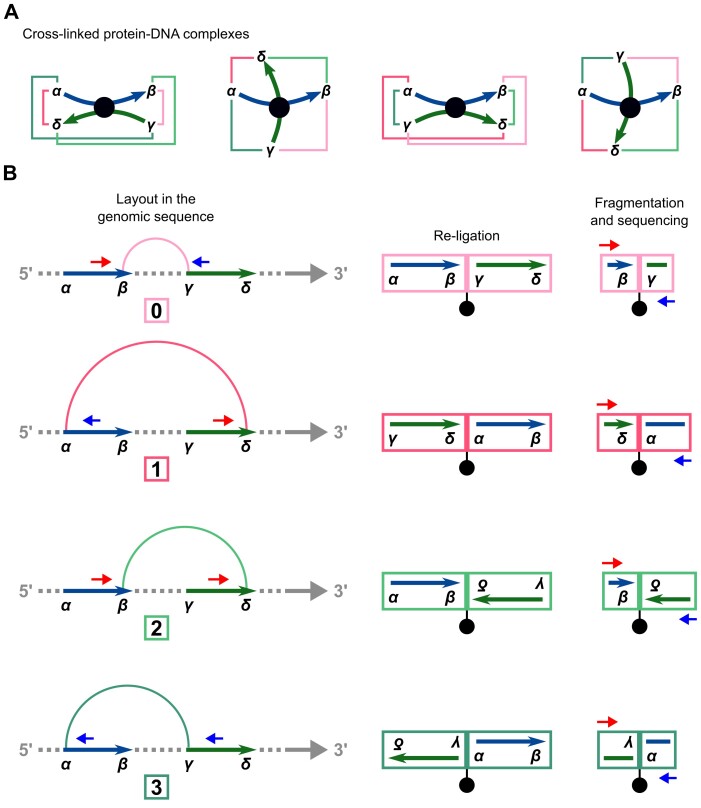
Cross-linking and restriction enzyme digestion results in protein–DNA complexes that are typically represented in a simplified way as two restriction fragments held together in the middle by a protein-mediated cross-link so that the ends of the fragments are in spatial proximity and can re-ligate with each other (Figure 1A). In most next-generation sequencing applications, paired-end sequencing yields mapped read pairs pointing inwards. However, due to restriction digestion and subsequent re-ligation, all four relative paired-end read orientations occur in Hi-C.

Figure 1.

Assignment of paired-end reads to chimeric fragment classes. (A) Simplified representations of four cross-linked protein–DNA complexes. Restriction fragments (curved arrows) are connected via protein-mediated cross-links (circles). The four possible re-ligations between the different restriction fragment ends (α, β, γ and δ) are shown as colored lines. Four different structures of complexes are indicated, with one of the two fragments being gradually rotated by 90°. (B) In this representation, the two restriction fragments from (A) are arranged sequentially on the genomic sequence and the four possible re-ligations are represented as arcs colored accordingly. To the right, the four corresponding biotinylated re-ligation products and chimeric fragments are shown. Chimeric fragments are sequenced from one side on the forward strand (small arrows pointing to the right) and from the other side on the reverse strand (small arrows pointing to the left). Mapping of paired-end reads to the reference sequence results in four different relative orientations of reads, each corresponding to one of the four chimeric fragment classes. See Supplementary Figure S1 for a more detailed schematic representation.

In our analysis, we focus on intrachromosomal interactions. For a given pair of restriction fragments, we label the ends of the upstream fragment α and β and those of the downstream fragment γ and δ. Any two of the four restriction fragment ends can potentially re-ligate, resulting in four classes of chimeric fragments, to each of which we assign a relative paired-end read orientation that implies information about which of the ends have been re-ligated (Figure 1B). In the first class (β-γ, which we will call ‘0’ for conciseness), the restriction fragment ends that face each other in the genomic sequence re-ligate. The resulting read pairs will thus point inwards. In the second class (α-δ, ‘1’), the fragment ends that face away from each other re-ligate. The resulting read pairs will thus point outwards. In the third and fourth case, the two ends that are either both on the 5′ or both on the 3′ terminus of the restriction fragments re-ligate. In contrast to the first two cases, the two DNA segments in the chimeric fragments have opposite orientations with respect to the genomic sequence. Therefore, only the reverse complement can be mapped for one or the other read. Thus, with the third class (β-δ, ‘2’) both reads map to the forward strand, and with the fourth class (α-γ, ‘3’), both reads map to the reverse strand.

We analyzed a large hematopoietic cell dataset (29) that includes sequencing data from Hi-C experiments for 8 cell types and CHi-C experiments for 17 cell types, with between 2 and 4 biological replicates for each cell type (Supplementary Table S2). The CHi-C experiments were performed with a bait set targeting the ends of >20 000 HindIII fragments containing a total of >30 000 annotated promoters. In previous work, we developed Diachromatic, a tool that can be used for initial processing and quality control of Hi-C and CHi-C data (15). We extended the output of Diachromatic so that for an interaction not just a single read pair count is reported, but four counts, one for each class of chimeric fragment. We applied Diachromatic to each biological replicate. We then pooled the biological replicates for each cell type by discarding interactions that occur for only one replicate and adding up the read pair counts of overlapping interactions separately by class (‘Materials and methods’ section). Overall, the read pairs are roughly evenly distributed across the four paired-end read orientations (Supplementary Table S3), but within individual interactions we often observe strong imbalances in the four counts.

Unbalanced interactions

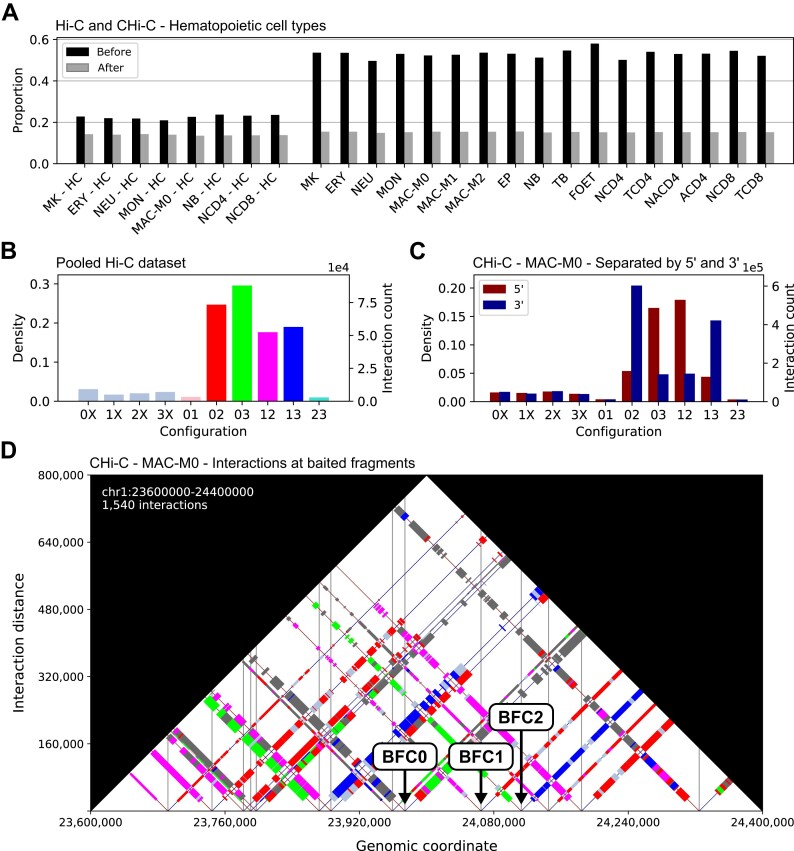
To determine whether interactions with unbalanced counts occur more often than expected by chance, we developed a randomization procedure (‘Materials and methods’ section). In each iteration, we randomize the four counts of each interaction according to a uniform distribution and then reclassify the randomized interactions as balanced or unbalanced. We applied our procedure with a classification threshold of 0.05 to the hematopoietic cell dataset, performing 1000 iterations for each replicate (Supplementary Table S4). In none of the permuted datasets did we observe a higher number of unbalanced interactions as compared to the original dataset. The numbers of classifiable interactions are much lower for Hi-C than for CHi-C. Among the classifiable interactions, the proportion of unbalanced interactions is substantially higher in the original datasets than in the corresponding permuted datasets, for both Hi-C and CHi-C (Figure 2A). However, the proportion of unbalanced interactions observed before randomization is much lower for Hi-C, indicating that the target enrichment step in CHi-C introduces additional unbalanced interactions.

Figure 2.

Unbalanced interactions and their configurations. (A) Proportions of unbalanced interactions before and after randomization for Hi-C experiments on eight and CHi-C experiments on 17 hematopoietic cell types. For this plot, we used a threshold of 0.05 to classify interactions as unbalanced or balanced. (B) Distribution of unbalanced interactions selcted at an FDR threshold of 5% across the 10 configurations for the Hi-C dataset for which we pooled interactions across eight hematopoietic cell types and (C) the CHi-C dataset for the cell type MAC-M0. For CHi-C, we additionally distinguished interactions based on whether they go from a baited fragment toward 5′ or 3′. (D) Visualization of configurations of interactions at baited fragments in a selected region on chromosome 1 for cell type MAC-M0. Balanced interactions are represented by gray rectangles and the rectangles for unbalanced interactions are colored according to their configuration. Vertical lines are drawn at the center positions of baited fragments. We identified two classes of baited fragments that can be distinguished based on their configuration patterns. For one class (BFC1) configurations 03 (green) and 13 (blue) predominate and for the other class (BFC2) configurations 12 (magenta) and 02 (red) predominate. We assign baited fragments that do not exhibit either pattern to class BFC0.

To select unbalanced interactions at an FDR threshold of 5%, we first use our randomization procedure to estimate the FDR for a range of classification thresholds. We then use the largest threshold for which the estimated FDR is still below 5% (‘Materials and methods’ section and Supplementary Figure S2). For CHi-C, between 1 995 781 and 3 394 515 unbalanced interactions are selected for the different cell types. In contrast, only between 5 and 1021 unbalanced interactions are selected for Hi-C, with <500 in five cases (Supplementary Table S5). We attribute this primarily to the much lower sequencing depth that is typically achieved for Hi-C. Therefore, we pooled the interactions across the eight hematopoietic cell types for which Hi-C experiments were performed (‘Materials and methods’ section). For the pooled Hi-C dataset, 297 282 unbalanced interactions are selected at an FDR threshold of 5%.

Configurations of unbalanced interactions

We noticed that among the unbalanced interactions there are many where the counts for two of the four paired-end read orientations are particularly high, while the other two are low. For a systematic investigation, we defined ten configurations of unbalanced interactions that differ in which two counts are the highest (‘Materials and methods’ section and Table 2). For the unbalanced interactions selected at an FDR threshold of 5%, we determined the distribution of interactions across the ten configurations. For both Hi-C (Figure 2B) and CHi-C, most interactions have the configurations 02, 03, 12 and 13. For CHi-C data, we additionally distinguished interactions based on whether they go from a baited restriction fragment towards 5′ or 3′ (Figure 2C). Interactions with configurations 03 and 12 predominantly go from baited fragments towards 5′, whereas interactions with configurations 02 and 13 predominantly go towards 3′.

To investigate how interactions with different configurations are distributed at individual baited restriction fragments, we visualize interactions, similar as in triangle heatmaps typically used for Hi-C data, as rectangles along the genomic axis, where the edge lengths correspond to the lengths of the two associated fragments and colors to the configuration (‘Materials and methods’ section). For the CHi-C data, we visualized interactions for various cell types in a number of genomic regions and discovered two ubiquitous configuration patterns at baited fragments (Figure 2D), which are consistent with the observations made when we integrated configurations of interactions genome-wide across all interactions (Figure 2C). In one pattern, the configurations 03 (green) and 13 (blue) predominate, whereas in the other pattern, the configurations 12 (magenta) and 02 (red) predominate.

Baited fragment classes

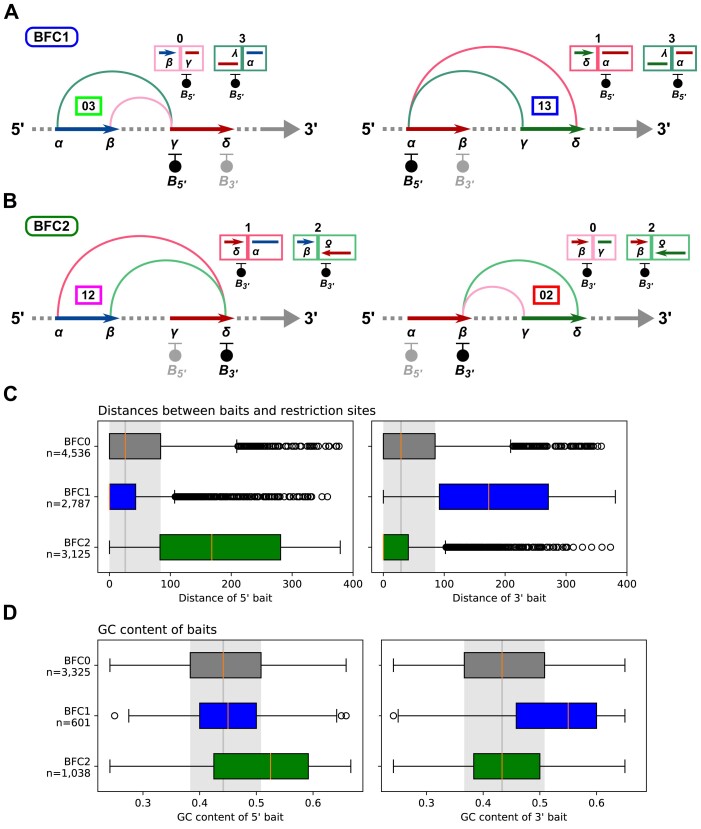
According to our assignment of paired-end read orientations to chimeric fragment classes (Figure 1B), the two configuration patterns differ in which end of a baited fragment occurs more frequently in the sequenced chimeric fragments. For the pattern with configurations 03 and 13 it is the 5′ end (Figure 3A), while for the pattern with configurations 12 and 02 it is the 3′ end (Figure 3B). Chimeric fragments of class 2 can only result from re-ligations between two 5′ ends of restriction fragments, while chimeric fragments of class 3 can only result from re-ligations between two 3′ ends of fragments. Therefore, to systematically divide the baited fragments into classes, we first determine the counts of the four chimeric fragment classes across all interactions at each given baited fragment and then assign a baited fragment to class BFC1 if the count for chimeric fragments of class 3 is twice as high as that for class 2. Conversely, if the count for chimeric fragments of class 3 is twice as high as that for class 2, we assign a baited fragment to class BFC2. Finally, we assign all remaining baited fragments to class BFC0 (‘Materials and methods’ section).

Figure 3.

Baited fragment classes and bait analysis. We have expanded our illustrations of re-ligations between restriction fragment ends and resulting chimeric fragments (Figure 1B) and arranged them according to the two observed configuration patterns (Figure 2D). The baits are drawn at the outermost ends of the restriction fragments ( and ). For each configuration, the corresponding chimeric fragments are shown along with the associated bait. (A) For BFC1, chimeric fragments associated with the 5′ end of the baited fragment predominate. (B) In contrast, for BFC2, chimeric fragments associated with the 3′ end of the baited fragment predominate. (C) Distributions of the distances between baits and the 5′ and 3′ ends of bilaterally baited BFC0, BFC1 and BFC2 fragments with shifted baits for the MAC-M0 CHi-C dataset. (D) Distributions of GC content (‘Materials and methods’ section) of baits at the 5′ and 3′ ends of BFC0, BFC1 and BFC2 fragments with unshifted baits for the CHi-C dataset for the same dataset.

On average, approximately two-thirds of the baited restriction fragments are classified as either BFC1 or BFC2 (Supplementary Table S6). We also determined the proportion of pairwise overlap for each of the 17 hematopoietic cell types and each of the three baited fragment classes. The division into the three classes is very similar for all cell types. In particular, in no case there was an overlap between BFC1 and BFC2 fragments (Supplementary Figure S5).

Bait analysis

We hypothesized that, in CHi-C, many unbalanced interactions result from uneven enrichment of the 5′ and 3′ ends of given baited fragments and therefore investigated the underlying baits (‘Materials and methods’ section). Generally, baits for CHi-C experiments should be designed such that there is one bait located at each end of a restriction fragment to be enriched. However, due to certain selection criteria for baits, such as GC content or mappability, for some fragments a bait can only be selected at one end. In addition, the target sequences of the baits should ideally be right next to the restriction sites of the fragments to be enriched. However, in some cases, in order to meet selection criteria, baits are shifted towards the restriction fragment center, causing a decrease in the efficiency of baits (Supplementary Figure S6). For the selection of the baits that we analyze here, a particularly strict selection criterion with regard to mappability was applied and a relatively large distance between baits and their restriction sites was tolerated (Table 4). We consider the selection criterion with the two consecutive Ns to be particularly strict because it ultimately results in baits having a maximum of only four Ns. In the entire genome, there are only very few N-periods <3 (between 22 and 64 for the different genome builds), which is why it is very unlikely that one or more N-periods are completely contained in a bait sequence (Supplementary Table S7). Therefore, generally only the edges of baits may overlap with N-periods by a maximum of two bases at each end. With a bait length of 120 nucleotides, this results in a maximum permitted N content of only 3.33%. With the criterion with the three consecutive bases masked by RepeatMasker, it is similar. There is no masked region <4 in the entire genome. A bait can therefore only overlap at the edges with a repeat-masked region, and the overlap at each end must not exceed three bases. With a bait length of 120 nucleotides, this results in a maximum allowed repeat content of only 5%. We would like to point out that we do not consider these criteria regarding mappability to be strict in the sense that the resulting baits will hybridize exclusively to their target fragments, which would be the ideal case, but in the sense that many baits have to be moved or even discarded to meet the criteria.

Table 4.

Bait selection criteria. Bait selection criteria for CHi-C experiments in human primary hematopoietic cells (29) and mouse embryonic stem cells (6)

	Human primary blood cells	Mouse embryonic stem cells
Max. dist.	330 bp	500 bp
GC content	25–65%	25–65%
Mappability	No more than 2 consecutive Ns	No more than 3 consecutive bases masked by RepeatMasker

For this analysis, we matched the baits to their target restriction fragments and divided these into three subsets: (I) Unilaterally baited fragments that have a bait at only one end, (II) bilaterally baited fragments that have baits at both ends with at least one bait shifted towards the fragment center, and (III) bilaterally baited fragments that have baits at both ends with neither of the baits shifted. For each of these subsets, we determined the distribution of fragments across BFC0, BFC1, and BFC2 (Table 5A). In the following, we report the results for the cell type MAC-M0. We obtain very similar results for the other cell types, as the baited fragment classifications differ only slightly among the 17 cell types (Supplementary Figure S5).

Table 5.

Bait analysis. (A) We divided baited fragments into three subsets: (I) Unilaterally baited fragments, (II) bilaterally baited fragments, where at least one bait is shifted towards the fragment center and (III) bilaterally baited fragments, where neither of the two baits is shifted. (B) To compare unilaterally to bilaterally baited fragments, we combined the counts for BFC1 and BFC2 fragments and the counts for fragments with shifted (II) and unshifted (III) baits. (C) For the unilaterally baited fragments, we determined the numbers of 5′ and 3′ baits. (D) To compare bilaterally baited fragments with shifted baits to those where neither bait is shifted, we combined the counts for fragments of BFC1 and BFC2

A: Uni- and bilaterally baited fragments with and without shifted baits
	BFC0		BFC1		BFC2		Total
I.	72	(1%)	3102	(48%)	3214	(44%)	6388	(29%)
II.	4536	(57%)	2787	(43%)	3125	(42%)	10 448	(48%)
III.	3325	(42%)	601	(9%)	1038	(14%)	4964	(23%)
Total	7933		6490		7377		21 800
B: Unilaterally vs. bilaterally baited fragments
	BFC0		BFC12				Total
I.	72	(1%)	6316	(46%)			6388	(29%)
II,III.	7861	(99%)	7551	(54%)			15 412	(71%)
Total	7933		13 867				21 800
C: Unilateral separated by 5′ and 3′
	5′ bait		3′ bait				Total
BFC0	36		36				72
BFC1	3091		11				3102
BFC2	12		3202				3214
Total	3139		3249				6388
D: Bilaterally baited fragments: shifted vs. unshifted
	BFC0		BFC12				Total
II.	4536	(58%)	5912	(78%)			10 448	(68%)
III.	3325	(42%)	1639	(22%)			4964	(32%)
Total	7861		7551				15 412

I. Unilaterally baited fragments

Overall, 29% of the baited fragments have a bait either only at the 5′ or at the 3′ end. Among the fragments of BFC0, this proportion is only 1%, whereas it is 46% for BFC1 and BFC2 (Table 5B; Fisher’s exact test; Prior odds ratio: 0.01; P ∼ 0). In addition, we distinguished unilaterally baited fragments depending on whether the bait is at the 5′ or 3′ end (Table 5C). For BFC0, the ratio of 5′ and 3′ baits is balanced. In contrast, fragments of BFC1 have almost exclusively 5′ baits, whereas fragments of BFC2 have almost exclusively 3′ baits. This result is consistent with our assignment of paired-end read orientations to chimeric fragment classes, according to which, for BFC1, chimeric fragments with the target sequence of the 5′ bait are more enriched (Figure 3A), whereas, for BFC2, chimeric fragments with the target sequence of the 3′ bait are more enriched (Figure 3B).

II. Bilaterally baited fragments with shifted baits

Among all baited fragments, the proportion of bilaterally baited fragments with at least one bait shifted towards the fragment center is 48% (Table 5A). Among the bilaterally baited fragments, this proportion is 68% (Table 5D). For the fragments of BFC0, it is 58%, whereas it is 78% for the fragments of BFC1 and BFC2 (Fisher’s exact test; Prior odds ratio: 0.38; P = 3.55 × 10⁻¹⁶⁷).

We also determined the distributions of the distances between baits and their restriction sites (Figure 3C). For the fragments of BFC0, the distance distributions for 5′ and 3′ baits differ only slightly (two-sided Wilcoxon signed-rank test; Rank sum: 5037633, P = 0.28). In contrast, for the fragments of BFC1, the distances for the 3′ baits are much larger than those for the 5′ baits (Rank sum: 142097, P ∼ 0). With the fragments of BFC2 it is the exact opposite. Here, the distances for the 5′ baits are much larger than those for the 3′ baits (Rank sum: 214 695, P ∼ 0). Since the efficiency of baits decreases with increasing distance from their restriction site, this result is also consistent with our assignment of paired-end read orientations to chimeric fragment classes.

III. Bilaterally baited fragments with unshifted baits

Overall, 23% of the baited fragments have unshifted baits at both ends (Table 5A). For these fragments, we determined the GC content of the baits (Figure 3D). For BFC0, the GC content distributions of the 5′ and 3′ baits do not differ significantly (two-sided Wilcoxon signed-rank test; Rank sum: 2 505 742, P = 0.10). In contrast, the 3′ baits of BFC1 fragments often have a higher GC content than the 5′ baits (Rank sum: 34 127, P = 1.82 × 10⁻³⁶). With the BFC2 fragments it is again the exact opposite. Here, the 5′ baits often have a higher GC content than the 3′ baits (Rank sum: 106 299, P = 6.01 × 10⁻⁵⁹). We also determined the repeat content of the baits (Supplementary Figure S7). More than 70% of the baits have zero repeat content, with the 3′ baits of BFC1 and the 5′ baits of BFC2 fragments having slightly higher repeat content on average, but at a low level.

Unbaited fragment analysis

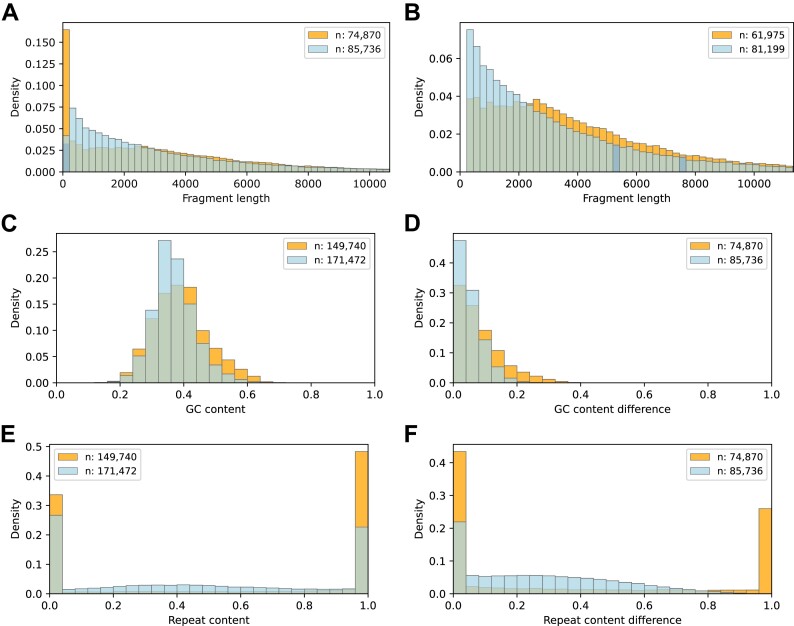
Up to this point, we limited our analysis to baited fragments and their baits. We also analyzed restriction fragments that are involved in interactions but not baited. A given restriction fragment can be involved in both balanced and unbalanced interactions. Therefore, we derived two disjoint sets of unbaited fragments, each containing fragments involved exclusively in either balanced or unbalanced interactions. For the MAC-M0 dataset, this yields 85 736 fragments from balanced interactions and 74 870 fragments from unbalanced interactions.

First, we compared the lengths of the fragments involved exclusively in either balanced or unbalanced interactions (Figure 4A). Although there are many particularly short fragments among the fragments from unbalanced interactions, these fragments are overall significantly longer than those from balanced interactions (Median (Mdn.) 2693 versus Mdn. 2296; Mann–Whitney U test; U: 3 244 871 871, P = 1.37 × 10⁻⁴). We removed fragments <250 bp from the two comparison sets (Figure 4B). After removal, it can be seen that fragments from balanced interactions predominate up to a fragment length of ∼2400 bp, and fragments from unbalanced interactions predominate for larger fragment lengths (Mdn. 3376 versus Mdn. 2474; U: 2 945 426 987, P ∼ 0).

Figure 4.

Unbaited fragment analysis. For the MAC-M0 CHi-C dataset, we selected two sets of unbaited fragments involved in either only balanced (light blue) or only unbalanced interactions (orange) and compared them with respect to length, GC and repeat content. (A) Fragment length distributions. (B) Fragment length distributions after removal of fragments <250 bp. (C) GC content distributions of fragment ends (120 bases from each end). (D) Distributions of the absolute differences in GC content of the two ends of given fragments. (E) Repeat content distributions of fragment ends. (F) Distributions of the absolute differences in repeat content of the two ends of given fragments.

Next, we compared the GC content of the fragment ends (120 bp from each end). For the fragments from unbalanced interactions, there is a slight but significant shift towards higher GC content (Figure 4C; Mdn. 0.38 versus Mdn. 0.36; U: 14 660 548 503; P ∼ 0). We also compared the absolute differences in GC content at the two ends of given fragments (Figure 4D). For the fragments from the unbalanced interactions, the GC content of the two ends differs significantly more than for the fragments from balanced interactions (Mdn. 0.07 versus Mdn. 0.04; U: 3 963 866 825; P ∼ 0).

Finally, we performed an analogous analysis for the repeat content of fragment ends. Fragments from unbalanced interactions have a significantly higher repeat content than those from balanced interactions (Mdn. 0.91 versus Mdn. 0.43; U: 14 836 969 699, P ∼ 0). Among both fragments from balanced and fragments from unbalanced interactions, most fragment ends have a repeat content of either 0 or 1. Among the fragments from unbalanced interactions, there are significantly more fragment ends with a repeat content of 1 (Figure 4E). Looking at the absolute difference in repeat content between the two ends of each fragment, fragments from unbalanced interactions with differences of 0 or 1 predominate. There is no fragment from a balanced interaction with an absolute difference of 1 (Figure 4F).

While the differences between balanced and unbalanced interacting restriction fragments are very pronounced in terms of length and repeat content, we observe much smaller but still statistically significant shifts in terms of GC content. We performed the same analysis for the Hi-C dataset, for which we pooled interactions across eight hematopoietic cell types, and made comparable observations regarding restriction fragment lengths as well as GC and repeat content of fragment ends (Supplementary Figure S8).

Impact of technical biases reflected in count imbalances

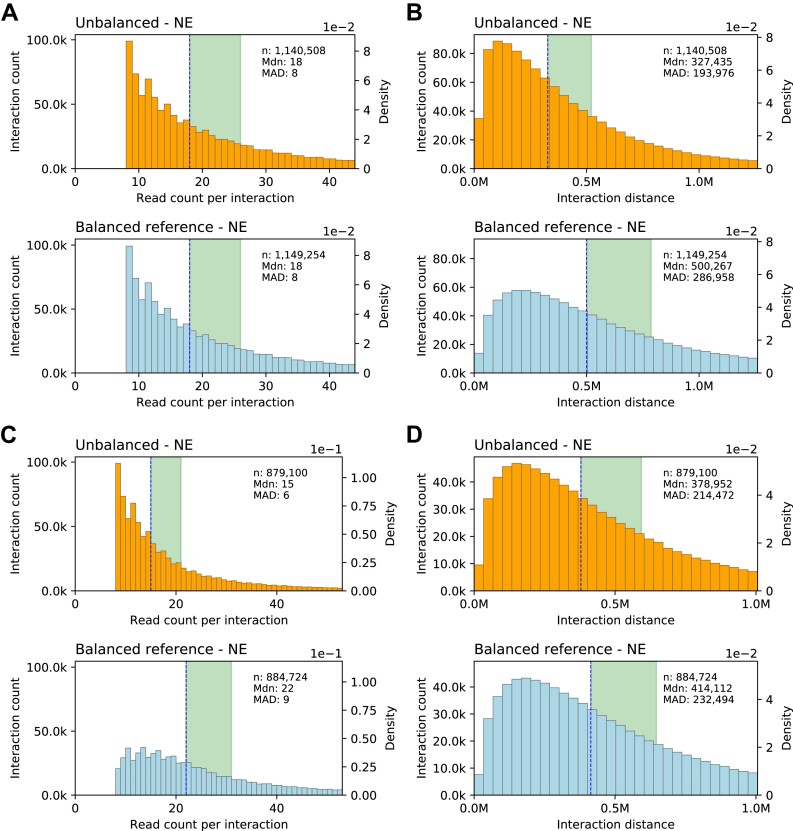
The read pair counts of interactions represent observed contact frequencies that are affected by technical biases of various kinds. The imbalances in the four read pair counts of interactions reflect biases arising from bait effects, varying restriction fragment lengths as well as differing GC content and mappability of the restriction fragment ends. On the other hand, there is a strong dependency between the interaction distance and the frequency of random contacts, with the frequencies being greatest at short distances and decreasing as the distance increases. We did not correct the data for distance-dependent contact frequencies but took advantage of this relationship to assess the impact of technical biases reflected in the imbalances of the four read pair counts of interactions. For each unbalanced interaction, we tried to find a balanced counterpart interaction with an identical total read pair count and, if successful, we added the interactions to two comparison sets, one for unbalanced and one for balanced interactions (‘Materials and methods’ section). For these sets, we then compared the distributions of the interaction distance.

For the unbalanced CHi-C interactions selected at an FDR threshold of 5%, this procedure yields two sufficiently large and equally sized comparison sets of unbalanced and balanced interactions that have nearly identical distributions of total read pair counts per interaction (Figure 5A). Given these nearly identical distributions and the strong dependency between interaction distances and contact frequencies, it would be expected that the distributions of distances for balanced and unbalanced interactions differ only slightly. However, compared to the balanced interactions, the distances of the unbalanced interactions are clearly shifted towards shorter distances (Figure 5B). This suggests that the contact frequencies of unbalanced interactions, as measured by their total read pair counts, are systematically underestimated, and that the imbalances in the four read pair counts of interactions reflect a substantial proportion of technical bias in CHi-C data.

Figure 5.

Impact of technical biases reflected in count imbalances. Distributions of read pair counts and interaction distances for CHi-C data derived from MAC-M0 cells. (A) Distribution of read pair counts per interaction for unbalanced and balanced reference interactions. (B) Corresponding distributions of interaction distances. (C) Distribution of read pair counts per interaction for unbalanced interactions and balanced reference interactions selected based on identical maximum read pair counts per interaction. (D) Corresponding distributions of interaction distances. This figure only shows the data for other-baited (NE) interactions. We make comparable observations for baited-other (EN) interactions (Supplementary Figure S9).

According to our assignment of paired-end read orientations (Figure 1B), the four read pair counts of an interaction represent the observed frequencies of the four possible re-ligations between the two associated restriction fragments. Each of the four counts reflects the same contact frequency, but is affected to varying degrees by various kinds of technical bias, resulting in unbalanced counts. We reasoned that the maximum of the four counts might be a more robust measure of contact frequencies than the total of the four counts.

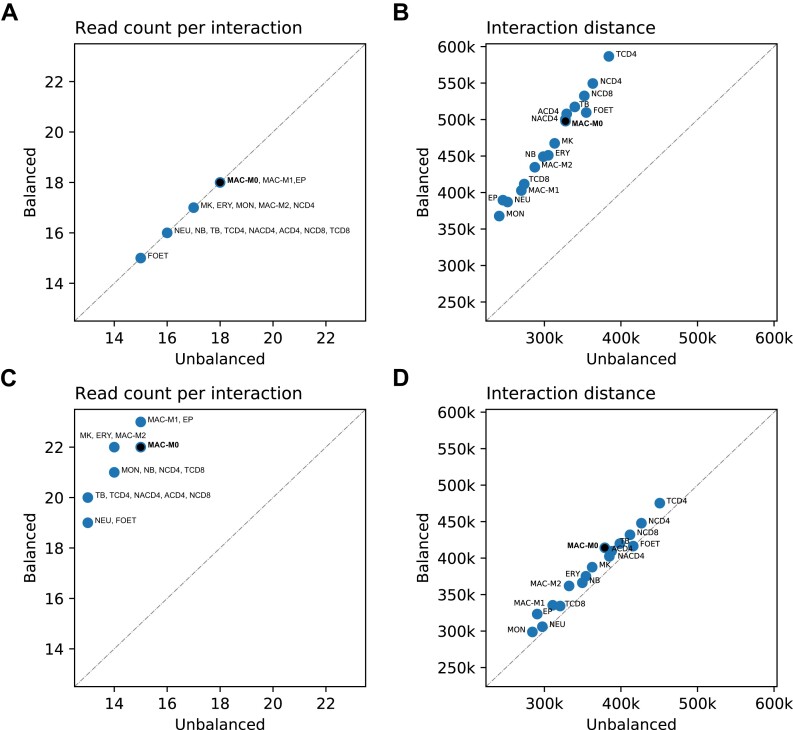
To verify our reasoning, we implemented an alternative procedure for the selection of two comparison sets in which we no longer choose balanced counterpart interactions with an identical total read pair count, but those with an identical maximum of the four counts. Using this selection procedure, the read pair counts of the balanced interactions, compared to those of the unbalanced interactions, are shifted towards higher counts (Figure 5C). This is to be expected since balanced interactions are characterized by the fact that the four counts differ only slightly; hence, the total number of counts is close to four times the maximum count, which is not the case for unbalanced interactions. Based solely on distance-dependent contact frequencies, it would be expected that the distances of the balanced interactions are shifted towards much shorter distances due to the higher total read pair counts per interaction. However, we observe that the distance distributions of balanced and unbalanced interactions differ only slightly (Figure 5D), suggesting that the maximum of the four counts represents a more unbiased measure of contact frequencies than the total of the four counts. We make comparable observations for all 17 cell types (Figure 6 and Supplementary Tables S8 and S9).

Figure 6.

Median total read pair counts and distances of interactions for 17 hematopoietic cell types. Median read pair counts per interaction and the median interaction distances for the 17 hematopoietic cell types. For the cell type MAC-M0, the medians correspond to those shown in Figure 5 at the top right of each histogram. (A) Median read pair counts per interaction for the two comparison sets of balanced and unbalanced interactions selected based on identical total read pair counts per interaction. (B) Corresponding median interaction distances. (C) Median read pair counts per interaction for the two comparison sets of balanced and unbalanced interactions selected based on identical maximum read pair counts. (D) Corresponding median interaction distances.

We also performed the analysis with the distance-dependent contact frequencies for the Hi-C dataset, for which we pooled interactions across eight hematopoietic cell types, and made observations comparable to those we made for the CHi-C datasets (Supplementary Figure S10).

Interaction calling using total or maximum counts

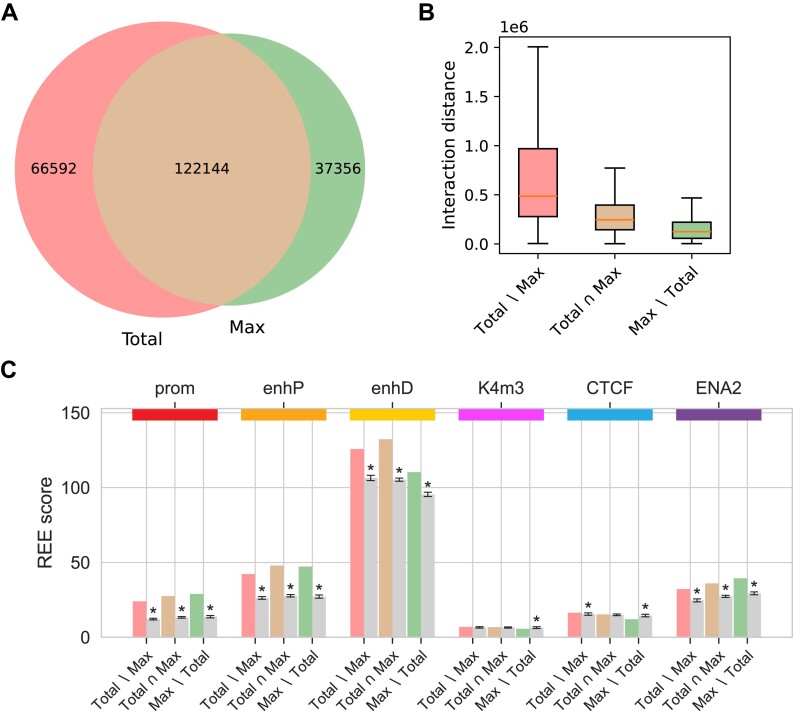
Each of the four read pair counts of an interaction reflects the same contact frequency, and their total is generally used to measure it. To explore the impact of imbalanced read pair counts on interaction calling, we prepared two CHiCAGO input datasets for the MAC-M0 cell type, which differ only in whether the total or only the maximum of the four read pair counts of interactions is taken into account (‘Materials and methods’ section). We then applied CHiCAGO with default settings and a score threshold of 5 to both datasets and compared the results. Most interactions are above the threshold for both maximum and total read pair counts, but there are also interactions that exceed the threshold only when using the total count, while others exceed the threshold only when using the maximum count (Figure 7A). Interactions identified only when using the maximum read pair count are much shorter than interactions identified when using the total count (Figure 7B). All subsets of the union of interactions identified using either the total or maximum counts (Total∖Max, Total∩Max, Max∖Total) are significantly enriched for ENCODE’s cCRE categories promoter, proximal enhancer, distal enhancer and enhancers from the Enhancer Atlas 2.0. Regulatory elements of the K4m3 and CTCF categories are not or only slightly enriched in most cases and even depleted in interactions that are only identified using the maximum counts (Figure 7C). The results for the promoter category are most likely biased because in the underlying experiment all promoters were targeted, which is why promoter–promoter interactions are enriched at both ends. Therefore, we performed the same analysis but without bait-to-bait interactions (Supplementary Figure S11). In this case, the promoter category is depleted in all interaction subsets, as expected. The proximal enhancer category is only slightly enriched across all interaction subsets, which is also to be expected because such elements by definition cannot be located further than 2000 bp from a transcription start site. However, distal enhancers and enhancers from the enhancer atlas are still significantly enriched.

Figure 7.

) Venn diagram of identified interactions. ( Interactions for the MAC-M0 cell type identified using CHiCAGO with default parameters and a score threshold of 5, based either on total or maximum counts. (A) Venn diagram of identified interactions. (B) Distances of interactions identified based on total counts only, both total and maximum counts, and maximum counts only. (C) Enrichment of interaction other-ends for ENCODE’s Candidate Cis-Regulatory Elements promoters (prom), proximal enhancers (enhP), distal enhancers (enhD), DNase-H3K4me3 (K4m3) and CTCF sites, as well as for enhancers from the Enhancer Atlas 2.0 (ENA2). The REE scores represent the number of other-ends of a given interaction subset that contain at least one regulatory element of a given category, normalized to the total length of all other-ends. The gray bars correspond to the mean REE score obtained after randomization of the other-ends (‘Materials and methods’ section). REE scores that are three standard deviations above or below the mean are considered significant and marked with an asterisk. The unnormalized values from the randomization procedure used to calculate the REE scores are shown in Supplementary Table S10.

Representativeness of the analyzed datasets

In this manuscript and the associated repository, we analyze datasets from the earliest publications on promoter capture Hi-C, for each of which the enzyme HindIII was used. Two of these publications are pioneering works (6,7) that should be cited whenever this protocol is reused, even when a different enzyme is used. We identified all publications that cited at least one of these two publications. From these, we retained only those whose abstract included the term ‘capture Hi-C’ because we assumed that such publications were more likely to have generated data. This left us with 64 publications, which we then reviewed manually (Supplementary Table S11). We found 28 publications for which CHi-C data were generated. In 21 of these, the enzyme HindIII was used, in five MboI, in one BglIII and in one both HindIII and MboI (not as a combination). The publications using HindIII were cited a total of 1297 times, while all others were cited only 168 times. Many of the subsequent publications replicated the CHi-C protocol from the pioneering publications either one-to-one or with minor modifications. In many cases, also the baits were selected according to identical criteria or taken one-to-one from the pioneer publications. In this way, terabytes of data were generated that very likely exhibit all the characteristics that we describe in our manuscript. Although this literature research is heuristic and incomplete, we believe it demonstrates that the datasets analyzed here are representative of a large proportion of available CHi-C data.

Discussion

To our knowledge, the different relative orientations of mapped paired-end reads previously have been used only to remove artifact read pairs resulting from un- or self-ligated restriction fragments (14,15). Here, we investigated the relative orientations of the valid chimeric read pairs. Depending on which ends of a given pair of restriction fragments re-ligate, a chimeric fragment is formed which belongs in one of four classes, to each of which we have assigned one of the four relative orientations of mapped paired-end reads (Figure 1B).

We have extended our tool Diachromatic described in a previous publication (15) to report the four read pair counts of each interaction separately by orientation and applied it to a large hematopoietic cell dataset. Overall, the different read pair orientations occur with roughly the same frequency, but for individual interactions we often observed strong imbalances. We named such interactions unbalanced and developed a framework to select them at a chosen FDR threshold and to analyze them with respect to various known sources of technical bias. For both Hi-C and CHi-C, unbalanced interactions occur much more often than expected by chance. However, at a given classification threshold of 0.05, there are far more classifiable interactions for CHi-C than for Hi-C. In part, we attribute this to the much lower sequencing depth typically achieved with Hi-C (Supplementary Table S2). Therefore, we pooled interactions across eight hematopoietic cell types for which Hi-C data are available. With an FDR threshold of 5%, only a few interactions are classified as unbalanced for the individual cell types, whereas there are >200 times as many unbalanced interactions for the pooled dataset. This suggests that unbalanced interactions in Hi-C arise from systematic effects that occur independently of the cell type. For CHi-C, many more interactions are classified as unbalanced than for Hi-C. Furthermore, the proportion of unbalanced interactions among the classifiable interactions is also much larger for CHi-C, suggesting that the target enrichment step introduces additional unbalanced interactions.

For CHi-C, we used the additional information from the four read pair counts of interactions to identify target restriction fragments that are predominantly enriched at only one of the two ends. By matching such fragments to the baits actually used for the experiments, we confirmed our assignment of paired-end read orientations to the possible re-ligations between two given restriction fragments (Table 1C) and gained insights that can inform bait design. The strict selection criterion regarding mappability with the two consecutive Ns used for the experiments analyzed here (Table 5), presumably results in many baits being shifted towards the center of the target fragments as well as baits that have been discarded, and thus in many unilaterally enriched target restriction fragments. Baits located too far from their restriction site are not effective because in such cases the target sequences in the re-ligation products are disrupted by random fragmentation and are therefore either only partially present or absent in the chimeric fragments to be enriched. The results on the GC contents of baits (Figure 4B) most likely reflect known sequencing and coverage biases (34,35). We included the results on repeat content for completeness. However, the repeat content of the vast majority of baits is zero, which is why no insights could be gained in this regard. We also analyzed additional data from CHi-C experiments in mice, each of which was performed with a bait set that targeted the ends of HindIII fragments containing promoters of 22 225 genes (6,36). We made observations comparable to those we made with the hematopoietic cell data (Supplementary Figures S12–S16 and Supplementary Tables S12–S14). The bait selection criteria used are very similar in both cases (Table 4). A strict selection criterion regarding mappability is applied and the maximum tolerated distance between baits and restriction sites is relatively large. When designing baits for CHi-C experiments, compromises have to be made. Regardless of which restriction enzyme is used, it is impossible to select baits for each desired target region that meet the criteria, which aim at high capture efficiency while avoiding off-target pull-downs (Supplementary Table S15). A less stringent selection criterion regarding mappability might reduce the number of unilaterally baited fragments or fragments with shifted baits, but on the other hand, the average quality of the baits could become worse. The analysis approach and software presented here can be used to characterize technical biases resulting from bait design, which can contribute to more informed decisions in bait selection.

Our analysis of unbaited fragments suggests that in addition to the bait effects, known technical biases that already arise from the Hi-C assay are reflected in read pair count imbalances of interactions. We focused on unbaited fragments that are involved in either balanced interactions or unbalanced interactions but not both. Many of the fragments from unbalanced interactions are very short (<250 bp). One possible explanation is that with such short fragments, cross-link mediating proteins might more frequently occupy one of the restriction sites, which could interfere with restriction digestion or re-ligation. Despite the fact that unbalanced interactions have more very short fragments, the fragments from unbalanced interactions are on average longer than those from balanced interactions. Fragments from balanced interactions predominate up to the length of 2400 bp, while fragments from unbalanced interactions predominate at longer lengths. This observation is in line with previous analyses indicating that longer restriction fragments might be more prone to random re-ligations (16). For a given pair of restriction fragments, each random re-ligation means one less observed contact, which can result in unbalanced interactions. Here, we analyzed a number of datasets from Hi-C and CHi-C experiments using the 6-cutter restriction enzyme HindIII, which generates in restriction fragments with an average length of ∼4 kb. Using 4-cutter enzymes such as DpnII results in shorter restriction fragments that might be less affected by this bias. However, further analyses are required to clarify to what extent the findings of this work can be transferred to 4-cutter enzymes. The distribution of GC content in fragment ends from unbalanced interactions is only slightly shifted towards higher values. However, this shift is highly significant, showing that biases arising from GC content are also reflected in read pair count imbalances of interactions. Looking at the repeat content of fragment ends, the differences between the two fragment sets are more pronounced. Compared to the fragments from balanced interactions, there are significantly more fragments from unbalanced interactions whose ends have a repeat content of 1. The difference is even more pronounced when considering the absolute differences in repeat content at the two ends of each fragment. There are no fragments from balanced interactions for which the absolute difference in repeat content of the two ends is close to 1. These results suggest that unmappable fragment ends contribute substantially to the technical bias in Hi-C and CHi-C data. However, further analysis is needed to better understand the relative weight of the contributions from the various sources of technical bias. We make comparable observations for the pooled Hi-C dataset in terms of fragment lengths, GC and repeat content (Supplementary Figure S8). This provides further evidence that the imbalances in the four read pair counts of interactions reflect not only technical biases arising from bait effects, but also those inherent in the Hi-C protocol.

To assess the impact of technical biases reflected in unbalanced read pair counts of interactions, we took advantage of the strong dependency between the distance and the frequency of interactions. We have demonstrated that unbalanced interactions are substantially shorter than balanced interactions. This suggests that the contact frequencies of unbalanced interactions, as measured by their total read pair counts, are systematically underestimated. We reasoned that the maximum of an interaction’s four read pair counts might be a more robust measure of its contact frequency than the total read pair count. Our considerations are based on the fact that the four read pair counts of an interaction represent the observed re-ligation frequencies, all reflecting the same contact frequency but being affected to different degrees by technical biases of various kinds. We verified our reasoning, again taking advantage of the distance-dependent contact frequencies, but using an alternative procedure to select the comparison sets of balanced and unbalanced interactions in which only the maximum of the four counts are taken into account. For two sufficiently large samples, the distribution of the total read pair counts per interaction for the balanced interactions is shifted towards the higher counts, as expected. However, the distance distributions of unbalanced and balanced interactions differ only slightly, suggesting that a large proportion of technical bias in CHi-C data can be eliminated by using only the maximum of the four counts.

Our approach can be used to assess technical biases reflected in imbalances in the observed re-ligation frequencies for given pairs of restriction fragments, i.e. interactions. However, it cannot be used to assess technical biases resulting from uneven enrichment of different target restriction fragments. Apart from that, it cannot be used to correct for distance-dependent contact frequencies. Existing methods such as CHiCAGO (20,22) or CHiCANE (23) model both technical bias and distance-dependent contact frequencies statistically. Technical bias is modeled as ‘visibility’ or ‘interactability’ of restriction fragments, which is estimated from the associated transchromosomal read pair counts. This approach is suitable to correct read pair counts of interactions for uneven enrichment of different target restriction fragments and thus implicitly also to correct for unilateral and bilateral enrichment of target restriction fragments. However, since transchromosomal read pairs largely result from random re-ligations, ‘interactability’ does not take into account the specific properties of given restriction fragment pairs. For example, long and short fragments may have different ligation efficiencies or compete differently on random re-ligations (16). The assignment of relative paired-end read orientations yields four counts of observed re-ligations for each interaction, the distribution of which reflects such properties and the resulting technical biases. Our approach can therefore be used to complement existing methods so that this additional information gained from the data is taken into account.

Although the total and maximum read pair counts of given interactions reflect the same contact frequency, CHiCAGO identifies different sets of interactions depending on which of the two counts is used (Figure 7). Interactions that are no longer identified when using only the maximum count are most likely due to reduced power because in this case three of the four counts are discarded. Interactions that are only identified using the maximum count are shorter than those identified using the total counts. Due to distance-dependent contact frequencies, shorter interactions are more difficult to detect and previous CHi-C analyses have primarily focused on long-range interactions. Nevertheless, it is widely accepted that short-range interactions can also have regulatory effects, such as in smaller-scale multi-connected enhancer-promoter hubs (37). Our ad hoc approach, using only the maximum counts as input for CHiCAGO, can identify short-range interactions enriched for enhancers from ENCODE’s cCREs and from the Enhancer Atlas 2.0 in addition to interactions that are identified using the standard approach with the totals of the four counts. However, further development is needed to make optimal use of all four counts.

Our literature research regarding representativeness suggests that a large proportion of available CHi-C datasets share the same characteristics as the HindIII datasets analyzed here. However, we point out that our results should not be extrapolated to datasets obtained with 4-cutter enzymes or enzyme cocktails, as we observed that the lengths of the restriction enzymes can have a significant impact on the distribution of the four read pair counts of interactions (Figure 4A and B).

Taken together, we have characterized a previously underutilized feature of Hi-C data and used it to assess technical biases arising from bait effects and shortcomings of the Hi-C assay. Our framework, software, and results have the potential to improve the design and interpretation of Hi-C and CHi-C experiments.

Data availability

The sequencing dataset on human primary hematopoietic cell types is available with data usage agreement at the EGA (EGAD00001002268). The datasets for the CHi-C experiments in mice are publicly available at the European Nucleotide archive (ERP008766 and ERP005386). The Diachromatic software is available under a GPL-3.0 license on GitHub (https://github.com/TheJacksonLaboratory/diachromatic) and on Zenodo (DOI: 10.5281/zenodo.10623971). The software developed for this work is available under an MIT license on GitHub (https://github.com/TheJacksonLaboratory/diachrscripts and on Zenodo (DOI: 10.5281/zenodo.10610460 and DOI: 10.5281/zenodo.13837266).

Supplementary data

Supplementary Data are available at NARGAB Online.

Funding

No external funding.

Conflict of interest statement. None declared.