Table 8. 1-(1H-Pyrrol-3-yl)ethanol Natural Internal Coordinates.

Description	Monomera	Unnormalized natural internal coordinateb
ring breathing	P	S1 = r(5,4) + r(1,5) + r(4,3) + r(2,1) + r(2,3)
ring stretching def.	P	S2 = r(5,4) + B r(1,5) + B r(4,3) + A r(2,1) + A r(2,3)
ring stretching def.	P	S3 = D r(1,5) – D r(4,3) + C r(2,1) – C r(2,3)
ring stretching def.	P	S4 = r(5,4) + A r(1,5) + A r(4,3) + B r(2,1) + B r(2,3)
ring stretching def.	P	S5 = C r(1,5) – C r(4,3) – D r(2,1) + D r(2,3)
C–C stretch	P ∩ E	S6 = r(5,6)
C–C stretch	E	S7 = r(6,7)
C–O stretch	E	S8 = r(6,8)
C–H stretch	P	S9 = r(1,9)
N–H stretch	P	S10 = r(2,10)
C–H stretch	P	S11 = r(3,11)
C–H stretch	P	S12 = r(4,12)
C–H stretch	E	S13 = r(6,15)
O–H stretch	E	S14 = r(8,17)
CH3 sym. stretch	E	S15 = r(7,13) + r(7,14) + r(7,16)
CH3 sym. stretch	E	S16 = 2r(7,13) – r(7,14) – r(7,16)
CH3 antisym. stretch	E	S17 = r(7,14) – r(7,16)
ring bending	P	S18 = θ(1,2,3) + A θ(2,1,5) + A θ(2,3,4) + B θ(1,5,4) + B θ(3,4,5)
ring shearing	P	S19 = (A – B) θ(2,1,5) – (A – B) θ(2,3,4) + (1 – A) θ(1,5,4) – (1 – A) θ(3,4,5)
C6–C5 P rock	P ∩ E	S20 = θ(6,5,4) – θ(6,5,1)
C7–C6–O bend	E	S21 = θ(8,6,7)
C5–C6 E wag	P ∩ E	S22 = θ(5,6,7) + θ(5,6,8)
C5–C6 E rock	P ∩ E	S23 = θ(5,6,7) – θ(5,6,8)
C–H rock	P	S24 = θ(9,1,2) – θ(9,1,5)
N–H rock	P	S25 = θ(10,2,3) – θ(10,2,1)
C–H rock	P	S26 = θ(11,3,4) – θ(11,3,2)
C–H rock	P	S27 = θ(12,4,5) – θ(12,4,3)
C–O–H bend	E	S28 = θ(17,8,6)
H–C–C rock	E	S29 = θ(15,6,7) + θ(15,6,8)
H–C–C wag	E	S30 = θ(15,6,7) – θ(15,6,8)
CH3 umbrella	E	S31 = θ(13,7,6) + θ(14,7,6) + θ(16,7,6) – θ(14,7,16) – θ(13,7,14) – θ(13,7,16)
CH3 rock	E	S32 = 2θ(13,7,6) – θ(14,7,6) – θ(16,7,6)
CH3 wag	E	S33 = θ(14,7,6) – θ(16,7,6)
CH3 scissor	E	S34 = 2θ(14,7,16) – θ(13,7,14) – θ(13,7,16)
CH3 def.	E	S35 = θ(13,7,14) – θ(13,7,16)
ring twisting	P	S36 = τ(1,5,4,3) + B τ(4,3,2,1) + B τ(3,2,1,5) + A τ(5,4,3,2) + A τ(2,1,5,4)
ring puckering	P	S37 = (1–A) τ(4,3,2,1) – (1–A) τ(3,2,1,5) – (B–A) τ(5,4,3,2) + (B–A) τ(2,1,5,4)
CH3 torsion	E	S38 = τ(13,7,6,8) + τ(14,7,6,8) + τ(16,7,6,8)
O–H torsion	E	S39 = τ(17,8,6,7)
P–E torsion	P ∩ E	S40 = τ(1,5,6,7) + τ(1,5,6,8) + τ(4,5,6,7) + τ(4,5,6,8)
C6–C5 P wag	P ∩ E	S41 = γ(6,5,1,4)
C–H wag	P	S42 = γ(9,1,2,5)
N–H wag	P	S43 = γ(10,2,3,1)
C–H wag	P	S44 = γ(11,3,4,2)
C–H wag	P	S45 = γ(12,4,5,3)

^a(P, E) = (pyrrole, ethanol).

^b(A, B, C, D) = 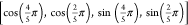.