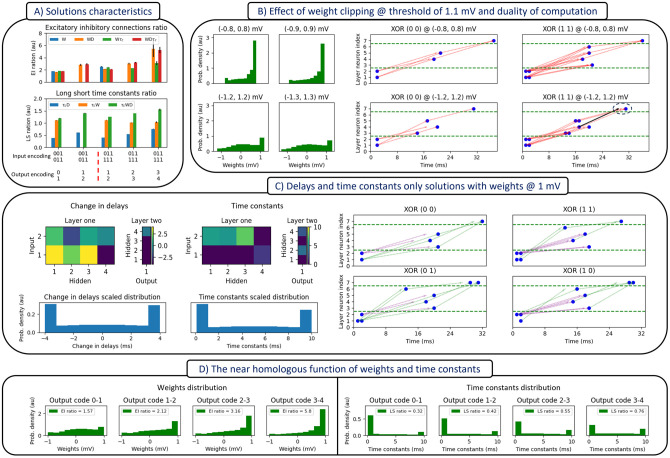
Fig 3. Properties of semi-temporal logic problems.

(A) Solutions characteristics; demonstrating the impact of the co-mutated parameters and the input-output encoding on the ratios of excitatory vs. inhibitory connections and long vs. short time constants. (B) The weight clipping range dictates the modality of computation and excitatory/inhibitory ratio. Left, distribution of weights in the network at various weight clipping ranges. Right, spiking raster plots illustrating the network behavior when the weight clipping range is below (top row) and above threshold (bottom row). (C) Delays and time constants alone can solve all logic problems with constant weights (1 mV). The heatmaps show the values of change in delays and time constants for the particular XOR problem in the accompanying spiking raster plots (right), while the histograms show the distributions for both parameters aggregated across all logic problems. Regarding delays, we mutate/adapt the change in delays and add it to a default value to acquire the total axonal delays (D) Weights and time constant distributions as a function of the output code. For more details, see Tables B, C and D in S1 Text and the related text.