Neighborliness of randomly projected simplices in high dimensions

Abstract

Let A be a d × n matrix and T = T^n-1 be the standard simplex in Rⁿ. Suppose that d and n are both large and comparable: d ≈ δn, δ ∈ (0, 1). We count the faces of the projected simplex AT when the projector A is chosen uniformly at random from the Grassmann manifold of d-dimensional orthoprojectors of Rⁿ. We derive ρ_N(δ) > 0 with the property that, for any ρ < ρ_N(δ), with overwhelming probability for large d, the number of k-dimensional faces of P = AT is exactly the same as for T, for 0 ≤ k ≤ ρd. This implies that P is 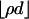-neighborly, and its skeleton 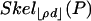is combinatorially equivalent to 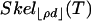. We also study a weaker notion of neighborliness where the numbers of k-dimensional faces f_k(P) ≥ f_k(T)(1 - ε). Vershik and Sporyshev previously showed existence of a threshold ρ_VS(δ) > 0 at which phase transition occurs in k/d. We compute and display ρ_VS and compare with ρ_N. Corollaries are as follows. (1) The convex hull of n Gaussian samples in R^d, with n large and proportional to d, has the same k-skeleton as the (n - 1) simplex, for k < ρ_N (d/n)d(1 + o_P(1)). (2) There is a “phase transition” in the ability of linear programming to find the sparsest nonnegative solution to systems of underdetermined linear equations. For most systems having a solution with fewer than ρ_VS(d/n)d(1 + o(1)) nonzeros, linear programming will find that solution.

1. Introduction

Let T = T^n-1 be the standard simplex in Rⁿ and let A be a uniformly distributed random projection from Rⁿ to R^d. Some time ago, Goodman and Pollack proposed to study the properties of n points in R^d obtained as the vertices of P = AT; this model was called by Schneider the Goodman–Pollack model of a random pointset. Independently, Vershik advocated a “Grassmann approach” to high-dimensional convex geometry and began to study the same object P, motivated by average-case analysis of the simplex method of linear programming.

Key insights into the properties of P were obtained by Affentranger and Schneider (1) and Vershik and Sporyshev (2). Both developed methods to count the number of faces of the randomly projected simplices P = AT. Affentranger and Schneider considered the case where d is fixed and n is large and showed the number of points on the convex hull if P grew logarithmically in n. Vershik and Sporyshev considered the situation where the dimension d was proportional to the number of points n and found that the low-dimensional face numbers of P behaved roughly like those of the simplex.

1.1. New Applications. In the years since refs. 1 and 2 first appeared, new connections arose, motivating a fresh study of this problem.

• The first connection involves properties of Gaussian “point clouds.” Work of Baryshnikov and Vitale (3) has shown that the Goodman–Pollack model is for certain purposes equivalent to the classical model of drawing n samples from a multivariate Gaussian distribution in R^d. Thus, results in this model tell us about the properties of multivariate Gaussian point clouds, in particular, the properties of their convex hull. High-dimensional Gaussian point clouds provide models of modern high-dimensional data sets. Much development of statistical models assumes these clouds behave as low-dimensional clouds; as we will see, low-dimensional intuition is wildly inaccurate.

• The second connection involves sparse solution of linear systems. In a companion paper (4), we considered the problem of finding the sparsest nonnegative solution to an underdetermined system of equations y = Ax, x ≥ 0, A a d × n matrix. We connected this with the problem of k-neighborliness of the polytope P₀ = conv(AT ∪ {0}); for more on neighborliness, see below. We showed that, if P₀ is k-neighborly, then for every problem instance (y, A) where y = Ax₀ with x₀ having at most k nonzeros, the sparsest solution can be obtained by linear programming.

Inspired by these two more recent developments, we study randomly projected simplices anew.

1.2. Neighborliness. The polytope P is called “k-neighborly” if every subset of k vertices forms a (k - 1)-face (ref. 5, Chap. 7). A k-neighborly polytope “acts like” a simplex, at least from the viewpoint of its low-dimensional faces. More formally, a k-neighborly polytope with n vertices has several properties of interest as follows:

• It has the same number of 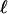-dimensional faces as the simplex T^n-1, 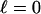,..., k - 1.

• The 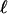-dimensional faces are all simplicial, for .

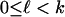• The (k - 1)-dimensional skeleton is combinatorially equivalent to the (k - 1)-skeleton of the simplex T^n-1.

Such properties can seem counterintuitive. Comparing T^n-1 ⊂ Rⁿ with P = AT^n-1 ⊂ R^d, we note that P is a lower-dimensional projection of T^n-1 and, it would seem, might “lose faces” as compared with T^n-1 because of the projection. For example, it might seem plausible that, under projection, some edges of T^n-1 might fall “inside” the convex hull conv(AT^n-1); yet if P is 2-neighborly, the plausible does not happen. Surprisingly, in high dimensions, the counterintuitive event of 2-neighborliness is quite typical. Even much more extreme things occur: we can have k-neighborliness with k proportional to d.

1.3. Asymptotic Analysis. We adopt the Vershik–Sporyshev asymptotic setting and consider the case where d is proportional to n and both are large. However, to better align with applications, and with our companion work (4, 6, 7), we use different notation than Vershik and Sporyshev in ref. 2. In a later section we will harmonize results. We assume 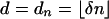and consider n large.

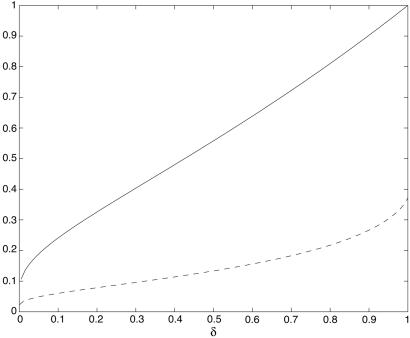
Our primary concern is the neighborliness phase transition. It turns out that, with overwhelming probability for large n, the polytope P = AT^n-1 typically has n vertices and is k-neighborly for k ≈ ρ_N(d/n)·d. The function ρ_N will be characterized and computed below (see Fig. 1). For example, Fig. 1 shows that if n = 2d and n is large, k-neighborliness holds for k ≤ 0.133d.

Fig. 1.

ρ_vs and ρ_N. The lower curve (dashed) shows the lower bound ρ_N(δ)on the neighborliness threshold, computed by methods described in this work. The upper curve (solid) shows Vershik–Sporyshev weak neighborliness threshold ρ_VS. matlab software is available from the authors.

To state a formal result, for a polytope Q, let 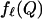denote the number of 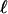-dimensional faces.

Theorem 1: Main Result. Let ρ < ρ_N(δ) and let A = A_d,n be a uniformly distributed random projection from Rⁿ to R^d, with d ≥ δn. Then

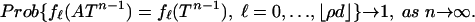[1.1]

In particular, this agreement of face numbers means that P is k-neighborly for k = ρ_N(δ)d(1 + o_P(1)).

We may distinguish this result from the pioneering work of Vershik and Sporyshev (2), who were interested in the question of whether, for k in a fixed proportion to n, the face numbers f_k(AT^n-1) = f_k(T^n-1)(1 + o_P(1)) or not. They also proved a threshold phenomenon for k in the vicinity of ρ_VSd, for some implicitly characterized ρ_VS = ρ_VS(d/n). Although Vershik and Sporyshev referred to “the neighborliness problem” in the title of their article, the notion they studied was not neighborliness in the sense of ref. 5 and classical convex polytopes but instead what we might call “weak neighborliness.” Such weak neighborliness asks whether, for a given random polytope P = AT^n-1, there are n vertices and whether the overwhelming majority of 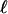-membered subsets of those vertices span 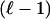-faces of P, for .

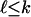For comparison with Theorem 1, note that the question of approximate equality of face numbers f_k(AT^n-1) = f_k(T^n-1)(1 + o_P(1)) is weaker than the exact equality studied here in Theorem 1; it changes at a different threshold in k/d. Vershik–Sporyshev's result can be stated as follows.

Theorem 2: Vershik–Sporyshev. There is a function ρ_VS(δ), characterized below, with the following property. Let d = d(n) ≈ δn and let A = A_d,n be a uniform random projection from Rⁿ to R^d. Then for a sequence k = k(n) with k/d ∼ ρ, ρ < ρ_VS(δ), we have

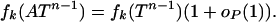[1.2]

We emphasize that our notation differs from Vershik and Sporyshev, who studied instead the inverse function δ_VS(ρ). Fig. 1 displays the weak-neighborliness phase transition function ρ_VS for comparison with the neighborliness phase transition ρ_N.

The Vershik–Sporyshev result is sharp in the sense that for sequences with k/d ∼ ρ > ρ_VS, we do not have the approximate equality 1.2. In this work, we will show how a proof of Theorem 2 can be made similar to the proof of Theorem 1.

1.4. Numerical Result. Our work contributes to the study of the neighborliness phase transition and to the numerical information about the Vershik–Sporyshev weak-neighborliness phase transition. Our matlab software for computing these curves is available from D.L.D. or J.T. on request. In particular, Fig. 1 depicts substantial numerical differences in the critical proportion ρ_VS and the lower bounds ρ_N. The most striking property of ρ_VS is that it crosses the line ρ = 1/2 near δ = 0.425 and increases to 1 as δ → 1. This property has implications for sparse solution of linear equations with n equations and 2n unknowns (see ref. 4). For comparison, we compute that

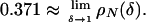[1.3]

1.5. Solid Simplices. There are two natural variations on the notion of simplex to which the above results also apply. The first, , is the convex hull of {0} and T^n-1. It is a “solid” n-simplex in Rⁿ but not a regular simplex, because the vertex at 0 is closer to the other vertices than they are to each other. The second, 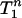, is the convex hull of the vector -α1 with T^n-1, where α solves (1 + α)² + (n - 1)α² = 2. It is also a solid n-simplex in Rⁿ, this time a regular one, with n + 1 vertices all spaced 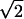apart. For applications where random projections of one or both of these alternate simplices could be of interest, we make the following remark.

Theorem 3. Theorems 1 and 2 hold for 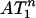, with the same functions ρ_N and ρ_VS and the comparable conclusions. Theorems 1 and 2 hold for 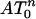, with the same functions ρ_N and ρ_VS and the comparable conclusions, provided “neighborliness” is replaced by “outward neighborliness.”

Outward neighborliness is a slight variation of the concept of neighborliness (see ref. 4). To save space we give the (simple) proof of Theorem 3 in the technical report (ref. 8, Appendix).

1.6. Applications. We briefly indicate how these new results give information about the applications sketched in Section 1.1.

1.6.1. Gaussian point clouds. Suppose we sample X₁, X₂,..., X_n i.i.d. according to a multivariate Gaussian distribution on R^d with nonsingular covariance. By Baryshnikov–Vitale (3), any affine-invariant property of the point configuration will have the same probability distribution under this model as it would under the model where A is a uniform random projection and X_i is the ith column of A. We conclude the following.

Corollary 1.1. Let δ ∈ (0, 1) be fixed and let 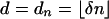. Let ρ < ρ_N(δ). Let X₁, X₂,..., X_n be i.i.d. samples from a Gaussian distribution on R^d with nonsingular covariance. Consider the convex hull P of 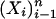. Then with overwhelming probability for large n,

• every X_i is a vertex of the convex hull P;

• every pair X_i, X_j generates an edge of the convex hull;

• ...

• every 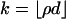points generate a (k - 1)-face of P.

In short, not only are the points on the convex hull, but all reasonable-sized subsets span faces of the convex hull.

This behavior is wildly different than the behavior that would be expected by traditional low-dimensional thinking. If we consider the case of d fixed and n tending to infinity, Affentranger and Schneider (1) showed that there are a constant times log(n)^(d-1)/2 points on the convex hull; in contrast, in the high-dimensional asymptotic considered here, all n points are on the convex hull.

1.6.2. Sparse solution by linear programming. Finding the sparsest nonnegative solution to y = Ax is an NP-hard problem in general when d < n. Surprisingly, many matrices have a sparsity threshold: for all instances y such that y = Ax has a sufficiently sparse nonnegative solution, there is a unique nonnegative solution, which can be found by linear programming. Interestingly, the neighborliness phase transitions ρ_N and ρ_VS describe the threshold behavior of typical matrices A. This connection is discussed at length in ref. 4. Consider the standard linear program

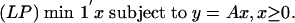Corollary 1.2. Fix ε, δ > 0. Let 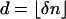, and let A be a d × n matrix whose columns are independent and identically distributed according to a multivariate normal distribution with nonsingular covariance. Let 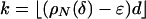. With overwhelming probability for large n, A has the property that, for every nonnegative vector x₀ containing at most k nonzeros, the corresponding y = Ax₀ generates an instance of the minimization problem (LP), which has x₀ for its unique solution.

In other words, for a typical A, for all problem instances permitting sufficiently sparse solutions, the linear programming problem (LP) computes the sparsest solution. Here “sufficiently sparse” is determined by ρ_N(d/n).

The weak-neighborliness threshold has implications in terms of “most” underdetermined systems. Consider the collection S₊(n, d, k) of all systems of linear equations with n unknowns, d equations, permitting a solution by ≤k nonzeros. As we explain in our companion paper (4), one can place a measure on S₊ in which different matrices with the same row space are identified and different vectors y are identified if their sparsest decompositions have the same support. The result is a compact space on which a natural uniform measure exists: the uniform measure on d-subspaces of Rⁿ times the uniform measure on k-subsets of n objects.

Corollary 1.3. Fix δ > 0, and set ρ < ρ_VS(δ). For large n, in the overwhelming majority of systems in S₊(n, δn, (ρδ)n), (LP) delivers the sparsest solution.

We read off of Fig. 1 that ρ_VS(1/2) > 0.55. Thus, for large n, in most n × 2n systems permitting a sparse solution with 55% as many nonzeros as equations, that is the solution delivered by (LP). This phenomenon is studied further by us in ref. 4 and material cited there.

In both such results about solutions of linear equations, Theorem 3's applicability to the solid simplices ATⁿ₀ is crucial.

1.7. Contents. In this work, we develop a viewpoint that allows us to prove Theorems 1 and 2 in the same way, and that is essentially parallel to proofs of face-counting results in ref. 7. Although necessarily our proofs have much to do with Vershik and Sporyshev's proof of Theorem 2, the viewpoint we adopt has the benefit of solving a range of problems, not only in this setting.

Section 2 proves Theorem 1, while Section 3 defined certain exponents used in the proof. Section 4 explains how the proof may be adapted to obtain Theorem 2. Theorem 3 is proven in ref. 8.

2. Random Projections of Simplices

We now outline the proof of Theorem 1. Key lemmas and inequalities will be justified in a later section.

2.1. Angle Sums. As remarked in the introduction, our proof proceeds by refining a line of research in convex integral geometry. Affentranger and Schneider (1) [see also Vershik and Sporyshev (2)] studied the properties of random projections P = AT where T is an (n - 1)-simplex and P is its d-dimensional orthogonal projection. Ref. 1 derived the formula

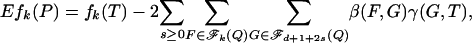where E denotes the expectation over realizations of the random orthogonal projection, and the sum is over pairs (F, G) where F is a face of G. In this display, β(F, G) is the internal angle at face F of G and γ(G, T) is the external angle of T at face G; for definitions and derivations of these terms see, e.g., Grünbaum, Chap. 14 (5) as well as refs. 9–11. Write

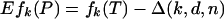[2.1]

with

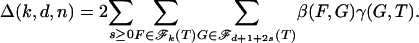[2.2]

2.2. Exact Equality from Expectation. We view Eq. 2.1 as showing that on average f_k(P) is about the same as f_k(T), except for a nonnegative “discrepancy” Δ. We will show that under the stated conditions on k, d, and n, for some ε > 0

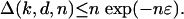[2.3]

Now as f_k(P) ≤ f_k(T),

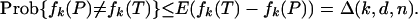Hence, Eq. 2.3 implies that with overwhelming probability, we get equality of f_k(P) with f_k(T), as claimed in the theorem. For the needed simultaneous result, that 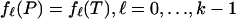, one defines events E_k = {f_k(P) ≠ f_k(T)} and notes that by Boole's inequality

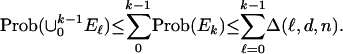The exponential decay of Δ(k, d, n) will guarantee that the sum converges to 0 whenever the (k -1)-th term does. Hence, by establishing Eq. 2.3 we get

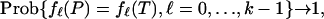as is to be proved.

To establish Eq. 2.3, we rewrite Eq. 2.2 as

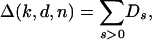where, for 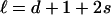, s = 0, 1, 2,...

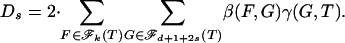We will show that, for ρ < ρ_N (still to be defined) and for sufficiently small ε > 0, then for n > n₀(ε; ρ, δ)

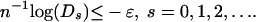Eq. 2.3 follows, as well as our main result.

2.3. Decay and Growth Exponents. Following Affentranger and Schneider (1) and Vershik and Sporyshev (2), observe the following:

• There are (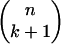) k-faces of T.

• For , there are (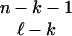) 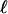-faces of T containing a given k-face of T.

• The faces of T are all simplices, and the internal angle 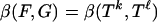, where T^d denotes the standard d-simplex.

Thus, we can write

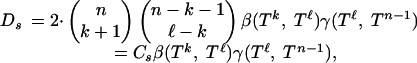say, with C_s the combinatorial prefactor.

We now estimate n^-1 log(D_s), decomposing it into a sum of terms involving logarithms of the combinatorial prefactor, the internal angle, and the external angle. Formally, we will define exponents Ψ_com, Ψ_int, and Ψ_ext so that for ε > 0, and n > n₀(ε, δ, ρ)

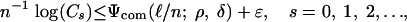and

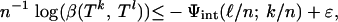[2.4]

uniformly in ;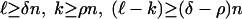

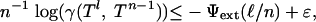[2.5]

uniformly in 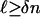. It follows that for any fixed choice of ρ, δ, for ε > 0, and for n ≥ n₀ (ρ, δ, ε) we have the inequality

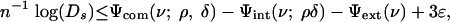[2.6]

valid uniformly in s. Exactly the same approach (with different details) has been used in ref. 7, and the approach is related to ref. 2.

To see where the exponents come from, we consider the simplest case, Ψ_com. Define the Shannon entropy

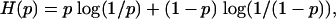noting that here the logarithm base is e, rather than the customary base 2. As did Vershik and Sporyshev (2) and also the authors of refs. 7 and 12, we note that

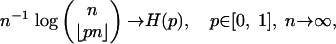[2.7]

so that H provides a convenient summary for combinatorial terms. Defining 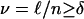, we have

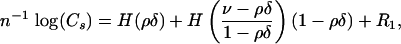[2.8]

with remainder R₁ = R₁ (s, k, d, n). Define then the growth exponent,

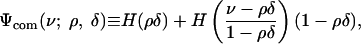describing the exponential growth of the combinatorial factors. It is banal to apply Eq. 2.7 and see that the remainder R₁ in Eq. 2.8 is o(1) uniformly in the range .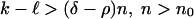

The definitions for the exponent functions Eqs. 2.4 and 2.5 are significantly more involved and are postponed to the following section. There it will be seen that these are continuous functions.

Define now the net exponent Ψ_net(ν; ρ, δ) = Ψ_com(ν; ρ, δ) - Ψ_int(ν; ρδ) - Ψ_ext(ν). We can define at last the mysterious ρ_N as the threshold where the net exponent changes sign. It can be seen that the components of Ψ_net are all continuous over sets {ρ ∈ [ρ₀, 1], δ ∈ [δ₀, 1], ν ∈ [δ, 1]}, and so Ψ_net has the same continuity properties.

Definition 1: Let δ ∈ (0, 1]. The critical proportion ρ_N(δ) is the supremum of ρ ∈ [0, 1] obeying

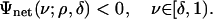Continuity of Ψ_net shows that if ρ < ρ_N then, for some ε > 0,

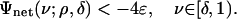Recall now Eq. 2.6. Then for all s = 0, 2,..., (n - d)/2 and all n > n₀(δ, ρ, ε)

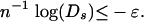Eq. 2.3 follows, and so also our main result.

3. Properties of Exponents

We now define the exponents Ψ_int and Ψ_ext and discuss properties of ρ_N.

3.1. Exponent for External Angle. Let Q denote the cumulative distribution function of a normal N(0, 1/2) random variable, i.e. X ∼ N(0, 1/2), and Q(x) = Prob{X ≤ x}. It has density 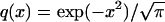. Writing things out explicitly,

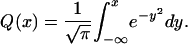[3.1]

For ν ∈ (0, 1], define x_ν as the solution of

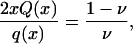[3.2]

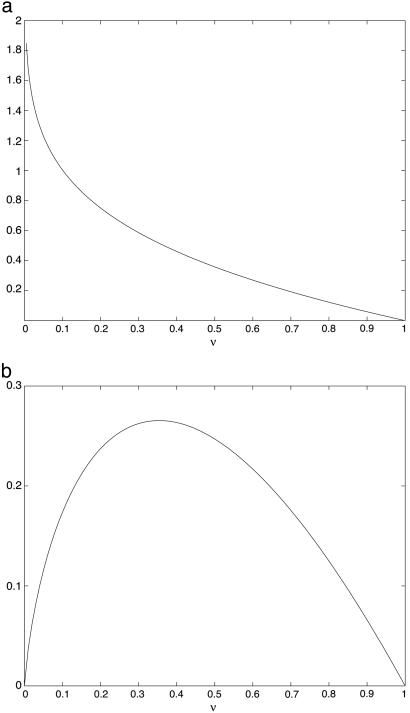
noting that possible values of x_ν are nonnegative. Since xQ is a smooth strictly increasing function ∼0 as x → 0 and ∼x as x → ∞, and q(x) is strictly decreasing, the function 2xQ(x)/q(x) is one–one on the positive axis, and x_ν is well-defined, and a smooth, decreasing function of ν. See Fig. 2 for a depiction.

Fig. 2.

Key notions associated with external angle. (a) The minimizer x_ν of Ψ_ν, as a function of ν. (b) The exponent Ψ_ext, a function of ν.

3.2. Exponent for Internal Angle. Let Y be a standard half-normal random variable HN(0, 1), with cumulant generating function Λ(s) = log(E exp(sY)). Very convenient for us is the exact formula

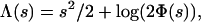where Φ is the usual cumulative distribution function of a standard Normal N(0, 1). The cumulant generating function Λ has a rate function [Fenchel–Legendre dual (13)]

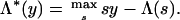Λ^* is smooth and convex on (0, ∞), strictly positive except at 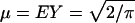. More details are provided in ref. 7.

For γ ∈ (0, 1) let

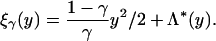The function ξ_γ(y) is strictly convex and positive on (0, ∞) and has a minimum at a unique y_γ in the interval 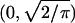. We define, for γ = ρδ/ν ≤ ρ,

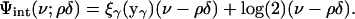For fixed ρ, δ, Ψ_int is continuous in ν ≥ δ. Most importantly, section 6 of ref. 7 gives the asymptotic formula

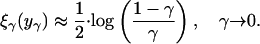[3.3]

3.3. Combining the Exponents. We now consider the combined behavior of Ψ_com, Ψ_int, and Ψ_ext. We think of these as functions of ν with ρ, δ as parameters. The combinatorial exponent Ψ_com involves a scaled, shifted version of the Shannon entropy, which is a symmetric, roughly parabolic shaped function. Ψ_com is the exponent of a growing function that must be outweighed by the sum Ψ_ext + Ψ_int.

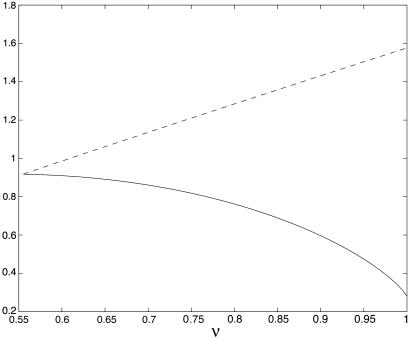
Fig. 3 shows both Ψ_com and Ψ_ext + Ψ_int with δ = 0.5555 and ρ = 0.145. The desired condition Ψ_net < 0 is the same as Ψ_com < Ψ_ext + Ψ_int and holds with plenty of slack except near ν = δ, where the two curves are close. We have ρ_N(δ) ≈ 0.145.

Fig. 3.

The exponents Ψ_com(ν; ρ, δ) and Ψ_int(ν; ρδ) + Ψ_ext(ν), for ρ = 0.145, δ = 0.5555. The graph of Ψ_com (solid line) falls below that of Ψ_int + Ψ_ext (dashed line), and so Ψ_net < 0.

3.4. Justifying the Exponents. It remains to justify Eqs. 2.4 and 2.5.

We sketch the argument for Eq. 2.5. The key point is the closed-form expression for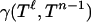

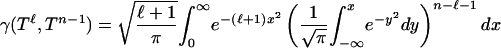(see ref. 1). We recognize the inner integral as involving Q from Eq. 3.1. Set 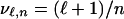. The integral formula can be rewritten as

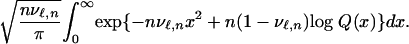[3.4]

The appearance of n in the exponent suggests to use Laplace's method; we define, for ν fixed,

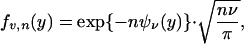with

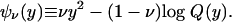We note that Ψ_ν is smooth and in the obvious way can develop expressions for its second and third derivatives. Applying Laplace's method to Ψ_ν in the usual way, but taking care about regularity conditions and remainders, gives a result with uniformity in ν. Arguing in a fashion paralleling section 5 of ref. 7, one obtains:

Lemma 3.1. For ν ∈ (0, 1) let x_ν denote the minimizer of Ψ_ν. Then

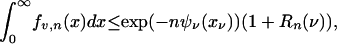where, for δ, η > 0,

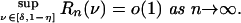The minimizer x_ν mentioned in this lemma is the same x_ν defined earlier in Eq. 3.2 in terms of the error function. Also, the minimum value identified in this lemma as driving the exponential rate is the same as our exponent Ψ_ext,

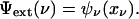[3.5]

Hence, Eq. 2.5 follows.

The decay estimate Eq. 2.4 for the internal angle was derived in ref. 7, and details can be found there. Vershik and Sporyshev (2) used a related but seemingly different approach. The argument starts from a closed-form integral expression for 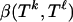. By ref. 14, 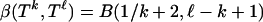, where

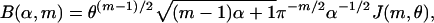[3.6]

with θ ≡ (1 - α)/α and

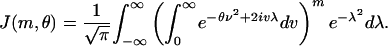[3.7]

It was shown in ref. 7 that Laplace's method applied to this last integral yields exponential bounds on the decay of β of the form Eq. 2.4.

3.5. Properties of ρ_N. We mention two key facts about ρ_N. First, the concept is nontrivial.

Lemma 3.2.

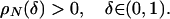[3.8]

Second, one can show that, although ρ_N(δ) → 0 as δ → 0, it goes to zero slowly.

Lemma 3.3. For η > 0,

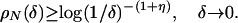These results require only a simple observation. Ref. 7 studied uniform random projections ACⁿ of the cross-polytope Cⁿ, namely the unit 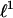ball in Rⁿ. A function 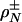was derived, giving the threshold below which a certain event E_n,ρ happens with overwhelming probability for large n. Under the event E_n,ρ the images under A of all 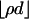-dimensional faces of C appeared as faces of AC. Viewing T^n-1 as a face of Cⁿ, when E_n,ρ holds, it follows that every low-dimensional face of T^n-1 must therefore appear as a face of AT^n-1, meaning that

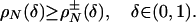Lower bounds completely parallel in form to those in Lemmas 3.2 and 3.3 were already proven for 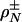in ref. 7. Hence, Lemmas 3.2 and 3.3 follow from those.

4. Weak Neighborliness

We now explain how the above proof can be adapted to handle Vershik–Sporyshev's result, Theorem 2.

Observe that 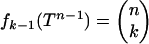; this combinatorial factor has exponential growth with n according to an exponent Ψ_face(ρδ) ≡ H(ρδ); thus, if k = k(n) ≈ ρδn,

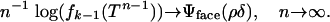We again define Ψ_net as in the proof of Theorem 1.

Definition 2: Let δ ∈ (0, 1]. The critical proportion ρ_VS(δ)isthe supremum of ρ ∈ [0, 1] obeying

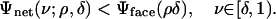[4.1]

Recall Section 2's definition Δ(k, d, n) = f_k-1(T) - f_k-1(AT) ≥ 0. The proof of Theorem 2 is based on observing that Eq. 4.1 implies

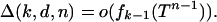[4.2]

We immediately get Eq. 1.2, showing that Eq. 4.1 implies Eq. 4.2 requires no new ideas; one proceeds as in Section 2 almost line by line, so we omit the exercise. □

We remark that the critical proportion ρ_VS defined in this way does not immediately resemble the result of Vershik and Sporyshev's result. Section 6 of ref. 6 explains how to translate between the two notational systems.