Increasing the power of functional maps of the medial temporal lobe by using large deformation diffeomorphic metric mapping

Abstract

The functional magnetic resonance imagery responses of declarative memory tasks in the medial temporal lobe (MTL) are examined by using large deformation diffeomorphic metric mapping (LDDMM) to remove anatomical variations across subjects. LDDMM is used to map the structures of the MTL in multiple subjects into extrinsic atlas coordinates; these same diffeomorphic mappings are used to transfer the corresponding functional data activation to the same extrinsic coordinates. The statistical power in the averaged LDDMM mapped signals is significantly increased over conventional Talairach–Tournoux averaging. Activation patterns are highly localized within the MTL. Whereas the present demonstration has been aimed at enhancing alignment within the MTL, this technique is general and can be applied throughout the brain.

Recent developments in observing the activation of brain regions by means of functional magnetic resonance imagery (fMRI) while different tasks are being processed are now providing a clear look at the working of the marvelous machinery of the brain. Such studies are expected to reveal an in-depth understanding of the intricate and effortless processing humans can perform while they go about their daily lives. Our own efforts in fMRI of the brain have focused on the study of the medial temporal lobe (MTL) during memory encoding and retrieval (1). Since the initial report of patient H.M. (2), research on human amnesic patients and on animal models of amnesia (see ref. 3 for review) has shown that structures in the medial portions of the temporal lobe, including the hippocampal region (CA fields of the hippocampus proper, dentate gyrus, and subiculum), the entorhinal cortex, the perirhinal cortex, and the parahippocampal cortex, play a vital role in declarative memory. Although it is clear that these structures, often referred to as the “MTL memory system” (4), play a vital and selective role in declarative memory, and although the connectivity of the system is relatively well understood (5), the precise contribution that each structure makes in the service of declarative memory is not well understood. With its relatively fine resolution (3–4 mm³), reasonably high sample rate (1–2 s per sample), and ability to isolate activity associated with specific trial types of interest or associated with specific behaviors, fMRI holds the promise of being able to make a significant contribution to our understanding of the roles of the various structures within the MTL.

The major difficulty for our work on active memory is that structures in the MTL demonstrate significant variability across individuals (6, 7). When aligned to the standard atlas of Talairach and Tournoux (8), this variability is both global and local, resulting in poor overlap across individuals, leading to reduced statistical power and reduced confidence in the location of any observed activity in extrinsic coordinates. More generally, we would argue that the confounding nature of human anatomical variability is one of the central methodological issues facing all investigators using fMRI to study the functional properties within the anatomical structures of the brain. Advances during the past decade have moved the structural imaging of the brain to the sub-1-mm scale of today's structural imagery, thereby presenting a major opportunity for the intrinsic atlas study of brain function, i.e., the comparison of functional responses gleaned within the same subject's anatomical coordinate systems. The validity of the intrinsic approach relies on the fact that rigid-body transformations (9–12) provide the crucial link between the coarse-resolution functional responses to the high-resolution structural and geometric measurements of the individual's own intrinsic coordinate systems.

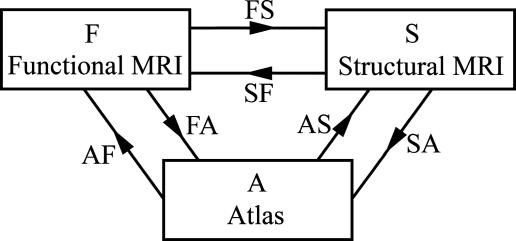
The intrinsic approach is in sharp contrast to extrinsic atlas studies arising by means of pooling functional responses from multiple anatomical coordinate systems coming from different individuals. The high baseline noise levels and relatively low resolution of fMRI technologies in comparison to standard structural MRI imaging modalities make it imperative to use cross-subject averaging to obtain clearer signals that represent activation of the individual structures. The intrinsic approach, of course, requires the valid extension of the rigid motions to their natural analogue, the infinite-dimensional diffeomorphisms, which we have been using extensively to map the shape of midbrain structures including the hippocampus and thalamus (13–16). The basic model for examining functional responses in extrinsic atlas coordinates is the compositional approach depicted in Fig. 1, in which the high-resolution structural representational MRI (sMRI) (S) is used as an intermediate substrate to transfer the individuals' fMRIs (F) to the common extrinsic atlas coordinate system (A). The arrows represent bijections between coordinates. The mapping labeled FS transforms the functional scan coordinates within the individuals structural scan by anatomically constraining the activation for a given individual to that individual's high-resolution cortical structure. The composition of transforms in the FS ○ SA uses the sMRI for correspondence to extrinsic atlas coordinates by first mapping the structural domain within the individual and then on the extrinsic coordinates by means of large deformation.

Fig. 1.

Functional, structural, and atlas domains connected by means of diffeomorphic mapping.

The construction of mappings ϕ: S → A to extrinsic coordinates is one of the principal foci of computational anatomy (16–19). The recent emergence of Beg's large deformation diffeomorphic metric mapping (LDDMM) method (20) provides the geodesic flow in the space of diffeomorphisms between anatomical configurations, allowing us to study anatomical configurations as a metric space. Such a construction of the transformation SA from structural to extrinsic atlas coordinates constrains the transformation so that connected sets remain connected, disjoint sets remain disjoint, and submanifold structures are preserved. This preservation is particularly important for averaging functional data where the bijective property of the maps ensures that artifacts because of superposition of functional data from neighboring regions are avoided.

In this paper, we demonstrate that LDDMMs provide a powerful means for recruiting signal response across multiple subjects in the MTL. A significant enhancement to our semiautomated image-based mappings is to define the intermediate data structure corresponding to region of interest (ROI) rough segmentations, augmenting the MRI imagery by a dense function that is relatively invariant to MRI calibration. We demonstrate that mappings based on these LDDMMs provide comparable structural detail to the MRI image mappings in the hippocampus, but enhanced detail in other MTL structures. We also demonstrate significant recruitment of response in the MTL by means of these structural maps.

Methods

All subjects were examined with both high-resolution structural MRI and the functional sequences. Talairach, local affine, and local LDDMM methods for registration were applied to optimize alignment to increase the statistical power and precision of localization within anatomically defined regions of the MTL. The maps generated were then applied to the functional response map of each subject. For each subject, segmentations of the participant's perirhinal cortex, temporopolar cortex, and entorhinal cortex were first defined bilaterally in 20 anatomical volumes according to the techniques described by Insausti et al. (6). The parahippocampal cortex was further defined bilaterally as the portion of the parahippocampal gyrus caudal to the perirhinal cortex and rostral to the splenium of the corpus callosum. The hippocampal region (the CA fields of the hippocampus, the dentate gyrus, and the subiculum) was also defined bilaterally. All anatomical ROI definitions were conducted after alignment to the Talairach atlas (8) by using afni (21) to perform the piecewise affine transformations prescribed in the atlas. This initial alignment provides the same low-dimensional initial alignments to each of the three techniques examined here without favoring any particular one.

To generate a template or extrinsic coordinate system to which all functional responses are mapped, the mapped set of all participants was merged based on segmentations minimizing a squared error registration distance. A single map within the MTL was created by calculating the mode of the M-ary maps across participants.

Functional Methods. In recent experiments of MTL activity during encoding and retrieval (1), participants studied a set of 100 color pictures of outdoor scenes while fMRI data were collected. After a 10-min delay, fMRI data collected while a recognition memory test was presented in which all 100 studied pictures and 100 novel foil pictures were presented, and participants were asked to judge whether each picture had been previously studied. A number of studies have demonstrated that although participants were initially studying stimuli such as pictures, the amount of activity in several MTL regions was correlated with their subsequent ability to remember having seen the item during the recognition memory test (22–29). Stark and Okado (1) demonstrated that this encoding-related activity was present not only when participants were attempting to study the pictures but also when participants were attempting to remember the pictures. For this encoding-related task, a second recognition memory test was administered outside the scanner to assess memory for the novel foil items that had been presented during the first recognition memory test (specifically, the correct rejections in which participants accurately judged that they had not initially studied the picture). Using the same technique to analyze the fMRI data at time of study based on subsequent memory ability, Stark and Okado (1) observed elevated levels of activity associated with incidental encoding of correct rejections during the retrieval task itself. That is, that activity during the first recognition task for correct rejections that were later remembered in this second test (CR-R) was greater than activity for correct rejections that were later forgotten (CR-F). This effect directly demonstrated that encoding-related activity during retrieval was masking or obscuring activity associated with successful recognition memory. The statistical maps for the incidental encoding-related contrast (CR-R vs. CR-F), the anatomically defined ROIs, and the structural MRI images were all taken from ref. 1 after rigid-body coregistration and transformation to the atlas of Talairach and Tournoux (8).

In all analyses presented here, the individual participant's beta coefficients from the multiple-regression statistical maps that correspond to the estimates of activity associated with each condition were resampled to 2.5 mm³ and subjected to a random-effects analysis by using pairwise t tests. The resulting statistical maps were thresholded at P ≤ 0.02 (t > 2.55) and a spatial-extent threshold was used (12 contiguous voxels, 188 mm³). These thresholds were as in ref. 1 and determined by using the AlphaSim component of afni (21) to correct for multiple comparisons (α < 0.05). The Monte Carlo simulations accounted for the number of voxels in the MTLs, their geometry, and the inherent smoothness of the data resulting from the size of the acquired voxels.

Data Correspondence or Distance Function. All registration or mapping algorithms to extrinsic atlas coordinates are based on a distance or correspondence function measuring the alignment of the mapping to the observable imagery (either sparse for landmarks or dense for imagery). The observable structural MRI imagery are dense functions I(x), x ∈ Ω, which are real gray-valued. To create an alignment or registration, the transformations ϕ are introduced on the background coordinates Ω, indexing the distance so as to make the observed imagery look similar to the extrinsic template imagery.

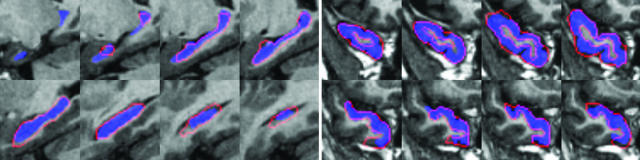
To generate MRI calibration-independent imagery for the mappings to extrinsic coordinates, the Stark group constructs ROI-based rough hand segmentations of the volumes, denoted as S(x), x ∈ Ω, which are one of M different labelings consisting of gray matter, subsuming each of the anatomically interesting relevant parts of the MTL, perirhinal cortex, temporopolar cortex, entorhinal cortex, and hippocampus, defined bilaterally (see Fig. 2). The rough segmentations are generally created in one pass, requiring much less time than the gold standard segmentations, and can be completed relatively quickly as a data preparation step. The segmentation imagery is smoothed with a Gaussian kernel p_σ(·) of σ = 0.5 voxel to stabilize the mapping algorithms so that the distance function is smooth and can be differentiated.

Fig. 2.

ROI rough hand segmentations of the hippocampus (Left) and other temporal lobe structures (Right). Red, boundaries of ROI segmentations used for the mapping algorithm; blue, the gold standard segmentations used for quantifying the accuracy of the mapping algorithms only.

The distance function indexed by the transformation ϕ used for registration takes two forms. For the MRI imagery I, I′ the associated distance used 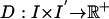is the squared-error distance 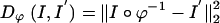. Landmarks are used for preconditioning the maps in which an ordered collection of points are defined x_k, x′_k, k = 1,..., N, with the 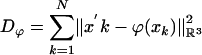. For the ROI segmentations, the masked volumes are smoothed with a Gaussian convolution kernel p_σ(·), σ = 0.5 voxel, before being matched with associated distance .

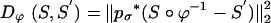Fig. 2 depicts the ROI rough hand segmentations of the hippocampus (Left) and other temporal lobe structures (Right).

Local ROI–Affine Method. The ROI affine alignment (ROI–Affine) method of Stark and Okado (1) registers subvolumes of anatomically defined regions of interest optimizing locally defined regional alignment by means of the 12-parameter affine transformation (3 rotations, 3 scales, 3 shears, and 3 translations). Unlike Talairach alignment, the 12-parameter generalized linear group with translation are locally defined to apply only to the ROIs. For this local definition, corresponding regions were cut from the rough segmentations containing the left and the right side of the MTL, including each subject as defined above. The objective function ROI–Affine is based on the overlap between the rough segmentation of the participant with the template coordinates, counting the identically labeled voxels after mapping and constructed to minimize the L₁ distance between ROI masks.^¶

The algorithm was coded into the minctracc program provided in the minc tool set (ftp://ftp.bic.mni.mcgill.ca). We refer to this algorithm here as the ROI–Affine method.

LDDMM. The LDDMM algorithm computes a transformation ϕ: Ω → Ω where is the 3D cube on which the data (structural and functional) are defined. The LDDMM computed transformation is the end point ϕ = ϕ₁ of a flow of vector fields v_t ∈ V, t ∈ [0, 1] given by the ordinary differential equation 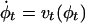, where ϕ₀ is identity ϕ₀(x) = x, x ∈ Ω. Enforcing smoothness on the vector fields v ∈ V ensures that the solution to the differential equation 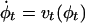, t ∈ [0, 1] is in the space of diffeomorphisms (30). Smoothness is enforced by constraining the L² norm of several derivatives of the flow vector field, admitting it to be an element of a Sobelev space with norm-square (20). The optimal ϕ is the minimum of the endpoint of the inexact matching problem

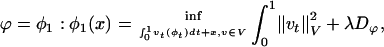[1]

where D_ϕ is defined on the ROI rough segmentations or the MRI imagery, and λ > 0 is the relative weight assignment. We term the mapping based on the ROI segmentations the ROI-LDDMM algorithm with distance function 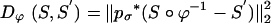. We term the mapping based on the MRI as MRI-LDDMM with distance function .

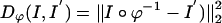Here ROI-LDDMM was applied to the same ROI hand segmentations as ROI-Affine, and MRI-LDDMM was applied to the MRI structural images. For the hippocampus and temporopolar cortex, the mappings are semiautomated, requiring the selection of landmarks as in refs. 31 and 32. For the temporopolar cortex, 11 landmarks are used.

Results

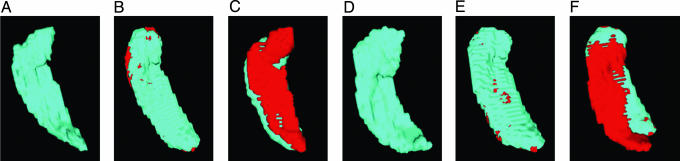
LDDMM Accuracy. Fig. 3 shows the accuracy of MRI-LDDMM for segmenting the hippocampus. As in ref. 31, all the errors in the mapping of the hippocampus occur in the boundary (partial voxel) of the structure.

Fig. 3.

Errors depicted in MRI volume for LDDMM and Talairach alignment. (A and D) The original target hippocampuses in each subject. (B and E) The discrepancy between the template mapped to the target by using the MRI-LDDMM. Errors are shown in red; notice the small errors near the boundary. (C and F) The discrepancy for the Talairach alignment, which exhibits errors (red) over the entire hippocampus.

Fig. 4 shows an alternative visualization of the improved alignment accuracy obtained by the LDDMM method. Shown are the results of averaging the ROIs of 15 participants' MTLs by using Talairach (Upper) and ROI-LDDMM (Lower) alignment in both coronal (Left) and sagittal (Right) cropped slices. For each participant, both their structural scan and a binary version of the ROI rough segmentation of their entire MTL were transformed by using each method. The average structural and the average segmentations across participants are shown. The overlaid colors range from red (1.0, indicating all participants agree this voxel is in the MTL) to blue (0.07, indicating only one participant labels this voxel as part of the MTL).

Fig. 4.

Comparisons of alignment accuracy visualizing the results of averaging the rough segmentations of 15 new participants' medial temporal lobes by using Talairach (Upper) and ROI-LDDMM (Lower) alignment in both coronal (Left) and sagittal (Right) cropped slices. The average structural and the average segmentations across participants are shown. The overlaid colors range from red (all participants agree this voxel is in the MTL) to blue (one participant labels this voxel as part of the MTL).

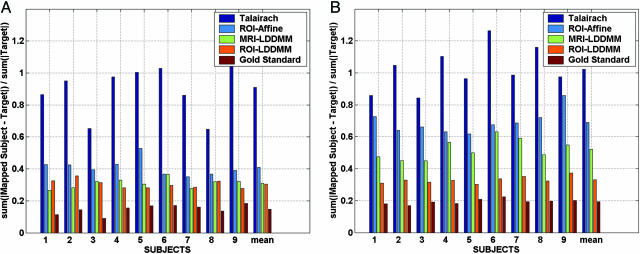
Fig. 5 shows the accuracy of each mapping technique, quantifying the techniques by using the error associated with aligning the segmentations. In each case, the template segmentation was mapped and interpolated as a positive-valued function onto the target segmentations. For each method, the L₁ distance (normalized by target volume) was computed between the mapped segmentations and the target segmentations.

Fig. 5.

L₁ error rate percentages of multiple subject hippocampi (A) and temporopolar cortices (B) for different registration methods. Error rates shown are L₁ errors interpolated as fractions between 0 and 1 and normalized by target volume. Error rates are ordered according to the Talairach alignment (highest dark blue), the ROI-Affine mapping (light blue), the MRI-LDDMM segmentation (green), and the rough segmentation based ROI-LDDMM (orange). As a gold standard comparison (baseline), the lowest error bars result from using the gold standard segmentation (which is never available) as the true registration function for the LDDMM.

The results indicate that the higher local dimensions of the LDDMM provide increased power in terms of segmentation accuracy. When the ROI is used, rough segmentations generally provide more information for the temporopolar cortex (Fig. 4, Left), which is an area of more ambiguous gray/white matter boundaries. To obtain a lower bound on segmentation accuracy, essentially the best possible, the dark red plots the error rate by using the “gold standard segmentations” in the mapping distance function itself (in general these segmentations are not available), comparing the accuracy of the resulting maps to these same gold standard segmentations. In this case the error rate of the LDDMM is strictly due to the numerical accuracy of the computational codes; this is a best achievable error rate using diffeomorphisms.

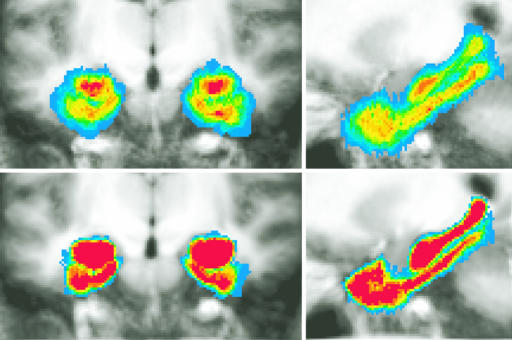
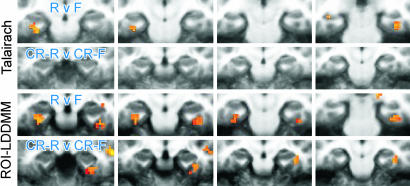
Recruiting Functional Responses in Extrinsic Coordinates. As posited in Fig. 1, the high-resolution structural information provides the opportunity to increase the detectability and resolvability of functional activity. Fig. 6 examines the cross-participant activation maps resulting from the different alignment techniques. As the methods for registration become progressively refined from Talairach and Tournoux to ROI-LDDMM, there is an increase in overlap of the functional signal across participants, leading to enhanced statistical power. Where the effect was not present at all after Talairach alignment, it appears after ROI-LDDMM alignment.

Fig. 6.

Areas showing significant activity during the recognition memory task associated with incidental encoding, shown as colored overlays on cropped coronal slices through the MTL (left of each image is left side of brain; there is a 4-mm gap between successive slices). Upper two rows show activity for two memory-related contrasts after Talairach alignment. Lower two rows show the same after ROI-LDDMM alignment. RvF, remembered vs. forgotten; CR-R v CR-F, correct rejections later remembered vs. correct rejections later forgotten.

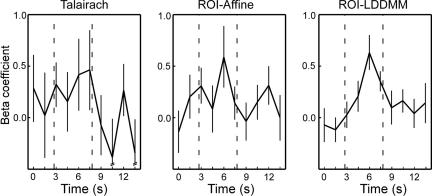
All three techniques identify a similar region of the right perirhinal cortex as being active at or near the statistical threshold in the correct rejections that were later remembered (CR-R) vs. correct rejections that were forgotten (CR-F) contrast. The most reliably active voxel was separately identified in each of the three group analyses (Talairach, t = 3.13; ROI-Affine, t = 3.71; ROI-LDDMM, t = 4.56). The hemodynamic response from each participant was extracted in each of the three data sets. Fig. 7 shows the average hemodynamic response across participants for each of the three techniques. This result demonstrates that not only are there a greater number of significant regions after ROI-LDDMM alignment (as in Fig. 6), but also that the activity within the region itself is greater in both magnitude (higher peak) and in signal-to-noise ratio (smaller standard error of the mean) after ROI-LDDMM alignment (Right) than after either ROI-Affine (Center) or Talairach (Left). Improved cross-participant alignment resulted in a less variable and more robust response in the group analysis. This change in the variability was statistically reliable in an analysis of cross-participant t tests, not isolated to the best voxel, but as general in nature. A Kolmogorov–Smirnov test on the 1,525 voxels within the MTL indicated a significant difference in the distributions of the absolute values of the cross-participant t statistics, with more extreme t values after ROI-LDDMM alignment (Z = 1.575, P < 0.02).

Fig. 7.

Plotted are the hemodynamic responses (as represented by the set of beta coefficients calculated by multiple regression in a deconvolution-style analysis) for the single voxel within the right perirhinal cortex that had the strongest (highest t value) signal for each technique. The three selected voxels were within several millimeters of each other.

Discussion

The current limitations of functional imaging technologies make it imperative to use the averaging of functional data to obtain clearer signals that represent activation of the individual structures. Methods for removing anatomical variability by means of representation of average information in extrinsic atlas coordinates requires the link of high resolution structural imagery to the fMRI scans measured intrinsic to the same subject. Low-dimensional transformation methods focusing on optimization by means of whole-brain alignment, such as the traditional Talairach techniques, are limited in their ability to account for local variability in the size, shape, and location of MTL structures. Increasing dimension of the mapping to extrinsic atlas coordinates by means of LDDMM increases the accuracy in localization of MTL response and, therefore, the statistical power. The LDDMM employs the most detailed transformations of human anatomy possible, essentially applying the transformations on the dense continuum attempting to transform the geometry of individual structures into the common extrinsic coordinates. Such dense geometric transformation of the MTL leads to substantial improvements in the localization of functional data activation with enhanced statistical power in cross-participant tests.

Specifically, we find:

1. The LDDMM provides a method for registering temporal lobe structures far more accurately than global registration methods such as Talairach alignment.

2. The improved alignment to extrinsic coordinates results in increased statistical power over traditional Talairach alignment as demonstrated by comparing the distribution of various cross-participant statistical maps within voxels of the MTL.

3. The MTL functional data strengthen results in ref. 1, demonstrating that MTL activity at the time of retrieval is associated with incidental memory encoding. Such effects are not observed with Talairach alignment, thereby demonstrating that global registration is not sufficient for normalizing out anatomical variability when studying function in temporal lobe structures.

We note, however, that at least two sources of variability or inaccuracy are not addressed in the current approach. First, the functional neuroanatomy across participants may vary and the precise localization of activity may differ between any two brains. Typical solutions to this problem (e.g., blurring of the functional data or the use of independent “localizer” or “reference” scans) will be quantitatively addressable only by means of methods that incorporate the improved structural alignment presented here. Second, distortions of the mapping between the functional coordinate system and the structural coordinate system are not addressed directly. Thus, deformations of the brain in functional data sets that arise from localized magnetic inhomogeneity or mislocalizations that arise from large draining vein signals are not corrected by the current approach. However, we note that advances in neuroimaging techniques to ameliorate these difficulties will still be faced with the anatomical variability addressed here.

There are two basic strategies being followed in the community that are tightly coupled, representing the coordinate systems of the brain by means of 3D volume coordinates for midbrain structures and 2D surface coordinates for cortical gyri. Connected subvolumes of the brain such as the deep nuclei (thalamus, hippocampus, ventricles, and others) are appropriately studied as 3D submanifolds. The neocortical mantle has a thin laminar structure, which implies a local surface coordinate system should provide significant advantages for fMRI studies. There is already a body of evidence that 2D cortical surface comparison in extrinsic coordinates increases the power of fMRI (33–39). Complementary to the approach described here, Zeineh et al. (40) have adapted cortical unfolding techniques on the spiral structure of the hippocampus and its adjacent cortical structures in the parahippocampal gyrus. Such a bijection to a locally registered intrinsic surface coordinate system has the potential to differentiate important information about the functional role of structures within the hippocampus itself. As resolution in the structural and functional MRIs increase, such a local intrinsic surface coordinate system approach will powerfully enhance the approach taken here with mappings to an extrinsic volume-based coordinate system.

The deep brain structures of the MTL are natural 3D subvolumes for mapping. Our mapping of the MTL functional data strengthens the ROI-Affine approach of Stark and Okado (1) demonstrating that MTL activity during retrieval is associated with incidental memory encoding. The only other study to look for this effect (41) used Talairach alignment and observed activity outside the MTL, but it failed to observe activity within the MTL. Such effects are robustly defined by means of ROI-LDDMM alignment. As the quality of anatomical alignment across participants increases, the quality of the cross-participant statistical analysis of the functional data increased commensurately. We note the ROI-LDDMM is a natural extension to the ROI-Affine method. To first order, the differential of the diffeomorphism is given by a rotation-scale-skew Jacobian matrix at every point in the continuum of the ROI. Of course, part of the diffeomorphism strategy is to constrain these locally defined Jacobians (an infinite number, not just one), so that the mapping is consistent (determinant, not changing sign or becoming singular) so that adjacent patches of tissue are transformed or displaced consistently relative to each other.

In the area of the mapping of temporal pole structures by MRI-LDDMM, we have previously performed extensive work studying the abnormalities of brain structure associated with various neuropsychiatric illnesses as manifest by structural changes in the hippocampus (31, 32, 42, 43). The significant departure here is (i) to use locally defined ROIs and (ii) to use the LDDMM mappings that generate the lowest-energy diffeomorphic path connecting anatomical structures in the space of all flows (20). We find the mapping errors to be consistent with those measured in these previous validation studies (31).

Returning to the Fig. 1 Left, a great deal of fMRI research uses statistical parametric mapping (44) in which subjects are mapped by means of some functional-atlas mapping ϕ: F → A into extrinsic atlas coordinates by using a low-dimensional basis. This work demonstrates the power of such an overall methodology by providing a mapping technique that focuses locally on the ROIs by means of the high-dimensional LDDMM mapping methods.