Abstract
This work explores the mathematical technique known as the Hirota bilinear transformation to investigate different wave behaviors of the nonlinear Rosenau equation, which is fundamental in the study of wave occurrences in a variety of physical systems such as fluid dynamics, plasma physics, and materials science, where nonlinear dynamics and dispersion offer significant functions. This equation was suggested to describe the dynamic behaviour of dense discrete systems. We use Mathematica to investigate these wave patterns and obtained variety of wave behaviors, such as M-shaped waves, mixed waves, multiple wave forms, periodic lumps, periodic cross kinks, bright and dark breathers, and kinks and anti-kinks. These patterns each depict distinct qualities and behaviors of waves, offering insights into the interactions and evolution of waves. The results found that free parameters have a substantial impact on travelling waves, including their form, structure, and stability. With the aid of this software, we potray the dynamics of these waves in 3Ds, contours and densities plots, which enables us to comprehend how waves move and take on various forms. The novel component is the application of Hirota’s bilinear approach to generate new form of solutions as highlighted above, analyse their interactions, and give better visualisations, which goes beyond prior soliton-focused investigations of the Rosenau problem. All things considered, our work advances our understanding of waves and nonlinear systems and demonstrates the value of mathematical techniques for understanding intricate physical phenomena. These results may have implications for a wide range of fields, including environmental science, engineering, and physics.
Keywords: Soliton, Rosenau equation, Hirota bilinear transformation, Periodic, Breather, Lump, Kink, M-shaped
Subject terms: Mathematics and computing, Physics
Introduction
Numerous physical modelling events have been shown to employ nonlinear partial differential equations (NLPDEs). The exact solutions to these equations are of great interest to researchers because they are crucial to comprehending the physical implications of several intriguing hypotheses. In order to solve these problems, a wide range of methods and procedures are developed and employed These includes but not limited to the variational iteration method1, the three-wave method2, the new modified extended direct algebraic technique3, the homotopy perturbation method4, the symmetry reductions method5, the Adomian decomposition method6, the extended tanh approach7, the Backlund transform technique8, the inverse scattering transform technique9, the 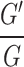 -expansion method10, the Riccati equation expansion method11, the auxiliary equation method12–15, the generalized exponential rational function (GERF) method16 and the advanced generalized expansion approach17.
-expansion method10, the Riccati equation expansion method11, the auxiliary equation method12–15, the generalized exponential rational function (GERF) method16 and the advanced generalized expansion approach17.
The well-known KdV equation could not account for the scenario of wave-wave and wave-wall interactions in the study of the dynamics of dense discrete systems18,19. To address this shortcoming of the KdV equation, the Rosenau equation was developed. We consider the Rosenau equation in the form20
 |
1 |
The dynamics of various Rosenau equations have been studied using a variety of numerical and analytic techniques. Park investigated the possibility of a solution to the Rosenau equation, and he explicitly provided the precise solution21. In their investigation of finite element Galerkin techniques for a Rosenau equation that resembles KdV, Chung and Ha establish the existence and uniqueness of the exact solutions and explore the error estimates22. Zuo gained solitons and periodic solutions of the Rosenau-KdV using the sine-cosine and the tanh methods23. Turgut Ak et al. devised the numerical technique for the Rosenau-KdV-RLW problem based on the collocation fnite element method with quintic B-splines24. Gao and Tian investigated the Rosenau similarity reductions and exact solutions using the conventional Lie symmetry technique25. They then employed the power series method to obtain analytical solutions. Abbaszadeh and Dehghan developed a two-grid interpolating element-free Galerkin method for solving the nonlinear Rosenau-regularized long-wave equation26. Razborova et al. studied shallow water waves using the Rosenau-KdV-RLW equation, they investigate the dynamics of soliton by the use of variational principle, ansatz method, and perturbation theory27. Ghilouf et al. have examined second-order and fourth-order difference schemes28,29. Avazzadeh et al. uses a meshless radial basis function (RBF) and finite-difference (FD) method to study solitary wave solutions in the generalised Rosenau-Korteweg-de Vries-regularized long wave equation30. Turgut Ak et al. investigate numerical solutions for the Rosenau-Korteweg-de Vries equation using the subdomain approach based on the sextic B-spline basis functions31. Using Petviashvili iteration, Erbay et al. solve the Rosenau equation numerically for solitary waves32. Their work shows rapid convergence and resilience to initial approximations. A multiple integral finite volume approach for solving the Rosenau-KdV equation is presented by Guo et al., they show that it is very accurate, conservation, reliable, and stable33. Chung and Pani have provided error estimates for complying C1-fnite element method34. Omrani et al. offer a Galerkin-Crank-Nicolson completely discrete technique for the Rosenau-Burgers problem and provide error estimates for a semi-discrete finite element method35. Using the extended auxiliary equation method, Alotaibi and Althobaiti obtain accurate travelling wave solutions of the Rosenau problem, which include exponential and Jacobi elliptic functions20.
The Hirota bilinear method have been employed by researchers such as Hossen et al., who in their work committed to identifying the interactions between lump and different solitary wave solutions of the B-type Kadomtsev-Petviashvili (BKP) generalised (3 + 1)-D Kadomtsev-Petviashvili (BKP) model, which is commonly encountered in plasma physics, fluid dynamics, and feebly dispersive media36. Additionally, Abdeljabbar et al. investigate a 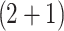 -D generalised Camassa-Holm-Kadomtsev-Petviashvili model. They derive a single lump wave, multi soliton solutions to the model, and present two, three, and four solitons. They also establish the double periodic breather waves, periodic line rogue waves, interaction between bell soliton and double periodic rogue waves, rogue and two bell solitons, two rogues, rogue and periodic wave, double periodic waves, two pair of rogue waves37. In order to improve the dynamics of nonlinear wave fields in mathematical physics and engineering, Hossen et al. investigate a higher-dimensional Breaking Soliton so;utions and offer novel bilinear forms and solutions utilising Bell polynomials, along with the derivation of rogue and solitary wave interactions38. It is evident that numerical techniques were employed in the majority of earlier studies. We attempt an analytical solution to the Rosenau equation in this paper. After a careful review of the literature, it was discovered that the Hirota bilinear transformation technique has not been used to analyse Eq. (1). Keeping this in mind, we effectively apply this strategy to Eq. (1).
-D generalised Camassa-Holm-Kadomtsev-Petviashvili model. They derive a single lump wave, multi soliton solutions to the model, and present two, three, and four solitons. They also establish the double periodic breather waves, periodic line rogue waves, interaction between bell soliton and double periodic rogue waves, rogue and two bell solitons, two rogues, rogue and periodic wave, double periodic waves, two pair of rogue waves37. In order to improve the dynamics of nonlinear wave fields in mathematical physics and engineering, Hossen et al. investigate a higher-dimensional Breaking Soliton so;utions and offer novel bilinear forms and solutions utilising Bell polynomials, along with the derivation of rogue and solitary wave interactions38. It is evident that numerical techniques were employed in the majority of earlier studies. We attempt an analytical solution to the Rosenau equation in this paper. After a careful review of the literature, it was discovered that the Hirota bilinear transformation technique has not been used to analyse Eq. (1). Keeping this in mind, we effectively apply this strategy to Eq. (1).
This manuscript is structured as follows. Section 2 describes the main steps of the method. In Sect.3, we apply this approach to solve the Rosenau problem. In section 4, we presents the graphical representation and analysis of the results. In section 5, we highlight the comparison of our findings with the existing literature of the Rosenau equation. The final part summaries the significant findings.
The method
One mathematical method for resolving NLPDEs is the Hirota bilinear transformation approach. It was initially developed in the 1970s by the mathematician Ryogo Hirota39. It is found to be a useful tool for generating soliton solutions in integrable systems. The fundamental idea behind it is to convert the original NLPDE into an algebraically and computationally solvable system of bilinear equations. Researchers like Zhao et al.40, Wang et al.41, Rizvi et al.42, Khan et al.43, Yan et al.44, Wazwaz45, Ma et al.46, Kumar and Mohan47, and more have used this method to solve a number of models in a variety of scientific fields, including fluid ions, plasma physics, ferromagnetic materials, etc.
We now give an overview of the method’s algorithm. The following describes the main steps of the method:
-
Step 1:
The Rosenau equation with two independent variables, x and t, is taken into consideration in the following form:
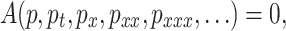 |
2 |
where  represents the wave function and A is a function in p(x, t) along with their highest order partial derivatives and nonlinear terms of p(x, t).
represents the wave function and A is a function in p(x, t) along with their highest order partial derivatives and nonlinear terms of p(x, t).
-
Step 2:
The precise solution to Eq. (2) is proposed by utilising the travelling wave equation:
 |
3 |
for constant  . By using Eq. (3), we transform Eq. (2) into the following nonlinear ordinary differential equations (ODEs):
. By using Eq. (3), we transform Eq. (2) into the following nonlinear ordinary differential equations (ODEs):
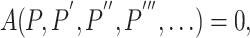 |
4 |
for polynomial A in 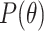 having derivatives
having derivatives  , etc is integrable differential equation.
, etc is integrable differential equation.
-
Step 3:
We integrate A in Eq. (4) in the context of
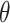 to the maximum extent possible while keeping the integral constants at 0.
to the maximum extent possible while keeping the integral constants at 0.
-
Step 4:
We presume the result obtained in stage (3) has solution of the form
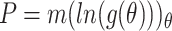 |
5 |
where  are functions for the various wave structures we are investigating.
are functions for the various wave structures we are investigating.
-
Step 5:
In this step, we use Mathematica to obtain
 , of Eq. (5) and put them into Eq. (4) to get the desired bilinear equation.
, of Eq. (5) and put them into Eq. (4) to get the desired bilinear equation.
-
Step 6:
With the assistance of Mathematica, we put the functions for the various wave forms under study into the equation obtained in stage (5). Subsequently, for each scenario, we expand, evaluate, and assemble similar terms together, setting them equal to 0. In the end, we solve this system of equations to get the potential categories of solutions for each scenario.
-
Step 7:
The categories of solutions are substituted into the various wave forms at stage (6). The outcome is then substituted in Eq. (5) to yield the solutions for
 .
.
-
Step 8:
.Finally, we substitute Eq. (3) into
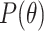 derived at step (7) to get the desired result(s).
derived at step (7) to get the desired result(s).
Application of the method
In this section, we apply our required method to produce exact solutions for the Rosenau equation.
The travelling wave transformation in Eq. (3) allow us to transform Eq. (1) into the nonlinear ODEs that follows:
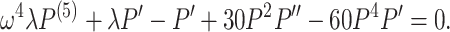 |
6 |
After integrating Eq. (6) once we have:
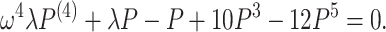 |
7 |
Assuming that the solution of Eq. (7) can be defined using the logarithm
 |
8 |
With the help of Mathematica, we calculate 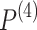 of Eq. (8) and replace it together with P into Eq. (7) to obtain the bilinear ODE:
of Eq. (8) and replace it together with P into Eq. (7) to obtain the bilinear ODE:
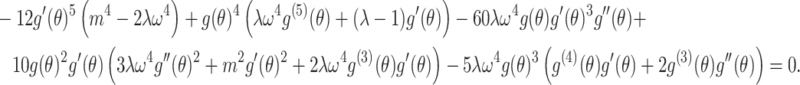 |
9 |
We input the functions for the different wave types under investigation into the equation found in step (9) with the help of Mathematica. Then, for each instance, we expand, evaluate, and arrange related terms together, setting them to 0. Ultimately, we solve this system of equations to obtain a number of potential categories for each instance.
Homoclinic breather: This wave structure is given by48
 |
10 |
By substituting Eq. (10) and its first five derivatives into Eq. (9), we obtained a simplified expression. We assemble similar terms together, and equate each expression’s coefficients to zero. We obtained the following sets of constant values, called categories:
Category 1: 
 ,
,
where h, m and 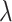 are free parameters and
are free parameters and 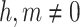 . By placing them in Eq. (10) and the outcome in Eq. (8), we obtain
. By placing them in Eq. (10) and the outcome in Eq. (8), we obtain
 |
11 |
where  Thus, in this instance, the homoclinic breather solutions of Eq. (1) are obtained as
Thus, in this instance, the homoclinic breather solutions of Eq. (1) are obtained as
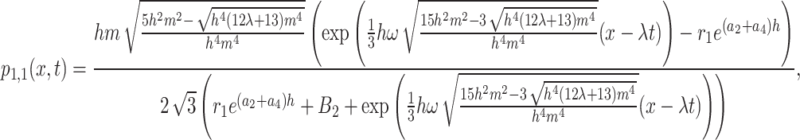 |
12 |
where 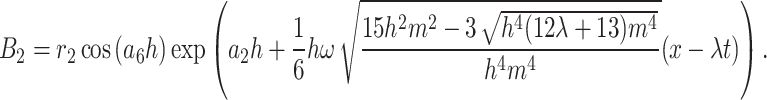
Category 2: 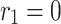 ,
, 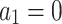 ,
,  .
.
where h,  and
and  are free parameters,
are free parameters,  and
and 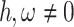 . By placing them in Eq. (13) and the outcome in Eq. (8), we obtain
. By placing them in Eq. (13) and the outcome in Eq. (8), we obtain
 |
13 |
Thus, in this instance, the homoclinic breather solutions of Eq. (1) are obtained as
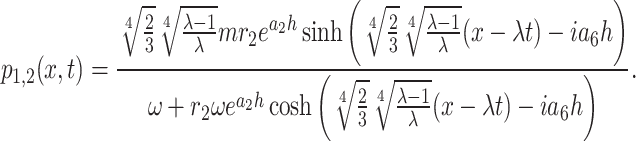 |
14 |
-
2.
Interaction via double exponents: This wave structure is given by48
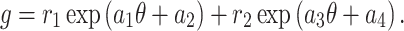 |
15 |
By substituting Eq. (15) and its first five derivatives into Eq. (9), we obtained a simplified expression. We assemble similar terms together, and equate each expression’s coefficients to zero. We obtained the following sets of constant values, called categories:
Category 1:  ,
, 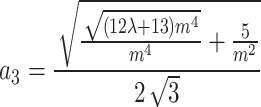 .
.
where m and 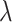 are free parameters and
are free parameters and  . By placing them in Eq. (15) and the outcome in Eq. (8), we obtain
. By placing them in Eq. (15) and the outcome in Eq. (8), we obtain
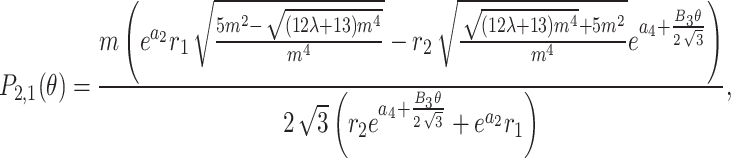 |
16 |
where 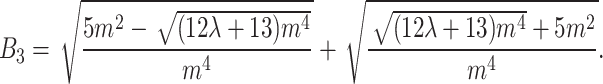 Thus, in this instance, the interaction via two exponents solutions of Eq. (1) are obtained as
Thus, in this instance, the interaction via two exponents solutions of Eq. (1) are obtained as
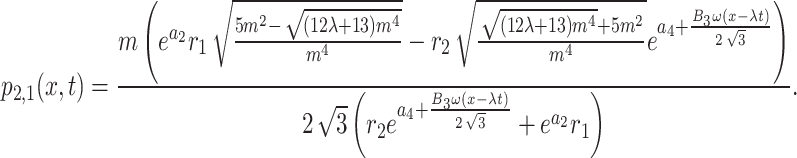 |
17 |
-
3.
Periodic Lump: This wave structure is given by49
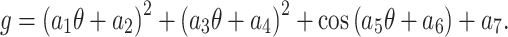 |
18 |
By substituting Eq. (18) and its first five derivatives into Eq. (9), we obtained a simplified expression. We assemble similar terms together, and equate each expression’s coefficients to zero. We obtained the following sets of constant values, called categories:
Category 1: 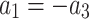 ,
, ,
,  ,
,  .
.
where 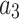 , m,
, m,  and
and 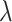 are free parameters and
are free parameters and 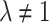 . By placing them in Eq. (18) and the outcome in Eq. (8), we obtain
. By placing them in Eq. (18) and the outcome in Eq. (8), we obtain
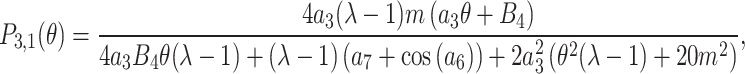 |
19 |
where  Thus, in this instance, the lump periodic solutions of Eq. (1) are obtained as
Thus, in this instance, the lump periodic solutions of Eq. (1) are obtained as
 |
20 |
Category 2: 
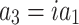 ,
, 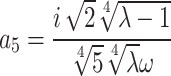 .
.
where  , m,
, m, 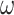 and
and  are free parameters and
are free parameters and  . By placing them in Eq. (18) and the outcome in Eq. (8), we obtain
. By placing them in Eq. (18) and the outcome in Eq. (8), we obtain
 |
21 |
Thus, in this instance, the lump periodic solutions of Eq. (1) are obtained as
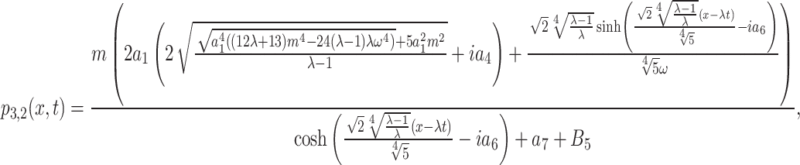 |
22 |
where 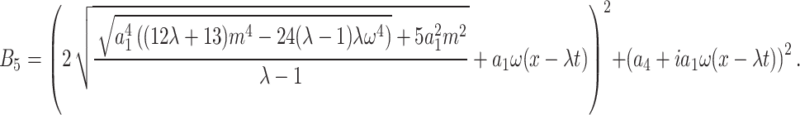
-
4.
Mixed type wave: This wave configuration is provided by49
 |
23 |
By substituting Eq. (23) and its first five derivatives into Eq. (9), we obtained a simplified expression. We assemble similar terms together, and equate each expression’s coefficients to zero. We obtained the following sets of constant values, called categories:
Category 1:
 .
.
where  and
and 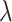 are free parameters,
are free parameters,  and
and 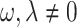 . Inserting them in Eq. (23) and then the result in Eq. (8), we have
. Inserting them in Eq. (23) and then the result in Eq. (8), we have
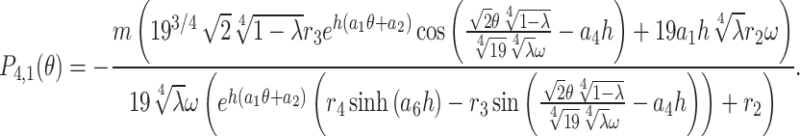 |
24 |
Therefore, the mixed type solutions of Eq. (1) in this instance are as follows:
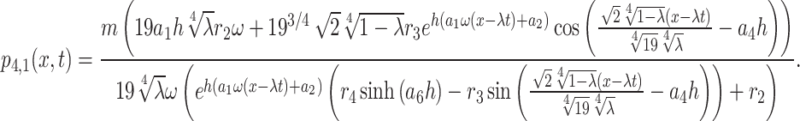 |
25 |
Category 2:
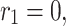 ,
, 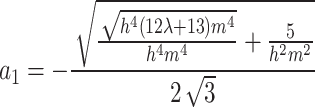 ,
, 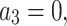 ,
, 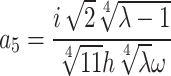 .
.
where h, m,  and
and 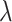 are free parameters
are free parameters 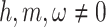 and
and 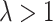 . Inserting them in Eq. (23) and then the result in Eq. (8), we have
. Inserting them in Eq. (23) and then the result in Eq. (8), we have
 |
26 |
where 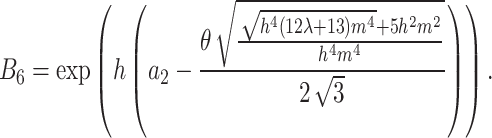 Therefore, the mixed type solutions of Eq. (1) in this instance are as follows:
Therefore, the mixed type solutions of Eq. (1) in this instance are as follows:
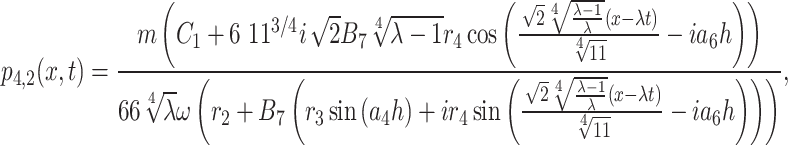 |
27 |
where 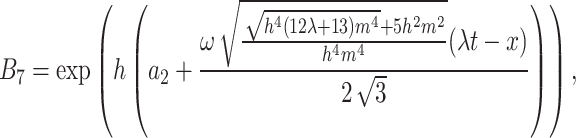

-
5.
Interaction of M-shaped with rogue and kink waves: This wave configuration is provided by50
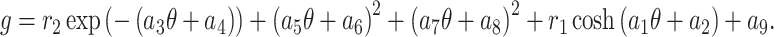 |
28 |
By substituting Eq. (28) and its first five derivatives into Eq. (9), we obtained a simplified expression. We assemble similar terms together, and equate each expression’s coefficients to zero. We obtained the following sets of constant values, called categories:
Category 1:
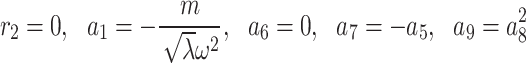 .
.
where  ,
,  , m,
, m,  and
and 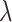 are free parameters,
are free parameters, 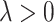 and
and 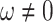 . Inserting them in Eq. (28) and then the result in Eq. (8), we have
. Inserting them in Eq. (28) and then the result in Eq. (8), we have
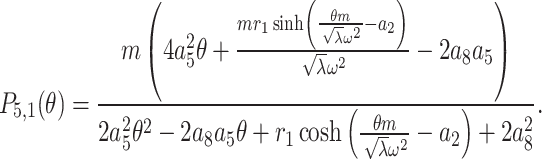 |
29 |
Therefore, the interaction of M-shaped with rogue and kink wave solutions of Eq. (1) in this instance are as follows:
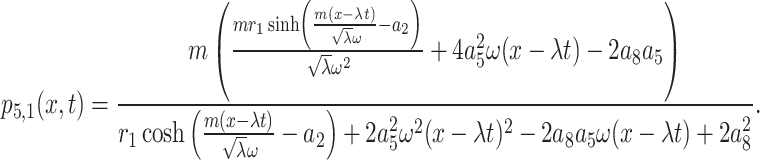 |
30 |
Category 2:
 ,
, 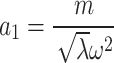 ,
, 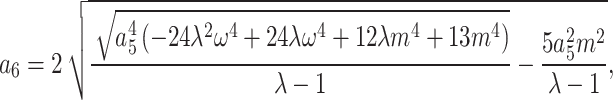
 ,
, 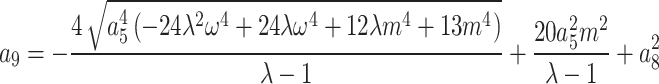 .
.
where 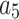 ,
, 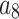 , m,
, m,  and
and 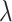 are free parameters,
are free parameters,  and
and  . Inserting them in Eq. (28) and then the result in Eq. (8), we have
. Inserting them in Eq. (28) and then the result in Eq. (8), we have
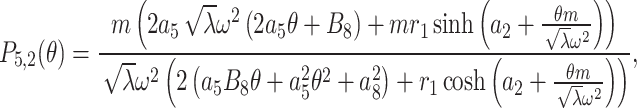 |
31 |
where 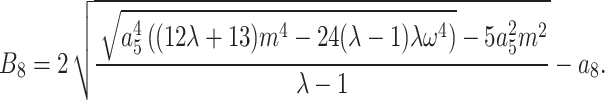 Therefore, the interaction of M-shaped with rogue and kink wave solutions of Eq. (1) in this instance are as follows:
Therefore, the interaction of M-shaped with rogue and kink wave solutions of Eq. (1) in this instance are as follows:
 |
32 |
-
6.
Interaction of M-shaped rational wave with one kink: This wave configuration is provided by50
 |
33 |
We substituted Eq. (33) and its derivatives up to the fifth order into Eq. (9) and simplified. Next, similar terms are combined, and each expression’s coefficients are set to zero. These sets of constant values (refer to as categories), were derived from this system of Eq.:
Category 1:
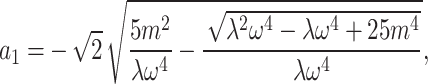
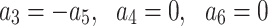 .
.
where 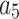 , m,
, m, 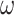 and
and 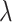 are free parameters and
are free parameters and 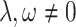 . After plugging them into Eq. (33) and the outcome into Eq. (8), we get
. After plugging them into Eq. (33) and the outcome into Eq. (8), we get
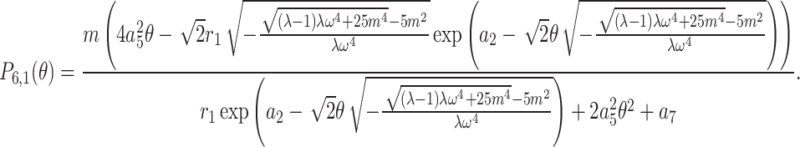 |
34 |
The interaction of M-shaped rational wave with one kink solutions to Eq. (1) in this case can therefore be found as
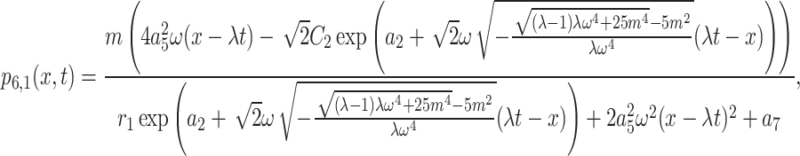 |
35 |
where 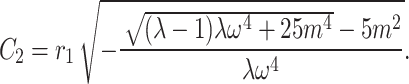
Category 2:
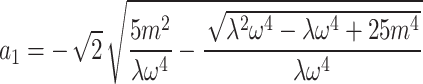 ,
, 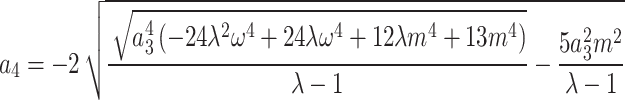 , ,
, , ,
, 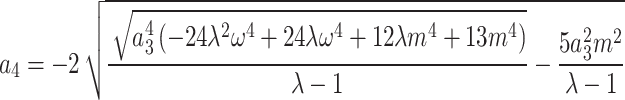 ,
, 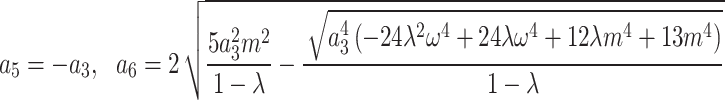 .
.
where 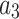 , m,
, m,  and
and 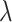 are free parameters,
are free parameters, 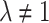 and
and 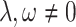 . After plugging them into Eq. (54) and the outcome into Eq. (11), we get
. After plugging them into Eq. (54) and the outcome into Eq. (11), we get
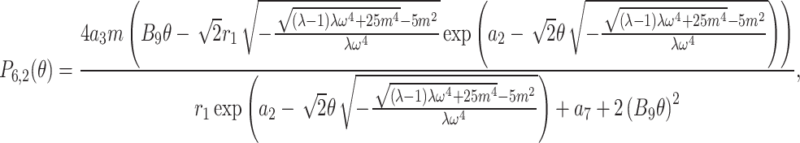 |
36 |
where  The interaction of M-shaped rational wave with one kink solutions to Eq. (1) in this case can therefore be found as
The interaction of M-shaped rational wave with one kink solutions to Eq. (1) in this case can therefore be found as
 |
37 |
where 
-
7.
Interaction of M-shaped rational wave with two kinks: This wave configuration is provided by50
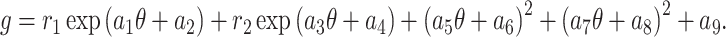 |
38 |
We substituted Eq. (38) and its derivatives up to the fifth order into Eq. (9) and simplified. Next, similar terms are combined, and each expression’s coefficients are set to zero. These sets of constant values (refer to as categories), were derived from this system of equations:
Category 1:
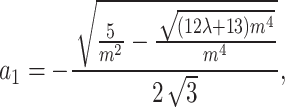
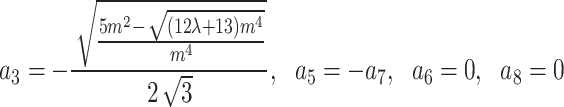 .
.
where 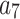 , m and
, m and 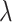 are free parameters and
are free parameters and  . After plugging them into Eq. (38) and the outcome into Eq. (8), we get
. After plugging them into Eq. (38) and the outcome into Eq. (8), we get
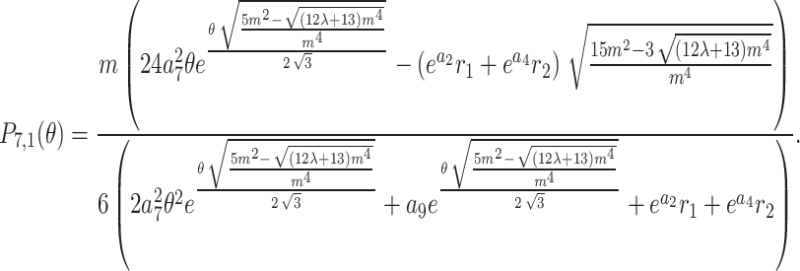 |
39 |
The interaction of M-shaped rational wave with two kinks solutions to Eq. (1) in this case can therefore be found as
 |
40 |
where 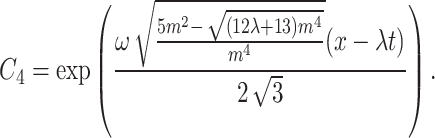
Category 2:
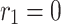 ,
, 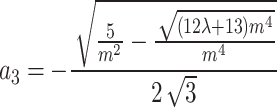 ,
, 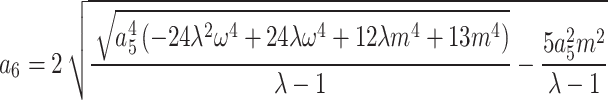 ,
, 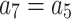 .
.
where 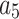 , m,
, m,  and
and 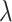 are free parameters,
are free parameters, 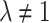 and
and 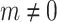 . After plugging them into Eq. (38) and the outcome into Eq. (9), we get
. After plugging them into Eq. (38) and the outcome into Eq. (9), we get
 |
41 |
where 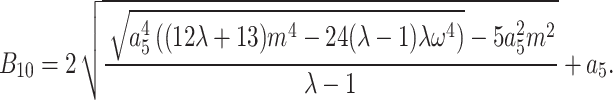 The interaction of M-shaped rational wave with two kinks solutions to Eq. (1) in this case can therefore be found as
The interaction of M-shaped rational wave with two kinks solutions to Eq. (1) in this case can therefore be found as
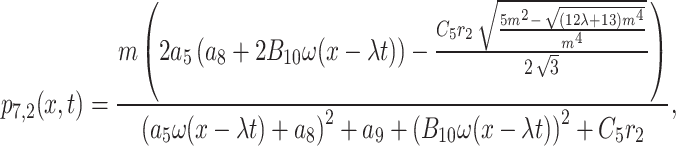 |
42 |
where 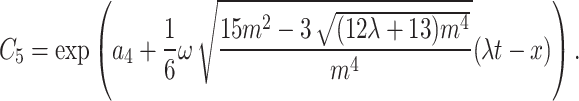
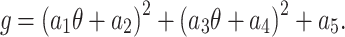 |
43 |
We substituted Eq. (43) and its derivatives up to the fifth order into Eq. (9) and simplified. Next, similar terms are combined, and each expression’s coefficients are set to zero. These sets of constant values (refer to as categories), were derived from this system of Eq.:
Category 1:
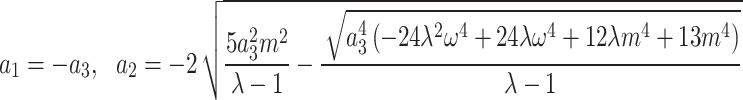 ,
, 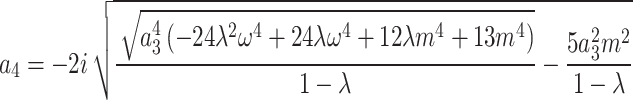 .
.
where 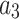 , m,
, m,  and
and 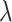 are free parameters and
are free parameters and 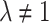 . After plugging them into Eq. (43) and the outcome into Eq. (8), we get
. After plugging them into Eq. (43) and the outcome into Eq. (8), we get
-
8.
M-shaped rational wave: This wave configuration is provided by51
 |
44 |
The M-shaped rational wave solutions to Eq. (1) in this case can therefore be found as
 |
45 |
-
9.
Multi waves: This pattern of waves is offered by48
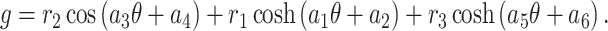 |
46 |
By substituting Eq. (46) and its first five derivatives into Eq. (9), we obtained a simplified expression. We assemble similar terms together, and equate each expression’s coefficients to zero. We obtained the following sets of constant values, called categories:
Category 1:
 ,
, 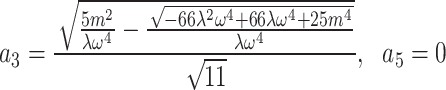 ,
,  .
.
where m,  and
and 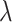 are free parameters and
are free parameters and  . Substituting them in Eq. (46) and then the outcome in Eq. (8), we have
. Substituting them in Eq. (46) and then the outcome in Eq. (8), we have
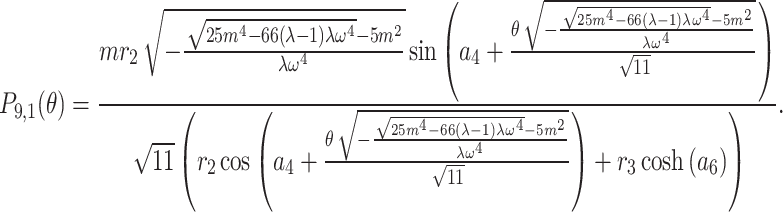 |
47 |
Therefore, in this instance, the multi wave solution of Eq. (1) is
 |
48 |
Category 2:
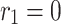 ,
, 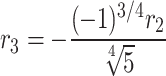 ,
,  .
.
where 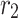 ,
,  and
and 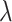 are free parameters,
are free parameters,  and
and 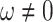 . Substituting them in Eq. (46) and then the result in Eq. (8), we have
. Substituting them in Eq. (46) and then the result in Eq. (8), we have
 |
49 |
Therefore, in this instance, the multi wave solution of Eq. (1) is
 |
50 |
-
10.
Periodic cross kink: This pattern of waves is offered by51
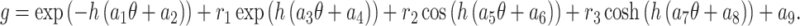 |
51 |
By substituting Eq. (10) and its first five derivatives into Eq. (9), we obtained a simplified expression. We assemble similar terms together, and equate each expression’s coefficients to zero. We obtained the following sets of constant values, called categories:
Category 1:
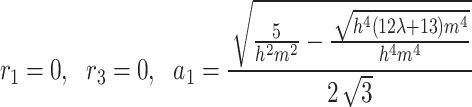 ,
, 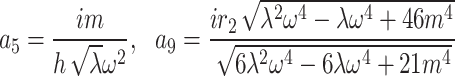 .
.
where 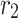 , h, m,
, h, m, 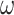 and
and 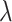 are free parameters,
are free parameters,  and
and 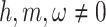 . Substituting them in Eq. (51) and then the outcome in Eq. (8), we have
. Substituting them in Eq. (51) and then the outcome in Eq. (8), we have
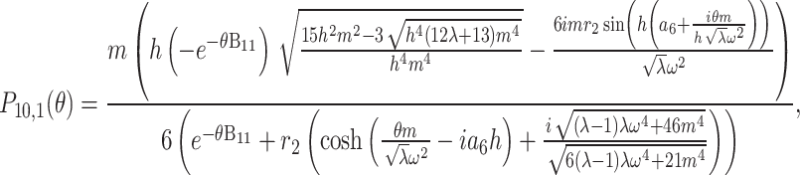 |
52 |
where 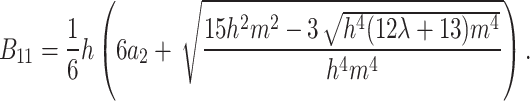 Therefore, in this instance, the periodic cross kink solution of Eq. (1) is
Therefore, in this instance, the periodic cross kink solution of Eq. (1) is
 |
53 |
Category 2:

 .
.
where 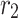 , h, m,
, h, m, 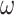 and
and 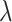 are free parameters,
are free parameters,  and
and 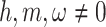 . Substituting them in Eq. (51) and then the result in Eq. (8), we have
. Substituting them in Eq. (51) and then the result in Eq. (8), we have
 |
54 |
Therefore, in this instance, the periodic cross kink solution of Eq. (1) is
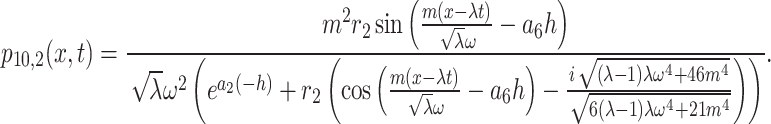 |
55 |
Analysing and graphically presenting the results
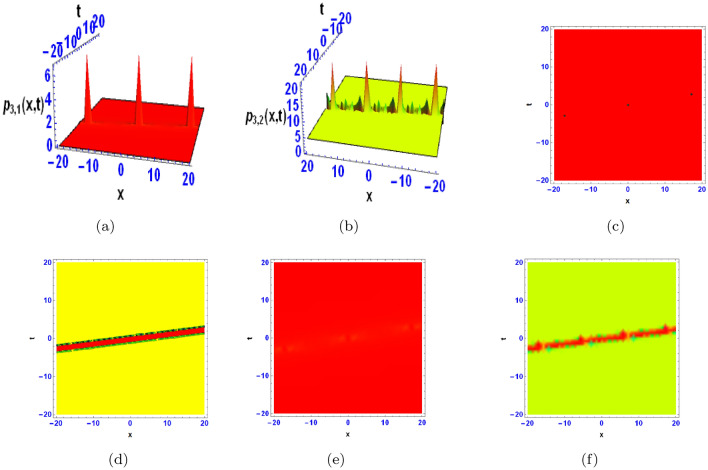
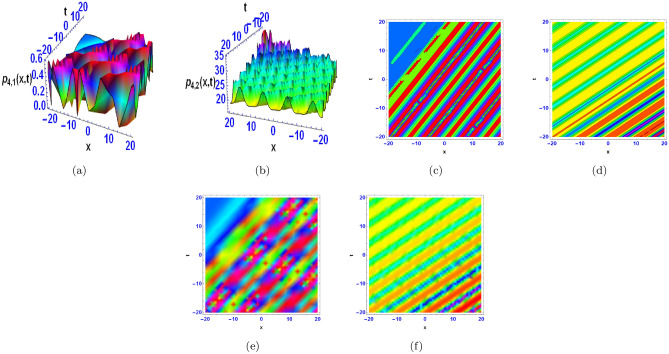
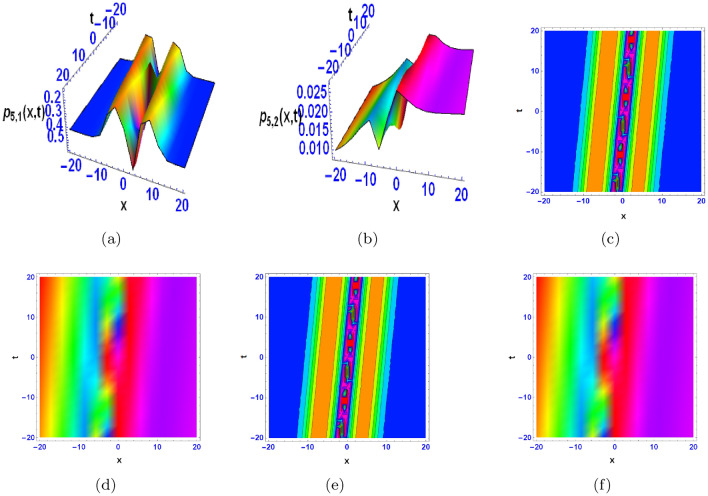
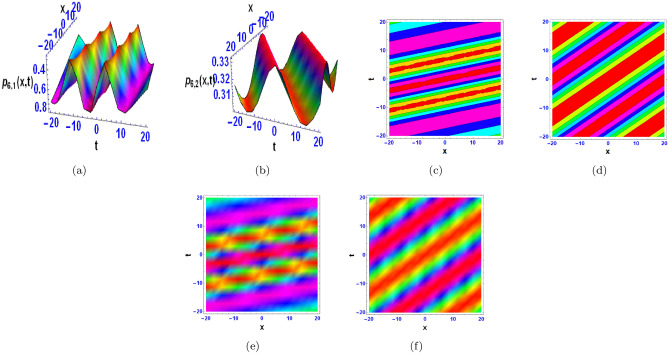
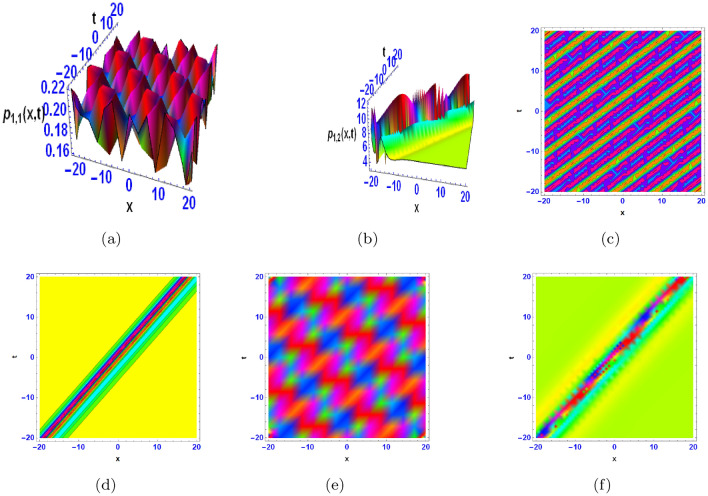
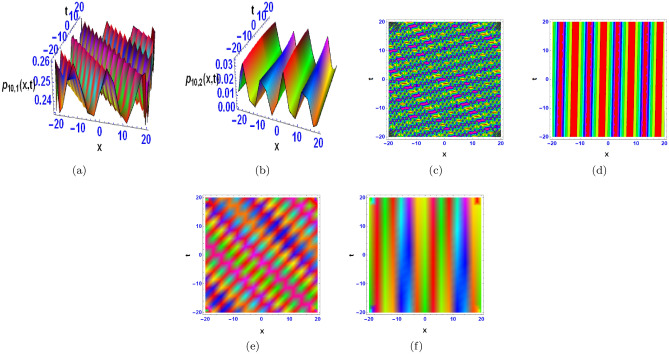
The three-dimensional (3D) figures, their corresponding contours and densities for the obtained solutions are constructed using Mathematica, and are displayed in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10, which aid in the visualisation of the solutions’ characteristics. Figure 1a shows a bright multiple breather wave, which indicate oscillatory localised waves that exchange energy between distinct modes on a periodic basis. They are frequently encountered in media having dispersion and nonlinearity. A bright breather wave with a flat kink is shown in Fig. 1b, indicating a hybrid dynamic by combining localised oscillations with a transition zone (kink) in the wave profile. Figure 2a shows an anti-kink wave, the inverse of a kink wave, which represents a localised transition in the opposite direction and is frequently encountered in media having symmetry breaking features. Periodic lump shaped waves are displayed in Fig. 3a and b. They are localised wave formations that occur on a regular basis and illustrate coherent energy localisation on a spatially periodic basis. Figure 4a depicts mixed wave of kink and breather like waves, emphasising interactions between a localised kink and oscillatory breather structures. Figure 4b shows mixed waves of kink and anti-kink waves, indicating a localised structure in which opposing transitions interact dynamically. Figure 5a and b show M-shaped waves with kinks and rogue waves, which represent a combination of acute localised transitions (kinks) and severe, transient wave episodes (rogue waves). Figure 6a and b show M-shaped waves with one kink, demonstrating sharp localised wave pattern with a solitary directional transition in the waveform. Figure 7a and b show M-shaped waves with two kinks, showing localised waves with dual directional transitions within a single structure, exhibiting complex dynamics. Figure 8a represents M-shaped wave, indicating a localised structure with an oscillating pattern mimicking a “M” shape, which is frequently a sign of nonlinear dispersion phenomena. Figure 9a displays multiple periodic breather waves, signifying an assortment of localised oscillating features that replicate in space or time. Figure 9b shows multiple periodic lump-like waves, with a succession of spatially localised waves repeating frequently.. Figure 10a and b indicate bright periodic cross kink waves, which show waves with periodic and transverse kink features and highlight complicated nonlinear relationships.
Fig. 2.
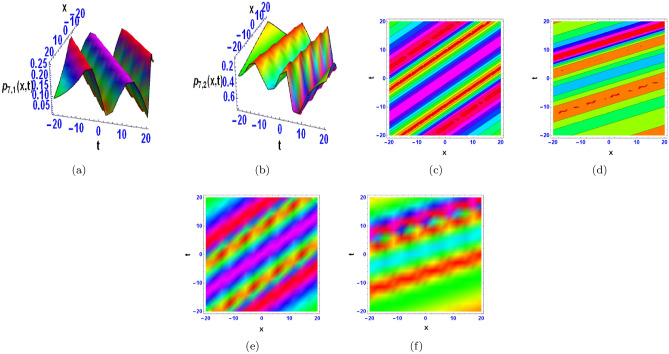
The 3D, contour and density diagrams represent the interaction via two exponent’s type wave.
Figure 3.
Displays the 3D, contour and density diagrams obtained from periodic lump-type wave.
Fig. 4.
The 3D, contour and density diagrams of the mixed-type wave are depicted.
Fig. 5.
The 3D, contour and density diagrams are obtained from the M-shaped interaction with rogue and kink waves.
Fig. 6.
Displays the 3D, contour and density diagrams of M-shaped rational wave with one kink.
Fig. 7.
Displays the 3D, contour and density diagrams of M-shaped rational wave with two kinks.
Fig. 8.
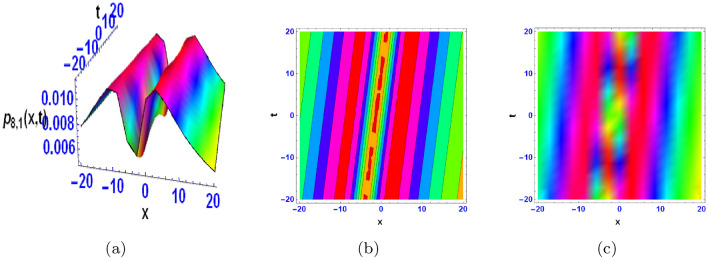
The 3D, contour and density diagrams represent the M-shaped rational wave.
Fig. 9.
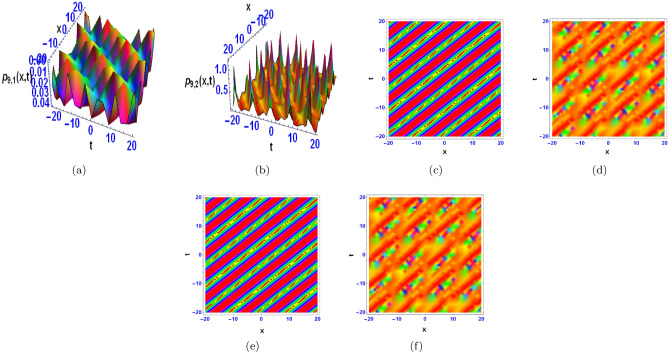
Displays the 3D, contour and density diagrams of multi-wave types.
The wave patterns that are described cover a broad spectrum of behaviours and medium-level structures. These consist of waves that exhibit sharp, localised shifts in amplitude or phase creating distinct bends, waves with abrupt flat changes in shape indicating disruptions in their regularity (bright breather wave with a flat kink), and waves with periodic oscillations and localised intensity peaks that stay stable over time (bright multiple breather wave). In addition, there are M-shaped waves with kinks and possibly rogue waves, indicating irregularities in wave behaviour; mixed waves combining kinks with breather or anti-kink characteristics; and simple M-shaped waves and those with multiple periodic breather or lump-like features. Periodic lump-shaped waves also display repeating rounded structures. Periodic kinks that intersect are indicated by the existence of bright periodic cross-kink waves, which may indicate intricate wave interactions or interference occurrences. Together, these explanations highlight how complex and varied wave dynamics are in real-world systems.
The contour plots that are produced help to visualise the wave profiles by displaying changes in both shape and intensity in different spatial areas at different times. By displaying differences in wave density before and after interactions, density plots facilitate the analysis of the impact of collisions and the creation of new waves. These graphs also make parameter tuning and optimisation easier because they illustrate how changes impact wave shape and density, which are crucial for optimising parameters and system performance. Additionally, wave quality in a range of fields can be validated, compared, and optimised through quantitative study using the contour and density plots.
Fig. 1.
The 3D, contour and density diagrams are obtained from the homoclinic breather-type wave.
Figure 1a depicts the solution 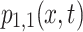 from Eq. (12) with chosen parameter values
from Eq. (12) with chosen parameter values 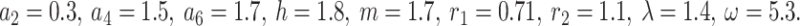 Figure 1b illustrates
Figure 1b illustrates 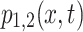 from Eq. (14) with parameter values
from Eq. (14) with parameter values 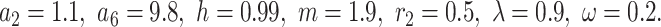 Figure 1c, d show the contour plots corresponding to Figure 1a, b respectively, while Figure 1e, f show their respective densities.
Figure 1c, d show the contour plots corresponding to Figure 1a, b respectively, while Figure 1e, f show their respective densities.
Figure 2a depicts the solution 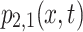 corresponding to Eq. (17) for selecting parameter values
corresponding to Eq. (17) for selecting parameter values 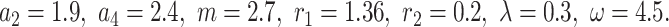 Figure 2b shows the contour of Fig. 2a, while Fig. 2c shows its density.
Figure 2b shows the contour of Fig. 2a, while Fig. 2c shows its density.
The solution 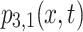 corresponding to Eq. (20) is depicted in Fig. 3a with the chosen parameter values
corresponding to Eq. (20) is depicted in Fig. 3a with the chosen parameter values  On the other hand, the solution
On the other hand, the solution  corresponding to Eq. (22) is displayed in Fig. 3b with the chosen parameter values
corresponding to Eq. (22) is displayed in Fig. 3b with the chosen parameter values 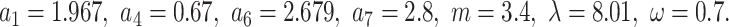 Fig. 3c, d portray the contour plots of Fig. 3a, b respectively, while Fig. 3e–f show their respective densities.
Fig. 3c, d portray the contour plots of Fig. 3a, b respectively, while Fig. 3e–f show their respective densities.
Based on the solution 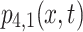 , corresponding to Eq. (25), Fig. 4a is obtained by selecting parameter values
, corresponding to Eq. (25), Fig. 4a is obtained by selecting parameter values  The solution
The solution 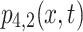 corresponding to Eq. (27) is shown in Fig. 4b for choosing parameter values
corresponding to Eq. (27) is shown in Fig. 4b for choosing parameter values  . Figure 4c, d show the contours of Fig. 4a, b respectively, while Fig. 4e–f show their respective densities.
. Figure 4c, d show the contours of Fig. 4a, b respectively, while Fig. 4e–f show their respective densities.
Figure 5a is depicted from the solution 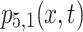 corresponding to Eq. (30) for chosen parameter values
corresponding to Eq. (30) for chosen parameter values 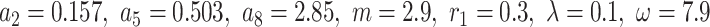 . Figure 5b is acquired from the solution
. Figure 5b is acquired from the solution 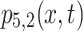 corresponding to Eq. (32) for parameter values
corresponding to Eq. (32) for parameter values 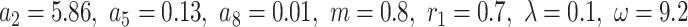 . Figure 5c, d show the contour plots of Fig. 5a, b respectively, while Fig. 5e–f show their respective densities.
. Figure 5c, d show the contour plots of Fig. 5a, b respectively, while Fig. 5e–f show their respective densities.
The solution 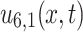 corresponding to Eq. (35) is shown in Fig. 6a for choosing parameter values
corresponding to Eq. (35) is shown in Fig. 6a for choosing parameter values  . The solution
. The solution 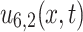 corresponding to Eq. (37) is shown in Fig. 6b for the parameter values
corresponding to Eq. (37) is shown in Fig. 6b for the parameter values 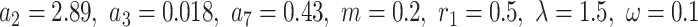 . Figure 6c–d show the contours of Fig. 6a, b respectively, while Fig. 6e–f show their respective densities.
. Figure 6c–d show the contours of Fig. 6a, b respectively, while Fig. 6e–f show their respective densities.
Figure 7a depicts the solution 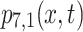 from Eq. (40) with chosen parameter values
from Eq. (40) with chosen parameter values 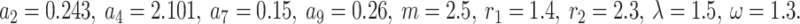 Fig. 7b illustrates
Fig. 7b illustrates 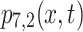 from Eq. (42) with parameter values
from Eq. (42) with parameter values 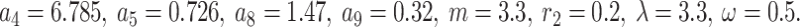 Fig. 7c–d show the contour plots corresponding to Fig. 7a, b respectively, while Fig. 7e–f show their respective densities.
Fig. 7c–d show the contour plots corresponding to Fig. 7a, b respectively, while Fig. 7e–f show their respective densities.
The solution  corresponding to Eq. (45) is depicted in Fig. 8a with the chosen parameter values
corresponding to Eq. (45) is depicted in Fig. 8a with the chosen parameter values  Fig. 8b portrays the contour plot of Fig. 8a, while Fig. 8c shows its density.
Fig. 8b portrays the contour plot of Fig. 8a, while Fig. 8c shows its density.
Based on the solution  , corresponding to Eq. (48), Fig. 9a is obtained by selecting parameter values
, corresponding to Eq. (48), Fig. 9a is obtained by selecting parameter values 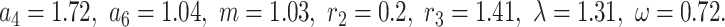 The solution
The solution  corresponding to Eq. (50) is shown in Fig. 9b for choosing parameter values
corresponding to Eq. (50) is shown in Fig. 9b for choosing parameter values 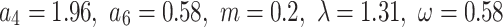 . Fig. 9c, d show the contours of Fig. 9a, b respectively, while Fig. 9e–f show their respective densities.
. Fig. 9c, d show the contours of Fig. 9a, b respectively, while Fig. 9e–f show their respective densities.
Fig. 10.
The 3D, contour and density diagrams represent the periodic cross-kink type wave.
Based on the solution  , corresponding to Eq. (53), Fig. 10a is obtained by selecting parameter values
, corresponding to Eq. (53), Fig. 10a is obtained by selecting parameter values 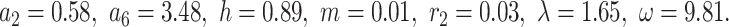 The solution
The solution  corresponding to Eq. (55) is shown in Fig. 10b for choosing parameter values
corresponding to Eq. (55) is shown in Fig. 10b for choosing parameter values  . Figure 10c, d show the contours of Fig. 10a, b respectively, while Fig. 10e–f show their respective densities.
. Figure 10c, d show the contours of Fig. 10a, b respectively, while Fig. 10e–f show their respective densities.
A Comparative analysis of the obtained solutions
Numerous numerical and analytical methods have been used to study the Rosenau equation in great detail, with an emphasis on its dynamics, stability, and solutions. Researchers like Park21 and Zuo23 used explicit techniques and methodologies like sine-cosine and tanh to generate soliton and periodic solutions. With contributions by Chung and Ha22, and Turgut Ak et al.24, finite element and collocation approaches have been used extensively, with a focus on error analysis and stability. Additional understanding of soliton dynamics has been gained through symmetry-based methods by Gao and Tian25, and iterative strategies like Petviashvili iteration by Erbay et al.32. Solitary solutions and shallow water waves have been investigated using sophisticated techniques, such as radial basis functions and variational principles, which have demonstrated accuracy and dependability. Numerical accuracy and soliton behaviours are the main topics of these investigations.
By contrast, we present a different method for solving the Rosenau equation: the Hirota bilinear transformation. This method considerably broadens the range of wave behaviours examined by revealing a variety of waveforms, including M-shaped waves, mixed waves, periodic lumps, breathers, and kinks/anti-kinks. Our study clarifies wave shape, stability, and interactions by examining the function of free parameters. These results extend the equation’s use in domains such as material science and fluid dynamics.
Conclusion
In this work, we gave a comprehensive study of the wave behaviours of the nonlinear Rosenau equation utilising the Hirota bilinear transformation and the help of Mathematica. Through our extensive examination, we have found a wide diversity of wave patterns, including M-shaped waves, mixed waves, bright and dark breathers, periodic lumps, and anti-kink. These patterns reveal deeply the complex dynamics of waves in a range of physical systems.
The relevance of our results goes beyond abstract mathematics and has immediate applications to real world phenomena. For example, M-shaped waves with kinks and potentially rogue waves are indicative of anomalies and unusual occurrences that may affect atmospheric or oceanic wave dynamics. Periodic lump-shaped waves indicate the presence of recurring structures in wave phenomena, which may be important to comprehend how waves propagate in fluid dynamics or materials science. The periodic kink intersections observed in bright periodic cross-kink waves provide insights into complex wave phenomena and interference events. These findings could be beneficial to studies on wave propagation in fibre optics or fields of electromagnetic waves, where disruptions are prevalent.
Also, our graphical representations, which include density plots, contour plots, and three-dimensional plots, enable a detailed understanding of wave profiles and their fluctuations over time and space. This ability is especially helpful in fields like environmental science, where research on wave patterns can provide details regarding the propagation of seismic waves, the distribution of wave energy, and the erosion of coastal areas.
The cutting-edge of this work is the employment of Hirota’s bilinear technique to develop novel types of solutions as discussed above, examine their relationships, and provide better representations, which goes beyond previous solitons obtained from the Rosenau equation. As a whole, this work advances the theoretical understanding of wave dynamics through mathematical technique of the Hirota bilinear transformation, and offers tangible interpretations and applications across multiple scientific fields. Our results have implications for a broad range of physical phenomena and industrial applications, ranging from wave-based technology optimisation to the prediction of extreme wave events.
Author contributions
B.C. writing original draft; M.Z.B. methodology and investigation; N.A . supervision and investigation and M.W.Y. review and editing and W.W.M review the article.
Data availability
All data generated or analysed during this study are included in this article.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Baboucarr Ceesay, Email: bceesay@utg.edu.gm.
Nauman Ahmed, Email: nauman.ahmed@math.uol.edu.pk.
References
- 1.He, J. Variational iteration method for delay differential equations. Commun. Nonlinear Sci. Numer. Simul.2(4), 235–236 (1997). [Google Scholar]
- 2.Liu, J. G. & Osman, M. S. Nonlinear dynamics for different nonautonomous wave structures solutions of a 3D variable-coefficient generalized shallow water wave equation. Chin. J. Phys.77, 1618–1624 (2022). [Google Scholar]
- 3.Shahzad, T. et al. On the analytical study of predator-prey model with Holling-II by using the new modified extended direct algebraic technique and its stability analysis. Results Phys.51, 106677 (2023). [Google Scholar]
- 4.He, J. H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng.178(3–4), 257–262 (1999). [Google Scholar]
- 5.Clarkson, P. A. & Mansfield, E. L. Algorithms for the nonclassical method of symmetry reductions. SIAM J. Appl. Math.54(6), 1693–1719 (1994). [Google Scholar]
- 6.Adomian, G. Solving frontier problems of physics: the decomposition method (Springer Science & Business Media, Cham, 2013). [Google Scholar]
- 7.Abdou, M. A. The extended tanh method and its applications for solving nonlinear physical models. Appl. Math. Comput.190(1), 988–996 (2007). [Google Scholar]
- 8.Rogers, C. & Shadwick, W. F. Bäcklund transformations and their applications (Academic Press, New York, NY, USA, 1982). [Google Scholar]
- 9.Novikov, S., Manakov, S. V., Pitaevskii, L. P. & Zakharov, V. E. Theory of solitons: the inverse scattering method (Springer Science & Business Media, Cham, 1984). [Google Scholar]
- 10.Shaikh, T. S. et al. Acoustic wave structures for the confirmable time-fractional Westervelt equation in ultrasound imaging. Results Phys.49, 106494 (2023). [Google Scholar]
- 11.Wang, Z. & Zhang, H. Q. A new generalized Riccati equation rational expansion method to a class of nonlinear evolution equation with nonlinear terms of any order. Appl. Math. Comput.186, 693–704 (2007). [Google Scholar]
- 12.Shahid, N. et al. Dynamical study of groundwater systems using the new auxiliary equation method. Results Phys.58, 107444 (2024). [Google Scholar]
- 13.Al-Amin, M., Islam, M. N. & Akbar, M. A. The closed-form soliton solutions of the time-fraction phi-four and (2+ 1)-dimensional Calogero-Bogoyavlenskii-Schiff model using the recent approach. Partial Differ. Equ. Appl. Math.5, 100374 (2022). [Google Scholar]
- 14.Rahman, M. A. et al. Mathematical analysis of some new adequate broad-ranging soliton solutions of nonlinear models through the recent technique. Partial Differ. Equ. Appl. Math.9, 100634 (2024). [Google Scholar]
- 15.Al-Amin, M., Islam, M. N., Ilhan, O. A., Akbar, M. A. & Soybas, D. Solitary wave solutions to the modified Zakharov-Kuznetsov and the (2+ 1)-dimensional Calogero-Bogoyavlenskii-Schiff models in mathematical physics. J. Math.2022(1), 5224289 (2022). [Google Scholar]
- 16.Afrin, F. U. Solitary wave solutions and investigation the effects of different wave velocities of the nonlinear modified Zakharov-Kuznetsov model for the wave propagation in nonlinear media. Partial Differ. Equ. Appl. Math.8, 100583 (2023). [Google Scholar]
- 17.Islam, M. N., Al-Amin, M., Akbar, M. A., Wazwaz, A. M. & Osman, M. S. Assorted optical soliton solutions of the nonlinear fractional model in optical fibers possessing beta derivative. Phys. Scr.99(1), 015227 (2023). [Google Scholar]
- 18.Rosenau, P. A quasi-continuous description of a nonlinear transmission line. Phys. Scr.34(6B), 827 (1986). [Google Scholar]
- 19.Rosenau, P. Dynamics of dense discrete systems: High order effects. Progress Theoret. Phys.79(5), 1028–1042 (1988). [Google Scholar]
- 20.Alotaibi, T. & Althobaiti, A. Exact wave solutions of the nonlinear Rosenau equation using an analytical method. Open Phys.19(1), 889–896 (2021). [Google Scholar]
- 21.Park, M. A. Pointwise decay estimates of solutions of the generalized Rosenau equation. J. Korean Math. Soc.29(2), 261–280 (1992). [Google Scholar]
- 22.Chung, S. K. & Ha, S. N. Finite element Galerkin solutions for the Rosenau equation. Appl. Anal.54(1–2), 39–56 (1994). [Google Scholar]
- 23.Zuo, J. M. Solitons and periodic solutions for the Rosenau-KdV and Rosenau-Kawahara equations. Appl. Math. Comput.215(2), 835–840 (2009). [Google Scholar]
- 24.Ak, T., Karakoc, S. & Biswas, A. Numerical scheme to dispersive shallow water waves. J. Comput. Theor. Nanosci.13(10), 7084–7092 (2016). [Google Scholar]
- 25.Gao, B. & Tian, H. Lie symmetry reductions and exact solutions to the Rosenau equation. Adv. Math. Phys.2014, 714635 (2014). [Google Scholar]
- 26.Abbaszadeh, M. & Dehghan, M. The two-grid interpolating element free Galerkin (TG-IEFG) method for solving Rosenau-regularized long wave (RRLW) equation with error analysis. Appl. Anal.97(7), 1129–1153 (2018). [Google Scholar]
- 27.Razborova, P., Moraru, L. & Biswas, A. Perturbation of dispersive shallow water waves with Rosenau-KdV-RLW equation and power law nonlinearity. Rom. J. Phys.59(7–8), 658–676 (2014). [Google Scholar]
- 28.Omrani, K. & Ghiloufi, A. An efficient computational approach for two-dimensional variant of nonlinear-dispersive model of shallow water wave. Eng. Comput.37, 2679–2688 (2021). [Google Scholar]
- 29.Ghiloufi, A. & Omrani, K. New conservative difference schemes with fourth-order accuracy for some model equation for nonlinear dispersive waves. Numer. Methods Partial Differ. Equ.34(2), 451–500 (2018). [Google Scholar]
- 30.Avazzadeh, Z., Nikan, O. & Machado, J. A. T. Solitary wave solutions of the generalized Rosenau-KdV-RLW equation. Mathematics8(9), 1601 (2020). [Google Scholar]
- 31.Ak, T., Karakoc, Battal G. & Triki, H. Numerical simulation for treatment of dispersive shallow water waves with Rosenau-KdV equation. Eur. Phys. J. Plus131, 1–15 (2016). [Google Scholar]
- 32.Erbay, H. A., Erbay, S. & Erkip, A. Numerical computation of solitary wave solutions of the Rosenau equation. Wave Motion98, 102618 (2020). [Google Scholar]
- 33.Guo, C., Wang, Y. & Luo, Y. A Conservative and Implicit Second-Order Nonlinear Numerical Scheme for the Rosenau-KdV Equation. Mathematics9(11), 1183 (2021). [Google Scholar]
- 34.Chunk, S. K. & Pani, A. K. Numerical methods for the rosenau equation: Rosenau equation. Appl. Anal.77(3–4), 351–369 (2001). [Google Scholar]
- 35.Omrani, K., Abidi, F., Achouri, T. & Khiari, N. A new conservative finite difference scheme for the Rosenau equation. Appl. Math. Comput.201(1–2), 35–43 (2008). [Google Scholar]
- 36.Hossen, M. B., Roshid, H. O., Ali, M. Z. & Rezazadeh, H. Novel dynamical behaviors of interaction solutions of the (3+ 1)-dimensional generalized B-type Kadomtsev-Petviashvili model. Phys. Scr.96(12), 125236 (2021). [Google Scholar]
- 37.Abdeljabbar, A., Hossen, M. B., Roshid, H. O. & Aldurayhim, A. Interactions of rogue and solitary wave solutions to the (2+ 1)-D generalized Camassa-Holm-KP equation. Nonlinear Dyn.110(4), 3671–3683 (2022). [Google Scholar]
- 38.Hossen, M. B., Roshid, H. O. & Ali, M. Z. Characteristics of the solitary waves and rogue waves with interaction phenomena in a (2+ 1)-dimensional Breaking Soliton equation. Phys. Lett. A382(19), 1268–1274 (2018). [Google Scholar]
- 39.Hirota, R. The direct method in soliton theory (No. 155). Cambridge University Press. (2004)
- 40.Zhao, J., Manafian, J., Zaya, N. E. & Mohammed, S. A. Multiple rogue wave, lump-periodic, lump-soliton, and interaction between k-lump and k-stripe soliton solutions for the generalized KP equation. Math. Methods Appl. Sci.44(6), 5079–5098 (2021). [Google Scholar]
- 41.Wang, M. et al. Lump, lumpoff, rogue wave, breather wave and periodic lump solutions for a (3+ 1)-dimensional generalized Kadomtsev-Petviashvili equation in fluid mechanics and plasma physics. Int. J. Comput. Math.97(12), 2474–2486 (2020). [Google Scholar]
- 42.Rizvi, S. T., Seadawy, A. R. & Ahmad, A. Study of lump, rogue, multi, M shaped, periodic cross kink, breather lump, kink-cross rational waves and other interactions to the Kraenkel-Manna-Merle system in a saturated ferromagnetic material. Opt. Quant. Electron.55(9), 813 (2023). [Google Scholar]
- 43.Khan, M. H., & Wazwaz, A. M. Lump, multi-lump, cross kinky-lump and manifold periodic-soliton solutions for the (2+ 1)-D Calogero-Bogoyavlenskii-Schiff equation.Heliyon 6(4). (2020) [DOI] [PMC free article] [PubMed]
- 44.Yan, X. W., Tian, S. F., Dong, M. J., Zhou, L. & Zhang, T. T. Characteristics of solitary wave, homoclinic breather wave and rogue wave solutions in a (2+ 1)-dimensional generalized breaking soliton equation. Comput. Math. Appl.76(1), 179–186 (2018). [Google Scholar]
- 45.Wazwaz, A. M. The Hirota’s direct method and the tanh-coth method for multiple-soliton solutions of the Sawada-Kotera-Ito seventh-order equation. Appl. Math. Comput.199(1), 133–138 (2008). [Google Scholar]
- 46.Ma, Y. L., Wazwaz, A. M. & Li, B. Q. Soliton resonances, soliton molecules, soliton oscillations and heterotypic solitons for the nonlinear Maccari system. Nonlinear Dyn.111(19), 18331–18344 (2023). [Google Scholar]
- 47.Kumar, S. & Mohan, B. A novel and efficient method for obtaining Hirota’s bilinear form for the nonlinear evolution equation in (n+ 1) dimensions. Partial Differ. Equ. Appl. Math.5, 100274 (2022). [Google Scholar]
- 48.Ceesay, B. et al. Modelling symmetric ion-acoustic wave structures for the BBMPB equation in fluid ions using Hirota’s bilinear technique. Symmetry15(9), 1682 (2023). [Google Scholar]
- 49.Ozsahin, D. U. et al. Multiwaves, breathers, lump and other solutions for the Heimburg model in biomembranes and nerves. Sci. Rep.14(1), 10180 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ceesay, B., Ahmed, N., Baber, M. Z. & Akgül, A. Breather, lump, M-shape and other interaction for the Poisson-Nernst-Planck equation in biological membranes. Opt. Quant. Electron.56(5), 853 (2024). [Google Scholar]
- 51.Rizvi, S. T. et al. Rogue, multi-wave, homoclinic breather, M-shaped rational and periodic-kink solutions for a nonlinear model describing vibrations. Results Phys.29, 104654 (2021). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analysed during this study are included in this article.