Data-driven exploration of weak coordination microenvironment in solid-state electrolyte for safe and energy-dense batteries

Abstract

The unsatisfactory ionic conductivity of solid polymer electrolytes hinders their practical use as substitutes for liquid electrolytes to address safety concerns. Although various plasticizers have been introduced to improve lithium-ion conduction kinetics, the lack of microenvironment understanding impedes the rational design of high-performance polymer electrolytes. Here, we design a class of Hofmann complexes that offer continuous two-dimensional lithium-ion conduction channels with functional ligands, creating highly conductive electrolytes. Assisting with unsupervised learning, we use Climbing Image-Nudged Elastic Band simulations to screen lithium-ion conductors and screen out five potential candidates that elucidate the impact of lithium coordination environment on conduction behavior. By adjusting the covalency competition between Metal−O and Li−O bonds within Hofmann complexes, we can manipulate weak coordination environment of lithium-ion for rapid conduction kinetics. Li | |sulfurized polyacrylonitrile (SPAN) cell using solid-state polymer electrolytes with predicted Co(dimethylformamide)₂Ni(CN)₄ delivers an initial discharge capacity of 1264 mAh g⁻¹ with a capacity retention of 65% after 500 cycles at 0.2 C (335 mA g⁻¹), at 30 °C ± 3 °C. The assembled 0.6 Ah Li | |SPAN pouch cell delivers an areal discharge capacity of 3.8 mAh cm⁻² at the second cycle with a solid electrolyte areal mass loading of 18.6 mg cm⁻² (mass-to-capacity ratio of 4.9).

The lack of microenvironment understanding results in unsatisfactory conductivity of solid polymer electrolytes. Here, authors report a data-driven exploration of weak coordination manipulation by plasticizer design for safe and energy-dense batteries.

Introduction

The use of solid-state batteries could address the safety concerns of conventional lithium-ion batteries with flammable liquid electrolytes. Pairing with lithium metal anode is promising for next-generation safe and energy-dense battery systems¹. Solid-state polymer electrolytes (SPEs) command significant commercial interest due to their flexibility, scalability, affordability, environmental friendliness, and good interface capability while their practical use is stifled by unsatisfactory ionic conductivity (10^–8 to 10^–5 S cm^–1) due to limited kinetics of segmental motion^2,3 (Fig. 1a). Plasticizing additives are expected to improve the ionic conductivity of SPEs. For example, the presence of residual dielectric solvents such as dimethylformamide (DMF), could facilitate the dissociation of lithium salts and improve transport kinetics^4,5. Unfortunately, the uncontrolled side reaction causes negative electrode corrosion, which, together with the continuous depletion of DMF, ultimately leads to poor stability of SPEs^6,7. Inorganic fillers have been added to SPEs to improve ionic conductivity by reducing the polymer crystallinity and constructing multiple pathways for lithium-ion (Li⁺) migration^8,9. Notably, certain fillers such as dielectric materials BaTiO₃ exhibit great affinity to residue sorbents and thus reduce the solvent decomposition^7,10. Despite the numerous reported strategies to improve ionic conductivity and sequester the residual solvent^11,12, the regulation mechanism particularly those influencing the Li⁺ coordination environment, remains unclear, substantially preventing the rational design of SPEs-based batteries¹³.

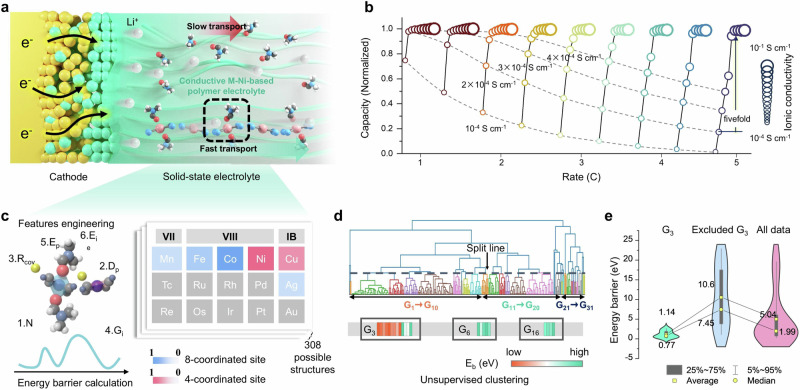
Fig. 1. CI-NEB simulations and machine learning methods for good Li⁺ conductor discovery.

a Schematic illustration of polymer electrolyte system and the need of high ionic conductivities. b The relationship between battery capacity, rate, and the ionic conductivity of the electrolytes where different colors indicate the charge/discharge rates from 1 C to 5 C and the sizes of spheres represent various ionic conductivities of the electrolytes. The dashed lines indicate the capacity with one specific ionic conductivity at various rates. c Construction of sample database and fingerprints constitute model features to predict E_b where blue and red elements represent octahedral sites M₁, and square planar sites M₂, respectively. N, D_p, R_cov, G_i, E_p, E_i indicate atomic number, dipole polarizability, covalent radius, group_id, Pauling energy, and first ionization energy, respectively. The blue, red, gray, white, and yellow spheres represent nitrogen, oxygen, carbon, hydrogen, and lithium, respectively. d Bottom-up tree (dendrogram) generating AHC algorithm where all Hofmann complexes are divided into 31 groups, labeled G₁-G₃₁, and different groups are denoted in different colors. Mapping the dendrogram to conductivity, revealing the distribution of 20 known structures where the orange and green bars represent low and high E_b, respectively. e Violin plots demonstrating E_b distribution.

Manipulating the interaction between inorganic fillers and solvents shows promise to balance ionic conductivity with mechanical strength while being durable by suppressing the solvent decomposition and generating a relatively stable inorganic-rich solid electrolyte interphase¹⁴. We designed layered Hofmann coordination complexes¹⁵ to functionalize DMF on Hofmann coordination frameworks as active ligands. This effectively sequesters the DMF and provides two-dimensional channels for fast ion transportation via a ligand-assisted mechanism. Besides, tunable substituting metal sites in the Hofmann complex make the possibility to modify the interaction with DMF ligands thus further regulating the lithium coordination environment. Based on the above considerations, Hofmann complexes were selected as a model system to investigate the influence of DMF regulation and elucidate a representative physical descriptor that mirrors the regulation mechanism on ionic conductivity.

Here, we use unsupervised learning and Climbing Image-Nudged Elastic Band (CI-NEB) simulations to screen series Hofmann structures for potentially fast Li⁺ conductors for solid-state batteries, as the workflow diagram demonstrated in Supplementary Fig. 1. The use of machine learning-driven modeling allowed for fast screening and prediction using a reference database of small-scale computations. To generate the dataset for the ML model, M₁ and M₂ were substituted to create 308 different candidates (22 M₁ × 14 M₂). M(DMF)₂Ni(CN)₄ (M = Mn²⁺, Fe²⁺, Co²⁺, Ni²⁺ or Cu²⁺) were selected for further investigation which shows an inverse volcano-type trend of diffusion barrier of ion migration, yielding the highest ionic conductivity of Co(DMF)₂Ni(CN)₄. SPEs-based cells with Co(DMF)₂Ni(CN)₄ exhibited the best electrochemical performance among those with different Hofmann structures, achieving stable Li plating/stripping in Li | |Li symmetric cell for 5000 h at 0.1 mA cm⁻² with an initial polarization of 27.9 mV. A 0.6 Ah pouch cell assembled with high-capacity sulfurized polyacrylonitrile (SPAN) cathodes, delivered an impressive areal capacity of 3.8 mAh cm⁻², suggesting the practical potential of SPEs with Co(DMF)₂Ni(CN)₄ for safe and energy-dense batteries. Electronic level understanding is further investigated to uncover the mechanistic rationale using a combination of density functional theory (DFT) calculations and experimental results, revealing a related relationship between the lithium coordination environment and ionic conductivity. Hofmann complexes with tunable metal sites allow us to controllably modulate a weakly Li⁺ coordination environment by manipulating the strong interaction with DMF due to the competitive coexistence of M − O and Li−O bonds with  the negative relationship between M − O and Li−O bonds. Consequently, the interaction of Li−O coupling could decipher the lithium coordination environment where weak coordination indicates a slow migration barrier. This work reveals the influence of the Li⁺ coordination environment in SPEs-based batteries by modulating the interaction with the coordination component, offering a rational viewpoint to meeting conductivity requirements and designing safe and energy-dense solid-state batteries.

Results and discussion

Machine-learning approach to rapidly screen Li⁺ conductors

To further clarify the necessity of improving ionic conductivity for SPEs, we employed the finite element method to explore the capacity of varying charge-discharge rates upon the electrolytes with different ionic conductivity (Fig. 1b). We find that battery performance shows distinct threshold ionic conductivities, within which the capacity experiences a multifold increase across a limited range. For example, in a battery system operating at 1 C, an increase in the ionic conductivity of electrolytes from 1 × 10^–4 S cm^–1 to 2 × 10^–4 S cm^–1 significantly enhances electrochemical performance, ranging from 75% to 98% of the theoretical capacity. These threshold conductivities rise with increasing cycling rates, showcasing a pronounced step-change in capacity improvement under fast charging conditions. Beyond the inflection point, the capacity increment becomes gradual, suggesting that the ionic conductivity does not correlate linearly with performance as a singular metric, but rather entails a minimum threshold that needs to be satisfied. Certain solid electrolyte systems, like sulfides and NASICONs, naturally exhibit exceptional ionic conductivity, eliminating conductivity as a bottleneck, their challenges pivot toward ensuring stability and enhancing interfacial compatibility. However, as for SPEs with inadequate conductivity, the focus shifts toward improving lithium transport kinetics to meet the requirements carrying higher current density^2,16.

CI-NEB could find transition states in ion diffusion, which is crucial for predicting the rates and paths of chemical reactions. By calculating the energy barrier from the reactant to the product, CI-NEB helps to quantify the maximum energy required for particle diffusion. The simulation is also demonstrated as a highly efficient predictive calculation method for determining the Li⁺ migration energy barrier (E_b) based on the Hoffman-DMF model system. DMF is engineered on Hoffman coordination frameworks as tethered ligands, allowing Hoffman-DMF to transport Li⁺ through a ligand-assisted mechanism. The layered 2D Hoffman-DMF M₁(DMF)₂M₂(CN)₄ has octahedral sites M₁ coordinated to four nitrogen atoms and two DMF ligands, and square planar sites M₂ coordinated to four carbon atoms. To generate the dataset for the ML model, M₁ and M₂ were substituted to create 308 different candidates (22 M₁ × 14 M₂, Fig. 1c). Due to the lack of Li⁺ diffusion data in Hoffman-DMF model systems, large-scale computing costs hinder the discovery of superionic conductors through computational simulation. However, the current ML method provides a possible solution to this problem. In view of the data scarcity of energy barriers diffused by Li⁺ in the Hoffman-DMF system, it is difficult to establish a reliable prediction model with supervised ML methods. Therefore, an unsupervised hierarchical clustering method is adopted in this work to overcome the issue of sparse data and establish a reliable prediction model based on the existing precious data. 1 eV is used as the threshold to judge the size of E_b. By calculating the diffusion energy barrier of Li⁺ in the Hoffman-DMF structure, a sample database containing 20 data is obtained (Supplementary Fig. 2). The 20 Hoffman-DMF structures are classified as either high or low E_b, of which 15 are labeled high E_b and 5 are labeled low E_b.

Of the candidate database identified, feature engineering to represent candidate materials is crucial to converting original data into training data. It is closely related to the output attributes E_b, to keep the consistency and collaboration of the ML results with expert knowledge. A low-dimensional component feature vector was applied to construct feature vectors, constructing a 24-dimensional feature vector for each candidate¹⁷. Each sample type is described with a vector of 24 numbers, which are visualized in the heat map after normalizing the feature vector (Supplementary Fig. 3). The fingerprint vector consists of six pivotal parameters, including atomic number, dipole polarizability, covalent radius, group_id, Pauling energy, and first ionization energy. Considering the combination of these features yields a total of 24 items per fingerprint vector as ML inputs (Supplementary Table 1). As marked by dotted boxes in Supplementary Fig. 4, there were significant differences among the features. The 24-dimensional feature vector can differentiate among candidate samples, which is useful for subsequent clustering. The unsupervised ML models clustered 308 different candidates into 31 groups (from G₁, G₂… to G₃₁), as shown by different colors in Fig. 1d corresponding to different groups. During this process, samples clustered in the same groups are expected to exhibit similar characteristics in ion conduction, and the known structures with low E_b were concentrated in G₃. Notably, samples with low E_b (< 1 eV) were clustered in the G₃ group, which group exhibits a relatively low median and the average value of E_b as violin plots shown in Fig. 1e. Consequently, the G₃ group potentially includes fast Li⁺ conductors which would be more conducive to the subsequent experimental investigation. Note that we specifically focus on the M-Ni-DMF system, with ionic conductivity as the key performance factor. However, for meaningful quantitative comparisons across various solid-state electrolytes, it is crucial to establish comprehensive coverage of all relevant parameters, including ionic conductivity, mechanical properties, and (electro)chemical stability. Future research endeavors should prioritize the development of comprehensive descriptor sets, enabling the systematic screening of diverse solid-state electrolyte systems.

Given the successful clustering of known Hofmann complexes by unsupervised learning models, it is expected that the other candidates clustered in G₃ will exhibit high ionic conductivity. We further conducted CI-NEB simulations to assess the conductivity of these candidates discovered from cluster G₃. The following section presents the experimental electrochemical performance and characterization with the purpose of validating the efficiency of CI-NEB simulations combined with unsupervised learning results and discovering the working mechanism of ML in predicting fast Li-ion conductors. The complexes M(DMF)₂Ni(CN)₄ (M = Mn²⁺, Fe²⁺, Co²⁺, Ni²⁺ or Cu²⁺), namely M-Ni-DMF (M = Mn, Fe, Co, Ni or Cu) exhibit low E_b with a volcano-type trend from Mn to Cu, yielding the highest conductivity and lowest E_b of Co-Ni-DMF. Selecting Hofmann complexes with the same anionic [Ni(CN)₄]²⁻ substituting the octahedral sites coordinates DMF ligands make the convenience for the investigations of Li-ion coordination environment to establish the rational design and kinetic modification of Li-ion migration.

Design, synthesis, and characterization of M(DMF)₂Ni(CN)₄ complex

CI-NEB simulations combined with unsupervised learning results indicate that samples in G₃ exhibit low E_b, and Li⁺ can move rapidly over the Hofmann complex along the 2D channels. Experimentally, we selected five Hofmann complexes M(DMF)₂Ni(CN)₄ (M = Mn²⁺, Fe²⁺, Co²⁺, Ni²⁺, or Cu²⁺) with similar structure morphology characteristics in G₃ for further investigation. Series M-Ni-DMF with the same anionic [Ni(CN)₄]²⁻ were fabricated via a ligand penetration method by substituting a series of transition metal sites bonding with two coordinated DMF molecules (Fig. 2a). The X-ray diffraction (XRD) patterns of M-Ni-DMF (Fig. 2b) fit well when substituting the octahedral metal site with different transition metals, indicating a similar crystal structure of M-Ni-DMF that can be indexed to the simulated pattern. The M-Ni-DMF structure shown in Supplementary Fig. 5 consists of 2D corrugated planes stacked above each other along the [001] axis, with absorbed DMF ligands in the interlayer region. The scanning electron microscopy (SEM) also confirms the 2D morphologic characteristic with similar sheet sizes (Supplementary Fig. 6). The precursors M(H₂O)₂Ni[CN]₄·xH₂O (denoted as M-Ni-H₂O) were synthesized via a coprecipitation method, followed by heat treatment to obtain M(H₂O)_xNi[CN]₄ (denoted as M-Ni-activate). The crystal H₂O and most of the absorbed H₂O were excluded, as the O–H and H–O–H signals disappeared in the Fourier transform infrared (FT-IR) spectra (Fig. 2c and Supplementary Fig. 7). Upon mixing the M-Ni precursor and DMF, DMF ligands diffuse into the precursor layer to assemble M-Ni-DMF with the emergence of strong C = O signals. The color change observed during the H₂O exclusion and DMF diffusion process indicates successful conversion of M-Ni-H₂O to M-Ni-DMF.

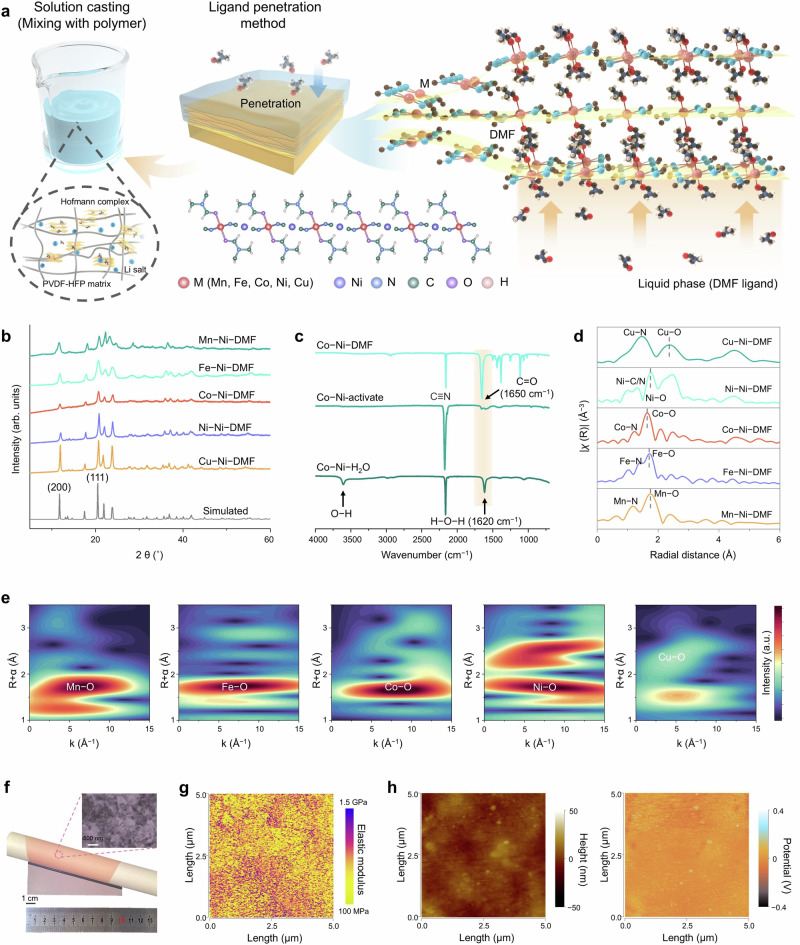
Fig. 2. Material synthesis and characterization.

a Schematic of the M-Ni-DMF fabricated by a ligand penetration method. The pink, blue, red, gray, and white spheres represent metal site, nitrogen, oxygen, carbon, and hydrogen, respectively. b XRD patterns of M-Ni-DMF. c FT-IR spectra of Co-Ni-H₂O, Co-Ni-activate, and Co-Ni-DMF. d k³-weighted Fourier transform of EXAFS analyses for M-Ni-DMF. e Wavelet-transform plots of M-Ni-DMF. f Digital photo of a roll of Co–Ni membrane. Inset: an SEM image demonstrating the uniformly dispersed Co-Ni-DMF in the composite electrolyte. Scale bar: 500 nm. g Elastic modulus distribution of M-Ni membrane measured by AFM. h AFM images of the M-Ni-DMF and PVDF composites and corresponding nano-infrared mapping spectra of the C = O vibration of DMF.

X-ray absorption near-edge structure (XANES) and extended X-ray absorption fine structure (EXAFS) analysis were used to investigate the variations in the local structure and electronic state of M-Ni-DMF. The octahedrally coordinated metal K edge from Mn to Cu shows the co-existence of M²⁺ and M³⁺_, indicating a significant electron transfer with the variation of 3 d orbital occupancy^18,19 (Supplementary Fig. 8). Operando k³-weighted Fourier transform of EXAFS depicts the local coordination environment of the M site (Fig. 2d and Supplementary Fig. 9). The first coordinated shells are assigned to the M‒N scattering paths where the second indicates M‒O coordination. Figure 2e shows wavelet transforms of M-Ni-DMF among the radial distance range of 1–3 Å, which corresponds to Metal-Oxygen (M-O) bonding. Among the five samples, M-Ni-DMF exhibits the shortest Co‒O bond length (1.65 Å) between the metal and oxygen of DMF ligand, indicating the strongest interaction between Co and DMF ligands. It is worth noting that Ni has an additional coordinated oscillation due to two possible electronic configurations in Ni-Ni-DMF: (1) octahedral site coordinated to four nitrogen atoms and two DMF ligands or (2) square planar site coordinated to four carbon atoms²⁰. The substitution of metal salts successfully achieves the assembling of series M-Ni-DMF with metal site bound to DMF ligands from Mn to Cu in the same phases, providing feasibility of the validation and physical understanding for the ML model. Additional X-ray photoelectron spectroscopy results for the supporting structural information are provided in Supplementary Figs. 10 and 11.

Solid-state electrolytes based on M-Ni-DMF, namely M-Ni (M = Mn, Fe, Co, Ni or Cu) electrolyte membranes, were fabricated by mixing them with lithium bis(fluorosulfonyl)imide (LiFSI) and poly(vinylidene fluoride-co-hexafluoropropylene) (PVDF-HFP). The membrane fabrication was controlled with the same content mass ratios, drying time, and drying condition. Series M-Ni membranes (approximately 120 μm thick) feature excellent flexibility, high strength (> 100 MPa), low cost¹², and scalability, suggesting their potential for practical use in safe and energy-dense electrolytes (Fig. 2f and Supplementary Figs. 12 and 13). High-resolution scanning electron microscope (SEM) images reveal that 2D M-Ni-DMF nanosheets are uniformly composited with PVDF-HFP and LiFSI matrix, forming uniform and continuous interfaces that facilitate Li⁺ migration. This meticulous compounding significantly enhances the mechanical integrity of the SPEs, effectively mitigating the risk of lithium dendrite penetration. Investigations using atomic force microscopy (AFM) demonstrated that the elastic modulus of the M-Ni membrane (Fig. 2g) is much higher than that of the PVDF-HFP electrolyte (Supplementary Fig. 14). Results suggest M-Ni membranes with the introduction of inorganic components can surpass 100 MPa. Furthermore, a combination of AFM and nano-infrared spectroscopy (nano-IR) techniques was used to delineate the surface texture and distribution of DMF, particularly detecting the C = O group (Fig. 2h). AFM analysis suggests the smooth surface morphology of the membranes with the surface roughness of only 50 nm. Different from the aggregated phenomenon of DMF for unmodified polymer system¹⁰, M-Ni-DMF nanosheets, and PVDF-HFP composites exhibit a uniform DMF distribution, as evidenced by substantial C = O signals throughout the plane, with fluctuation coinciding with morphology variation. The uniform distribution indicated that M-Ni-DMF nanosheets are well-composited with PVDF-HFP without significant clustering and such a homogeneous structure is advantageous to forming continuous ionic conduction channels.

Discovering potential solid-state electrolyte for lithium-metal battery

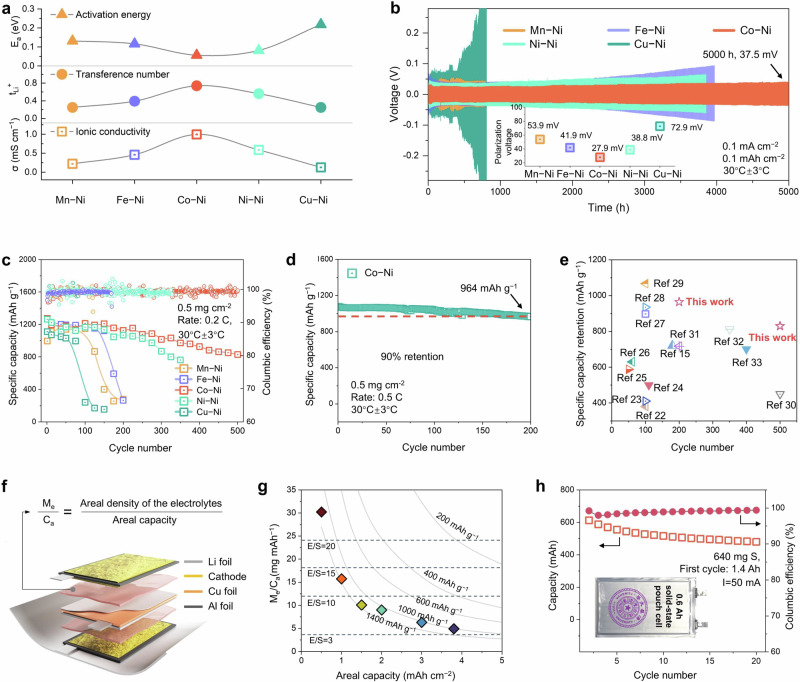
The clusters labeled as G₃ in Fig. 1 represent 2D Hofmann complexes that are expected to exhibit higher lithium conduction behavior compared to other complexes. Based on a combination of CI-NEB and machine learning prediction, the E_b for the series M-Ni-DMF, ranging from Mn to Cu, is approximately 0.32, 0.21, 0.19, 0.40, and 2.03 eV, respectively. To verify the availability and predicted low E_b of the materials, we conducted systematic measurements to investigate lithium mobility characteristics (Supplementary Figs. 15–18). Figure 3a summarizes the ionic conductivity (σ), Li⁺ transference number (t_Li⁺), and activation energy (E_a) from Arrhenius plots. From Mn to Cu in the 3d row of the periodic table, σ and t_Li⁺ of M-Ni-based electrolytes follow a volcano trend, while E_a follows an inverted trend. These trends are consistent with the predicted results generated by CI-NEB. Co-Ni exhibits high ionic conductivity of σ (0.99 mS cm^–1) and t_Li⁺ (0.74) at room temperature (30 °C ± 3 °C) and a low E_a (0.056 eV). These results suggest the effective Li⁺ mobility due to the fast percolating pathway along the 2D channel that the Li⁺ can take through the system. The Li|electrolyte|Li symmetric cells were then subjected to alternate Li plating and stripping cycles, with a similar volcano trend in initial polarization voltage, yielding a minimum polarization of 27.9 mV for Co-Ni. The Li | |Li symmetric battery stably cycles for 5000 h at 0.1 mA cm⁻² with a slight polarization increment. However, those using Mn-Ni, Fe-Ni, Ni-Ni, and Cu-Ni show enlarged polarization or even short circuits after 780, 4000, 3850, and 770 h, respectively (Fig. 3b). Continuous Li⁺ migration paths and corresponding energy barriers, as well as anodic stability, can comprehensively improve the full cell performance of M-Ni based composite electrolytes. When paired with high-capacity positive electrodes, such as sulfurized polyacrylonitrile (SPAN) cathodes, the benefits of fast Li⁺ conduction behavior are highlighted due to the more efficient use of active materials in solid-state cells. Cyclic voltammetry (CV) measurement demonstrated the irreversible capacity loss in the first cycle, primarily coming from an extra reaction between Li⁺ and C = N/C = C bonds and the decomposition of free DMF (Supplementary Fig. 19). A simple comparison of CV profiles in the second cycle shows that the current density first increased and then decreased as the predicted volcano trend from Mn to Cu, suggesting Co-Ni demonstrated the highest current response. The improvements in the current response indicate a large capacity of the conversion reactions, verifying the optimal electrochemical performance of Co-Ni cells. In Fig. 3c, the cycling stability of M-Ni electrolytes is compared, showing that Co-Ni cell exhibits prolonged cycle life with a reversible capacity of 829.6 mAh g⁻¹ after 500 cycles at 0.2 C (335 mA g⁻¹). In contrast, other cells, particularly Cu-Ni cells, experience significant capacity decay within the first 200 cycles. This stability trend is consistent with theoretical predictions. Upon the cycling, Co-Ni demonstrated declined impedance under different depths of discharge and states of charge, as investigated by in situ electrochemical impedance spectroscopy measurements (Supplementary Fig. 20). Improved Li⁺ transport kinetics decrease the internal resistance, which is further confirmed in galvanostatic intermittent-titration voltage measurements (Supplementary Fig. 21). The overpotential between actual and equilibrium voltage tested confirms that Co-Ni had mostly the smallest internal resistance with a low reaction barrier. Previous studies have shown that continuous side interaction between DMF and Li metal can lead to DMF depletion and unstable solid electrolyte interphase, resulting in premature capacity decay. Benefiting the effective confinement of DMF, series electrolytes exceed the stable electrochemical window of about 4.6 V (Supplementary Fig. 22). Co-Ni with a coordinated DMF through Hofmann complexes could considerably prevent the side reaction, together with high conductivity, thus exhibiting better stability. Cycling under 0.5 C (837.5 mA g⁻¹), Co-Ni cell retains 90.0% of its capacity after 200 cycles with an average capacity decay of only 0.05% per cycle (Fig. 3d). In terms of specific capacity and cycle life, our results based on Co-Ni electrolytes achieve improved capacity retention and prolonged lifespan compared to previously reported batteries with sulfur-based electrodes (Fig. 3e and Supplementary Table 2).

Fig. 3. Electrochemical performance of Li − S batteries.

a Comparison of ionic conductivity (σ), Li⁺ transference number (t_Li⁺), and activation energy (E_a). b Long-term cycling of symmetric Li | |Li cells using M-Ni SPEs at a current density of 0.1 mA cm⁻² at 0.1 mAh cm⁻². c Cycling performances and Coulombic efficiencies of Li|M-Ni|SPAN cells at 0.2 C (335 mA g⁻¹) for 500 cycles with a sulfur loading of 0.5 mg cm^–2. d Cycling performance of Li|Co-Ni|SPAN cell at 0.5 C (837.5 mA g⁻¹) with a sulfur loading of 0.5 mg cm^–2. e Comparison of specific capacity after cycling and cycle life with previously reported results^14,41–52. f Schematic diagram illustrating the configuration of the pouch cell and the proposed mass-to-capacity ratio (m_e/c_a) to evaluate the achievable energy density of a practical cell. g Relationship between areal capacity and m_e/c_a with liquid-state and solid-state electrolytes. The colored rhombuses were measured with cathode sulfur loadings to be 0.5, 1, 1.5, 2, 3, and 4 mg cm^–2, respectively. The gray lines are the fitting data of our solid-state electrolytes when the cathodes deliver various specific capacities, while the dashed lines indicate liquid electrolytes with various electrolyte-to-sulfur ratios (E/S ratios). h Cycling performances of the pouch cell. Inset: Photograph photo of the 0.6 Ah pouch cell.

M-Ni membranes feature excellent flexibility, scalability, and (electro)chemical stability, making them potentially suitable for large-scale industrialization in practical applications such as pouch cells. Practical use scenarios, particularly with thick negative electrode configurations, could highlight the benefits of highly conductive M-Ni in solid-state batteries. A solid-state pouch cell (6 cm × 10 cm in dimension) was prepared by loading the negative electrodes (5 cm × 8 cm in dimension) overcoming the benchmark areal capacity of commercialized lithium-ion batteries of 3 mAh cm⁻², achieving good cycling stability even with such high areal loading^21,22. To increase the capacity loading further, the positive and negative electrodes (areal sulfur loading of 4 mg cm^–2) were stacked with the electrolyte membranes in between, as the configuration of the pouch cell shown in Fig. 3f. There was an irreversible capacity loss with an initial capacity of 1.4 Ah in the first cycle, primary coming from an extra reaction between Li⁺ and C = N/C = C bonds and the decomposition of free DMF. The pouch cell had a capacity of 0.613 Ah in the second cycle (equivalent to an areal capacity of 3.8 mAh cm⁻²), working 20 cycles with a high average Coulombic efficiency of about 99% (Fig. 3h). To unify a status evaluating and comparing various electrolytes, both liquid-state and solid-state, electrolytes, for promising practical commercialization, here we proposed the concept of mass-to-capacity ratio (m_e/c_a). The m_e/c_a (mg mAh⁻¹) is defined as the areal mass density of the electrolytes (mg cm⁻²) divided by the areal capacity of the cell (mAh cm⁻²) the m_e/c_a metric effectively captures the efficiency of electrolyte usage relative to the battery’s capacity. According to the equation, a lower m_e/c_a ratio signifies a reduced electrolyte weight per unit of carried capacity, indicating a leaner proportion of electrolytes within the entire battery assembly. Quantifying the mass-to-capacity ratio provides comparable information among various electrolytes and battery systems in the goal of energy-dense energy storage solutions. Co-Ni-based electrolyte had considerable m_e/c_a of 4.9 mg mAh⁻¹, which is equivalent to a liquid-state electrolyte with a low electrolyte-to-sulfur ratio of about 4 μL mg⁻¹, exemplifies its competitive edge for integration into high-energy-density battery systems (Fig. 3g). Note that the density of normally used liquid electrolyte is 1.2 g cm⁻³ and suppose that the specific capacity in liquid-state Lithium-sulfur battery could reach 1000 mAh g⁻¹.

Developing energy-dense and safe solid-state batteries to enhance the thermal runaway prevention capabilities of energy storage systems remains a challenge. In addition to the development of high-performance electrolytes, careful consideration and optimization of key parameters in positive and negative electrode design are also necessary. Specifically, the energy density and cycling performance of Ah-level solid-state pouch cells can be improved through various methods. These include improving homogeneity by optimizing mass production process parameters, enhancing the transport characteristics of ions and electrons by designing positive electrodes with optimized tortuosity, conductivity, and electrocatalytic properties, and bolstering stability by protecting lithium anode.

Electronic-level understanding rationalizes predictive performance

As predicted by CI-NEB assisted with ML, Co-Ni with low E_b exhibits significantly higher conductivity, resulting in improved Li⁺ migration kinetics and stable anodic properties. Based on previous studies, our series of Hofmann-DMF materials not only helps to form a durable solid electrolyte interphase by preventing DMF decomposition but follows a rotational behavior to promote Li⁺ conduction kinetics through a ligand-assisted transport mechanism. The incompletely removed DMF exhibits a strong shielding effect, which aids in the dissociation of lithium-salt (ion-dipole pairs) due to its strong polarity and high donor number²³. Although the effectiveness of the dissociation of lithium salts and Li⁺ transport of DMF has been reported, the reasons for the difference in kinetics, the impact on Li⁺ transport kinetics, and the descriptors of coordination environment regulation remain unclear²⁴. In addition to searching for potential solid-state composite electrolytes, we applied DFT calculations and advanced characterization to uncover the working mechanism and electronic-level insight into the chemistry of ion migration.

The Hofmann coordination frameworks feature cations in octahedral sites that can be covalently bound to two DMF ligands, forming M − O bonds through the orbital overlap between the metal d orbitals (or p orbitals for metals such as magnesium) and oxygen p orbitals. Figure 4a illustrates the molecular orbital couplings between the octahedral metal sites and their surroundings in Hofmann frameworks with M-O and M-N bonds formed through the hybridization of anion p and metal 3 d, 4 s, and 4 p orbitals. The bonding orbitals included a_1g, t_1u, σ₁ and σ₂, while the antibonding orbitals included a_1g*, t_1u*, σ₁*, and σ₂*, as well as the non-bonding metal t_2g. The bonding states a_1g, t_1u, σ₁, and σ₂ exhibit anion character, while the antibonding states show metal character. Therefore, the occupation of metal d orbitals correspondingly influences the anti-bonding states, where the lower anti-bonding filling results in strong M-O couplings and strong affinity to DMF. The binding energy of DMF increases and then decreases from Mn to Cu, reaching a maximum value of 1.1 eV at Co-Ni-DMF (Supplementary Fig. 23). The high binding energy of Co-Ni-DMF suggests strong affinity to DMF of Co, which consists of a shorter M − O bond in Fig. 2d. The interaction trend with DMF is strongly correlated to the up-shift of d band center, which is probably a result of local electron transfer from the neighboring square planar Ni sites and C/N atoms in Hofmann frameworks (Fig. 4b and Supplementary Fig. 24). This was further validated using scanning transmission X-ray microscope stack imaging technique (STXM) and corresponding Co L edge spectra, where Co exhibits the mix valence state with both Co²⁺ and Co³⁺ (Fig. 4c). Transition metals with higher d band center leads to fewer occupation in anti-bonding states, thus strengthening the interaction between octahedral metal sites and DMF with more effective d-p orbital hybridization of M − O bonds²⁵.

Fig. 4. Electronic-level understanding.

a The degeneracy of molecular orbital between metal and O in M-Ni-DMF. b STXM image of Co-Ni-DMF and corresponding color-coded spatial distribution of Co L edge spectra. Scale bar: 4 μm. c Projected densities of states of d band of octahedral metal sites in M-Ni-DMF (M = Mn, Fe, Co, Ni, Cu). d Schematic illustration of how the coordination competition between octahedral cations and lithium in overlapping with oxygen p orbitals results in lithium coordination environment tuning. Substitutional cations with improved d band center correspondingly improve the anti-bonding state of M-O coupling and thus weaken Li-O coupling. Insets: Bonding and anti-bonding state change of M − O and O−Li bonds. e O K edge X-ray absorption spectra of M-Ni-DMF (M = Mn, Fe, Co, Ni, Cu). The shaded region centered at ∼ 530 eV represents the feature assigned to O 1 s excitation to the M 3 d − O 2p hybridized state. Theoretical and experimental confirmation of oxygen interaction strength with iCOHP_M-O and K-edge-based excitation area. f ⁷Li ssNMR spectra of fresh M−Ni electrolytes and after cycling Li | |Li symmetric batteries for 100 times at a current density of 0.1 mA cm⁻² at 0.1 mAh cm⁻², at 30 °C ± 3 °C.

Thermogravimetric analysis- Fourier transform infrared-gas chromatography-mass spectrometry (TGA-FTIR-GC-MS) was used to experimentally verify the binding strength with DMF in M-Ni-DMF. The escape characteristics of pyrolysis gas volatiles were investigated during the heating process to determine the strength of the interaction with DMF (Supplementary Figs. 25 and 26). A stronger interaction with DMF indicates more difficult escaping features, corresponding to the higher pyrolysis temperature. A prominent peak at m/z = 73 indicated the presence of DMF as the major pyrolysis product of M-Ni-DMF. The M-Ni-DMF powder showed a gradual decay of the carbonyl (O = C) peak at 1650 cm^–1, which is indicative of caprolactam. The decomposition temperature of DMF in M-Ni-DMF (M from Mn to Cu) followed a volcano trend, with Co-Ni-DMF exhibiting the strongest tethering effect to anchor the DMF. A relatively low content of DMF in Cu-Ni-DMF consists of EXAFS results that Cu-O shows weak intensity with strong disorder fluctuation.

Hofmann-DMF provides 2D channels for Li⁺ migration through a DMF ligand-assisted transport mechanism, and thus we further investigate the lithium coordination characteristics¹⁰. Interestingly, lithium interacts with the oxygen of DMF ligands, with orbital overlap between the lithium s orbitals and oxygen p orbitals. This suggests coordination competition between the Li and octahedral cations for overlapping with the oxygen p orbitals (Fig. 4d). Consequently, substituting the octahedral sites results in different M − O coupling, which leads to a difference in electron transfer (Supplementary Fig. 27) at the oxygen of DMF. This, in turn, affects the strength of the Li−O bond. The competitive coexistence of M − O and Li−O bonds is responsible for the negative relationship between M − O and Li−O bond strength and lithium affinity shows an inversed volcano trend from Mn to Cu²⁶. In the Co-Ni-DMF sample with the largest DMF binding energy out of the five samples, we observed a weak interaction between Li and O ions accompanied by the weakest binding energy of 1.02 eV (Supplementary Fig. 28).

The coordination competition was further confirmed by the projected crystal orbital Hamilton population (pCOHP) and integrated crystal orbital Hamilton population (iCOHP). The iCOHP of M − O bonds shows a volcano-type trend from Mn to Cu, while Li−O bonds show an inverted volcano trend, reaching the extreme values for Co-Ni-DMF with the strongest M − O bond and weakest Li−O. Particularly, the more anti-bonding states of the Co-O bond shift up above the Fermi level with less occupation, indicating that the Co-O is stronger than other M − O bonds. In contrast, the anti-bonding state of the Li−O bond in Co-Ni-DMF shifts below the Fermi level and is filled, yielding a relatively weakest Li−O bond. The competition of M and Li coordination with O suggests a negative correlation between M − O bond strength and Li−O bond strength.

The stronger interaction with DMF in M-Ni-DMF may induce electrons transferring differs of O attracted to the coordinated metal atoms, hence leading to variation of band occupation of O. The O 2p − M 3 d hybridization states were investigated by O K edge X-ray absorption pre-edge, reflecting the excitation from the O 1 s to the hybridized unoccupied O 2p − M 3 d state, approximately corresponds to particle O 2p projected DOS lying above the Fermi level (shaded region in Fig. 4e). The area under the pre-edge peaks for K edges provided information on unoccupied occupancy which reflects the bonding strength of M − O^27,28. Good agreement can be seen between the ICOHP results in DFT calculation and O K edge pre-edge area, that pre-edge range increased with the strong interaction and less occupied O 2p − M 3 d state. This sequence is consistent with the order of the calculated binding energy.

We conjecture that the Li⁺ coordination behaviors can be modulated by tuning the interactions with DMF during transport, such as by substituting the metal sites in Hofmann complexes. Solid-state nuclear magnetic resonance (ssNMR) was further conducted to investigate the Li⁺ coordination environment by tracking ⁷Li signals (Fig. 4f). In the ⁷Li NMR spectra, a lower peak represents a relatively weaker coordination of Li⁺ with the surrounding DMF ligands^29,30. The coordination trend of various M-Ni followed in the order of Cu-Ni (– 1.34 ppm) <Mn-Ni (– 1.27 ppm) < Ni-Ni (– 1.25 ppm) < Fe-Ni (– 1.22 ppm) < Co-Ni (– 1.15 ppm). Upon galvanostatic plating/stripping tests for 100 cycles, the Li | |Li symmetric batteries were disassembled in an argon-filled glovebox to ensure an inert atmosphere. Upfield-shifted signals were observed in M-Ni of ⁷Li ssNMR spectra, indicating more deshielded lithium nuclei LiFSI dissociation and Li⁺ coordination interaction resulting in a reduced electron cloud around Li⁺. Notably, Co-Ni exhibited the largest chemical shift after Li plating/stripping, suggesting a weak coordination environment, which is well accorded with the calculated coordination strength between Li⁺ and O.

Transition metals with higher d band centers and fewer filled anti-bonding states form strong M–O bonds, altering the distribution of electronic states around oxygen and thus reducing the M–O coupling. Li⁺ weakly interacts with O suggesting more movable Li⁺ easier out of coordination and migrate along the 2D channels. This enables weakly Li⁺ coordinating electrolytes to have high conductivity. In addition, metal sites can locally trap DMF and effectively impede DMF deposition at negative electrodes, which facilitates cycling stability. Weakly Li⁺ coordination environment, as occurs in Co-Ni-DMF compromises ionic conductivity with low E_b but improves durability with less DMF decomposition. For the development of SPEs capable of conducting ions efficiently, one key is to reduce their binding strength to the surroundings by modulating the ion coordination environment.

In conclusion, while many fillers have been reported to improve ionic conductivity and confine the residual solvent, the regulation mechanism of the lithium-ion coordination environment, remains unclear, which hinders the rational design to further improve the ionic conductivity of SPEs to meet the practical application. In this study, we used unsupervised learning and CI-NEB calculations to develop a workflow for rapidly screening Li⁺ conductors and investigating descriptor deciphers of the ion motion. Using Hofmann complexes as a model system, M-Ni-DMF (M=Mn, Fe, Co, Ni, or Cu) are predicted to facilitate Li⁺ migration (E_b < 1 eV) with the order of the calculated E_b of an inverted volcano trend. This trend is verified experimentally, and SPEs-based cells with Co-Ni-DMF exhibited excellent performance in Li  | |Li symmetric measurement (5000 h at 0.1 mA cm⁻²) and good cycling stability in full cells (90% capacity retention after 200 cycles at 0.5 C). M-Ni-DMF provides 2D channels with DMF ligands and lays the foundation for DMF confinement, Li⁺ coordination, and ligand-assisted Li⁺ migration, facilitating the tuning of Li⁺ conductivity. Notably, a 0.6 Ah pouch cell with a high areal capacity of 3.8 mAh cm⁻² and a low m_e/c_a (4.9 mg mAh⁻¹) demonstrates its potential for a next-generation safe and energy-dense energy storage system. DFT calculations reveal the competitive mechanism between M − O and Li−O bonds, which can be used to construct the weakly coordinated Li⁺ environment by tuning the interaction with the oxygen of DMF. Co-Ni-DMF with strong M − O bonds could not only tether DMF in the local area but weaken the coordination strength with Li⁺ and thus facilitate its migration. Consequently, the interaction strength between the coordinated component (such as O) and Li⁺ can serve as a descriptor for comprehending the energy barrier of Li⁺ migration where weak coordination suggests an easier migration. Modulating the coordination environment by tuning interaction with atoms or substances that solvate Li⁺ provides a rational viewpoint for improving lithium conductivity³¹. Based on the above-integrated approach, the combination of CI-NEB and machine learning guidance accelerates the theoretical discovery of candidate Li⁺ conductors for solid-state batteries, contributing to the development of safe and energy-dense energy storage systems.

Methods

COMSOL Multiphysics simulations

The finite-element method is conducted using the COMSOL Multiphysics 6.2 platform to develop the simulation model, which consists of a lithium-ion battery and a single-ion conductor interface. This setup incorporates a lithium-ion battery interface with the charge balance model configured for a single-ion conductor, commonly used for solid electrolytes³².

The interface, with the single-ion conductor charge balance model, considers the following aspects: (1) Charge transport in the electrode and electrolyte governed by Ohm’s Law; (2) Material transport within the spherical particles forming the electrodes described by Fick’s Law; and (3) Butler–Volmer kinetics for electrode equilibrium potential³³. These processes are represented by Fick’s Law and the Butler–Volmer equations, respectively:

$${\mathrm{j}}_{\mathrm{i}}=-{\mathrm{D}}_{\mathrm{i}}\nabla {\mathrm{c}}_{\mathrm{Li}}$$ 1

where J_i is the flux of lithium ions, c_Li is the concentration of lithium ions, and D_i is the diffusion coefficient of lithium ions.

$$\mathrm{j}={\mathrm{j}}_{\mathrm{ex}}\left[\exp \left(\frac{{\mathrm{\alpha }}_{\mathrm{a},\mathrm{j}}{\mathrm{F}\mathrm{\eta }}_{\mathrm{j}}}{\mathrm{RT}}\right)-\exp \left(-\frac{{\mathrm{\alpha }}_{\mathrm{c},\mathrm{j}}{\mathrm{F}\mathrm{\eta }}_{\mathrm{j}}}{\mathrm{RT}}\right)\right]$$ 2

where ${\alpha }_{a,j}$ and ${\alpha }_{c,j}$ are charge transfer coefficients of negative and positive electrodes, respectively, and j_ex is exchanged current density, η_j is overpotential.

The model domain was divided into the lithium metal phase (85 μm), SPEs phase (45 μm), and the positive electrode domain (65 μm), in which the geometry is one-dimensional and the model is isothermal. The behavior at various discharge currents and solid electrolyte conductivities is analyzed with the constant current cut-off voltage charging method, where the internal polarization voltage of the battery varies under different conditions. The actual discharge capacity is obtained by multiplying the discharge current density and the actual discharge time.

Unsupervised learning

In this work, an agglomerative hierarchical clustering algorithm (AHC) is used to complete the unsupervised learning of the Hoffman-DMF structure. AHC is a bottom-up clustering method, AHC evaluates the similarity between samples by calculating the correlation between features, and sums each of the two most similar samples into a group, while generating new features for this group, and so on, so that the layer by layer of clustering is merged. AHC forms a bottom-up tree pattern through this square. In this work, the Euclidean distance between the features of different samples is used as a similarity measure. Different from other clustering methods, AHC can get the whole clustering process at one time, and does not need to recalculate when aggregated into different numbers of categories according to requirements, which saves a lot of computing resources and is more flexible.

Climbing Image-Nudged Elastic Band (CI-NEB) calculation

The Vienna Ab initio Simulation Package (VASP) is used to perform first-principles calculations. The optimization of the Hoffman-DMF system is achieved using the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional within the framework of the generalized gradient approximation (GGA) and employing projector-augmented wave (PAW) atomic potentials^34–37.

The CI-NEB calculation in this work is implemented based on the variational transition state theory (VTST) software package³⁸. The diffusion energy barrier of Li⁺ is obtained by calculating the total energy of the system when Li⁺ migrates to different positions in Hoffman-DMF. The ionic conductivity of the Hoffman-DMF structure is evaluated by the value of the energy barrier.

Preparation of M(DMF)₂Ni(CN)₄

0.193 g of K₂[Ni(CN)₄] (purity: > 99%, Aldrich) was dispersed in 20 mL deionized water and stirred for 1 h. To substitute the octahedral cation sites, about 0.7 mmol Mn²⁺, Fe²⁺, Co²⁺, Ni²⁺, or Cu²⁺ and 0.176 g of dihydrate tri-sodium citrate (purity: > 99%, Aldrich) were mixed and dispersed in 20 mL deionized water and stirred for 1 hour. After mixing the two solutions followed by 4 hours of magnetically stirring, the mixture was then aged at 30 °C ± 3 °C for 8 h to obtain the precipitates M(H₂O)₂Ni[CN]₄·xH₂O. The as-obtained precipitates were washed with de-ionized water and ethanol dried at 30 °C ± 3 °C, followed by thermal dehydration treatment to remove H₂O and obtain the powder precursors M(H₂O)_xNi[CN]₄. M(DMF)₂Ni(CN)₄ were then fabricated via a ligand penetration method by immersing the M(H₂O)_xNi[CN]₄ precursors into 2 mL DMF solution(purity: > 99.8%, Aldrich), followed by drying at 60 °C under negative pressure argon atmosphere for 6–8 h to remove the residual DMF. Upon the entire procedure, there were color changes of the power to visually demonstrate the removal of H₂O and the penetration of DMF.

Preparation of solid-state electrolytes

All the fabrication processes, including the preparation of polymer electrolytes, SPAN cathode, and the assembly of batteries, were done in an Argon-filled glovebox with O₂ and H₂O content <0.01 ppm to avoid oxygen and moisture in the air. The solid-state electrolytes were prepared through a solution-casting method. PVDF-HFP (M.w. ~ 400,000, Maclin)) were dissolved 2 mL of DMF solution, followed by heating at 80 °C for 2 hours. M(DMF)₂Ni[CN]₄ and 0.3 g of LiFSI (purity: > 99.9%, DoDoChem) were mixed in 2 mL of DMF solution, followed by mixing with PVDF-HFP solution. After 10 h of magnetically stirring to acquire a homogeneous slurry, the mixture was cast onto a glass substrate with a doctor blade and then dried at 60 °C for 8 h to evaporate the DMF and obtain series M-Ni membranes. The as-prepared M-Ni membranes were cut into disks with a 19 mm punch.

Preparation of SPAN cathode

SPAN composite was synthesized by mixing sulfur (Alfa Aesar) and polyacrylonitrile (Mw = 150,000, Aldrich) in a 1:1 weight ratio, followed by heat treatment in an argon-filled furnace at 450 °C for 6 h. For the preparation of positive electrodes, the cathode slurry was prepared by mixing SPAN composite, carbon nanotubes (> 95%, XFNANO), PVDF-HFP, and LiFSI in a weight ratio of 5:1:2:2 in DMF solution after SPAN and carbon nanotubes grinding in a mortar for at least 30 min. SPAN cathodes were prepared by coating the homogeneous slurry onto an Al foil and dried at 60 °C for 6 h. The process was all conducted in a glove box with an atmosphere of O₂ < 0.01 ppm and H₂O < 0.01 ppm. Coin cells with as-prepared M-Ni electrolytes were assembled with a pressure of 50 kg cm⁻². For Li | |SPAN cell measurement, the positive electrode is punched into circular discs with a diameter of 12 mm, pairing with high-purity Li foil (500 µm, 15.6 mm, 99.9%, Canrd). Except for the tests mentioned specifically, all batteries are tested in a temperature-controlled battery testing cabinet at 30 °C ± 3 °C.

Material characterization

XRD analysis was conducted on a Smartlab SE to observe the crystal structures. SEM was conducted on SU 8010 to investigate sample morphology. Thermo gravimetric analysis (TGA) was conducted on TGA2 at a heating rate of 5 °C min⁻¹ under a N₂ atmosphere. FT-IR spectrums were measured on Thermo Nicolet Avatar 320 Spectrometer over a wavenumber range of 400–4000 cm^–1. The gas chromatography-mass spectrometry instrument was operated using QMS403D (NETZSCH). X-ray photoelectron spectroscopy (XPS) spectrums were measured on AXI Sultra DLD using Al-Kα radiation. Mn, Fe, Co, Ni, Cu, K edge XANES, and EXAFS measurements were performed at Canadian Light Source (CLS), using the X-ray Micro-characterization beamline (SXRMB, 06B1-1). The STXM and Mn, Fe, Co, Ni, Cu L edge, and O K edge measurements were conducted using the SXRMB (10ID-1). The atomic force microscopy-nano-infrared spectroscopy measurements were conducted on Bruker Nano IR3-s. The ⁷Li ssNMR spectra of electrolytes before and after Li plating/stripping were obtained on an Agilent-NMR-vnmrs600 spectrometer equipped with a highly homogeneous PremiumCOMPACT magnet (600 MHz 1H, 14.1 Tesla).

Electrochemical performance measurements

The electrochemical measurements were conducted on the LAND battery testing system (CT 2001A) or Bio Logic workstation (VMP3). The ionic conductivities and activation energies of the electrolytes were measured with stainless steel (SS, 15 mm, 0.5 mm, Canrd) symmetric SS|SPEs|SS cells. For electrochemical impedance spectroscopy (EIS) and in situ EIS tests, the frequency range was set between 1 MHz and 0.1 Hz with a voltage amplitude of 10 mV. A quasi-stationary potential was performed to stabilize the system at the open-circuit voltage for a duration of 30 minutes before the EIS measurement begins. In situ EIS measurements were conducted using a potentiostatic mode with the control of the potential applied for 5 minutes during charge/discharge. The ionic conductivities can be calculated according to the equation of:

$$\mathrm{\sigma }=\mathrm{L}/\left(\mathrm{R}\times \mathrm{S}\right)$$ 3

where σ is the ionic conductivity, L and S are the thickness and area of SPEs, R is the impedance value from Nyquist plots.

The activation energy E_a was conducted based on the temperature dependencies of $\sigma$, over temperature range from 30 °C to 90 °C with 10 °C intervals. E_a can be calculated according to the Arrhenius equation of:

$$\mathrm{\sigma }={\mathrm{Ae}}^{-\mathrm{Ea}/{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}$$ 4

where σ is the ionic conductivity, E_a is the activation energy, A is the pre-exponential factor, k_B is the Boltzmann constant, and T is the absolute temperature.

The transference number t_Li⁺ was electrochemically determined by the Bruce–Vincent method. The Li|SPEs|Li symmetric batteries were prepared and measured with AC impedance and potentiostatic polarization (ΔV  =  10 mV) for 3000 s. t_Li⁺ can be calculated according to the equation:

$${\mathrm{t}}_{{\mathrm{Li}}^{+}}=\frac{{\mathrm{I}}_{\mathrm{S}}\left(\mathrm{\Delta }\mathrm{V}-{\mathrm{I}}_0{\mathrm{R}}_0\right)}{{\mathrm{I}}_0\left(\mathrm{\Delta }\mathrm{V}-{\mathrm{I}}_{\mathrm{S}}{\mathrm{R}}_{\mathrm{S}}\right)}$$ 5

where t_Li⁺ is the transference number, ΔV is the polarization potential (10 mV), I₀ and I_s are the initial and steady-stable currents (μA), and R₀ and R_s are the initial and steady-stable impedance (Ω).

Li | |Li symmetric cells were assembled by sandwiching the electrolyte between two fresh Li foils (500 µm, 15.6 mm, 99.9%, Canrd). The solid-state full cells were assembled with SPAN cathode, the M–Ni-based electrolyte, and the lithium foil, cycling between 1.0 and 3.0 V. Galvanostatic intermittent titration (GITT) tests were put forward at a constant current of 0.1 mA for 15 min, followed by a pulse of the duration of 30 min to collect the potential response. Cyclic voltammetry (CV) was performed in the voltage window 1.0 to 3.0 V at a scanning rate of 0.1 mV s⁻¹. Linear sweep voltammetry (LSV) measurement. The electrochemical windows of M-Ni electrolytes were obtained by LSV test using Li|M-Ni|SS cells at a scanning rate of 1 mV s⁻¹.

The pouch cell assembling process involves several key steps: electrode preparation, electrode stacking, tab welding, and pouch sealing. For pouch cells, the cathode slurry was uniformly coated on both sides of the Al foil with a sulfur loading of 4 mg cm⁻² using a doctor blade (5 cm × 8 cm in dimension for each layer). The pouch cell assembling was carried out in a dry room with a dew point maintained at approximately − 50 °C or even lower to ensure optimal conditions and prevent moisture damage during the manufacturing process. The positive and negative electrodes (100 μm, Canrd) were stacked layer by layer for each four layers in the cell core to further improve the sulfur loading. Perforated Al and Cu foils (9 μm, Canrd) were used as the current collectors of positive and negative electrodes to connect external circuits by welding the Al and Ni tab (Canrd), respectively. Finally, the cells were packed with Al-plastic film (6 cm × 10 cm in dimension) with a vacuum sealing process. The pouch cells were tested at 5 MPa operational pressure at 30 °C ± 3 °C.

DFT calculations

DFT calculations were performed using VASP with GGA-PBE functional^34,36,37. PAW potentials and plane wave basis set were chosen to describe the ionic cores and valence electrons, with an energy cutoff of 500 eV. The valence electron configurations used in this work are 1s¹ (H), 2s¹ (Li), 2s²2p² (C), 2s²2p³ (N), 2s²2p⁴ (O), 4s²3d⁵ (Mn), 4s²3d⁶ (Fe), 4s²3d⁷ (Co), 4s²3d⁸ (Ni) and 4s¹3d¹⁰ (Cu), respectively. The electronic energy was converged when the total energy change was smaller than 10⁻⁵ eV. The DFT + U method was used to consider strong correlation effects of d electrons where U_eff values for Mn, Fe, Co, and Ni were set to be 3.6, 4.6, 5.0, and 5.1 eV, respectively.

The binding energy of DMF in Hofmann complexes is computed as:

$${\mathrm{E}}_{\mathrm{b}}={\mathrm{E}}_{\mathrm{M}-\mathrm{Ni}-\mathrm{DMF}}-{\mathrm{E}}_{\mathrm{M}-\mathrm{Ni}}-{\mathrm{E}}_{\mathrm{DMF}}$$ 6

where E_M–Ni–DMF, E_M–Ni, and E_DMF are the energy of the M–Ni–DMF, M–Ni, and DMF, respectively.

The binding energy of Li with Hofmann complexes is computed as:

$${\mathrm{E}}_{\mathrm{b}}={\mathrm{E}}_{\mathrm{total}}-{\mathrm{E}}_{\mathrm{M}-\mathrm{Ni}-\mathrm{DMF}}-{\mathrm{E}}_{\mathrm{Li}}$$ 7

where E_total, E_M–Ni–DMF, and E_Li are the energy of the lithium adsorbed on M–Ni–DMF surface, M–Ni–DMF, Li, respectively. A uniform background charge was added to ensure that Li remained in its normal charge states for all calculations³⁹.

The d band center is defined by the following equation:

$${\mathit{ϵ}}_{\mathbf{d}}=\frac{{\int }_{-\infty }^{\infty }{\mathbf{n}}_{\mathbf{d}}\left(\mathit{ϵ}\right)\mathit{ϵ}\mathbf{d}\mathit{ϵ}}{{\int }_{-\infty }^{\infty }{\mathbf{n}}_{\mathbf{d}}\left(\mathit{ϵ}\right)\mathbf{d}\mathit{ϵ}}$$ 8

Author contributions

Z.L. conceived the idea. G.Z., Y.Z., and J.L. directed the project. Z.L., K.T., and X.W. performed DFT calculations. K.T., A.C., L.S., and X.W. performed ML calculations. H.Q. performed COMSOL simulations. Z.L., X.X., X.W., and Y.S. synthesized materials, characterized materials, and analyzed data. J.W. conducted the XAS and STXM experiments. Z.H., R.G., and C.C. helped with electrochemical measurements and pouch cell assembling. Z.L., Y.Z., and G.Z. co-wrote and revised the manuscript. All authors contributed to the interpretation of the results.

Peer review

Peer review information

Nature Communications thanks Jingjie Yeo, and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

All data supporting the research in this paper are available in the main text and Supplementary Information, and source data can be obtained through requests from corresponding authors. Source data are provided in this paper.

Code availability

Code and some related data information can be found at https://github.com/taokehao/SE-DMF_Cluster⁴⁰. For raw data, please contact https://www.aimslab.cn.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-55633-9.