Assembly of polymorphic genomes: Algorithms and application to Ciona savignyi

Abstract

Whole-genome assembly is now used routinely to obtain high-quality draft sequence for the genomes of species with low levels of polymorphism. However, genome assembly remains extremely challenging for highly polymorphic species. The difficulty arises because two divergent haplotypes are sequenced together, making it difficult to distinguish alleles at the same locus from paralogs at different loci. We present here a method for assembling highly polymorphic diploid genomes that involves assembling the two haplotypes separately and then merging them to obtain a reference sequence. Our method was developed to assemble the genome of the sea squirt Ciona savignyi, which was sequenced to a depth of 12.7× from a single wild individual. By comparing finished clones of the two haplotypes we determined that the sequenced individual had an extremely high heterozygosity rate, averaging 4.6% with significant regional variation and rearrangements at all physical scales. Applied to these data, our method produced a reference assembly covering 157 Mb, with N50 contig and scaffold sizes of 47 kb and 989 kb, respectively. Alignment of ESTs indicates that 88% of loci are present at least once and 81% exactly once in the reference assembly. Our method represented loci in a single copy more reliably and achieved greater contiguity than a conventional whole-genome assembly method.

Genome sequencing is undergoing explosive growth, driven by improvements in both laboratory methods and computational analysis. A key aspect has been the continuing development of algorithms for assembling large and complex genomes from whole-genome shotgun (WGS) data (Myers et al. 2000; Batzoglou et al. 2002; Huang et al. 2003; Jaffe et al. 2003; Mullikin and Ning 2003; Pop et al. 2004). For most of the species selected for sequencing so far, it has been possible to collect WGS data from either a single haplotype or several nearly identical haplotypes. These species are inbred (e.g., worm, fly, mouse, rat), haploid (e.g., yeasts, bacteria), or have a very low effective population size (e.g., human) (Fleischmann et al. 1995; Myers et al. 2000; Venter et al. 2001; Mural et al. 2002; Waterston et al. 2002; Gibbs et al. 2004). Genome assembly algorithms to date have largely been developed for such organisms. The situation is more complicated for polymorphic organisms. If genome assembly of inbred organisms is akin to solving a large jigsaw puzzle, the assembly of polymorphic organisms is like starting with a mixture of pieces from several closely related but different puzzles.

Many diploid organisms (probably most) have polymorphism rates that are much higher than the ∼0.1% rate for humans. Polymorphism rates are expected to scale roughly with effective population size (Nordborg 2003). For marine animals and insects, that can mean polymorphism rates at least two orders of magnitude higher than for humans.

Several authors have already noted that polymorphism within a WGS data set complicates the assembly process. For example, the sequenced strain of the mosquito (Anopheles gambiae) is inbred along 92% of its genome (one haplotype) and outbred in localized islands comprising the last 8% (two haplotypes). Assemblies of this genome display lower quality precisely in the islands of heterozygosity (Holt et al. 2002). For species sequenced from a wild individual, such as the puffer fish (Fugu rubripes; 7× sequencing depth, 0.4% heterozygosity) and the sea squirt (Ciona intestinalis; 7× sequencing depth, 1.2% heterozygosity), assembly contiguity and completeness is significantly lower than would have been expected in the absence of heterozygosity, although factors such as repeat content, segmental duplications, and library quality could also affect assembly quality (Aparicio et al. 2002; Dehal et al. 2002). For the fungus Candida albicans (7.1× sequencing depth, 0.4% heterozygosity), high heterozygosity was the main cause of assembly difficulty (Jones et al. 2004). Several other polymorphic species are the subject of recent or ongoing genome projects, and polymorphism has complicated these endeavors as well. For these polymorphic species and many others scheduled for sequencing, the WGS libraries can be constructed using DNA from exactly two haplotypes. Thus, there is a significant need for methods for assembling polymorphic diploid genomes.

We present here a method for the assembly of diploid genomes with very high heterozygosity, 1 substitution per 20 bases and 1 deletion/insertion event per 100 bases. In our approach, we assemble the two haplotypes separately, and then merge the haplotype assemblies to choose a single representative at each locus. The method is implemented as extensions to the Arachne assembly program (Batzoglou et al. 2002; Jaffe et al. 2003). These extensions introduce a new constraint called “the splitting rule” that reinforces the tendency of Arachne to separate polymorphic haplotypes during assembly. As a result of this constraint, most loci are present exactly twice in the resulting intermediate assemblies. We then collapse this twofold redundancy by establishing long-range correspondences between haploid scaffolds, using these correspondences to form larger structures called diploid scaffolds, then explicitly choosing a single representative at each locus.

We developed this method to assemble the diploid genome of the sea squirt Ciona savignyi, a model system for vertebrate development (Johnson et al. 2004). Sequence data corresponding to more than 12× coverage were generated from a single highly heterozygous individual using a WGS method. We describe the genome assembly resulting from applying our method to these data. The assembly represents loci in a single copy more reliably and achieves greater contiguity than conventional whole-genome assembly methods.

Analysis using default algorithm

WGS data and default assembly

Whole-genome assembly is a computational method for obtaining the nucleotide sequence of an entire genome by piecing together sequencing reads obtained by whole-genome shotgun (WGS) sequencing. Typically, WGS data are obtained by randomly shearing genomic DNA, selecting for fragments of a certain size, inserting these fragments in an appropriate cloning vector (e.g., plasmids for 4-kb inserts or Fosmids for 40-kb inserts), then sequencing both ends of the insert. Thus, WGS reads typically come in pairs that represent nucleotide sequences whose relative orientation and approximate distance are known. A now-standard approach to whole-genome assembly is to use overlaps between sequencing reads to computationally merge these sequencing reads into contigs, i.e., contiguous stretches of DNA with no gaps. When two reads from a pair lie in different contigs, the pairing of these two reads implies a relative orientation and position for the two contigs. This leads to the formation of larger structures called scaffolds, in which one or more contigs are separated by gaps of approximately known length.

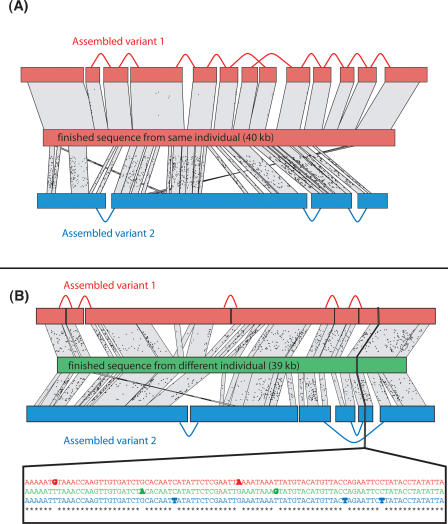
The 190-Mb genome of Ciona savignyi was sequenced from two WGS libraries with 5-kb and 40-kb insert sizes, constructed from the DNA of a single wild, diploid individual from the San Francisco Bay (see Supplemental material). We generated 12.7× sequence coverage and 58× in physical coverage, of which 17× is from long inserts. We then performed an assembly using the Arachne assembler (Batzoglou et al. 2002; Jaffe et al. 2003). The resulting assembly exhibited a total contig length of 412 Mb, more than twice the estimated genome size; the largest scaffolds had a median coverage of 5.1×, roughly half the expected coverage. Furthermore, when the contigs and scaffolds are aligned to the entire assembly, the majority of them align to two related sites: themselves and a second location with substantial divergence. When finished sequence obtained from cloned DNA from the same organism is aligned to the assembly (see below), it shows a near-exact match with one of the two sites (Fig. 1).

Figure 1.

Typical alignments of the two assembled variants to finished clones from the same individual (A) and from a different individual (B). Finished sequence from the same individual aligns very well to one of the two assembled variants but differs significantly from the second variant. In contrast, finished sequence from another individual represents a third variant, and the three pairwise distances are similar. These observations indicate that the two assembled variants are haplotypes, not paralogs. BLASTN alignments are shown as parallelograms, nucleotide mismatches are shown as small dots.

In principle, these results could have been caused by either widespread paralogy (such as a recent whole-genome duplication) or a high level of heterozygosity. We resolved this ambiguity by aligning 350 kb of finished sequence, representing seven random clones, obtained from a pool of other Ciona savignyi individuals from the same geographic source (Fig. 1). If the two related sites were paralogs representing different loci, the finished sequence from a different individual would be expected to closely match one of the two related sites. Instead, we observed in each case that the finished sequence differed significantly from both related sites: the divergences between the three sequences formed a star phylogeny with three edges of comparable length.

These data support the conclusion that the assembled variants represent the two haplotypes of the individual from which the WGS libraries were constructed, and that the finished sequence from a different individual represents a third haplotype.

Heterozygosity within the sequenced individual

We next sought to characterize more fully the nature and degree of heterozygosity of the sequenced diploid individual. For this, we produced finished or nearly finished sequence corresponding to both haplotypes from the individual used for WGS sequencing. Specifically, we obtained sequence from seven loci, resulting in 542 kb from the two haplotypes or ∼270 kb from each haplotype. The regions of haplotype overlap at the seven loci is ∼200 kb, and thus the total genomic footprint of the 14 clones is ∼340 kb. By aligning and comparing the two haplotypes at these loci, we measured an average substitution rate of 4.6%—60 times the rate in humans (see Methods). We also investigated large indel events and quantified the variability in local substitution rate.

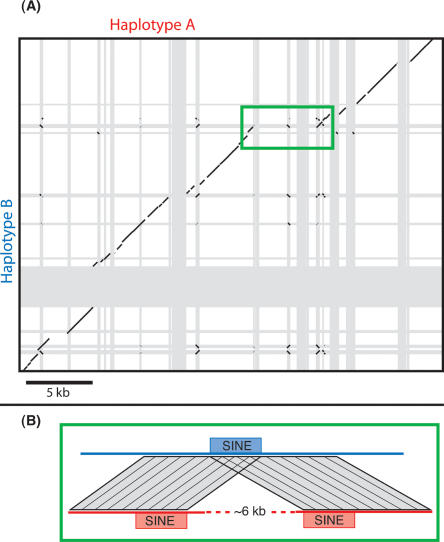
The two haplotypes frequently differ by large indels, i.e., sequence regions from hundreds to thousands of base pairs long that are present in only one of the two haplotypes (Fig. 2). In many cases, these differences can be identified as the recent insertion of transposable elements. In one case the difference appears to be due to a deletion mediated by recombination of nearby SINE elements, but in other cases the cause of the indel was not immediately evident. In total, the large indels between the two haplotypes comprise about one-sixth of the total number of aligning bases (28 kb out of 158 kb).

Figure 2.

(A) Alignment of finished sequence from the two haplotypes, superimposed on the annotation of repetitive DNA (gray bars). In many cases the haplotype-specific sequence and its boundaries coincide with repetitive sequence, indicating that a repetitive DNA element (often a SINE) has inserted in one of the two haplotypes. Black lines indicate all BLASTN alignments between finished sequence from the two haplotypes. (B) Illustration of the repetitive sequences and alignments flanking a 6-kb interval specific to haplotype A. This is consistent with a deletion in haplotype B mediated by recombination through SINE elements.

The heterozygosity rate was not only high, but also highly variable across regions. Regional variability has also been noted in Ciona intestinalis (Aparicio et al. 2002). Of the 1559 observed 50-base pair windows, the mean number of substitutions is μ = 2.3 (4.6%), with a variance of σ²= 6.1. This polymorphism within species is consistent with a geometric distribution (μ = 2.3, σ² = 7.5), not a Poisson distribution (μ = 2.3, σ² = 2.3) as has been seen for divergences between species (Waterston et al. 2002). The fit to a geometric distribution agrees with the predictions of population genetics: Assuming a freely mixing population of constant size (the panmyctic model), theory predicts that the coalescence time within each 50-base pair window is exponentially distributed, and thus the number of substitutions is geometrically distributed (Nordborg 2003). The implication for genome assembly is that sequencing reads of opposite haplotype will sometimes be identical in their region of overlap (low heterozygosity and short coalescence time), and sometimes differ significantly (high heterozygosity and long coalescence time).

Results with algorithm for polymorphic genomes

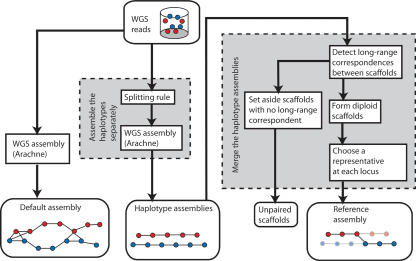
Given the high rate of heterozygosity in Ciona savignyi, we set out to develop a method to assemble WGS reads from exactly two highly diverged haplotypes. As shown in Figure 3, our method has two main components: (part 1) assembling the haplotypes separately (resulting in the haplotype assemblies) and (part 2) merging the separately assembled haplotypes to form the reference assembly.

Figure 3.

Our method for diploid genome assembly. The multistep process has two main components, which were motivated by an analysis of the default assembly using Arachne. First, we assemble the two haplotypes separately by applying a new algorithm called “the splitting rule” prior to the formation of contigs and scaffolds. This forces the two haplotypes to assemble separately. Second, we merge the two haplotypes by detecting long-range correspondences between haploid scaffolds, forming diploid scaffolds, and then choosing the best representative at each locus. When we cannot unambiguously determine the partner of a haploid scaffold, we set it aside as an unpaired scaffold.

More specifically, we introduce a new method called “the splitting rule” that causes overlaps between reads of opposite haplotype to be ignored during the formation of contigs and scaffolds. The goal is to force the two haplotypes to assemble separately in part 1.

We then accomplish the merger of the separately assembled haplotypes in part 2 in three steps. First, we use dynamic programming to select long collinear blocks of alignments between a haploid scaffold and its partner of the opposite haplotype. Second, we use collinear blocks as the atomic units and form larger structures called “diploid scaffolds.” For this, we use haploid scaffolds to relay from one collinear block to the next. Third, we select a representative path through each diploid scaffold. These paths through the diploid scaffolds compose the reference assembly. When the haplotype partner of a haploid scaffold cannot be determined, we set it aside as an unpaired scaffold. Further details are provided below.

Assembly results

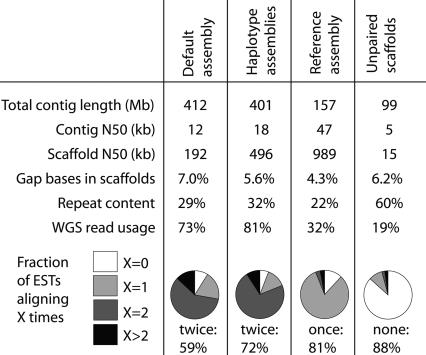
We applied our method to the ∼13× WGS data set from the diploid Ciona savignyi individual and compared these results to the default assembly (Fig. 4). The N50 contig and scaffold sizes both improved, from 12 kb and 192 kb in the default assembly to 47 kb and 989 kb in the reference assembly. The total contig length decreased from 412 Mb to 157 Mb, consistent with most loci being represented singly rather than doubly. To test this, we sequenced 84,000 ESTs, aligned them to each assembly, and determined whether each aligned 0, 1, 2, or >2×. These EST alignments confirm that most loci are represented only once in the assembly: 81% of ESTs align exactly once to the reference assembly, and 88% align at least once. The ESTs aligning multiply to the reference assembly appear to represent duplicated loci, not artificial duplication introduced by the assembly process (see Supplemental material).

Figure 4.

The results of applying our method for diploid genome assembly to the ∼13× WGS data set for Ciona savignyi. The majority of ESTs align exactly twice to the default assembly using Arachne, indicating a tendency for the two haplotypes to assemble separately. The fraction of ESTs aligning twice has increased in the haplotype assemblies, consistent with the goal of separating the haplotypes more cleanly. The process of merging the haplotype assemblies had three effects: representing the vast majority of loci exactly once instead of twice, increasing the scaffold size, and increasing the contig size. We also report the unpaired scaffolds, for which we were unable to determine their partner of the opposite haplotype—on average they are small, highly repetitive, and depleted for EST alignments.

The haplotype assemblies are more complete than the reference assembly, with 95% of ESTs aligning (the remaining 5% may be due to strain differences), and therefore the haplotype assemblies are also available for download. Ideally, all ESTs aligning to the haplotype assemblies would also be present in the reference assembly. However, among ESTs not aligning to the reference assembly, 4% align to the unpaired scaffolds and 3% align to the mirror image of the reference assembly (the unchosen haplotype). See Supplemental material for a more in-depth analysis of EST alignments.

The effect of the splitting rule can be seen by comparing the default assembly to the haplotype assemblies. As expected, the fraction of loci represented exactly twice in the assembly (measured by the number of times an EST aligns) has increased, indicating that the splitting rule caused the haplotypes to separate more cleanly in the assembly. We also observed an increase in contig sizes, scaffold sizes, and WGS read usage. These improvements appear to be side effects of the cleaner haplotype separation.

Between the haplotype assemblies and the reference assembly were three intermediate stages (Figs. 3, 4). First, we formed collinear blocks of alignments relating the vast majority of sequence in the haplotype assemblies with its partner of the opposite haplotype. At this point we set aside the unpaired scaffolds that contained no collinear block of alignments. Second, we formed diploid scaffolds by using the haploid scaffolds to relay between collinear blocks of alignments; the increase in scaffold size between the haplotype assemblies and the reference assembly is attributable to this step. Third, we chose a reference path through each diploid scaffold. The choice of reference path gave us the freedom to choose the better-assembled haplotype at each position of a diploid scaffold, leading to the increase in contig size between the haplotype assemblies and the reference assembly. The N50 size of haplotype segments (sequences uninterrupted by either a contig gap or a switch between haplotypes) is 21.4 kb. Choosing a reference path also collapsed the twofold redundancy; for example, in the reference assembly, 81% of ESTs align to exactly one location, indicating that the vast majority of loci are represented uniquely.

We then characterized the properties of the unpaired scaffolds, which total 99 Mb (Fig. 4). We found that these unpaired scaffolds are depleted for coding regions: only 5% of ESTs have an alignment to the unpaired scaffolds but not to the reference assembly. In addition, the unpaired scaffolds are typically small, having an N50 scaffold size of only 15 kb, and are highly enriched for repetitive sequence (Fig. 4). An independent analysis confirms that the unpaired scaffolds are highly enriched for repetitive sequence (see Supplemental material). These two properties of the unpaired scaffolds—small size and high repeat content—appear to be the reason we could not identify their haplotype partner.

Assembly validation

We validated the assembly process at several scales by examining the resulting assemblies. At the nucleotide level, we used the finished sequence from both haplotypes at seven loci to evaluate the accuracy of the haplotype assemblies. On a larger scale, we identified 14 loci that indicate large differences between the assembled haplotypes, then performed PCR assays to validate each locus.

Validation with finished sequence

In a highly polymorphic species, assembly validation at the nucleotide level requires comparing the draft sequence with finished sequence from the same haplotype. In particular, the draft sequences must each represent a single haplotype. Thus, we validated only the haplotype assemblies at the nucleotide level. The finished and nearly finished sequences used as a reference were the 14 Fosmid clones totaling 542 kb from the same individual described above. These Fosmids form overlapping pairs at seven distinct loci, with one Fosmid of each haplotype per pair. When compared with the sequence of each haplotype, the sequence of the Fosmid agrees with the order and orientation of contigs in the scaffold in every case, and in nine cases adjacent contigs overlap at their ends by a median of 25 base pairs.

At the nucleotide level, we obtained alignments between the haplotype assembly and 522 kb out of the 542 kb of finished sequence (96%). These alignments are highly accurate, with almost all discrepancies occurring at regions of the assembly that have been assigned low quality scores. Specifically, we defined a position to be of low quality if it or any of the five flanking bases in either direction are of quality Q <45 as assigned by Arachne (assembly quality files are also available for download). By this definition, 18% of the haplotype assemblies and 13% of the reference assembly are of low quality. In the remaining high-quality regions, the discrepancies were 15 isolated single-nucleotide differences (of which four are at mononucleotide runs); a 2-base pair indel; two islands of sequence mismatches (four differences in 20 base pairs, seven differences in 120 base pairs); a”recombination” event in which the terminal 600 base pairs of a contig match the opposite haplotype perfectly; and the terminal 1800 base pairs of a contig not aligning to the finished sequence. [Also, in an ambiguous case, a variable number of tandem repeats (VNTR) region of period 45 is repeated 36 times in the finished sequence and only 27 times in the assembly]. The overall rate of mismatches or indels is 5 × 10^–5 per base (28/542 kb), and discrepant regions comprise 0.4% of the sequence (2.4 kb/542 kb).

At regions marked as low quality, the error rate was higher. We found 108 isolated single-base differences (a rate of 1 per 5 kb) and 44 clusters of several mismatches with median length of ∼60 base pairs and total length ∼5 kb. About half of these low-quality discrepancies are in the terminal 200 base pairs of a contig.

PCR verification of large-scale heterozygosity

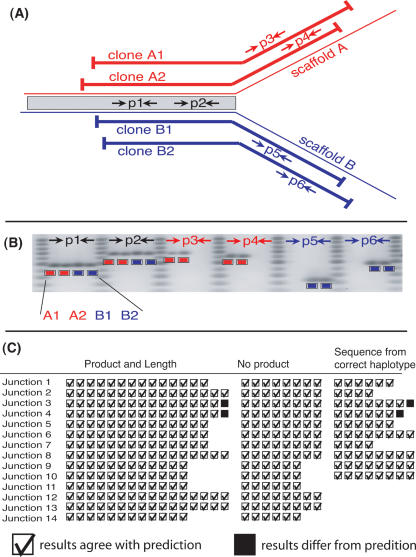
We observed large-scale differences between the assembled haplotypes and sought to determine whether these differences represented actual heterozygosity or misassembly. First, we selected 14 critical junctions—points at which a collinear block terminates far from the end of either of the haploid scaffolds it relates—that manifest varied examples of large-scale differences, such as inversions over 100 kb. At each critical junction, we then selected and characterized 40-kb Fosmid clones from each haplotype to confirm their agreement with the assembly.

Specifically, at each critical junction we used the placement of end reads in the haploid scaffolds to select four 40-kb Fosmid clones (two from haplotype A and two from haplotype B) that span the critical junction (Fig. 5). If the assembly is correct, the sequence of each clone should be identical to the sequence of its matching haploid scaffold. Thus, all four clones at the critical junction should correspond in the region where the haploid scaffolds correspond, and diverge where the haploid scaffolds diverge. To test this, we designed six PCR assays: two assays within the region of correspondence that should amplify in all four clones, two assays within the region of divergence that should amplify only in the haplotype A clones, and two assays in the region of divergence that should amplify only in the haplotype B clones. All four clones spanning the critical junction were then interrogated with all six PCR assays. If the sequence of the clones supports the assembly, we would expect a product (of the predicted length) in 16 of the 24 reactions, and the absence of a product in eight of the 24 reactions. In addition, we sequenced all PCR products and checked that PCR products from a clone align best (or at least as well) to the scaffold of the same haplotype.

Figure 5.

Experimental design for validating the assembly at critical junctions, sample results, and summary of results from 14 critical junctions. At a critical junction (at which the haploid scaffolds correspond up to a point and then cease to correspond) we select two 40-kb clones from each haplotype spanning the junction. We check that the draft sequences correspond to the clone sequences by designing six PCR assays that are applied to each clone (A). For these 24 assays, we predict a product and its length in 16 assays and the absence of a product in eight assays, as in the sample results (B). We also sequenced the PCR products at 10 of the critical junctions and checked that they align best to the draft sequence of the correct haplotype. Accounting for variations in experimental design, we made predictions for 304 PCR assays (see Supplemental material). We observed only two discrepant PCR product lengths, and the nucleotide sequence of these two products was also discrepant (C). The overwhelming agreement between prediction and observation supports the interpretation that the large-scale haplotype differences are real and that we assembled them correctly.

We interrogated all 14 critical junctions by PCR and sequenced the PCR products at 10 of the 14 critical junctions (Fig. 5). We found that in all but two cases, the presence or absence of a PCR product agreed with the prediction, and in all but these same two cases the sequence of the PCR product aligned best to the scaffold of the predicted haplotype. The overwhelming agreement between prediction and experiment indicates that the large-scale haplotype differences are real and that we assembled them correctly.

Assessment of assembly quality

The Ciona savignyi assembly displayed close agreement with 542 kb of finished sequence, with no major misassemblies and high accuracy at the nucleotide level. At a larger scale, haploid scaffolds of opposite haplotype generally agreed over large collinear blocks of alignments; the sites of large-scale disagreement seem to represent heterozygosity in the individual sequenced by WGS. At an even larger scale, haploid scaffolds showed close agreement with preliminary genetic maps of Ciona savignyi (M. Hill and A. Sidow, pers. comm.). A direction for further improvement of this assembly would be to reduce the fraction of sequence that is unpaired and thereby more fully segregate the sequence into a unique representative for each locus and the redundant copy from the other haplotype.

Description of assembly algorithm

In this section, we describe our assembly method in more detail. The method has two broad steps: assembling the two haplotypes separately, then merging the two haplotypes to produce a reference assembly in which genomic loci are represented uniquely.

The splitting rule

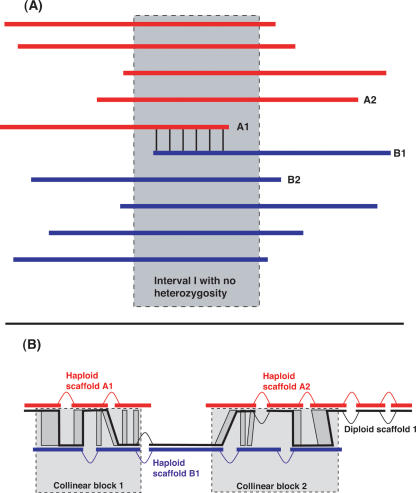
The first step of our method is to construct haploid contigs and haploid scaffolds, each of which is intended to consist of reads that are all from the same haplotype. For this step, we intervened between the Arachne steps of computationally detecting overlaps between sequencing reads, and using these overlaps to construct sequence contigs. Our modification applies a new filter, called the splitting rule, to detect and erase those read-read overlaps between sequencing reads of opposite haplotype (Fig. 6).

Figure 6.

The splitting rule (A) and a diploid scaffold (B). (A) Suppose that the red reads are of one haplotype and the blue reads are of the other haplotype, and that all reads have computationally detected overlaps with all other reads of the same color. In principle, the red reads should assemble in one contig, and the blue reads in another contig. However, if A1 and B1 overlap only in a region of haplotype identity, then A1 and B1 will also have a computationally detected overlap. When Arachne builds contigs, this overlap would trigger algorithms designed to prevent assembly through repeats and break both the red and blue scaffolds. The splitting rule was devised to recognize this situation and sever the overlap between A1 and B1 prior to the formation of contigs, thus allowing the red and blue contigs to assemble separately. See text for details. (B) In general, a diploid scaffold is an alternation between regions represented by a single haploid scaffold and regions represented by a collinear block of alignments relating two haploid scaffolds. For example, the diploid scaffold in B has two collinear blocks and three regions represented by a single haplotype. Within each collinear block, the reference path (thick black line) is chosen to minimize the number of contig gaps.

If the two haplotypes are identical in a region I, and two reads A1 and B1 of opposite haplotype overlap solely within I, then there is no way to determine that these two reads are of opposite haplotype without considering a wider context (Fig. 6). The splitting rule gains this wider context by using other sequencing reads overlapping A1 and B1 to infer a local partition of the sequencing reads into two haplotypes. Specifically, we define (X∼Y) to mean that X and Y overlap, O(X,Y) to refer to the interval of their overlap, and (X!∼Y) to mean that they do not overlap. We consider all read-read overlaps and reject any overlaps (A1∼B1) for which there are two additional reads, A2 and B2, establishing a local two-haplotype structure (A1 and A2 as one haplotype and B1 and B2 as the other) that is consistent with all other contextual information. Algebraically, we erase (A1∼B1) if the following two conditions are satisfied:

1. There are two additional reads, A2 and B2, that locally establish two distinct haplotypes A and B:

   1. O(A2∼A1) properly contains O(A1∼B1), and
   2. O(B2∼B1) properly contains O(A1∼B1), and
   3. (A2!∼B1) and (A1!∼B2).

2. For all reads C matching either A1 or B1 and containing O(A1∼B1), C matches either the A haplotype or the B haplotype, or both:

   1. (C∼A1) and (C∼A2), or
   2. (C∼B1) and (C∼B2), or
   3. Both (a) and (b) (i.e., C is completely within the region I of homozygosity).

Merging the haplotypes into a reference assembly

The second step of our method is to merge the haploid scaffolds of opposite haplotype and report a reference genome assembly. We accomplish this by detecting long-range correspondences between haploid scaffolds of the same genomic region but opposite haplotypes, stitching these corresponding haploid scaffolds together to form diploid scaffolds, and finally choosing a single reference sequence to represent each diploid scaffold.

Detecting correspondences between haploid scaffolds

To establish long-range collinearity between haploid scaffolds of opposite haplotype, we performed an all versus all alignment of the haploid scaffolds and clustered these alignments into long runs of collinear alignments. We performed the alignment using Megablast, with a word size of 24 and default parameters otherwise (Zhang et al. 2000). To remove alignments corresponding to high-copy genomic repeats, we loosely filtered the raw alignments by computing the total depth of alignments at each position of a haploid scaffold and rejecting any alignment not containing at least 200 bases in a region of depth 6 or less.

To cluster the filtered alignments into runs of collinear alignments, we used dynamic programming to select, for each haploid scaffold S, the sequence of nonoverlapping alignments on S that is maximally collinear. The objective function for quantifying collinearity is the sum of the scores of alignments as assigned by Megablast, minus a switching penalty of 12,000 for pairs of adjacent alignments that disrupt strict collinearity. Such disruptions include adjacent pairs of alignments to different target scaffolds, adjacent pairs of alignments with different orientations relative to the same target scaffold, or adjacent alignments on the query scaffold that are overlapping or in a different order on the target scaffold. We divide this optimal sequence of alignments at each disruption of collinearity, resulting in (n + 1) nonoverlapping runs of collinear anchors, where n is the number of disruptions in the optimal path across S.

The runs of collinear alignments found by dynamic programming are not necessarily reciprocal, and we filter to retain those that are. That is, we retain a run of collinear anchors from A to B only if there is also a run of collinear anchors from B to A that overlaps the original over more than half its length. We then intersect the ranges of reciprocal runs of alignments, retaining the corresponding alignments to create a collinear block. As a result of requiring all collinear blocks to be reciprocal, no part of a haploid scaffold can be part of more than one collinear block. Collinear blocks relate corresponding genomic regions in the two haplotypes, which are represented by haploid scaffolds.

Constructing diploid scaffolds

In principle, we would like to represent each chromosome as a single collinear block relating the two haplotypes. To approximate this goal, we form connected structures called diploid scaffolds in which regions represented by collinear blocks alternate with regions represented by a single haploid scaffold (Fig. 6). We form these diploid scaffolds by treating the collinear blocks as atomic units and deciding at each end of the collinear block whether to terminate the diploid scaffold (e.g., if the two haploid scaffolds diverge at the large scale) or to extend the diploid scaffold using one of the two haploid scaffolds (e.g., if there is no evidence of large-scale divergence). Specifically, we apply local rules at each end of each collinear block:

1. If one of the two haploid scaffolds extends for less than 40 kb from the end of the collinear block, we extend using the haploid scaffold that extends further.

2. If both haploid scaffolds extend 40 kb or more beyond the end of the collinear block, we terminate the diploid scaffold at the end of the collinear block.

Logically, the application of these local rules could lead to a diploid scaffold forming a closed loop; we explicitly check for this condition but have never encountered it.

Collapsing diploid scaffolds into reference scaffolds

Diploid scaffolds represent information about both haplotypes for the loci within collinear blocks—potentially useful information—but downstream genome analyses typically require a single representative at each locus. To collapse each diploid scaffold into a single reference sequence, we choose a path through each collinear block of alignments that determines the better-assembled variant at each locus, switching from one haploid scaffold to the other only at the endpoints of individual alignments within collinear blocks (Fig. 6). Among all possible paths, we choose the path that minimizes the number of gaps between contigs and, as a secondary criterion, switches haplotypes least frequently. Thus, the reference assembly is a mosaic of the two separately assembled haplotypes.

Discussion

Whole-genome assembly from multiple-haplotype WGS data is fundamentally different from, and more difficult than, the assembly of single-haplotype WGS data. We have described here a method for the case of exactly two haplotypes, and applied this method to assemble the Ciona savignyi genome from 12.7× WGS sequence. Because our method first assembles the two haplotypes separately, it requires about twice the sequencing depth that is typical for WGS assembly. Using the full 12.7 WGS sequence available for Ciona savignyi, our method provides a substantial improvement over the default assembly using Arachne, yielding an assembly with improved long-range continuity and in which the vast majority of loci are represented uniquely. The improvement results primarily from exploiting the fact that there are exactly two haplotypes present in the data.

From an algorithmic perspective, the knowledge that exactly two haplotypes are present is an enormous advantage. For example, half of the overlaps between sequencing reads are between two reads of the same haplotype, and by using sequencing quality scores we only need to consider overlaps with near-perfect sequence identity. In addition, each sequence is confounded by at most one other variant; once the two haplotypes at a locus have been identified, a sequencing read from that locus must exactly match sequence from one of the two haplotypes.

One alternative method for polymorphic assembly is to assemble all haplotypes in a consensus sequence from the start. This is the approach of the JAZZ assembler, which was used to assemble the moderately polymorphic genomes of Ciona intestinalis and Fugu rubripes (Aparicio et al. 2002; Dehal et al. 2002). It does not require the presence of exactly two haplotypes in the WGS data set, but neither can it take full advantage of this characteristic if present.

A second alternative method for polymorphic assembly is the approach developed by Jones and colleagues (2004) to assemble the diploid genome of Candida albicans. In this approach, developed specifically for the case of two haplotypes, the haplotypes assembled together in contigs at most loci and only required merging at the exceptional loci. This approach depends on the much lower heterozygosity rate of Candida albicans, and would likely not work for Ciona savignyi, which has an 11-fold higher heterozygosity rate.

Ideally, it would be desirable to have methods for assembling polymorphic diploid genomes that can be applied regardless of the level and variability of heterozygosity. We are optimistic that this is achievable, but believe that it will require more than cosmetic refinements of traditional algorithms that were designed for genomes with little or no polymorphism. In such traditional algorithms, even the most basic data structures of “contigs” and “scaffolds” presume that a single haplotype is present. Instead, it would be better to introduce more natural data structures at the earliest stages of assembly, which allow the two haplotypes to assemble together at regions of low or zero heterozygosity and bifurcate at regions of high heterozygosity, and only project to contigs and scaffolds as the final step.

At present, polymorphic WGS assemblies cannot be produced at the same accuracy and completeness that is now routine for haploid WGS data sets, even in the case of only two haplotypes at high coverage. In addition, not all polymorphic species can be sequenced from a single individual containing only two haplotypes, e.g., polyploid plants and species for which several individuals are required to gather sufficient DNA for genome sequencing. Thus, alternative sequencing strategies for polymorphic species need to be explored. One alternative is BAC-by-BAC sequencing, which should cost ∼35% less than sequencing to twice the usual coverage by WGS (although the burden of handling the many individual clones and libraries is substantial). Regardless of polymorphism, each individual BAC could be sequenced and assembled using standard methods. However, BAC-by-BAC strategies depend on the ability to select a single BAC representing each locus. Conventional fingerprinting methods for clone path selection might or might not be possible depending on the degree to which the clone fingerprints are polymorphic. Because fingerprint mapping is a small investment relative to sequencing, it is well worth trying. A second BAC-by-BAC sequencing strategy, requiring several time-consuming iterations, is to sequence a small collection of long-insert clones to seed the genome, end-sequence a much larger library of clones, and use the end-sequences to walk out from the seed clones. See the work by Jones et al. (2004) for a complementary discussion of sequencing strategies for polymorphic genomes.

We are optimistic that with continued algorithmic and sequencing advances, diploid genome assembly will become as routine as haploid assembly now is. Our results represent initial steps in that direction.

Methods

Finished sequence from the same individual

The 14 finished and nearly finished clones from the same Ciona savignyi individual are from the 40-kb Fosmid WGS library. These clones were selected manually in seven pairs so that, within each pair, the two Fosmids overlap by at least 20 kb and represent opposite haplotypes. Nine of the 14 clones are finished (GenBank phase 3) and five are nearly finished (GenBank phase 2). All 14 clones (∼560 kb) were used for assembly validation. Accession numbers, phase information (phase 2 or 3), pairing at loci, and usage in figures are shown in Supplemental Table 1.

Measurement of substitution rates

We aligned the finished sequence from the two haplotypes using the BLASTZ computer program (Schwartz et al. 2003). There were 158 kb of aligned bases within the alignments scoring at least 100,000 (this score corresponds to ∼1300 aligned bases). To remove spurious alignments in the neighborhood of alignment gaps, we filtered the alignments by dividing the consensus alignment into 60-base pair windows, rejecting any 60-base pair window containing a gap, then observed the central 50 base pairs of all remaining windows. We observed 3565 substitutions within 77,950 base pairs (1559 windows), corresponding to a heterozygosity rate for substitutions of 4.6%.

Validation using finished sequence from the same individual

For each finished clone, we identified the haploid scaffold to which it primarily aligns, then retained all BLAST alignments scoring at least 2000 between the finished clone and its corresponding haploid scaffold. In particular, we rejected alignments between the finished clone and the haploid scaffold of opposite haplotype. At the large scale, we verified the order and orientation of contigs using dot-plots of these alignments. At the nucleotide level, we recorded all differences between the finished sequence and draft sequence. We also noted any instances where an alignment terminated prior to the end of either the finished sequence contig or the draft sequence contig. Two high-quality discrepancies within 20 base pairs of the end of a finished sequence contig are not reported since they probably represent errors in the finished sequence.

Finished sequence from different individuals

The seven finished sequence clones from other Ciona savignyi individuals are BAC clones averaging ∼50 kb. The BAC library was constructed from DNA collected from sperm of 25 Ciona savignyi individuals from the San Francisco Bay. The accession numbers are: AC092520, AC092560, AC092561, AC102146, AC117993, AC117995, and AC153355. The clone shown in Figure 1B is AC153355.

EST sequencing

We sequenced ∼85,000 Ciona savignyi ESTs from several specimens collected from the Sea of Japan. We filtered these ESTs to exclude ∼10,000 mitochondrial ESTs and ∼250 ESTs of length <100 base pairs. We aligned using BLAT (Kent 2002) with default parameters, retaining all alignments for which the number of matching bases exceeds 80% of the length of the EST. The accession numbers at the DNA Data Bank of Japan are BW509979–BW594280.

Identifying repeats by alignment depth

To annotate the repeats in Figure 1 we aligned the finished sequence clones to the haplotype assemblies using BLASTN (Altschul et al. 1997), with default parameters, filtered to retain alignments of >150 base pairs; we annotated as repeat any base of the finished sequence that is present in 10 or more alignments. To estimate the repetitive content of a set of the assemblies, we used BLAT (Kent 2002) because of its greater speed. For these alignments, we retained all aligning gap-free blocks of 150 base pairs or more and counted the fraction of bases aligning to a depth of at least 10.