Abstract
Poly(dimethylsiloxane) is currently the material of choice for rapidly fabricating microfluidic devices. As the size of these devices decreases, a significant hydrodynamic flow is generated due to permeation of fluid through the channel walls. We develop a theoretical model verified by single bead tracking experiments, which demonstrates that large flow rates (>10 μm/s) can be passively generated in a straight microchannel filled with water. Realizing that this flow may be unwanted in some applications, we present a method to eliminate it by inhibiting mass transfer of water into the poly(dimethylsiloxane) walls. Furthermore, we explore applications to harness this passively generated flow inside a microfluidic device such as bead stacking, chemical concentration, and passive pumping.
Keywords: fluid dynamics, soft lithography
Over the last 10 years, there has been a burst of activity in the field of microfluidics and lab-on-chip devices (1). Much of this growth can be attributed to the pioneering work of Effenhauser (2) and Whitesides (3), who showed that inexpensive fluidic devices could be easily fabricated in poly(dimethylsiloxane) (PDMS) by replica molding from a microfabricated template. Consequently, PDMS has become the material of choice for making microfluidic devices (4-6).
Although the use of PDMS in microfluidics is relatively new, this material has been used extensively in applications that require gas- or vapor-permeable membranes (7). PDMS is highly permeable to organic solvents, making solvent-PDMS compatibility one of the main drawbacks of using PDMS for fluidic devices (8). Permeation of solvent into the PDMS channel walls becomes increasingly more important as device size decreases because the surface area to volume ratio increases. Current research on cells and single molecules requires creation of devices that are only a few microns to hundreds of nanometers in height [e.g., the DNA cytometry device of Chou et al. (9) has height of 3 μm]. The resulting microfluidic flow from the permeation flux will be important in these thin devices, but it has not been studied. However, some have observed other solvent permeation effects in microchannels. In one example, protein crystallization in aqueous droplets has been observed at unexpected initial concentrations because the permeation of water through the PDMS increases the concentration in the droplets over time (10). Until now, water permeability into the PDMS has been considered negligible for most microfluidic applications; however, we will show that this small but finite permeability generates a significant flow in thin (O[μm]) channels.
For nanoscale applications that require sealed microchannel walls, this permeation-driven flow clearly must be eliminated. Conversely, the permeation-driven flow provides an alternative approach to passive flow applications. Several groups have previously demonstrated passive flow processes by filling one reservoir with liquid and leaving the other empty and open to air so that the liquid evaporates at the pinned contact line at the empty reservoir. Some examples include evaporation-driven pumping (11), microsphere crystallization (12), and sample concentrating (13, 14). A permeation-driven flow can provide similar results using a driving flux at the channel walls instead of at the outlet air interface.
In this work, we model and study permeation-driven flow and its applications. We model the mass transfer of water from the microchannel into the PDMS and use the lubrication approximation to solve for the gap-averaged velocity for the case of a single rectangular channel connecting two fluid reservoirs. We experimentally validate the flow model by tracking single Brownian beads using fluorescence microscopy. Because this flow may be undesirable for many applications, we present a simple method to eliminate it. We also discuss ways to exploit this phenomenon to passively drive pumping in a microfluidic device, concentrate samples, and self-assemble particles.
Model
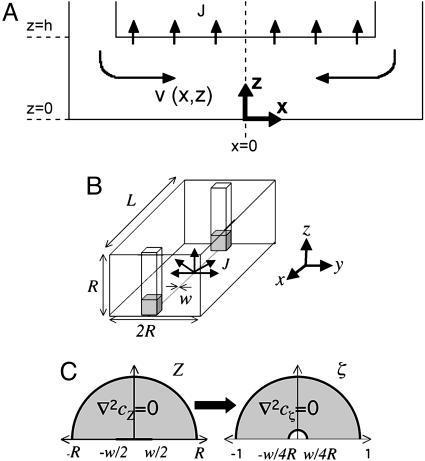
Solvent permeation into the walls of a microchannel creates an incoming flow fed by the channel reservoirs at both ends. Our goal is to model this flow and the mass transfer driving it. Fig. 1A shows the microchannel geometry as viewed from the side, and Fig. 1B shows a 3D view. The microchannel, which connects two evenly filled reservoirs, has length L, width w, and height h, and the PDMS thickness surrounding the microchannel is R. The length scales we study are L ∼ O[cm], R ∼ O[mm], w ∼ O[100 μm], and h ∼ O[μm]. We use Cartesian coordinates with origin at the floor of the channel center and with the x-axis oriented along the length of the channel, the y-axis oriented along the width of the channel, and the z-axis normal to the channel floor. Aside from the glass channel floor, all surfaces are PDMS, characteristic of softlithography microfluidic devices. Because PDMS is permeable to water, there is a net flux J of water molecules out of the microchannel and into the PDMS, which drives a converging microfluidic flow v(x, z) in this geometry.† We neglect y-dependence of the velocity because h/w << 1.
Fig. 1.
Microchannel geometry and coordinate systems. (A) Side view of the PDMS microchannel on the microfluidic length scale h. (B) A 3D view of the PDMS microchannel on the mass transfer length scale R. (C) Conformal mapping of the microchannel geometry.
We use the lubrication approximation (15) to model this 2D converging flow. This approximation reduces the Navier-Stokes equation to
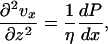 |
[1] |
which is valid in the limits h/L << 1 and Re h/L << 1, where Re = hvxρ/η, ρ is fluid density, and η is the fluid viscosity. For general conditions in this work (e.g., w = 50 μm, h = 2 μm, and L = 2.5 cm), the lubrication approximation is valid everywhere except the O[μm] entry and side wall regions. The boundary conditions used are symmetry at x = 0, no slip at z = 0 and z = h, no penetration at z = 0, and a flux balance at z = h so that vz(x, z = h) = J/ρ.
The permeation-induced velocity profile can be found by solving Eq. 1 and the continuity equation. Averaging the parabolic profile vx over the channel height gives
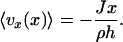 |
[2] |
Thus, the permeation-driven microfluidic flow rate will grow linearly as the distance from the symmetry (or stagnation) plane increases, and it depends inversely on the height of the microchannel. The magnitude and time dependence of this flow depend on the mass transfer rate of the solvent (water) into PDMS.
The mass transfer of water in PDMS has been previously studied (16), and results suggest near-Fickian diffusion with a diffusion coefficient D ∼ 10-9 m2/s. On the length scale of the mass transfer (R), the channel width w appears very small, so that the mass transfer is primarily radial diffusion (Fig. 1B). We model the mass transfer of water into the PDMS using constant-D Fickian diffusion as follows:
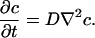 |
[3] |
We seek both steady-state and transient solutions for the flux J = -D▿c|ceiling of water molecules leaving the channel, where ▿c|ceiling is the concentration gradient at the channel ceiling, i.e., (-w/2 < y < w/2, z = h). On the mass-transfer scale, h ∼ 0 so that the diffusion problem in PDMS reduces to diffusion from a thin 2D slab with a finite width w. We assume that the outer PDMS boundary can be modeled as a cylindrical boundary of radius R and c(R) << co, where co is the room temperature saturation concentration of water in PDMS. The latter is a good assumption for PDMS stored at typical room conditions. The other boundary condition at the channel ceiling is nontrivial: c(-w/2 < y < w/2, z = 0) = co. However, this geometry is similar to a classical problem of the potential flow of fluids near cracks in porous rocks (17).
We construct the steady-state concentration profile as done in ref. 17 by using a conformal map (18). By using this result, we will then show how to compute the mean flux of water molecules leaving the channel. As is done in most conformal mapping problems, we translate our 2D geometry (yz-plane) to the complex plane (Z = y + iz) and define a complex concentration (potential) so that 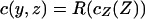 . The conformal map
. The conformal map 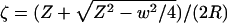 maps the channel source, i.e., the segment (-w/2 < y < w/2, z = 0) into a semicircle of radius w/4R in the ζ-plane (Fig. 1C). The exterior PDMS boundary of radius R is mapped to a semicircle of radius 1, so we are left with a straightforward diffusion problem in the ζ-plane. Solving ▿2cζ(ζ) = 0 with boundary conditions cζ(w/4R) = co and cζ(1) = 0 gives
maps the channel source, i.e., the segment (-w/2 < y < w/2, z = 0) into a semicircle of radius w/4R in the ζ-plane (Fig. 1C). The exterior PDMS boundary of radius R is mapped to a semicircle of radius 1, so we are left with a straightforward diffusion problem in the ζ-plane. Solving ▿2cζ(ζ) = 0 with boundary conditions cζ(w/4R) = co and cζ(1) = 0 gives
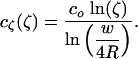 |
[4] |
Note that the concentration profile depends only logarithmically on R, justifying our simplification of the external boundary. We can convert back to the Z-plane and take the real part of this complex concentration potential to get the steady state concentration profile c(y, z). For |Z| >> w/2, c(y, z) is the same as that around a cylinder with radius w/4
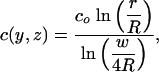 |
[5] |
where 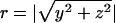 . With this profile, we can compute the flux of water at some position r as follows: J(r) = -Ddc/dr. At steady state, there is no accumulation of water in the PDMS. Therefore, we can compute the flux at some distance from the source where we know that Eq. 5 is valid and use a mass balance relation to derive the mean flux at the microchannel ceiling. From this method, we find that at steady state
. With this profile, we can compute the flux of water at some position r as follows: J(r) = -Ddc/dr. At steady state, there is no accumulation of water in the PDMS. Therefore, we can compute the flux at some distance from the source where we know that Eq. 5 is valid and use a mass balance relation to derive the mean flux at the microchannel ceiling. From this method, we find that at steady state
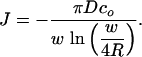 |
[6] |
Note that the steady-state flux will decrease as w increases because J ∼ 1/(w ln(w/R)).
Next, we examine the unsteady mass transfer. For the transient case, at times t >> w2/4D (which is t >> 1 s here), the concentration profile asymptotically approaches the profile around a cylinder of radius w/4 (17). Therefore, we construct a similarity solution of Eq. 3 using the effective radius of w/4 for the inner channel, obtaining a transient concentration profile
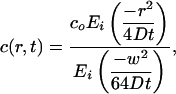 |
[7] |
where Ei is the exponential integral Ei function. We stress that for r > w/2, this solution is asymptotically valid for our exact geometry for times w2/4D << t << R2/D. To calculate the flux at some position r, we evaluate -D∂c/∂r
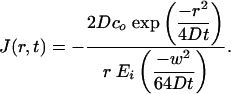 |
[8] |
To obtain the transient flux at the microchannel, we now consider the limits of Eq. 8 as r approaches w/2 and t >> w2/4D. For any sufficiently small r (i.e., 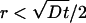 ), we have r2/(4Dt) << 1 so that the exponential in Eq. 8 is ≈1. Expanding Ei near zero to leading order gives J(r, t) ∼ 1/(r ln (Dt/w2)) near the channel during this transient period of interest. Performing a mass balance at two radii, it is easy to see that there is no local accumulation of water in this PDMS region near the channel during this transient period. Therefore, as a reasonable approximation, we can use the same mass balance technique used for the steady-state analysis to determine the flux at the microchannel ceiling. The transient flux [valid for w2/4D << t << R2/D] is
), we have r2/(4Dt) << 1 so that the exponential in Eq. 8 is ≈1. Expanding Ei near zero to leading order gives J(r, t) ∼ 1/(r ln (Dt/w2)) near the channel during this transient period of interest. Performing a mass balance at two radii, it is easy to see that there is no local accumulation of water in this PDMS region near the channel during this transient period. Therefore, as a reasonable approximation, we can use the same mass balance technique used for the steady-state analysis to determine the flux at the microchannel ceiling. The transient flux [valid for w2/4D << t << R2/D] is
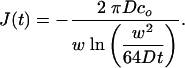 |
[9] |
Eqs. 6 and 9 predict the flux at times t >> R2/D and w2/4D << t << R2/D, respectively. With this insight into the mass transfer of water into the PDMS, we can now analyze the induced microfluidic flow. In our analysis, we experimentally determine co and use D as a fitting parameter whose value is bound by values reported in ref. 16.
Experimental Methods
The experimental observable is the gap average velocity 〈vx〉. We extract this value using fluorescence microscopy to track the position of small 0.11-μm-diameter Brownian tracer beads in the flow.
Solution. A solution of 2 × 10-4% fluorescent carboxylate-modified polystyrene microspheres (diameter = 0.11 μm, Molecular Probes) in ultrapure water (Milli-Q, Millipore) was prepared for observation. Before loading into the microchannels, this solution was vortexed for 30 s and sonicated for 30 s (Aquisonic 50HT, VWR Scientific). Bead aggregation was not observed.
Channel Preparation. PDMS microchannels were fabricated by softlithography (3). A 10:1 PDMS: crosslinking agent (Sylgard 184, Dow) was degassed for 60 min at 15″ Hg vacuum pressure. The PDMS then was poured onto a Si master wafer with the negative of the microchannel geometry embedded in a layer of AZ 5214 image reversal photoresist (Clariant, Muttenz, Switzerland). The Si wafer was pretreated with a fluorinated silane monolayer (United Chemical Technologies, Bristol, PA) to prevent cured PDMS from sticking to the Si master. After pouring, the PDMS was allowed to degas for an additional hour at 15″ Hg. The PDMS then was cured at 65°C for 24 h. Reservoirs (4 × 4 mm) were cut at each end of the cured PDMS microchannel with a scalpel, and the microchannel was placed onto a clean glass slide (soaked 15 min in 1 M NaOH, rinsed with ultrapure water, and treated with 100 W RF plasma for 60 s). Unless otherwise noted, the length of each microchannel was L = 25 mm. Ten microliters of the bead solution was added to the reservoirs, and the channel filled within a minute. The reservoirs were replenished with 5 μl approximately every 2 h. Significant sagging of the PDMS ceiling was not observed as 1.6-μm beads uniformly passed through a 2.0-μm-high channel, and bead diffusion experiments showed no correlation with y-position away from the walls. We gravimetrically measured the solubility of water in PDMS to be co = 40 mol/m3 at 21°C in agreement with ref. 16.
Observation. The device was placed on an inverted microscope (Axiovert 200, Zeiss), and the tracer beads were observed through a ×100, 1.4 numerical aperture oil-immersion objective. Images were captured with an electron-beam-charge-coupled device camera (C7190-20, Hamamatsu) and nih image software. Room conditions were steady at 21 ± 0.5°C and 33 ± 3% relative humidity. We determined the gap average velocity for each presented data point by computing the velocity of 15 tracer beads in the x-direction. To do this velocity calculation, we determined the center of mass position of a bead at two different times, requiring that Δx ∼ 35-70 μm depending on the velocity. The gap average velocity for a bead was then Δx/Δt. Note that a typical value of Δt was 1 s in the 2-μm-high channels. In this time, a bead can diffuse ≈4 μm in the z-direction, which assures us that we are measuring the gap average velocity. These measurements were made at y positions at least 5 μm from the side walls, where we confirmed that the 〈vx〉 profile was independent of y.
Results
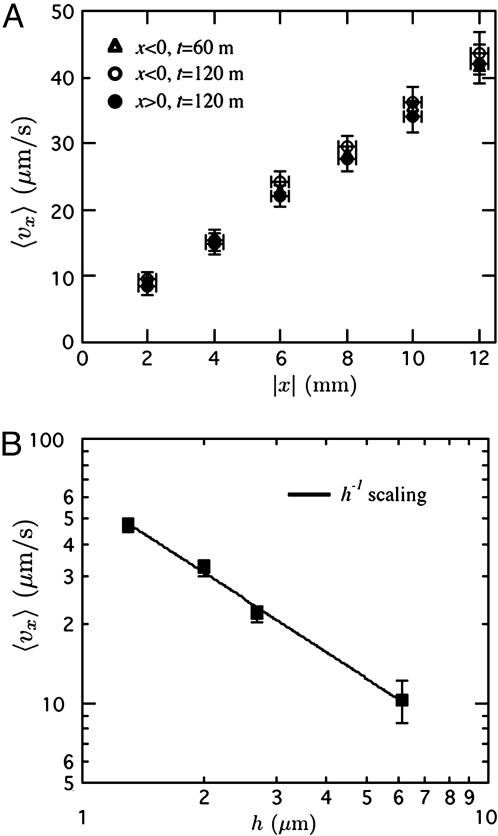
Microfluidics. We investigated the dependence of 〈vx〉 on x and h to validate the lubrication approximation analysis by tracking the velocity of 0.11-μm beads in the PDMS microchannels. Fig. 2A shows the steady-state permeation velocity as a function of the distance |x| from the microchannel center. The dimensions of this microchannel were w = 50 μm, h = 2 μm, and R = 1.5 mm. The velocity clearly increases linearly with |x| and, noting that both x < 0 and x > 0 data are present, it is symmetric about x = 0. From the slope, we calculate the flux to be J = 7 × 10-6 kg/(m2s), which is (for an order of magnitude reference) ≈20% of the evaporation rate of water at these conditions. Fig. 2B shows the steady-state permeation velocity at x = 9.5 mm. The velocity scales as h-1 as predicted and is much more pronounced in thin channels. Together, these experiments confirm that the steady-state microfluidic velocity can be modeled by the lubrication approximation. Next, we examine how this flow depends on the mass transfer.
Fig. 2.
Experimental steady-state permeation flow results. (A) Steady permeation velocity as a function of distance from the center (|x| = 0) in a microchannel with w = 50 μm, h = 2 μm, and R = 1.5 mm. (B) Steady permeation velocity (evaluated at t = 150 min, x = 9.5 mm) as a function height in microchannels with w = 50 μm and R = 5 mm.
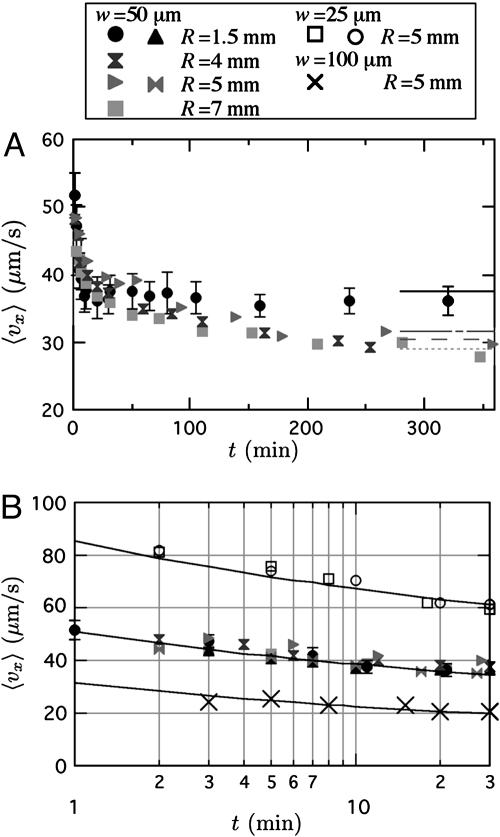
Mass Transfer. By using Eq. 2 and the expressions for J(t) and J from our model, we can predict the transient and steady-state permeation velocities, respectively. We compare the model predictions with experimental results in Fig. 3. Fig. 3A shows the time-dependent permeation velocity at x = 9.5 mm as a function of PDMS thickness. Lines are included at long times showing the expected steady-state velocities for each R using the measured value of co = 40 mol/m3 and a fitting parameter D = 8.5 × 10-10 m2/s. This best fit D for transient and steady data is in the range observed in recent diffusion experiments in PDMS (16). Importantly, note that the steady-state velocities are weakly dependent on R, as predicted by Eq. 6, which is a consequence of radial diffusion from a thin line. Also, note that permeation can deliver steady velocities for several hours. In Fig. 3B, we focus on the short-time transient velocity and include channels of various widths. The line accompanying each constant-width data set uses Eq. 9, again using co = 40 mol/m3 and D = 8.5 × 10-10 m2/s. Note that the wider channels do have lower induced velocities as expected. Additionally, the transient scaling has a much flatter fall-off with time than the t-1/2 scaling predicted for planar diffusion, a consequence of the logarithmic time scaling (Eq. 9) of radial diffusion. Finally, note that the w = 50 μm data for various R show uniform behavior during the transient penetration into the PDMS, which is expected because the outer boundary condition has no effect at times t << R2/D.
Fig. 3.
Experimental time-dependent permeation flow results. (A) Permeation velocity (x = 9.5 mm) as a function of time and PDMS thickness in microchannels with w = 50 μm and h = 2 μm. Lines are the calculated steady-state velocities (Eqs. 2 and 6) for each R (moving down, R = 1.5, 4, 5, and 7 mm) using D = 8.5 × 10-10 m2/s. Only one set of the self-similar error bars is shown for clarity. (B) Transient permeation velocity for different channel widths with h = 2 μm. Lines are the calculated transient velocities (Eqs. 2 and 9) by using D = 8.5 × 10-10 m2/s.
Discussion
Comparison with Poiseuille Flow. Figs. 2 and 3 show strong experimental support that the models presented can reliably predict the permeation-induced microflow. We can compare the gap average velocity to that of a mean Poiseuille velocity UPoiseuille to get a better feel for when this flow is important
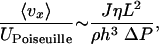 |
[10] |
where ΔP is an externally applied pressure drop. At large values of this parameter, e.g., for very thin channels, the permeation-induced velocity will dominate the applied pressure driven flow. More specifically, for h < 10 μm, 〈vx〉/UPoiseuille ≫ 1 for the flow induced by a 1-mm hydrostatic head. Therefore, it is impossible to create a stagnant fluid environment in thin, untreated PDMS channels. Consequently, knowledge of permeation-induced flow is extremely important for designing the next generation of O[μm] microdevices in PDMS.
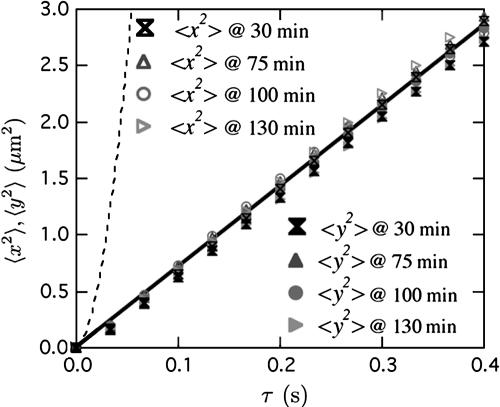
Eliminating the Flow. For many applications in O[μm]-sized PDMS channels, permeation-induced flow is undesirable. Therefore, it would be useful to try to eliminate it by inhibiting the mass transfer of water into the PDMS. The simplest way is to supersaturate the PDMS with water by soaking it in a bath of heated water. We soak a PDMS microchannel in 50°C water for 24 h, rinse it, gently dry it, and then use it as in the above experiments. We observe that after a short equilibration time of 10-20 min (presumably to resoak a thin layer of PDMS that has dried during handling), the permeation-driven flow subsides. We show this result by tracking the mean square displacements (〈Δx2〉 and 〈Δy2〉) of the tracer beads vs. lag time τ (Fig. 4) using 120 s of total trajectory time for each time series at a position x = 9.5 mm in the microchannel. For reference, we include the 〈Δx2〉 expected at x = 9.5 mm if the permeation-driven flow persisted (dashed line). Without flow, we expect that both 〈Δx2〉 and 〈Δy2〉 equal 2Dbeadτ expected from the Stokes-Einstein relation. For times up to 2 h, both 〈Δx2〉 and 〈Δy2〉 equal 2Dbeadτ, and the flow is not detectable. This 2-h passivation time is approximately the time it takes for this piece of supersaturated PDMS to dry at room conditions. More robust passivation methods such as using a coating of parylene (19) or Teflon (20) would be desirable as research in PDMS devices moves to the micro- and nanoscale.
Fig. 4.
Mean square displacement (MSD) vs. time of the tracer beads in a presoaked PDMS microchannel with w = 50 μm, h = 2 μm, and R = 5 mm. Open symbols are for the x-direction, and filled symbols are for the y-direction. Data are taken at several times after filling the microchannel at the position x = 9.5 mm. The dashed line is the expected MSD if the permeation-driven flow persisted, and the solid line is the Stokes-Einstein MSD.
Applications. We have already mentioned the potential to use this flow for passive pumping, because it can deliver a steady flow for several hours. In fact, it is possible to passively generate a converging flow in a single channel, a difficult feat by conventional techniques. A steady converging flow could prove to be a powerful way to quantify chemical interactions at the channel center where two different streams would meet. For example, it may prove useful to monitor chemical reactions or gel-formation phenomenon at the channel center.
Other possible applications that we are able to demonstrate are passively stacking colloids and passively concentrating chemicals. Fig. 5 shows light microscopy images of passively fabricated crystalline microstructures. To form these arrays, we applied 2% solutions of various bead sizes to the reservoirs of a thin PDMS microchannel (w = 50 μm, h = 2 μm, R = 5 mm, and L = 1 cm). The permeation-driven flow carried the beads toward the center of the channel where they assembled into the displayed structures. Note that the interface between bead layers is not perfectly straight. We speculate that the small component of the velocity in the y-direction can lead to a larger bead concentration profile at the walls and, hence, nonuniform stacking at the interface. With this assembly technique, we have created a microstructure with controllable pore size, a potentially useful tool for biomolecule separations (e.g., DNA). This bead-stacking method also will be useful for microbead catalyst processes (21) because beads can be stacked at the center of a channel without the need for any supporting weirs. Consequently, beads much smaller than typical microfabrication limits could be used for these catalytic/enzymatic processes. In comparison with other bead-stacking techniques, permeation-driven stacking is limited to thin channels but has the advantage of forming layered microstructures in the center of a channel without supporting weirs.
Fig. 5.
Observation of permeation-driven bead packing (bead diameters of 0.75, 1.0, and 1.6 μm) in a channel with h = 2 μm. Both images are taken on the left side of the symmetry plane, and the crystal interface propagates from right to left.
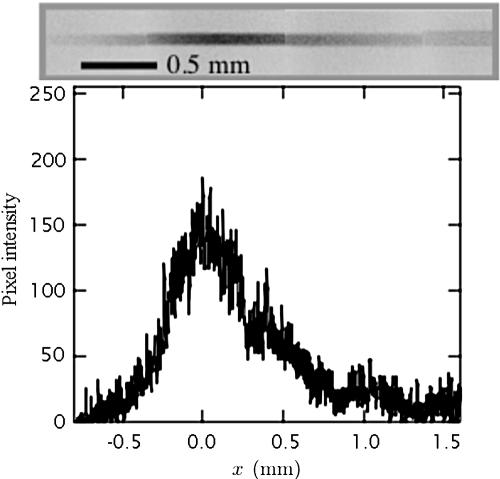
In addition to forming stacked microstructures, we can concentrate chemical species with this flow. Concentrating chemicals is particularly important in microdetection devices because the small sample volume combined with potentially low species concentrations leaves very few species for detection (13). Concentration is also important at the beginning of many separation processes (e.g., DNA) that require an initial highly concentrated plug of material. Permeation-driven flow offers a way to concentrate chemicals at specific regions in a channel. For example, a symmetric “T” design could concentrate species at the channel intersection, where they can be driven by a field for a separation application. The characteristic concentrating length scale is 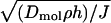 , where Dmol is the diffusivity of the desired concentrated molecule in water. At this length scale, diffusive fluxes and convective fluxes balance near the stagnation plane. Because Dmol grows as molecular size decreases, this length scale may be much larger than molecular dimensions. The typical channels in this work would be able to concentrate molecules in regions with lengths on the order of 0.5 mm for a small molecule like fluorescein to 50 μm for a macromolecule like λ-DNA. To show chemical concentration, we load the left reservoir of a 2-μm-high channel with water and the other with 2 × 10-2 % fluorescein. Assuming that the fluorescein concentration is proportional its fluorescence light intensity, we can quantify the degree of concentration of the fluorescein at the center of the microchannel. Fig. 6 shows the centerline (y = 0) pixel intensity as a function of distance from the channel center (x = 0) 60 min after loading the dilute fluorescein solution. The image is a magnification of the center of the actual channel where darkness corresponds to high intensity. Care was taken not to saturate our 8-bit intensity resolution and to capture short (<2 s) images so that photobleaching was not a factor. After the pixel intensity was noise filtered, the inlet fluorescein had a baseline intensity of 10. At the channel center, the intensity averages to a value near 150, corresponding to ≈15× concentration of the fluorescein. This result agrees with a back-of-the-envelope calculation using Eq. 2 for the degree of concentration for a 0.5-mm-long sample volume at the center of this channel.
, where Dmol is the diffusivity of the desired concentrated molecule in water. At this length scale, diffusive fluxes and convective fluxes balance near the stagnation plane. Because Dmol grows as molecular size decreases, this length scale may be much larger than molecular dimensions. The typical channels in this work would be able to concentrate molecules in regions with lengths on the order of 0.5 mm for a small molecule like fluorescein to 50 μm for a macromolecule like λ-DNA. To show chemical concentration, we load the left reservoir of a 2-μm-high channel with water and the other with 2 × 10-2 % fluorescein. Assuming that the fluorescein concentration is proportional its fluorescence light intensity, we can quantify the degree of concentration of the fluorescein at the center of the microchannel. Fig. 6 shows the centerline (y = 0) pixel intensity as a function of distance from the channel center (x = 0) 60 min after loading the dilute fluorescein solution. The image is a magnification of the center of the actual channel where darkness corresponds to high intensity. Care was taken not to saturate our 8-bit intensity resolution and to capture short (<2 s) images so that photobleaching was not a factor. After the pixel intensity was noise filtered, the inlet fluorescein had a baseline intensity of 10. At the channel center, the intensity averages to a value near 150, corresponding to ≈15× concentration of the fluorescein. This result agrees with a back-of-the-envelope calculation using Eq. 2 for the degree of concentration for a 0.5-mm-long sample volume at the center of this channel.
Fig. 6.
Centerline (y = 0) fluorescence intensity of fluorescein concentrating near the center of a microchannel (w = 50 μm, h = 2 μm, R = 5 mm, and L = 2.5 cm) after 60 min of flow. The composite image is the series of four snapshots about x = 0 used to obtain these data, with high intensity corresponding to dark areas.
In summary, we have presented a model and experimental validation of a previously undescribed microfluidic flow driven by permeation of a solvent into a PDMS wall. Results show that the process can be described by the lubrication approximation and radial diffusion, which explains the increase in flow with decreasing channel height and the weak dependence of the flow on the PDMS thickness. In many circumstances, this flow is undesirable, but we have shown that it can be eliminated by inhibiting the mass transfer of the solvent into the PDMS. Conversely, we demonstrate that this flow can be harnessed for several passive flow applications like pumping, stacking microspheres, and concentrating chemicals. Permeation-driven flow is a powerful and unexplored technology to manipulate fluids and colloids on the micro- and nanoscale. But equally as important, as PDMS devices move from micro- to nanoscale, this flow will dominate externally driven flows. Therefore, knowledge of what drives it and what stops it is invaluable to the success of these future devices.
Acknowledgments
We thank Prof. V. M. Entov for stimulating discussions and for referring us to ref. 17. This work was supported by National Science Foundation CAREER Grant CTS-0239012.
Author contributions: G.C.R. and P.S.D. designed research, performed research, contributed new reagents/analytic tools, analyzed data, and wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviation: PDMS, poly(dimethylsiloxane).
Footnotes
The same analysis can be applied to permeation-driven flow in a channel closed at one end.
References
- 1.Beebe, D. J., Mensing, G. A. & Walker, G. M. (2002) Annu. Rev. Biomed. Eng. 4, 261-286. [DOI] [PubMed] [Google Scholar]
- 2.Effenhauser, C. S., Bruin, G. J. M., Paulus, A. & Ehrat, M. (1997) Anal. Chem. 69, 3451-3457. [DOI] [PubMed] [Google Scholar]
- 3.Xia, Y. & Whitesides, G. M. (1998) Angew. Chem. Int. Ed. 37, 550-575. [DOI] [PubMed] [Google Scholar]
- 4.McDonald, J. C., Duffy, D. C., Anderson, J. R., Chiu, D. T., Wu, H., Schueller, O. J. A. & Whitesides, G. M. (2000) Electrophoresis 21, 27-40. [DOI] [PubMed] [Google Scholar]
- 5.Quake, S. R. & Scherer, A. (2000) Science 290, 1536-1540. [DOI] [PubMed] [Google Scholar]
- 6.McDonald, J. C. & Whitesides, G. M. (2002) Acc. Chem. Res. 35, 491-499. [DOI] [PubMed] [Google Scholar]
- 7.Robb, W. L. (1968) Ann. NY Acad. Sci. 146, 119-137. [DOI] [PubMed] [Google Scholar]
- 8.Lee, J. N., Park, C. & Whitesides, G. M. (2003) Anal. Chem. 75, 6544-6554. [DOI] [PubMed] [Google Scholar]
- 9.Chou, H.-P., Spence, C., Scherer, A. & Quake, S. (1999) Proc. Natl. Acad. Sci. USA 96, 11-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zheng, B., Roach, L. S. & Ismagilov, R. F. (2003) J. Am. Chem. Soc. 125, 11170-11171. [DOI] [PubMed] [Google Scholar]
- 11.Goedecke, N., Eijkel, J. & Manz, A. (2002) Lab Chip 2, 219-223. [DOI] [PubMed] [Google Scholar]
- 12.Kim, E., Xia, Y. N. & Whitesides, G. M. (1996) Adv. Mater. 8, 245-247. [Google Scholar]
- 13.Walker, G. M. & Beebe, D. J. (2002) Lab Chip 2, 57-61. [DOI] [PubMed] [Google Scholar]
- 14.Walker, G. M. & Beebe, D. J. (2002) Lab Chip 2, 131-134. [DOI] [PubMed] [Google Scholar]
- 15.Deen, W. M. (1998) Analysis of Transport Phenomena (Oxford Univ. Press, New York).
- 16.Watson, J. M. & Baron, M. G. (1996) J. Membr. Sci. 110, 47-57. [Google Scholar]
- 17.Barenblatt, G. I., Entov, V. M. & Ryzhik, V. M. (1990) Theory of Fluid Flows Through Natural Rocks (Kluwer, Boston).
- 18.Schinzinger, R. & Laura, P. A. A. (2003) Conformal Mapping: Methods and Applications (Dover, New York).
- 19.Shin, Y. S., Cho, K., Lim, S. H., Chung, S., Park, S. J., Chung, C., Han, D. C. & Chang, J. K. (2003) J. Micromech. Microeng. 13, 768-774. [Google Scholar]
- 20.Lau, K. K. S. & Gleason, K. K. (2000) J. Fluorine Chem. 2000, 119-126. [Google Scholar]
- 21.Seong, G. H. & Crooks, R. M. (2002) J. Am. Chem. Soc. 124, 13360-13361. [DOI] [PubMed] [Google Scholar]