The superconductivity and electron-doping effect in MgP₂H₁₄ hydrides

Summary

Room temperature superconductivity has become the tireless pursuit of scientists due to its epoch-making significance. Inspired by the recently predicted high superconductivity in LiP₂H₁₄, we identify a new superconductor MgP₂H₁₄ by substituting Li with Mg and prove its stability. The superconducting critical temperature (T_c) and electron-phonon coupling (EPC) parameters (λ) of MgP₂H₁₄ under 280 GPa are predicted to be ∼166 K and ∼1.65, respectively; the high superconductivity of MgP₂H₁₄ mainly arises from the strong electron-phonon interaction between H 1s electrons and the H-associated vibration. Furthermore, in hydrogen-based superconductors, the hydrogen sublattice will gain more electrons by doping extra metal atoms or replacing the original metals with higher valence electrons metals. However, if these electrons do not form newly occupied states on the hydrogen energy level near the Fermi level, the superconductivity will not improve further. Our findings provide clues for designing and modulating the superconductivity.

Graphical abstract

Highlights

• •Doping electrons in hydride superconductors will cause H to gain more electrons
• •If the doped electrons fail to increase the H-PDOS, T_c won’t be improved
• •In the case of similar atomic masses in hydrides, low $⟨{\omega }^2⟩$ are favorable for EPC
• •T_c of MgP₂H₁₄ benefits from the coupling between H-associated vibration and H electron

Condensed matter physics; Superconductivity; Photon-electron interaction

Introduction

The breakthrough of room temperature superconductivity barrier is bound to bring unprecedented innovation in the energy field. According to the Bardeen-Cooper-Schrieffer (BCS) theory,¹ metallic hydrogen was predicted to be a potential room temperature superconductor.² However, the pressure required for realizing hydrogen metallization is exceptionally high and difficult to achieve.³ As an alternative route, chemical pre-compression proposed by Ashcroft holds that introducing another element into hydrogen will chemically pre-compress the system under certain circumstances, allowing the hydride to enter the metallic phase earlier than the metallic hydrogen and retain a certain degree of superconductivity.⁴ Based on this principle, a series of hydrogen-dominant high-temperature superconductors were predicted, and some were successfully synthesized in the past 20 years,^5,6,7,8,9,10 which has rekindled the hope to realize room temperature superconductivity and has sparked enthusiasm for the search for more promising superconducting materials in hydrides.

As the available chemical space expands and additional degrees of freedom become possible, ternary hydrides are gaining increasing attention to increase T_c and enhance stability over a wider pressure range.¹¹ In 2020, Li et al. identified that the T_c of LiP₂H₁₄ reaches up to 169 K at 230 GPa.¹² As the electron donor, Li atoms play an important role in stabilizing the crystal structure and enhancing the phonon-mediated superconductivity of the Li-P-H system. Traced back to the simplified Hopfield expression $\lambda =N\left(E_f\right)⟨I^2⟩/M⟨{\omega }^2⟩$,¹³ where N(E_f) is the calculated electronic density of states (DOS) at the Fermi level, $⟨I^2⟩$ is the mean square of the electron-phonon matrix element averaged over the Fermi level, M is the atomic mass, and $⟨{\omega }^2⟩$ is the mean square of the phonon frequencies. Normally, heavier atoms might suppress superconductivity due to their low Debye temperature.¹⁴ But sometimes, heavier atoms tend to be accompanied by lower phonon frequencies (soft phonons), which may improve the strength of the electron-phonon coupling (EPC) and thus enhance the T_c.¹⁵ For example, the phonon frequency of LiP₂H₁₄ was greatly reduced and its T_c was improved after substituting Li with Be or Na atoms, T_c (LiP₂H₁₄) < T_c (BeP₂H₁₄) < T_c (NaP₂H₁₄). Inspired by this result, we try to replace the Li with heavier atoms to see if the superconductivity can be further improved. In this paper, we replaced Li in LiP₂H₁₄ with Mg, K, Ca, Rb, and Sr to calculate their phonon dispersion curve at 200, 240, and 300 GPa. However, only MgP₂H₁₄ is found to be dynamically stable at 300 GPa.

Under an appropriate chemical environment, introducing extra electrons via metal doping can enable the antibonding states of H₂ or H₃ molecules to accept electrons and achieve molecular dissociation; in this case, the energy of H electrons will be closer to the Fermi level, which will give rise to an increased H-derived DOS at the Fermi level and thus improve the H-based superconductor.¹⁶ Mg atoms have one additional valence electron compared with Li atoms; hence, Mg substitute for Li in LiP₂H₁₄ is equivalent to doping electrons in the system. Besides, Mg and Be atoms have the same number of valence electrons, but Mg is less electronegative, which may be beneficial for the hydrogen lattice to gain more electrons and hence stabilize the structure under lower pressure and improve the superconductivity.^16,17 MgP₂H₁₄ may be a promising superconductor with T_c higher than NaP₂H₁₄ and LiP₂H₁₄ since it doped with more electrons. With this wonderful expectation, we investigated the stability, electronic properties, EPC, and superconductivity of MgP₂H₁₄ systematically.

Computational methods

The first principles based on the density functional theory (DFT)¹⁸ and density functional perturbation theory (DFPT)¹⁹ were employed to execute all calculations by using the Quantum ESPRESSO package.²⁰ The exchange-correlation function was parameterized by the Perdew-Burke-Ernzerhof (PBE)²¹ model to describe the electron interactions. The Mg 2s²2p⁶3s², P 3s²3p³, and H 1s¹ configurations were treated as valence electrons. The first-order potential perturbation and dynamical matrices were calculated using DFPT on an irreducible 4 × 4 × 4 q-point mesh. The norm-conserving pseudopotentials²² were used with a kinetic energy of 80 Ry and Monkhorst-Pack k meshes with a grid spacing of 2π × 0.02 Å⁻¹ (16 × 16 × 16) are adopted to achieve a good convergence. A denser k-point mesh of 32 × 32 × 32 was employed to calculate the electron-phonon matrix elements. The ab initio molecular dynamics (AIMD)²³ simulation with NVT (N for the number of particles, V for volume, and T for temperature) ensemble and Nose-Hoover thermostat was performed to prove its thermodynamic stability in 300 K, the time step was 2fs, the primitive cell was expanded to 2 × 2×2. The setting of the exchange-correlation function, valence electrons, pseudopotentials, and energy cutoff in AIMD simulation are consistent with the DFT calculation above. The crystal orbital Hamilton population (COHP)²⁴ was exploited to describe the pair interactions by using the LOBSTER code.²⁵

The isotropic Migdal-Eliashberg (ME) equation^26,27,28 was employed to calculate the superconducting gap and T_c by using the electron-phonon Wannier (EPW) code.²⁹ The denser homogeneous k-point mesh of 64 × 64 × 64 and q-point mesh of 16 × 16 × 16 were employed to solve the isotropic ME equation during the Wannier interpolation. Twenty-three atomic orbitals of MgP₂H₁₄ (consisting of H-s, Mg-s, P-s, and P-p orbitals) were used to construct the maximally localized Wannier functions (MLWF).³⁰

More computational details for calculating the superconducting parameters can be seen in the supplemental information. Phonon spectra and phonon DOS in Figures S1 and S2 are calculated by using the CASTEP code (more computation details can be seen in the caption of Figures S1 and S2),³¹ all the rest of the phonon properties are calculated by using the Quantum ESPRESSO package.

Results and discussions

Lattice structure and stability

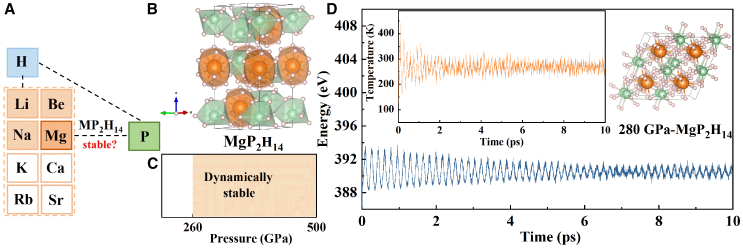
By substituting the Li atom in $R\overline{3}$ LiP₂H₁₄ with M (M = Mg, K, Ca, Rb, Sr), we investigated the dynamical stability of five kinds of MP₂H₁₄ by calculating the phonon dispersion curves under 200 , 240 , and 300 GPa, respectively (see Figures 1A and S1). However, for several specific pressure points (200, 240, and 300 GPa) we calculated, except for MgP₂H₁₄ that is dynamically stable under 300 GPa, the phonon spectra of other MP₂H₁₄ systems exhibit a large number of imaginary modes (see Figure S1). Based on this, we conduct a detailed study on MgP₂H₁₄.

Figure 1.

Crystal structure and stability of MgP₂H₁₄

(A) The stability of MP₂H₁₄ (M = Li, Be, Na, Mg, K, Ca, Rb, Sr).

(B) Crystal structure of MgP₂H₁₄ with the space group of $R\overline{3}$ at 280 GPa, consisting of P-centered H₉ cages and Mg-centered H₁₄ cages.

(C) MgP₂H₁₄ is dynamically stable in the pressure range of 260–500 GPa, the detailed data of phonon spectra can be found in the supplemental information.

(D) The total free energy and temperature as a function of time during the ab initio molecular dynamics (AIMD) simulation (lasting for 10 ps at 300 K).

The optimized structure of MgP₂H₁₄ consists of Mg-centered H₁₄ cages and P-centered H₉ cages, without independent H₂ units (see Figure 1B), which lays a good foundation for its high superconductivity since many cases have proven that clathrate structure is beneficial to superconductivity.^7,32,33 To further explore the dynamical stability of MgP₂H₁₄ under pressure, we calculated the phonon spectra and phonon DOS of MgP₂H₁₄ at 0, 260, 340, 420, and 500 GPa (see Figures S1A and S2). The results show that there are substantial imaginary modes at 0 and 240 GPa and no imaginary modes at 260, 340, 420, and 500 GPa, indicating that MgP₂H₁₄ is dynamically stable in the pressure range of 260–500 GPa but unstable when the pressure is below 240 GPa (see Figure 1C). To determine the thermodynamic stability, AIMD simulations were performed under 280 GPa. As shown in Figure 1D, we observed that all of the atoms only vibrate slightly around their equilibrium positions, the fluctuations of the total free energy and temperature as a function of time are within a narrow range, indicating that MgP₂H₁₄ is thermodynamically stable at 300 K under 280 GPa.

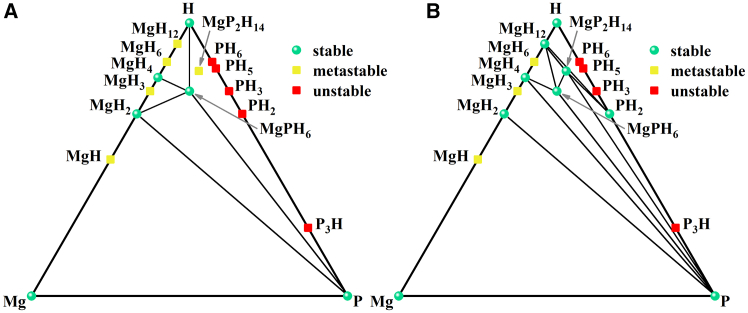
We further explore the thermal stability and the possibility of the experimental synthesis of MgP₂H₁₄ by calculating the formation enthalpy to construct the ternary phase diagram at 280 GPa after considering the zero-point energy (ZPE). The ZPE plays an important role in determining the energetics of H-rich materials because of the high vibrational frequency of H. The ΔH_zero value of MgP₂H₁₄ is defined as follows:

$$\Delta H_{\text{zero}}=\Delta H+\Delta ZPE$$ (Equation 1)

where ΔH is the formation enthalpy of MgP₂H₁₄, which can be estimated as follows:³⁴

$$\Delta H\left({\text{MgP}}_2{\mathrm{H}}_{14}\right)=H\left({\text{MgP}}_2{\mathrm{H}}_{14}\right)-H\left(\text{Mg}\right)–2H\left(\mathrm{P}\right)–14H\left(\mathrm{H}\right)$$ (Equation 2)

where the H(MgP₂H₁₄), H(Mg), H(P), and H(H) are the enthalpy for MgP₂H₁₄, pure elements Mg, P, and H at 280 GPa. As shown in Figure 2, MgP₂H₁₄ and MgH₁₂ become thermodynamically metastable under 280 GPa once ZPE correction is included, indicating that it is necessary to consider ZPE correction in Mg-P-H systems. MgPH₆,³⁵ MgH₄,³⁶ and MgH₂³⁷ are thermodynamically stable whatever with and without ZPE correction. Besides, the results show that MgP₂H₁₄ may be synthesized by the elemental Mg, P, and H (or MgH₂) as the first two paths listed below, but MgP₂H₁₄ is thermally unstable since it may decompose into the energetically more favorable MgH₄ or MgPH₆ at 280 GPa (the ΔH_zero values for corresponding decomposition pathways are listed as follows, herein, only the thermally stable phase was considered as decomposition product), implying a metastable feature. This does not mean that MgP₂H₁₄ cannot be synthesized experimentally, after all, 20% of synthesized materials are metastable in the Inorganic Crystal Structure Database,³⁸ but the synthesis process of metastable phases may be a bit challenging, such as the synthesis of diamond. In addition, it can be seen that P₃H, PH₃, PH₅, and PH₆ have positive formation enthalpy against the elemental P and H, indicating that Mg plays a positive role in stabilizing the P-H systems.

MgP₂H₁₄ → Mg + 2P + 14H–4.281 eV,

MgP₂H₁₄ → MgH₂ + 2P + 12H–0.112 eV,

MgP₂H₁₄ → MgH₄ + 2P + 10H + 0.087 eV,

MgP₂H₁₄ → MgPH₆ + P + 8H + 0.322 eV.

Figure 2.

The phase diagrams of Mg_xP_yH_z relative to elemental Mg, P, H, and binary Mg-H, and P-H systems at 280 GPa

(A) The convex hull after considering the zero-point energy.

(B) The convex hull without considering the zero-point energy. Green solid circles and yellow squares indicate stable and metastable phases, respectively, and red squares indicate unstable phases relative to elemental Mg, P, and H. The source and detailed information of the corresponding structure are summarized in Table S1 in supplemental information.

Electronic structures

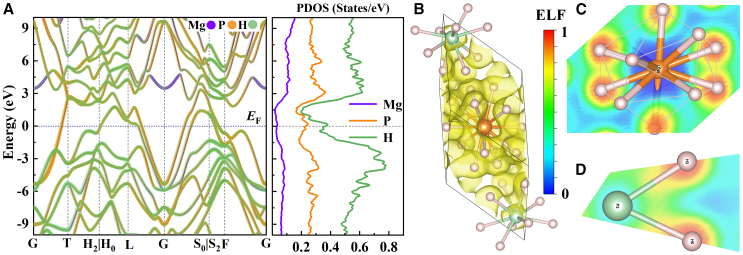
The predicted MgP₂H₁₄ system is metallic at 280 GPa as confirmed by the electronic band structure on account of two bands across the Fermi level (see Figure 3), these two bands exactly form obvious σ bands that attributed to the hybridization of P-p and H-s orbitals (see Figure S3). There is a small peak of electronic DOS located slightly above the Fermi level, which is associated with the inflection point of a quite small band fraction close to the L point. The electrons near the Fermi level are mainly contributed by the s orbitals of H atoms and p orbitals of P atoms and there is strong hybridization between them. One of the most typical characteristics of hydrogen-rich superconductors is that their electrons near the Fermi level are mainly contributed by the H atom,³⁹ this feature is particularly obvious in the MgP₂H₁₄ system. The orbitals of H in MgP₂H₁₄ contribute about 58.4% to the electronic DOS at the Fermi level, while the Mg contributes very little to the electronic DOS near the Fermi level.

Figure 3.

The electronic structure of MgP₂H₁₄

(A) The electronic band structure and the partial density of states of MgP2H14 at 280 GPa, the projected weight of each orbital are shown in different colors, and the widths of the lines are proportional to the weights.

(B) The electron localization function (ELF) present in the primitive cell (where the isosurface level is set with 0.5).

(C) The ELF near Mg and H atoms.

(D) The ELF near P and H atoms for MgP₂H₁₄ at 280 GPa (the degree of localization is shown in the color column, where the red and blue areas indicate the highest and lowest localized electrons, respectively).

As illustrated intuitively in Figure 3B, the electrons in MgP₂H₁₄ are mainly concentrated around H atoms, in addition, Figure 3C shows that the electron localization function (ELF) around P is below 0.5, the ELF around H is above 0.8, the ELF between P and H is about 0.7, and the shared electron pairs are biased toward H atoms, indicating that P-H bond is a polar bond in which ionic and covalent properties coexist. Figure 3D shows that the ELF around Mg is close to 0, indicating that Mg and H are mainly bonded with an ionic bond. A small amount of electron cloud overlap between H and H indicates a weak covalent bond. The Bader charge shows that both Mg and P atoms will donate electrons to H atoms (see Table S2), and Mg atoms donate more electrons than P atoms, indicating that Mg and P atoms may play an important role in stabilizing the hydrogen-rich structure so that MgP₂H₁₄ can maintain dynamically stable within a wide range of pressures. As the pressure increases, both the P-H bond and Mg-H bond length decrease gradually, and the Bader charge of P atoms increases significantly however the Mg atoms decrease slightly, which may be due to the P atom being closer to the H atoms and are covalently bonded to each other and hence the distribution of electrons is more susceptible to pressure. In order to further understand the bonding nature, we also exploit the COHP and integrated COHP (ICOHP) to quantify the interatomic interactions. As depicted in Figure 4, the negative and positive projected COHP values indicate bonding and antibonding interactions, respectively, the ICOHP up to the Fermi level can reflect the atom pair interaction strength. We note that P-H, H-H, Mg-P, and Mg-P bonding interactions are obvious, the P-H bonding occupies the largest portion in states below the Fermi level. Besides, the Mg-P and Mg-H interactions near the Fermi level are weaker than the P-H and H-H interactions, indicating that the effect of P-H and H-H interactions on EPC may be larger.³⁵

Figure 4.

The density of states and projected crystal orbital Hamilton populations

(A) The total density of states (TDOS).

(B and C) (B) The projected crystal orbital Hamilton populations (COHP) and (C) its integration ICOHP for MgP₂H₁₄ under 280 GPa. Mg-H, P-H, H-H, and Mg-H correspond to the averaging contacts between Mg and H in Mg-centered H₁₄ cages, P and H in P-centered H₉ cages, the first coordination shell H-H, and the nearest neighbor Mg-P, respectively.

(D and E) The TDOS for MP₂H₁₄ (M = Li, Be, Mg, Na) under 280 and 400 GPa.

(F and G) The projected electronic density of states of H near the Fermi level in the NaP₂H₁₄ (H_Na), MgP₂H₁₄ (H_Mg), BeP₂H₁₄ (H_Be), and LiP₂H₁₄ (H_Li) under 280 and 400 GPa.

As shown in Figure 5, the calculated Fermi surface (FS) displays that there are two bands across the Fermi level, which form the hole-like Fermi-surface sheets, indicating that the predominant carrier type influencing superconductivity is holes and the electronic transport properties should largely rely on its anionic electrons. The Fermi velocities of the n = 1 band are significantly larger than that of the n = 2 band. Moreover, we can see that the two metallic bands are highly dispersive along G-T-H₂, G-S₀, and S₂-F-G paths, but a quite small fraction of the n = 1 band shows an inflection point close to the L point near the Fermi level, similar to the “flat band-steep band” scenario, which provides a nearly vanishing Fermi velocity to part of the conduction electrons and thus favorable for the formation of Cooper pairs.^40,41 The Fermi-surface nesting function could describe the degree of parallelism for a set of FSs. On the very parallel FSs, the electronic wave vectors are linked in large quantities by the same phonon wave vectors, which improve the effective coupling and is beneficial for high superconductivity.⁴² Regrettably, except for a high peak at G point, the Fermi nesting function of the entire Brillouin zone in MgP₂H₁₄ is relatively small (see Figure 5D).

Figure 5.

Fermi surface (FS) and its nesting function

(A) The FS of MgP₂H₁₄ presents in the first Brillouin zone under 280 GPa. The relative Fermi velocity υ_F on FS is represented by the color scale, where the red and blue color stands for the high and low Fermi velocities, respectively.

(B and C) The FS sheet for the two bands (n = 1, 2).

(D) The FS nesting function ξ along the high-symmetry path.

Electron-phonon coupling and superconductivity

To determine the superconducting critical temperature, we solved the Allen-Dynes modified McMillan equation (AD)^14,43 firstly, the T_c of MgP₂H₁₄ is predicted to be 155 K, which is higher than that of LiP₂H₁₄ (solving by AD). As shown in Figure 6, the optical modes at high frequency are mainly contributed by the lightest H atoms, while the heavier Mg and P atoms play an important role in the phonon modes below 650 cm⁻¹. The Eliashberg spectral function α²F(ω) and electron-phonon integral λ(ω) show that the EPC of MgP₂H₁₄ is mainly contributed by high- and medium-frequency vibrational modes of H (account for 61%), indicating the coupling between the H-associated vibration and electrons from H 1s orbitals determines the superconductivity of MgP₂H₁₄. By mapping the mode-resolved phonon linewidth ${\gamma }_{\mathbf{q}v}$ onto the phonon spectra, we found a significantly soft mode (A) with a large ${\gamma }_{\mathbf{q}v}$ at L point near 380 cm⁻¹. As the pressure increases, this soft mode gradually disappears (see Figures S4 and S5). In order to illustrate the origin of the phonon softening and large phonon linewidth at L point, we display the vibrational modes of this soft mode in Figure 6D. The A mode (the single degenerate state symmetric to the principle axis) with a vibrational frequency of ∼380 cm⁻¹ at the L point is mainly associated with the bending vibration of the H sublattice, the vibration of the P atoms is almost negligible. In order to study the pressure dependence of superconductivity, we also calculated the superconductivity of MgP₂H₁₄ under 350 GPa and 400 GPa. As shown in Figure 7A, both the T_c and λ of MgP₂H₁₄ decrease with increasing pressure, besides, the decline is more pronounced in the pressure range of 280–350 GPa, which may be related to the disappearance of the soft mode, particularly the soft mode in the L high-symmetry point.

Figure 6.

Phonon properties and electron-phonon coupling

(A) Phonon dispersion curves with the projection of phonon linewidth ${\gamma }_{qv}$ using the color scale.

(B) Eliashberg spectral function α²F(ω) as well as the integrated EPC parameter λ(ω) of MgP₂H₁₄ at 280 GPa.

(C) Phonon density of states projected on Mg, P, and H atoms.

(D) Vibrational patterns for phonon modes A (indicated by the pink arrow), where the aqua arrows represent the direction of atomic vibration.

Figure 7.

Superconductivity under pressure (μ^∗ = 0.10)

(A) the critical superconducting temperature T_c and EPC strength λ as a function of pressure.

(B) The superconducting energy gap as a function of temperature under 280 GPa.

Considering that the total λ of MgP₂H₁₄ is up to 1.65, the McMillan equation is not suitable for predicting the T_c of the system with EPC higher than 1,⁴³ we also calculated the T_c by solving the isotropic ME equation through the MLWF interpolation approach since the ME equation usually gives a better description for systems with strong EPC.⁴⁴ As shown in Figure S6, the Wannier-interpolated electron band structure matches well with that calculated by using the DFT calculation, which can serve as evidence for good interpolation results and ensure the accuracy of subsequent calculation results. By solving the isotropic ME equation, the maximum value of the superconducting gap is calculated to be ∼30 meV (see Figure 7B), MgP₂H₁₄ is predicted to be a potential high-temperature superconductor with an estimated T_c of 166 K with a typical Coulomb pseudopotential parameter μ^∗ = 0.1 at 280 GPa.

For comparison, the EPC parameter λ, the logarithmic average phonon frequency ${\omega }_{\log }$, the electronic DOS at the Fermi level (N(E_f)), and the T_c of MP₂H₁₄ (M = Mg, Na, Be, Li) are summarized in Table 1. The λ and ω_log of MgP₂H₁₄ change by about 50% when pressure increases from 280 to 400 GPa, indicating EPC strength and phonon frequencies are strongly affected by pressure. $⟨\omega ⟩$ and $⟨{\omega }^2⟩$ are calculated to quantify the contribution of electrons and phonons to the EPC, respectively, the results show that both $⟨\omega ⟩$ and $⟨{\omega }^2⟩$ increase with the increase of pressure. Compared with LiP₂H₁₄ under 400 GPa, the higher superconductivity observed in MgP₂H₁₄ under 400 GPa may be related to its higher N(E_f). However, at 400 GPa, the T_c and λ of MgP₂H₁₄ are significantly lower than that of NaP₂H₁₄, two reasons may explain this result well. Firstly, NaP₂H₁₄ possesses a higher H-PDOS (H-projected DOS) at the Fermi energy (E_F) as shown in Figure 4G, which is beneficial for superconductivity.³⁹ Secondly, the ω_log of NaP₂H₁₄ is much lower than MgP₂H₁₄, thus we can deduce that the $⟨{\omega }^2⟩$ may be lower and the λ may be higher according to the Hopfield expression mentioned in the introduction.

Table 1.

The calculated EPC parameter λ, the first moment of Eliashberg function $⟨\omega ⟩$, square root of the average square phonon frequencies $⟨{\omega }^2⟩$^1/2, logarithmic average frequency ω_log, DOS at Fermi level, and superconducting critical temperature T_c for MgP₂H₁₄, LiP₂H₁₄, BeP₂H₁₄, and NaP₂H₁₄ under pressure, T_c is obtained from solving the Allen-Dynes modified McMillan equation (herein, we default f₁f₂ = 1 when λ < 1) and isotropic Migdal Eliashberg equations, with the typical Coulomb pseudopotential μ^∗ = 0.10

System	P	λ	$⟨\omega ⟩$	$⟨{\omega }^2⟩$1/2	ωlog	N(Ef)	TcAD	f1f2TcAD	TcME	Reference
	(GPa)		(K)	(K)	(K)	(states/Ry/fu)	(K)	(K)	(K)
MgP2H14	280	1.65	1281	1481	1072	6.43	133	154	166	this work
	350	1.12	1691	1870	1464	6.43	120	130	–	this work
	400	1.02	1840	2030	1578	6.54	114	122	–	this work
NaP2H14	400	1.45	–	–	1101	6.28	139	–	159	Ref.10
BeP2H14	400	1.13	–	–	978	5.73	90	–	99	Ref.10
LiP2H14	400	0.85	–	–	1494	4.96	84	–	90	Ref.10
	300	1.06	–	–	1350	5.48	112	–	125	Ref.10
	230	1.69	–	–	956	6.08	143	–	169	Ref.10

As shown in Table 2, Mg/Be elements have one additional valence electron than Na/Li elements and could donate more electrons to the hydrogen lattice, the calculated Bader charge confirms this. However, the computed results indicate the T_c (BeP₂H₁₄)>T_c (LiP₂H₁₄), while T_c (NaP₂H₁₄)>T_c (MgP₂H₁₄) at 400 GPa, which suggests that the larger the number of doping electrons does not necessarily mean higher superconductivity. As shown in Figure 4, an extra valence electron makes the E_F of MgP₂H₁₄ and BeP₂H₁₄ shift toward lower energies than that of LiP₂H₁₄ and NaP₂H₁₄. If the Fermi level is situated in a narrow pseudogap and the total density of states (TDOS) near the Fermi level is shaped like the graph of a quadratic function, N(E_f) will be strongly influenced via substituting atoms with more valence electrons, thus affecting the superconductivity. However, in the LiP₂H₁₄ structure, due to the wide pseudogap and some small peaks near the Fermi level, the DOS at the Fermi level does not increase obviously with the increase of the valence electrons of the metal atoms. Extensive research indicated that introducing extra electrons by doping other metals in a binary hydrogen-rich system with H₂ molecules is beneficial to breaking the H₂ molecules and thus improving the superconductivity of the system.^12,45,46 However, in this work, there are no H₂ molecules in the original LiP₂H₁₄ system, besides, the introduction of extra electrons does not greatly improve the TDOS and H-PDOS at the Fermi level, moreover, Mg and Na have similar masses, but the ω_log of Na is much smaller than that of Mg, which is conducive to large EPC parameter, those may be the reason why the superconductivity has not been further improved after replacing Na with Mg in NaP₂H₁₄.

Table 2.

The Bader charge (e) of MgP₂H₁₄, NaP₂H₁₄, BeP₂H₁₄, and LiP₂H₁₄ at 280 and 400 GPa

System	MgP2H14		NaP2H14		BeP2H14		LiP2H14
Pressure	Mg	P	Na	P	Be	P	Li	P
280 GPa	+1.4636	+1.0269	+0.6570	+1.1580	+1.6699	+1.1625	+0.7888	+1.3984
400 GPa	+1.4221	+1.4353	+0.6357	+1.5537	+1.6558	+1.6035	+0.7637	+1.8527

Conclusions

A novel ternary hydride MgP₂H₁₄ with clathrate structures was identified by substituting the Li atom in LiP₂H₁₄ with the Mg atom. The phonon calculation shows that MgP₂H₁₄ is dynamically stable in the 260–500 GPa pressure range. The formation enthalpy calculation verified that MgP₂H₁₄ is thermodynamically metastable. Remarkably, the EPC strength (λ ≈ 1.65) and T_c (∼166 K) of MgP₂H₁₄ at 280 GPa are comparable to that of the LiP₂H₁₄ at 230 GPa. The interaction between the high- and medium-frequency vibrations associated with the hydrogen sublattice and the electrons induces strong EPC, resulting in high-temperature superconductivity. Considering the superconductivity of MP₂H₁₄ (M = Mg, Na, Be, Li), the number of valence electrons of each element, and the number of electrons that hydrogen lattice gained comprehensively, we find that doping with more electrons does not necessarily enhance the superconductivity of the system. When trying to improve the superconductivity of a hydrogen-rich system by introducing extra electrons by doping metal elements or substituting an atom with one possessing different valence electrons, the existence form of H in the parent system, the position of the Fermi level, the changing trend of DOS near the Fermi level, as well as the size of the pseudogap should be considered comprehensively. Supposing the introduction of extra electrons greatly improves the TDOS and H-PDOS at the Fermi level or greatly reduces the mean square of the phonon frequencies, the superconductivity will be improved, otherwise, it is unable. These results provide some clues to guide the exploration of novel high-temperature superconductors.

Limitations of the study

The results of this paper are predicted under the harmonic approximation, without going beyond the harmonic approximation to test whether there is phonon renormalization at 280 GPa and if this renormalization changes the value of the T_c. The superconducting critical temperature is calculated by solving the isotropic ME equation, the role of anisotropic effect is not further considered.

Resource availability

Lead contact

Further information and resource requests should be directed to the lead contact, Juan Gao (gao.juan.xnjd@my.swjtu.edu.cn).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• •The lead contact will share all data reported in this paper upon request.
• •This paper does not report the original code.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Acknowledgments

This work was supported by the Fundamental Research Funds for the Central Universities (no. 2682024ZTPY054). Numerical computations were performed on Hefei Advanced Computing Center.

Author contributions

J.G., writing – original draft, formal analysis, investigation, visualization, conceptualization. Q.-J.L., writing – review & editing, supervision, funding acquisition. D.-H.F., validation, methodology, data curation. Z.-T.L., software, resource, project administration.

Declaration of interests

The authors declare no competing interests.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
Quantum-ESPRESSO	Giannozzi et al.,20	www.quantum-espresso.org/
Wannier90	Mostofi et al.,30	www.wannier.org/
CASTEP	Clark et al.,31	https://www.castep.org/
LOBSTER	Maintz et al.,25	http://www.cohp.de/
Electron-Phonon Wannier	Poncé et al.,29	https://epw-code.org/
FERMISURFER	Kawamura,47	http://fermisurfer.osdn.jp/

Experimental model and study participant details

There is no experimental model and participant in this study.

Method details

Specific methods

The calculations were conducted using the plane wave pseudopotential method implemented in the QUANTUM ESPRESSO package. To simulate the electron-ion interactions, we employed optimized norm-conserving Vanderbilt pseudopotentials (ONCVPSP). The exchange and correlation potential were described using the generalized gradient approximation (GGA-PBE). We set the wave function cutoff energy to 80 Ry and the charge density cutoff energy to 320 Ry, Gaussian smearing is set as 0.02 Ry. A kinetic energy of 80 Ry and Monkhorst-Pack k meshes with a grid spacing of 2π×0.02Å−1 (16 × 16 × 16) are adopted to achieve a good convergence in the self-consistent calculation. The first-order potential perturbation and dynamical matrices were calculated using density functional perturbation theory (DFPT) on an irreducible 4 × 4 × 4 q-point mesh.

Electronic structure calculations

• •Density Functional Theory (DFT) calculations were performed using Quantum ESPRESSO.
• •The electronic structure was calculated with a plane-wave basis set and an energy cutoff of 80 Ry.
• •A Monkhorst-Pack k-point mesh of 16×16×16 was used for Brillouin zone integration.
• •To estimate Fermi surfaces (FSs) and visualize the results, we used Wannier90 interpolation, followed by visualization with the FERMISURFER software.
• •The crystal orbital Hamilton population (COHP) was exploited to describe the pair interactions by using the LOBSTER code.

Electron-phonon coupling (EPC) calculation

• •Electron-phonon coupling (EPC) was analyzed using the Eliashberg spectral function, and the electron-phonon coupling constant, λ.
• •A denser k-point mesh of 32 × 32 × 32 was employed to calculate the electron-phonon matrix elements.

The superconducting transition temperature (T_c) calculation

• •The superconducting transition temperature (T_c) was estimated using the Allen Dynes modified McMillan formula.
• •The isotropic Migdal-Eliashberg (ME) equation was also employed to calculate the superconducting gap and T_c using the Electron-Phonon Wannier (EPW) code. The denser homogeneous k-point mesh of 64 × 64 × 64 and q-point mesh of 16 × 16 × 16 were employed to solve the isotropic ME equation during the Wannier interpolation. Twenty-three atomic orbitals of MgP₂H₁₄ (consisting of H-s, Mg-s, P-s, and P-p orbitals) were used to construct the maximally localized Wannier functions (MLWF).

ab initio molecular dynamics (AIMD) simulation

• •The ab initio molecular dynamics (AIMD) simulation with NVT (N for the number of particles, V for volume, and T for temperature) ensemble and Nose-Hoover thermostat was performed to prove its thermodynamic stability in 300 K, the time step was 2fs, the primitive cell was expanded to 2×2×2.

All computational parameters and methods were selected to optimize the balance between computational cost and accuracy.

Quantification and statistical analysis

Superconducting properties were quantified using Density Functional Theory (DFT) calculations with Quantum ESPRESSO. Electronic structures were calculated with a plane-wave basis set and a [specify energy cutoff, e.g., 80 Ry] energy cutoff, using a Monkhorst-Pack k-point mesh of [specify grid density, e.g., 16×16×16]. Phonon calculations were conducted using density functional perturbation theory (DFPT), and electron-phonon coupling (EPC) was analyzed via the Eliashberg function and coupling constant λ. The superconducting transition temperature (T_c) was estimated using the Allen Dynes modified McMillan formula and isotropic Migdal-Eliashberg (ME) equation. All computational parameters and methods were optimized for accuracy.

Additional resources

Additional resources, including supplementary data, computational codes, and detailed methodological protocols, are available upon request from the lead contact. All supplementary materials are intended to enhance the reproducibility and transparency of the study, providing comprehensive insights into the experimental and computational approaches employed. For access to these resources, please contact [lead contact, Juan Gao (E-mail: gao.juan.xnjd@my.swjtu.edu.cn)]. The supplementary data include raw and processed data files, input files for computational simulations, and step-by-step protocols for the methodologies described in this study. These resources aim to support further research and validation efforts within the scientific community.

Published: February 7, 2025