Nonempirical Adiabatic Connection Correlation Functional from Hartree–Fock Orbitals

Abstract

We present a nonempirical strategy to construct a correlation functional rooted in the Møller–Plesset (MP) adiabatic connection (AC) formalism for the strong-interaction regime, which satisfies both the weak- and strong-interaction limits and describes accurately the uniform electron gas (UEG) model. The functional is based on Hartree–Fock (HF) orbitals and employs only the UEG and helium atom as model systems; thus, it can be considered a nonempirical and nonlinear generalization of post-HF approaches based on the second-order perturbation theory (MP2) correlation. The functional describes the correlation of atoms with 1 mHa/electron accuracy, and it is also accurate for jellium surface energies. Accurate tests using a nearly complete basis set on diverse systems and properties (atomization/interaction energies, dispersion forces, and ionization potentials) have shown an excellent performance of the functional that corrects the MP2 overbinding without error cancellation. The present investigation can open the way for the development of a new generation of post-HF functionals based on nonlinear MP2 contributions and strong-correlation ingredients.

Theoretical electronic calculations in quantum chemistry and solid-state physics have greatly advanced modern material science and technology by validating state-of-the-art experiments and forecasting future trends.¹⁻⁴ Improving theoretical many-body methods is therefore a continuously progressing research field that is essential for achieving higher accuracy within feasible computational costs. Within the many possible method development pathways, the adiabatic connection (AC) formalism⁵⁻¹¹ is a powerful framework for developing both density functional theory (DFT)^12,13 and wave-function-based methods¹⁴⁻¹⁸ in electronic structure calculations.

In DFT, the AC formalism has been extensively used to construct accurate exchange-correlation (XC) functionals, including hybrid^10,19,20 and double-hybrid (DH) functionals,²¹ as well as Görling–Levy (GL) perturbation corrections.^22,23 Additionally, the random phase approximation (RPA) and its AC-based extensions have further advanced correlation energy calculations.²⁴⁻²⁸ More recently, adiabatic connection integrand interpolation (ACII) methods,²⁹⁻⁵³ which interpolate between the weak- and strong-interaction limits, have been introduced. The ACII approaches include the second-order GL term, and thus these methods belong to the fifth rung of the Jacobs ladder.⁵⁴

A primary computational limitation of DFT-ACII methods lies, however, in their density requirement since DFT-AC is formally based on the exact density. This requirement typically necessitates a self-consistent Kohn–Sham (KS) calculation or, more commonly, the use of preliminary calculated ad hoc orbitals and eigenvalues. The former approach is computationally hard and expensive, as correlated optimized effective potential (OEP) calculations are required,⁴⁷ whereas methods based on the latter may significantly affect the accuracy and reliability of the final results,^41,53 introducing complexities that are difficult to control.

This issue is addressed by the AC formalism for wave function methods, referred as Møller–Plesset (MP)-AC methods.⁵⁵⁻⁵⁹ This approach retains the advantages of DFT-AC, particularly the ability to construct high-level functionals that incorporate information from both the weak- and strong-correlation regimes while relying on the well-defined framework of Hartree–Fock (HF) orbitals. The importance of the HF ground-state has been also shown in the density-corrected DFT.⁶⁰ Recently, MP-AC has attracted increasing interest for its potential in the development of advanced wave function computational methods, being applied to study correlation in different regimes, including asymmetric Hubbard dimers,⁶¹ and to provide a reliable indicator for the accuracy of the second-order term in MP perturbation theory.⁶² Moreover, a closely related methodology has been used to improve dynamical correlation in multireference wave function methods.¹⁶⁻¹⁸ Additionally, MP-AC methods have recently been successfully employed to develop efficient computational approaches, which achieved highly accurate results especially for dispersion interactions,^63,64 but only thanks to empirical parameters.

The MP-AC scheme can also be seen as a resummation of the MP series, effectively introducing a curvature to the otherwise linear MP2 AC curve. Despite its popularity, MP2 has known limitations: it cannot be applied to systems with vanishing gaps (e.g., metals) or in cases of strong correlation, particularly due to its inability to capture collective nonadditive correlations.⁶⁵ This results in poor descriptions of noncovalent interactions involving polarizable molecules,⁶⁶ especially in π–π stacking,⁶⁷ and leads to increasingly large errors for larger complexes.^68,69

To address MP2’s limitations, several variants have been proposed, including spin-component-scaled (SCS),⁷⁰ spin-opposite-scaled (SOS),⁷¹ and many others.⁷² Additionally, regularization schemes⁶⁵ have been introduced to manage issues with the small energy gap. However, all of these methods incorporate empirical parameters and do not fully address the core challenges of capturing higher-order correlations and strong correlation effects. A similar limitation is present in DH functionals where empirical parameters are required for high accuracy.⁷³⁻⁷⁵ This underscores the importance of developing a nonempirical MP-AC approach as a key area of ongoing research.

General Theoretical Framework

In this work, we consider the traditional quantum-chemistry correlation energy (E^HF_c), i.e., the difference between the true total energy and the HF limit. In the MP-AC theory^55−58,62 this can be written as

1

2

with α being the coupling constant, 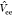being the electron–electron interaction operator, 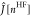and 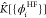being the Coulomb and exchange operators, U[n^HF] and E^HF_x[{ϕ^HF_i}] the Hartree and the HF-exchange energies, and Ψ_α being the minimizing wave function of the Hamiltonian 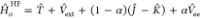, where T̂ and are the kinetic energy and external potential operators, respectively. In the weak-interaction limit (α → 0), the coupling-constant-dependent correlation integrand behaves as⁵⁶

3

where E^MPn_c is the nth term of the MP perturbation series.¹⁴ In the strong-interaction limit (α → ∞) it goes as⁵⁶

4

with⁵⁶⁻⁵⁸

5

where E_el[n] is the electrostatic energy in the strong-interaction regime.⁵⁶⁻⁵⁸

A classical minimization of E_el[n] as well as accurate variational estimates of both W^HF_1/2[n^HF] and W^HF_3/4[n^HF] have been shown in refs (56−58). These procedures are, however, computationally cumbersome and very expensive. More practical gradient expansions for E_el[n^HF] and W^HF_1/2[n^HF] as well as an interpolation formula of W^HF_3/4[n^HF] have also been developed.⁵⁷⁻⁵⁹

Using the asymptotic behaviors of eqs 3 and 4, MP-ACII (or HF-ACII to highlight the HF density dependence) methods can be obtained, similarly to what is done in the DFT case, constructing a proper interpolation function for W^HF_c,α[n^HF] between the two limits (α → 0 and α → ∞). In this way W^HF_c,α[n^HF] turns out to be a nonlinear function of E^MP2_c, E^HF_x, and the three strong-interaction ingredients, and so it is the total correlation energy after the α integration (see eq 1). Thus, in general we can write

6

where the dependence on the HF density is not explicitly reported for simplicity.

In the past few years, some HF-ACII functionals have been proposed. They all have the simplified form , that is, they only employ E^MP2_c, E^HF_x and an approximated and/or empirical expression for W^HF_c,∞[n^HF] and they neglect instead any information from W^HF_1/2 and W^HF_3/4. Among these functionals, we mention the Seidl–Perdew–Levy (SPL) functional,³² the SPL2 method,⁶⁴ and the MPACF1 correlation energy.⁶⁴ SPL was originally developed as the DFT-ACII method but has also been often employed in the MP-AC framework by simply replacing GL2 with MP2 and the exact Kohn–Sham exchange and density with the corresponding HF quantities. On the other hand, SPL2 and MPACF1 are semiempirical formulas developed in the formal MP-AC context. All these functionals correctly recover the first term of the weak-interaction expansion of eq 3 (i.e., 2E^MP2_cα), but none of them can correctly recover the strong-interaction limit of eq 4. In fact, only MPACF1 uses a modest approximation for W^HF_c,∞[n^HF], while the SPL and SPL2 do not formally describe any term of the right-hand side of eq 4 at all. We also note that both SPL2 and MPACF1 have been developed and optimized for the calculation of interaction energies (or more generally, energy differences) so that none of them can be expected to yield accurate total energy values for molecular systems.

In this article, we focus on the full expression in eq 6 to develop a functional that exhibits correct asymptotic behavior at both the weak- and strong-interaction limits. Our approach follows a structured four-step path: (i) defining the three strong-interaction components, (ii) constructing an interpolation function for the asymptotic case of the uniform electron gas (UEG), (iii) addressing spin dependence, and (iv) developing the final interpolation function for general systems beyond the UEG.

Development of Strong-Interaction Functionals

We start by considering their second-order gradient expansions (GE2):⁵⁸

7

8

where 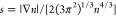is the reduced density gradient, which is invariant under the uniform density scaling, and A^HF = −1.44423075, μ^GE2_el ≈ 0.399, C^HF = 2.8687, and μ^GE2_1/2 ≈ 1.601; see ref (58). These GE2 are accurate for systems where the slowly varying density regime dominates, such as large atoms or jellium clusters, as shown in Figures 4 and 7 of ref (58). To improve for small systems, we propose the following GGA models:

9

10

where in both cases the enhancement factor has the general form⁴⁷

11

with κ(s) = c/(1 + s²) and where μ = μ^GE2_el, c = 20 for E^GGA_el, while μ = μ^GE2_1/2, c = 14 for W^GGA_1/2.

These values have been obtained fitting the exact strong-interaction results for noble atoms⁵⁸ as shown in Figure S1. The factor βf(ζ) is a spin-dependent correction, which will be fixed at point (iii) below (note that ζ = (n_↑ – n_↓)/n is the relative spin polarization).

As for W^HF_3/4, we employ instead the accurate interpolation formula proposed in refs (57 and 59):

12

where R_k is the position of atom k with nuclear charge Z_k and ϵ_3/4(σ) = −2.002 – 1.588σ + 0.394σ² and σ = (1 + ζ²)/2. Such an ingredient (which can be easily computed) is not present in any of the AC methods or in any DFT functionals. However, it has been shown that the density at the atomic nuclei can be an important ingredient to describe the electronic correlation.⁷⁶ Note that eq 12 is an upper bound (in absolute value) as there could be systems where, e.g., by symmetry, the minimizing positions are not on all the nuclear cusps.⁵⁸ But, as discussed in ref (58), it is reasonable to assume that in a large system there is one minimizing position at each nucleus.

Interpolating Function for the UEG

We consider the UEG as a model system, which includes cases with a vanishingly small gap and slowly varying density as well as the asymptotic condition E^MP2_c → –∞. This scenario is crucial for our construction, as it provides an asymptotic constraint for the general interpolation formula we aim to develop in eq 6.

To recover the correct behavior for the AC interpolating function, we propose the formula

13

where b = b[n^HF], c = c[n^HF], and g = g[n^HF] are functionals of the HF density (through W^HF_c,∞, W^HF_1/2, and W^HF_3/4), while d₁ and d₂ are numerical coefficients. Note that eq 13 reduces to the UEG-ISI expression of ref (52) when d₁ = d₂ and g = 0. To define the functionals b, c, and g, we impose the asymptotic conditions for the weak- and strong-interaction limits, i.e., that W^uegIHF_c,α vanishes for small α and fulfills the expansion of eq 4 up to order α^–3/4 for large α. Thus, we obtain

14

15

16

with

17

We note that in the UEG, where W^HF_3/4 vanishes,⁵⁷ the g term always vanishes. Nevertheless, the inclusion of this term in eq 13 is essential for the recovery of the expansion of eq 4 up to order α^–3/4; we thus retain this term for the importance it will have in the slowly varying density regime.

To fix the coefficients d₁ and d₂, we fit the correlation energy per particle ϵ^uegIHF_c = (1/N)∫¹₀W^uegIHF_c,αdα to the UEG correlation energy per particle as described by the Perdew–Wang (PW) correlation formula⁷⁷ (ϵ^PW_c). To this purpose, we define the integrated error

18

where r_s = (3/(4πn))^1/3 is the bulk parameter. To compute ϵ^uegIHF_c we furthermore used the fact that for the spin-unpolarized UEG W^HF_c,∞/N = A^HFn^1/3 + E_x/N and W^HF_1/2/N = C^HFn^1/2, where E_x/N = −0.4582/r_s is the UEG exchange, so that . The absolute minimum of the Err(d₁, d₂) is found at d₁ = 1457.2 and d₂ = 132.15 (see Figure S4). Note that instead for the case d₁ = d₂, which recovers the original expression of UEG-ISI, the value of Err(d₁, d₂) is always larger; this remarks on the significant difference between the DFT-AC and the MP-AC.

To verify our fit, we report in the top panel of Figure 1 the UEG correlation energy per particle ϵ_c versus the bulk parameter r_s for the spin-unpolarized case, as obtained with different methods (the same plots, zoomed in the high-density region, are reported in Figure S2).

Figure 1.

Negative of the correlation energy per particle (−ϵ_c, in log scale) versus the bulk parameter r_s, for (a) the spin-unpolarized (ζ = 0) and (b) the fully spin-polarized (ζ = 1) UEG. We also show the results of MPACF1⁶⁴ and SPL.³²

We see that both UEG-ISI and uegIHF perform very well and the improvement with respect to other HF-ACII, such as MPACF1 and SPL, is very significant (SPL2 is not even reported and it is one order of magnitude worse than MPACF1, which, for the UEG, differs from SPL by 2E_x). Thus, the uegIHF expression reproduces the UEG correlation energy with very high accuracy. Note that for the atomic and molecular systems investigated in this work, we found that q ≳ 0.28 so that the important region for the UEG parametrization is r_s ≳ 0.08; thus, the description of UEG logarithmic divergence for r_s → 0 is not necessary.⁵²

Spin Dependence

To treat the spin dependence we consider the function

19

which has been often used in the construction of the spin dependence of correlation functionals.^77,78 This function enters into the definition of the W^GGA_1/2 functional of eq 10 together with coefficient β. To fix the numerical value of β we consider the fully spin-polarized UEG model system and we minimize for this case the error Err(d₁, d₂) (now with d₁ and d₂ fixed to their optimal values). We find that the best result is obtained for β = 1.05. This is shown in Figure S3 as well as in the bottom panel of Figure 1, where we plot the correlation energy per particle of the fully spin-polarized UEG as a function of r_s as obtained for different methods. The W^GGA_1/2 spin dependence from ref (59) is not so accurate for the spin-polarized UEG (see Figure S4). Note also that eq 57 of ref (59) is based on the minimizing positions, whereas we use here GGA approximation, and that the W^GGA_1/2 spin dependence has a very small/negligible impact on the correlation energy of the atoms and molecules systems considered in this work.

The HFAC24 Functional

The uegIHF model fulfills the asymptotic expansion in the strong-interaction regime, but it does not satisfy the correct weak-interaction limit of eq 3. This traces back to the fact that in the UEG, which was used as the model system for this formula, E^MP2_c diverges and cannot be included as a valid parameter. Thus, we need to recover the correct first-order term in the weak-interaction limit, still preserving the correct strong-interaction behavior. To do this, we define the HFAC24 AC integrand model as an interpolation between the desired limits, using the formula

20

where

21

with κ = 0.3 being a parameter fixed to the exact correlation of the helium atom. Note that the denominator of G(α) is just a numerical continuous approximation of the Heaviside function, which forces that 2αE^MP2_c > W^uegIHF_c,α otherwise G(α) vanishes and HFAC24 recovers uegIHF. This limit is also obtained in the strong-interaction limit, when G(α) is vanishing exponentially. Thus, HFAC24 correctly recovers the expansion in eq 4.

On the other hand, in the weak-interaction limit, i.e., α → 0, we have G → 1 and we correctly have W^HFAC24_c,α → 2αE^MP2_c (where we have neglected the Heaviside term and also used the fact that in this limit W^uegIHF_c,α ∝ α). Nevertheless, a peculiar case is still obtained in the weak-interaction limit if E^MP2_c exceeds a critical threshold. This case is not pertinent to thermochemistry but it can be of interest for static-correlation⁵³ or large atoms (see in the following). A detailed analysis can be found in Section 5 of the SI, which also shows that the HFAC24 total correlation energy, via eq 1, is a strong nonlinear function of E^MP2_c. When E^MP2_c = 0, HFAC24 vanishes exactly, which is the exact behavior for any one-electron system as well as for perfect insulators.⁵³Equation 21, which defines the interpolating function for the correlation energy, is a very simple function (just the error-function) as compared with the general expression in eq 6. Nevertheless, we show in the following that very accurate correlation energies can be obtained for different systems and properties. Note that the HFAC24 functional, as well as all other HF-ACII approaches, are non-size-consistent for dissociation into non-equal fragments. However, a size-consistent correction (SCC) can be easily applied.⁴²

Numerical Results

To test the HFAC24 functional, we considered a diverse set of applications, including total energies of atoms, semi-infinite jellium-surface correlation energies, H₂ dissociation, and several thermochemistry benchmarks for organic molecules. We recall that the HFAC24 functional was not trained on any of the above systems.

Total Energies of Atoms

Results for neutral atoms are summarized in Figure 2 and reported in Table S3. We considered neutral atoms from He to Ba (with 2 ≤ Z ≤ 56), for which there are accurate MP2 correlation energies,⁷⁹⁻⁸² as well as accurate reference correlation energies.⁸³ All the other input ingredients (E^HF_x, W^HF_c,∞, W^HF_1/2, W^HF_3/4) have been computed with accurate numerical HF orbitals,⁸⁴ and they are reported in Table S2. Results from the Perdew–Burke–Ernzerhof (PBE)⁸⁵ and Tao–Perdew–Staroverov–Scuseria (TPSS)⁸⁶ density functionals have also been computed with the same accurate numerical HF orbitals⁸³ (see instead Table S4 for SCF results and comparison with CCSD(T) values).

Figure 2.

Errors on correlation energy per electron (in mHa) for different methods for neutral atoms from He to Ba (with 2 ≤ Z ≤ 56). Full data are reported in Table S3. The inset reports the MAE for the different methods.

Overall, HFAC24 shows very high accuracy, achieving a mean absolute error (MAE) of only 1.0 mHa, significantly improving upon MP2 and outperforming SPL. The HFAC24 accuracy is also about twice as high as that of semilocal DFT approaches. Results for SPL2 and MPACF1 are much worse (see Table S3). This is not surprising, recalling that both these methods had been developed targeting energy differences (especially in the context of weak interactions); therefore, systematic errors can be largely expected when dealing with total energies.

Figure 2 also shows important features of the HF-ACII functionals when compared to MP2. The SPL functional always gives a smaller absolute correlation than MP2, which is not correct, because in most cases the exact absolute correlation is larger than MP2. Instead, the HFAC24 functional gives larger absolute correlation than MP2 for small atoms (e.g., Z < 20) and smaller for large atoms (e.g., Z > 20). And this is exactly the correct behavior.^82,87 Thus, the HFAC24 functional correctly predicts this crossing, thanks to its nonlinear dependence on E^MP2_c.

To further analyze these results, Figure 3 displays the difference between the correlation integrand per electron W^HFAC24_c,α/N and the MP2 one, for selected atoms (He, Ne, Ar, Zn, Kr, and Xe; for a detailed analysis see also Figures S6–S8). The curves follow the exact slope 2αE^MP2_c for small α, where they are concave as shown in Figure S8, then diverge from the MP2 behavior for larger α, aligning with W^uegIHF_c,α. The area under each curve represents the energy difference E^HFAC24_c – E^MP2_c: this is negative for light atoms (He, Ne, Ar), where E^ref_c ≤ E^MP2_c, and it is positive for larger atoms (Zn, Kr, Xe), where E^ref_c ≥ E^MP2_c, showing that HFAC24 provides the appropriate corrections based on atom size.

Figure 3.

Difference ΔW_c,α = (W^HFAC24_c,α – 2E^MP2_cα)/N as a function of the coupling strength α for several atoms (He, Ne, Ar, Zn, Kr, and Xe).

Semi-Infinite Jellium-Surface Correlation Energies

Results for jellium surfaces,^88,89 given in Table 1, further validate the HFAC24 functional. In these systems, where E^MP2_c → –∞, HFAC24 recovers the uegIHF functional. Inspection of the table shows indeed that the HFAC24 correlation functional performs remarkably well, being better than PBE (TPSS is almost equivalent); on the contrary, SPL, SPL2, and MPACF1 are failing quite badly, especially for r_s = 2 and 3. The strong accuracy of HFAC24 likely stems from the reliability of the GGA models used for the strong-interaction terms.

Table 1. Jellium Surface Correlation Energies (erg/cm²)^a.

^aThe diffusion Monte Carlo (DMC) estimates are from refs (88 and 89). Color legend according to the absolute relative error (ARE): ARE ≤ 20% green, 20% < ARE ≤ 100% yellow, 100% < ARE red.

H₂ Dissociation

The dissociation curve of H₂ within a spin-restricted formalism, shown in Figure 4, is a prototype critical test of strong correlation.^{41,47,53,90−94} Near equilibrium (see inset of Figure 4), all methods perform reasonably well, yet HFAC24 provides the closest match to the reference. At large bond distances, MP2 diverges, as all DH or scaled MP2 approaches, and SPL2 and MPACF1 perform poorly, while HFAC24 remains stable and smooth, although it overestimates the dissociation (but improves over HF). This overestimation is mainly due to the UEG parametrization. In fact, when changing the d₁, d₂ parameters, it is possible to improve this feature, as also indicated by the performance of SPL, which was constructed considering the H₂ dissociation.³² This suggests that future improvements may incorporate additional constraints for H₂ dissociation alongside UEG constraints, potentially balancing this behavior.

Figure 4.

Dissociation of the H₂ in a spin-restricted formalism for different methods over a wide range of interatomic distances (in log scale). The inset shows the bonding region.

Thermochemistry Benchmarks for Organic Molecules

Finally, we computed molecular systems. We note that for calculating the thermochemical properties of molecules, the choice of basis set is critical when the MP2 energy is involved. For accurate MP2 correlation calculations, a large basis set or an extrapolation scheme^41,95 is essential. Additionally, HF-ACII methods rely on the total correlation energy, necessitating the inclusion of core electrons and core–valence interactions. This is important because HFAC24 depends on the ratio between the E_MP2 correlation and strong-interaction density functionals (E^uegIHF_c); see eq 21. For accuracy, both components must include core and core–valence effects and be equally well-converged with respect to the basis set. While this requirement does not affect linear methods like (scaled-) MP2 or DH functionals (where core effects generally cancel in interaction energy calculations), HF-ACII methods are nonlinear functions of MP2 and require a SCC correction,⁴² therefore they do not benefit from such cancellations. In future work, we will investigate these basis set effects and extrapolation schemes in greater detail. Here, we have used a nearly complete basis set (CBS), the 5ZaPa-NR-CV basis set,⁹⁶ which can reproduce the all-electron MP2 correlation with an error less than 2%. This implies that only calculations with less than 10 atoms can be reasonably done, while many standard quantum-chemistry benchmarks^97,98 are out-of-reach. Nevertheless, important insight on the accuracy of the HFAC24 functional can be obtained. Results in the 5ZaPa-NR-CV basis set will also serve as a benchmark reference for extrapolation techniques. We have thus developed a benchmark that can be run with the 5ZaPa-NR-CV basis set on conventional computational resources and it is balanced in terms of system sizes and properties. It consists of 11 tests divided in five groups: total energy of the H–Ar atoms (TE18), atomization energies (AE6, dimers), energy differences (isomers, G21IP′), electrostatic bonded molecular dimers (CT7, DI6, HB16), and weakly bonded dimers (ngd, A24mt, A24di). See the Computational Details for the definitions of these tests.

Table 2 compares, for a range of thermochemical tests, the MAE (upper part) and the mean signed error (ME, lower part) of HFAC24 and several DFT functionals (PBE,⁸⁵ TPSS,⁸⁶ B3LYP,^19,99 B2-PLYP¹⁰⁰), SOS-MP2⁷¹ and SCS-MP2,⁷⁰ as well as the previous HF-ACII SPL,³² SPL2,⁶⁴ and MPACF1⁶⁴ (full results are reported in Tables S5–S20). For all DFT methods for nonbonded interactions we added the D3 dispersion correction.¹⁰¹

Table 2. Mean Absolute Errors (MAE, upper part) and Mean Errors (ME, lower part), in kcal/mol, for Several Thermochemical Benchmark Tests: T18, AE6, Dimers, G21IP′, CT7, DI6, HB16, ngd, A24mt, and A24di, for Different Methods^a.

^aThe last column reports the LRMAE (see Computational Details). Results better than MP2 are in boldface. MAE color legend: dark green (best functional or close to it), green (MAE top 30%), red (MAE worst 30%), otherwise yellow. ME color legend: blue (negative), green (close to zero), red (positive).

Overall, previous HF-ACII methods perform well for all noncovalent interactions but are rather poor for total energies and atomization energies. Indeed, these methods work well thanks to error cancellation. Recall that SPL2 (MPACF1) has 4(2) empirical parameters obtained by fitting dispersion systems,⁶³ whereas SPL has no parameters but it is not based on the correct eqs 4 and 5. On the contrary, HFAC24 stands out with consistent improvements over MP2 for most of the tests and outperforms SOS-MP2/SCS-MP2 as well as semilocal and hybrid functionals. This is also shown by the value of the LRMAE, which describes the relative improvement (negative LRMAE) or worsening (positive LRMAE) with respect to MP2 (see Computational Details for exact definition), that is significantly negative for HFAC24. The global performance of HFAC24 is comparable to that of B2PLYPD, which contains two empirical parameters and employs dispersion correction. Instead, HFAC24 is not parametrized with any molecule and does not use any dispersion correction.

In more detail, for atomization energies (AE6 and dimers), MP2 tends to overbind most of the systems (ME ≈ +MAE), while SPL, SPL2, and MPACF1 always underbind (ME ≈ −MAE). In contrast, HFAC24 yields highly accurate atomization energies, with an MAE comparable to (slightly better than) TPSS, and more importantly without large error cancellation with the isolated atom counterpart. Clearly, B2PLYP is more accurate thanks to its empirical parameters. For isomers, SOS-MP2 is the most accurate approach, yet HFAC24 is still better than MP2, PBE, and TPSS. For ionization potentials (G21IP′), HFAC24 has the same performance of B2PLYP, while all other DFT and HF-ACII approaches are significantly less accurate. For CT7 and DI6, HFAC24 significantly improves over MP2, which always overbinds. SPL and other HF-ACII methods are very accurate, whereas all DFT methods are quite poor. For hydrogen bonds (HB16), MP2 is already almost exact.¹⁰² MP2 in general overbinds, but there are many cases where it underbinds. In general the interaction energy of HFAC24 for nonbonded interactions is lower than MP2, thus HFAC24 works better when MP2 overbinds, but this is not the case for hydrogen bonds. In this case, HF-ACII performs better. Nevertheless, the accuracy of HFAC24 is comparable to that of B2PLYPD and much better than the SOS-MP2 and SCS-MP2 approaches. Similar considerations also hold for ngd and the A24mt test, where the ME of MP2 is close to zero. The ngd test is a hard test as the interaction energies are very small: the MAE is thus small but the relative errors are all very large (see Tables S15 and S16). The A24di contains systems with a larger dispersion where MP2 overbinds. Thus, HFAC24 consistently achieves the lowest MAE (as B3LYPD), even a little smaller than that of SPL2 and MPACF1. Finally, we point out that HFAC24 is never in the worst 30% region (red entries in Table 2) of the considered functionals (like B2PLYPD).

Concluding Remarks

In this work, we developed the HFAC24 correlation functional within the Møller–Plesset adiabatic connection formalism, designed to perform well in both weak- and strong-interaction regimes, as well as for the uniform electron gas. Through rigorous testing on systems such as jellium surfaces, atoms, ions, and various molecules, HFAC24 consistently corrects the MP2 overbinding and demonstrated enhanced accuracy across a broad range of applications, including atomization energies, energy differences, and noncovalent interactions.

The main distinctive features of the HFAC24 functional are that it achieves accurate performance in thermochemistry (i) without any empirical parameters from molecular systems, (ii) without any error cancellation between incorrect total energy and atomic energies, and (iii) without divergence for vanishing-gap systems. These properties originate from a combination of a proper MP2 nonlinearity and the correct strong-correlation ingredients: this is clearly different with respect to empirical DH^73−75,103 or empirically scaled MP2 approaches,⁷² which use a fixed scaling of a linear MP2 term, as well as to all previous HF-ACII approaches.

Looking ahead, several avenues could further enhance the method, including developing a more adaptable expression for the E^MP2_c = –∞ limit that extends beyond the UEG model, and exploring more sophisticated interpolation schemes beyond the simple eq 21, eventually considering also a local interpolation along the adiabatic-connection path,⁴⁰ which could help to address the problems of size consistency and vanishing local gaps. Note that the development of other HF-ACII functionals, once the HF and MP2 calculations are done and stored, is much faster than that of conventional DFT approaches, as no additional SCF or correlated calculations are required.

Of course, further work will be necessary to enable the application of HFAC24 to larger and more complex systems. Currently, the method’s strongly nonlinear treatment of MP2 contributions, coupled with the need to compute the W^HF_3/4 term, necessitate the use of large basis sets, limiting its broader applicability. Efforts to develop efficient and dedicated computational protocols to address these limitations are already underway.

Despite this practical limitation, the results of the present work underscore the benefits of our approach, which leverages the adiabatic connection formalism with HF orbitals while satisfying the correct asymptotic conditions. This robust, nonempirical scheme promises to extend the reach of accurate electronic structure calculations and supports further advances in computational methods based on the adiabatic connection framework. Additionally, the GGA models of the strong-interaction leading terms developed here serve as valuable functionals for wave function methods, and the results obtained in the nearly-CBS basis set can be used as a reference for extrapolation schemes.

Computational Details

All molecular calculations have been performed with the acmxc script¹⁰⁴ and a development version of the program package TURBOMOLE,^105,106 where we implemented the functionals in eqs 9 and 10. For the SPL, SPL2, and MPACF1 models, the required strong-interaction quantity has been obtained using the original PC model.³⁰ In MP2 calculations, we have employed the resolution of identity (RI) approximation;^107,108 all electrons have been correlated (including core). Unless otherwise specified, all calculations have been performed using the nearly complete 5ZaPa-NR-CV basis set.⁹⁶ Such a large basis set was required to minimize basis set truncation errors in MP2 energies and to compute W^HF_3/4 with acceptable accuracy (see Table S2). This latter quantity depends on the electron density values at the nuclear positions, which is difficult to converge in conventional medium-size Gaussian basis set calculations. Auxiliary basis sets for Coulomb and correlations have been obtained using the automatic generation procedure,^109,110 as implemented in the Basis Set Exchange software.¹¹¹ For DFT we used gridsize 4. All open-shell ground-state calculations were done in a spin-unrestricted formalism. For all molecular systems, basis set superposition error effects have been corrected using the counterpoise procedure (cp) of Boys–Bernardi.¹¹² All results without cp are reported in the SI, together with some previous results from the literature. The SCC correction⁴² is used for all HF-ACII functionals, using the non-cp values, which are correct in the dissociation limit.

Details of the Tests

We considered several standard benchmarks from the literature which, in some cases, have been reduced considering the following constraints: no more than 2000 basis functions per system, only atoms in the first and second row (where 5ZaPa-NR-CV is available), no spin contamination (as for open-shell systems we are using the UHF ground-state), and no multireference (MR) effects. For AE6,^113,114 we used the nonrelativistic reference values with core correction of ref (114). The dimers test is composed by all the dimers (29) of the W4-11-woMR database,¹¹⁵ excluding CN, in which the spin contamination is very large in UHF. The isomers test is composed by the systems in Tables SI–SVIII of ref (115) (also known as ISOMERIZATION20⁹⁷), but removing system 1, which has MR effects, and systems 13 and 19 where the spin contamination is very large in UHF. The G21IP′ test is the original G21IP¹¹⁶ excluding CS and CO, where the UHF solution of the ion is spin-contaminated. The charge transfers (CT7),¹¹⁷ dipole interactions (DI6),¹¹⁷ hydrogen bond interactions (HB16)¹¹⁸ are not modified. The ngd test is composed by the noble gas dimers test NGDWI21,¹¹⁹ but excluding the systems with the Kr atom. The mixed-type (A24mt) and dispersion-dominated (A24di) systems are subsets of the A24 benchmark.¹²⁰ For A24mt and A24di, we used all the corrections of ref (120), but relativistic effects, which are not considered here.

LRMAE

The LRMAE of method m is the MAE relative to the MP2, i.e., LRMAE_m = ∑¹¹_j = 1w_jlog(MAE^j_m/MAE^j_MP2), where w_j = 1 for TE18, w_j = 1/2 for all covalent tests, and w_j = 1/3 for all noncovalent tests, so that each of the five groups have the same weights.

Semi-Infinite Jellium Surfaces

We considered semi-infinite jellium surfaces with bulk parameters r_s = 2–6. All calculations use local density approximation (LDA) orbitals. The exchange energy has been computed using these orbitals and the exact exchange formula.¹²¹

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.4c03593.

• Errors for the strong-correlation GGA functionals; interpolating function for the UEG; fit of the d₁ and d₂ parameters for the uegIHF functional; fit of the spin coefficient β; details of the HFAC24 interpolating formula; atomic data (table with all HFAC24 ingredients and additional plot of W_c(α)); full results for TE18, isomers, and G21IP tests; full results for the AE6 and dimers tests, with tables with/without the BSSE correction; and full results for CT7, DI6, HB16, ngd, A24mt, and A24di tests, with tables with/without the BSSE correction and with/without dispersion correction for DFT functionals (PDF)

• Transparent Peer Review report available (PDF)

The authors declare no competing financial interest.