Fig. 1A–D.

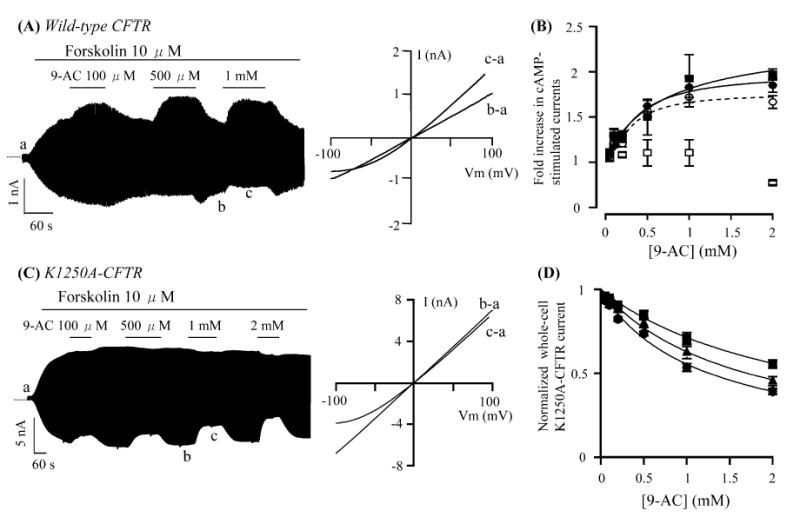
Effects of anthracene-9-carboxylic acid (9-AC) on whole-cell cystic fibrosis transmembrane conductance regulator (CFTR) currents. A A whole-cell wild-type CFTR current trace in the presence of 10 μM forskolin and various concentrations of 9-AC. I-V relationships shows net CFTR currents in different conditions as marked in the left panel. B Dose-response relationships of 9-AC potentiation effects. Net potentiation effects in wild-type CFTR were calculated by correcting for the inhibitory effects obtained from recordings of 9-AC on K1250A-CFTR currents. y_comp = y_raw/(1 − x/100), where y_comp, is the compensated value; y_raw, the measured fold increase; x, the percentage inhibition of whole-cell K1250A-CFTR currents with 1 mM 9-AC at a pipette potential (V_p) of +100 mV or −100 mV. Open circles: y_raw for 1 mM 9-AC at +100 mV; filled circles: y_comp at +100 mV; open squares: y_raw at −100 mV; filled squares: y_comp at −100 mV. C A whole-cell K1250A-CFTR current trace. I-V relationships show net K1250A-CFTR currents in the presence or absence of 9-AC. D Dose-response relationships of the inhibitory effect on K1250A-CFTR currents at three different voltages. Filled squares: −60 mV; filled triangles: −80 mV; filled circles: −100 mV. All values are represented by mean±SEM (n=3). Lines were fitted using the Hill equation: y=1+(y_max − 1)/[1+(K_d/x)ⁿ] or y=1/[1+(x/K_i)ⁿ], where y is normalized current; y_max the maximal response; x the concentration of 9-AC; K_d the half-maximal concentration of potentiation; K_i the half-maximal concentration of inhibition; and n is the Hill coefficient