Abstract
Arithmetic fluency is regarded as a foundational math skill, typically measured as a single construct with pencil-and-paper-based timed assessments. We introduce a tablet-based assessment of single-digit fluency that captures individual trial response times across several embedded experimental contrasts of interest. A large (n = 824) cohort of 3rd- 7th grade students (ages 7–13 years) completed this task, revealing effects of operation and problem size in “common” problems (i.e., 5 + 3) often examined in studies of mathematical cognition. We also characterize performance on “exceptional” problems (i.e., 4 + 4), which are typically included in fluency tests, yet excluded from most cognitive studies. Overall, individuals demonstrated higher fluency on exceptional problems compared to common problems. However, common problems better predicted standardized tests scores and exhibited distinct patterns of speed-accuracy tradeoffs relative to exceptional problems. The affordances of tablet-based assessment to quantify multiple cognitive dynamics within chained fluency testspresent several advantages over traditional assessments, thus enriching the study of arithmetic fluency development at scale.
Subject terms: Education, Human behaviour
Introduction
In recent years, the field of cognitive science and neuroscience have looked to generate large-scale datasets to better understand how cognitive development unfolds in diverse, representative populations1–3. A challenge for these studies, which include data from thousands of participants, is administering rapid yet valid assessments of cognitive abilities that capture nuanced views of cognitive constructs within a domain. To this end, in the present study, we introduce a novel, tablet-based assessment capturing fluency in single-digit arithmetic within a large, diverse cohort of third, fifth, and seventh grade students.
Due to the importance of single-digit arithmetic for later success in the domain of mathematics4–6, educators and researchers have developed a range of assessments designed to efficiently assess a learner’s fluency with these types of problems. Assessments of single-digit fluency are critical for understanding the relationship of basic numerical cognition and math achievement, as opposed to assessments of mixed and multi-digit arithmetic, which often require strategic flexibility7 and domain-general cognitive processes8,9.
In the domain of education, single-digit fluency is frequently assessed using pencil-and-paper assessments, which operationalize fluency as the number of correct answers provided in a given amount of time (typically 1–3 min). Many such measures exist including the Woodcock-Johnson test of math fluency10, Math4Speed11, and the Wechsler Individual Achievement Test12. These assessments place an emphasis on accuracy and can be thought of as a measure of chained-fluency where students answer as many problems as they can in a given time frame to form a single global fluency score based on the total number of correct responses.
In particular, many studies have used the Woodcock-Johnson math fluency subtest as a way to measure math ability13,14, diagnose learning disabilities, such as developmental dyscalculia15–17, and predict achievement on high-stakes standardized tests18,19. The widespread use of the Woodcock-Johnson across multiple, large-scale studies illustrates the utility of chained-fluency assessments for efficiently assessing large populations of learners. However, the global fluency scores generated by chained-fluency assessments do not consider item-level properties and may be influenced by several factors. While some of these constructs might be specific to mathematics (i.e., fluency across different arithmetic operations), global fluency scores may also be impacted by other factors, such as fatigue and motivation, that may not be as relevant for specifically understanding the fine-grained cognitive mechanisms underlying mental arithmetic.
In contrast to these chained-fluency assessments, studies of numerical cognition based in cognitive psychology have leveraged discrete-trials paradigms to explore cognitive constructs in single-digit arithmetic. These approaches typically leverage trial-by-trial accuracy and reaction time data to define single-digit fluency as the amount of time needed for an individual to execute elementary cognitive processes to arrive at a solution20. Whereas chained-fluency assessments typically place more emphasis on accuracy as a measure of mastery, discrete-trials paradigms allow for the examination of both the reaction time and accuracy dynamics of single-digit arithmetic. Whereas, accuracy-based approaches and curriculum standards tend to suggest that fluency with single-digit arithmetic does not develop after early elementary school21, evidence from discrete-trials research has demonstrated that although accuracy plateaus in mid-to-late elementary school, reaction time dynamics continue to evolve during this time period20,22,23. These results suggest that each subsequent year of engagement with mathematics keeps reactivating, integrating, and automating the elementary mental operations underlying single-digit arithmetic.
In addition to these developmental dynamics, studies using discrete-trials paradigms have also revealed that individuals demonstrate higher fluency on addition problems compared to subtraction24 and that fluency decreases as a function of problem size25. Furthermore, discrete-trials studies examining specific operations, such as identity (N ± 0; e.g., 4 + 0), successor (N ± 1; e.g., 6 − 1) or ties (N ± N; e.g., 2 + 2), have found these problems elicit different significantly higher accuracies and lower reaction times compared to other problems26. These problems are thought by some researchers to be solved using rapid fact retrieval or the application procedural rules27–29, whereas other problems are thought to be solved using a mix of computational strategies and fact retrieval, depending on the individual’s ability in mathematics30.
When we examine the set of items present in both chained-fluency assessments and discrete-trials research, it is apparent that there is a class of problems that are common across both paradigms10,12. The problems included in both chained-fluency assessments and discrete-trials research, henceforth known as common problems, follow lawful patterns based on the operation and problem size of the problem at hand25. However, performance on identity, successor, and tie problems is largely independent from problem features known to impact common problems, such as operand distance, operation, and problem size27,31. Thus, most studies of numerical cognition using discrete-trials paradigms exclude these “exceptional” problems from their analyses32–34.
Despite the omission of exceptional problems from discrete-trials research, general measures of single-digit arithmetic that combine performance from both common and exceptional problems have been shown to predict later success in math4,35,36. However, as previously mentioned, these global fluency metrics do not differentiate between common and exceptional problems and it remains unclear how fluency with these different problem types relates to broader achievement in mathematics. Interestingly, differences in brain activation while verifying the solution to common problems has been shown to predict math scores on a standardized exam37, highlighting the importance of fluency with common problems for broader math achievement. However, this result provides no insight into the relationship between exceptional problems and math achievement and raises questions about the utility of these items in chained-fluency assessments.
In the present study, we introduce a novel, tablet-based assessment of single-digit fluency that looks to capitalize on the strengths of both chained-fluency and discrete-trials assessments of arithmetic fluency in an efficient manner that is compatible with the time constraints of large-scale studies. With just a few minutes of assessment time, this tablet-based paradigm can rapidly generate raw fluency scores similar to those provided by chained-fluency assessments like the Woodcock-Johnson. However, in addition to accuracy, this novel form of assessment also measures reaction time for each trial, as well as other item-level characteristics, such as operation, problem size, and problem type (i.e., common and exceptional). The use of trial-by-trial recordings enables us to identify various constructs within single-digit arithmetic reported by past discrete-trials studies. The segmentation of chained-fluency data into discrete events enables us to move beyond traditional raw scores and develop a more nuanced view of the development of single-digit arithmetic and its relationship to broader mathematics achievement.
Using this novel tablet-based paradigm, we have three primary research objectives: (1) establish the reliability and validity of the single-digit fluency paradigm, (2) use the trial-level data to understand the differential relationships between math achievement and fluency with common and exceptional problems, and (3) combine combining reaction time and accuracy data to better understand the cognitive mechanisms underlying single-digit arithmetic. We first look to validate the tablet-based assessment by calculating split-half reliability and criterion validity of our single-digit fluency assessment, as well as replicate well-established constructs within arithmetic fluency, in a large cohort of 3rd, 5th, and 7th grade students.
To replicate well-established constructs within arithmetic fluency, we conduct several trial-level comparisons across various item-level features, including operation and problem size. Within each grade level, we expect to observe increased fluency with addition problems compared to subtraction24 and a negative relationship between problem size and single-digit fluency25. We also expect to capture fluency differences between the set of common and exceptional problems26.
In addition to replicating these established effects from the discrete-trials literature, we also look to examine how fluency with common and exceptional problems differentially relate to a student’s performance on a high-stakes standardized mathematics test. We hypothesize that metrics combining accuracy and reaction time data from common problems will be most predictive of student performance on high-stakes standardized tests, in line with the chained-fluency literature.
We also look to leverage the unique combination of speed and accuracy data afforded by our tablet-based assessment to conduct an exploratory characterization of the speed-accuracy tradeoffs in single-digit arithmetic. Recent work by Domingue et al.38 has suggested that depending on the assessment, increased time usage on a given item may not necessarily be related to increases in accuracy, and in some cases may relate to decreased accuracy. In our case, we look to apply this approach to examine speed-accuracy tradeoffs across both common and exceptional problems and gain insight into the cognitive mechanisms underlying fluency with these different problem types.
Past work has suggested that exceptional problems become consolidated as arithmetic facts or learned as procedural rules more readily than common problems27,31,39. Because exceptional problems are more easily mastered, they typically elicit much faster reaction times compared to common problems, which rely on slower computational procedures30,40. Based on this literature, we hypothesize that a curvilinear speed-accuracy profile will emerge for single-digit arithmetic problems, as observed in Domingue et al.38, but that this curve will appear more linear for exceptional problems. We also expect that the speed-accuracy curves for each problem type will appear more similar in both older students and students with higher levels of mathematics achievement.
Results
Evaluating the reliability and validity of the single-digit fluency assessment
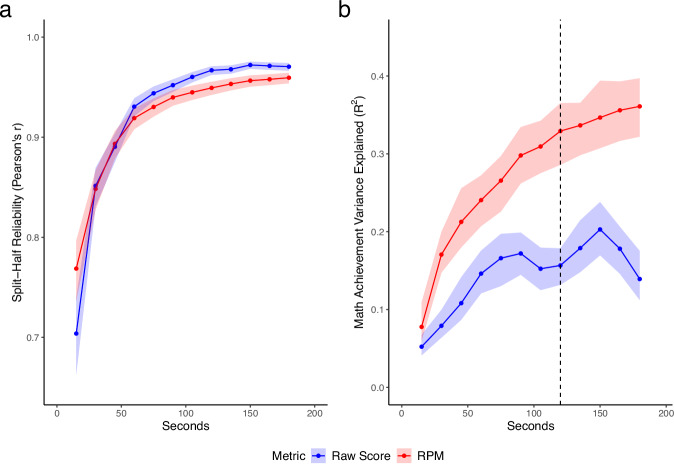
Before examining any cognitive constructs within the single-digit fluency module, we first looked to establish the reliability and criterion validity of our novel tablet-based assessment. To combine speed and accuracy data, we computed the total number of correct responses per minute (RPM) for each individual (Note: when computed across all problem types, this measure is perfectly correlated with total correct responses). Across the entire 3-min session, RPM proved highly reliable (r = 0.97; Fig. 1, left panel). Exploring the reliability of the temporal subsets of the data revealed that RPM is highly reliable with 2 min of fluency data (r = 0.95) and moderately reliable with even just 1 min of data (r = 0.92).
Fig. 1. Overview of the reliability and criterion validity of raw score (blue) and RPM (red) using different temporal subsets of the data.
Shaded areas represent 95% confidence intervals. a Spearman-Brown adjusted split-half reliability of the raw score and RPM metric for different temporal subsets of the single-digit arithmetic assessment. b Explained variance in scores on high-stakes math exams explained by raw score and RPM metrics from different subsets of the single-digit arithmetic task. The vertical line represents the number of seconds of data after which the variance explained by RPM increases by less than 1% compared to the previous point.
We also looked to establish the criterion validity of this novel assessment of arithmetic fluency by predicting a student’s performance on the Smarter Balanced Assessment System for California (SBAC; see “Methods” for more details) using the RPM metrics calculated from the same time increments as the reliability analysis. We found that 3 min of single-digit fluency served to explain roughly 36% of the variance in standardized test scores (Fig. 1, right panel). Additionally, we found that using subsets of the data derived from just the first minute or first 2 min of the fluency assessment served to explain over 24% and 32% of the variance in test scores, respectively.
Chained-fluency assessment on a tablet replicates known effects from discrete-trials
After establishing the reliability of our tablet-based fluency assessment, we then looked to assess whether our tablet-task could replicate established effects found in the numerical cognition literature, specifically problem size, operation, and problem type20,25,27,32. To do so, for each individual, we calculated RPM within our three constructs of interest and then constructed two linear-mixed effects models to evaluate the relationship between these constructs and RPM (see “Methods” for more detail about modeling approach).
To account for individual differences in fluency, each model included a random intercept for each participant. In addition to this random effect, one model included fixed-effects of problem size, operation, and their interaction, while the other included a single fixed-effect of problem type. We included fixed-effects of operation and problem size in a single model to account for the fact that subtraction problems generally have smaller solutions than addition, meaning that operation is confounded by problem size. All reported p values in these models were FDR-corrected36 to account for multiple comparisons (adjusted pcrit = 0.05).
The model examining the effects of problem size and operation revealed significant main effects of problem size, operation, and grade. Students tended to speed up when solving smaller problems, with an average decrease in RPM of 2.03 problems per minute with a one-unit increase in problem size (R2partial = 0.020, t(10,780) = −16.47, padj < 0.001; Fig. 2a). This model also revealed that, on average, students correctly answered addition problems at a slightly, yet significantly, faster rate compared to subtraction problems (R2partial = 0.003, t(10,800) = −6.62, padj < 0.001, Fig. 2a) and older students demonstrated increased fluency compared to younger students (R2partial = 0.020, t(2807) = 12.38, padj < 0.001).
Fig. 2. Mean correct responses per minute across various item level features. Shading represents one standard error.
a Overview of fluency as measured by correct responses per minute as a function of problem size and operation. Each line represents a grade cohort. b Differences in single-digit fluency by problem type (common or exceptional) across the six grade levels represented in the sample.
In addition to these main effects, this model also revealed a subtle, yet, significant interaction between problem size and operation (R2partial = 0.007, t(10,800) = 9.90, padj < 0.001), suggesting that the slope of the problem size effect was slightly greater for subtraction problems. This model also revealed negligible interaction effects between operation and grade (R2partial = 0.001, t(10,800) = −4.01, padj < 0.001) and between problem size, operation, and grade (R2partial < 0.001, t(10,800) = 3.36, padj = 0.009).
The second model that we fit looked to evaluate the differences in fluency between common problems and exceptional problems, which are traditionally excluded from numerical cognition studies. This model revealed significant main effects of both problem set and grade cohort. Students, on average, responded correctly to exceptional problems at a faster rate than common problems (R2partial = 0.050, t(691) = −15.02, padj < 0.001, Fig. 2, right panel). As with the other two models, we again found that the older students, on average, exhibited significantly higher fluency compared to younger students (R2partial = 0.186, t(830) = 13.52, padj < 0.001). Furthermore, there was subtle yet significant interaction between problem set and grade cohort (R2partial = 0.001, t(691) = −2.00, padj = 0.045).
Tablet derived correct responses per minute (RPM) better predicts math achievement than traditional scores from chained fluency assessment
After replicating past effects from the discrete-trials literature, we then determined whether our tablet-based assessment also replicated predictions of math achievement found in the chained-fluency literature18,19. We also looked to build on this replication by directly comparing the predictive strength of our RPM fluency metrics with that of a traditional raw fluency score, similar to those calculated by chained-fluency assessments, like the Woodcock-Johnson10. For each individual, we generated a traditional raw fluency score by summing the total number of correct responses provided during the single-digit fluency module. We also calculated two RPM sub-scores: one based on performance for common problems and another one based on performance for exceptional items. We used the SBAC score as a measure of math achievement (see “Methods” for description of SBAC).
We first conducted correlation analyses to explore the relationships with math achievement. Pearson’s r showed that the two RPM metrics significantly correlated with math achievement (common RPM r = 0.67, p < 0.001); (exceptional RPM r = 0.59, p < 0.001). The traditional raw score notably showed the weakest correlation of all metrics (r = 0.42, p < 0.001). We compared the z-transformed r values using Pearson and Filon’s z-test, which revealed that all three arithmetic fluency metrics were significantly different from each other (all p < 0.001). This suggests that, although math achievement is correlated with traditional raw scores on single-digit fluency assessments, RPM metrics, especially for common problems, are more highly correlated with achievement on high-stakes standardized mathematics exams.
Although these correlations suggest a link between the RPM measures and math achievement, they do not account for demographic or cognitive factors that may also relate to performance on standardized math exams. To better understand the relationship between Arithmetic Fluency and math achievement, we then constructed a series of linear models predicting SBAC score. We first build a model with grade, parental income, three measures of domain-general executive function, and the traditional raw score from the math fluency task to predict SBAC scores (standardized beta-weights estimated by this model are presented in Table 1, left column). This model showed significant effects of grade, household income, Flanker, Spatial Span, and traditional raw score from the Arithmetic Fluency task (all p < 0.001) and served to explain roughly 45% of the variance in SBAC scores (Table 1).
Table 1.
Model comparisons show that including RPM problem types explains more variance in SBAC scores
| Traditional Raw Score |
Common RPM |
Exceptional RPM |
Common + Exceptional RPM | |
|---|---|---|---|---|
| Predictors | Estimates | Estimates | Estimates | Estimates |
| (Intercept) | 0.04 (0.030) | 0.03 (0.028) | 0.03 (0.029) | 0.03 (0.028) |
| Grade | 0.09** (0.040) | 0.04 (0.037) | 0.007 (0.040) | 0.02 (0.038) |
| Household Income | −0.37*** (0.031) | −0.27*** (0.030) | −0.33*** (0.031) | −0.27*** (0.030) |
| Basic Response Time | 0.07 (0.037) | 0.07* (0.034) | 0.06 (0.036) | 0.07* (0.034) |
| Flanker | 0.19*** (0.045) | 0.10* (0.042) | 0.12** (0.044) | 0.10* (0.042) |
| Spatial Span | 0.11** (0.033) | 0.10** (0.030) | 0.10** (0.032) | 0.10** (0.030) |
| Traditional Raw Score | 0.27*** (0.033) | – | – | – |
| RPM Common | – | 0.48*** (0.035) | – | 0.47*** (0.057) |
| RPM Exceptional | – | – | 0.40*** (0.039) | 0.01 (0.061) |
| Observations | 599 | 599 | 599 | 599 |
| R2 | 0.457 | 0.543 | 0.491 | 0.543 |
| R2adj. | 0.452 | 0.538 | 0.486 | 0.537 |
Coefficients represent standardized beta-weights with standard error in parentheses.
Significance codes: ***p < 0.001, **p < 0.01, *p < 0.05.
We then looked to test the hypothesis that fluency metrics that combine speed and accuracy, such as RPM, predict standardized test scores better than traditional raw scores typically provided by chained-fluency assessments. To do so, we generated two additional models using either RPM for common or exceptional problems as a predictor instead of the traditional raw score, while controlling for the same demographic and domain general cognitive measures as the first model. Both of these models proved to explain more variance in standardized test scores than the raw score model. The model that included exceptional RPM as a predictor explained roughly 50% of the variance in test scores (R2adj = 0.486), while the model that included common RPM explained 54% of the variance in test scores (R2adj = 0.538), suggesting that measures that are sensitive to both speed and accuracy better predict test scores than measures based solely on accuracy.
We then constructed a full model that included both common and exceptional RPM as predictors. Although this model did not explain more variance than the common RPM model (R2adj = 0.545), a likelihood-ratio test revealed that the full model fit the data better than the reduced models (F(591) = 66.896, p < 0.001). Additionally, when comparing the full RPM model and the traditional raw score model, we found that the full RPM model explained 8.5% more variance in standardized test scores than the raw score model (ΔR2adj < 0.098). Further, a Cox test to compare the non-nested linear models showed that the full RPM model fit the data significantly better than the raw score model (z = −17.470 p < 0.001). Examining the standardized beta-weights of this model revealed that RPM on common problems was by far the strongest predictor of SBAC scores, even when considering measures of executive function and parental income (see Table 1 for full results). Overall, these models suggest that fluency metrics that combine speed and accuracy, such as RPM, are the best predictors of achievement on standardized mathematics exams.
Dynamics between speed and accuracy vary based on problem type, grade, and math achievement
In addition to the analyses above that provide evidence for differentiated processing between common and exceptional problem types, we also leveraged the trial-level accuracy and reaction time data afforded by our tablet-based paradigm to analyze speed-accuracy dynamics within the single-digit arithmetic task. Full details of this approach are outlined in the “Methods” section and in Domingue et al.38 but briefly, each individual’s response to each single-digit arithmetic question is modeled as a function of their reaction time on that item and the probability of them providing a correct response, as generated by an item-response model. The predictions from this model can then be plotted to qualitatively examine, on average, how the probability of a correct response changes with increases in reaction time. This approach moves beyond the comparison of reaction time and allows for a more nuanced view of performance on different types of arithmetic problems.
Past analyses of cognitive tasks have found that simple items tend to elicit linear speed-accuracy curves, which suggests that these items are solved through rapid, homogeneous cognitive processes. More complex items, in contrast, tend to elicit curvilinear speed-accuracy curves, suggesting slower cognitive processes which leave room for strategy shifts, working memory decay, and the depletion of cognitive resources41. Based on these findings, we hypothesized that the shape of the SAT curves would differentiate common from exceptional problems. Specifically, we expected common problems to involve a range of more complex and time-consuming cognitive processes, thereby producing curvilinear profiles, whereas we expected exceptional problems to generate more linear SAT profiles.
We first fit speed-accuracy curves for common and exceptional single-digit problems across the entire sample. Plotting these curves revealed distinct shapes for the curves describing common and exceptional problems (Fig. 3a). More specifically, the speed-accuracy curve describing exceptional problems (blue line) illustrates a traditional speed-accuracy tradeoff, whereby the longer an individual takes to solve a problem, the more likely they are to respond correctly. On the other hand, the speed-accuracy curve for common problems (red curve) has a more curvilinear shape, which suggests that after a certain amount of time, the likelihood of an individual providing a correct response actually decreases with additional time spent on the problem.
Fig. 3. Speed-accuracy profiles for common (blue) and exceptional (red) problems.
The x-axis represents reaction time and the y-axis represents the probability that an individual answers correctly to a given item. a Speed-accuracy profiles for common and exceptional problems across the entire sample. b Speed-accuracy profiles for common and exceptional problems based on grade level. c Speed-accuracy profiles for common and exceptional problems based on achievement on a high-stakes standardized mathematics exam. Shading represents 95% confidence interval.
To better understand how these speed-accuracy curves differ by educational experience and academic achievement, we then fit the same models as above within each grade cohort and achievement group, as measured by grade-normalized achievement quartiles on the SBAC exam. Across the grade cohorts, we see that the curve describing common problems becomes more similar to that describing exceptional problems in the older students compared to the younger students. We also observe this similarity across the two curves in the highest achievement group, where both curves take on a more linear shape. Interestingly, however, in the lowest achievement group, these curves both take on a more curvilinear shape and only become more linear in the higher achievement groups.
We then looked to quantify the difference between speed and accuracy across the two problem sets by fitting both linear and quadratic functions to the SAT data. In the full sample, the addition of a quadratic term for the model describing common problems explained more variance compared to the linear model (R2 = 0.198), whereas the quadratic term in the model describing exceptional problems explained far less additional variance (R2 = 0.070). When we quantify the SAT by achievement quartiles or grade, we observe that in the youngest students and lowest achieving quartiles the inclusion of a quadratic term drastically increases the variance explained for both common and exceptional problems. However, as we move up the age or achievement groups, the change in variance explained due to a quadratic term dramatically drops for exceptional problems but less so for common problems (see Supplementary Fig. 4 for overview).
We further tested the impact of a quadratic term on explaining the SAT curve across each decile of math achievement. Paired sample t-tests comparing the change in R2 revealed that the inclusion of a quadratic term to describe the SAT curve for common problems significantly increased the amount of variance explained compared to exceptional problems (d = 0.65, t(9) = 2.057, p = 0.035). All together, these figures suggest that in older students and higher achieving students both common and exceptional problems demonstrate a speed-accuracy tradeoff, whereas in younger students and lower achieving students, these problems elicit different responses.
Discussion
In the present study, we developed a novel tablet-based task to explore fine-grained mental arithmetic abilities at various stages of education. Through this single-digit arithmetic task, we examined how fluency develops in a large cohort of 3rd, 5th, and 7th grade students with respect to various problem-level contrasts adopted from cognitive studies of mathematical cognition such as operation, problem size, and problem type (i.e. whether a problem belongs to the set of single-digit arithmetic problems commonly investigated in these studies, or to the set of exceptional problems typically excluded from such studies). Additionally, we examined how fluency with common and exceptional problems differentially relate to performance on high-stakes standardized math exams. Finally, we leveraged the item-level reaction time and accuracy data afforded by our tablet-based paradigm to explore the relationship between speed and accuracy within single-digit arithmetic.
We observed significant main effects of grade, operation, problem size, and problem type on correct RPM. Consistent with previous findings in the literature35, older participants answered more questions correctly per second than younger participants. Additionally, our analysis examining the effects of operation and problem size on arithmetic fluency also replicated established effects from the literature. Generally, addition has been found to be easier than subtraction and the distance between operands tends to correlate with reaction time25,33,34.
When we separated the single-digit arithmetic problems into distinct types—exceptional problems, such as identity, successor, and tie problems, and problems that belong to the common set of problems found both in the discrete-trials numerical cognition literature26 and chained-fluency measures of single-digit arithmetic– we consistently observed that participants across all three grade cohorts answered more exceptional problems correctly per minute than common problems, in line with Ashcraft42. All together, these results suggest that our tablet-based paradigm can effectively replicate discrete-trials paradigms and capture the cognitive constructs within the domain of single-digit arithmetic observed in past research.
In addition to replicating these known effects, we also used data from our tablet-based assessment to replicate associations between performance on chained-fluency assessments, such as the Woodcock-Johnson, and achievement on a state-mandated standardized mathematics test18,19. To explore the specific relationship between standardized test scores and measures arithmetic fluency, we constructed a series of linear models that controlled for covariates that have been linked to academic achievement, such as SES or domain-general cognitive abilities9,43. However, we also expanded on past findings by comparing the specific relationships between match achievement and fluency with common and exceptional problems. Overall, we fit four models; one that used a traditional raw score, much like the scores provided by traditional chained-fluency assessments of single-digit fluency, as the primary predictor of interest and three others that used common RPM, exceptional RPM, or both as the primary predictors.
Interestingly, across all four regression models, RPM metrics derived from the arithmetic fluency assessment proved to be the strongest predictor of standardized test scores, even when controlling for household income and domain general executive functions. This link between arithmetic fluency and mathematics achievement across all four models illustrates the importance of fundamental mathematical skills, such as arithmetic fluency, for higher level mathematics achievement44. However, when we compared our regression models, we found that models that included RPM metrics explained a higher proportion of the variance in standardized test scores compared to the traditional raw score model, suggesting that tablet-based measures that capture both speed and accuracy better predict individual achievement than pencil and paper measures that simply record the total number of correct responses.
Furthermore, although exceptional RPM served to explain over 40% of the variance in standardized test scores on its own, the combined RPM model revealed that common RPM was the strongest predictor of standardized test scores, even when controlling for domain-general cognitive skills or socioeconomic status. This suggests that the responses to exceptional problems on chained-fluency assessments may not necessarily be the most informative for understanding individual math achievement. However, it bears mentioning that exceptional items are generally easier and may serve as an attention check or confidence boost for individuals who may struggle with math anxiety.
Additionally, we leveraged the trial level data captured by our tablet-based assessment to explore the speed-accuracy dynamics across different problem types and subsets of our sample. Visual inspection of the speed-accuracy profiles of common and exceptional problems revealed that, across all participants, exceptional problems demonstrate a more linear relationship, and common problems take on a curvilinear speed-accuracy profile. As presented in Fig. 3, exceptional problems elicit a typical speed-accuracy tradeoff, whereby the probability of an individual providing a correct response increases with the amount of time they spend on a given item. On the other hand, analysis of exceptional problems led to more curvilinear speed-accuracy curves that suggested that after a certain amount of time, the probability of a correct response actually decreased with additional time.
Past work examining speed-accuracy tradeoffs has suggested that homogenous cognitive processes, such as fact retrieval, produce linear speed-accuracy curves, whereas more complex processes that involve multiple strategies and cognitive resources result in more curvilinear speed-accuracy profiles41. In the case of mental arithmetic, when children first begin solving single-digit arithmetic problems, they initially rely on slower procedural strategies20,45–48 before consolidating problems into a rapidly accessible arithmetic fact repository after repeated practice20,25,42,49,50. However, it has been suggested that individuals consolidate exceptional problems, as either arithmetic facts or procedural rules, more rapidly than common problems27,31,39. Taken together, these past findings and the speed-accuracy curves observed in the present study suggest that individuals are likely engaging in fact retrieval when solving exceptional problems and relying on a range of computational strategies when solving common problems.
Interestingly, we also find that higher achieving students demonstrate more linear speed-accuracy profiles for both common and exceptional problems, whereas lower achieving students demonstrate curvilinear profiles for both problem types. It could be the case that in the present sample high achieving individuals rely on rapid retrieval-based strategies to solve both common and exceptional problems, whereas lower achieving individuals have only rapid access to exceptional problems and rely on slower computational processes to solve common problems. In fact, past work has shown that learners who struggle in mathematics struggle to retrieve arithmetic facts from memory and rely on counting procedures to solve these more complex problems51.
However, it also bears mentioning that, according to the Overlapping Waves theory52, as learners develop new arithmetic strategies, they do not simply discard one strategy and move on to the next strategy but rather use an overlapping combination of both new strategies and those they have already mastered. Based on this, when solving problems, learners will have multiple strategies at their disposal to arrive at the correct answer. However, these various strategies will be employed more frequently depending on the age and experience of the learner and may relate differently to achievement in the domain of mathematics.
Nevertheless, the results from both the regression models and speed-accuracy analyses suggest the consolidation of more complex single-digit arithmetic problems into math facts serves as a key building block from which individuals can begin to solve more sophisticated math problems, such as the ones found on standardized tests. We observed a clear distinction between common and exceptional problems across all grade ranges and levels of academic achievement. However, it bears repeating that in students with higher levels of mathematics achievement, the differences in the speed-accuracy profiles between the two problem types decrease, suggesting a potential shift in the cognitive strategies used to solve common problems.
Findings from the neuroimaging literature, which have observed distinct cortical networks responsible for arithmetic fact retrieval and procedural strategies46, provide evidence for this proposed shift. The networks associated with single-digit arithmetic differ between children and adults53 and patterns of brain activity vary between children who primarily rely on procedural strategies and children who use fact retrieval to solve arithmetic problems54. Interestingly, when engaging in mental arithmetic, individuals with higher scores on a standardized math exam demonstrate increased activation in regions associated with fact retrieval, whereas lower performing individuals demonstrated higher levels of activation in cortical regions involved in numerical processing37. Furthermore, developmental differences in a range of neural circuits, including parietal-frontal circuits involved in working memory and hippocampal circuits involved in declarative memory, have been linked to distinct patterns of mathematical cognition55,56 and increased parietal specialization has been observed older individuals engaging in arithmetic more fluently compared to younger individuals57. All together, this evidence suggests there is a shift in brain activation associated with expertise in mathematics. The sensitivity of our tablet-based assessment to differences in the speed-accuracy curves generated by common and exceptional problems presents an initial step towards developing a behavioral metric that corresponds with the fronto-parietal shift observed in past neuroimaging studies.
The more nuanced view of math development afforded through these distinct problem types will provide a clearer picture of the developmental dynamics of arithmetic fluency and has several implications for educational practice. Whereas existing chained-fluency assessments only identify a general weakness, the trial-level data afforded by the present tablet-based assessment can help pinpoint specific aspect(s) of arithmetic in which a learner might need additional support. By identifying these areas, the present tablet-based assessment can open the door for the development of personalized teaching strategies and tailored interventions to help learners improve in the aspects of arithmetic in which they most need support. For example, a recent study found that learners diagnosed with dyscalculia showed no difficulties solving problems requiring fact retrieval but did have difficulties solving problems that required procedural operations58. The present tablet-based assessment allows educators to identify students struggling with procedural operations and intervene appropriately.
Furthermore, the present assessment captured these effects after just 3 min of use and did not require any manual scoring, suggesting that similar tablet-based approaches to assessing arithmetic fluency lend themselves well to contexts that may not have the requisite time or resources to distribute, administer, and score traditional pencil-and-paper tests or sophisticated experimental software. This will not only allow for practitioners to rapidly and efficiently assess their students but also allows for researchers to study numerical cognition at a population level. For a range of logistical and practical reasons, numerical cognition studies relying on discrete-trials paradigms do not lend themselves well to large-scale studies and are therefore limited in their generalizability. However, the current results demonstrate how tablet-based assessments allow for a more nuanced understanding of the cognitive mechanisms underlying single-digit arithmetic at scale and open the door for the development of similar tools that can be made accessible to the larger education and research communities.
Despite the insights into mental arithmetic afforded by the present results, they must be interpreted within the context of a few limitations. First, although the present sample includes a diverse set of participants, some participants were missing demographic information and thus omitted from our analyses. This omission may bias the results the present sample thus limiting generaliz to the broader population. Although sensitivity analyses suggested that the observed effects of operation, problem size, and problem type did not change when these excluded participants were included in the analysis, future research should look to replicate these findings in an independent sample. Furthermore, the participants in the present analysis are all from the same geographic region and the results may not generalize to other geographic contexts. Nevertheless, future large-scale studies, such as the Adolescent Brain and Cognitive Development study (ABCD)1, that were adapted from these specific tablet-based behavioral assessments will likely be well-positioned to serve as a more valid generalization dataset the present results.
Additionally, the design of the present fluency assessment leads to some limitations in our comparisons of raw score and RPM metrics. Because the filler multiplication trials were excluded from our analyses, the top performers were all capped at a maximum raw score of 62, whereas their RPM metrics had more variability, due to the incorporation of reaction time data. The higher correlation between RPM and standardized test scores compared to raw scores may be partially due to the decreased variance present in raw scores for the highest performers. Although various sensitivity analyses demonstrated, across various temporal subsets of the data and different participant groupings, that RPM consistently explained more variance in test scores that raw scores (Supplementary Figs. 6, 7), future iterations of this assessment may consider removing the presence of filler trials to allow for a more direct comparison of RPM and raw scores.
Furthermore, the data from this assessment cannot fully explain the cognitive mechanisms underlying arithmetic fluency. Although our speed-accuracy curves allow us to speculate that high achieving students may rely on fact retrieval to solve both common and exceptional problems, whereas struggling learners may rely more heavily on procedural calculations, we cannot determine the exact cognitive mechanisms each individual uses to solve arithmetic problems without specifically asking participants how they solved a given problem. Despite this limitation, the present tablet-based approach to assessing fluency allows for the application of discrete-trials methodologies in large-scale studies to develop a more nuanced view of single-digit arithmetic compared to traditional chained-fluency assessments.
In summary, we used a novel assessment of arithmetic fluency accounts for different types of single-digit arithmetic problems to explore mental arithmetic in a large cohort of 3rd, 5th, and 7th grade students. This assessment proved reliable and replicated established effects from the numerical cognition literature, such as effects of operation, problem size, and problem type. Furthermore, fluency in both common and exceptional problems, as measured by RPM, were more strongly linked to achievement on standardized math exams compared to traditional global raw scores. Fluency with common problems also partially mediated the relationship between parental income and math achievement. Additionally, these different problem types elicited different speed-accuracy profiles, though these profiles became more similar in high achieving students. All together, this nuanced approach to arithmetic fluency is crucial to better assess where diverse populations of individual learners such as that found in the ABCD study, stand on their journeys as emerging mathematicians.
Methods
Participants
The participants in the present study come from the first time point of a 2-year accelerated longitudinal study exploring the development of various cognitive and academic abilities in third to eighth grade students in one of nine schools from northern California. Overall, 977 students completed the tablet based arithmetic modules at the first time point. Across the three grade levels, 53 individuals were identified as outliers and excluded from the analysis.
Outliers were determined in agreement with other analyses using this sample22,59,60 and were defined as individuals with either mean accuracy or reaction time that fell outside three median absolute deviations61 of the median performance for a given grade cohort. Furthermore, to avoid analyzing data where participants repeatedly and rapidly entered random responses, trials where with a response in less than 200 milliseconds were excluded from the analysis. Overall, after cleaning the data, participants completed between 17 and 51 addition or subtraction problems.
We measured socioeconomic status using parental income. Though we did not have access to exact parental income information, participants were classified as low-income using the definition employed by the state of California of coming from a household earning less than 70% of the state median income59,60. Using this binary scale, we dummy coded participants with low-income parental income as 1 and participants with average/above average parental income as 0. Based on this definition, 287 participants were classified as low income, 542 as average income or higher. Two schools in the sample declined to share demographic information about their students (n = 100). To avoid biasing results through imputation of demographic variables62, we excluded individuals without this information from our analyses.
The final sample consisted of 824 students who successfully completed the single-digit arithmetic task and provided information about socioeconomic status. Within this final sample, there were 230 third graders (mean age = 8.73 years old, standard deviation = 0.32), 226 fifth graders (mean age = 10.60 years old, standard deviation = 0.37), and 468 seventh graders (mean age = 12.51 years old, standard deviation = 0.38). The final sample was 31.1% Asian, 24.6% Latinx, 16.4% white, 4.9% Filipino, 4.1% two or more races, and 1.7% Black. Additionally, 8.73% of the participants received some form of Special Education services at school. Furthermore, the final sample consisted of data from 339 female participants, 345 male participants.
Each student also provided information about their yearly performance on the mathematics portion of the Smarter Balanced Assessment (SBAC). In the state of California, this exam is completed annually by students in 3rd grade through 8th grade and again in 11th grade. This exam is a computer adaptive test based on Common Core State Standards designed to measure a student’s ability to apply their knowledge in the domain of mathematics across multiple grade-level standards63.
Tablet-based single-digit arithmetic task
Participants completed the present single-digit arithmetic task as part of a larger tablet-based assessment that probed various cognitive and academic abilities. These assessments were administered in a group setting within each classroom and supervised by their teachers and members of the research team. Within each classroom, each participant was provided an individual tablet device to complete these assessments. The single-digit arithmetic module was part of a suite of individual mathematics modules that also included a dot enumeration task, an arithmetic verification module, and a double-digit arithmetic task, which we will not discuss here. All participants completed the dot enumeration task immediately before the single-digit fluency module. This fixed order was intentionally designed to ensure that subjects were warmed up64 on quickly executing touch responses on the digital number pad before the single digit fluency task began.
In the single-digit arithmetic task, participants spent 3 min responding to single-digit arithmetic problems. These problems were presented on a tablet device using custom software. To respond to each problem, participants used an on-screen keypad to type their responses before hitting enter (Fig. 4). Within the 3-min timeframe, participants were instructed to answer each problem as quickly and as accurately as possible. Arithmetic problems were randomly drawn without replacement from a set of 62 addition and subtraction problems designed to resemble those found on the Woodcock-Johnson III Tests of Achievement10 (see Supplementary Material for overview of items). However, unlike the worksheet used in the Woodcock-Johnson, problems appeared on the screen one at a time. Responses could be altered in the event of a realizing a mistake was made (e.g., pressing the wrong number key) by pressing a delete button before submitting the final answer (Fig. 4). As with the Woodcock-Johnson, time spent on such actions are included in fluency estimates. Participants could not advance to the next problem until a response was provided. Students were not provided with any feedback after submitting their responses.
Fig. 4. Schematic representation of the tablet-based single-digit fluency task.

Participants were presented with a series of problems at the top of the screen and asked to provide a response using the keypad at the bottom of the screen.
Similar to the Woodcock-Johnson, if participants completed the entire contiguous set of addition and subtraction problems, they began to respond to multiplication problems. This approach ensured that all participants ended at the same time, thereby facilitating large-group administration, as well as minimizing overt opportunities for peer comparison. Roughly 25% of all participants exhausted the addition and subtraction items in the problem bank before the 3 min had elapsed and therefore responded to a mix of multiplication, addition, and subtraction trials until the end of the 3 min assessment period. To ensure that our analyses focused exclusively on fluency with addition and subtraction, we treated all problems, regardless of operation type, presented after the first multiplication problem as filler trials and did not include these in our primary analyses (see Supplementary Table 1 for overview of filler items and number of students who responded to them). After removing outlier and filler trials, participants completed between 17 and 51 addition or subtraction problems, overall.
Additionally, the limitations of the task design raise questions about the extent all participants may change their fluency toward the end of a 3 min challenge (i.e., fatigue effects). The data for the participants who exhausted the addition and subtraction item bank may be somewhat biased as they completed the 62 item test bank of interest before the end of the 3 min where presumably the fatigue effects would be most pronounced. To understand the extent of this potential bias, we contrasted the first, second, and 3rd minutes of the top performance quartile (i.e., those who engaged with filler trials) and the second quartile of performers (i.e., the highest performers who did not exhaust the item bank). When we compared the minute-by-minute fluency for these two groups, we found significant group differences, as well as consistent fatigue effects, but no evidence that the two groups differed in the extent to which they slowed down (Supplementary Fig. 5).
The structure of the filler trials also presents some issues in generating fair comparisons between raw scores and RPM, especially in the fastest participants who exhausted the 62-item problem bank before the allotted 3 min had passed. To ensure that the variance in the raw scores for the top performing individuals was not arbitrarily reduced due to the maximum possible score of 62, we centered our main analyses on the first 126 s of each participants data, the, the point at which the very fastest participant first exhausted the bank of 62 contiguous addition and subtraction problems. To ensure the consistency of the results between the 126 s and 180 s samples, we also ran our primary analyses on the full data set, excluding filler trials (Supplemental Text). These two sets of analyses were largely consistent.
Single-digit fluency problems were classified as one of two types: common and exceptional. Common problems consist of items found in both the discrete-trials literature and chained fluency assessments, which have traditionally been studied in past investigations into single-digit fluency. Exceptional problems consist of problems that all participants, regardless of grade, have likely committed to memory as either arithmetic fact or procedural rules. These problems included ties (a number plus or minus itself, e.g., 3 + 3), the successor function (a number plus or minus one, e.g., 3 + 1), and the identity function (a number plus or minus 0, e.g., 3 + 0). All other problems were classified as belonging to the common set, which likely require procedural calculation to solve. In addition to these fluency types, we also classified items based on their operation and the distance between the two operands. Problem size was defined as the sum of the two operands, in line with past studies65,66 and operation type was limited to addition and subtraction.
It should be noted that in the analysis we made sure to analyze operation in conjunction with solution size. This is because subtraction, especially in single-digit arithmetic, will result in smaller solutions than addition. In the current study, the number of small subtraction problems greatly exceeded the number of small addition problems and the number of large additions greatly exceeded the number of large subtractions. Due to this imbalance across solution size and operation, we ensured to analyze these two factors in conjunction with one another to account for any solution size effects that might be obscuring operation effects.
We defined reaction time as the time it took a participant to press the first button, instead of the submit button. This is due to the fact that for items that resulted in a double-digit answer (i.e., 8 + 3), participants had to enter two digits to correctly record their final answer, which would necessarily result in slower reaction times for these items compared to items with single-digit answers. To validate this decision, we compared the difference between time to first button press and overall reaction time across common and exceptional problems. This revealed that the difference between time to first button press and overall reaction time was not different across the two problem types (t(2712) = −1.291, p = 0.197), suggesting that for all problems, participants began their response once they had reached a solution in their head and were not making on-the-fly calculations as they entered their response on the tablet (Supplementary Fig. 1).
Correct responses per minute
One of the challenges in assessing arithmetic fluency is navigating the speed-accuracy trade-off. To consider both the speed and accuracy with which students responded, we computed a composite metric that combined information about both reaction time and accuracy to gauge arithmetic fluency. Similar to the procedure outlined by Vandierendonck67, we computed Correct RPM for each contrast for each participant. RPM is computed using the formula:
| 1 |
where ct is the total number of correct responses provided for condition, t, and the denominator refers to the sum of all the reaction times for condition t. RPM then gives us a metric of the number of correct RPM. For example, an RPM equal to 20 would indicate that a participant answered twenty questions correctly per minute.
It should be noted that the RPM for the entire 3-minute assessment is perfectly correlated with traditional raw scores (total correct responses) calculated by chained-fluency assessments. However, by using event segmentation to calculate RPM, we can better characterize fluency across all problem types and make comparisons across individuals, grade cohorts, and problem types.
Furthermore, we also examined cross-sectional performance on the single-digit arithmetic at the first observation using reaction time (RT) and accuracy separately, which was calculated as the percentage of items answered correctly (Supplementary Figs. 2, 3).
Flanker task
The Flanker Task68 measured selective attention in participants. For this task, participants were presented with an array of five letters (A, B, C, or D) and asked to identify the center letter, while ignoring the four flanking letters. Participants recorded their response by tapping the button that corresponded to the center letter. The session began with 20 practice trials to learn the response mapping, 20 additional practice trials, and then 50 experimental trials. The initial maximum response time for this task was 800 ms.
Spatial span task
The Spatial Span Task was based off of the Corsi Block Stimuli Task69 and probed an individual’s visuospatial working memory. In this task, participants viewed an array of 20 black circles. These circles were then sequentially cued by changing color to green. In the Forward condition, participants were prompted to tap the circles in the order in which they were cued. In the Backward condition, the circles were highlighted in blue instead of green and participants were prompted to tap the circles in the reverse order in which they were cued. The experimental portion of both conditions was divided into levels. Participants started out on the first having to recall a three dot sequence. After correctly completing two consecutive trials of a given level, participants would advance to the next level where they would be prompted to recall an additional cue. After two consecutive incorrect trials, the task ended. We then added performance on the Forward and Backward conditions to obtain a composite Spatial Span measure for each participant.
Reliability and validity analysis
To assess the internal reliability and criterion validity of our single-digit fluency measure, we constructed a series of temporal subsets of our data. These subsets began with just the first 15 s of the assessment and increased in length by 15 s until the entire dataset was used. Within each subset, we calculated both a raw score using the total number of correct responses, as well as our RPM metric. Both of these metrics were computed using only addition and subtraction problems and excluded responses from filler trials that occurred after the initial 62 addition and subtraction items. To assess the internal reliability of our single-digit fluency measure, we calculated the Spearman-Brown adjusted split-half reliability70,71 of the correct RPM and raw score using data from each first temporal subset of the dataset.
To establish the criterion validity of our tablet-assessment, we fit a series of linear mixed-effects models predicting SBAC performance from each participant’s overall fluency. As with the reliability analysis, we began by fitting our model from the first 15 s of the assessment and sequentially added 15 more seconds of data until we reached the full 3-minute sample. We chose mixed-effects models because they account for interindividual differences not captured by ordinary least squares models. These SBAC for each individual, i, was modeled as follows:
| 2 |
Where,
Where γ is the mean SBAC score across all participants and the individual deviation from the intercept, vi, is assumed to be normally distributed with mean 0 and standard deviation σ. We first built a baseline random-effect model predicting standardized-test scores with no fixed effect of RPM and each participant as a random effect. This baseline model allowed us to establish the total amount of variance in test scores at the individual level across the entire sample. We then constructed a second model that included the RPM from each temporal subset of the single-digit fluency module as a fixed effect. We then calculated the change in variance in SBAC scores explained at the individual level between the full and reduced model.
Modeling known effects from numerical cognition literature
To examine the effects of problem size, operation, and problem type on RPM, we again fit a series of mixed-effects models that included a random intercept to account for individual differences in fluency and various fixed effects, including our predictors of interest, as well as covariates of grade and household income.
The model examining the effects of operation and problem size on RPM was specified as follows:
| 3 |
where,
Where γ is the mean RPM across all participants and the individual deviation from the intercept, vi, is assumed to be normally distributed with mean 0 and standard deviation σ.
Similarly, the model examining the effect of problem type on RPM was specified as follows:
| 4 |
Where,
Where γ is the mean RPM for a given problem type across all participants and the individual deviation from the intercept, vi, is assumed to be normally distributed with mean 0 and standard deviation σ.
Predicting SBAC achievement
To examine the specific relationship between arithmetic fluency and math achievement, we constructed a series of linear models predicting SBAC score. For each of these models, the independent variables were standardized to allow for the comparison of effects across models. Due to issues with model convergence, we opted to use ordinary least squares regression models for this analysis. We first built a baseline model predicting SBAC from grade, parental income, Basic Reaction Time (BRT), Flanker, Spatial Span, and traditional raw score from the math fluency task. Traditional raw score was derived by taking the total number of correct responses across the 3-minute session. We then fit three additional models that replaced traditional raw scores with either RPM on common problems, RPM on exceptional problems, or RPM on both common and exceptional problems (entered as individual predictors).
Speed-accuracy analysis
We conducted our analysis of speed and accuracy within the single-digit fluency module using the approach outlined in Domingue et al.38. Briefly, for each individual and single-digit fluency item, a Rasch mode72 is fit to estimate the probability of a correct response as a function of two parameters: latent individual ability, θj, and item difficulty, δi. These probability estimates, along with estimates from a flexible b-spline basis mapping of reaction time, are then entered into a linear fixed-effects model to model the within-person associations between accuracy and time-usage.
As highlighted in Domingue et al.38, the use of the b-spline basis function is important for capturing potential curvilinear associations between time usage and accuracy, while the linear fixed-effects model allows for computational flexibility while controlling for various time-invariant covariates. It is important to note, however, that this approach does not account for variation in item difficulty within a given category, nor does it allow for potential shifts in individual ability over the course of the assessment. After fitting the model with these assumptions, the model predictions can be plotted as speed-accuracy curves and qualitatively analyzed to describe the relationship between speed and accuracy. When exploring the speed-accuracy profiles for different problem types or subgroups of our overall sample, we simply filtered the data to include only our problem type and group of interest before fitting the speed-accuracy models to the data.
All analyses were carried out using R version 4.2.173 and linear-mixed effects models were fit with the lme4 package (version 1.1.30)74.
Supplementary information
Acknowledgements
This research was supported by funding from The Stanford Educational Neuroscience Initiative (2017-01) awarded to B.D.M. (Principal Investigator [PI]), Stanford Wu Tsai Neurosciences Institute Seed Grant (SNI-SG1-16) awarded to B.D.M. (co-PI) and a National Science Foundation, Science of Learning Collaborative Networks Grant (NSFSLCN-1540854) awarded to the project iLEAD consortium: Adam Gazzaley (PI), Melina R. Uncapher (Lead Co-PI) and (co-PIs) Joaquin Anguera, Silvia Bunge, Fumiko Hoeft, Bruce D. McCandliss, Jyoti Mishra, and Miriam Rosenberg-Lee. This study was conducted under approval from the Stanford University and University of California San Francisco Institutional Review Boards. Furthermore, the authors would like to thank the students, teachers, parents, and district officials for the time and contributions to this research.
Author contributions
E.R., M.G., A.V.R., and B.D.M. contributed to the conceptualization and design of the study. B.D.M. and Project iLead were involved with the data collection. E.R., M.G., A.V.R., and B.D.M. analyzed the data. E.R., M.G., A.V.R., and B.D.M. contributed to the writing of the manuscript. E.R., M.G., A.V.R., and B.D.M. contributed to the editing and revisions of the manuscript, and all read and approved the submitted version.
Data availability
The data that supported this study are available upon request from the iLead consortium authors and completion of a data use agreement. The data are not publicly available due to privacy and ethical restrictions. This study was not preregistered.
Code availability
The code used for these analyses is publicly available at: https://github.com/earoy/tablet_based_fluency/.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A list of authors and their affiliations appears at the end of the paper.
Contributor Information
Ethan Roy, Email: ethanroy@stanford.edu.
Project iLead Consortium:
Joaquin A. Anguera, Silvia A. Bunge, Adam Gazzaley, Fumiko Hoeft, Jyoti Mishra, Miriam Rosenberg-Lee, and Melina R. Uncapher
Supplementary information
The online version contains supplementary material available at 10.1038/s41539-025-00314-5.
References
- 1.Casey, B. J. et al. The adolescent brain cognitive development (ABCD) study: Imaging acquisition across 21 sites. Dev. Cogn. Neurosci.32, 43–54 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Alexander, L. M. et al. An open resource for transdiagnostic research in pediatric mental health and learning disorders. Sci. Data4, 170181 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nooner, K. et al. The NKI-Rockland sample: a model for accelerating the pace of discovery science in psychiatry. Front. Neurosci.6, 152 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Duncan, G. J. et al. School readiness and later achievement. Dev. Psychol.43, 1428–1446 (2007). [DOI] [PubMed] [Google Scholar]
- 5.Ritchie, S. J. & Bates, T. C. Enduring links from childhood mathematics and reading achievement to adult socioeconomic status. Psychol. Sci.24, 1301–1308 (2013). [DOI] [PubMed] [Google Scholar]
- 6.Rivera-Batiz, F. L. Quantitative literacy and the likelihood of employment among young adults in the United States. J. Hum. Resour.27, 313–328 (1992). [Google Scholar]
- 7.Hickendorff, M. Dutch sixth graders’ use of shortcut strategies in solving multidigit arithmetic problems. Eur. J. Psychol. Educ.33, 577–594 (2018). [Google Scholar]
- 8.Clements, D. H., Sarama, J. & Germeroth, C. Learning executive function and early mathematics: directions of causal relations. Early Child. Res. Q.36, 79–90 (2016). [Google Scholar]
- 9.Cragg, L. & Gilmore, C. Skills underlying mathematics: the role of executive function in the development of mathematics proficiency. Trends Neurosci. Educ.3, 63–68 (2014). [Google Scholar]
- 10.Wendling, B. J., Schrank, F. A. & Schmitt, A. J. Educational Interventions Related to the Woodcock-Johnson III Tests of Achievement (Assessment Service Bulletin No. 8). Rolling Meadows, IL: Riverside Publishing (2007).
- 11.Loenneker, H. D. et al. (Math4Speed: A freely available measure of arithmetic fluency. Canadian Journal of Experimental Psychology / Revue canadienne de psychologie expérimentale. Advance online publication. 10.1037/cep0000347 (2024). [DOI] [PubMed]
- 12.Wechsler, D. Wechsler Preschool and Primary Scale of Intelligence 4th edn (The Psychological Corporation, 2012).
- 13.Berteletti, I. & Booth, J. R. Perceiving fingers in single-digit arithmetic problems. Front. Psychol.6, 226 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Haist, F., Wazny, J. H., Toomarian, E. & Adamo, M. Development of brain systems for nonsymbolic numerosity and the relationship to formal math academic achievement. Hum. Brain Mapp.36, 804–826 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Butterworth, B. The development of arithmetical abilities. J. Child Psychol. Psychiatry46, 3–18 (2005). [DOI] [PubMed] [Google Scholar]
- 16.Mather, N. & Wendling, B. J. Instructional Implications from the Woodcock–Johnson IV Tests of Achievement. in WJ IV Clinical Use and Interpretation (eds Flanagan, D. P. & Alfonso, V. C.) Ch. 6, 151–190. 10.1016/B978-0-12-802076-0.00006-2 (Academic Press, 2016).
- 17.Wilkey, E. D., Pollack, C. & Price, G. R. Dyscalculia and typical math achievement are associated with individual differences in number-specific executive function. Child Dev.91, 596–619 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fyfe, E. R., Rittle-Johnson, B. & Farran, D. C. Predicting success on high-stakes math tests from preschool math measures among children from low-income homes. J. Educ. Psychol.111, 402–413 (2019). [Google Scholar]
- 19.Davis-Kean, P. E., Domina, T., Kuhfeld, M., Ellis, A. & Gershoff, E. T. It matters how you start: early numeracy mastery predicts high school math course-taking and college attendance. Infant Child Dev.31, e2281 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ashcraft, M. H. The development of mental arithmetic: a chronometric approach. Dev. Rev.2, 213–236 (1982). [Google Scholar]
- 21.Education, C. D. of. California Common Core State Standards: Mathematics (California Department of Education, 2013).
- 22.Guillaume, M. et al. Groupitizing reflects conceptual developments in math cognition and inequities in math achievement from childhood through adolescence. Child Dev. cdev.13859. 10.1111/cdev.13859 (2022). [DOI] [PubMed]
- 23.Gliksman, Y., Berebbi, S. & Henik, A. Math fluency during primary school. Brain Sci.12, 371 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Boets, B. & Smedt, B. D. Single-digit arithmetic in children with dyslexia. Dyslexia16, 183–191 (2010). [DOI] [PubMed] [Google Scholar]
- 25.Groen, G. J. & Parkman, J. M. A chronometric analysis of simple addition. Psychol. Rev.79, 329 (1972). [Google Scholar]
- 26.LeFevre, J.-A. et al. Multiple routes to solution of single-digit multiplication problems. J. Exp. Psychol. Gen.125, 284 (1996). [Google Scholar]
- 27.Fayol, M. & Thevenot, C. The use of procedural knowledge in simple addition and subtraction problems. Cognition123, 392–403 (2012). [DOI] [PubMed] [Google Scholar]
- 28.Uittenhove, K., Thevenot, C. & Barrouillet, P. Fast automated counting procedures in addition problem solving: when are they used and why are they mistaken for retrieval? Cognition146, 289–303 (2016). [DOI] [PubMed] [Google Scholar]
- 29.Siegler, R. S. Strategy diversity and cognitive assessment. Educ. Res.18, 15–20 (1989). [Google Scholar]
- 30.Ashcraft, M. & Ashcraft, M. H. Cognitive arithmetic: a review of data and theory. Cognition44, 75–106 (1992). Cognition 44, 75–106. [DOI] [PubMed] [Google Scholar]
- 31.LeFevre, J., Shanahan, T. & DeStefano, D. The tie effect in simple arithmetic: an access-based account. Mem. Cogn.32, 1019–1031 (2004). [DOI] [PubMed] [Google Scholar]
- 32.LeFevre, J.-A., Sadesky, G. S. & Bisanz, J. Selection of procedures in mental addition: reassessing the problem size effect in adults. J. Exp. Psychol. Learn. Mem. Cogn.22, 216 (1996). [Google Scholar]
- 33.Campbell, J. I. & Xue, Q. Cognitive arithmetic across cultures. J. Exp. Psychol. Gen.130, 299 (2001). [DOI] [PubMed] [Google Scholar]
- 34.De Smedt, B., Holloway, I. D. & Ansari, D. Effects of problem size and arithmetic operation on brain activation during calculation in children with varying levels of arithmetical fluency. NeuroImage57, 771–781 (2011). [DOI] [PubMed] [Google Scholar]
- 35.Jiban, C. L. & Deno, S. L. Using math and reading curriculum-based measurements to predict state mathematics test performance: are simple one-minute measures technically adequate? Assess. Eff. Interv.32, 78–89 (2007). [Google Scholar]
- 36.Siegler, R. S. et al. Early predictors of high school mathematics achievement. Psychol. Sci.23, 691–697 (2012). [DOI] [PubMed] [Google Scholar]
- 37.Price, G. R., Mazzocco, M. M. M. & Ansari, D. Why mental arithmetic counts: brain activation during single digit arithmetic predicts high school math scores. J. Neurosci.33, 156–163 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Domingue, B. W. et al. Speed–accuracy trade-off? Not so fast: marginal changes in speed have inconsistent relationships with accuracy in real-world settings. J. Educ. Behav. Stat.47, 576–602 (2022). [Google Scholar]
- 39.Baroody, A. J. The development of procedural knowledge: an alternative explanation for chronometric trends of mental arithmetic. Dev. Rev.3, 225–230 (1983). [Google Scholar]
- 40.Barrouillet, P. & Thevenot, C. On the problem-size effect in small additions: can we really discard any counting-based account? Cognition128, 35–44 (2013). [DOI] [PubMed] [Google Scholar]
- 41.Chen, H., De Boeck, P., Grady, M., Yang, C.-L. & Waldschmidt, D. Curvilinear dependency of response accuracy on response time in cognitive tests. Intelligence69, 16–23 (2018). [Google Scholar]
- 42.Ashcraft, M. H. Is it farfetched that some of us remember our arithmetic facts? J. Res. Math. Educ.16, 99–105 (1985). [Google Scholar]
- 43.Sirin, S. R. Socioeconomic status and academic achievement: a meta-analytic review of research. Rev. Educ. Res.75, 417–453 (2005). [Google Scholar]
- 44.Nunes, T., Bryant, P., Barros, R. & Sylva, K. The relative importance of two different mathematical abilities to mathematical achievement. Br. J. Educ. Psychol.82, 136–156 (2012). [DOI] [PubMed] [Google Scholar]
- 45.De Smedt, B. Individual differences in arithmetic fact retrieval. in Development of Mathematical Cognition 219–243. 10.1016/B978-0-12-801871-2.00009-5 (Elsevier, 2016).
- 46.Siegler, R. S. Individual differences in strategy choices: good students, not-so-good students, and perfectionists. Child Dev. 59, 833–851 (1988). [PubMed]
- 47.Carpenter, T. P. & Moser, J. M. The acquisition of addition and subtraction concepts in grades one through three. J. Res. Math. Educ.15, 179–202 (1984). [Google Scholar]
- 48.Geary, D. C., Bow-Thomas, C. C. & Yao, Y. Counting knowledge and skill in cognitive addition: A comparison of normal and mathematically disabled children. J. Exp. Child Psychol.54, 372–391 (1992). [DOI] [PubMed] [Google Scholar]
- 49.Campbell, J. I. D. Architectures for numerical cognition. Cognition53, 1–44 (1994). [DOI] [PubMed] [Google Scholar]
- 50.Butterworth, B., Zorzi, M., Girelli, L. & Jonckheere, A. R. Storage and retrieval of addition facts: the role of number comparison. Q. J. Exp. Psychol. Sect. A54, 1005–1029 (2001). [DOI] [PubMed] [Google Scholar]
- 51.Geary, D. C., Hoard, M. K. & Bailey, D. H. Fact retrieval deficits in low achieving children and children with mathematical learning disability. J. Learn. Disabil.45, 291–307 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Siegler, R. S. Children’s learning. Am. Psychol.60, 769 (2005). [DOI] [PubMed] [Google Scholar]
- 53.Arsalidou, M., Pawliw-Levac, M., Sadeghi, M. & Pascual-Leone, J. Brain areas associated with numbers and calculations in children: Meta-analyses of fMRI studies. Dev. Cogn. Neurosci.30, 239–250 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cho, S., Ryali, S., Geary, D. C. & Menon, V. How does a child solve 7 + 8? Decoding brain activity patterns associated with counting and retrieval strategies. Dev. Sci.14, 989–1001 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Menon, V. Memory and cognitive control circuits in mathematical cognition and learning. Prog. Brain Res.227, 159–186 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Menon, V. Working memory in children’s math learning and its disruption in dyscalculia. Curr. Opin. Behav. Sci.10, 125–132 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Rivera, S. M., Reiss, A. L., Eckert, M. A. & Menon, V. Developmental changes in mental arithmetic: evidence for increased functional specialization in the left inferior parietal cortex. Cereb. Cortex15, 1779–1790 (2005). [DOI] [PubMed] [Google Scholar]
- 58.Bagnoud, J. Developmental changes in size effects for simple tie and non-tie addition problems in 6- to 12-year-old children and adults. J. Exp. Child Psychol.201, 104987 (2021). 15. [DOI] [PubMed] [Google Scholar]
- 59.Younger, J. W. et al. Better together: novel methods for measuring and modeling development of executive function diversity while accounting for unity. Front. Hum. Neurosci.17, 1195013 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Younger, J. W. et al. Development of Executive Function in Middle Childhood: A Large-Scale, In-School, Longitudinal Investigation. https://osf.io/xf489; 10.31234/osf.io/xf489 (2021).
- 61.Leys, C., Ley, C., Klein, O., Bernard, P. & Licata, L. Detecting outliers: do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol.49, 764–766 (2013). [Google Scholar]
- 62.Li, P., Stuart, E. A. & Allison, D. B. Multiple imputation: a flexible tool for handling missing data. JAMA314, 1966 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.CAASPP Description—CalEdFacts (CA Dept of Education). https://www.cde.ca.gov/ta/tg/ai/cefcaaspp.asp.
- 64.Odic, D., Hock, H. & Halberda, J. Hysteresis affects approximate number discrimination in young children. J. Exp. Psychol. Gen.143, 255 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Mauro, D. G., LeFevre, J.-A. & Morris, J. Effects of problem format on division and multiplication performance: division facts are mediated via multiplication-based representations. J. Exp. Psychol. Learn. Mem. Cogn.29, 163 (2003). [DOI] [PubMed] [Google Scholar]
- 66.LeFevre, J.-A. & Morris, J. More on the relation between division and multiplication in simple arithmetic: Evidence for mediation of division solutions via multiplication. Mem. Cogn.27, 803–812 (1999). [DOI] [PubMed] [Google Scholar]
- 67.Vandierendonck, A. A comparison of methods to combine speed and accuracy measures of performance: a rejoinder on the binning procedure. Behav. Res. Methods49, 653–673 (2017). [DOI] [PubMed] [Google Scholar]
- 68.Eriksen, B. A. & Eriksen, C. W. Effects of noise letters upon the identification of a target letter in a nonsearch task. Percept. Psychophys.16, 143–149 (1974). [Google Scholar]
- 69.Corsi, P. M. Human Memory and the Medial Temporal Region of the Brain. McGill University (1972).
- 70.Spearman, C. Correlation calculated from faulty data. Br. J. Psychol.3, 271 (1910). [Google Scholar]
- 71.Brown, W. Some experimental results in the correlation of mental abilities 1. Br. J. Psychol.3, 296–322 (1910). 1904-1920. [Google Scholar]
- 72.Georg, R. Probabilistic Models for Some Intelligence and Attainment Tests (Danmarks Paedagogiske Institut, 1960).
- 73.R Core Team. R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, 2022).
- 74.Bates, D., Mächler, M., Bolker, B. & Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw.67, 1–48 (2015). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that supported this study are available upon request from the iLead consortium authors and completion of a data use agreement. The data are not publicly available due to privacy and ethical restrictions. This study was not preregistered.
The code used for these analyses is publicly available at: https://github.com/earoy/tablet_based_fluency/.