Lateral Diffusion of CO₂ in Leaves Is Not Sufficient to Support Photosynthesis

Abstract

Lateral diffusion of CO₂ was investigated in photosynthesizing leaves with different anatomy by gas exchange and chlorophyll a fluorescence imaging using grease to block stomata. When one-half of the leaf surface of the heterobaric species Helianthus annuus was covered by 4-mm-diameter patches of grease, the response of net CO₂ assimilation rate (A) to intercellular CO₂ concentration (C_i) indicated that higher ambient CO₂ concentrations (C_a) caused only limited lateral diffusion into the greased areas. When single 4-mm patches were applied to leaves of heterobaric Phaseolus vulgaris and homobaric Commelina communis, chlorophyll a fluorescence images showed dramatic declines in the quantum efficiency of photosystem II electron transport (measured as F_q′/F_m′) across the patch, demonstrating that lateral CO₂ diffusion could not support A. The F_q′/F_m′ values were used to compute images of C_i across patches, and their dependence on C_a was assessed. At high C_a, the patch effect was less in C. communis than P. vulgaris. A finite-volume porous-medium model for assimilation rate and lateral CO₂ diffusion was developed to analyze the patch images. The model estimated that the effective lateral CO₂ diffusion coefficients inside C. communis and P. vulgaris leaves were 22% and 12% of that for free air, respectively. We conclude that, in the light, lateral CO₂ diffusion cannot support appreciable photosynthesis over distances of more than approximately 0.3 mm in normal leaves, irrespective of the presence or absence of bundle sheath extensions, because of the CO₂ assimilation by cells along the diffusion pathway.

Leaf CO₂ assimilation rates in C3 plants are sensitive to the intercellular CO₂ concentration (C_i) primarily because of the poor affinity of Rubisco for CO₂ (e.g. Evans and von Caemmerer, 1996). The rate of diffusion of CO₂ into or out of the leaf depends on the partial pressure gradient and the resistance of the diffusion pathway from outside the leaf to the site of fixation, the chloroplasts. This pathway comprises the well-understood boundary layer and stomatal components and a less well-understood internal resistance, r_i (for clarification of terminology, see Evans and von Caemmerer, 1996). Understanding r_i is very important, as it determines the drop in CO₂ molar fraction between the substomatal space and the chloroplast, which is about 70 to 100 μmol mol⁻¹ (e.g. Parkhurst and Mott, 1990; Evans and Loretto, 2000; Singsaas et al., 2003). The value of r_i is therefore critical to many aspects of photosynthetic modeling, for example, correct estimation of key photosynthetic model parameters (Parkhurst and Mott, 1990; Singsaas et al., 2003; Manter and Kerrigan, 2004; Warren 2004), assessment of the importance of carbonic anhydrase in chloroplastic CO₂ diffusion (e.g. Gillon and Yakir, 2000), and prediction of photosynthetic gains from engineering C4 photosynthesis in C3 cells (von Caemmerer, 2003).

While numerous studies have attempted to determine r_i in different species, there is as yet no complete model of it (Singsaas et al., 2003), and we need more information on its basis (Long and Bernacchi, 2003). The r_i is the combination of an air space gaseous resistance, r_ias, and a liquid phase resistance from the cell wall to the chloroplast, r_liq. The air space diffusion resistance, r_ias, should reflect the leaf structure, particularly the porosity, cell shape, and density of packing. At the scale of a few cells, r_ias must be anisotropic, given the typical arrangement of packed vertical cylindrical cells in the palisade and more loosely arranged cells in the spongy mesophyll tissue (porosities in the two tissues are typically 15%–30% and 25%–65%, respectively; e.g. Terashima, 1992; Terashima et al., 1996). The r_ias must also depend on the pathway, which is partly determined by the pattern of stomatal apertures. For example, if groups of stomata are closed in particular areas of the leaf, lateral CO₂ diffusion could become important (Terashima, 1992; Parkhurst, 1994), whereas homogeneous stomatal apertures result in CO₂ diffusion being predominately vertical over the small distance of the thickness of the leaf (or, for amphistomatous leaves, one-half of the thickness). At a larger scale of a few millimeters, in heterobaric leaves, bundle sheath extensions divide the leaf into numerous isolated gas compartments called areoles (Esau, 1977), and these extensions apparently restrict lateral CO₂ diffusion during photosynthesis. This is suggested by the heterogeneous patterns of CO₂ assimilation observed in such leaves (e.g. Downton et al., 1988; Terashima et al., 1988). Therefore, r_ias is believed to be greater in heterobaric leaves compared with homobaric leaves in which these extensions are absent (Terashima et al., 1988; Parkhurst, 1994). Heterobaric leaf anatomy under certain conditions is associated with patchy stomatal behavior, which can be defined as stomata in “adjacent regions differing by exhibiting mean values that differ significantly” (p. 323; Weyers and Lawson, 1997). The importance of patchy stomatal behavior to net CO₂ assimilation rate (A) and to the calculation of C_i, particularly during water stress, has been extensively debated (e.g. Terashima, 1992; Parkhurst, 1994). However, even when leaves are not “patchy,” there can be significant spatial trends in stomatal aperture in both homobaric and heterobaric leaves so that lateral CO₂ diffusion could be important (Terashima et al., 1988; Weyers and Lawson, 1997).

There are rather few published empirical values for r_ias or its reciprocal, the air space conductance for CO₂, g_ias. The upper limits to vertical g_ias can be estimated from the value of the diffusion coefficient of CO₂ (D_c) in still air, and the overall mesophyll porosity and the leaf thickness. Taking ranges of values of the latter two parameters from the comprehensive survey of 56 species by Slaton and Smith (2002; e.g. 10%–30% porosity and 0.1–0.6 mm thickness) gives a g_ias range of 4.7 to 0.26 cm s⁻¹ (equivalent to molar conductances of 1.9–0.11 mol m⁻² s⁻¹). Values measured have usually been at the lower end of this range (0.14–0.33 mol m⁻² s⁻¹; Pieruschka et al., 2005). There are two possible factors causing these values: the tortuosity of the path length, which may reduce diffusion by 50% or more (Parkhurst and Mott, 1990; Syvertsen et al., 1995; Terashima et al., 1996), and the narrow diameter of the air spaces, causing more collision with cell walls (Leuning, 1983). There are even fewer estimates of lateral g_ias. Using respiration measurements, Pieruschka et al. (2005) recently determined much lower values that differ substantially between homobaric Vicia faba leaves (26 mmol m⁻² s⁻¹) and heterobaric Phaseolus vulgaris leaves (0.3 mmol m⁻² s⁻¹). However, it is difficult to determine what such g_ias values mean for two reasons. First, such conductance values are equal to the diffusion coefficient of the gas in air divided by the length of the path of diffusion, which is not precisely known and is likely to vary, particularly during patchy stomatal closure. Second, the basic conductance or resistance model breaks down when diffusion occurs in a medium with distributed sources or sinks (Parkhurst, 1994), and in the light the sinks vary markedly with C_i (particularly under CO₂ limiting conditions). It is therefore crucial to consider both the sink activity along the pathway and the physical limitation (resistance to diffusion determined by leaf anatomy) in determining intercellular diffusion rates (Parkhurst, 1994; Evans and von Caemmerer, 1996).

Parkhurst (1977) developed a three-dimensional (3-D) model of photosynthetic CO₂ uptake to estimate r_ias and concluded that intercellular diffusion is slow and thus can be an important factor limiting CO₂ assimilation rate (Parkhurst, 1977, 1994). However, Parkhurst's theoretical conclusions have had only limited experimental confirmation, as it has not been possible to measure CO₂ concentration profiles inside leaves and thereby estimate vertical or lateral diffusion and determine the effects of different anatomies and the effect of sink strength on CO₂ diffusion. In this work, we applied artificial patches of silicon grease to block stomata and examined the contribution of lateral diffusion using gas exchange. We also used the approach of Meyer and Genty (1998) combining gas exchange measurements and chlorophyll a fluorescence imaging to map the resulting two-dimensional (2-D) distribution of C_i across the leaf surface. In the patched area, diffusion through the stomata was eliminated; consequently, CO₂ supply for photosynthesis in the mesophyll under the patch was provided solely by lateral diffusion from the tissues surrounding the patch. Using this technique, it was possible to map C_i at a spatial resolution of 0.15×0.15 mm and study the lateral diffusion of CO₂ in leaves. We also developed a 2-D CO₂ diffusion model that included the activity of sinks along the pathway to estimate the effective lateral CO₂ diffusion coefficient, D_c′, from these data. We focused on two amphistomatous species with different leaf anatomy: P. vulgaris, a dicotyledonous species with heterobaric vein anatomy, and Commelina communis, a monocotyledonous, homobaric species. It is clear from the results that lateral diffusion over distances longer than 0.3 mm is not sufficient to provide for normal CO₂ assimilation rates in either of these two species and that vertical diffusion over short distances in normal conditions dominates CO₂ fluxes inside the leaf. The results also allay recent concerns that lateral diffusion through the leaf may cause errors in leaf photosynthetic measurements in small chambers (Long and Bernacchi, 2003).

RESULTS

Gas Exchange Demonstration of Limited Lateral Diffusion

When diffusion through the stomata was prevented by covering both sides of one-half of a leaf of sunflower (Helianthus annuus) with grease, the response of A to increasing ambient CO₂ concentration, C_a, showed that A was approximately halved (Fig. 1A). However, the shape was essentially the same as that for the leaf prior to covering, with the rate saturating at approximately the same C_a. Closer inspection shows that the ratio of A for the half-covered leaf (A^c) to that for the complete leaf (A) was slightly higher than one-half (0.53), which might indicate that some CO₂ did diffuse into the covered area to contribute to assimilation. However, this difference in ratio is equivalent to an additional 0.9-mm zone along the boundary between greased and untouched areas photosynthesizing at the full rate, which is within the accuracy of placement of the grease and chamber. The transpiration ratio T^c/T was very similar to the assimilation ratio (data not shown), showing that the grease was preventing diffusion through stomata and thereby affecting both CO₂ and H₂O equally.

Figure 1.

Response of net CO₂ assimilation rate, A, to increasing ambient CO₂ concentration, C_a, for sunflower leaves, with (•) and without (○) parts of the leaf being covered with grease. The right-hand axis (▵) indicates the ratio of A in covered (A^c) and not-covered (A) leaves. A, One-half of the total leaf area covered (both surfaces; •); B, the whole of the lower surface of the leaf covered (•); C, one-half of the leaf covered in 4-mm-diameter grease patches (both surfaces; •). Conditions: PPFD = 1,000 μmol m⁻² s⁻¹; leaf temperature = 25°C; water vapor in the leaf chamber approximately 15 mmol mol⁻¹; O₂ = 21%.

The substantial effect on the CO₂ assimilation rate of covering one-half of a leaf on both sides contrasts markedly with just covering the whole lower surface alone (Fig. 1, compare A and B). With the lower surface covered, A^c/A was only a minimum of 0.7, and more than 0.9 across most of the range of C_a from present atmospheric concentrations upwards. Sunflower leaves are amphistomatous, with typical ratios of lower to upper surface stomatal conductance of 1.7 (Morison, 1998), so that the upper surface stomata were able to supply CO₂. Indeed, they opened slightly more, as the transpiration ratio T^c/T was approximately 0.6 over the whole C_a range. Therefore, the drop in calculated C_i was only 40 μmol mol⁻¹ (at C_a = 360 μmol mol⁻¹). The A/C_i response was identical for normal leaves and those with the lower surface greased, showing that there was no effect of the treatment other than on the diffusion through stomata.

Figure 1A suggested that lateral diffusion across the short boundary (2 cm long) between greased and ungreased portions was slight. When a much larger boundary zone was created by covering approximately one-half of the leaf area with grease in small, 4-mm-diameter patches evenly distributed across the leaf surfaces, the A/C_i curve was markedly different (Fig. 1, compare C to A). Although A was approximately one-half at C_a = 370 μmol mol⁻¹, as C_a increased, A increased, showing no saturation, even up to C_a = 2,000 μmol mol⁻¹. The ratio A^c/A changed from 0.3 at 100 μmol mol⁻¹ C_a to 0.81 at 2,000 μmol mol⁻¹. However, transpiration was not affected by changing C_a as T^c/T remained close to 0.5 throughout, showing that it was not diffusion through the stomata that was changing with C_a. The changing ratio A^c/A therefore demonstrates that the higher C_a increased CO₂ diffusion laterally through the mesophyll. The effect produced a substantial increase in A because the distributed small patches provided a total perimeter length of 28 cm. However, even for this length perimeter, the additional photosynthesis at the highest C_a was equivalent to supplying CO₂ to a mesophyll zone only 0.6 mm wide photosynthesizing at the maximum rate.

Chlorophyll Fluorescence Imaging

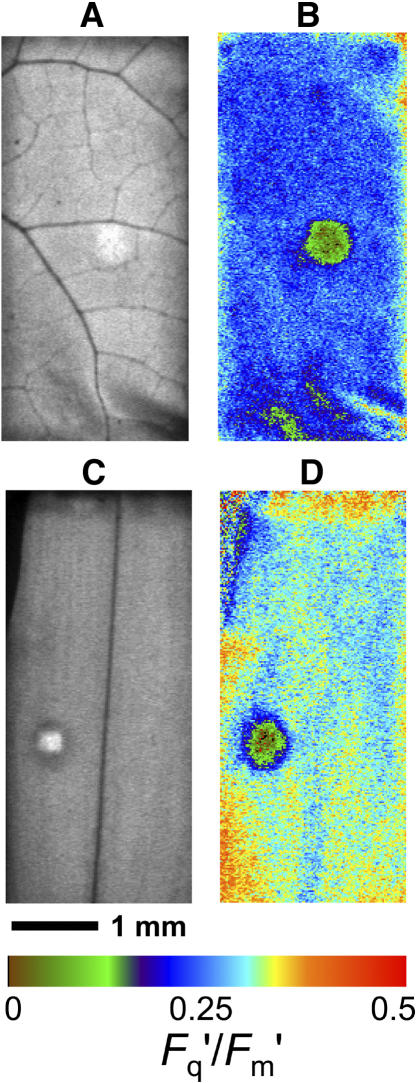
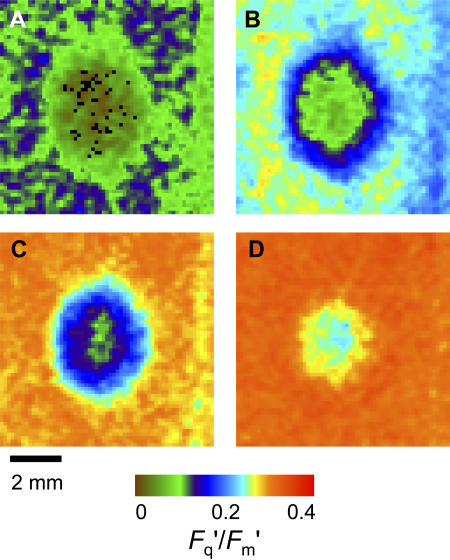
The CO₂ diffusion into patched areas of leaves was examined in detail with chlorophyll a fluorescence imaging. We contrasted the effect of the patch in the heterobaric P. vulgaris with the effect in the homobaric species C. communis. The imaging system clearly resolved in detail differences across the 10-cm² area of leaf enclosed, with vein patterns very evident in the steady-state fluorescence image F′ (Fig. 2, A and C). The effect of a grease patch on the photosynthesis of the leaf was also clearly visible through F′ and in the image constructed of F_q′/F_m′ or the operating quantum efficiency of PSII electron transport (Fig. 2, B and D) in both P. vulgaris and C. communis.

Figure 2.

Images of chlorophyll fluorescence for 10-cm² leaf areas enclosed in a chamber (4.6×2.2 mm) during simultaneous gas exchange measurement. A and B are for P. vulgaris, and C and D are for C. communis leaves with a single 4-mm-diameter grease patch applied to both leaf surfaces. PPFD = 400 μmol m⁻² s⁻¹; leaf temperature = 25°C; 1% O₂; CO₂ = approximately 320 μmol mol⁻¹. Images A and C are for F′ (arbitrary gray scale). Images in B and D are for F_q′/F_m′, with the colored bar indicating how the range of values is mapped to the color palette; mean values are 0.239 and 0.300, respectively.

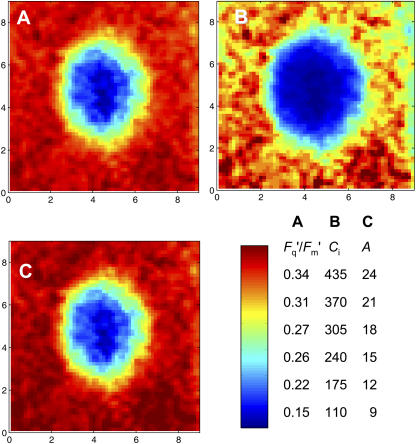
When an image of F_q′/F_m′ for a patch and surrounding region is viewed in more detail (Fig. 3A), it is striking that the F_q′/F_m′ declines very steeply within a few pixels (<0.5 mm) of the edge of the patch and is <0.18 across a large area of the patch, with an approximate diameter of 2 mm. Note also that the F_q′/F_m′ values in the area surrounding the patch are quite uniform (range 0.33–0.36). Using the calibration relationship determined prior to patching between whole image mean F_q′/F_m′ and gas exchange-derived C_i (Fig. 11), we calculated C_i for each pixel after a patch was applied. The calculated C_i (Fig. 3B) in the middle region of the patched area is very low, <50 μmol mol⁻¹, and the gradient at the edge is approximately 320 μmol mol⁻¹ mm⁻¹. The calculated image of A (Fig. 3C) essentially shows the same pattern as F_q′/F_m′ (as suggested by the linear relationship between A and F_q′/F_m′ in Fig. 11A), with a dramatic drop in photosynthesis in the patched area, and demonstrates that lateral diffusion of CO₂ was restricting photosynthesis.

Figure 3.

Effect of a 4-mm-diameter grease patch on photosynthesis in part of a leaf of C. communis. Grease was applied to both leaf surfaces. C_a = 643 μmol mol⁻¹; C_i = 342 μmol mol⁻¹; g_s = 85 mmol m⁻² s⁻¹; PPFD = 400 μmol m⁻² s⁻¹. Axes shown are image scales in millimeters. Color bar is shown with relevant scales. A, Image of measured PSII efficiency (F_q′/F_m′). B, Map of intercellular CO₂ concentration, C_i, across the patch, calculated from A as described in “Materials and Methods.” C, Map of net CO₂ assimilation rate, A, calculated from B.

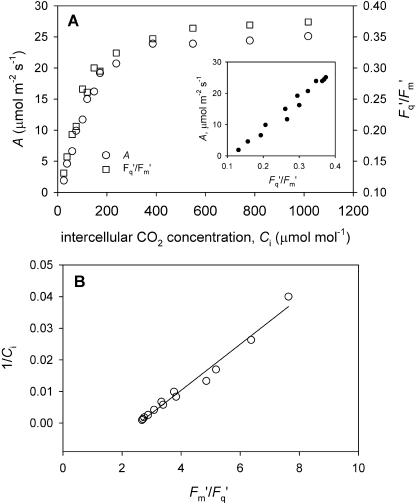
Figure 11.

A, Example calibration information: relationships between net CO₂ assimilation rate (A), F_q′/F_m′ (PSII quantum efficiency), and intercellular CO₂ concentration (C_i) for P. vulgaris. PPFD 400 μmol m⁻² s⁻¹; leaf temperature = 25°C; 1% O₂. Insert graph in A is data replotted as A versus F_q′/F_m′. B, Data from A replotted as the double reciprocal plot, 1/C_i against F_m′/F_q′.

Obviously if there is any lateral diffusion, the CO₂ molar fraction inside the patch and, consequently, A will depend on the molar fraction in the surrounding leaf (C_i) and therefore on the C_a. As C_a is increased, C_i outside the patch should increase, driving more lateral CO₂ diffusion. This effect is examined in Figures 4 and 5 for P. vulgaris and Figures 6 and 7 for C. communis. As expected, F_q′/F_m′ in the unpatched area responded to C_i (Fig. 4), increasing to 0.46 as C_i was increased to >1,200 μmol mol⁻¹ and dropping to 0.18 at C_i = 57 μmol mol⁻¹. However, across this wide C_i range, the effect of the patch is evident in all the images (Fig. 4), although the area of leaf affected by the patch diminished as the adjacent C_i increased, indicating some lateral diffusion. The C_i values across the patches calculated from the F_q′/F_m′ data are shown by the symbols in Figure 5 (the lines are modeled data; see later). Although the minimum C_i in the middle of the patch increased slightly with increasing CO₂, even at a C_i of 1,270 μmol mol⁻¹ in the rest of the leaf, C_i in the middle of the patch was as low as 40 μmol mol⁻¹ (Fig. 5B). In all cases, the patch affected a slightly larger area than the patch itself, presumably because there was no lateral CO₂ supply outward from the patched area. This effect is not so evident at the lowest C_i because there is only a small lateral CO₂ gradient close to the CO₂ compensation molar fraction.

Figure 4.

Images of PSII efficiency (F_q′/F_m′) in part of a leaf of P. vulgaris (approximately 8 × 8 mm) with a 4-mm-diameter grease patch applied to both sides at different external CO₂ concentrations (C_a). PPFD was 400 μmol m⁻² s⁻¹. C_a and intercellular CO₂ concentration, C_i, values determined for the unpatched portion of the leaf were as follows: A, C_a = 97, C_i = 57; B, C_a = 270, C_i = 166; C, C_a = 360, C_i = 227; and D, C_a = 1,780, C_i = 1,270 μmol mol⁻¹. The colored bar indicates how the range of F_q′/F_m′ values is mapped to the color palette.

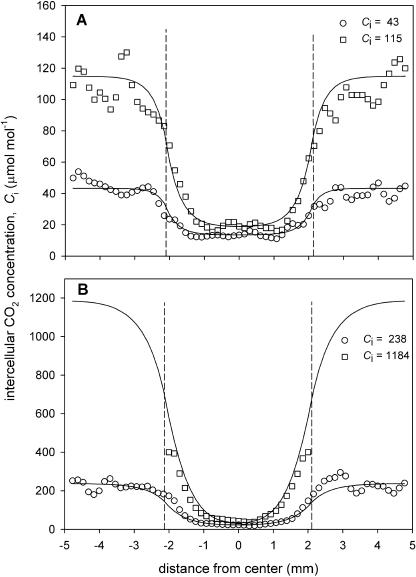
Figure 5.

Transects of intercellular CO₂ concentration, C_i, across a 4-mm-diameter grease patch applied to part of a leaf of P. vulgaris. Symbols indicate the mean C_i values calculated from the F_q′/F_m′ images shown in Figure 4 for three rows of 0.15-×0.15-mm pixels on a horizontal transect. Lines show the C_i values estimated from a model of lateral CO₂ diffusion (see text for details). The fitted CO₂ diffusion coefficient reduction factors , φ, for the curves in A were 9.4% (lower) and 10.8% (upper), and in B were 15.8% (lower) and 8.5% (upper). C_i values shown are those for the unpatched leaf area. For the highest C_a, C_i values above 400 μmol mol⁻¹ could not be reliably estimated from F_q′/F_m′. Dotted vertical lines indicate the position of the patch.

Figure 6.

Images of PSII efficiency (F_q′/F_m′) in part of a leaf of C. communis (approximately 8×8 mm) with a 4-mm-diameter grease patch applied to both sides at different external CO₂ concentrations (C_a). PPFD was 400 μmol m⁻² s⁻¹. C_a and intercellular CO₂ concentration, C_i, values determined for the unpatched portion of the leaf were as follows: A, C_a = 145, C_i = 50; B, C_a = 383, C_i = 154; C, C_a = 643, C_i = 342; and D, C_a = 1,790, C_i = 1,375 μmol mol⁻¹. The colored bar indicates how the range of F_q′/F_m′ values is mapped to the color palette.

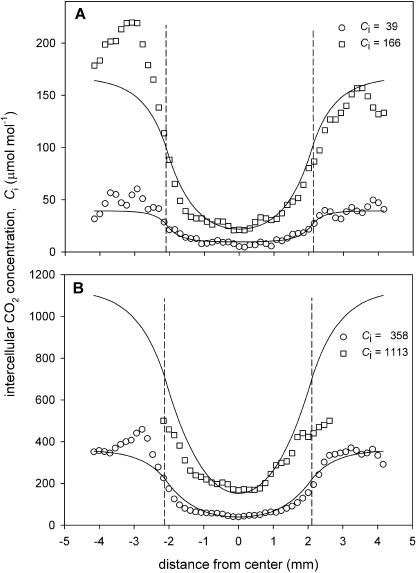
Figure 7.

Transects of intercellular CO₂ concentration, C_i, across a 4-mm-diameter grease patch applied to part of a leaf of C. communis. Symbols indicate the mean C_i calculated from the F_q′/F_m′ images shown in Figure 6. Lines show the C_i values estimated from a model of lateral CO₂ diffusion, with a fitted CO₂ diffusion coefficient reduction factor, φ, of (A) 16.5% (lower) and 33.7% (upper), and (B) 25.5% (lower) and 23.2% (upper). C_i values shown are those for the unpatched leaf area. Other details are as in Figure 5.

When patches were applied to C. communis leaves (Fig. 6), the C_i concentrations in the surrounding leaf required to reduce the patch-affected area were considerably lower than in P. vulgaris. At the highest C_i (1,375 μmol mol⁻¹), blocking the stomata only affected F_q′/F_m′ in an area about one-half of the patch diameter (Fig. 6D). The C_i transect graphs (Fig. 7) showed that the minimum C_i in the patch was <50 μmol mol⁻¹ for the three lowest CO₂ molar fractions, but at the highest C_i of 1,375 it was 171 μmol mol⁻¹.

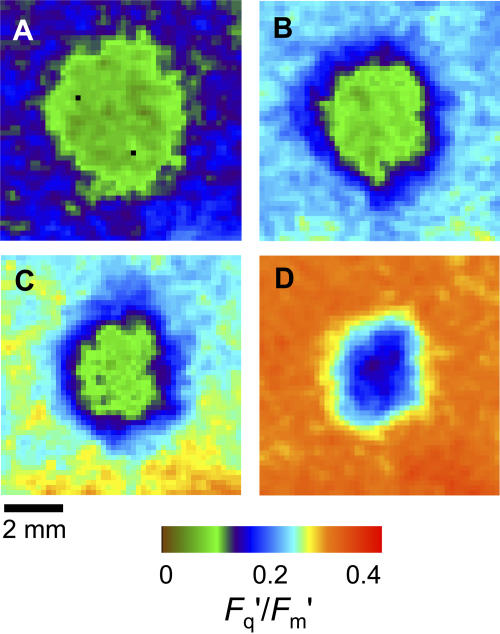
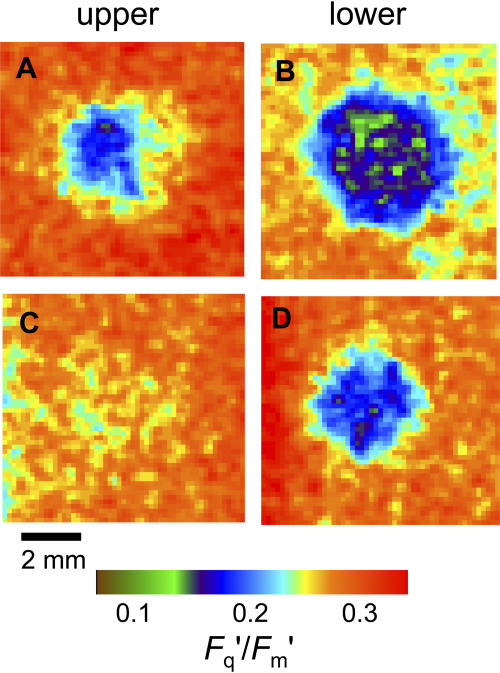
Both of the species examined are amphistomatous, with similar leaf thicknesses and mesophyll sizes (Table I). However, both have much higher stomatal frequencies on the lower side than on the upper (Table I), as is usual in most herbaceous species, which consequently have typical conductance ratios of g_s^l/g_s^u ≥ 2. Therefore, we hypothesized that patches on the upper surface alone would have less effect on F_q′/F_m′ than patches applied to the underneath. This is confirmed by the images shown in Figure 8. For P. vulgaris, a patch on the upper surface (Fig. 8A) had only a small effect, both in the maximum drop in F_q′/F_m′ and in the size of the area affected. At higher C_a (approximately 900 μmol mol⁻¹; data not shown), the effect on F_q′/F_m′ of a patch on the upper surface alone could be almost eliminated. Note that the effect of both sides being patched (e.g. Fig. 4B) appears much more than the sum of the effect of the two sides singly; we believe this is caused by the compensation effect of the stomata opening further in the side that is not blocked, although we cannot quantify this from the gas exchange data that combines both surfaces. The limit to this effect is presumably reached at maximum stomatal aperture. In C. communis, there was almost no effect on F_q′/F_m′ of patching the upper surface only (Fig. 8C), and this was the case at a range of C_a values (data not shown). When the lower surface alone was patched, the effect was smaller than in P. vulgaris. It might be noted that the species difference in comparative patch effect between the two surfaces is contrary to the differences in stomatal frequency ratios (Table I, 5.0 compared to 3.4). However, what determines the severity of the C_i depletion when only one surface is patched is g_s of the remaining active surface, and previous measurements have shown that maximum g_s in C. communis is about twice that in P. vulgaris (Lawson et al., 1998a).

Table I.

Anatomical characteristics of P. vulgaris and C. communis leaves used for the grease patch experiments

Measurements were taken on fully expanded primary P. vulgaris leaves and from main axis C. communis leaves. Leaf thickness and porosity were measured from leaf cross sections and stomatal density from leaf epidermal impressions. Means are of four leaves; ses are shown in parentheses.

Measurement	P. vulgaris	C. communis
Leaf thickness (μm)	410 (±33)	460 (±30)
Tissue thickness (μm)a
Upper epidermis	31.6 (±1.4)	54.9 (±3.7)
Palisade	79.3 (±4.4)	70.2 (±2.2)
Spongy mesophyll	100.5 (±2.8)	88.6 (±7.9)
Lower epidermis	22.5 (±2.8)	46.6 (±1.4)
Porosity %b	36.4 (±1.4)	40.9 (±1.2)
Stomatal density (mm−2)
Upper leaf surface	21.3 (±2.2)	13.6 (±0.47)
Lower leaf surface	106.5 (±6.4)	46.8 (±2.2)
Lower/upper ratio	5.00	3.44

^aTissue thickness was measured on individual cells, so they sum to less than the leaf thickness measured on whole leaf sections.

^bPorosity was calculated as the percentage of the total leaf cross-sectional area of leaf comprising air spaces.

Figure 8.

Images of PSII efficiency (F_q′/F_m′) with 4-mm-diameter artificial grease patches applied to different leaf surfaces in P. vulgaris (A and B) and C. communis (C and D). Images approximately 8×8 mm. PSII efficiency measured from upper surface with patch on upper surface only (A and C) or lower surface only (B and D). C_a and C_i values for the unpatched leaf from gas exchange measurements were as follows: A, C_a = 268, C_i = 158; B, C_a = 243, C_i = 122; C, C_a = 315, C_i = 171; and D, C_a = 315, C_i = 171 μmol mol⁻¹. The colored bar indicates how the range of F_q′/F_m′ values is mapped to the color palette.

The resulting differences in C_i when upper or lower surfaces are patched are shown in Figure 9. The constant value across much of the patch when the lower surface was patched, even though not near the CO₂ compensation concentration, indicates the supply of CO₂ from the upper surface. For P. vulgaris, this minimum C_i value of 40 μmol mol⁻¹ can be compared directly with the value of 15 μmol mol⁻¹ observed in similar conditions when both surfaces were patched (Fig. 5A). For C. communis, the comparison is between 75 and 21 μmol mol⁻¹ (Fig. 7A). Although direct comparison of values between the species is not possible due to the different C_a used, the ratio of the minimum C_i in the patch to the C_i value in the surrounding leaf is a useful comparator: when the lower surface was patched, the ratio was substantially smaller for P. vulgaris than C. communis (0.33 and 0.44, respectively).

Figure 9.

Transects of intercellular CO₂ concentration, C_i, across 4-mm-diameter patches applied to part of a leaf of P. vulgaris (top) or C. communis (bottom). Legend indicates whether patches applied to either upper or lower leaf surface only.

A 2-D photosynthesis and diffusion model was developed to analyze lateral CO₂ movement in patched leaves (Supplemental Appendix). The steeply changing values of C_i at the margins of the patch and the minimum value across much of the patch were accurately reproduced by the model. The root mean square relative error between model and estimated C_i values along horizontal transects across the patches, as exemplified in Figures 5 and 7, was typically <30%, although at high C_a it was larger because C_i values >400 μmol mol⁻¹ cannot be reliably determined from F_q′/F_m′ due to saturation (Fig. 11A).

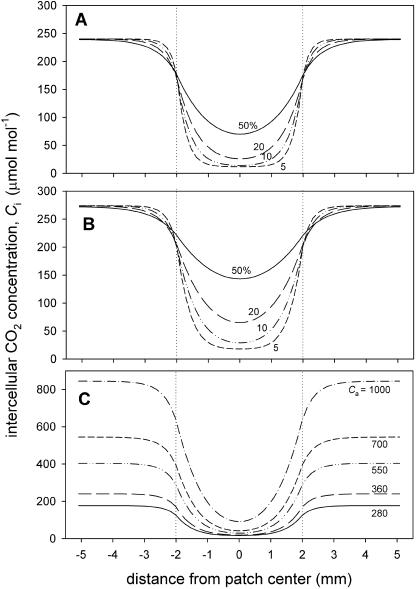
The key aspect of the model is the calculation of net photosynthetic CO₂ consumption along the diffusion path because this is a major determinant of C_i as illustrated in Figure 10, A and B. When photosynthetic capacity is high (Fig. 10A), even if diffusion was as rapid as in free air in a 50% porosity medium (i.e. a diffusion reduction factor, φ, of 50%), the model shows that a patch blocking stomata on both sides would cause pronounced depletion of C_i in the middle of the patch to 70 μmol mol⁻¹, 30% of that calculated for adjacent leaf areas. This demonstrates the importance of the sink strength in determining CO₂ gradient under the patch. More realistically, mesophyll porosity is approximately 30% to 40% (see Table I and introduction), and the path length between closely packed, cylindrical cells must be more tortuous than in free air. Assuming that the path length is increased by π/2 implies that the maximum D_c′ inside a 35% porosity leaf should be about 22% of that in free air. Even at lower A rates, φ of 20% would cause very large depletion (Fig. 10B). In our experiments, the A values at C_a = 360 μmol mol⁻¹ were similar to, or a little lower than, the higher rate case illustrated in Figure 10A. While there was some considerable variation in the values determined from the model for an individual patch image, for C. communis leaves the mean φ was 22.0% and for P. vulgaris 12.4% (means of four and five leaves, respectively, estimated at a range of four to seven C_a values for each leaf; ses of 2.7 and 1.8, means significantly different, P = 0.032, two-tailed t test). The small ses for the φ values reflect in part the variation between leaves but also suggest that the model provides a good description of diffusion in the leaf, given the widely different external CO₂ conditions examined. Using the appropriate value for D_c (Supplemental Appendix), these φ values correspond to CO₂ diffusion coefficients of 134 μmol m⁻¹ s⁻¹ for C. communis and 73 μmol m⁻¹ s⁻¹ for P. vulgaris, which reflect differences in leaf anatomy between the two species.

Figure 10.

Transects of intercellular CO₂ concentration, C_i, across a 4-mm-diameter patch (limits indicated by dotted vertical lines) calculated from the diffusion model. A and B show results for different reduction factor values, φ, for the CO₂ diffusion coefficient D_c at fixed C_a (360 μmol mol⁻¹) and either high (A) or low (B) net CO₂ assimilation capacities (as indicated by the rate outside the patch of 23.5 and 12.1 μmol m⁻² s⁻¹, respectively). Numbers indicate φ in percentages. Model parameters were as follows: A, g_s^c = 200 mmol m⁻² s⁻¹, leaf thickness = 400 μm, a = 45 μmol m⁻² s⁻¹, b = 160 μmol mol⁻¹, c = 3.0 μmol m⁻² s⁻¹; and B, g_s^c = 140 mmol m⁻² s⁻¹, a = 20 μmol m⁻² s⁻¹, b = 90 μmol mol⁻¹, c = 3.0 μmol m⁻² s⁻¹ (see “Materials and Methods”). C shows C_i values for different C_a, using parameters from the high A case in A, with φ = 15%; C_a values are indicated.

The effect of changing C_a on the modeled C_i profile across a patch is shown in Figure 10C using φ = 15%, a value between those determined here for the two species. Clearly, even at high C_a (1,000 μmol mol⁻¹), there is very large depletion in the patch, and the change in shape of the profiles is very similar to that evident in Figures 5 and 7.

DISCUSSION

The gas exchange data with sunflower (Fig. 1) demonstrates that lateral diffusion of CO₂ within a leaf is low: covering both sides of one-half of a leaf with grease caused a 50% decrease in net CO₂ uptake, which remained essentially unchanged from C_a = 100 μmol mol⁻¹ to C_a = 2,000 μmol mol⁻¹. Moreover, reducing the surface of a leaf by one-half by covering both sides with 4-mm-diameter patches of grease also caused a 50% decrease in A at C_a = 370 μmol mol⁻¹. But in this case the inhibitory effect of patches was progressively removed by increasing C_a (Fig. 1C), and extrapolation suggests that A of patched leaves would be the same as nonpatched leaves at C_a equals approximately 7,000 μmol mol⁻¹. The much larger perimeter of the greased area when small patches were used therefore allowed enhanced diffusion of CO₂ from the nonpatched to the patched area. This result recalls that of Terashima et al. (1988), who found that cutting V. faba leaf discs treated with abscisic acid into quarters restored the response of A to increased C_a, saturating at similar C_a values as found here. However, the difference is that sunflower is considered a heterobaric species while V. faba is homobaric and relatively porous (e.g. 53% porosity compared to 32% for P. vulgaris in the measurements of Pieruschka et al. [2005]). Indeed, both sunflower experiments showed that, at high C_a, large lateral CO₂ gradients well in excess of 2,000 μmol mol⁻¹ mm⁻¹ occurred between nonpatched and patched areas, suggesting high resistances to lateral diffusion.

Imaging the PSII efficiency (F_q′/F_m′) of the mesophyll when stomata were blocked with grease patches allowed us to assess lateral CO₂ diffusion in photosynthesizing leaves, over distances determined by the image pixel size of 0.15×0.15 mm. The images of the drop in F_q′/F_m′ underneath artificial patches shown in Figures 2 to 4 and 8 are striking. As there was a linear relationship between A and F_q′/F_m′ in our experimental conditions (Fig. 11B), the sharp declines in F_q′/F_m′ at the edges of patches demonstrate that there was not sufficient lateral CO₂ diffusion over distances of more than 0.3 to 0.5 mm to support substantial photosynthesis in either C. communis or P. vulgaris, agreeing with the gas exchange data for sunflower. Furthermore, we used the relationship between mean F_q′/F_m′ and mean C_i to calculate pixel values of C_i under patches. These showed that there were large lateral gradients in C_i across a patch margin (>250 μmol mol⁻¹ mm⁻¹ at normal C_a, much larger at high C_a). These lateral gradients are considerably larger than the vertical gradients across leaves of approximately 100 μmol mol⁻¹ mm⁻¹, given by Terashima (1992) and Parkhurst et al. (1988). Furthermore, while lateral diffusion was clearly more effective in the homobaric C. communis than in the heterobaric P. vulgaris, lateral fluxes were still very low. Images of grease patches applied to two other species, tobacco (Nicotiana tabacum) and sunflower (homobaric and heterobaric, respectively), showed the same severe inhibition of A (data not shown). We conclude that even if bundle sheath extensions are absent, lateral CO₂ diffusion at these spatial scales (representing between five and 25 mesophyll cells) is insufficient for appreciable photosynthesis at normal C_a. Obviously, mesophyll cell packing will affect the speed of lateral diffusion and photosynthetic rate will affect the C_i depletion. Therefore, it is likely that there would be a difference in D_c′ between palisade and spongy mesophyll tissues (Parkhurst, 1986; Terashima, 1992). The fluorescence measurements were only from the upper leaf surface and, therefore, primarily of the palisade tissue. However, as blocking stomata reduced F_q′/F_m′ in the palisade, it is clear that lateral diffusion in the leaf as a whole is slow enough to restrict photosynthesis, and the spongy tissue does not therefore act as an effective high permeability CO₂ supply route for the palisade, as has been suggested (Parkhurst, 1986).

Our results suggest that the internal air space resistance, r_ias, between substomatal cavity and mesophyll is dominated by the vertical pathway, and lateral diffusion plays little part. Indeed, both the sunflower data (Fig. 1) where there was minimal effect on A when the stomata in one surface were blocked and the image in Figure 8C for C. communis when the upper surface only was blocked demonstrate that vertical diffusion over the thickness of the leaf is clearly effective. This is obviously a result of the vertical orientation of palisade mesophyll cells and the dense spacing of stomata. Leaves are usually thin, typically 0.2 to 1.0 mm thick, and we should expect that diffusion over longer distances is a limitation, particularly laterally.

It should be noted that we used only moderate light intensity for these experiments with C. communis or P. vulgaris to have sufficient sensitivity in the response of F_q′/F_m′ to CO₂ (Fig. 11A). Although the A rates were moderate, at higher light intensity the much larger CO₂ sinks would mean an even steeper gradient of CO₂ across patch perimeters. However, in normal O₂ concentrations, photorespiration would reduce the CO₂ depletion so that the minimum values would presumably only drop as low as 50 to 100 μmol mol⁻¹, i.e. close to the normal compensation CO₂ molar fraction. A second point is that our calculated images of C_i are derived from gas exchange measurements, so the C_i value is actually the mean substomatal CO₂ concentration. It is this that we have modeled. As pointed out in several articles (e.g. Terashima et al., 2001), the CO₂ concentration within the mesophyll air spaces in photosynthesizing leaves is lower than the substomatal concentration, although the effect is likely to be least in thin, amphistomatous leaves as examined here. The F_q′/F_m′ measurements are those from the upper mesophyll cells and the stomatal conductance in these leaves is usually substantially lower on the upper surface, so in the unpatched areas of leaf we may be slightly overestimating the CO₂ concentration close to the imaged mesophyll. The overestimation depends on vertical diffusion, and the actual C_i in the intercellular air spaces is likely to be 10 to 20 μmol mol⁻¹ lower than the measured C_i (e.g. Parkhurst and Mott, 1990; Evans and Loretto, 2000; Singsaas et al., 2003).

The modeling analysis suggests that the effective lateral CO₂ diffusion coefficient inside the leaves (D_c′) is approximately 10% to 25% of that for free air. While this is in the range expected from typical values of mesophyll porosity (see introduction) and the likely increase in path-length tortuosity, there are some uncertainties in the exact D_c′ values. First, the model estimates are very sensitive to the physical patch size, which is difficult to determine exactly as it spreads out slightly during application. Second, estimates of D_c′ also depend slightly on the stomatal conductance values used, and in some cases C_i values estimated from the model for areas outside the patch overestimated those derived from gas exchange for the whole leaf area in the chamber. This is probably caused by heterogeneity in conductance across the leaf. Third, the C_i profiles are sensitive to the parameters of the A/C_i relationship but relatively insensitive to the φ value (Fig. 10, compare A and B). Nevertheless, we found higher values of φ in leaves of C. communis than in P. vulgaris (22% and 12% of that in free air, respectively), reflecting anatomical differences. These two species are usually classified as homobaric and heterobaric, respectively. However, in view of their many anatomical differences as monocot and dicot species, it is simplistic to attribute the differences in D_c′ to the presence or absence of bundle sheath extensions, especially as no species is completely homobaric because primary veins exhibit bundle sheath extensions (Weyers and Lawson, 1997). Similarly, several articles have attempted to relate diffusion resistances to various measures of the air space porosity inside leaves. Here, measurements on transverse sections did not show any significant differences in porosity between the species (Table I). In addition, it is noticeable that while the F_q′/F_m′ images in Figures 2 to 4 and 6 show the patch effect to be circular in the dicot P. vulgaris, those for C. communis are slightly elongated in the vertical direction (parallel to the leaf length and corresponding to the venation direction). This suggests that there is a difference in D_c′ depending on the direction of diffusion. Obviously D_c′ is determined by permeability and not porosity alone, which would require a full assessment of air space volume and the volume of air spaces and their connectivity from transverse, longitudinal, and paradermal sections.

There have been suggestions recently that lateral diffusion of CO₂ in leaves can be sufficient to cause errors in gas exchange measurements because of gases external to the chamber diffusing through the clamped leaf into the chamber (Jahnke and Krewitt, 2002; Pons and Welschen, 2002; Long and Bernacchi, 2003). For example, Jahnke and Krewitt (2002) found an effect of the CO₂ concentration outside the chamber on the respiration of mature tobacco leaves The chamber Jahnke and Krewitt used had an 8-mm-wide gasket, so the observed effect implies a high D_c′, which would affect many chamber systems (e.g. the LI-COR 6400 standard chamber has a gasket width of 6 mm). However, their measurements were done with high CO₂ gradients in respiring tissue. In illuminated leaves, as our results show, CO₂ assimilation by cells along the pathway depletes the CO₂ so that diffusion over more than a few tenths of a millimeter is ineffective. Indeed, the data of Pons and Welschen (2002), which showed that light saturated rates of photosynthesis in leaves of homobaric Plantago major were not affected by chamber perimeter length while respiration was, confirms this point. Therefore, the images in Figures 4 and 6 should restore confidence in gas exchange measurement of moderate photosynthetic rates with small chambers with large perimeter to area ratios. It is more likely that leakage at the leaf/gasket interface and difficulties in illumination conditions around the edge of chambers are potential problems for such chambers.

Recently, values for lateral g_ias have been determined by Pieruschka et al. (2005) using respiration measurements, and they showed marked differences between homobaric (V. faba and tobacco) and heterobaric (P. vulgaris and Glycine max) leaves. We have not used our data to estimate g_ias because of the inherent problems with the conductance model when considering diffusion in a system with sinks and sources (see introduction and Parkhurst [1994]). Instead, we prefer to characterize the diffusivity within leaves by φ (the ratio of the diffusion coefficient for CO₂ inside the leaf, D_c′, to that for free air, D_c), derived from a diffusion model. Pieruschka et al. (2005) calculated D_c′ from their measurements of g_ias and the diffusion pathway length in respiring leaves. For the two homobaric species they examined, tobacco and V. faba, D_c′ was approximately 75 and 200 μmol m⁻¹ s⁻¹, respectively. The φ value of 22% for C. communis measured here produces a comparable diffusion coefficient value of 134 μmol m⁻¹ s⁻¹. However, the φ value of 12% for the heterobaric P. vulgaris here corresponds to 73 μmol m⁻¹ s⁻¹, which is much higher than their estimate of approximately 2 μmol m⁻¹ s⁻¹. Pieruschka et al. (2005) indicate that these low diffusivities were at the limit of their measurement accuracy; in addition, their analysis approach does not allow for sinks or sources of CO₂ in the pathway.

The need to include sinks and sources has previously led to the development of several diffusion models for leaves, and Parkhurst made a major contribution (e.g. Parkhurst, 1977). Parkhurst and Mott (1990) developed Parkhurst's original 3-D model to describe the effect of gas mixtures on intercellular CO₂ diffusion. A 3-D model could be adapted for the analysis of the artificial “patch” results. However, such a model would be highly dependent on the nonlinear response of A to C_i (the source term in the model), which will vary with light penetration and between different cell types. As we do not have any experimental data on the variation of light and photosynthetic characteristics with depth in the leaves examined here, nor the detailed anatomical information required to estimate vertical variation in D_c′, we would have to make assumptions and fit the required parameters with the model. The considerable uncertainties that would result are not merited since our main objective is characterization of lateral diffusion. We used a 2-D model that averages A and C_i through the leaf thickness, which is obtained by integrating the 3-D diffusion equation over the leaf depth (see Gallouët and Herbin [2005] for details). There are, of course, some drawbacks in using the 2-D model instead of the 3-D implementation (Gallouët and Herbin, 2005), and the depth-averaged model cannot give any quantitative information on the vertical diffusion. Interestingly, the Parkhurst and Mott (1990) 3-D model simulated measured A responses well when they used an effective diffusion reduction factor, φ of 25%, similar to the 22% value that we found fit our observations for C. communis. This gives some confidence in the validity of the different modeling approaches used here and by Parkhurst. Other leaf diffusion models have been developed, but they have been for very small leaf slices with a single stoma or a few stomata, (e.g. Pachepsky and Acock, 1996), or have found that lateral diffusion is very small compared to vertical diffusion on the small lateral scales considered (e.g. Aalto and Juurola, 2002).

Finally, we have shown that application of grease at similar scales to those of natural patches (Lawson et al., 1998b) produces “patches” of A even in homobaric leaves. Indeed, Terashima et al. (1988) previously showed some patchy starch formation in the homobaric V. faba, although it was less marked than in sunflower (for review of other examples for homobaric leaves, see Terashima, 1992). We have not determined D_c′ for a species as porous as V. faba; however, the model calculations in Figure 10 show that closed stomata will substantially reduce photosynthesis even if D_c′ is as high as 50% of that for free air. Such a high D_c′ is clearly unlikely. Therefore, these natural and artificial examples of patchiness of A demonstrate that it is patchy stomatal apertures that determine if A heterogeneity occurs, not differences in lateral CO₂ diffusion, as is often inferred (e.g. Syvertsen et al., 1995; Evans and von Caemmerer, 1996). This suggests to us that the key difference between homobaric and heterobaric leaves is that in heterobaric leaves the areoles are isolated hydraulically and thus can show patchy stomatal behavior (Mott et al., 1999), whereas in homobaric leaves the stomata are not hydraulically isolated and show more gradual trends in stomatal aperture (Weyers and Lawson, 1997).

CONCLUSION

Our results confirm for lateral CO₂ diffusion the theoretical calculations and suggestions of Parkhurst (1977, 1994) that intercellular diffusion in leaves is slow and thus can limit CO₂ assimilation rate. Both gas exchange data and F_q′/F_m′ images of patched leaves lead us to conclude that, in the light, lateral CO₂ diffusion cannot support appreciable photosynthesis over distances of more than 0.2 to 0.5 mm in normal leaves. Although there are differences in the lateral diffusivity between leaves with different anatomy, if stomata are blocked or closed in actively photosynthesizing leaves, the CO₂ assimilation by cells along the diffusion pathway prevents significant lateral CO₂ transfer.

MATERIALS AND METHODS

Plant Material

Seeds of Commelina communis (originally supplied by Lancaster University), sunflower (Helianthus annuus L. cv LG53.80M; LG Seeds), and Phaseolus vulgaris L. cv Vilbel (Nickerson Seeds) were sown in a peat and loam-based compost (F2; Levington Horticulture) and grown in a heated glasshouse. Measurements were made on attached fully expanded primary leaves of P. vulgaris plants that were 3 to 4 weeks old and on the youngest fully expanded leaves of C. communis and sunflower plants that were 5 to 6 weeks old. Temperature was maintained above 20°C at night and rarely exceeded 30°C during the day. The plants were well watered throughout. Supplemental lighting (350 μmol m⁻² s⁻¹) was provided from 07 h to 19 h by sodium vapor lights.

A/C_i Measurements with One-Half of the Leaf Covered

Responses of A to internal CO₂ concentration (A/C_i curves) were measured for leaves of sunflower using a portable gas exchange system (Li-6400 [LI-COR] with standard leaf chamber and red and blue LED light source). Initially leaves were allowed to stabilize for approximately 30 min to the leaf chamber conditions, where CO₂ was maintained at 400 μmol mol⁻¹, 21% O₂, leaf temperature of 25°C, photosynthetic photon flux density (PPFD) of 1,000 μmol m⁻² s⁻¹, and water vapor pressure difference of 1.1 ± 0.2 kPa. After stabilization, an A/C_i curve was constructed by first decreasing and then increasing the chamber CO₂ concentration (C_a). Then one-half of the leaf area (both surfaces) was covered with grease (High Vacuum; BDH), either as one contiguous block from the midline of the leaf area in the chamber or in 20 4-mm-diameter patches applied to the leaf. The leaf was placed back in the chamber in an identical position and allowed to stabilize for approximately 30 min. After stabilization, a second A/C_i curve was constructed, identical to that described above.

Chlorophyll a Fluorescence Imaging with Single Patches

Images of chlorophyll a fluorescence were obtained on attached leaves, essentially as described by Barbagallo et al. (2003), using a CF Imager (Technologica), with a spatial resolution of approximately 0.15 × 0.15 mm. The orange LEDs in the imaging system (output spectra 580–700 nm, peak wavelength 648 nm) provided a PPFD of 400 μmol m⁻² s⁻¹. Steady-state fluorescence (F′) was continuously monitored, while maximum fluorescence in the actinic light (F_m′) was measured during an 800-ms exposure to a saturating pulse of 4,800 μmol m⁻² s⁻¹ Using the images captured at F′ and F_m′, images of PSII photosynthetic efficiency (F_q′/F_m′ = (F_m − F′)/F_m′) were constructed by the imaging software. Simultaneous measurements of gas exchange were taken using a 10-cm² area stirred leaf chamber [model PLC(B); PP Systems] with a low reflectance window (Edmund Optics) attached to a portable infrared gas analysis system (CIRAS1; PP Systems). Leaves were illuminated and imaged from above. Leaves were placed in the chamber and allowed to stabilize for at least 30 min to the chamber conditions, which were CO₂ molar fraction of 370 μmol mol⁻¹, water vapor pressure of approximately 1.8 kPa, and leaf temperature of 24°C to 27°C giving leaf-air vapor pressure differences in the range 0.7 to 1.4 kPa. Oxygen concentration was maintained at 1% throughout by supplying air from a cylinder of 1% oxygen in nitrogen (BOC Gases). Gas exchange measurements were recorded just before the saturating pulse was applied. On each leaf measured, a calibration curve was constructed first as described below. Then a single patch 4 mm in diameter was applied to the adaxial, abaxial, or both leaf surfaces as required using neoprene foam discs cut to the appropriate size with cork borers, mounted onto forceps, and evenly covered with silicon grease. The leaves were again allowed to stabilize to the chamber conditions, and images and gas exchange measurements were then taken at various C_a when assimilation rate was stable. As a single 4-mm-diameter patch represented only 1.3% of the area of the leaf in the chamber, we assumed that the gas exchange values accurately reflected the conditions in the unpatched area of the leaf. Using ungreased discs, we verified that the pressure applied during patching did not show any subsequent damage effects in fluorescence images, and we verified that the grease alone had no effect on dark-adapted PSII efficiency.

Treatment of Data

To determine the relationship between PSII quantum efficiency (F_q′/F_m′) and C_i, gas exchange measurements were recorded simultaneously with chlorophyll fluorescence on leaves without patches at varying external CO₂ concentration and 1% O₂ concentration. The PSII quantum efficiency was averaged across the image, and variations were typically small (see Fig. 2 for examples). The example in Figure 11A illustrates that as photorespiration was suppressed at this low O₂ concentration, both A and F_q′/F_m′ were very similarly shaped saturation functions of C_i and linearly related (inset graph). In these conditions, a double reciprocal plot between 1/C_i and 1/(F_q′/F_m′) or F_m′/F_q′ gave a close linear relationship (Fig. 11B), so that C_i could be determined from F_q′/F_m′. In all cases, the calibrations used were linear, reproducible, and r² values were >0.95. We assumed these relationships would hold constant whether a patch was present or absent. We verified that even after 10 to 15 min of exposure in some cases to low CO₂ concentration in the center of the patch combined with the low O₂ concentration, there were no changes in the A versus C_i relationship that would otherwise invalidate our C_i estimation procedure.

Using the CF imager software, parts of the F_q′/F_m′ images with the patch and some surrounding leaf areas were isolated, smoothed using a loss-less, low-pass spatial filter, and the data transferred to Matlab (version 6.0 or 7.0; MathWorks). The calibration curve was then used to compute the C_i value for each pixel. For comparison between conditions and with modeled results, average transects were calculated from three rows of pixels along the horizontal axis passing through the center of the patch image.

Modeling Lateral Diffusion

Given the even light distribution used, the spatial pattern of C_i under the patch depends on the effective lateral diffusion coefficient D_c′, the stomatal conductance to CO₂ (g_s^c) outside the patch, and the CO₂ assimilation rate, A, at different points along a distance from the boundary of the area being considered to the patch center. Since A is dependent on C_i only (at constant light and temperature) and C_i can be estimated from F_q′/F_m′ using the calibration procedure (above), A can be determined at each point. As g_s^c may be measured (assumed constant over the whole surface), the main unknown is D_c′. A 2-D mathematical model was therefore developed by R. Herbin and E. Gallouët (Supplemental Appendix) to estimate D_c′ and account for sinks and sources along the diffusion path. The 3-D diffusion equation was integrated over the depth of the leaf (the z dimension) to obtain a 2-D diffusion equation, the unknown of which is the value of C_i averaged through the depth of the leaf. To do so, we approximate integrals in z by a one-point quadrature formula (for details, see Gallouët and Herbin, 2005). The resulting 2-D model is equivalent to writing a balance equation for the diffusion fluxes in control volumes that run through the whole depth of the leaf replacing the point values of A and C_i by their mean value in the z direction (Supplemental Appendix). At the scale of the image pixels and the patches used here, we consider that treating the epidermis and stomata as simple porous boundaries, characterized by a conductance to CO₂ without details on stomatal size and distribution, is reasonable. The model used a hyperbolic function relating A to C_i (A = [(aC_i)/(b + C_i)] − c) and used the finite volume method for the discretization of the diffusion equation (Eymard et al., 2000) considering fluxes in discrete radial segments centered on the middle of the patch.

A fixed point monotonic method was used to solve the resulting set of equations and compute C_i values for each discrete segment, and these were compared with the horizontal transects through the patch of fluorescence-derived C_i values (see above). An iterative procedure was then used to estimate the diffusion coefficient reduction factor (φ) value that produced the best fit between experimental and model values of C_i. The model was to analyze the experimental results; the sole fitted parameter was φ, which was independently fitted to results at different C_a and for different leaves. Average values of φ were computed for the two species examined from the different leaves. Further details of the model derivation and its fitting using Matlab version 6 are given in the Supplemental Appendix and in Gallouët (2004) and Gallouët and Herbin (2005).

Leaf Sections

Sections taken from the middle part of the lamina were fixed overnight in gluteraldehyde (Agar Scientific) before being dehydrated by immersing them for 10 min each in a graded alcohol series (25%, 50%, 75%, 80%, 90%, and 100% ethanol). Following a second rinse in 100% ethanol, the sections were placed in 1:1 ethanol:LR White resin (London Resin) for 6 h. The sections were then placed in 100% LR White resin for several days, embedded in fresh resin in gelatin capsules, and polymerized overnight at 60°C. Thin transverse sections (10 μm) were cut using an ultramicrotome, placed on microscope slides, and stained with 0.1% aqueous solution of toluidine blue (BDH). Measurements of leaf thickness, cell length, and air space as a fraction of total area (porosity) were made using image analysis software (ImageJ; National Institutes of Health) on images of sections from four leaves from different plants taken at ×200 magnification with a digital microscope camera.

Stomatal Density

Stomatal density was determined in the midleaf lamina on four leaves of different plants for both the upper and lower epidermal surfaces. For C. communis, the lower or upper epidermis was peeled from the intact leaf and mounted onto a slide in water. Stomatal complexes in 4-×1-mm² areas were counted using a standard microscope at magnification of ×200. For P. vulgaris, silicone rubber impressions were taken of the abaxial and adaxial leaf surfaces of four leaves with dental impression material (Xantropren VL plus; Heraeus Kulzer) according to the method of Weyers and Johansen (1985). The impressions were divided into two 10- × 10-mm areas for each leaf, from which positives were made with clear nail varnish spread onto microscope slides. Stomatal numbers per area were counted in four fields of view following the systematic sampling strategy outlined by Poole and Kürschner (1999) using a microscope and eye piece graticule at ×400 magnification.