Robustness of Ancestral Sequence Reconstruction to Among-site and Among-lineage Evolutionary Heterogeneity

Abstract

Ancestral sequence reconstruction is typically performed using homogeneous evolutionary models, which assume that the same substitution propensities affect all sites and lineages. These assumptions are routinely violated: heterogeneous structural and functional constraints favor different amino acids at different sites, and these constraints often change among lineages as epistatic substitutions accrue at other sites. To evaluate how violations of the homogeneity assumption affect ancestral sequence reconstruction under realistic conditions, we developed site-specific substitution models and parameterized them using data from deep mutational scanning experiments on three protein families; we then used these models to perform ancestral sequence reconstruction on the empirical alignments and on alignments simulated under heterogeneous conditions derived from the experiments. Extensive among-site and -lineage heterogeneity is present in these datasets, but the sequences reconstructed from empirical alignments are almost identical when heterogeneous or homogeneous models are used for ancestral sequence reconstruction. Using models fit to deep mutational scanning data from distantly related proteins in which mutational effects are very different also has a minimal impact on ancestral sequence reconstruction. The rare differences occur primarily where phylogenetic signal is weak—at fast-evolving sites and nodes connected by long branches. When ancestral sequence reconstruction is performed on simulated data, errors in the reconstructed sequences become more likely as branch lengths increase, but incorporating heterogeneity into the model does not improve accuracy. These data establish that ancestral sequence reconstruction is robust to unincorporated realistic forms of evolutionary heterogeneity, because the primary determinant of ancestral sequence reconstruction is phylogenetic signal, not the substitution model. The best way to improve accuracy is therefore not to develop more elaborate models but to apply ancestral sequence reconstruction to densely sampled alignments that maximize phylogenetic signal at the nodes of interest.

Introduction

Ancestral sequence reconstruction (ASR) has become an important strategy in molecular evolution for experimentally testing hypotheses about the properties of ancient proteins and the genetic and biochemical mechanisms by which those properties evolved during history (Thornton 2004; Liberles 2007; Merkl and Sterner 2016; Hochberg and Thornton 2017; Mascotti 2022). ASR finds the most probable ancestral sequence at any node on a phylogenetic tree, given an alignment of extant proteins, a phylogeny and branch lengths, and a stochastic substitution model that describes the relative rates of sequence change among the possible amino acid or nucleotide states (Yang et al. 1995). Previous research has evaluated the robustness of inferred ancestral sequences to using different alignment methods (Vialle et al. 2018) and to uncertainty about the phylogenetic tree (Hanson-Smith et al. 2010; Groussin et al. 2015). Here we address the sensitivity of ASR to model misspecification—the inevitable mismatch between the substitution model used for ASR and the true processes of historical sequence evolution. We examine two forms of evolutionary complexity that are seldom incorporated into substitution models for ASR: differences among sites in the propensity for each amino acid state to evolve, and among-lineage differences in these propensities.

The vast majority of ancestral reconstructions have been performed using site-homogeneous models, in which all amino acid sites in the protein have the same vector of expected frequencies of the 20 amino acids and the same matrix of relative rates of substitution between them. These models are typically estimated from very large sequence databases, with fixed parameters that represent a best-fit set of frequencies and rates across all sites in a wide variety of proteins with different structures, functions, and histories (e.g. Jones et al. 1992; Whelan and Goldman 2001; Le and Gascuel 2008). The assumption of site-homogeneity embodied in these models is routinely violated (Naser-Khdour et al. 2019; Zou and Zhang 2019), because sites within a protein are subject to different structural and functional constraints (Kimura and Ohta 1974; Worth et al. 2009; Grahnen et al. 2011; Yeh et al. 2014). For example, hydrophobic amino acids are favored in the protein core but not at exposed surface sites, and amino acids have different propensities to be found in helices, sheets, and loops because they favor different protein backbone angles. As a consequence, the frequencies of amino acid states and the rates at which each state is exchanged for the others are highly heterogeneous across sites (Halpern and Bruno 1998; Ashenberg et al. 2013; Echave et al. 2016); we refer to this phenomenon as among-site compositional heterogeneity. When tree topologies are inferred using homogeneous models that do not incorporate among-site compositional heterogeneity, long-branch attraction artifacts can result (Lartillot et al. 2007; Feuda et al. 2017; Schrempf et al. 2020; Szánthó et al. 2023), and heterogeneous models that include compositional heterogeneity typically fit sequence data better and can reduce topological errors (Lartillot and Philippe 2004; Si Quang et al. 2008).

A second form of model violation is among-lineage compositional heterogeneity. Epistatic interactions may cause the effects of mutations at a site to depend on the genetic background into which they are introduced. In this case, the constraints that affect each site will change across the tree as sequences diverge at other sites (Pollock et al. 2012; Zou and Zhang 2019). Epistatic interactions are clearly widespread during protein evolution, causing the effects of particular mutations to differ among related proteins (Breen et al. 2012; Gong et al. 2013; Bank et al. 2016; Park et al. 2022). Unincorporated lineage-specific heterogeneity can cause incorrect inferences of phylogenetic relationships (Foster 2004; Jayaswal et al. 2014).

The effect of these two forms of model violation on ASR has not been thoroughly evaluated. Several studies have shown that the choice among various site-homogeneous models has very small impacts on reconstructed ancestral sequences and their accuracy (Pupko et al. 2007; Del Amparo and Arenas 2022; Sennett and Theobald 2024). These models are generally very similar to each other, however, with minor differences that are attributable to averaging over different large protein datasets. The only work to directly address unincorporated compositional heterogeneity among sites has been a series of computational studies in which sequence evolution was simulated under a simple biophysically based model of site-heterogeneous effects on protein stability; the model used for ASR had very small effects on the inferred ancestral sequences or their predicted stabilities (Arenas et al. 2015; Arenas et al. 2017; Arenas and Bastolla 2020). We are aware of no studies that evaluated the effects of lineage-specific heterogeneity on ASR. It is therefore unknown how empirical forms of among-site and among-lineage compositional heterogeneity affect the robustness and accuracy of sequences inferred by ancestral reconstruction.

Here we evaluate the effect of these forms of model violation on ASR. We incorporate realistic forms of compositional heterogeneity by using data from experimental deep mutational scanning (DMS) experiments, which directly characterize the functional effect of introducing every possible amino acid state at each site in a protein. For three example protein families, we used DMS data to parameterize site-specific (SS) heterogeneous substitution models and then used these models for ASR. To assess robustness of ASR to including/excluding compositional heterogeneity, we compared ancestral sequences reconstructed using the SS DMS model to those reconstructed using conventional site-homogeneous models. To assess the effect on ASR accuracy, we simulated sequence evolution of these protein families using the corresponding SS DMS model, and then compared the true ancestral sequences to those inferred using site-homogeneous and site-heterogeneous models. We assessed the effect of among-lineage compositional heterogeneity by evaluating accuracy and robustness of ASR using SS models that were parameterized using DMS experiments performed on distantly related proteins within the same family.

Results

Experimentally Informed Site-Specific Substitution Models

To incorporate realistic forms of among-site compositional heterogeneity into ASR, we developed a SS substitution model that can be parameterized using data from DMS experiments that measure the effect of every possible amino acid mutation at every site in a protein. Conventional site-homogeneous models specify a 20 × 20 matrix of instantaneous substitution rates by which each amino acid y replaces an amino acid x, and this matrix applies to all sites in the protein. Our SS models specify a unique rate matrix for every site in the protein. Our approach follows that of Bloom (2014a, 2014b), who developed a SS model of nucleotide substitution which was parameterized using experimental data on the fitness effect of mutations at each site. The major modifications in our approach relative to Bloom's are to accommodate amino acid alignments (rather than nucleotide or codon alignments) and to incorporate DMS measurements of function rather than direct measurements of fitness.

Like Bloom's, our model uses the formalism of Halpern and Bruno (1998), in which the rate of substitution from amino acid x to y is simply the rate of x mutating into y, multiplied by the probability of this mutation being fixed in the population (Fig. 1). Our model assumes that amino acid mutation rates are homogeneous across sites; these rates are determined by nucleotide mutation rates acting through the standard genetic code and are represented using a general time-reversible model. The probabilities of fixation are site-specific and are derived from the functional effects of each amino acid mutation measured in the DMS experiment. A simple sigmoid relationship is used to convert effects on function to fitness effects; this model represents purifying selection to maintain function, with fitness that plateaus at an upper bound as function increases, and plateaus at a lower bound of zero as function decreases (Chou et al. 2011; Bank 2022). Fitness effects determine fixation probabilities via the classic Kimura equation. Finally, we capture any unaccounted-for variation in the total rate of substitution among sites using a discrete gamma model (Yang 1994). The free parameters of the model—eight rate parameters of the nucleotide mutation model, three free parameters that determine the exact shape of the sigmoid curve, and the shape parameter of the gamma distribution—are estimated from the alignment data by maximum likelihood. This model was used for branch length optimization and ASR on a specified topology, not for identifying the topology itself.

Fig. 1.

Graphical summary of SS substitution model generation. The SS substitution model specifies the instantaneous rate of substitution of any amino acid x by any other y at each site a (blue box). Each substitution rate is the product of the rate at which mutation produces an amino acid change (pink box) and the probability that the change will be fixed (green box). The mutation rate, which is homogeneous across sites, is parameterized from the sequence alignment assuming a general time-reversible model of nucleotide mutation and the standard genetic code. The fixation probability is parameterized by transforming experimental data on the functional effects of each amino acid state at each site using a simple logistic function-to-fitness relationship.

Protein Systems Analyzed

We used our SS model to investigate the accuracy and robustness of ASR using three example protein families. These families were selected because they all have high-quality DMS datasets, well-resolved phylogenetic trees, and robust multiple sequence alignments. They differ dramatically in their biological functions, the types of phenotypes measured, the rates at which they evolve, and the timescale encompassed by their phylogenies (Fig. 2a).

Fig. 2.

Protein families selected for analysis in this work. a) Reduced phylogenetic trees of SR (left), RBD (middle), and HA (right) protein families. The proteins used for DMS experiments that yield the best fit to the alignment are blue; the proteins used for DMS with the second-best fit, which was used for analyzing among-lineage compositional heterogeneity in SRs and HAs, are green. Number of terminal branches per clade in parenthesis, see supplementary fig. S1 to S3, Supplementary Material online for detailed topologies. b) Examples of the differences in equilibrium frequencies estimated by the best-fitting site-homogeneous models (top row) versus the best-fitting SS models (middle row) and second-best fit SS model (bottom row). Only a subset of sites is shown. For SS equilibrium frequencies at all sites, see supplementary figs. S4 to S6, Supplementary Material online.

The first system is the DNA-binding domain of steroid hormone receptors (SRs), a family of transcription factors in animals (Beato et al. 1995; Mangelsdorf et al. 1995; Klinge 2018). Park et al. (2022) inferred the phylogeny of this protein family (supplementary fig. S1, Supplementary Material online)—the common ancestor of which existed >600 mya—and experimentally measured the effects of all amino acid replacements at each of the 76 sites in the DNA-binding domain on DNA-binding using a fluorescent reporter assay in yeast. DMS experiments were performed on mutant libraries of several extant and reconstructed ancestral proteins as genetic backgrounds. Here we fit SS models using the libraries constructed in two distantly related paralogs with ∼50% sequence identity—the estrogen receptor of the annelid Capitella teleta and the mineralocorticoid receptor of Homo sapiens. We refer to these fitted models as SS-ER and SS-MR, respectively.

The second system is the receptor-binding domain (RBD) of the spike glycoprotein of Sarbecoviruses, which mediates binding to the ACE2 receptor and viral entry into mammalian cells (Walls et al. 2020). Starr et al. (2020) inferred the RBD phylogeny (supplementary fig. S2, Supplementary Material online) from SARS-CoV-1, SARS-CoV-2, and related viruses and used a yeast display system to assay the binding affinities to human ACE2 of variants of SARS-CoV-2 containing all amino acid replacements at all 182 sites of the RBD. We used these data to fit the SS substitution model for this protein (SS-SARS). This phylogeny spans a few decades of viral evolution but involves substantial sequence divergence because the protein evolves rapidly.

The third system, the influenza hemagglutinin (HA) protein, binds host glycoproteins and mediates membrane fusion into endosomes (Russell 2008; Gamblin et al. 2021). Hilton inferred the phylogenetic tree from an alignment of 90 HA family members representing 15 HA subtypes (Hilton and Bloom 2018) (supplementary fig. S3, Supplementary Material online). Fitness effects of a library of all single-amino acid replacements at all 550 sites in the protein were measured using a DMS assay that quantifies variant frequency before and after viral passage. DMS libraries were engineered and assessed in two different backgrounds with sequence identity 43%—the HA subtypes H1 (Doud and Bloom 2016) and H3 (Lee et al. 2018). We used both of these datasets to fit SS models (SS-H1 and SS-H3). Like the SARS RBD, the HA phylogeny spans several decades of rapid evolution.

Reconstructed Sequences are Robust to Unincorporated Among-site Heterogeneity

To characterize the robustness of ASR to incorporating or excluding compositional heterogeneity in the substitution model, we inferred ancestral sequences at every node on all three phylogenies using the SS model and compared the sequence to that reconstructed using the best-fitting site-homogeneous model. In each case, we used the tree topology reported in the original publications (see supplementary figs. S1 to S3, Supplementary Material online). For the SR and HA datasets, there are two DMS libraries in different backgrounds in each family and therefore two SS models: our initial assessment used the model that fits the alignment best using AIC (Table 1). We also reconstructed ancestral sequences using a Poisson model, in which all amino acid exchange rates are equal, as a reference case for a model that incorporates neither compositional heterogeneity nor any bias in the substitution process among amino acids. At each site in every ancestral node on the tree, we inferred the maximum a posteriori (MAP) state. To incorporate statistical uncertainty, we also inferred the set of plausible states, defined as the union of the set of MAP states at all sites and the set of alternative plausible states (all other states with posterior probability (PP) > 0.2) (Eick et al. 2017).

Table 1.

Fit of substitution models to sequence data

System/Model	Log-likelihood	AIC	ΔAIC	No. of parameters
SR	…	…	…	…
SS-ER	−1689.7	3403.4	0	12
SS-MR	−1768.2	3560.4	157.1	12
JTTa	−1787.4	3614.8	211.4	20
Poisson	−2042.0	4086.1	682.7	1
RBD	…	…	…	…
SS-SARS	−1875.4	3774.9	0	12
WAGa	−2090.4	4220.8	446.0	20
Poisson	−2322.8	4647.6	872.7	1
HA	…	…	…	…
SS-H1	−21339.4	42702.8	0	12
SS-H3	−21516.0	43056.0	353.2	12
FLUa	−21711.4	43462.8	760.0	20
Poisson	−24825.8	49653.5	6950.7	1

All models include a Γ4 distribution.

^aIncludesML estimates of amino acid frequencies (+X).

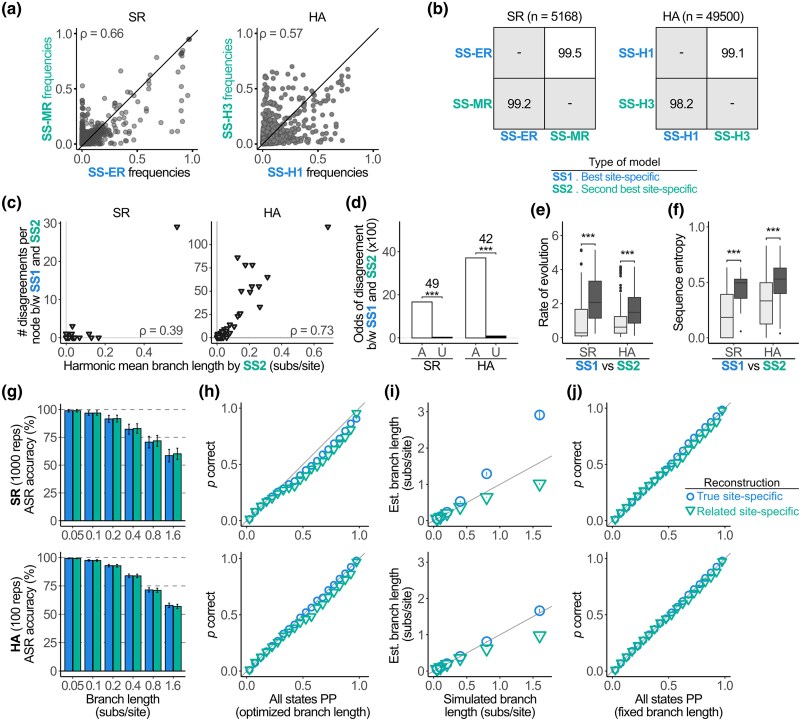
The SS models fit the data much better than the homogeneous models do, with much higher likelihoods and superior AIC scores (Table 1). Despite these differences, the inferred ancestral sequences are almost identical irrespective of the model used in all three datasets. Across all ancestors reconstructed in all three proteins, more than 98% of sites are reconstructed with the same MAP amino acid when the SS model, the site-homogeneous model, and even the Poisson model are used (Fig. 3a, lower diagonal). When statistical uncertainty is incorporated using the set of plausible states, >99% of sites have identical reconstructions across models (Fig. 3a, upper diagonal). Of the few sites that differ among reconstructions, about half are resolved by incorporating statistical uncertainty using the set of plausible states; at these sites, the difference between the models is merely to prefer one plausible but uncertain state over the other.

Fig. 3.

Robustness of ancestral sequences to unincorporated model heterogeneity. a) Percentage of states across all nodes that are identically reconstructed states between models. Below diagonal, identity between MAP states reconstructed using the model specified for the column and that specified for the row. Above diagonal, identity when ambiguity is incorporated: the fraction of sites is shown at which the MAP state using the model specified for the column is a member of the set of plausible states using the model for the row. Plausible states are defined as having PP > 0.2. n, total number of reconstructed sites in each protein system across all nodes. b) Odds that ancestral reconstructions disagree between homogeneous and SS models, defined as the number of sites with disagreements to the number of sites that agree. Odds are shown separately for sites with a maximum parsimony reconstruction that is ambiguous (A) or unambiguous (U). Odds ratios between categories are shown, defined as the odds of disagreement for parsimony-ambiguous sites divided by the odds for parsimony-unambiguous sites. ***P < 0.001 by Fisher's exact test for SR and RBD and χ² test for HA (see supplementary table S2, Supplementary Material online). c) Relationship between disagreements and branch lengths. Each point represents the reconstructed sites in the inferred sequence of one ancestral node, plotted by the number of sites with disagreements between SS and homogeneous models, and the harmonic mean of the three branch lengths that connect to the node. ρ, Spearman's correlation coefficient. d to e) The distribution of evolutionary rates (d) or sequence entropy (e) is shown for sites with identical reconstructions between SS and site-homogeneous models (light gray) and disagreeing reconstructions (dark gray). The rate for each site was estimated as the posterior mean rate given the best-fit model of gamma-distributed among-site rate variation. Sequence entropy was calculated as Shannon entropy using log-base 21 (to reflect an alphabet of 20 amino acid states plus gaps). ***P < 0.001 by a two-sample Kolmogorov–Smirnov test (see supplementary table S3, Supplementary Material online).

ASR is therefore largely robust to violation of the assumption of compositional homogeneity by using site-homogeneous models. The fact that even the Poisson model gives almost identical reconstructions suggests that ASR in these proteins is insensitive to virtually all aspects of the substitution model (except for among-site rate variation, which was included in all models tested).

Phylogenetic Signal is the Primary Determinant of ASR

Why are reconstructions nearly identical across models, even though the SS model fits the data so much better and compositional heterogeneity is rampant in the data? We reasoned that phylogenetic signal, not the substitution model, may be the primary determinant of ASR. Phylogenetic signal is defined as the retention of the states found in an ancestral node in the nodes that are connected to it (Derrickson and Ricklefs 1988; Blomberg and Garland 2002). Phylogenetic signal degrades as branches become long and sites become saturated with substitutions. When phylogenetic signal is strong, there is a single most-parsimonious state, which minimizes the number of sequence changes on branches near the node being reconstructed. In this case, evolutionary models would yield different ancestral reconstructions only if one model is so strongly biased that the occurrence of convergent substitutions along nearby branches to a particular state is more probable than retention of the ancestral state (or if the models are so differentially biased that they predict convergence to different non-parsimonious states). Unless the branches are very long, these are very unlikely scenarios. By contrast, when phylogenetic signal is absent—when all neighboring nodes have different states—then there will be several equally parsimonious ancestral states, each of which implies the same number of substitutions on neighboring branches. In that case, biases in the model and the lengths of the branches will together choose which of these states is the maximum likelihood state.

This hypothesis predicts that disagreements among models should occur primarily at sequence sites and ancestral nodes where phylogenetic signal is weak or absent. Several measures of phylogenetic signal corroborate this prediction. First, disagreements between the SS and best site-homogeneous models are highly enriched at sites where the maximum parsimony reconstruction is ambiguous (odds ratios between 40 and 400 for the three datasets, Fig. 3b, supplementary table S2, Supplementary Material online). Second, the number of disagreements between models per node on the tree increases strongly with the length of the branches connected to the node (Fig. 3c). Finally, disagreements between models about ancestral reconstructions are much more likely at sites with fast evolutionary rates and low sequence conservation: The estimated rate of evolution is an average of 3- to 16-fold faster at sites with disagreements than at sites where the models agree, and the average Shannon entropy is greater by a factor of 1.6 to 9.4 (Fig. 3d and e, supplementary table S3, Supplementary Material online).

We also observed that sites ambiguously reconstructed using ML are also overwhelmingly those that have ambiguous maximum-parsimony reconstructions (odds ratios between 65 and 760, supplementary table S4, Supplementary Material online). This observation explains why most disagreements among models occur at sites where the state preferred by one model is within the set of plausible states inferred by the other (Fig. 3a). Partially retained phylogenetic signal results in a limited set of equally parsimonious states, and the different models prefer different states within this set.

Taken together, these data indicate that phylogenetic signal, rather than the substitution model, is the primary determinant of inferred ancestral states. When phylogenetic signal is strong, the maximum likelihood reconstruction is the most parsimonious state (MP), and the model's influence on the PP distribution of ancestral states is relatively weak. Incorporating compositional heterogeneity into the model changes the ancestral state only under conditions that erase the ancestral state in most descendant lineages, such as at nodes connected to long branches and at sites that evolve rapidly.

ASR Accuracy is Unaffected by Unincorporated Among-site Heterogeneity

Although different models yield very similar reconstructions, incorporating heterogeneity might improve accuracy at the sites where models disagree. Accuracy cannot be assessed using real proteins, because the true ancestral sequences are unknown. We therefore simulated phylogenetic evolution under realistic forms of compositional heterogeneity derived from the DMS experiments. For each of our three protein model systems, we simulated evolution of proteins of the same length as the real proteins, using the estimated parameters of the best-fitting SS model (Fig. 4a, Table 1, supplementary table S1, Supplementary Material online). At each site, a state is seeded at one node from the model's equilibrium distribution; the sequence then evolves across each branch of the tree according to the SS Markov model, and the “true” state at every internal and terminal node is recorded. Accuracy of ASR was measured as the percentage of sites at which the MAP reconstructed state matches the true ancestral state (Fig. 4b). To understand how branch lengths affect ASR, we used a simple four-taxon tree with equal branch lengths ranging from 0.05 to 1.6 substitutions per site, which encompasses virtually all branch lengths on the trees for the empirical datasets (see supplementary figs. S1 to S3, Supplementary Material online).

Fig. 4.

ASR accuracy is largely robust to among-site compositional heterogeneity. a) Workflow to simulate SS evolution and assess the accuracy of ancestral reconstruction. For each replicate, an ancestral sequence was seeded from the empirical SS model and allowed to evolve across the tree under that model. The trees have equal branch lengths, and simulations were performed across a range of lengths. The resulting alignment was then analyzed by maximum likelihood given the true topology and either the SS model, the best-fitting site-homogeneous model, or the Poisson model; branch lengths and free parameters were optimized by ML, ancestral sequences were inferred and compared to the true ancestral sequences. b) Accuracy of ancestral reconstructions given the true SS model (blue), best site-homogeneous model (magenta), and Poisson (yellow) at all the simulated branch lengths. Column height shows the mean of replicates; error bars, SD. The number of replicates per system and per branch length is specified. c) Reconstruction errors outnumber disagreements between models. Each circle represents one set of branch lengths and is plotted by the mean number of erroneous reconstructions by the site-homogeneous model and the mean percentage of disagreements between the SS and best site-homogeneous reconstructions across replicates. The size of each circle represents the branch length (from 0.05 to 1.6 substitutions per site). Gray line, y = x. d) Percentage of reconstructions for which site-homogeneous and SS models assigned the same erroneous state (green), SS and site-homogeneous assigned different erroneous states (blue), and only SS (orange) or only site-homogeneous (pink) assigned an erroneous state.

For all three systems, the simulation results show that nearly identical accuracy is achieved when ASR is performed using the SS model that generated the data, the best-fit homogeneous model, or even the Poisson model (Fig. 4b, supplementary Supp. table S5, Supplementary Material online). At short branch lengths (≤0.2), all models yield highly accurate reconstructions that are nearly indistinguishable from each other. Accuracy declines as branch lengths increase irrespective of the model used, consistent with our finding that phylogenetic signal is the major determinant of inferred sequences. In two of the three proteins, the best SS model is slightly more accurate on average at longer branch lengths, but the difference is very small. Even at the longest branch length (1.6 subs/site per branch), the difference in ASR accuracy between the SS model and the best-fitting site-homogeneous model is ∼1% point (supplementary table S5, Supplementary Material online), equivalent to about 1 to 4 more errors per protein. Even Poisson reconstructions are, at worst, less accurate than ancestral sequences inferred using the true model by ∼3% points.

The models have similar accuracy because they largely infer the same sequences. The reconstructed MAP states are highly similar between models, especially at short to moderate branch lengths (Fig. 4c). There are more errors than disagreements (Fig. 4c), because most sites with an erroneous reconstruction involve both models choosing the same incorrect state (Fig. 4d). The next most common outcome—which accounts for <10% of reconstructions—is for both models to err at a site but to choose different ancestral states. The least common outcome is for one model to get the reconstruction right and the other to get it wrong, and even at these sites the two models have similar error rates.

Site-homogeneous reconstructions are therefore virtually as accurate as SS reconstructions across a wide range of phylogenetic conditions. Failure to incorporate realistic levels of among-site heterogeneity into the substitution model does not strongly affect the accuracy of the reconstructions, and it rarely affects the amino acid that is inferred.

Phylogenetic Signal Determines the Accuracy of ASR

Because phylogenetic signal is the primary determinant of the identity of ancestral sequences, we hypothesized that the major source of ASR error would be misleading phylogenetic signal—convergence or reversal that makes the MP incorrect. To test this hypothesis, we examined the frequency of ASR error in our simulations at sites where phylogenetic signal is true (i.e. the MP state matches the true ancestral state), misleading (the MP state differs from the true state), or ambiguous (without a unique MP state, Fig. 5a).

Fig. 5.

Misleading phylogenetic signal is the main cause of error in ASR. a) Scheme for classifying phylogenetic signal by the correspondence of the maximum parsimony reconstruction (MPR) to the true ancestral state at a given site. Each subtree shows an example of an ancestral node with its true state (middle circle) and three connected nodes with their true states; the MPR given the states at the connected nodes is also shown. The phylogenetic signal of a site is true if the MPR matches the true ancestral state because the state is retained in the majority of connected nodes (left); misleading if the MPR is different from the true ancestral state ancestor due to convergence/reversion (center); and ambiguous if there is no single MPR due to the lack of historical resolution (right). b) Loss of phylogenetic signal and accumulation of misleading/ambiguous phylogenetic signal as a function of branch lengths. Each data point represents a set of replicate simulations, plotted by the branch length for the simulation and the percentage of MPRs that are true (squares), misleading (circles), or ambiguous (triangles). c) Percentage of errors in reconstructed ancestral states classified by their phylogenetic signal as described in a. Data from SS and site-homogeneous models are shown in blue and magenta, respectively. d) Of reconstructions with misleading phylogenetic signal, the percentage at which the MAP state and the MPR are identical and erroneous is shown.

As predicted, the error rate in ASR depends on the phylogenetic signal. At short branch lengths, virtually all phylogenetic signal—and therefore all MP reconstructions—are true, and ASR error rates are very low (Fig. 5b and c). As branch length increases, the error rates of both methods increase. At most sites with ASR errors, the phylogenetic signal is misleading—that is, the MP reconstruction is false because of convergence and reversal—and the MAP state in these cases virtually always matches the erroneous MP reconstruction. Errors also occur sometimes when phylogenetic signal is ambiguous, especially when branches are long, but to a lesser extent than when the signal is misleading.

The SS and homogeneous models are similarly sensitive to the loss of true phylogenetic signal. The SS model is very slightly more accurate when phylogenetic signal is misleading but slightly less accurate when the signal is true (Fig. 5c and d). These models are more likely to choose a non-parsimonious state, presumably because at some sites they have stronger biases than the homogeneous models (Fig. 2b).

Taken together, these data show that ASR error is rare when branch lengths are short—so phylogenetic signal is strong and true. When branch lengths are long, the most common cause of error is convergence and reversal, not model misspecification. Neither SS nor site-homogeneous models can overcome misleading phylogenetic signal.

Model Misspecification Inflates Confidence in ASR When Phylogenetic Signal is Weak

When using ASR, we want to know not only the best estimate of the ancestral state but also the statistical support for it. The measure of confidence in reconstructed ancestral sequences is the PP, which expresses the probability that a state is correct, given the data, model, phylogeny, and prior probabilities.

To assess the effect of model violation on PPs, we binned the reconstructed states from our simulations by their inferred PP and then computed the fraction of states in each bin that match the true ancestral state (Fig. 6a). When branch lengths are short, both SS and site-homogeneous models yield PPs that closely match the probability that the inferred state is correct. As branch lengths become longer, site-homogeneous models yield PPs that overestimate the accuracy of MAP states. PPs from SS models are less inflated. Overestimation by either model is most extreme at moderate levels of confidence: states with an inferred PP = 1.0 are almost always correct, but when PP is between 0.50 and 0.95, the probability that the state is correct tends to be lower than the PP (Fig. 6b, supplementary fig. S7, Supplementary Material online).

Fig. 6.

Posterior probabilities (PP) of ancestral states are inflated because of branch length estimation errors. Comparisons of mean ASR PP versus the fraction of correct reconstructions from simulations given the true SS model (blue circles) or the best site-homogeneous model (magenta triangles) Gray line, y = x. a) PPs are most inflated when branch lengths are long, irrespective of the model used. Each shape plots the mean PP of the MAP state and the fraction of correct reconstructions for replicate simulations under one set of branch length; shape size is proportional to the branch length (from 0.05 to 1.6 substitutions/site). Error bars, SD of PP. b) For reconstructions at branch length = 0.8, all possible ancestral states were binned by PP. Each shape plots the fraction of correct states among reconstructions in a PP bin. For other branch lengths, see supplementary fig. S7, Supplementary Material online. c) Relationship of true branch lengths to the estimated branch length using each model; each shape plots the mean estimated branch length; error bars, SD. d) Same as b when branch lengths used for ASR are fixed to the true length.

PPs are conditioned on the substitution model, its parameters, the tree topology, and its branch lengths. The simulated data were generated using a SS model, so overestimation of confidence by site-homogeneous models could be caused directly by a mismatch between the model used for ASR and the true model; however, confidence was also overestimated in the SR and RBD protein families even when the true SS models were used (Fig. 6a and b). In every case, the true tree topology was used for ASR. We therefore hypothesized that inflated PPs were caused by differences between the inferred and true branch lengths. Consistent with this possibility, overconfidence is most severe when branch lengths are long, and under these conditions the branch length estimates are most inaccurate (Fig. 6c).

To directly test whether the inflation of PPs is caused indirectly by being conditioned on inaccurate estimates of branch lengths, we repeated ASR but this time fixed branch lengths to the true values that were used to generate the simulations. Under these conditions, overconfidence using site-homogeneous models is dramatically reduced, and bias using SS is virtually eliminated (Fig. 6d). Branch length misestimation is therefore the primary cause of overconfident PPs.

PPs may therefore overestimate the probability that an ancestral state is true when branch lengths are long, especially when site-homogeneous models are used. This phenomenon is an indirect result of model violation: its primary cause lies not in its effect on the ASR calculation itself but in the estimation of branch lengths by oversimplified models, on which the ASR is conditioned.

ASR is Robust to Unincorporated Among-lineage Compositional Heterogeneity

Finally, we investigated the effects on ASR of among-lineage heterogeneity in amino acid preferences. Differences in the effects of mutations at among homologous proteins in a family are caused by epistatic interactions between mutations at each site and the historical substitutions that occurred on the tree as lineages diversified (Lunzer et al. 2010; Breen et al. 2012; Kaltenbach et al. 2015). To incorporate realistic levels of among-lineage heterogeneity, we parameterized SS evolutionary models using DMS experiments that measured the effects of mutations when introduced into distantly related homologous proteins in the SR and HA family (see Fig. 2a, supplementary figs. S1 and S3, Supplementary Material online; only one DMS experiment was available for the RBD family). In both protein families, the SS equilibrium frequencies are poorly correlated between the models from the pair of homologous proteins (Fig. 7a, supplementary figs. S4 and S6, Supplementary Material online), and the preferred amino acid state differs between the two models at 29% and 64% of sites. Extensive among-lineage heterogeneity is therefore present.

Fig. 7.

Among-lineage compositional heterogeneity does not affect ASR. a) Comparison of the SS equilibrium frequencies between models fitted to experimental data from different proteins on the same phylogeny. Each point represents one amino acid state at one site in the protein, plotted by its equilibrium frequency for each of the two SS models. ρ, Spearman's correlation coefficient. b) Percentage of sites across all nodes with identically reconstructed states between models. Lower diagonal, identity between MAP states. Upper diagonal, identity when ambiguity is incorporated as in Fig. 3a. c) Relationship between length of branches connected to a node and the number of disagreements between SS models at that node. Each point represents the reconstruction at one ancestral node. ρ, Spearman's correlation coefficient. d) Odds that SS reconstructions disagree at sites where the parsimony reconstruction is ambiguous (A) or unambiguous (U). Odds ratios between categories are shown; ***P < 0.001 by Fisher's exact test for SR and χ² test for HA (See supplementary table S6, Supplementary Material online). The distribution of evolutionary rates (e) or sequence entropy (f) is shown for sites with identical reconstructions between SS models (light gray) and disagreeing reconstructions (dark gray). ***P < 0.001 by a two-sample Kolmogorov–Smirnov test (See supplementary table S7, Supplementary Material online). g) Accuracy of ancestral reconstructions given the true SS model (blue) and the SS model parameterized using the closely related protein (green). Column height shows the mean of replicates; error bars, SD. The number of repetitions per system and per branch length is shown. h) For reconstructions at branch length = 0.8, all possible ancestral states were binned by PP. Each shape plots the fraction of correct states among reconstructions in a 5% bin. i) Relationship of true branch lengths to the estimated branch length using each model; each shape plots the mean estimated branch length; error bars, SD. j) Same as panel h, but the branch lengths used for ASR are fixed to the true length.

Despite these differences, performing ASR with the paralogous models yields almost identical results. For the empirical alignments in both families, reconstructions are >98% identical between the models; this identity increases to >99% when alternative plausible reconstructions are included (Fig. 7b). In both protein families, the small number of disagreements again appears to be caused primarily by the loss of phylogenetic signal, because disagreements are strongly enriched at sites and nodes with long branches, fast rates, high entropy, and parsimony-ambiguous reconstructions (Fig. 7c to f). These results indicate that realistic forms of among-lineage heterogeneity have a very minor effect on ASR, changing the reconstruction only when phylogenetic signal is weak.

To understand how unincorporated among-lineage compositional heterogeneity affects the accuracy of ASR, we simulated sequence evolution as described in the previous sections using the SS model parameterized from the DMS experiment on one protein in the family, but we now performed ASR using the SS model parameterized from the experiment on the distantly related homolog (Fig. 2b, Table 1). Accuracy did not change when using the different model under any conditions examined (Fig. 7g).

As for the accuracy of posterior probabilities, using the SS model from a distantly related homolog yielded PPs that slightly exceed the probability that an inference is correct (Fig. 7h). This phenomenon again appears to be primarily attributable to underestimates of branch lengths, because fixing the branch lengths to their true values when performing ASR almost entirely eliminates the inflated confidence (Fig. 7i and j).

These results indicate that model misspecification caused by realistic among-lineage compositional heterogeneity in these families has a minimal effect on the robustness or accuracy of ancestral sequence reconstructions. The functional effects of mutations differ substantially among homologous proteins because of epistatic interactions with historical substitutions, but these differences have little effect on inferred ancestral states.

Discussion

Our data show that ancestral sequences inferred by ASR are largely robust to realistic forms of unincorporated among-site and among-lineage compositional heterogeneity, so long as the alignments contain reasonable phylogenetic signal. Using conventional site-homogeneous substitution models to perform ASR on real sequence alignments yields reconstructed sequences that are nearly identical to those reconstructed using SS models that incorporate compositional heterogeneity observed in functional experiments. Models parameterized using experiments from distantly related proteins also yield nearly identical ancestral sequences, indicating that incorporating among-lineage heterogeneity is also inconsequential. Simulation experiments confirm these results and show that all models have nearly identical ASR accuracy. The only exception is when branches are very long and phylogenetic signal is lost; in that case, accuracy remains virtually identical, but different models may make different errors.

We do not claim that the SS models we derived from experimental data represent the “true” evolutionary model. Rather, our purpose was to incorporate into ASR a reasonable approximation of among-site heterogeneity in functional constraints and then compare the results to ASR using models that exclude this compositional heterogeneity. These SS models dramatically improve the statistical fit to sequence alignments in all three protein families that we studied, but they barely change ancestral sequence reconstructions or their accuracy. It therefore seems unlikely that, if we precisely knew the among-site differences in selective constraints that pertained during history, incorporating them would strongly affect ASR or its accuracy.

Our findings are consistent with the limited prior work in this area. A recent study found that sequences inferred by ASR and their accuracy are very similar irrespective of the particular site-homogeneous model used (<1% percentage point difference even when sequences differ at 50% of sites) (Del Amparo and Arenas 2022). Another study developed a biophysical model to account for SS effects on protein stability (SSS); when sequences were simulated under the SSS model and ASR was then performed, accuracy was nearly identical irrespective of whether the model used for ASR was the true SSS generating model or a variety of site-homogeneous models (Arenas et al. 2017).

We found that phylogenetic signal, rather than the substitution model, is the primary determinant of ASR. When phylogenetic signal is present, the most parsimonious reconstruction is almost always assigned as the MAP state, irrespective of the model used; models yield different reconstructions only when branches are very long and/or rates are very high. These observations can be easily understood by considering how phylogenetic signal affects the probability of ancestral state reconstructions. Consider a case with strong phylogenetic signal, such that a focal ancestral node and all three neighboring nodes share the ancestral state. The likelihood of the maximum-parsimony state at the focal node is the product of the likelihoods that the state will not change along all connecting branches. With an unbiased model, the likelihood of no-change on a branch will always be greater than that of a change to a particular state, so the product of the no-change likelihoods will be much greater than the product of the likelihoods of three convergent changes. The only way for the MAP state to differ from the maximum-parsimony state is if the model's bias overcomes this difference, which is very unlikely unless the branches are very long and the bias extremely strong. By contrast, when phylogenetic signal is absent—that is, all neighboring nodes have different states—then any reconstruction requires multiple changes on the descendant branches; which one of these has the highest PP depends entirely on branch lengths and biases in the model.

Our analyses show that the primary cause of error in ASR is not model misspecification but the loss of true phylogenetic signal, especially the generation of misleading signal on long branches via convergence and reversal. When phylogenetic signal is strong, reconstructions are accurate regardless of model used; even the completely uninformative Poisson model performs almost as well as SS and site-homogeneous models. When phylogenetic signal is misleading because of convergence or reversal, reconstructions are inaccurate, again regardless of model choice. When phylogenetic signal is ambiguous, some reconstructions err stochastically; the state inferred can be sensitive to model choice, but no model is systematically more accurate than others.

Although the misspecification caused by using site-homogeneous models has little overall effect on ASR and its accuracy, the model used does changes the reconstruction at a small fraction of sites. Our data show that most of this model-related ambiguity in ancestral states can be incorporated by using the AltAll strategy for addressing statistical uncertainty in ASR (Eick et al. 2017). That is, most ambiguity caused by model misspecification overlaps with stochastic ambiguity; this is expected, because both forms of uncertainty occur when phylogenetic signal is weak (Eick et al. 2017). We therefore recommend that the AltAll strategy be used to incorporate both forms of uncertainty. This strategy should be used with caution for nodes with weak signal, because it identifies ambiguously reconstructed sites based on their PPs, which can be overestimated when oversimplified models are used (Sennett and Theobald 2024).

The goal of ASR is typically not to infer the exact ancestral sequence but to assess the protein's biochemical and functional properties. We did not experimentally characterize the sequences reconstructed using SS models, so we cannot rule out the possibility that the small number of model-dependent differences among reconstructed sequences could affect these properties. Several lines of evidence, however, suggest that disagreements between models are unlikely to strongly affect function. First, disagreements are strongly enriched at fast-evolving, high-entropy sites with weak phylogenetic signal; these patterns occur primarily at sites that are subject to weak functional constraints. Second, experiments show that AltAll reconstructions generally have the same functional properties as the MAP reconstructions (Eick et al. 2017), and we show here that these AltAll sequences incorporate most of the differences caused by using different models. Third, two experimental studies have shown that the biochemical and functional properties of reconstructed ancestral proteins are virtually identical when the reconstructions are conditioned on different models (Ugalde et al. 2004; Arenas et al. 2017).

Our data suggest that there is little to gain by developing and using SS models for the purpose of ASR. There is no need to perform laborious DMS experiments to parameterize empirical SS models. Even fitting heterogeneous models like the CAT model to sequence alignments, which is computationally costly, is unlikely to be beneficial for ASR per se, although these models may improve inference of tree topology and branch lengths (Lartillot and Philippe 2004; Si Quang et al. 2008; Schrempf et al. 2020; Szánthó et al. 2023). Our finding that among-lineage compositional heterogeneity caused by epistatic interactions has a negligible effect on ASR and its accuracy means that there is no apparent need for ASR models to explicitly incorporate epistatic interactions. Further research is warranted, however, to understand how among-lineage changes in the functional effects of mutations may affect inference of topologies, branch lengths, and ancestral sequences. Explicit epistatic models parameterized by empirical data (Di Bari et al. 2024) could advance those efforts.

The most effective way to improve the accuracy of ASR in practice is to maximize phylogenetic signal by densely sampling sequences around the nodes of interest. This strategy, which is also effective for improving phylogenetic inference per se (Hillis 1996; Hillis 1998; Zwickl and Hillis 2002), will increase the accuracy of reconstructed states, reduce ASR disagreements among models, and improve the correspondence between the calculated PP of an ancestral state and the probability that it is true. In some cases, however, it may be impossible to implement this strategy, if no extant sequences exist to break up long branches near nodes of interest. In such cases, phylogenetic signal is irreparably weak, and ASR should be approached with caution or not performed at all.

Although our findings are reassuring, ASR is by no means foolproof. Some errors in ASR are inevitable because of convergence, reversal, and stochastic error, especially when phylogenetic signal is weak. The keys to reliable ASR are to curate alignments in which extant sequences retain rich evidence of ancestral states, to critically characterize whatever uncertainty remains, and to avoid using ASR when the sequences of ancient proteins has been largely erased by the passage of time.

Materials and Methods

Experimentally Informed SS Model Fitting

The SS probabilistic model incorporating information from DMS functional experiments is based on the approach developed by Bloom (2014b, 2014a). The key differences are (i) Bloom's model used experimental measurements of fitness effects of mutations to estimate the probability that a mutation will be fixed, whereas our model uses measured effects on function and a simple function-to-fitness transformation; and (ii) Bloom's model estimated nucleotide mutation rates from nucleotide-based alignment data, whereas our model uses a general time-reversible model of nucleotide substitution and the genetic code to estimate the rate of producing amino acid changes by mutation from amino acid-based alignment data.

The model consists of a matrix, q, at each site a, which specifies for that site the instantaneous rates at which each of the twenty amino acids x is substituted to the 19 other amino acids y. Each rate $q_{a,xy}$ is the product of the rate at which an amino acid replacement is produced by mutation $({\mu }_{xy})$ times the probability that the mutation will be fixed $(f_{a,xy})$ (Halpern and Bruno 1998):

$$q_{a,xy}=k\times {\mu }_{xy}\times f_{a,xy},$$ (1)

k is a normalization factor which scales the total rate of substitution so that the length of any branch equals the expected number of substitutions per site on that branch. The mutation rates do not vary among protein sites, whereas the fixation probabilities do, thus incorporating SS differences in the functional/fitness effects of each amino acid mutation.

Mutation Rates

Each mutation rate ${\mu }_{xy}$ from amino acid x to amino acid y can be decomposed into the equilibrium frequency of amino acid y  $({\pi }_y)$ and the exchangeability from x to y  $({\rho }_{xy})$:

$${\mu }_{xy}={\rho }_{xy}\times {\pi }_y,$$ (2)

With 20 amino acids, a time-reversible version of this model would require 209 free parameters—190 for the exchangeabilities and 19 for the equilibrium frequencies. The problem can be simplified by specifying the amino acid model in terms of the four possible nucleotides and the genetic code that maps DNA states to amino acids. We adopt this approach and use the general time-reversible model of nucleotide mutation and the standard genetic code. The equilibrium frequency ${\pi }_y$ of any amino acid y is the sum of the frequencies of all the codons that code for y, denoted as codon(y):

$${\pi }_y=\sum _{\mathrm{codon}\in \mathrm{codon}(y)}{\pi }_{\mathrm{codon}},$$ (3)

The frequency of a codon, denoted $\alpha \beta \gamma$ to specify the nucleotide at each of the codon's three positions, is the product of the frequencies of the three nucleotides in the general time-reversible model:

$${\pi }_{\mathrm{codon}}={\pi }_{\alpha }{\pi }_{\beta }{\pi }_{\gamma },$$ (4)

The exchangeability ${\rho }_{xy}$ between any two amino acids x and y is calculated from the exchangeabilities for single-nucleotide changes that can cause a codon for x to become a codon for y. Consider a change from a particular codon for x that contains nucleotide a (codon x_a) to a codon for y that contains nucleotide b (codon y_b). The exchangeability for that codon change is the exchangeability of the nucleotide mutation:

$${\rho }_{\mathrm{codon}(x_{\alpha })\mathrm{codon}(y_{\beta })}={\rho }_{\alpha \beta },$$ (5)

The total exchangeability from amino acid x to amino acid y is the sum of the exchageabilities for all single-nucleotide changes from codons for x to codons for y, each weighted by the relative frequency of codon x_a among all codons for x:

$${\rho }_{xy}=\sum {\rho }_{\mathrm{codon}(x_{\alpha })\mathrm{codon}(y_{\beta })}{\displaystyle \frac{{\pi }_{\mathrm{codon}(x_{\alpha })}}{{\sum }_i{\pi }_{\mathrm{codon}{(x)}_i}},}$$ (6)

The rate of mutation between codons that require more than 1 nucleotide substitution is fixed at zero.

SS Probability of Fixation

As in Bloom's model, the probability that a mutation will be fixed is calculated from its selection coefficient, using the Kimura equation for a diploid population of size N:

$$f_{a,xy}={\displaystyle \frac{4N{s}_{a,xy}}{1-e^{-4N{s}_{a,xy}}},}$$ (7)

where s_a,xy represents the selection coefficient for the replacement of x by y (Kimura 1962; McCandlish and Stoltzfus 2014) [equation (5)]. N determines the extent to which substitutions implied on the phylogeny are attributed to fitness differences or drift.

In Bloom's model, the fitness effect of each amino acid replacement at each site was measured directly in a DMS experiment, and selection coefficients could be directly calculated from them. In our datasets, protein function was measured, so we inferred fitness effects and selection coefficients from functional measurements using a simple function-to-fitness transformation. We use a simple sigmoid representation of purifying selection, which imposes an upper-bound fitness (above which increases in function cause no further improvement in fitness) and a lower bound (below which reductions in function cause no further fitness decrement). Specifically, the growth rate $r_{a,x}$ of a genotype carrying amino acid state x at site a is related to the experimentally measured functional value $F_{a,x}$ for that genotype using the sigmoid relationship:

$$r_{a,x}(F)={\displaystyle \frac{r_{\max }}{1+e^{-m(F_{a,x}-F_{1/2})}},}$$ (8)

where r_max is the upper-bound growth rate, F_1/2 is the midpoint (the function associated with half-maximal growth), and m determines the slope of transition from lower to upper bound. These free parameters apply to all states and all sites.

These inferred growth rates allow selection coefficients to be calculated for any substitution from amino acid x to y at site a:

$$s_{a,xy}=r_{a,y}-r_{a,x},$$ (9)

Altogether, the substitution model contains the eight free parameters of the general time-reversible nucleotide mutation model, the slope and midpoint of the function-to-fitness transformation, and the selection tuning parameter N  $r_{\max }$. (When equations (6) and (7) are substituted into equation (5), the product Ns in equation (5) is formulated in terms of N  $r_{\max }$, so this product can be treated as a single parameter.) These free parameters, along with the branch lengths, are estimated from the data by maximum likelihood as part of the phylogenetic optimization process; they take on the values that maximize the probability of observing all the sequence data, given the observed functional effects of mutations, the genetic code, and the tree topology.

SS Equilibrium Frequencies

For the SS models, the steady-state equilibrium frequencies of each amino acid at every site $({\mathrm{\Phi }}_{a,y})$ serve as the priors for empirical Bayesian ancestral reconstruction (Yang et al. 1995). They can be derived from the model as follows:

$${\mathrm{\Phi }}_{a,y}={\displaystyle \frac{{\pi }_y\times e^{4N{r}_{a,y}}}{Z},}$$ (10)

Where Z is a normalization factor that ensures that the frequencies of all 20 states at a site sum to one $({\sum }_y{\mathrm{\Phi }}_{a,y}=1).$ Logo plots of SS equilibrium frequencies were generated using ggseqlogo (Wagih 2017).

We also included among-site rate heterogeneity using a four-category discretized gamma distribution (Yang 1996), which requires estimation of a single additional free parameter (the shape parameter of the gamma distribution).

This model was implemented in Python as DMSPhyloAA and is publicly available at github.com/JoeThorntonLab/site-specific-asr. DMSPhyloAA can also perform ML optimization and ancestral reconstruction using a provided site-homogeneous model. Custom scripts to implement our model were necessary because most packaged methods for ASR do not use the origin-fixation formalism.

Empirical Datasets, Model Selection, ASR, and Analysis

Alignments, phylogenetic trees, and DMS datasets were all obtained from previous publications. Sites with >50% gaps were removed from the alignments and their corresponding positions in the DMS datasets were eliminated. Missing data in the DMS datasets were considered to have no functional effect relative to the wild-type state at the corresponding site. The tree and alignment obtained from Park et al. (2022) were reduced to include sequences only from the steroid receptor family. The HA nucleotide alignment obtained from Hilton and Bloom (2018) was translated into amino acid sequences while maintaining the position of alignment gaps.

For each dataset, the best-fitting site-homogeneous model given the published topology was identified using ProtTest 3.4.2 and the corrected Akaike Information Criterion; all available models (JTT, LG, DCMut, MtREV, MtMam, MtArt, Dayhoff, WAG, RtREV, CpREV, Blosum62, VT, HIVb, HIVw, and FLU) were compared (Guindon and Gascuel 2003; Darriba et al. 2011). Equilibrium frequencies for the site-homogeneous models were estimated from the data by maximum likelihood (+X) with RAxML 8.2 (Stamatakis 2014). The four-category discretized gamma distribution was also incorporated with site-homogeneous models (Yang 1996).

All ancestral sequence reconstructions were performed using DMSPhyloAA, given the published topology, while optimizing branch lengths and free model parameters. For alignment sites containing gaps in some sequences, maximum parsimony was used to determine whether a gap or sequence state should be present or absent. If a state is inferred to be present, the particular state was reconstructed by ML; if a state is inferred to be a gap, it is reconstructed as a gap irrespective of the model used.

For the analysis of phylogenetic signal, parsimony-based ASR was performed using Mesquite 3.70 (Maddison and Maddison 2021). The reconstruction of a site at a node was classified as parsimony-ambiguous if there are multiple equally parsimonious states, and unambiguous if there is a single MP state.

The average distance of node to its immediate neighbors was calculated as the harmonic mean of the branch lengths coming off it. The harmonic mean reduces the effect of outliers, thus providing a conservative measurement of distance.

The rate of evolution per site under each site-homogeneous model was estimated using PhyML 3.0 (Guindon and Gascuel 2003; Guindon et al. 2010). The alignment Shannon entropy was calculated using the amino acid frequency per site using a logarithm base 21 (20 amino acid states + gaps).

SS Sequence Evolution Simulation, ASR, and Analyses

To simulate sequences under SS models, we implemented a script, simulate_alignment, which uses the simSeq function of the R package phangorn 2.11.1 (Schliep 2011) Using the fitted SS model parameters for each dataset, we simulated sequence evolution on four-taxa trees with equally sized branch lengths. For datasets with DMS experiments in multiple backgrounds, we used the model parameterized by the DMS experiment that yields the highest likelihood across the entire alignment/phylogeny. For each branch length condition, we simulated 1,000 alignments for SR, 500 for RBD, and 100 for HA. The number of replicate simulations per protein family was varied because DMSPhyloAA processing time depends strongly on sequence length.

ASR was then performed given each simulated alignment, using the true generating tree topology. SS reconstructions were obtained with DMSPhyloAA. For site-homogeneous reconstructions, the best-fitting site-homogeneous model for each alignment was identified using ProtTest 3.4.2, empirical frequencies were estimated using RAxML 8.2 (Stamatakis 2014), and PAML 4.9j (Yang 1997; Yang 2007) was used to estimate branch lengths and reconstruct ancestral sequences. Parsimony-based ancestral reconstructions were obtained using the ancestral.pars(type = “MPR”) function of phangorn 2.11.1 (Schliep 2011). Sites were classified as “unambiguous” if there is a single MP state or as “ambiguous” if there are multiple equally parsimonious states.

PP accuracy was evaluated by binning every possible reconstructed state at each node by their PP in 5% increments and calculating the fraction of true ancestral states in each bin. Bins with <200 elements were discarded. The effect of branch length optimization on PP estimation was assessed by fixing branch lengths to their true values during ASR on an independent set of simulations made at 0.8 substitutions/site.

Supplementary Material

Supplementary material is available at Molecular Biology and Evolution online.

Funding

This work was supported by National Institutes of Health grants R35-GM145336, R01-GM131128, and R01-GM121931 (J.W.T.), and a Samsung Graduate Fellowship (Y.P.).

Data availability

Data and code for analysis of the empirical datasets as well as summarized tables of the simulated data are available in github.com/JoeThorntonLab/site-specific-asr. Examples of ten replicates of simulated RBD evolution at 0.8 substitutions/site were included along with the scripts used to summarize data. ChatGPT-4o was used to optimize the performance and memory usage of all data analysis scripts used in this manuscript.