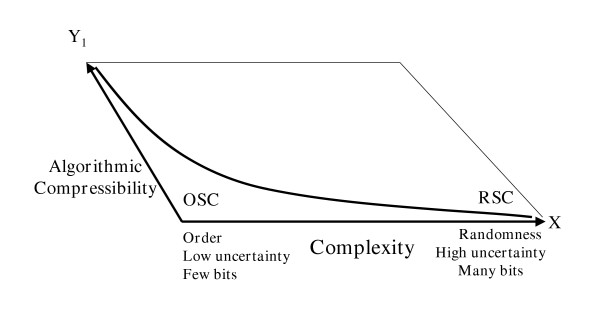
Figure 2.

The adding of a second dimension to Figure 2 allows visualization of the relationship of Kolmogorov algorithmic compressibility to complexity. The more highly ordered (patterned) a sequence, the more highly compressible that sequence becomes. The less compressible a sequence, the more complex is that sequence. A random sequence manifests no Kolmogorov compressibility. This reality serves as the very definition of a random, highly complex string.