Table 1.
Mapping Rules[Note]
| Case | Distance d | Range of t |
| 1 | 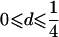 |
0⩽t<2π |
| 2 | 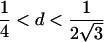 |
0<t⩽2arctan(3-1/2-a-A)2arctan(3-1/2-a+A)⩽t⩽2arctan(-3-1/2+b-B)-2arctan(3-1/2-b-B)⩽t<ππ⩽t⩽2π |
| 3 | 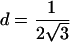 |
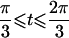 π⩽t⩽2π π⩽t⩽2π
|
| 4 | 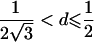 |
2arctan(3-1/2-a+A)⩽t⩽2arctan(-3-1/2+b+B)2π-2arctan(3-1/2-b+B)⩽t⩽2π-2arctan(-3-1/2+a+A) |
| 5 | 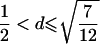 |
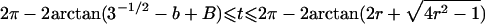 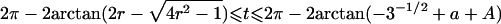
|
Note.— Valid IBD distributions are calculated in terms of polar coordinates (d,t) with origin in (f0,f1,f2)=(1/4,1/2,1/4). These rules specify, for any d, the valid angles t (in radians), so that the pair (d,t) maps back to a valid IBD sharing value. Except for the first area, which describes a whole circle, distances d correspond to the union of different circle segments. In addition, 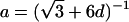 ,
, 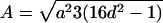 ,
, 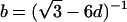 , and
, and 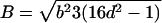 .
.
