Abstract
In this study, we propose a novel improved Dung Beetle Optimizer called Environment-aware Chaotic Force-field Dung Beetle Optimizer (ECFDBO). To address DBO’s existing tendency toward premature convergence and insufficient precision in high-dimensional, complex search spaces, ECFDBO integrates three key improvements: a chaotic perturbation-based nonlinear contraction strategy, an intelligent boundary-handling mechanism, and a dynamic attraction–repulsion force-field mutation. These improvements reinforce both the algorithm’s global exploration capability and its local exploitation accuracy. We conducted 30 independent runs of ECFDBO on the CEC2017 benchmark suite. Compared with seven classical and novel metaheuristic algorithms, ECFDBO achieved statistically significant improvements in multiple performance metrics. Moreover, by varying problem dimensionality, we demonstrated its robust global optimization capability for increasingly challenging tasks. We further conducted the Wilcoxon and Friedman tests to assess the significance of performance differences of the algorithms and to establish an overall ranking. Finally, ECFDBO was applied to a 3D path planning simulation in UAVs for safe path planning in complex environments. Against both the Dung Beetle Optimizer and a multi-strategy DBO (GODBO) algorithm, ECFDBO met the global optimality requirements for cooperative UAV planning and showed strong potential for high-dimensional global optimization applications.
Keywords: dung beetle optimizer, improvement strategies, CEC2017, path planning, cooperative UAVs
1. Introduction
Unmanned aerial vehicles (UAVs) have experienced rapid development and have been widely deployed in various domains since their inception. UAVs have been applied in such specialized areas as soil information collection and irrigation decision support in agriculture [1], deterring birds, connecting nodes in communication networks, monitoring the marine environment [2], and urban planning [3]. Three-dimensional (3D) path planning is a critical component of autonomous UAV missions, as it directly determines whether a UAV can navigate complex environments safely and efficiently to reach its destination [4]. An optimized flight path must not only avoid terrain obstacles but also minimize travel distance while adhering to the dynamic constraints of the aircraft. These requirements make path planning particularly challenging in 3D spaces with complex terrain and numerous static obstacles [5]. It is also essential to consider flight altitude, camera angle, overlap rate, and obstacle avoidance to enable comprehensive 3D observation and accurate modeling, especially in areas with varying topography or dense urban structures [6,7,8,9].
Among the classical global path planning algorithms, the grid-based search methods (e.g., A*) are capable of finding the optimal paths in static environments, but they incur large memory overhead and are sensitive to the environment scale, making them unsuitable for planning in vast 3D space [10,11,12,13,14,15,16]. The artificial potential field methods are highly respected for their simplicity and computational speed, and have been used for UAV obstacle avoidance; however, pure potential field methods do not guarantee global optimality and are prone to falling into local minima in complex terrains, leading the path to ‘deadlocks’ [17,18]. Another class of sampling-based expansion algorithms, namely Rapidly exploring Random Trees (RRT) and its improved variant RRT*, can effectively expand paths in continuous space, but RRT makes it difficult to strike a balance between path optimality and obstacle safety, thus may still produce excessively long or non-smooth paths [19]. To address these problems, researchers have proposed various improvements to RRT; for example, Guo et al. introduced a fuzzy control strategy to optimize the sampling process and developed the FC-RRT* algorithm to improve search efficiency and safety in complex 3D environments [20]. In conclusion, traditional algorithms often face such problems as high computational costs and being prone to falling into suboptimal solutions in challenging terrains and scenarios with many obstacles.
In recent years, intelligent optimization algorithms have been increasingly applied in UAV path planning owing to their strong global search capabilities [21]. Genetic algorithms (GA), which are naturally adept at multi-objective optimization, have been employed in planning UAV paths under multiple tasks or constraints. For example, Pehlivanoglu et al. devised an improved GA for UAV coverage missions [22]. Particle Swarm Optimization (PSO) algorithms [23,24] have gained widespread attention because of their fast convergence and small number of parameters. Researchers have proposed numerous variants tailored to UAV path-planning needs, including phase-angle-encoded PSO [25,26,27], quantum-behaved PSO [28], and discrete PSO [29,30]. Differential evolution (DE) algorithms excel in global search capability, and some scholars have proposed hybrid DE algorithms in combination with strategies such as grey wolf optimization to plan 3D paths in complex mountainous terrain [31]. Additionally, swarm intelligence methods like Ant Colony Optimization (ACO) [32] and Artificial Bee Colony (ABC) [33] have been applied to UAV obstacle-avoidance path planning. However, single-strategy meta-heuristics often suffer from getting trapped in local optima or lacking sufficient convergence precision. Original PSO, for instance, is prone to converge prematurely, while ACO’s communication-based modeling incurs substantial computational overhead, limiting its real-time application [34]. In addition, researchers have explored various types of plants, animals, and insects in nature and invented various meta-heuristic algorithms. Inspired by the foraging behavior of coatis, Dehghani M et al. proposed the Coati Optimization Algorithm (COA) [35]. Arora S et al. modeled the food search and mating behavior of butterflies and proposed and tested the Butterfly Optimization Algorithm (BOA) [36] based on the foraging strategy of butterflies. Zhong et al. proposed the Beluga Whale Optimization (BWO) algorithm, inspired by the collective behavior of beluga whales [37]. Duan and Qiao introduced the Pigeon-Inspired Optimization (PIO) algorithm, based on the navigational behavior of pigeon flocks. PIO has been successfully applied to flight-robot path planning [38]. Recently, the Nutcracker Optimization Algorithm (NOA) was proposed, simulating the spatial memory and random foraging behavior of nutcracker birds in their seed search, caching, and retrieval process [39]. Liu and Cai et al. proposed a hybrid multi-strategy artificial rabbit optimization (HARO) [40]; by simulating spherical and cylindrical obstacle models, they achieved efficient and stable UAV path planning in complex environments. Therefore, these advancements highlight an emerging research focus: refining algorithms to meet the specific demands of UAV path planning by striking a more effective balance between global exploration capability and local optimization precision.
In response to the above optimization requirements, Dung Beetle Optimizer (DBO) offers a novel perspective for UAV path planning. First proposed by Xue and Shen in 2022 [41], DBO draws inspiration from the behavioral patterns of dung beetles, incorporating five typical behavioral mechanisms—rolling, dancing, foraging, stealing, and reproducing. When applied to three examples of engineering optimization, DBO also achieved superior results compared to benchmark algorithms; the potential of it for practical applications is further confirmed. Owing to these advantages, DBO has attracted increasing attention in the field of path planning and is considered a promising approach for solving complex optimization tasks such as 3D UAV path planning.
Despite the strong performance of the original DBO, subsequent research has revealed certain limitations when the algorithm is applied to high-dimensional and complex search spaces. Responding to these shortcomings, scholars have proposed several enhanced variants of the Dung Beetle Optimizer. For single-UAV path planning, Shen et al. introduced the Multi-strategy Dung Beetle Optimizer (MDBO) [42]. In 2024, Tang et al. proposed RCDBO, an enhanced DBO variant for robotic path planning [43]. Another notable variant is GODBO, introduced by Wang et al. [44], which enhances exploration through opposition-based learning and multiple strategies centered on the current best solution. Results indicated clear improvements in both convergence precision and speed. Similarly, SSTDBO, proposed by Hu et al. [45], was designed to overcome the original DBO’s deficiencies in population diversity, global detection ability, and convergence precision.
For multi-UAV cooperative planning, Zhang et al. proposed the Multi-strategy Improved Dung Beetle Optimizer (MIDBO) for UAV task allocation [46]. In another study, Shen Q. et al. extended DBO to the multi-objective optimization domain by introducing the Directed Evolution Non-dominated Sorting Dung Beetle Optimizer (DENSDBO-ASR) [47]. This algorithm was applied to cooperative multi-UAV path planning and achieved excellent results in both convergence precision and solution set diversity. Collectively, these enhancements demonstrate that integrating chaos theory, evolutionary operators, and distribution-based mechanisms can substantially boost the performance of DBO, making it more suitable for high-dimensional and complex path-planning tasks.
Many researchers have proposed various DBO improvement algorithms, such as MDBO, SSTDBO, and GODBO. However, there are still some problems that need to be solved in high-dimensional, complex search spaces and in actual UAV 3D path planning tasks. For example, SSTDBO can maintain population diversity in the early stages of the search, but it easily falls into local optima due to the fast convergence of strategies, especially in scenarios with more than 50 dimensions. The premature convergence of the algorithm is especially obvious. Second, MDBO is prone to premature population convergence in high-dimensional, complex environments, making it difficult to escape local optima. Furthermore, GODBO enhances exploration capability by applying multi-strategy learning to the current optimal solution. However, it struggles to escape local optimization in multi-constraint UAVs. GODBO enhances exploration capability by applying multi-policy learning to the current optimal solution. However, it exhibits high computational overhead in multi-constraint UAV tasks, affecting the algorithm’s real-time performance and practicality.
In summary, the Dung Beetle Optimizer offers both advantages and limitations in UAV path planning. On the one hand, DBO integrates diverse biological behavior mechanisms, which makes DBO have strong global exploration and local exploitation capabilities. Particularly, strategy-enhanced variants of DBO have shown improved adaptability to complex terrain, enabling safer and more efficient path planning in large-scale 3D environments [48]. On the other hand, the original DBO is still prone to premature convergence and becoming trapped in local optima. In environments with complex obstacle distributions, this can lead to insufficient search diversity and difficulty escaping suboptimal regions [49]. Furthermore, as UAV path planning is inherently a high-dimensional optimization problem, the computational cost of DBO increases with problem scale, making it essential to balance convergence speed and algorithm efficiency in practical applications. For these challenges, we propose a novel improved DBO variant for 3D UAV path planning in environments with complex terrain and static obstacles. The algorithm integrates three core strategies: nonlinear contraction of chaotic perturbation, which significantly inhibits premature convergence; an intelligent boundary-handling mechanism that realizes an “energy wall” rebound at the obstacle boundary in a gradient-guided manner to improve the algorithm’s ability to adapt to a dynamic environment; and an attraction-repulsion force-field variability strategy that adjusts adaptively with iterations. This strategy effectively balances global search and local development, resulting in better convergence accuracy and computational efficiency for high-dimensional complex problems and multi-constraint UAV path planning. This study makes the following specific contributions:
An Environment-aware Chaotic Force–field Dung Beetle Optimizer (ECFDBO) is proposed by us, which augments the original Dung Beetle Optimizer (DBO) with three novel improvement strategies: chaotic perturbation mixed nonlinear contraction, environment-aware boundary handling, and dynamic attraction–repulsion field mutation. It ensures stable performance in high-dimensional search spaces.
ECFDBO was subjected to multi-perspective, multi-run experiments by us on the CEC2017 (Dim = 30, 50, and 100) suite to assess its robustness and effectiveness. Wilcoxon and Friedman’s tests demonstrate that ECFDBO’s performance differences among seven state-of-the-art metaheuristics are statistically significant.
We formulate the multi-UAV coordination task as a multi-constrained optimization problem with several key constraints based on the application of UAV tasks in remote sensing. Additionally, we apply the cooperative path-planning model to four distinct environments to validate its simulated effectiveness.
The rest of the paper is structured as follows. Section 2 reviews the preliminary knowledge of the original DBO algorithm. Section 3 details the three novel improvement mechanisms introduced in ECFDBO. Section 4 analyzes the computational complexity of the proposed algorithm. Section 5 presents benchmark results on the CEC2017 suite and accompanying statistical tests. Section 6 describes the UAV simulation experiments and discusses the results. Section 7 concludes the paper and outlines directions for future work.
2. Preliminary Knowledge
The DBO algorithm is derived from the survival behavior of dung beetles in their natural environment. The algorithm plays an important role in achieving global dominance by simulating the rolling of a dung ball by a beetle and the subsequent redirection of movement by implementing a dancing behavior. The beetles adopt this behavior when encountering obstacles, thus preventing falling into local traps. Female dung beetles establish a localized exploration area by hiding dung balls and laying eggs. Following this initial foraging behavior, the young dung beetles mimic the adults and thus perform a fine search in a small area. Finally, competitive behavior occurs between individuals, accelerating the approach to the optimal solution. This phenomenon is illustrated in Figure 1.
Figure 1.
Dung Beetle Optimizer.
2.1. Population Initialization
The Dung Beetle Optimizer initializes its population in a randomized manner, where each dung beetle’s position corresponds to a potential solution to the optimization problem. For the dimensional optimization problem, the position of the -th dung beetle is denoted as , and the population of dung beetles of size can be denoted as , as shown in Equation (1).
| (1) |
2.2. Rolling Stage
2.2.1. Obstacle-Free Mode
In the absence of obstacles, a rolling dung beetle simulates its natural counterpart by carrying a dung ball multiple times its size on its back and moving in a straight line in flat or slightly undulating terrain with the help of sun or moonlight. This phase focuses on “covering a wider search space with large steps.” The ball’s position is updated according to Equation (2).
| (2) |
where simulates the inertia of the dung beetle continuing in its original direction, is randomly selected to reflect small deflections in the rolling direction due to natural disturbances such as wind and terrain, , are the current worst individual locations, which encourages the dung beetle to move away from the inferior region by increasing the distance to the worst solution, and maintains the continuity of the algorithm in the current optimal neighborhood.
2.2.2. Obstacle Mode
When a dung beetle encounters an obstacle during rolling and cannot continue in its original direction, it performs a “dancing” behavior—rotating on its dung ball and pausing momentarily to recalibrate its path. The position update rule corresponding to this dancing behavior is defined in Equation (3).
| (3) |
It has been demonstrated that the magnitude of the movement in the new direction is proportional to the difference between the two positions of the dung beetle before and after. Furthermore, the value of takes on a characteristic that produces diversity from zero deflection to large steering. This helps the algorithm to jump out of the trap and avoid falling into local optimization.
2.3. Reproduction Behavior
Female dung beetles will set aside a safe spawning area for their young within a certain distance from the main path of the colony—close to the food source but avoiding detection by predators. The algorithm dynamically defines the upper and lower boundaries of the spawning area centered on the current local optimal position , as shown in Equation (4).
| (4) |
where ; , denote the lower and upper bounds of the optimization problem; as the iteration advances ( decreases gradually), the spawning area shrinks from a wide area to a narrow area, which is conducive to fine mining near the optimal solution. A single spawn location is generated per iteration, as shown in Equation (5).
| (5) |
where is the position information of the -th spawn ball at the -th iteration; and are two independent random vectors of size . Egg balls are strictly confined to spawning areas.
2.4. Foraging Behavior
Some of the dung beetles leave the spawning area to forage on the ground, representing the algorithm’s diverse and smaller step-size fine search around the high-quality area. It also dynamically defines the foraging area centered on the global optimization , as shown in Equation (6).
| (6) |
where , are the lower and upper bounds of the optimal foraging area, respectively. The position of the small dung beetle is updated by measuring normal perturbation and linear interpolation, as shown in Equation (7).
| (7) |
where is a random number following a normal distribution; is a random vector in the range .
2.5. Stealing Behavior
In high-density areas, some dung beetles attempt to “steal” dung balls from others to quickly acquire resources. In the algorithm, this behavior corresponds to a jump-based position update that drives individuals toward convergence on the global best solution. The position update rule for this stealing behavior is defined in Equation (8).
| (8) |
where is a random vector of size obeying a normal distribution and is a constant controlling the jump amplitude. Pseudo code such as the Algorithm 1.
The Pseudo-Code of DBO:
| Algorithm 1: DBO (Dung Beetle Optimizer) |
| Input: population size: N; problem dimension: d; search boundary: [lb, ub]; maximum number of iterations: Tmax; fitness function: f(x) Output: Optimal position: Xbest |
| 1: Initialize Xi ∼ Uniform(lb, ub) for i = 1…N ←Calculated using Equation (1) 2: Evaluate fi = f(Xi), set Xbest = argmin fi, Xworst = argmax fi 3: for t = 1 to Tmax do 4: p = ⌊0.2·N⌋ 5: // Rolling stage 6: for i = 1 to p do 7: if rand() < 0.9 then 8: Xi ←Calculated using Equation (2) 9: else 10: Xi ←Calculated using Equation (3) 11: end if 12: end for 13: // Reproduction stage 14: R = 1 − t/Tmax 15: [Lb*, Ub*] ←Calculated using Equation (4) 16: for i = p + 1 to p + m do 17: Xi ←Calculated using Equation (5) 18: end for 19: // Foraging stage 20: for i = p + m+1 to p + m+q do 21: Xi ←Calculated using Equation (6) 22: end for 23: // Stealing stage 24: for i = p + m+q + 1 to N do 25: Xi ←Calculated using Equation (7) 26: end for 27: // Boundary check 28: for i = 1 to N do 29: Xi = clip(Xi, lb, ub) 30: end for 31: Evaluate all fi, update Xbest, Xworst 32: end for 33: return Xbest |
3. Proposed Algorithm
According to the No Free Lunch theorem [50], different algorithms perform variably on different problems, so there is a continual need for novel optimization strategies in academic research.
3.1. Chaotic Perturbation Mixed Nonlinear Contraction Mechanisms
In the ecological behavior of dung beetles, real individuals exhibit remarkable dynamic spatial adaptability. When a population cooperates around a core resource (the dung ball), its range of activity follows a spiral contraction pattern, gradually shrinking over time. This spatial focusing strategy creates a negatively correlated feedback mechanism with an individual’s energy reserves, causing their radius of motion to decrease at a nonlinear rate, showing a preferential guarding of vested resources and conservative local search behavior.
Inspired by this, a chaotic perturbation–based nonlinear contraction mechanism is designed to enhance the foraging behavior in the algorithm. The specific update rule is provided in Equation (9).
| (9) |
| (10) |
| (11) |
is the nonlinear shrinkage factor; is the chaotic perturbation factor; is the shrinkage strength parameter; is the attenuation factor; denotes the current iteration optimal solution; is the globally optimal solution; maps random numbers to smooth bounded ranges to avoid oscillations due to large step sizes. controls the steepness of the curve, with larger values of being more sensitive to small changes. Exponential decay term : Suppresses the step size of large -values, creating a “small step size for high frequency, large step size for low frequency” search pattern.
The generates a non-monotonic and asymmetric perturbation pattern within the interval , producing differentiated disturbance intensities at positions and . Compared with other chaotic mappings, this approach has lower computational cost and does not require iterative sequence generation. The use of two independent random variables (one governing the perturbation strength and the other controlling the search direction) forms a two-dimensional probabilistic space, which adds a broader range of search patterns than would be possible with a single random number. This design has proven effective in overcoming local optima in constrained search corridors.
3.2. Environment-Aware Boundary-Handling Strategy
In the original DBO algorithm, when an individual violates the search boundary, a simple truncation or directly setting the transboundary component to a boundary value is often used to ensure feasibility. There are two main problems with this approach: information loss: directly “trimming” individuals may destroy their original directional and positional information, especially in the critical region, which may lead to some valuable search information being ignored; and too much randomness: the lack of directional guidance when resetting to the boundary may destroy convergence.
Inspired by this, we designed an environment-aware boundary-handling strategy that treats the boundary as an “energy wall” and intelligently rebounds particles along the gradient field upon collision, using a three-phase process: collision detection (identifying the transgressed dimension), gradient sensing (calculating the gradient of the objective function at the boundary), and intelligent rebounding (adjusting the position along the direction of gradient descent). Specifically, as in Equation (12):
For individual in dimension transgression:
| (12) |
The center difference method is used to avoid double counting:
| (13) |
where : rebound factor; : gradient direction in the dimension; : unit vector in the dimension; : minor perturbation.
This environment-aware boundary-handling strategy significantly enhances the performance of the optimization algorithm on constrained problems through a gradient-guided intelligent rebound mechanism. On the one hand, by maintaining the directionality of the search, particles rebound along the direction of the gradient of the objective function when they cross the boundary, thus avoiding the loss of information caused by the traditional random reset, and prompting the search process to always be directed toward the favorable region; on the other hand, through the adaptive step-size adjustment, the fine search is conducted near the boundary in order to enhance the exploitation of the boundary region, effectively avoiding the premature convergence and at the same time maintaining the diversity of the populations.
3.3. Dynamic Attraction–Repulsion Force-Field Mutation Strategy
The original DBO algorithm relies only on attraction to the global optimal solution, which leads to rapid population aggregation and loss of diversity, thereby increasing the risk of premature convergence. Moreover, all dimensions are updated synchronously, which cannot deal with nonlinear correlation between variables, and the fixed or linear decay step mechanism is difficult to adapt to the demand of multi-stage optimization.
Based on this, a dynamic attraction–repulsion force field strategy is designed: the suboptimal solution with the top 10% fitness is selected as the source of repulsion so that the algorithm is able to perform a fine local search when it is close to the global optimization, and at the same time the repulsion force is utilized to prevent premature aggregation and maintain population diversity. The repulsive force strength is enhanced with iterations as specified in Equation (14):
| (14) |
Intelligent mutation rules:
| (15) |
where is the time-varying attractive weight; is the time-varying repulsive weight; is the set of suboptimal solutions in the top of fitness; is the nonlinear step size; is the adaptive factors perturbation; this strategy is favorable in the weak-field region (): fine search with small step sizes; and in the strong-field region (): fast moving with large step sizes. In the case of the multiple-peak function: the repulsive field effectively prevents premature convergence, and in the case of the single-peak function: the attractive field accelerates the convergence rate. Pseudo code such as the Algorithm 2.
The Pseudo-Code of ECFDBO:
| Algorithm 2: ECFDBO (Environment-aware Chaotic Force-field Dung Beetle Optimizer) |
| Input: population size: N; problem dimension: d; search boundary: [lb, ub]; maximum number of iterations: Tmax; fitness function: f(x) Output: Optimal position: Xbest |
| 1: Initialize {Xi}₁ⁿ ∼ Uniform (lb, ub) 2: Evaluate fi, set Xbest 3: for t = 1…Tmax do 4: // Construct the set of suboptimal solutions Q 5: Sort {Xi} by fitness, let Q ← best K = max (3, ⌊0.1·N⌋) 6: for each i = 1…N do 7: Compute 8: Fi ← Fg − Fr← Calculated using Equation (14) 9: if rand () < pm then 10: η ←Calculated using Equation (15) 11: Xi ←Attraction–Repulsion Mutation 12: else 13: // Chaos Steps Update 14: Xi ← Calculated using Equation (9) 15: end if 16: Xi ← SmartReflect(Xi, lb, ub, ε) ← Calculated using Equation (12) 17: end for 18: {Xi}← DBO_ Stage({Xi}) // Rolling, Reproduction, Foraging, Stealing 19: Evaluate all fi, update Xbest 20: end for 21: return Xbest |
4. Complexity Analysis
The time complexity is an important index of the computational efficiency of the algorithm, assuming that the population size is , the problem dimension is , and the number of iterations is . The complexity of the original DBO algorithm is mainly influenced by the population initialization complexity () and the complexity of the iteration process (), and the time complexity of the DBO algorithm is shown in Equation (16).
| (16) |
ECFDBO adds three key strategies to the original DBO algorithm. The total complexity of its dynamic attraction–repulsion variation strategy: , where are suboptimal solutions; the complexity of the individual behavior update: ; and the complexity of the environment-aware boundary processing strategy: , where is the time complexity of a single adaptation. For each updated individual, it is necessary to check whether variables are out of bounds and correct them, but usually the proportion of out-of-bounds individuals is limited and the actual complexity is far less than the upper bound, so the time complexity can be approximated as . The ECFDBO time complexity is calculated as shown in Equation (17)
| (17) |
From the analysis, it is evident that the complexity of ECFDBO increases from linear to quadratic growth of the original algorithm, primarily due to the attraction–repulsion field. Despite the increase in time complexity, this increase is acceptable under modern computing conditions. The introduced strategy reduces the probability of the algorithm falling into a local optimization and improves the overall convergence performance so that the increased time cost in exchange for a significant improvement in performance is reasonable and worthwhile in most practical optimization scenarios.
5. CEC2017 Test
The CEC series of test suites, recommended by the IEEE CEC Conference, has become a standard evaluation platform in swarm intelligence and evolutionary algorithms, ensuring fair and reproducible comparisons among different algorithms. In order to fully evaluate ECFDBO’s performance advantages, ECFDBO algorithms, and some classical and novel meta-heuristic algorithms are compared based on the CEC2017 test suite, which has wide recognition. All experiments of this research work were performed on Windows 10 64-bit, Intel(R) Core (TM) i5-12400 processor (2.50 GHz), 16 GB RAM, and MATLAB R2023a.
5.1. CEC2017 Introduction
The CEC2017 test suite aims to provide a fair and systematic performance evaluation of the newly proposed optimization algorithms. The test suite contains 29 standardized single-objective real-parameter optimization functions (the F2 function has been officially removed due to instability), including two single-peak functions (F1–F3) to test the global convergence capability of the algorithm; seven multi-peak functions (F4–F10) to test the global exploration capability of the algorithm; ten hybrid functions (F11–F20) to evaluate the performance of the algorithm by combining different basis functions; and 10 composition functions (F21–F30) to test the robustness and adaptability of the algorithm to highly complex and nonlinear problems. Both simple convex functions are covered, and high-dimensional complex combinations are introduced to ensure the reliable performance of the algorithm in diverse search spaces. The shift and rotation transformations are applied to all basis functions, and the search domain is uniformly set to: to force the algorithm to find the optimal solution in a large range.
5.2. Comparison with Mainstream Optimization Algorithms
In order to facilitate the testing of the convergence capability, global exploitation capability, and robustness of the new improved algorithm, a total of seven comparison algorithms are compared and analyzed on the CEC2017 test component using five novel metaheuristic algorithms, namely BWO [37], COA [35], PIO [38], BOA [36], and NOA [39], as well as the original DBO [41] algorithm and a novel variant of DBO, namely GODBO [44]. Parameter settings are shown in Table 1. The test parameters are 30 populations, 500 iterations, and 30, 50, and 100 dimensions, and the results are evaluated on five performance indicators: mean, standard deviation, best, median, and worst. The optimal solution for each function is shown in bold.
Table 1.
Parameter settings.
| Algorithm | Parameter |
|---|---|
| ECFDBO | = 0.07 |
| BWO | = 0.1, = (1 − 0.5 × t/iter)× rand, = 3/2, = 0.05 |
| COA | No internal hyperparameters |
| PIO | = Maxiter − Nc1 |
| BOA | = 0.8, = 0.1, = 0.01 |
| NOA | = 0.2 |
| GODBO | = 0.2, = 1.25 |
| DBO | = 0.2 |
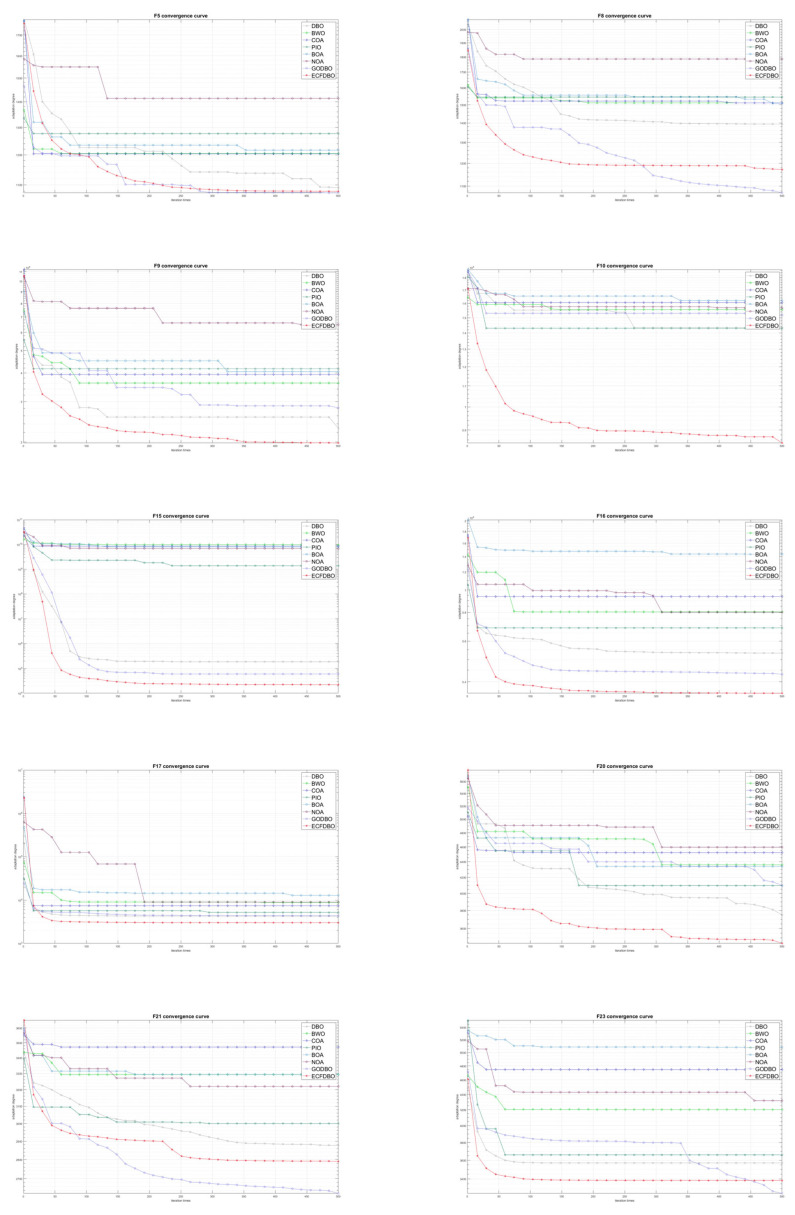
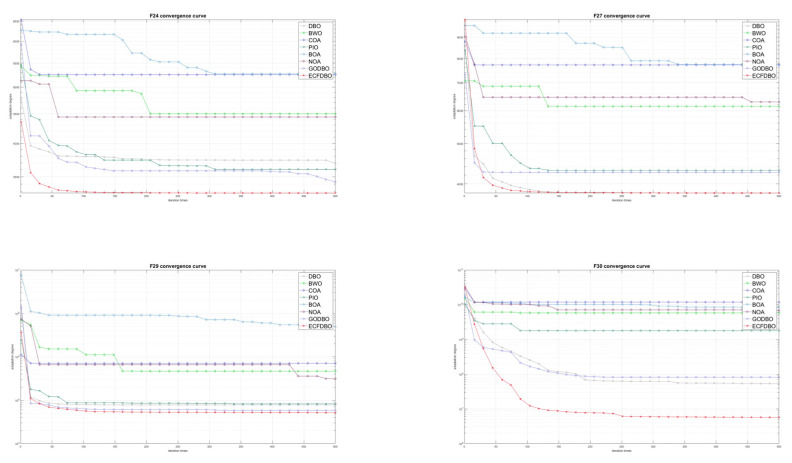
As shown in Table 2 and Figure A1, in the 30-dimensional CEC2017 benchmark, the ECFDBO algorithm achieved the best average performance on most of the test functions. Among the 29 test functions, ECFDBO achieved the best performance on 18 functions, while GODBO performed best on the remaining 11 functions. It is worth noting that, with the exception of GODBO, none of the other algorithms compared can outperform ECFDBO on any function; for example, on the typical complex benchmark function F1, the average value of ECFDBO is only 63,942.51, while the suboptimal algorithm DBO is as high as 2.64 × 108, and the rest of the algorithms are even in the order of 1010, which is an extremely wide gap, showing the significant advantage of ECFDBO in convergence precision. On simpler benchmarks such as the F5 function, although GODBO slightly outperforms ECFDBO (with means of 657.68 vs. 800.48), ECFDBO still significantly surpasses all other algorithms. In terms of standard deviation, ECFDBO achieved minimum values for 15 functions, followed by BWO with 7 functions. On the complex hybrid function F12, ECFDBO’s standard deviation is 1,863,468, which is 102 better than the second best algorithm, DBO with 1.19 × 108. On the F29 function, ECFDBO’s 271.7949 is only less than 50 different from the first place GODBO, and in the remaining optimal, median, and worst values, ECFDBO has 15, 19, and 17 optimal function values, respectively, all of which are ranked first among all algorithms. Overall, ECFDBO shows clear dominance on the 30-dimensional problem: six of the seven algorithms compared are outperformed by ECFDBO on almost all functions, and only GODBO is able to follow ECFDBO on some functions.
Table 2.
F1–F30 Benchmark Function Test Results (dim = 30).
| ECFDBO | BWO | COA | PIO | BOA | NOA | GODBO | DBO | ||
|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 63,942.51 | 5.3 × 1010 | 6.01 × 1010 | 2.39 × 1010 | 5.61 × 1010 | 6.94 × 1010 | 70,930,059 | 2.64 × 108 |
| std | 25,681.63 | 3.89 × 109 | 7.05 × 109 | 4 × 109 | 8.45 × 109 | 7.01 × 109 | 91,756,810 | 1.52 × 108 | |
| best | 26,987.47 | 4.5 × 1010 | 4.35 × 1010 | 1.71 × 1010 | 3.7 × 1010 | 5.09 × 1010 | 98,021.64 | 8,135,863 | |
| worst | 63,480.11 | 5.37 × 1010 | 6.04 × 1010 | 2.31 × 1010 | 5.63 × 1010 | 6.86 × 1010 | 49,093,779 | 2.57 × 108 | |
| median | 136,598.9 | 5.86 × 1010 | 7.33 × 1010 | 3.7 × 1010 | 7.02 × 1010 | 8.4 × 1010 | 4.57 × 108 | 5.65 × 108 | |
| F3 | mean | 9633.591 | 81,544.45 | 84,950.16 | 93,315.5 | 82,745.1 | 167,120.2 | 84,780.36 | 99,466.21 |
| std | 3718.314 | 6400.38 | 5554.423 | 11,092.81 | 7651.117 | 18,639.5 | 9399.648 | 44,057.83 | |
| best | 4364.107 | 65,363.83 | 68,694.54 | 65,001.02 | 64,619.64 | 128,257.5 | 61,888.87 | 48,642.91 | |
| worst | 9190.556 | 82,800.58 | 86,511.15 | 94,228.91 | 83,836.86 | 167,579.1 | 87,999.2 | 88,573.77 | |
| median | 20,079.23 | 89,699.18 | 92,190.43 | 140,987.2 | 94,910.4 | 201,649.3 | 98,912.04 | 276,108.9 | |
| F4 | mean | 507.3657 | 12,623.19 | 15,825.34 | 2722.201 | 20,935.8 | 18,256.86 | 580.2727 | 661.3345 |
| std | 36.80775 | 1638.889 | 2792.877 | 942.6409 | 3621.418 | 3024.038 | 78.66037 | 116.997 | |
| best | 413.7077 | 7410.967 | 7205.844 | 1384.752 | 13,918.25 | 11,069.96 | 473.5652 | 492.5788 | |
| worst | 499.465 | 12,837.3 | 16,777.87 | 2499.828 | 20,571.39 | 18,053.4 | 567.4128 | 640.5954 | |
| median | 593.5448 | 14,671.85 | 19,562.26 | 5098.445 | 26,488.42 | 23,726.71 | 842.6524 | 913.3457 | |
| F5 | mean | 800.4774 | 927.4693 | 913.1074 | 861.2371 | 912.0203 | 994.2789 | 657.6842 | 747.3314 |
| std | 66.09734 | 20.75242 | 30.04247 | 35.8504 | 26.87911 | 30.76318 | 51.81988 | 46.88862 | |
| best | 689.4502 | 866.6334 | 859.8462 | 815.4365 | 861.6815 | 891.0154 | 582.831 | 670.1164 | |
| worst | 787.3878 | 928.829 | 913.4338 | 856.991 | 912.5462 | 1002.681 | 644.9905 | 749.2904 | |
| median | 941.7984 | 959.2968 | 979.8217 | 937.9318 | 957.8257 | 1033.27 | 796.3756 | 823.7392 | |
| F6 | mean | 656.6684 | 692.5882 | 692.5231 | 664.002 | 689.7923 | 700.5578 | 632.6684 | 651.2531 |
| std | 10.41309 | 3.796584 | 6.053389 | 9.607602 | 6.46441 | 6.283517 | 7.125919 | 14.1612 | |
| best | 638.408 | 683.9351 | 680.0325 | 647.6615 | 672.0864 | 687.1371 | 620.9715 | 625.9021 | |
| worst | 656.0106 | 692.5493 | 692.5136 | 662.3847 | 690.1579 | 700.4147 | 630.7543 | 651.611 | |
| median | 682.1257 | 700.5901 | 706.2709 | 684.4867 | 698.8628 | 709.9328 | 649.3964 | 689.0801 | |
| F7 | mean | 1153.35 | 1399.737 | 1426.264 | 1480.295 | 1399.608 | 2509.026 | 956.4392 | 1033.291 |
| std | 95.01219 | 31.46096 | 56.81814 | 69.98394 | 39.21844 | 146.9285 | 59.31968 | 96.73882 | |
| best | 984.1991 | 1324.88 | 1192.911 | 1319.496 | 1303.075 | 2124.928 | 854.8254 | 861.6912 | |
| worst | 1155.905 | 1405.592 | 1431.847 | 1488.556 | 1397.56 | 2510.022 | 949.4535 | 1023.429 | |
| median | 1363.504 | 1455.351 | 1492.507 | 1591.572 | 1475.421 | 2819.798 | 1099.998 | 1237.708 | |
| F8 | mean | 1025.492 | 1150.519 | 1144.503 | 1150.445 | 1140.776 | 1240.074 | 956.0772 | 1023.584 |
| std | 55.48367 | 17.49316 | 26.30245 | 31.96821 | 22.10053 | 31.092 | 59.19539 | 53.63345 | |
| best | 932.3506 | 1115.986 | 1067.319 | 1051.653 | 1078.164 | 1152.245 | 876.1469 | 933.177 | |
| worst | 1017.925 | 1151.833 | 1147.954 | 1147.037 | 1146.534 | 1241.165 | 938.4419 | 1024.154 | |
| median | 1136.266 | 1196.125 | 1181.328 | 1205.558 | 1168.874 | 1295.581 | 1083.507 | 1126.276 | |
| F9 | mean | 9736.612 | 11,225.61 | 11,006.85 | 11,206.31 | 11,285.16 | 19,537.19 | 3953.867 | 6765.347 |
| std | 2383.204 | 1012.324 | 1454.668 | 2377.326 | 1176.202 | 2469.75 | 1464.371 | 1543.686 | |
| best | 5041.098 | 8552.426 | 8263.224 | 7715.942 | 8045.321 | 13,774.64 | 1759.752 | 4228.991 | |
| worst | 9855.975 | 11,336.28 | 11,214.13 | 10,825.41 | 11,383.51 | 19,132.04 | 3849.641 | 6651.009 | |
| median | 15,743.02 | 13,329.95 | 13,500.85 | 18,884.46 | 13,336.9 | 23,146.73 | 7918.796 | 9490.701 | |
| F10 | mean | 5713.745 | 8901.387 | 8736.062 | 8948.604 | 9224.094 | 9078.285 | 6807.646 | 6231.936 |
| std | 664.7464 | 357.743 | 476.0732 | 447.7387 | 346.0579 | 310.5175 | 1617.939 | 944.1829 | |
| best | 4282.283 | 8159.714 | 7632.897 | 7856.555 | 8399.939 | 7874.633 | 3640.744 | 4264.357 | |
| worst | 5621.71 | 8961.451 | 8780.951 | 8953.611 | 9296.556 | 9103.181 | 6538.687 | 5975.079 | |
| median | 7289.91 | 9538.599 | 9513.005 | 9625.635 | 9659.249 | 9465.218 | 9083.362 | 8844.381 | |
| F11 | mean | 1292.336 | 8200.144 | 9024.436 | 4832.391 | 9120.109 | 12,833.55 | 1401.827 | 1742.403 |
| std | 69.0754 | 1516.37 | 1678.05 | 1121.911 | 2668.268 | 2871 | 142.0839 | 575.7978 | |
| best | 1164.307 | 4821.051 | 6320.424 | 2628.512 | 5682.718 | 5379.799 | 1234.603 | 1346.82 | |
| worst | 1285.529 | 8306.735 | 8685.513 | 4614.778 | 8221.468 | 13,228.65 | 1375.095 | 1613.581 | |
| median | 1441.465 | 11,521.07 | 12,781.11 | 7008.444 | 16,082.06 | 17,555.23 | 1911.36 | 4505.651 | |
| F12 | mean | 2,519,837 | 1.16 × 1010 | 1.3 × 1010 | 2.05 × 109 | 1.33 × 1010 | 1 × 1010 | 1.05 × 108 | 75,765,766 |
| std | 1,863,468 | 2.18 × 109 | 3.2 × 109 | 6.39 × 108 | 3.25 × 109 | 2.26 × 109 | 2.56 × 108 | 1.19 × 108 | |
| best | 192,565.7 | 8.3 × 109 | 7.21 × 109 | 8.47 × 108 | 6.78 × 109 | 5.96 × 109 | 2,916,036 | 2,025,324 | |
| worst | 2,047,460 | 1.17 × 1010 | 1.28 × 1010 | 2.04 × 109 | 1.31 × 1010 | 1.01 × 1010 | 20,653,606 | 27,026,788 | |
| median | 8,109,615 | 1.6 × 1010 | 1.96 × 1010 | 4.15 × 109 | 2.14 × 1010 | 1.41 × 1010 | 1.09 × 109 | 6.04 × 108 | |
| F13 | mean | 25,844.73 | 6.55 × 109 | 8.69 × 109 | 6.77 × 108 | 1.3 × 1010 | 5.64 × 109 | 1.15 × 108 | 11,920,817 |
| std | 20,870.87 | 2.1 × 109 | 4.36 × 109 | 2.49 × 108 | 6.3 × 109 | 1.5 × 109 | 6.03 × 108 | 20,468,936 | |
| best | 3899.699 | 2.83 × 109 | 2.84 × 109 | 1.85 × 108 | 3.88 × 109 | 2.1 × 109 | 41,537.44 | 46,900.35 | |
| worst | 18,980.97 | 6.51 × 109 | 7.8 × 109 | 6.19 × 108 | 1.22 × 1010 | 5.79 × 109 | 224,277.8 | 1,574,382 | |
| median | 72,569.17 | 1.05 × 1010 | 2.02 × 1010 | 1.22 × 109 | 2.83 × 1010 | 9.46 × 109 | 3.31 × 109 | 71,958,593 | |
| F14 | mean | 32,334.97 | 4,257,854 | 3,960,435 | 815,745.2 | 4,297,723 | 3,025,255 | 283,592.4 | 209,998.4 |
| std | 26,512.96 | 2,620,007 | 3,167,737 | 583,094.9 | 4,097,839 | 1,467,041 | 382,286.9 | 185,649 | |
| best | 2309.498 | 592,077.2 | 557,713 | 90,371.21 | 144,606.2 | 667,300.7 | 10,666.78 | 10,345.24 | |
| worst | 25,730.5 | 3,906,692 | 3,948,395 | 681,304.7 | 2,568,498 | 2,860,144 | 136,500.5 | 166,456.7 | |
| median | 89,428.44 | 14,500,690 | 14,945,409 | 2,395,542 | 19,757,277 | 7,075,432 | 1,673,009 | 881,024.9 | |
| F15 | mean | 13,198.82 | 3.28 × 108 | 8.58 × 108 | 1.52 × 108 | 5.68 × 108 | 8.21 × 108 | 65,525.93 | 285,280.7 |
| std | 12,461.62 | 1.9 × 108 | 5.73 × 108 | 91,543,844 | 5.76 × 108 | 4.38 × 108 | 53,997.25 | 1,102,114 | |
| best | 1908.749 | 13,466,524 | 45,179,493 | 34,061,391 | 37,393,246 | 1.09 × 108 | 2920.75 | 7399.019 | |
| worst | 9093.7 | 3.34 × 108 | 7.62 × 108 | 1.13 × 108 | 3.63 × 108 | 8.15 × 108 | 58,370.11 | 59,707.92 | |
| median | 43,755.35 | 8.69 × 108 | 2.91 × 109 | 4.03 × 108 | 2.37 × 109 | 1.71 × 109 | 177,445.2 | 6,109,350 | |
| F16 | mean | 2879.769 | 5819.178 | 6364.759 | 4098.702 | 7467.678 | 5202.702 | 3115.283 | 3288.972 |
| std | 344.4561 | 410.5533 | 906.3894 | 348.0564 | 1430.561 | 352.1852 | 420.6608 | 435.3645 | |
| best | 2175.863 | 4673.785 | 5161.759 | 3114.32 | 4054.969 | 4353.857 | 2333.674 | 2172.459 | |
| worst | 2899.125 | 5900.782 | 6260.549 | 4115.118 | 7507.335 | 5263.261 | 3055.136 | 3317.381 | |
| median | 3567.785 | 6616.584 | 8789.34 | 4960.323 | 9887.666 | 5749.903 | 4083.444 | 4184.224 | |
| F17 | mean | 2516.491 | 4475.714 | 5249.251 | 2971.063 | 10974.59 | 3581.037 | 2582.441 | 2679.382 |
| std | 262.9417 | 763.2336 | 3076.794 | 154.6144 | 11,398.86 | 228.1887 | 289.5168 | 272.8822 | |
| best | 2054.322 | 3156.685 | 3006.496 | 2702.383 | 3899.054 | 3086.8 | 1904.785 | 2203.731 | |
| worst | 2571.811 | 4347.132 | 3900.741 | 2999.47 | 7324.974 | 3562.245 | 2597.015 | 2706.697 | |
| median | 3159.862 | 6487.527 | 17,638.14 | 3241.072 | 59,337.9 | 4019.663 | 3276.592 | 3195.838 | |
| F18 | mean | 715,402.3 | 54,249,832 | 59,452,992 | 11,870,742 | 49,325,991 | 40,892,718 | 1,948,317 | 4,033,524 |
| std | 817,243.3 | 27,073,426 | 53,818,539 | 7,421,462 | 44,586,033 | 19,512,922 | 3,992,745 | 5,215,681 | |
| best | 41,453.47 | 6,640,996 | 1,889,149 | 2,794,686 | 6,903,898 | 5,674,777 | 35,531.39 | 78,313.29 | |
| worst | 486,623.9 | 53,683,497 | 49,593,129 | 10,764,934 | 31,256,161 | 39,061,988 | 860,592.8 | 1,839,512 | |
| median | 3,439,557 | 1.12 × 108 | 2.11 × 108 | 30,407,745 | 1.86 × 108 | 1.06 × 108 | 20,309,921 | 23,672,496 | |
| F19 | mean | 21,262.95 | 4.85 × 108 | 7.77 × 108 | 2 × 108 | 6.64 × 108 | 1.17 × 109 | 4,097,332 | 5,784,654 |
| std | 18,941.24 | 2.03 × 108 | 5.22 × 108 | 96,177,925 | 4.79 × 108 | 4.63 × 108 | 11,501,863 | 18,081,030 | |
| best | 2583.758 | 92,132,654 | 59,577,484 | 40,201,933 | 89,876,191 | 2.88 × 108 | 2193.569 | 2638.476 | |
| worst | 16,050.65 | 4.87 × 108 | 7.96 × 108 | 2.14 × 108 | 6.08 × 108 | 1.22 × 109 | 116,303.4 | 404,450.8 | |
| median | 56,775.43 | 9.58 × 108 | 2.71 × 109 | 4.2 × 108 | 2.24 × 109 | 1.97 × 109 | 50,617,202 | 98,073,607 | |
| F20 | mean | 2656.364 | 3033.38 | 3094.954 | 3036.89 | 3118.8 | 3100.258 | 2697.781 | 2742.864 |
| std | 239.1146 | 130.2307 | 168.8114 | 119.101 | 92.77931 | 110.8192 | 226.7765 | 260.9707 | |
| best | 2272.189 | 2771.009 | 2554.983 | 2787.174 | 2897.134 | 2857.476 | 2300.289 | 2235.967 | |
| worst | 2647.291 | 3043.592 | 3139.187 | 3045.243 | 3119.75 | 3110.219 | 2628.047 | 2707.018 | |
| median | 3128.032 | 3296.213 | 3339.509 | 3352.285 | 3288.163 | 3338.99 | 3137.841 | 3249.261 | |
| F21 | mean | 2580.126 | 2723.701 | 2747.425 | 2615.562 | 2751.371 | 2754.239 | 2465.95 | 2561.324 |
| std | 73.88951 | 48.44362 | 45.47191 | 27.57139 | 48.36754 | 23.98249 | 45.84667 | 48.4529 | |
| best | 2447.708 | 2517.947 | 2648.155 | 2564.386 | 2623.924 | 2706.618 | 2377.878 | 2471.764 | |
| worst | 2572.032 | 2732.73 | 2752.298 | 2617.724 | 2755.723 | 2760.237 | 2468.811 | 2558.892 | |
| median | 2731.755 | 2792.62 | 2855.607 | 2663.135 | 2825.202 | 2790.236 | 2560.656 | 2655.951 | |
| F22 | mean | 6787.768 | 8871.049 | 9576.702 | 5759.646 | 7151.263 | 9518.539 | 4205.682 | 6215.286 |
| std | 1677.095 | 484.1969 | 764.6035 | 2399.439 | 1026.057 | 723.9233 | 2613.766 | 2311.638 | |
| best | 2303.192 | 7887.258 | 6769.96 | 3515.935 | 4850.228 | 7868.123 | 2311.7 | 2364.278 | |
| worst | 7116.831 | 8882.628 | 9874.276 | 4697.181 | 7126.808 | 9654.074 | 2427.148 | 7212.762 | |
| median | 8901.377 | 9708.593 | 10,688.6 | 10,792.8 | 9364.771 | 10,622.98 | 9568.586 | 9886.574 | |
| F23 | mean | 3014.155 | 3333.174 | 3651.941 | 2990.432 | 3575.073 | 3402.129 | 2915.651 | 3014.023 |
| std | 97.72177 | 50.0228 | 148.0593 | 29.88314 | 187.2047 | 60.65244 | 112.0721 | 86.11765 | |
| best | 2787.788 | 3226.259 | 3351.357 | 2935.955 | 3025.996 | 3276.915 | 2762.188 | 2864.823 | |
| worst | 2996.712 | 3337.957 | 3632.102 | 2989.931 | 3596.07 | 3403.872 | 2871.606 | 3007.588 | |
| median | 3250.481 | 3430.545 | 3998.319 | 3056.997 | 3864.495 | 3505.623 | 3139.631 | 3177.673 | |
| F24 | mean | 3161.378 | 3613.339 | 3787.649 | 3158.17 | 4161.534 | 3645.135 | 3113.082 | 3182.059 |
| std | 102.5177 | 79.48947 | 185.5656 | 42.43335 | 238.4944 | 75.61685 | 90.56529 | 75.59769 | |
| best | 2965.589 | 3496.282 | 3365.74 | 3082.772 | 3590.092 | 3434.83 | 2979.835 | 3044.666 | |
| worst | 3173.165 | 3596.364 | 3808.872 | 3159.029 | 4152.174 | 3653.606 | 3097.128 | 3162.987 | |
| median | 3327.024 | 3762.824 | 4200.671 | 3240.074 | 4590.274 | 3824.527 | 3310.4 | 3336.49 | |
| F25 | mean | 2896.548 | 4480.734 | 5323.274 | 4724.265 | 5704.686 | 8804.558 | 2923.458 | 2999.593 |
| std | 15.91772 | 199.7949 | 350.8185 | 380.5895 | 641.2731 | 863.4685 | 30.39884 | 77.06749 | |
| best | 2883.728 | 3962.203 | 4410.293 | 4017.356 | 4641.95 | 7384.903 | 2885.076 | 2894.905 | |
| worst | 2889.672 | 4477.085 | 5326.115 | 4702.903 | 5546.177 | 8584.713 | 2924.395 | 2983.4 | |
| median | 2950.292 | 4847.75 | 5965.091 | 5495.495 | 7193.241 | 10803.07 | 3023.588 | 3210.79 | |
| F26 | mean | 7455.369 | 10,646.15 | 11,735.05 | 6895.655 | 11,882.12 | 11,251.12 | 6034.232 | 7158.672 |
| std | 1340.177 | 561.0557 | 861.7151 | 959.6498 | 788.1217 | 822.3199 | 997.3035 | 785.1776 | |
| best | 2816.789 | 9133.756 | 9854.465 | 5176.728 | 10,765.61 | 9540.23 | 3676.833 | 5295.298 | |
| worst | 7586.724 | 10,689.68 | 11,804.83 | 7168.295 | 11,911.44 | 11,502.11 | 5888.133 | 7151.111 | |
| median | 9757.087 | 11,751.22 | 13,408.35 | 8646.077 | 13,352.94 | 12,632.54 | 8731.387 | 8632.776 | |
| F27 | mean | 3290.302 | 4034.996 | 4495.708 | 3404.736 | 4395.659 | 4132.721 | 3349.182 | 3347.978 |
| std | 45.08133 | 151.9417 | 395.5547 | 55.45793 | 363.7561 | 122.9201 | 79.86542 | 70.67476 | |
| best | 3213.545 | 3652.449 | 3830.985 | 3293.771 | 3752.556 | 3903.359 | 3261.087 | 3249.935 | |
| worst | 3272.556 | 4059.076 | 4402.444 | 3403.038 | 4458.546 | 4138.376 | 3323.077 | 3336.538 | |
| median | 3392.306 | 4294.696 | 5635.099 | 3520.293 | 5352.941 | 4402.514 | 3634.885 | 3534.849 | |
| F28 | mean | 3252.387 | 6458.329 | 7659.126 | 4566.759 | 8163.217 | 7789.137 | 3352.866 | 3604.37 |
| std | 42.03031 | 325.0748 | 701.5746 | 459.2043 | 500.8554 | 776.3482 | 75.75684 | 687.9095 | |
| best | 3200.329 | 5574.211 | 6126.061 | 4073.511 | 7047.834 | 6335.197 | 3265.205 | 3299.473 | |
| worst | 3250.148 | 6521.058 | 7650.086 | 4413.026 | 8244.752 | 7842.011 | 3324.336 | 3392.65 | |
| median | 3373.517 | 7105.451 | 8955.831 | 5831.231 | 9021.743 | 9020.772 | 3558.877 | 6272.067 | |
| F29 | mean | 4429.617 | 6895.76 | 8345.137 | 5101.263 | 13,156.87 | 6395.72 | 4214.615 | 4549.805 |
| std | 271.7949 | 711.9064 | 1580.409 | 304.2742 | 6171.057 | 428.0731 | 229.5287 | 392.7875 | |
| best | 3947.653 | 5733.582 | 5557.795 | 4427.106 | 6837.421 | 5507.769 | 3817.121 | 3800.398 | |
| worst | 4455.078 | 6874.303 | 8501.48 | 5147.45 | 11,409.63 | 6436.563 | 4261.45 | 4548.292 | |
| median | 4972.681 | 8645.288 | 12397.94 | 5690.939 | 34917.82 | 7228.335 | 4635.857 | 5311.23 | |
| F30 | mean | 48,500.77 | 1.16 × 109 | 1.78 × 109 | 1.23 × 108 | 1.22 × 109 | 6.8 × 108 | 1,780,797 | 7,762,810 |
| std | 41,110.94 | 3.57 × 108 | 1.19 × 109 | 50,993,436 | 5.91 × 108 | 2.22 × 108 | 2,843,252 | 22,587,572 | |
| best | 6351.341 | 5.08 × 108 | 1.04 × 108 | 35,740,734 | 3.27 × 108 | 2.09 × 108 | 30,084.02 | 13,525.09 | |
| worst | 31,118.47 | 1.15 × 109 | 1.35 × 109 | 1.15 × 108 | 1.1 × 109 | 6.98 × 108 | 570,931.4 | 1,081,845 | |
| median | 151,815.9 | 1.96 × 109 | 5.45 × 109 | 2.4 × 108 | 2.48 × 109 | 1.1 × 109 | 10,298,184 | 1.23 × 108 |
As shown in Table 3 and Figure A2, the overall dominance of ECFDBO is further extended in the 50-dimensional benchmark test. The result statistics for the 29 tested functions show that ECFDBO achieves the best average performance value on 19 functions, while the remaining 10 functions are still dominated by GODBO. None of the other algorithms outperform ECFDBO on any function, reflecting the fact that ECFDBO remains a solid leader in higher dimensions. For example, on the F9 function, ECFDBO has a mean of 2.63 × 104, while the second-best GODBO is about 1.87 × 104 higher, and the remaining algorithms’ values are generally more than an order of magnitude higher. This indicates that as the dimensionality increases, some algorithms such as BWO and COA show deterioration in performance, with their average errors and rankings significantly lagging behind those of ECFDBO; in contrast, ECFDBO and GODBO are still able to maintain good adaptation to complex functions. In terms of standard deviation, ECFDBO achieves the lowest fluctuation on 14 functions, and the second-best BWO is the most stable on 5 functions; in the complex single-peak function F1, the standard deviation of ECFDBO is about 2.36 × 106, while the value of GODBO is more than 7.03 × 108, with a magnitude difference of more than 102. In the rest of the best, median, and worst values, ECFDBO also achieves the first place with 18, 17, and 18, while GODBO is in the second place with 10, 9, and 10. In the high-dimensional environment of 50 dimensions, the ECFDBO algorithm still shows the overall leading performance advantage. Its average convergence precision continues to be the best and is slightly better than the performance in 30 dimensions. In the extreme cases of optimal/worst, ECFDBO wins with the majority function, showing good robustness.
Table 3.
F1–F30 Benchmark Function Test Results (dim = 50).
| ECFDBO | BWO | COA | PIO | BOA | NOA | GODBO | DBO | ||
|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 4,780,258 | 1.06 × 1011 | 1.09 × 1011 | 9.65 × 1010 | 1.09 × 1011 | 1.71 × 1011 | 1.18 × 109 | 9.19 × 109 |
| std | 2,359,295 | 5.01 × 109 | 9.86 × 109 | 1.39 × 1010 | 7.88 × 109 | 1.07 × 1010 | 7.03 × 108 | 1.69 × 1010 | |
| best | 1,512,934 | 9.37 × 1010 | 8.91 × 1010 | 6.82 × 1010 | 9.01 × 1010 | 1.5 × 1011 | 4.25 × 108 | 4.64 × 108 | |
| worst | 3,928,363 | 1.06 × 1011 | 1.1 × 1011 | 9.83 × 1010 | 1.1 × 1011 | 1.73 × 1011 | 1 × 109 | 3.77 × 109 | |
| median | 10,522,602 | 1.15 × 1011 | 1.25 × 1011 | 1.22 × 1011 | 1.22 × 1011 | 1.94 × 1011 | 3.35 × 109 | 7.07 × 1010 | |
| F3 | mean | 87,516.16 | 249,766.4 | 197,257.9 | 264,701.7 | 316,388.5 | 329,198.4 | 322,936.4 | 248,865.5 |
| std | 32,122.38 | 36,977.68 | 21,021.17 | 29,715.68 | 149,694.8 | 33,740.95 | 58,986.33 | 54,829.01 | |
| best | 36,759.7 | 189,932.7 | 162,315.7 | 179,046.2 | 170,203 | 248,425.4 | 193,637.4 | 145,758.5 | |
| worst | 73,523.75 | 251,556.4 | 195,704.8 | 266,654.4 | 272,373.2 | 331,103.4 | 314,708 | 247,962.2 | |
| median | 162,429.7 | 351,854.8 | 238,114.7 | 311,972.1 | 865,964.3 | 382,355.9 | 513,354.7 | 393,175.2 | |
| F4 | mean | 609.8426 | 34,119.13 | 39,293.57 | 15,732.3 | 41,410.92 | 51,193.12 | 912.5862 | 1194.075 |
| std | 60.86762 | 3216.901 | 5100.663 | 5187.062 | 3473.452 | 8197.951 | 159.1647 | 299.3094 | |
| best | 489.1183 | 22,722.15 | 30,096.17 | 7784.69 | 31,673.1 | 37,072.26 | 654.7685 | 663.9026 | |
| worst | 617.0304 | 34,459.92 | 39,746.09 | 14,700.99 | 40,911.51 | 53,136.07 | 878.393 | 1115.647 | |
| median | 800.1924 | 39,085.95 | 48,427.4 | 31,976.03 | 49,882.52 | 63,973.42 | 1351.225 | 1895.822 | |
| F5 | mean | 1023.086 | 1196.792 | 1194.138 | 1243.679 | 1176.389 | 1447.111 | 831.1338 | 995.0373 |
| std | 111.8223 | 18.2011 | 32.05341 | 28.3418 | 26.20114 | 33.46087 | 81.35437 | 99.21457 | |
| best | 837.5148 | 1151.511 | 1134.758 | 1167.687 | 1104.998 | 1368.81 | 700.8344 | 821.8647 | |
| worst | 1044.548 | 1198.489 | 1197.412 | 1241.588 | 1184.553 | 1455.214 | 817.1006 | 1005.631 | |
| median | 1273.856 | 1221.935 | 1243.223 | 1313.445 | 1218.404 | 1507.044 | 1044.84 | 1153.54 | |
| F6 | mean | 673.1587 | 703.0555 | 702.3727 | 691.9153 | 705.7748 | 720.2816 | 647.1692 | 670.9763 |
| std | 6.741626 | 4.470917 | 4.770088 | 9.732927 | 5.495881 | 4.579695 | 7.042482 | 9.649086 | |
| best | 659.9427 | 689.8744 | 687.6308 | 673.5214 | 686.885 | 708.4121 | 634.3791 | 643.4003 | |
| worst | 673.5805 | 703.072 | 704.0603 | 693.1564 | 705.456 | 720.9183 | 647.4455 | 670.9801 | |
| median | 688.3811 | 710.4015 | 707.9847 | 711.0534 | 715.5399 | 727.7279 | 663.3866 | 687.7654 | |
| F7 | mean | 1677.512 | 1989.602 | 2070.307 | 2113.629 | 2008.223 | 4750.685 | 1335.724 | 1401.825 |
| std | 129.802 | 43.66188 | 41.57328 | 77.63079 | 52.39592 | 171.1507 | 181.3475 | 134.9587 | |
| best | 1415.056 | 1864.435 | 1960.993 | 1884.382 | 1841.49 | 4404.823 | 1075.477 | 1139.746 | |
| worst | 1692.121 | 1994.192 | 2074.903 | 2120.844 | 2001.787 | 4751.85 | 1307.007 | 1407.649 | |
| median | 1973.952 | 2069.746 | 2130.137 | 2199.236 | 2110.807 | 5066.757 | 1893.642 | 1700.882 | |
| F8 | mean | 1351.27 | 1512.373 | 1495.853 | 1563.182 | 1512.089 | 1749.039 | 1169.113 | 1279.896 |
| std | 85.06685 | 17.77129 | 27.11427 | 36.59189 | 24.964 | 42.2352 | 124.1553 | 117.3652 | |
| best | 1132.023 | 1467.454 | 1448.889 | 1487.389 | 1436.219 | 1623.599 | 1024.438 | 1068.045 | |
| worst | 1332.628 | 1511.177 | 1496.799 | 1568.833 | 1512.149 | 1756.379 | 1111.142 | 1312.018 | |
| median | 1524.114 | 1545.217 | 1545.219 | 1624.462 | 1555.27 | 1810.891 | 1443.049 | 1485.358 | |
| F9 | mean | 26,315.19 | 39,713.01 | 39,487.92 | 43,652.74 | 40,148.12 | 64,453.51 | 18,684.12 | 27,981.46 |
| std | 5710.865 | 2801.281 | 2733.521 | 6709.924 | 3165.292 | 6313.14 | 5930.056 | 7751.885 | |
| best | 14,120 | 30,240.19 | 34,025.13 | 29,168.84 | 30,667.48 | 44,678.95 | 10,217.21 | 14,544.16 | |
| worst | 26,145.71 | 40,060.17 | 39,455.94 | 43,719.75 | 40,167.54 | 65,672.73 | 18,116.57 | 27,353.29 | |
| median | 39,054.82 | 44,701.06 | 44,175.14 | 54,292.88 | 45,526.84 | 76,863.93 | 33,371.21 | 43,059.4 | |
| F10 | mean | 9036.244 | 15,023.68 | 15,408.3 | 15,529.49 | 15,601.81 | 15,607.16 | 12,851.33 | 11,442.55 |
| std | 1028.188 | 463.9161 | 452.2438 | 447.2961 | 565.7118 | 364.0358 | 2916.489 | 2387.653 | |
| best | 6960.834 | 13,673.81 | 14,072.49 | 14,574.59 | 14,099.78 | 14,972.36 | 7474.548 | 8069.785 | |
| worst | 9123.119 | 15,059.99 | 15,410.71 | 15,589.28 | 15,670.62 | 15,660.5 | 14,533.69 | 11,116.4 | |
| median | 10,696.68 | 15,644.29 | 16,156.46 | 16,218.35 | 16,541.27 | 16,122.54 | 15,705.3 | 15,258.18 | |
| F11 | mean | 1456.014 | 22,646.18 | 25,955.2 | 16,038.51 | 24,384.56 | 37,752.18 | 3113.923 | 5406.151 |
| std | 101.1321 | 1911.871 | 2606.749 | 4284.927 | 2959.744 | 6875.879 | 685.7545 | 4643.407 | |
| best | 1307.773 | 18,668.89 | 19,768.28 | 9414.711 | 15,229.5 | 19,129.47 | 1899.894 | 2176.385 | |
| worst | 1438.399 | 22,946.78 | 26,342.5 | 15,599.38 | 25,237.19 | 38,325.34 | 3226.607 | 3474.322 | |
| median | 1667.795 | 25,295.74 | 30,296.26 | 26,549.58 | 28,484.62 | 49,140.39 | 4584.315 | 19,830.63 | |
| F12 | mean | 21,208,223 | 6.3 × 1010 | 8.9 × 1010 | 1.41 × 1010 | 8.17 × 1010 | 6.76 × 1010 | 3.98 × 108 | 9.58 × 108 |
| std | 11,394,622 | 1.05 × 1010 | 1.46 × 1010 | 2.63 × 109 | 1.76 × 1010 | 9.25 × 109 | 4.05 × 108 | 8.38 × 108 | |
| best | 7,817,785 | 3.66 × 1010 | 5.51 × 1010 | 8.37 × 109 | 5.32 × 1010 | 4.61 × 1010 | 31,344,196 | 31,725,817 | |
| worst | 19,125,871 | 6.25 × 1010 | 9.14 × 1010 | 1.39 × 1010 | 8.61 × 1010 | 6.79 × 1010 | 2.88 × 108 | 6.88 × 108 | |
| median | 48,400,214 | 8.33 × 1010 | 1.13 × 1011 | 2.09 × 1010 | 1.13 × 1011 | 8.4 × 1010 | 1.75 × 109 | 3.61 × 109 | |
| F13 | mean | 65,586.63 | 4.12 × 1010 | 4.74 × 1010 | 4.37 × 109 | 4.13 × 1010 | 2.85 × 1010 | 1.93 × 108 | 1.61 × 108 |
| std | 44,267.62 | 8.42 × 109 | 1.62 × 1010 | 1.31 × 109 | 1.72 × 1010 | 4.54 × 109 | 5.22 × 108 | 2.28 × 108 | |
| best | 13,035.42 | 2.71 × 1010 | 1.55 × 1010 | 1.89 × 109 | 1.66 × 1010 | 1.92 × 1010 | 114,020.3 | 2,961,075 | |
| worst | 51,812.64 | 4.15 × 1010 | 4.68 × 1010 | 4.28 × 109 | 3.65 × 1010 | 2.87 × 1010 | 22,893,078 | 65,134,665 | |
| median | 144,709.6 | 5.91 × 1010 | 8.47 × 1010 | 6.93 × 109 | 7.87 × 1010 | 3.76 × 1010 | 2.57 × 109 | 9.92 × 108 | |
| F14 | mean | 327,094.4 | 70,972,878 | 1.21 × 108 | 4,716,715 | 1.57 × 108 | 31,301,009 | 3,210,835 | 4,034,978 |
| std | 206,097.4 | 26,730,785 | 1.07 × 108 | 2,287,260 | 1.16 × 108 | 16,751,125 | 4,229,751 | 4,957,667 | |
| best | 62,115.75 | 10,693,642 | 5,875,508 | 1,233,774 | 16,131,250 | 9,128,897 | 304,722.2 | 148,710.7 | |
| worst | 311,704.9 | 71,552,201 | 79,985,985 | 4,621,592 | 1.2 × 108 | 27,603,229 | 1,954,626 | 1,928,327 | |
| median | 859,561.4 | 1.44 × 108 | 4.11 × 108 | 12,215,340 | 4.41 × 108 | 85,198,632 | 23,139,889 | 17,643,989 | |
| F15 | mean | 20,076.14 | 6.39 × 109 | 8.42 × 109 | 1.85 × 109 | 9.56 × 109 | 7.81 × 109 | 1,194,628 | 99,311,999 |
| std | 12,505.08 | 1.61 × 109 | 3.71 × 109 | 7.37 × 108 | 2.88 × 109 | 2.2 × 109 | 4,993,285 | 3.24 × 108 | |
| best | 3435.915 | 3.34 × 109 | 2.86 × 109 | 3.12 × 108 | 3.54 × 109 | 2.44 × 109 | 16,137.75 | 38,951.08 | |
| worst | 19,200.35 | 6.16 × 109 | 8.49 × 109 | 1.85 × 109 | 9.96 × 109 | 8.04 × 109 | 95,439.28 | 222,537.5 | |
| median | 55,648.57 | 9.84 × 109 | 2.03 × 1010 | 3.18 × 109 | 1.53 × 1010 | 1.1 × 1010 | 27,128,857 | 1.76 × 109 | |
| F16 | mean | 4149.21 | 8913.883 | 10,551.97 | 6367.51 | 11,540.07 | 8841.368 | 4350.922 | 4647.712 |
| std | 449.7375 | 713.0557 | 1734.323 | 517.7536 | 1392.449 | 475.2364 | 620.8001 | 733.0185 | |
| best | 2885.242 | 7250.674 | 7519.845 | 5428.665 | 8080.71 | 7966.537 | 3034.95 | 3140.566 | |
| worst | 4161.454 | 8945.439 | 10,219.52 | 6349.436 | 11,493.53 | 8814.252 | 4308.845 | 4797.013 | |
| median | 4885.024 | 10,160.04 | 14,156.68 | 7510.284 | 14,834.54 | 9721.609 | 5773.102 | 6039.062 | |
| F17 | mean | 3925.459 | 7852.056 | 12,419.1 | 5903.533 | 17,758.61 | 16,857.18 | 3714.467 | 4287.897 |
| std | 400.7181 | 1469.263 | 9511.617 | 524.5195 | 11,094.1 | 7660.292 | 376.9633 | 575.6267 | |
| best | 3266.528 | 5184.302 | 4962.228 | 4893.874 | 6891.405 | 6954.543 | 2801.898 | 2809.991 | |
| worst | 3885.232 | 7429.907 | 10,080.37 | 5944.598 | 15,095.38 | 17,259.1 | 3752.541 | 4376.222 | |
| median | 4527.253 | 11,919.57 | 54,864.4 | 7012.83 | 47,128.53 | 43,756.89 | 4383.183 | 5328.389 | |
| F18 | mean | 3,741,347 | 1.58 × 108 | 2.06 × 108 | 56,514,657 | 1.8 × 108 | 1.7 × 108 | 8,681,295 | 10,596,914 |
| std | 2,325,907 | 63,623,326 | 1.04 × 108 | 25,410,815 | 92,081,400 | 53,349,251 | 9,155,939 | 9,242,248 | |
| best | 723,232.6 | 52,320,253 | 77,846,397 | 19,530,349 | 57,970,648 | 75,065,695 | 724,814.8 | 1,571,896 | |
| worst | 3,132,272 | 1.59 × 108 | 1.82 × 108 | 51,753,001 | 1.41 × 108 | 1.72 × 108 | 5,021,894 | 7,209,046 | |
| median | 10,168,401 | 3.36 × 108 | 5.33 × 108 | 1.11 × 108 | 4.29 × 108 | 2.91 × 108 | 42,010,779 | 39,489,195 | |
| F19 | mean | 22,177.84 | 3.65 × 109 | 4.7 × 109 | 6.87 × 108 | 4.44 × 109 | 3.52 × 109 | 3,340,464 | 8,448,320 |
| std | 15,848.02 | 8.07 × 108 | 1.74 × 109 | 2.54 × 108 | 1.8 × 109 | 7.66 × 108 | 5,014,682 | 10,142,526 | |
| best | 2419.492 | 1.99 × 109 | 1 × 109 | 2.68 × 108 | 1.72 × 109 | 1.14 × 109 | 12,709.89 | 258,850.9 | |
| worst | 23,607.7 | 3.62 × 109 | 4.73 × 109 | 6.82 × 108 | 3.92 × 109 | 3.53 × 109 | 1,037,733 | 4,918,391 | |
| median | 44,662.61 | 5.31 × 109 | 7.28 × 109 | 1.18 × 109 | 8.35 × 109 | 4.8 × 109 | 19,438,061 | 39,488,873 | |
| F20 | mean | 3644.941 | 4157.516 | 4297.97 | 4367.142 | 4365.791 | 4512.71 | 3788.856 | 3724.264 |
| std | 405.6563 | 182.891 | 195.1588 | 236.7496 | 218.3726 | 156.6324 | 432.4924 | 269.4832 | |
| best | 2731.173 | 3642.467 | 3861.911 | 3678.193 | 3747.012 | 4093.051 | 2791.965 | 3237.719 | |
| worst | 3730.817 | 4153.203 | 4339.08 | 4388.035 | 4407.163 | 4520.621 | 3857.83 | 3697.314 | |
| median | 4448.922 | 4476.917 | 4654.814 | 4731.953 | 4701.596 | 4894.467 | 4418.513 | 4227.031 | |
| F21 | mean | 2854.438 | 3211.012 | 3266.611 | 2971.814 | 3230.192 | 3246.853 | 2689.216 | 2836.455 |
| std | 104.4249 | 40.49479 | 91.52014 | 48.47485 | 61.12815 | 34.9707 | 110.5395 | 77.75509 | |
| best | 2624.227 | 3095.647 | 3044.184 | 2876.981 | 3144.784 | 3169.299 | 2492.846 | 2695.025 | |
| worst | 2870.038 | 3215.319 | 3261.033 | 2972.478 | 3221.754 | 3253.185 | 2665.487 | 2831.948 | |
| median | 3047.414 | 3267.575 | 3445.266 | 3083.429 | 3357.7 | 3314.383 | 2909.121 | 2953.604 | |
| F22 | mean | 10,998.8 | 16,980.06 | 17,249.4 | 16,679.94 | 17,358.84 | 17,391.27 | 13,652.73 | 12,998.59 |
| std | 840.0132 | 408.6059 | 515.1264 | 2123.499 | 786.7584 | 417.0635 | 2907.168 | 2632.685 | |
| best | 9175.088 | 16,194.08 | 16,400.35 | 7408.293 | 13,847.85 | 16,508.11 | 9287.273 | 8554.412 | |
| worst | 10,922.91 | 17,105.06 | 17,387.52 | 17,186.66 | 17,511.75 | 17,358.62 | 12,992.19 | 12,206.8 | |
| median | 12,981.21 | 17,617.41 | 18,030.33 | 18,131.47 | 18,188.65 | 18,118.71 | 17,712.53 | 17,233.74 | |
| F23 | mean | 3581.643 | 4128.582 | 4620.601 | 3510.33 | 4719.551 | 4298.04 | 3307.936 | 3534.21 |
| std | 206.2312 | 91.56528 | 189.0447 | 68.58512 | 192.4512 | 124.7457 | 129.4303 | 133.5617 | |
| best | 3210.139 | 3939.255 | 4212.774 | 3411.791 | 4076.143 | 4022.329 | 3161.893 | 3350.576 | |
| worst | 3583.159 | 4138.696 | 4653.107 | 3497.276 | 4730.426 | 4302.796 | 3268.264 | 3537.664 | |
| median | 3952.577 | 4266.704 | 4987.475 | 3681.977 | 5042.447 | 4499.2 | 3650.281 | 3956.54 | |
| F24 | mean | 3731.615 | 4570.291 | 4977.045 | 3600.492 | 5383.01 | 4623.296 | 3516.178 | 3755.547 |
| std | 182.5002 | 145.2558 | 319.1224 | 58.59646 | 363.3184 | 151.54 | 256.9348 | 134.312 | |
| best | 3515.322 | 4265.015 | 4471.506 | 3480.267 | 4864.839 | 4229.267 | 3166.45 | 3428.635 | |
| worst | 3694.558 | 4581.483 | 4947.526 | 3600.111 | 5382.951 | 4625.649 | 3453.59 | 3798.043 | |
| median | 4218.938 | 4826.476 | 5813.129 | 3707.121 | 6419.906 | 4884.136 | 4227.354 | 3985.79 | |
| F25 | mean | 3110.898 | 14,313.62 | 15,991.59 | 14,126.02 | 16,062.94 | 33,891.03 | 3248.244 | 4482.356 |
| std | 35.02985 | 642.6781 | 1098.787 | 2319.172 | 1040.241 | 2965.027 | 78.15422 | 2045.493 | |
| best | 3039.404 | 12,625.6 | 13,102.36 | 8969.727 | 13,429.07 | 24,792.33 | 3123.983 | 3140.849 | |
| worst | 3115.631 | 14,328.07 | 15,887.54 | 14,173.48 | 16,125.58 | 34,648.34 | 3243.365 | 3573.945 | |
| median | 3192.159 | 15,495.95 | 17,971.18 | 18,126.43 | 18,101.86 | 38,039.97 | 3434.72 | 10,113.06 | |
| F26 | mean | 12,568.05 | 16,850.6 | 17,622.64 | 17,458.21 | 17,780.67 | 21,232.97 | 7701.159 | 10,970.81 |
| std | 1580.866 | 378.2373 | 535.129 | 2077.685 | 615.3835 | 1315.065 | 2403.614 | 1118.15 | |
| best | 9295.756 | 16,187.63 | 16,391.97 | 11,932.34 | 15,771.89 | 18,804.74 | 4126.587 | 8835.321 | |
| worst | 12,811.02 | 16,858.82 | 17,703.9 | 17,938.19 | 17,869.69 | 21,437.78 | 7611.067 | 11,041.12 | |
| median | 17,119.85 | 17,673.45 | 18,813.64 | 19,701.78 | 18,878.72 | 23,754.6 | 12,024.9 | 13,645.62 | |
| F27 | mean | 3808.675 | 6063.492 | 7074.102 | 4337.961 | 6850.284 | 6255.282 | 4020.108 | 3984.485 |
| std | 235.8524 | 455.9033 | 910.8321 | 196.7503 | 807.757 | 321.4446 | 209.8758 | 213.1498 | |
| best | 3484.347 | 5243.028 | 5646.505 | 4030.389 | 5131.224 | 5697.883 | 3657.32 | 3623.358 | |
| worst | 3811.76 | 6093.332 | 6923.087 | 4318.229 | 6767.458 | 6244.369 | 4020.047 | 3939.278 | |
| median | 4270.054 | 6871.226 | 8560.403 | 4815.071 | 8550.204 | 6939.098 | 4531.801 | 4417.38 | |
| F28 | mean | 3365.325 | 12,358.22 | 14,036.87 | 9989.373 | 14,426.55 | 15,690.86 | 3964.528 | 6578.806 |
| std | 37.49875 | 722.2068 | 1214.651 | 1047.597 | 1115.615 | 1440.892 | 1197.622 | 2123.016 | |
| best | 3298.155 | 9369.051 | 12,230.38 | 7433.328 | 12,290.5 | 12,654.15 | 3371.988 | 3527.566 | |
| worst | 3369.195 | 12,457.72 | 13,653.71 | 9811.273 | 14,322.91 | 15,661.53 | 3764.248 | 6543.57 | |
| median | 3456.389 | 13,161.69 | 16,948.66 | 12,382.35 | 17,099.86 | 18,663.63 | 10,185.55 | 10,123.58 | |
| F29 | mean | 5497.258 | 29,545.38 | 156,637.6 | 8103.622 | 309,734.5 | 25,633.53 | 5625.994 | 6369.865 |
| std | 590.1981 | 17,812.2 | 192,179.3 | 635.5026 | 341,597 | 9502.369 | 632.0883 | 889.2101 | |
| best | 4439.055 | 10,118.99 | 25,201.37 | 6565.725 | 28,361.95 | 13,564.98 | 4492.346 | 4770.456 | |
| worst | 5484.536 | 25,437.29 | 79,776.49 | 8036.524 | 144,237.5 | 23,549.28 | 5650.587 | 6220.656 | |
| median | 7052.816 | 75,688.88 | 999,331.1 | 9552.535 | 1,209,936 | 55,501.01 | 6680.621 | 9653.24 | |
| F30 | mean | 2,795,529 | 5.14 × 109 | 8.39 × 109 | 1.2 × 109 | 7.06 × 109 | 5.73 × 109 | 29,677,057 | 48,080,697 |
| std | 1,351,722 | 1.11 × 109 | 3.87 × 109 | 3.56 × 108 | 2.87 × 109 | 1.39 × 109 | 29,781,941 | 41,573,944 | |
| best | 903,013.9 | 2.54 × 109 | 2.27 × 109 | 6.3 × 108 | 1.76 × 109 | 2.99 × 109 | 4,194,733 | 3,665,377 | |
| worst | 2,509,618 | 5.03 × 109 | 7.53 × 109 | 1.12 × 109 | 7.05 × 109 | 5.69 × 109 | 15,930,412 | 26,709,720 | |
| median | 6,397,697 | 7.53 × 109 | 1.68 × 1010 | 2.14 × 109 | 1.23 × 1010 | 7.88 × 109 | 1.02 × 108 | 1.49 × 108 |
As shown in Table 4 and Figure A3, in the 100-dimensional benchmarks, the performance of the algorithms is more clearly differentiated: ECFDBO remains the best on most functions, with the best average optimization on a total of 20 functions; GODBO is still the main contender, with a slight edge on 8 functions; and there is an unexpected optimization of the COA algorithm on F3, with an average of 3.51 × 105 for COA and 5.56 × 105 for ECFDBO, suggesting that ECFDBO may fall into a local optimization on this particular function. Nevertheless, ECFDBO still performs best on most functions. For example, on the F7 function, which has a complex multi-peak structure, ECFDBO averages 3.29 × 103, significantly outperforming all algorithms except GODBO (2.75 × 103); even on the F3 function, which has a dominant COA, ECFDBO ranks 4th without significant performance degradation. In terms of standard deviation, best, median, and worst, ECFDBO wins again with 14, 18, 17, and 18 times, respectively. Especially in terms of standard deviation, the suboptimal algorithm BWO has only 5 optimal times, GODBO is only dominated by one function, F29, and DBO has even failed completely, creating a substantial performance gap with ECFDBO. Overall, ECFDBO shows more stable and efficient optimization in 100 dimensions compared to 30 dimensions and 50 dimensions.
Table 4.
F1–F30 Benchmark Function Test Results (dim = 100).
| ECFDBO | BWO | COA | PIO | BOA | NOA | GODBO | DBO | ||
|---|---|---|---|---|---|---|---|---|---|
| F1 | mean | 7.45 × 108 | 2.59 × 1011 | 2.73 × 1011 | 2.69 × 1011 | 2.61 × 1011 | 4.84 × 1011 | 3.7 × 1010 | 8.06 × 1010 |
| std | 3.24 × 108 | 5.57 × 109 | 9.06 × 109 | 1.3 × 1010 | 1.46 × 1010 | 1.66 × 1010 | 1.34 × 1010 | 6.3 × 1010 | |
| best | 2.28 × 108 | 2.46 × 1011 | 2.54 × 1011 | 2.33 × 1011 | 2.27 × 1011 | 4.41 × 1011 | 1.82 × 1010 | 2.93 × 1010 | |
| worst | 6.31 × 108 | 2.6 × 1011 | 2.75 × 1011 | 2.7 × 1011 | 2.62 × 1011 | 4.84 × 1011 | 3.61 × 1010 | 4.57 × 1010 | |
| median | 1.61 × 109 | 2.68 × 1011 | 2.88 × 1011 | 2.91 × 1011 | 2.84 × 1011 | 5.17 × 1011 | 6.51 × 1010 | 2.5 × 1011 | |
| F3 | mean | 556,312.7 | 377,040 | 351,483 | 475,644.8 | 511,431.5 | 783,361.5 | 414,625.3 | 595,729.4 |
| std | 155,549.4 | 50,453.21 | 16,245.01 | 176,121 | 174,033.4 | 87,093.05 | 106,216.4 | 250,553.3 | |
| best | 284,156.4 | 332,419.6 | 310,093.1 | 366,642.5 | 359,050.2 | 608,466.1 | 362,163.9 | 322,179.9 | |
| worst | 574,389.5 | 362,168.8 | 356,070.1 | 366,718 | 435,797 | 778,483.9 | 391,103.9 | 511,466.6 | |
| median | 964,242.4 | 560,682.7 | 374,778.9 | 883,061.5 | 947,707.4 | 975,420 | 951,696.2 | 1,369,806 | |
| F4 | mean | 1103.319 | 100,125.8 | 109,569.4 | 70,926.48 | 113,669.9 | 174,227.7 | 3727.137 | 19,936.42 |
| std | 109.6269 | 7489.947 | 11,451.92 | 16,469.75 | 10,194.13 | 14,779.12 | 1350.386 | 20,626.2 | |
| best | 948.5583 | 85,618.23 | 87,562.86 | 39,553.18 | 90,745.05 | 147,507.9 | 1956.474 | 3387.313 | |
| worst | 1076.578 | 101,194.6 | 108,947.3 | 72,477.39 | 115,869.6 | 174,697.2 | 3401.511 | 8784.596 | |
| median | 1481.919 | 110,236.8 | 126,735.7 | 100,351.8 | 130,039.5 | 198,696.7 | 9386.499 | 71,595.01 | |
| F5 | mean | 1744.406 | 2120.383 | 2130.764 | 2219.419 | 2091.949 | 2741.801 | 1684.584 | 1692.849 |
| std | 294.6566 | 22.99016 | 35.44666 | 55.07385 | 50.9796 | 66.98955 | 226.6237 | 205.015 | |
| best | 1373.308 | 2049.402 | 2060.307 | 2109.29 | 1936.35 | 2556.87 | 1284.559 | 1344.777 | |
| worst | 1714.638 | 2123.877 | 2133.904 | 2223.298 | 2106.804 | 2756.277 | 1692.64 | 1613.662 | |
| median | 2269.237 | 2159.801 | 2191.759 | 2307.57 | 2145.858 | 2837.671 | 2112.396 | 2048.001 | |
| F6 | mean | 678.0402 | 712.5224 | 713.1258 | 717.9441 | 712.8578 | 740.7731 | 665.6168 | 683.7687 |
| std | 8.109982 | 2.330429 | 3.682679 | 5.089617 | 3.313486 | 3.780802 | 9.107656 | 13.90364 | |
| best | 666.344 | 707.813 | 701.4139 | 707.4029 | 706.6868 | 729.5406 | 650.24 | 657.0897 | |
| worst | 677.4142 | 712.1859 | 713.4107 | 720.0742 | 713.603 | 741.2842 | 664.9418 | 685.7911 | |
| median | 698.8027 | 717.3 | 717.6363 | 725.4998 | 718.7438 | 747.9626 | 699.5684 | 707.3842 | |
| F7 | mean | 3293.137 | 3884.255 | 4032.22 | 4143.678 | 3944.478 | 11,069.35 | 2753.51 | 3015.819 |
| std | 200.926 | 61.64376 | 52.51027 | 104.3898 | 69.1295 | 479.8582 | 202.3837 | 256.7895 | |
| best | 2614.124 | 3761.538 | 3921.182 | 3800.1 | 3804.844 | 9824.999 | 2370.676 | 2389.143 | |
| worst | 3309.688 | 3879.63 | 4026.939 | 4147.419 | 3950.498 | 11,177.42 | 2698.88 | 3022.455 | |
| median | 3736.915 | 3984.399 | 4133.647 | 4285.594 | 4083.88 | 11,755.91 | 3180.337 | 3526.901 | |
| F8 | mean | 2222.104 | 2599.935 | 2598.42 | 2663.825 | 2578.03 | 3117.185 | 1903.055 | 2153.67 |
| std | 202.2045 | 34.72153 | 56.75434 | 48.33201 | 38.17371 | 73.77207 | 200.1381 | 254.3752 | |
| best | 1717.655 | 2526.253 | 2448.614 | 2550.778 | 2508.156 | 2964.277 | 1645.144 | 1722.929 | |
| worst | 2221.624 | 2602.339 | 2615.513 | 2667.069 | 2582.048 | 3115.349 | 1838.554 | 2236.892 | |
| median | 2620.501 | 2680.056 | 2705.458 | 2736.03 | 2661.689 | 3234.99 | 2372.973 | 2498.944 | |
| F9 | mean | 60,455.35 | 80,183.84 | 81,018.74 | 99,296.14 | 86,041.04 | 165,765.3 | 77,050.36 | 73,587.85 |
| std | 18655 | 4820.338 | 4885.766 | 6903.58 | 3395.674 | 10,464.62 | 8062.067 | 12,965.47 | |
| best | 27,080.32 | 65,379.89 | 69,477.43 | 78,988.2 | 80,435.73 | 142,076.6 | 58,765.57 | 35,460.35 | |
| worst | 60,669.35 | 80,472.15 | 80,475.79 | 102,981.4 | 85,766.82 | 165,432.2 | 77,127.33 | 75,350.98 | |
| median | 103,171.6 | 87,361.81 | 91,129.78 | 107,492 | 92,480.88 | 185,227.9 | 89,292.5 | 94,984.11 | |
| F10 | mean | 18,753.74 | 32,411.89 | 32,823.04 | 33,026.71 | 33,190.84 | 33,492.99 | 31,613.64 | 28,054.6 |
| std | 1731.832 | 578.5304 | 855.6955 | 632.246 | 635.5477 | 566.0072 | 2337.055 | 4967.889 | |
| best | 15,986.87 | 31,194.72 | 30,940.53 | 31,454.9 | 31,740.45 | 32,155.73 | 22,861.36 | 18,960.93 | |
| worst | 18,962.75 | 32,577.92 | 32,940.26 | 33,120.2 | 33,221.75 | 33,575.51 | 32,405.64 | 29,006.16 | |
| median | 23,201.87 | 33,521.24 | 34,038.48 | 34,043.18 | 34,294.1 | 34,400.95 | 33,363.61 | 33,813.22 | |
| F11 | mean | 30,562.76 | 375,307.3 | 251,568.9 | 234,786.9 | 435,013.7 | 361,867.1 | 278,041 | 229,312.4 |
| std | 6570.78 | 79,545.43 | 66,685.19 | 40,111.28 | 200,693.6 | 58,812.15 | 76,660.37 | 54,000.11 | |
| best | 19,355.85 | 253,923.3 | 143,315.6 | 125,476.8 | 165,383.3 | 250,249.2 | 134,985.8 | 151,359.1 | |
| worst | 29,760.43 | 368,621.2 | 225,813.5 | 239,133.6 | 361,261.8 | 364,866.1 | 276,670.5 | 220,557.2 | |
| median | 43,382 | 516,893.2 | 437,470.1 | 319,686.3 | 991,459 | 463,055.7 | 478,738.9 | 335,987.1 | |
| F12 | mean | 3.35 × 108 | 1.92 × 1011 | 2.03 × 1011 | 8.9 × 1010 | 1.91 × 1011 | 2.31 × 1011 | 3.21 × 109 | 7.15 × 109 |
| std | 1.47 × 108 | 1.23 × 1010 | 1.81 × 1010 | 1.77 × 1010 | 2.33 × 1010 | 2.12 × 1010 | 1.07 × 109 | 2.48 × 109 | |
| best | 1.23 × 108 | 1.6 × 1011 | 1.65 × 1011 | 5.96 × 1010 | 1.39 × 1011 | 1.73 × 1011 | 1.71 × 109 | 1.37 × 109 | |
| worst | 3.26 × 108 | 1.95 × 1011 | 2.04 × 1011 | 9.01 × 1010 | 1.94 × 1011 | 2.37 × 1011 | 2.84 × 109 | 6.64 × 109 | |
| median | 6.28 × 108 | 2.07 × 1011 | 2.39 × 1011 | 1.33 × 1011 | 2.36 × 1011 | 2.62 × 1011 | 5.34 × 109 | 1.52 × 1010 | |
| F13 | mean | 699,034 | 4.38 × 1010 | 4.9 × 1010 | 1.56 × 1010 | 4.62 × 1010 | 5.55 × 1010 | 1.01 × 108 | 3.83 × 108 |
| std | 1,404,644 | 3.91 × 109 | 5.34 × 109 | 3.05 × 109 | 5.96 × 109 | 4.91 × 109 | 1.46 × 108 | 2.85 × 108 | |
| best | 38,284.6 | 3.67 × 1010 | 3.65 × 1010 | 6.95 × 109 | 3.2 × 1010 | 4.24 × 1010 | 195,268 | 79,403,252 | |
| worst | 89,752.62 | 4.46 × 1010 | 4.86 × 1010 | 1.53 × 1010 | 4.71 × 1010 | 5.63 × 1010 | 53,102,300 | 2.98 × 108 | |
| median | 4,738,688 | 5.04 × 1010 | 6 × 1010 | 2.16 × 1010 | 5.63 × 1010 | 6.33 × 1010 | 6.02 × 108 | 1.29 × 109 | |
| F14 | mean | 3,357,850 | 85,212,469 | 1.02 × 108 | 68,947,180 | 1.51 × 108 | 1.76 × 108 | 5,119,034 | 19,596,326 |
| std | 2,371,169 | 29,998,080 | 34,349,981 | 22,965,475 | 91,411,206 | 43,582,925 | 3,686,515 | 14,389,273 | |
| best | 942,121.9 | 31,318,902 | 44,596,733 | 15,755,741 | 45,787,788 | 88,132,376 | 1,248,844 | 3,347,050 | |
| worst | 2,366,674 | 81,087,973 | 89,294,636 | 70,365,901 | 1.21 × 108 | 1.76 × 108 | 4,347,843 | 16,060,509 | |
| median | 10,420,191 | 1.57 × 108 | 1.82 × 108 | 1.41 × 108 | 3.93 × 108 | 2.66 × 108 | 18,256,524 | 68,172,667 | |
| F15 | mean | 78,930.7 | 2.34 × 1010 | 2.51 × 1010 | 5.57 × 109 | 2.41 × 1010 | 2.23 × 1010 | 13,072,258 | 61,298,556 |
| std | 219,072.8 | 3.02 × 109 | 4.33 × 109 | 1.12 × 109 | 5.12 × 109 | 5.04 × 109 | 21,948,861 | 79,951,870 | |
| best | 12,611.07 | 1.36 × 1010 | 1.51 × 1010 | 3.66 × 109 | 1.27 × 1010 | 1.39 × 1010 | 52,749.1 | 406,195.4 | |
| worst | 26,017.69 | 2.42 × 1010 | 2.57 × 1010 | 5.56 × 109 | 2.41 × 1010 | 2.24 × 1010 | 3,704,249 | 38,353,874 | |
| median | 1,220,023 | 2.84 × 1010 | 3.21 × 1010 | 8.21 × 109 | 3.38 × 1010 | 2.96 × 1010 | 77,559,893 | 3.09 × 108 | |
| F16 | mean | 7420.488 | 22,623.58 | 25,147.88 | 14,599.08 | 26,320.23 | 24,164.12 | 7951.092 | 8898.95 |
| std | 1072.346 | 1437.168 | 3156.294 | 843.7633 | 2172.911 | 1644.561 | 1032.6 | 1284.48 | |
| best | 5570.599 | 19,049.66 | 19,358.85 | 12,878.89 | 19,940.45 | 19,856.09 | 5912.598 | 6313.505 | |
| worst | 7379.487 | 22,827.85 | 25,509.03 | 14,565.16 | 26,451.68 | 24,062.32 | 7705.267 | 8900.273 | |
| median | 9546.879 | 25,581.13 | 30,852.49 | 16,755.66 | 30,537.53 | 27,797.61 | 10,722.2 | 11,774.85 | |
| F17 | mean | 6750.273 | 5,120,658 | 11,568,266 | 19,556.08 | 18,571,373 | 4,215,614 | 8014.545 | 9561.856 |
| std | 607.155 | 3,202,454 | 10,391,713 | 7302.894 | 12,013,187 | 2,973,714 | 1475.525 | 1472.375 | |
| best | 5389.357 | 1,038,674 | 719,282.4 | 11,665.35 | 431,620.6 | 253,709.6 | 5894.588 | 6670.773 | |
| worst | 6734.364 | 4,444,374 | 9,134,410 | 17,682.34 | 19,581,069 | 3,070,116 | 7672.809 | 9609.199 | |
| median | 7765.744 | 11,556,604 | 38,037,312 | 39,841.93 | 57,540,752 | 10,549,137 | 13,547.69 | 12,806.76 | |
| F18 | mean | 7,110,332 | 2.01 × 108 | 3.2 × 108 | 1.23 × 108 | 2.6 × 108 | 3.31 × 108 | 13,751,662 | 31,038,738 |
| std | 2,779,528 | 53,722,189 | 1.74 × 108 | 33,787,632 | 1.06 × 108 | 1.03 × 108 | 8,773,563 | 21,182,188 | |
| best | 2,437,016 | 87,289,245 | 38,115,404 | 61,624,382 | 67,995,553 | 1.5 × 108 | 2,827,917 | 5,159,165 | |
| worst | 6,988,379 | 1.97 × 108 | 2.93 × 108 | 1.18 × 108 | 2.57 × 108 | 3.23 × 108 | 11,671,407 | 29,795,728 | |
| median | 12,595,111 | 3.26 × 108 | 7.19 × 108 | 1.98 × 108 | 5.18 × 108 | 5.3 × 108 | 34,595,900 | 88,488,020 | |
| F19 | mean | 161,629.1 | 2.24 × 1010 | 2.72 × 1010 | 5.25 × 109 | 2.62 × 1010 | 2.45 × 1010 | 23,478,427 | 82,678,768 |
| std | 150,792.2 | 2.39 × 109 | 4.2 × 109 | 1.01 × 109 | 3.76 × 109 | 2.58 × 109 | 18,582,036 | 71,810,474 | |
| best | 17,306.4 | 1.72 × 1010 | 2.03 × 1010 | 3.31 × 109 | 1.84 × 1010 | 1.95 × 1010 | 235,256.2 | 1,656,899 | |
| worst | 129,312 | 2.26 × 1010 | 2.76 × 1010 | 5.24 × 109 | 2.62 × 1010 | 2.42 × 1010 | 19,932,316 | 60,757,956 | |
| median | 770,506.8 | 2.66 × 1010 | 3.52 × 1010 | 6.7 × 109 | 3.3 × 1010 | 3.02 × 1010 | 72,024,184 | 3.6 × 108 | |
| F20 | mean | 6336.572 | 7815.554 | 7936.265 | 8023.333 | 8061.241 | 8370.703 | 7436.64 | 7428.492 |
| std | 730.5444 | 237.0489 | 322.0247 | 365.498 | 302.5378 | 229.1073 | 532.3598 | 657.3067 | |
| best | 4856.539 | 7222.014 | 7237.683 | 7322.811 | 7465.892 | 7798.554 | 5956.323 | 6130.059 | |
| worst | 6494.878 | 7841.19 | 7978.25 | 8028.876 | 8092.769 | 8389.837 | 7606.706 | 7453.894 | |
| median | 7347.281 | 8218.618 | 8376.735 | 8735.5 | 8550.418 | 8715.894 | 8196.152 | 8526.579 | |
| F21 | mean | 4091.623 | 4753.532 | 5054.394 | 4138.902 | 4835.805 | 4827.72 | 3545.287 | 4007.131 |
| std | 202.3991 | 117.0087 | 215.807 | 120.4908 | 219.0194 | 101.6755 | 164.3183 | 179.7956 | |
| best | 3706.605 | 4460.952 | 4449.178 | 3924.682 | 4400.545 | 4541.913 | 3209.056 | 3581.077 | |
| worst | 4139.599 | 4766.447 | 5106.211 | 4141.252 | 4823.088 | 4850.111 | 3529.698 | 3982.011 | |
| median | 4547.738 | 4954.546 | 5383.477 | 4358.611 | 5245.605 | 4975.327 | 3936.363 | 4318.997 | |
| F22 | mean | 21,835.86 | 34,804.59 | 35,405.42 | 35,512.35 | 35,802.49 | 35,768.79 | 30,883.39 | 29,201.22 |
| std | 1578.262 | 499.9623 | 454.6997 | 673.7102 | 563.8343 | 648.3102 | 5023.191 | 4840.573 | |
| best | 18,345.09 | 33,725.21 | 34,380.09 | 33,911.83 | 34,512.62 | 34,051.68 | 21,219.49 | 21,274.95 | |
| worst | 22,189.25 | 34,807.9 | 35,414.25 | 35,587.18 | 35,893.79 | 35,799.74 | 33,186.59 | 28,547.36 | |
| median | 24,528.11 | 35,643.73 | 36,446.65 | 36,867.86 | 36,636.76 | 36,958.27 | 35,643.22 | 35,948.67 | |
| F23 | mean | 4522.377 | 6128.485 | 6706.252 | 4726.073 | 6666.565 | 6624.233 | 4458.082 | 4862.778 |
| std | 227.661 | 206.8003 | 311.8774 | 144.3862 | 298.6917 | 208.8306 | 334.0317 | 183.4844 | |
| best | 4069.015 | 5697.221 | 5925.037 | 4526.84 | 6167.803 | 6166.97 | 3866.858 | 4401.4 | |
| worst | 4541.962 | 6160.689 | 6759.413 | 4682.834 | 6672.552 | 6635.941 | 4401.469 | 4880.059 | |
| median | 4985.777 | 6464.255 | 7374.691 | 5104.453 | 7176.801 | 7003.271 | 5053.456 | 5160.213 | |
| F24 | mean | 5857.826 | 9342.537 | 10,841.56 | 5860.021 | 11,614.26 | 10,528.28 | 5506.501 | 6235.145 |
| std | 378.8069 | 367.4904 | 824.4215 | 249.144 | 1349.797 | 673.2516 | 544.6357 | 411.0967 | |
| best | 5095.272 | 8696.912 | 8963.08 | 5409.182 | 8609.48 | 9354.27 | 4438.242 | 5502.835 | |
| worst | 5875.381 | 9381.774 | 10,730.26 | 5886.524 | 11,526.34 | 10,473.02 | 5462.246 | 6121.079 | |
| median | 6719.068 | 10,217.76 | 12,762.6 | 6386.001 | 13,823.65 | 11,594.64 | 6438.321 | 7131.038 | |
| F25 | mean | 3769.489 | 27,856.39 | 29,869.98 | 29,312.02 | 30,582.81 | 85,464.15 | 5939.275 | 10,182.26 |
| std | 111.1321 | 1252.448 | 2092.453 | 3198.363 | 1622.11 | 7145.521 | 722.1818 | 7108.135 | |
| best | 3560.144 | 25,277.26 | 26,005.69 | 21,133.68 | 27,172.64 | 66,896.08 | 4862.769 | 4884.121 | |
| worst | 3761.928 | 27,753.1 | 29,784.64 | 29,816.04 | 30,471.82 | 87,164.45 | 5813.634 | 7050.382 | |
| median | 4054.049 | 30,542.99 | 33,982.04 | 35,071.9 | 33,326.43 | 99,108.89 | 7745.367 | 30,475.37 | |
| F26 | mean | 31,009.52 | 50,936.92 | 53,737.98 | 43,732.13 | 57,798.14 | 63,818.11 | 21,038.14 | 26,878.31 |
| std | 4110.581 | 1176.966 | 2254.596 | 8990.192 | 2389.712 | 4546.23 | 3950.96 | 3906.133 | |
| best | 21,423.14 | 48,574.34 | 48,509.41 | 30,908.45 | 54,023.07 | 56,471.55 | 13,467.27 | 19877.39 | |
| worst | 31,427.39 | 50,935.76 | 54,026.64 | 44,323.95 | 58,188.65 | 63,397.93 | 21,286.16 | 26,315.97 | |
| median | 37,732.05 | 53,129.96 | 57,818.87 | 58,175.37 | 61,513.28 | 74,691.44 | 31,846.06 | 33,541.61 | |
| F27 | mean | 4049.225 | 12,738.09 | 14,612.9 | 6633.679 | 15,466 | 12,099.81 | 4588.784 | 4665.642 |
| std | 237.415 | 887.3229 | 1847.36 | 462.838 | 1183.631 | 821.7461 | 437.8651 | 558.4765 | |
| best | 3622.841 | 11,001.37 | 9956.104 | 5859.08 | 12,395.44 | 10027.23 | 3820.702 | 3734.622 | |
| worst | 4011.685 | 12,881.18 | 14,617.13 | 6603.605 | 15,331.31 | 12,476.57 | 4517.536 | 4706.624 | |
| median | 4536.897 | 14,634.92 | 18,357.8 | 7681.489 | 17,298.81 | 13,150.6 | 5615.708 | 6164.552 | |
| F28 | mean | 3928.902 | 27,579.2 | 30,966.01 | 32,360.48 | 37,253.33 | 53,180.92 | 6247.656 | 18,748.06 |
| std | 175.0026 | 932.4787 | 1115.262 | 2089.106 | 1964.436 | 3257.289 | 1052.154 | 6524.976 | |
| best | 3719.935 | 25,065.01 | 28,118.09 | 25,031.75 | 33,693.31 | 44,544.13 | 4336.486 | 6136.359 | |
| worst | 3912.315 | 27,677.51 | 31,323.85 | 33,469.65 | 37,559.39 | 53,123.78 | 6163.077 | 20,628.16 | |
| median | 4428.841 | 29,593.04 | 32,652.56 | 34,467.5 | 40,517.02 | 58,373.92 | 9215.413 | 30,822.45 | |
| F29 | mean | 8480.565 | 452,072.2 | 705,440.1 | 36,007.73 | 920,606.3 | 856,033 | 9526.919 | 11,454.74 |
| std | 1080.918 | 180,448.5 | 485,272.9 | 20,755.47 | 470,669.8 | 403,997.3 | 898.0878 | 1669.909 | |
| best | 5932.02 | 93,201.62 | 72,902.48 | 20,394.78 | 258,530.2 | 123,197.8 | 7963.642 | 8446.091 | |
| worst | 8524.741 | 435,448.8 | 582,095.4 | 30,908.54 | 882,911.5 | 898,083 | 9369.629 | 11,355.29 | |
| median | 11,096.79 | 718,608.2 | 2,136,675 | 129,997.7 | 2,325,186 | 2,057,818 | 11,796.08 | 15,180.8 | |
| F30 | mean | 3,917,708 | 3.94 × 1010 | 4.42 × 1010 | 7.01 × 109 | 4.13 × 1010 | 3.86 × 1010 | 1.43 × 108 | 2.89 × 108 |
| std | 1,861,671 | 5.48 × 109 | 6.62 × 109 | 1.1 × 109 | 5.24 × 109 | 4.95 × 109 | 1.37 × 108 | 1.37 × 108 | |
| best | 1,659,875 | 2.29 × 1010 | 2.86 × 1010 | 4.93 × 109 | 2.49 × 1010 | 2.63 × 1010 | 11,050,311 | 59,217,772 | |
| worst | 3,252,883 | 4.16 × 1010 | 4.43 × 1010 | 7.01 × 109 | 4.18 × 1010 | 3.97 × 1010 | 91,981,143 | 2.85 × 108 | |
| median | 9,756,674 | 4.64 × 1010 | 5.49 × 1010 | 9.38 × 109 | 5.05 × 1010 | 4.56 × 1010 | 5.76 × 108 | 6.86 × 108 |
Combining the experimental results in 30, 50, and 100 dimensions, ECFDBO consistently leads in average performance, stability, and extreme cases, demonstrating good scalability and robustness as dimensionality increases, and it shows better overall solution quality and stability of results on the CEC2017 test set. As the dimensionality of the problem increases, the difference in solution accuracy between the algorithms widens significantly. ECFDBO achieving the lowest mean and std for most of the test functions in all dimensions, indicating that its converged solutions are closer to the global optimization with less variation. As the dimensions increase from 30 to 100, ECFDBO grows steadily from 18, 19 to 20 functions to reach the optimal mean. This shows that ECFDBO adapts well to dimensional extensions and maintains strong solving power on high-dimensional problems. In contrast, other algorithms such as BOA, BWO, PIO, etc. show a significant decrease in solution accuracy as dimensionality increases. This reflects that these algorithms are prone to local optimization or unstable convergence in high-dimensional complexity, while ECFDBO effectively alleviates the performance degradation caused by the increase in dimensionality through improved strategies.
5.3. Wilcoxon and Friedman Statistical Tests
In order to provide a more in-depth and systematic statistical analysis of the experimental results, the Wilcoxon and Friedman tests were introduced in this study to quantify the significance of the performance differences between the ECFDBO algorithm and the seven comparison algorithms. Specifically, the Wilcoxon test performs a test on the paired observations of ECFDBO and each comparison algorithm in the dataset, where the difference in performance between the two algorithms is considered statistically significant if the p-value obtained from the test is <0.05 (shown in bold) when the significance level is ; otherwise, the difference is not statistically significant. The Friedman test aggregates the rankings of all algorithms across the functions in the CEC2017 benchmark suite and computes their average ranks. This process evaluates whether the overall differences among multiple algorithms across multiple test functions are statistically significant, thereby providing a global, nonparametric statistical basis for algorithm comparisons.
Based on Table 5, Table 6 and Table 7, the Wilcoxon test shows that ECFDBO has a significant advantage over most of the algorithms. Overall, the differences between ECFDBO and the seven algorithms BWO, COA, PIO, BOA, NOA, GODBO, and DBO reached a significant level (p < 0.05) in the function-by-function comparison with each of the compared algorithms in 30 dimensions, which proves that the results of ECFDBO are significantly better than these algorithms. The three algorithms, BWO, COA, and NOA, all showed significant differences during the comparison process with ECFDBO one by one. PIO had only two functions (F23 and F24), and BOA had one function (F22). GODBO had four functions (F17, F18, F20, and F24) and did not show significant differences, while the original DBO showed advantages with ten functions. When the number of dimensions reaches 50, ECFDBO has more significant advantages, including the original DBO and GODBO, which were second to ECFDBO in the previous 30 dimensions, and the advantages of ECFDBO over the original DBO and GODBO are further extended in the 50-dimensional benchmark. The remaining algorithms have more significant differences with ECFDBO; for example, the p-value is close to 0 for BWO and COA, etc. Four algorithms even show significant differences with ECFDBO in all 29 functions, proving that ECFDBO has a clear lead in higher dimensions. The performance improvement of ECFDBO over all seven algorithms compared to 100 dimensions was significantly better than the other algorithms, with a total of 11 functions with p-values > 0.05. It is worth noting that although the GODBO algorithm achieved the best results on individual functions in the previous test, the overall gap between it and ECFDBO is still extremely obvious—ECFDBO achieved 20 wins against GODBO in 100 dimensions. It can be seen that as dimensionality increases, ECFDBO outperforms all comparators in the statistical sense.
Table 5.
Wilcoxon test (dim = 30).
| Function | BWO vs. ECFDBO | COA vs. ECFDBO | PIO vs. ECFDBO | BOA vs. ECFDBO | NOA vs. ECFDBO | GODBO vs. ECFDBO | DBO vs. ECFDBO |
|---|---|---|---|---|---|---|---|
| F1 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.08 × 10−11 | 3.02 × 10−11 |
| F3 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F4 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.25 × 10−5 | 1.01 × 10−8 |
| F5 | 4.2 × 10−10 | 5.97 × 10−9 | 0.00062 | 5.97 × 10−9 | 4.08 × 10−11 | 1.55 × 10−9 | 0.001953 |
| F6 | 3.02 × 10−11 | 3.34 × 10−11 | 0.007617 | 4.08 × 10−11 | 3.02 × 10−11 | 2.37 × 10−10 | 0.082357 |
| F7 | 4.98 × 10−11 | 8.99 × 10−11 | 3.69 × 10−11 | 5.49 × 10−11 | 3.02 × 10−11 | 6.12 × 10−10 | 1.64 × 10−5 |
| F8 | 7.39 × 10−11 | 2.87 × 10−10 | 3.16 × 10−10 | 2.61 × 10−10 | 3.02 × 10−11 | 5.27 × 10−5 | 0.958731 |
| F9 | 0.000399 | 0.010763 | 0.039167 | 0.000526 | 3.69 × 10−11 | 1.96 × 10−10 | 1.11 × 10−6 |
| F10 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.005828 | 0.021506 |
| F11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.000318 | 2.37 × 10−10 |
| F12 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 5.57 × 10−10 | 7.38 × 10−10 |
| F13 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.61 × 10−10 | 7.39 × 10−11 |
| F14 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 7.69 × 10−8 | 1.47 × 10−7 |
| F15 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.42 × 10−6 | 1.31 × 10−8 |
| F16 | 3.02 × 10−11 | 3.02 × 10−11 | 7.39 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.030317 | 0.000168 |
| F17 | 3.34 × 10−11 | 4.08 × 10−11 | 4.18 × 10−9 | 3.02 × 10−11 | 3.69 × 10−11 | 0.332855 | 0.05012 |
| F18 | 3.02 × 10−11 | 3.69 × 10−11 | 3.69 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.185767 | 0.000149 |
| F19 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.00238 | 9.06 × 10−8 |
| F20 | 6.53 × 10−8 | 9.26 × 10−9 | 3.35 × 10−8 | 2.23 × 10−9 | 3.5 × 10−9 | 0.53951 | 0.166866 |
| F21 | 3.2 × 10−9 | 3.82 × 10−10 | 0.016285 | 4.2 × 10−10 | 6.07 × 10−11 | 3.65 × 10−8 | 0.3871 |
| F22 | 1.69 × 10−9 | 3.82 × 10−10 | 0.003501 | 0.78446 | 1.61 × 10−10 | 0.006377 | 0.982307 |
| F23 | 3.69 × 10−11 | 3.02 × 10−11 | 0.464273 | 1.78 × 10−10 | 3.02 × 10−11 | 0.001058 | 0.888303 |
| F24 | 3.02 × 10−11 | 3.02 × 10−11 | 0.641424 | 3.02 × 10−11 | 3.02 × 10−11 | 0.070127 | 0.501144 |
| F25 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.59 × 10−5 | 2.87 × 10−10 |
| F26 | 4.08 × 10−11 | 3.02 × 10−11 | 0.035137 | 3.02 × 10−11 | 4.08 × 10−11 | 8.29 × 10−6 | 0.08771 |
| F27 | 3.02 × 10−11 | 3.02 × 10−11 | 3.5 × 10−9 | 3.02 × 10−11 | 3.02 × 10−11 | 0.000268 | 0.000812 |
| F28 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.1 × 10−8 | 2.37 × 10−10 |
| F29 | 3.02 × 10−11 | 3.02 × 10−11 | 1.69 × 10−9 | 3.02 × 10−11 | 3.02 × 10−11 | 0.003848 | 0.251881 |
| F30 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 8.48 × 10−9 | 5.19 × 10−7 |
Table 6.
Wilcoxon test (dim = 50).
| Function | BWO vs. ECFDBO | COA vs. ECFDBO | PIO vs. ECFDBO | BOA vs. ECFDBO | NOA vs. ECFDBO | GODBO vs. ECFDBO | DBO vs. ECFDBO |
|---|---|---|---|---|---|---|---|
| F1 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F3 | 3.02 × 10−11 | 3.34 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.69 × 10−11 |
| F4 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 8.99 × 10−11 | 4.5 × 10−11 |
| F5 | 8.1 × 10−10 | 3.82 × 10−9 | 3.82 × 10−10 | 8.48 × 10−9 | 3.02 × 10−11 | 1.31 × 10−8 | 0.297272 |
| F6 | 3.02 × 10−11 | 3.34 × 10−11 | 6.52 × 10−9 | 3.34 × 10−11 | 3.02 × 10−11 | 3.69 × 10−11 | 0.347828 |
| F7 | 7.39 × 10−11 | 3.34 × 10−11 | 3.34 × 10−11 | 6.07 × 10−11 | 3.02 × 10−11 | 7.12 × 10−9 | 2.02 × 10−8 |
| F8 | 9.76 × 10−10 | 1.31 × 10−8 | 5.49 × 10−11 | 9.76 × 10−10 | 3.02 × 10−11 | 4.42 × 10−6 | 0.059428 |
| F9 | 1.61 × 10−10 | 1.33 × 10−10 | 3.82 × 10−10 | 1.21 × 10−10 | 3.02 × 10−11 | 1.34 × 10−5 | 0.379036 |
| F10 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.28 × 10−5 | 7.2 × 10−5 |
| F11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F12 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 5.49 × 10−11 | 5.49 × 10−11 |
| F13 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 8.99 × 10−11 | 3.02 × 10−11 |
| F14 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.82 × 10−10 | 2.57 × 10−7 |
| F15 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.55 × 10−9 | 6.07 × 10−11 |
| F16 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.1809 | 0.004637 |
| F17 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.085 | 0.002891 |
| F18 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.015014 | 0.000284 |
| F19 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 5.46 × 10−9 | 3.02 × 10−11 |
| F20 | 1.87 × 10−7 | 1.1 × 10−8 | 5 × 10−9 | 4.57 × 10−9 | 1.78 × 10−10 | 0.122353 | 0.589451 |
| F21 | 3.02 × 10−11 | 3.34 × 10−11 | 2.68 × 10−6 | 3.02 × 10−11 | 3.02 × 10−11 | 1.03 × 10−6 | 0.347828 |
| F22 | 3.02 × 10−11 | 3.02 × 10−11 | 1.86 × 10−9 | 3.02 × 10−11 | 3.02 × 10−11 | 0.000526 | 0.002755 |
| F23 | 3.69 × 10−11 | 3.02 × 10−11 | 0.149449 | 3.02 × 10−11 | 3.02 × 10−11 | 2 × 10−6 | 0.283778 |
| F24 | 3.02 × 10−11 | 3.02 × 10−11 | 0.000587 | 3.02 × 10−11 | 3.02 × 10−11 | 0.000399 | 0.149449 |
| F25 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.2 × 10−10 | 4.5 × 10−11 |
| F26 | 2.87 × 10−10 | 4.98 × 10−11 | 9.26 × 10−9 | 4.08 × 10−11 | 3.02 × 10−11 | 2.03 × 10−9 | 4.08 × 10−5 |
| F27 | 3.02 × 10−11 | 3.02 × 10−11 | 1.69 × 10−9 | 3.02 × 10−11 | 3.02 × 10−11 | 0.00077 | 0.004226 |
| F28 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.15 × 10−10 | 3.02 × 10−11 |
| F29 | 3.02 × 10−11 | 3.02 × 10−11 | 4.08 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.290472 | 7.74 × 10−6 |
| F30 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.46 × 10−10 | 2.15 × 10−10 |
Table 7.
Wilcoxon test (dim = 100).
| Function | BWO vs. ECFDBO | COA vs. ECFDBO | PIO vs. ECFDBO | BOA vs. ECFDBO | NOA vs. ECFDBO | GODBO vs. ECFDBO | DBO vs. ECFDBO |
|---|---|---|---|---|---|---|---|
| F1 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F3 | 7.22 × 10−6 | 6.53 × 10−7 | 0.046756 | 0.162375 | 4.69 × 10−8 | 0.000141 | 0.994102 |
| F4 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F5 | 6.28 × 10−6 | 4.12 × 10−6 | 6.01 × 10−8 | 1.09 × 10−5 | 3.02 × 10−11 | 0.549327 | 0.761828 |
| F6 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.26 × 10−7 | 0.082357 |
| F7 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 6.72 × 10−10 | 2.6 × 10−5 |
| F8 | 1.41 × 10−9 | 1.55 × 10−9 | 8.15 × 10−11 | 5.46 × 10−9 | 3.02 × 10−11 | 2.15 × 10−6 | 0.520145 |
| F9 | 3.26 × 10−7 | 2.2 × 10−7 | 2.61 × 10−10 | 8.48 × 10−9 | 3.02 × 10−11 | 2.6 × 10−5 | 0.001857 |
| F10 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.34 × 10−11 | 4.62 × 10−10 |
| F11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F12 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F13 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.37 × 10−10 | 3.02 × 10−11 |
| F14 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.029205 | 1.29 × 10−9 |
| F15 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.47 × 10−10 | 3.34 × 10−11 |
| F16 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.051877 | 6.77 × 10−5 |
| F17 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.43 × 10−5 | 2.61 × 10−10 |
| F18 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.000587 | 1.6 × 10−7 |
| F19 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.5 × 10−11 | 3.02 × 10−11 |
| F20 | 4.98 × 10−11 | 4.5 × 10−11 | 3.34 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 7.69 × 10−8 | 1.11 × 10−6 |
| F21 | 3.34 × 10−11 | 3.34 × 10−11 | 0.371077 | 4.08 × 10−11 | 3.34 × 10−11 | 1.33 × 10−10 | 0.111987 |
| F22 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.57 × 10−9 | 2.92 × 10−9 |
| F23 | 3.02 × 10−11 | 3.02 × 10−11 | 0.000301 | 3.02 × 10−11 | 3.02 × 10−11 | 0.411911 | 6.05 × 10−7 |
| F24 | 3.02 × 10−11 | 3.02 × 10−11 | 0.982307 | 3.02 × 10−11 | 3.02 × 10−11 | 0.011228 | 0.000952 |
| F25 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F26 | 3.02 × 10−11 | 3.02 × 10−11 | 9.06 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 | 3.2 × 10−9 | 0.000356 |
| F27 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 8.2 × 10−7 | 3.32 × 10−6 |
| F28 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.34 × 10−11 | 3.02 × 10−11 |
| F29 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 0.000178 | 3.82 × 10−9 |
| F30 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
As shown in Table 8, the Friedman test shows that the ECFDBO algorithm has a lower average rank than the other algorithms on all dimensions, and the bright spot is that GODBO and the original DBO are ranked second and third on all dimensions. From this, it can be seen that the superiority of ECFDBO is not due to randomness but has reliable statistical support. There are almost no algorithms that can match or exceed ECFDBO’s overall performance in any dimension. This means that the performance improvement of ECFDBO over every other algorithm is statistically significant, with advantages over BWO, COA, and NOA being particularly prominent, and a reliable lead over second-tier algorithms such as GODBO and DBO. Thus, it can be quantitatively confirmed that ECFDBO significantly outperforms the seven meta-heuristic algorithms compared to the CEC2017 test set as a whole, demonstrating robust optimization capabilities in all dimensions. For this statistical advantage, the excellent performance of the ECFDBO algorithm on each benchmark function fully demonstrates its effectiveness and competitiveness in solving complex optimization problems.
Table 8.
Friedman test in different dimensions.
| Test Functions and Dimensions | Algorithm and the Friedman Test | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | ECFDBO | BWO | COA | PIO | BOA | NOA | GODBO | DBO | |
| CEC2017-30D | Friedman | 2.1241 | 5.2759 | 6.2828 | 4.1517 | 6.3724 | 6.3034 | 2.3655 | 3.1241 |
| Rankings | 1 | 5 | 6 | 4 | 8 | 7 | 2 | 3 | |
| CEC2017-50D | Friedman | 2.0276 | 4.8690 | 6.0690 | 4.4621 | 6.4345 | 6.4897 | 2.5379 | 3.1103 |
| Rankings | 1 | 5 | 6 | 4 | 7 | 8 | 2 | 3 | |
| CEC2017-100D | Friedman | 1.9931 | 4.6414 | 5.8483 | 4.6483 | 6.2207 | 6.8138 | 2.4621 | 3.3724 |
| Rankings | 1 | 4 | 6 | 5 | 7 | 8 | 2 | 3 | |
5.4. Contribution of the Improvement Strategies
ECFDBO brings three key improvement strategies for the DBO algorithm to enhance its performance.
Chaotic Perturbation Mixed Nonlinear Contraction Mechanisms: ECFDBO introduces chaotic sequence perturbation into the iterative process and adopts a nonlinearly decreasing convergence factor to regulate the search step size so as to dynamically balance global exploration and local exploitation. Chaotic sequences can effectively increase the population diversity and improve the global search capability of the algorithm due to their ergodicity and randomness. In the early stage of the algorithm, the chaotic perturbation helps ECFDBO to explore the solution space more extensively to avoid falling into the local optimization prematurely, and as the iteration proceeds, the perturbation amplitude gradually shrinks according to the nonlinear function, which helps the algorithm to perform a fine search near the optimal solution at a later stage, thus improving the convergence precision. This adaptive perturbation mechanism makes up for the lack of perturbation means in the original algorithm: lack of population perturbation, the algorithm can easily fall into the local optimization and missing the opportunity to search other regions. Therefore, chaotic perturbation combined with nonlinear contraction strengthens the global exploration capability and late convergence stability of ECFDBO in complex multi-peak environments, dramatically reducing the solution deviation and improving the robustness of the results.
Environment-Aware Boundary-Handling Strategy: For the problem of candidate solutions crossing the boundary, ECFDBO adopts an environment-aware boundary-handling mechanism. When an individual crosses the boundary of the defined area, the algorithm does not simply cut it back to the boundary or reset the random value but adjusts it according to the environmental information at the time the individual crosses the boundary so as to maintain the feasibility of the solution without losing diversity. Proper boundary handling is critical to the performance of population intelligence algorithms, and ECFDBO’s boundary handling takes into account the fitness environment of the individual’s region, intelligently pulling out-of-bounds solutions back into potentially favorable regions of the search space rather than blindly discarding or zeroing them. This ‘environment-aware’ approach improves the efficiency of the algorithm’s search near the boundary, avoiding the traditional hard boundary handling that can cause individuals to oscillate or stagnate at the boundary.
Dynamic Attraction–Repulsion Force-Field Mutation Strategy: ECFDBO introduces a mutation operator that simulates the effects of attractive and repulsive forces to speed up convergence while maintaining population diversity. The strategy applies an ‘attractive force’ to the high-quality solutions to bring the surrounding individuals closer to them so as to use the global optimal information to guide the search and improve the speed of local convergence; at the same time, it applies a ‘repulsive force’ to the over-aggregated individuals to push them away from their current position to encourage the population to spread to unexplored areas and maintain the global search capability. Through Attractive -repulsive mutation, the population of ECFDBO can consistently jump out of local traps while approaching the global optimization. It makes the algorithm rarely stagnate in local extremum traps of complex functions and speeds up the optimality search process of the global optimization.
In the relationship between the 3D path planning task of unmanned aerial vehicles (UAVs) and the CEC2017 test experiments: In terms of the correspondence of problem characteristics, ECFDBO significantly outperforms the comparative algorithms in the 30D/50D/100D tests of CEC2017, demonstrating its remarkable high-dimensional optimization capabilities. Given that UAV path planning involves optimizing dozens of variables simultaneously in a 3D space, such as path length, threat avoidance, and altitude constraints, the high-dimensional optimization capabilities of ECFDBO can effectively address such problems. The excellent performance of ECFDBO in the multi-peak functions (F4-F10) and hybrid functions (F11-F20) of CEC2017 enables it to help UAVs find a globally safe path amidst the “traps” of local optimal solutions formed by multiple obstacles. The intelligent boundary-handling mechanism of ECFDBO, as evidenced by its performance in the constrained functions of CEC2017, ensures that UAVs strictly comply with physical constraints such as the flight altitude range and minimum path length. Regarding the problem goals, the advantages of ECFDBO in terms of convergence speed and results in CEC2017 guarantee that UAVs can quickly find the optimal solution during path planning. The comprehensive advantages of ECFDBO in the composite functions (F21-F30) can assist UAVs in generating optimal paths under conditions of multiple conflicting constraints.
6. Collaborative 3D Path Planning Simulation
Path planning in complex spatial environments is a critical step for UAV navigation in remote sensing missions. It ensures that the UAV safely and efficiently travels from one location to another while satisfying all mission-related constraints and requirements [51]. Based on these considerations, the model developed in this study is constructed as follows.
6.1. Problem Statement
6.1.1. Flight Path Distance
In order to make the operation of UAVs more relevant to actual needs, the path planning should be based on different application scenarios for goal setting and constraints. Since we focus on remote sensing and surface monitoring, etc., we assume that there are a total of UAVs, and the path of each UAV consists of a series of discrete points, and the flight path of the UAVs is represented as a list consisting of a number of discrete points, : the set of path points of the UAV, where ; the total flight path length of the flight path of the UAV is represented as Equation (18):
| (18) |
Let the sum of the theoretical shortest path lengths of all UAV origins and destinations be , where the path cost from the origin to the destination is expressed as Equation (19):
| (19) |
where is the adjustment factor. By minimizing , it is possible to minimize the total range of the planned path, thus increasing the efficiency of the flight.
6.1.2. Security and Threat Constraints
In complex environments, UAVs must avoid static obstacles or airborne threats to ensure flight safety, where safety constraints are defined as cylindrical and spherical zones. Assuming there are obstacles in the environment, each obstacle is represented by a cylindrical zone with horizontal projected circular center coordinates of and radius of (). The safety radius of the UAV itself is denoted as , and the safety distance to be maintained outside the collision zone of the UAV and the obstacle is defined as . Let the closest distance to the center of an obstacle when the flight segment passes through the projection area of the obstacle be (e.g., Figure 2). Based on the distance of the UAV relative to the obstacle, the threat cost function of the flight segment relative to the obstacle can be defined as in Equation (20) below:
| (20) |
where
Figure 2.
Cylinder threat.
(1) If , the UAV has entered the collision zone of the obstacle, then the cost is taken as to indicate a collision;
(2) If , the UAV is far enough away from the obstacle, take ;
(3) If , the UAV has not collided but has entered the dangerous zone around the obstacle, and a penalty is applied to the path. The cost in this case is inversely proportional to the deviation from the distance and can be set to .
In summary, the total threat cost of the entire flight path relative to all obstacles can be cumulatively added to the threat surrogate value of each flight segment under each obstacle as in Equation (21):
| (21) |
For at waypoint , if detected inside the -th threat sphere, distance is calculated; For spherical region 1, given a constant , the cost contribution can be defined as ; For spherical region 2, the following equation is used, assuming that spherical region 2 has a radius of : and that the cumulative traversal cost per UAV in all threat regions is , where denotes the set of threat regions detected at point . The total threat traversal cost is then given by Equation (22):
| (22) |
With the threat-cost model described above, the cost will increase if the UAV’s path is too close to an obstacle, so the path planning will be directed away from the obstacle, and safety constraints will be met.
6.1.3. Cost of Flight Altitude
In practice, in complex environments, the flight altitude of a UAV usually needs to be limited to a certain altitude based on the accuracy requirements of sensors or remote sensing equipment such as detection radar. The mission requirements (e.g., clarity of aerial imagery, sensor accuracy) will specify a minimum altitude and a maximum altitude as the lower and upper limits of the safe flight altitude for the UAV and make the median safe value . e.g., Figure 3.
Figure 3.
Cost of flight altitude.
The altitude constraint is therefore included in the cost function of the path planning. For the altitude of at each of its track points , let the penalty function be defined as Equation (23):
| (23) |
That is, if the waypoint altitude is within the permissible range , the cost is taken as the deviation from the median of the range to encourage the UAV to fly in the middle of the permissible altitude range, and the altitude cost of the path can be obtained by summing the altitude costs of the path for all the waypoints along the path, then the altitude cost model of the flight is given by Equation (24):
| (24) |
Modelling in this way ensures that the planned paths strictly adhere to the upper and lower altitude limits specified by the mission, with appropriate penalties for approaching the altitude limits, thus improving the mission fitness of the paths.
6.1.4. Path Smoothness
To ensure a smooth UAV path, UAVs need to avoid violent steering and climb/dive maneuvers as much as possible. For this, two metrics, horizontal steering angle and climb angle, are introduced to quantify path smoothness, and their effects are incorporated into the cost function, e.g., Figure 4.
Figure 4.
Path Smoothness.
Firstly, the horizontal steering angle is defined as the degree of turning of the path in the horizontal plane: for the three consecutive waypoints , and in the path, their projection points on the horizontal plane are , and , respectively, then the horizontal steering angle can be defined as the angle between the projected segments and , i.e., the magnitude of the horizontal steering angle, which is calculated using Equation (25):
| (25) |
Secondly, the angle of climb is used to describe the degree of inclination of the path in the vertical direction and can be defined as the angle of climb or descent of the segment with respect to the horizontal plane. It is usually calculated using Equation (26):
| (26) |
where is the height difference between adjacent waypoints and is the projected length of the segment in the horizontal plane. On the basis of these two angles, the change in declination and elevation angle is determined for each between its successive waypoints, defining the indicator function as in Equation (27):
| (27) |
| (28) |
| (29) |
where and are the change in declination and pitch angle, respectively, for segment . Equation (28) is the angular constraint cost. By working together to form a cost function as in Equation (29), these two parts of the cost ensure that the generated path is smooth enough in 3D space to satisfy the UAV’s maneuverability constraints.
6.1.5. Time Synchronization Constraint
For , the total duration of its voyage is , where is the average speed of the UAV. Then the time synchronization cost is defined by Equation (30):
| (30) |
where is the time synchronization weighting factor and the target synergy time is .
6.1.6. Space Collision Costs
As in Figure 5, assuming collision detection between different UAVs, the number of times that the distance between and is detected to be less than the safe distance at the same time or time period is denoted as , where is the spatial synergy or collision weight factor. The spatial synergy cost model can be written as Equation (31):
| (31) |
Figure 5.
Safe distance for drones coordination.
6.1.7. Minimum Path Segment Interval Constraint
For each flight distance of , when , is a predetermined minimum allowable path segment length, the indicator function and the cost function can be defined as Equations (32) and (33):
| (32) |
| (33) |
Taking into account the path distance, obstacle threat, safety altitude range, and path smoothness, a comprehensive cost function (Equation (34)) for path planning can be established:
| (34) |
where , , , …, are the weighting parameters of each cost component, which can be set according to the mission requirements and unit scale differences. Up to this point, the UAV cooperative 3D path planning problem is transformed into an optimization problem with a comprehensive cost function F as the objective.
Restrictions:
Waypoints and are fixed to the given start and end points;
For each waypoint , must be satisfied, where is the area in which the UAV can fly.
6.2. Simulation Experiment
In this experiment, two terrain maps and two threat layouts are set up, four application scenarios are simulated and validated, the UAV formation consists of three UAVs, and ECFDBO is used to compare the GODBO and the original DBO algorithms that performed well in the test. The experimental settings are population size N = 30, iteration number D = 200, and fitness function weights 0.05, 0.05, 2, 0.7, 0.7, 0.6, 0.9, 0.9, etc. In this experimental phase, the aim is to plan a safe path; therefore, safety-related costs such as security and threat constraints, collisions, and time synchronization are given high weights to ensure the safety and coordination of the task. In practical application, design can be carried out according to specific needs. The path points are set to 15 × 3. The layout of the experimental scenarios is shown in Figure 6.
Figure 6.
Layout of the four simulated scenarios.
We applied the eight algorithms to the four scenarios in Figure 6 for experimental validation, and each scenario was run independently 10 times, and the MEAN and BEST metrics of each algorithm were counted separately. From Table 9, we can see that in Scenario 1, ECFDBO has an average score of 1.5688, which is just behind COA (1.4832) and BWO (1.5763), but its best score (0.7681) is much better than all the algorithms except GODBO (0.3057). This shows that in simple environments, ECFDBO can not only maintain a more stable global search level but also better explore the optimal solution space. As the complexity of Scenario 2 increases, the average fitness of most algorithms increases. At this time, ECFDBO’s average fitness of 1.5242 remains low, and its optimal fitness reaches 0.1660, which is the lowest among all algorithms. In Scenario 3, ECFDBO’s best = 0.8294 is in first place. Scenario 4 further increases the search difficulty, and the mean and optimal values of most algorithms are significantly higher than those in Scenario 3. ECFDBO’s mean = 1.4131 and best = 0.8181 are still robust, while GODBO (mean = 2.9202, best = 2.1725) and the other algorithms fluctuate more in comparison. The optimal values are bolded in the table.
Table 9.
Comparison of fitness values of various algorithms.
| DBO | BWO | COA | PIO | BOA | NOA | GODBO | ECFDBO | ||
|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | mean | 2.2316 | 1.5763 | 1.4832 | 2.0817 | 2.6013 | 2.7279 | 1.2346 | 1.5688 |
| best | 1.4468 | 1.5651 | 1.4044 | 1.7332 | 1.9031 | 2.6730 | 0.3057 | 0.7681 | |
| Scenario 2 | mean | 2.4209 | 1.5498 | 3.7070 | 3.0094 | 12.9084 | 9.0949 | 2.4308 | 1.5242 |
| best | 2.0802 | 1.4630 | 2.1446 | 1.8516 | 9.2956 | 6.6315 | 1.7541 | 0.166 0 | |
| Scenario 3 | mean | 1.7941 | 1.7472 | 1.8963 | 1.3048 | 2.9077 | 2.4024 | 1.7808 | 1.3504 |
| best | 1.4477 | 1.707 | 1.7199 | 0.9515 | 2.0745 | 1.8298 | 1.1031 | 0.8294 | |
| Scenario 4 | mean | 2.3057 | 1.7660 | 2.5658 | 3.4131 | 7.1357 | 7.5692 | 2.9202 | 1.4131 |
| best | 2.0574 | 1.7369 | 2.2404 | 2.5915 | 4.5966 | 5.4114 | 2.1725 | 0.8181 |
The fitness iteration curves are shown in Figure 7. Scenario 1 terrain is relatively simple; obstacles are scarce and scattered; each algorithm can easily find a safe and feasible path. In terms of the convergence curve (Figure 7a), ECFDBO and GODBO converge to the lowest track cost during the early iterations and tend to be stable and optimal in about 40–70 generations; the final path cost of the original DBO is slightly higher than that of the former two. This shows that in a simple environment, each algorithm can find a better solution. Regarding path planning results, the three-dimensional paths (Figure 8a) and top view (Figure 9a) show that all three algorithms generally share similar paths and effectively avoid obstacles. ECFDBO has fewer inflection points and good smoothness; DBO’s planned path, while safe and feasible, is slightly stiff at some turns and has more track corners than ECFDBO. This is because the global search pressure of each algorithm in simple scenarios is not large; DBO can find feasible paths, but its local optimization ability is slightly inferior, and the path smoothness is somewhat poor. From the height profile (Figure 10a), it is evident that ECFDBO provides the best optimal altitude control. In general, ECFDBO finds the optimal path in Scenario 1, which verifies the algorithm’s effectiveness in simple environments.
Figure 7.
Comparison of fitness curves.
Figure 8.
3D display of path.
Figure 9.
Vertical display of path.
Figure 10.
Height profile display of path.
Scenario 2 increases the number of safety constraints compared with Scenario 1, thus increasing the difficulty of path planning. From the convergence performance (Figure 7b), ECFDBO converges rapidly to the minimum cost in about 60 generations, showing excellent global optimization speed. DBO and GODBO converge in about 20–40 generations, but their minimum costs are slightly higher than that of ECFDBO. This indicates that the search accuracy of ECFDBO is significantly better than that of the other algorithms in this scenario. The path comparisons (Figure 8b and Figure 9b) reveal that all three algorithms exhibit varying degrees of constraint violation. However, ECFDBO demonstrates the optimal overall planning trend, effectively bypassing obstacles while remaining closer to the terrain. It can be seen from the top view that ECFDBO’s path shows a reasonable “S”-shaped smooth turn when crossing obstacle gaps, with continuous inflection points and uniform curvature. GODBO’s planned path is suboptimal, exhibiting slight zigzagging in the same region and significantly violating altitude constraints, indicating insufficient step-size control during local searches. In contrast, DBO generates a significantly longer detour, characterized by sharp bends near multiple obstacles and a less smooth and compact path. This indicates that the original DBO tends to produce oscillations near obstacles as environmental complexity increases. In contrast, ECFDBO effectively avoids over-corrected paths due to its chaotic disturbance and refined control through a nonlinear scaling strategy. In Figure 10b, ECFDBO still maintains good altitude. Therefore, ECFDBO not only converges faster in Scenario 2 but also plans a lower cost and smoother path.
As the terrain in Scenario 3 becomes more complex, the requirements for global exploration and fine obstacle avoidance are higher. The convergence curve (Figure 7c) shows that ECFDBO still maintains the fastest convergence rate and approaches the optimal solution at about 100 generations. The fitness curves of GODBO and DBO remain significantly higher than that of ECFDBO in the whole iteration process, indicating that they fall into local optimization. It is obvious that ECFDBO has a more stable optimization ability and global convergence effect in a complex terrain environment. From the path shape (Figure 8c), the three algorithms successfully plan the path through the complex terrain, but the differences are significant: ECFDBO’s track avoidance strategy is more intelligent, and it starts to adjust the altitude and direction before entering the narrow channel to achieve a high-quality solution; GODBO and DBO take a more conservative approach; their paths are close to the edge of the terrain, resulting in a ‘sliding along the wall’ phenomenon. The top view (Figure 9c) clearly shows that ECFDBO’s path maintains a more uniform buffer distance from obstacle boundaries, while GODBO’s path even exhibits dangerous behavior. ECFDBO adopts intelligent boundary handling, and when particles approach the boundary, they are guided by a gradient to actively stay away from the “danger wall,” avoiding the “collision–retreat–re-collision” circuitous phenomenon of traditional DBO. In addition, the ECFDBO track turns more smoothly, with only necessary direction changes and no obvious back-and-forth twists; in contrast, the path generated by DBO contains several small loops, indicating that its particles were trapped in local search areas and missed better paths.
Scenario 4 adds safety constraints to the complex scenario, including multiple adjacent obstacles. A comparison of algorithm convergence (Figure 7d) shows that although the problem in this scenario is complex, ECFDBO can still converge to the vicinity of global optimization within about 120 generations and obtain the lowest path cost; GODBO converges to the final solution at a slightly higher cost; the DBO convergence curve stays at a higher cost value for a long time, showing an obvious premature convergence tendency and only obtaining suboptimal solutions. From a three-dimensional perspective (Figure 8d), the path planning results of each algorithm can be visually compared. ECFDBO successfully opens up a nearly direct path while avoiding obstacle clusters: when approaching complex obstacle clusters, the path does not plunge into crowded areas but chooses a relatively open detour corridor in advance and then bypasses obstacle clusters with smooth curves. This “round-before-through” strategy makes the ECFDBO path compact and efficient both in the top plane (Figure 9d) and in the height profile (Figure 10d): the curved path closely follows the globally optimal ideal path, with little excess detour and height fluctuation. In contrast, GODBO’s path has many sharp turns in this complex environment: from the top view, its path has made sharp turns close to right angles in order to avoid some obstacles, which not only increases the range but also causes the path not to be smooth; more seriously, it can be found in Figure 8d that GODBO’s planned path even has a “knotting” phenomenon. The path quality of the original DBO is the worst: DBO falls into local search in front of the obstacle group due to a lack of an effective disturbance-jumping mechanism, and finally, the planned track takes a large circle to reach the target, and the path cost is much higher than ECFDBO. ECFDBO stands out precisely because of its environment-aware boundary strategy: when particles approach an obstacle boundary, the algorithm does not simply truncate their coordinates but uses gradient information to bounce them away from the obstacle by a certain distance. This mechanism reduces the detour of repeated correction after collision with obstacles so that the ECFDBO track can keep smooth progress in complex areas. To sum up, ECFDBO achieves global optimal planning with the shortest path length, the lowest total cost, and the smoothest and safest path in the most complex Scenario 4, which fully proves the value of the improved strategy proposed in this paper in practical complex path planning.
In the above experiments in 3D environments of varying difficulty, the ECFDBO algorithm is able to converge to points with lower path generation values in all scenarios. Especially in complex environments, the advantages of ECFDBO over the original DBO and GODBO are more obvious—its global exploration capability ensures that the algorithm does not fall into suboptimal solutions in localized regions of obstacles, while the intelligent boundary handling and chaotic perturbation mechanisms improve path smoothing and reduce ineffective detours. The final results show that ECFDBO is able to more reliably plan safe and efficient 3D UAV paths, meeting the path optimality and smoothness requirements for practical tasks.
7. Conclusions
The Environment-aware Chaotic Force-field Dung Beetle Optimizer (ECFDBO) proposed in this paper significantly enhances the global optimization capability and convergence accuracy compared with the original DBO algorithm by employing three innovative strategies. Furthermore, ECFDBO is applied to plan remote sensing application paths in different complex environment scenarios. The results show that the ECFDBO algorithm can find the global optimal path in a complex environment with a faster convergence speed. These studies show that ECFDBO has broad prospects in the field of high-dimensional global optimization and can provide more efficient and reliable solutions for the autonomous navigation of unmanned aerial vehicles in complex environments. Nowadays, machine learning algorithms, such as reinforcement learning, are widely used for bionic robot path planning. Lin and Li et al. proposed a novel fixed-horizon constrained reinforcement learning (RL) framework [52] to ensure vehicle safety and strike a balance between accomplishing goals and providing comfort. Additionally, they proposed a sample efficient teacher-advice mechanism with Gaussian process (TAG) [53] to address the challenges of low sample efficiency and exploration difficulties in reinforcement learning. The above methods may be used for UAV path planning in the future.
Appendix A
This appendix section consists of a classical convergence curve for CEC2017 (dim = 30, 50, 100). Provides visual evidence for the basic function tests in Section 5, including typical single-peak functions F1/F3, simple multi-peak functions F5/F8/F9/F10, hybrid functions F15/F16/F17/F20, and composition functions F21/F23/F24/F27/F29/F30.
Figure A1.
Convergence trends of classical functions in CEC 2017 (dim = 30).
Figure A2.
Convergence trends of classical functions in CEC 2017 (dim = 50).
Figure A3.
Convergence trends of classical functions in CEC 2017 (dim = 100).
Author Contributions
Conceptualization, X.Z. and R.L.; methodology, R.L. and X.Z.; investigation, X.Z. and R.L.; writing—original draft preparation, R.L.; writing—review and editing, X.Z. and R.L.; supervision, S.L. and X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
The original contributions presented in this study are included in the article. further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflicts of interest.
Funding Statement
This research was supported by the research grant from the National Key Research and Development Program of China (2024YFB3312204).
Footnotes
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
References
- 1.Ndlovu H.S., Odindi J., Sibanda M., Mutanga O. A systematic review on the application of UAV-based thermal remote sensing for assessing and monitoring crop water status in crop farming systems. Int. J. Remote Sens. 2024;45:4923–4960. doi: 10.1080/01431161.2024.2368933. [DOI] [Google Scholar]
- 2.Yang Z., Yu X., Dedman S., Rosso M., Zhu J., Yang J., Xia Y., Tian Y., Zhang G., Wang J. UAV remote sensing applications in marine monitoring: Knowledge visualization and review. Sci. Total Environ. 2022;838:155939. doi: 10.1016/j.scitotenv.2022.155939. [DOI] [PubMed] [Google Scholar]
- 3.Guan S., Zhu Z., Wang G. A review on UAV-based remote sensing technologies for construction and civil applications. Drones. 2022;6:117. doi: 10.3390/drones6050117. [DOI] [Google Scholar]
- 4.Debnath D., Hawary A.F., Ramdan M.I., Alvarez F.V., Gonzalez F. QuickNav: An effective collision avoidance and path-planning algorithm for UAS. Drones. 2023;7:678. doi: 10.3390/drones7110678. [DOI] [Google Scholar]
- 5.Meng Q., Qu Q., Chen K., Yi T. Multi-UAV Path Planning Based on Cooperative Co-Evolutionary Algorithms with Adaptive Decision Variable Selection. Drones. 2024;8:435. doi: 10.3390/drones8090435. [DOI] [Google Scholar]
- 6.Maboudi M., Homaei M.R., Song S., Malihi S., Saadatseresht M., Gerke M. A review on viewpoints and path planning for UAV-based 3-D reconstruction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023;16:5026–5048. doi: 10.1109/JSTARS.2023.3276427. [DOI] [Google Scholar]
- 7.Zhang Z., Zhu L. A review on unmanned aerial vehicle remote sensing: Platforms, sensors, data processing methods, and applications. Drones. 2023;7:398. doi: 10.3390/drones7060398. [DOI] [Google Scholar]
- 8.Nex F., Remondino F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014;6:1–15. doi: 10.1007/s12518-013-0120-x. [DOI] [Google Scholar]
- 9.Mazaheri H., Goli S., Nourollah A. A Survey of 3D Space Path-Planning Methods and Algorithms. ACM Comput. Surv. 2024;57:1–32. doi: 10.1145/3673896. [DOI] [Google Scholar]
- 10.Dechter R., Pearl J. Generalized best-first search strategies and the optimality of A. J. ACM. 1985;32:505–536. doi: 10.1145/3828.3830. [DOI] [Google Scholar]
- 11.Hart P.E., Nilsson N.J., Raphael B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968;4:100–107. doi: 10.1109/TSSC.1968.300136. [DOI] [Google Scholar]
- 12.Mandloi D., Arya R., Verma A.K. Unmanned aerial vehicle path planning based on A* algorithm and its variants in 3d environment. Int. J. Syst. Assur. Eng. Manag. 2021;12:990–1000. doi: 10.1007/s13198-021-01186-9. [DOI] [Google Scholar]
- 13.Bai X., Jiang H., Cui J., Lu K., Chen P., Zhang M. UAV path planning based on improved A∗ and DWA algorithms. Int. J. Aerosp. Eng. 2021;2021:4511252. doi: 10.1155/2021/4511252. [DOI] [Google Scholar]
- 14.Chen J., Li M., Yuan Z., Gu Q. An improved A* algorithm for UAV path planning problems; Proceedings of the IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC); Chongqing, China. 12–14 June 2020; pp. 958–962. [Google Scholar]
- 15.Sun S., Wang H., Xu Y., Wang T., Liu R., Chen W. A Fusion Approach for UAV Onboard Flight Path Management and Decision Making Based on the Combination of Enhanced A* Algorithm and Quadratic Programming. Drones. 2024;8:254. doi: 10.3390/drones8060254. [DOI] [Google Scholar]
- 16.Huang C. A Novel Three-Dimensional Path Planning Method for Fixed-Wing UAV Using Improved Particle Swarm Optimization Algorithm. Int. J. Aerosp. Eng. 2021;2021:7667173. doi: 10.1155/2021/7667173. [DOI] [Google Scholar]
- 17.Heidari H., Saska M. Collision-free path planning of multi-rotor UAVs in a wind condition based on modified potential field. Mech. Mach. Theory. 2021;156:104140. doi: 10.1016/j.mechmachtheory.2020.104140. [DOI] [Google Scholar]
- 18.Di B., Zhou R., Duan H. Potential field based receding horizon motion planning for centrality-aware multiple UAV cooperative surveillance. Aerosp. Sci. Technol. 2015;46:386–397. doi: 10.1016/j.ast.2015.08.006. [DOI] [Google Scholar]
- 19.Noreen I., Khan A., Habib Z. Optimal path planning using RRT* based approaches: A survey and future directions. Int. J. Adv. Comput. Sci. Appl. 2016;7:97–107. doi: 10.14569/IJACSA.2016.071114. [DOI] [Google Scholar]
- 20.Guo Y., Liu X., Yang Y., Zhang W. FC-RRT*: An improved path planning algorithm for UAV in 3D complex environment. ISPRS Int. J. Geo. Inf. 2022;11:112. doi: 10.3390/ijgi11020112. [DOI] [Google Scholar]
- 21.Phung M.D., Ha Q.P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization. Appl. Soft Comput. 2021;107:107376. doi: 10.1016/j.asoc.2021.107376. [DOI] [Google Scholar]
- 22.Pehlivanoglu Y.V., Pehlivanoglu P. An enhanced genetic algorithm for path planning of autonomous UAV in target coverage problems. Appl. Soft Comput. 2021;112:107796. doi: 10.1016/j.asoc.2021.107796. [DOI] [Google Scholar]
- 23.Roberge V., Tarbouchi M., Labonté G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inform. 2012;9:132–141. doi: 10.1109/TII.2012.2198665. [DOI] [Google Scholar]
- 24.Kennedy J. Handbook of Nature-Inspired and Innovative Computing: Integrating Classical Models with Emerging Technologies. Springer; Boston, MA, USA: 2006. pp. 187–219. [Google Scholar]
- 25.Fu Y., Ding M., Zhou C. Phase angle-encoded and quantum-behaved particle swarm optimization applied to three-dimensional route planning for UAV. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2011;42:511–526. doi: 10.1109/TSMCA.2011.2159586. [DOI] [Google Scholar]
- 26.Wei-Min Z., Shao-Jun L., Feng Q. θ-PSO: A new strategy of particle swarm optimization. J. Zhejiang Univ. Sci. A. 2008;9:786–790. doi: 10.1631/jzus.A071278. [DOI] [Google Scholar]
- 27.Hoang V.T., Phung M.D., Dinh T.H., Ha Q.P. Angle-encoded swarm optimization for uav formation path planning; Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); Madrid, Spain. 1–5 October 2018; pp. 5239–5244. [Google Scholar]
- 28.Sun J., Fang W., Wu X., Palade V., Xu W. Quantum-behaved particle swarm optimization: Analysis of individual particle behavior and parameter selection. Evol. Comput. 2012;20:349–393. doi: 10.1162/EVCO_a_00049. [DOI] [PubMed] [Google Scholar]
- 29.Phung M.D., Quach C.H., Dinh T.H., Ha Q. Enhanced discrete particle swarm optimization path planning for UAV vision-based surface inspection. Autom. Constr. 2017;81:25–33. doi: 10.1016/j.autcon.2017.04.013. [DOI] [Google Scholar]
- 30.Onwubolu G.C., Babu B.V., Clerc M. Discrete particle swarm optimization, illustrated by the traveling salesman problem. New Optim. Tech. Eng. 2004;47:219–239. [Google Scholar]
- 31.Yu X., Jiang N., Wang X., Li M. A hybrid algorithm based on grey wolf optimizer and differential evolution for UAV path planning. Expert Syst. Appl. 2023;215:119327. doi: 10.1016/j.eswa.2022.119327. [DOI] [Google Scholar]
- 32.Yu X., Chen W.N., Gu T., Yuan H., Zhang H., Zhang J. ACO-A*: Ant colony optimization plus A* for 3-D traveling in environments with dense obstacles. IEEE Trans. Evol. Comput. 2018;23:617–631. doi: 10.1109/TEVC.2018.2878221. [DOI] [Google Scholar]
- 33.Xu C., Duan H., Liu F. Chaotic artificial bee colony approach to Uninhabited Combat Air Vehicle (UCAV) path planning. Aerosp. Sci. Technol. 2010;14:535–541. doi: 10.1016/j.ast.2010.04.008. [DOI] [Google Scholar]
- 34.Debnath D., Vanegas F., Sandino J., Hawary A.F., Gonzalez F. A Review of UAV Path-Planning Algorithms and Obstacle Avoidance Methods for Remote Sensing Applications. Remote Sens. 2024;16:4019. doi: 10.3390/rs16214019. [DOI] [Google Scholar]
- 35.Dehghani M., Montazeri Z., Trojovská E., Trojovský P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl. Based Syst. 2023;259:110011. doi: 10.1016/j.knosys.2022.110011. [DOI] [Google Scholar]
- 36.Arora S., Singh S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019;23:715–734. doi: 10.1007/s00500-018-3102-4. [DOI] [Google Scholar]
- 37.Zhong C., Li G., Meng Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl. Based Syst. 2022;251:109215. doi: 10.1016/j.knosys.2022.109215. [DOI] [Google Scholar]
- 38.Duan H., Qiao P. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning. Int. J. Intell. Comput. Cybern. 2014;7:24–37. doi: 10.1108/IJICC-02-2014-0005. [DOI] [Google Scholar]
- 39.Abdel-Basset M., Mohamed R., Jameel M., Abouhawwash M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl. Based Syst. 2023;262:110248. doi: 10.1016/j.knosys.2022.110248. [DOI] [Google Scholar]
- 40.Liu B., Cai Y., Li D., Lin K., Xu G. A Hybrid ARO Algorithm and Key Point Retention Strategy Trajectory Optimization for UAV Path Planning. Drones. 2024;8:644. doi: 10.3390/drones8110644. [DOI] [Google Scholar]
- 41.Xue J., Shen B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023;79:7305–7336. doi: 10.1007/s11227-022-04959-6. [DOI] [Google Scholar]
- 42.Shen Q., Zhang D., Xie M., He Q. Multi-strategy enhanced dung beetle optimizer and its application in three-dimensional UAV path planning. Symmetry. 2023;15:1432. doi: 10.3390/sym15071432. [DOI] [Google Scholar]
- 43.Tang X., He Z., Jia C. Multi-strategy cooperative enhancement dung beetle optimizer and its application in obstacle avoidance navigation. Sci. Rep. 2024;14:28041. doi: 10.1038/s41598-024-79420-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zilong W., Peng S. A multi-strategy dung beetle optimization algorithm for optimizing constrained engineering problems. IEEE Access. 2023;11:98805–98817. doi: 10.1109/ACCESS.2023.3313930. [DOI] [Google Scholar]
- 45.Hu W., Zhang Q., Ye S. An enhanced dung beetle optimizer with multiple strategies for robot path planning. Sci. Rep. 2025;15:4655. doi: 10.1038/s41598-025-88347-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhang R., Chen X., Li M. Multi-UAV cooperative task assignment based on multi-strategy improved DBO. Clust. Comput. 2025;28:195. doi: 10.1007/s10586-024-04912-7. [DOI] [Google Scholar]
- 47.Shen Q., Zhang D., He Q., Ban Y., Zuo F. A novel multi-objective dung beetle optimizer for Multi-UAV cooperative path planning. Heliyon. 2024;10:e37286. doi: 10.1016/j.heliyon.2024.e37286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Chen Q., Wang Y., Sun Y. An improved dung beetle optimizer for UAV 3D path planning. J. Supercomput. 2024;80:26537–26567. doi: 10.1007/s11227-024-06414-0. [DOI] [Google Scholar]
- 49.Lv F., Jian Y., Yuan K., Lu Y. Unmanned Aerial Vehicle Path Planning Method Based on Improved Dung Beetle Optimization Algorithm. Symmetry. 2025;17:367. doi: 10.3390/sym17030367. [DOI] [Google Scholar]
- 50.Wolpert D.H., Macready W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1:67–82. doi: 10.1109/4235.585893. [DOI] [Google Scholar]
- 51.Ait Saadi A., Soukane A., Meraihi Y., Benmessaoud Gabis A., Mirjalili S., Ramdane-Cherif A. UAV path planning using optimization approaches: A survey. Arch. Comput. Methods Eng. 2022;29:4233–4284. doi: 10.1007/s11831-022-09742-7. [DOI] [Google Scholar]
- 52.Lin K., Li Y., Chen S., Li D., Wu X. Motion planner with fixed-horizon constrained reinforcement learning for complex autonomous driving scenarios. IEEE Trans. Intell. Veh. 2023;9:1577–1588. doi: 10.1109/TIV.2023.3273857. [DOI] [Google Scholar]
- 53.Lin K., Li D., Li Y., Chen S., Liu Q., Gao J., Jin Y., Gong L. Tag: Teacher-advice mechanism with gaussian process for reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2024;35:12419–12433. doi: 10.1109/TNNLS.2023.3262956. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The original contributions presented in this study are included in the article. further inquiries can be directed to the corresponding author(s).