A bayesian network model for neurocognitive disorders digital screening in Chinese population: development and validation study

Abstract

Background

Neurocognitive disorders (NCDs), classified under the ICD-10 codes F00-F09, are a category of mental disorders associated with brain disease, injury, or systemic conditions leading to cerebral dysfunction. NCDs represent a significant disease burden and an increasingly critical global public health challenge. Early screening for neurocognitive disorders is conducive to improving patients’ quality of life and reducing healthcare costs. Therefore, there is an urgent need to develop an inexpensive and convenient screening model for neurocognitive disorders that can be applied to large populations to improve the efficiency of neurocognitive disorders screening.

Methods

This study aimed to construct a classification model for screening neurocognitive disorders (NCDs) based on cross-sectional electronic health record data from the Cheeloo Whole Lifecycle eHealth Research-based Database (2015–2017). Eligible participants were adults aged 18 years or older, without prior diagnosis of neurocognitive disorders at baseline, covering multiple cities in Shandong Province, China. Among 1,626,817 individuals initially screened, 4,518 diagnosed NCD cases were included for model building and validation. Participants were assigned to a training set or a validation set based on their geographic locations. A Bayesian network classification model was developed by initially screening variables through univariate logistic regression. Gender and the top 30 variables with the highest coefficient of determination () in explaining the variance in NCD status were retained for model construction. Subsequently, the optimal network structure was identified using the Tabu search algorithm guided by Bayesian Information Criterion, with parameters estimated by maximum likelihood estimation. The model’s performance was benchmarked against a multivariable logistic regression model. The model’s performance was validated through ROC curves, calibration curves, and decision curves analysis. Sensitivity analyses were performed by introducing random missingness into the dataset to evaluate robustness of Bayesian network model and multivariable logistic regression model.

Results

The final Bayesian network model included 31 variables in total, of which eight were directly connected to the neurocognitive disorders node in the learned Bayesian network structure. The Bayesian network model had good predictive discrimination, with AUC of 0.849 (95% CI; 0.839-0.859), 0.821 (95% CI; 0.803-0.840) and 0.800 (95% CI; 0.785-0.815) in the training, testing and validation sets, respectively. The calibration curves were well calibrated, and the decision curve analysis demonstrated its clinical applicability. In sensitivity analysis, the AUC of the Bayesian network model was 0.791 (95% CI; 0.777-0.806), with good robustness to missing data.

Conclusions

The findings of this study indicated that the established Bayesian network model could identify factors directly related to neurocognitive disorders and accurately predicted the risk of neurocognitive disorders in primary healthcare settings. The Bayesian network model is applicable to screening for neurocognitive disorders in large-scale electronic health record systems among adult populations. The proposed Bayesian network model incorporates 31 variables spanning demographic and clinical variables and demonstrates robustness to missing data, supporting its potential utility in clinical decision-making contexts.

Supplementary Information

The online version contains supplementary material available at 10.1186/s12888-025-07189-1.

Introduction

Neurocognitive disorders (NCDs) are a class of conditions characterized by acquired cognitive impairment attributable to brain pathology. NCDs encompass both mild and major neurocognitive disorders, reflecting a continuum from subtle cognitive deficits to significant dementia [1, 2]. NCDs affect more than 55 million individuals worldwide, with this number expected to reach approximately 139 million by 2050 [3]. In China, the burden is particularly severe due to the large population and rapidly aging demographic [4]. An estimated 15 million individuals in China are living with dementia, accounting for approximately one-quarter of global cases [5–7]. Consequently, the high prevalence and heavy burden of NCDs in China and worldwide have made the early detection and prevention a public health priority [8–10].

Early identification and intervention in NCDs are crucial for effectively improving patients’ quality of life and reducing the disease burden [11]. However, existing tools for NCDs screening and diagnosis are insufficient for large-scale early detection, especially in low-resource primary care environments. Global estimates suggest up to 75% of dementia cases are missed, rising to 90% in low-resource settings [12]. To improve early detection, clinicians rely on brief cognitive screening tools such as the Mini-Mental State Examination (MMSE) and Montreal Cognitive Assessment (MoCA). A community-based meta-analysis found that the MMSE identified dementia with pooled sensitivity equal to 0.73 and pooled specificity equal to 0.83 [12]. Beyond cognitive testing, various neuroimaging and fluid biomarkers have been explored to enhance diagnostic accuracy. A systematic review of structural MRI in Alzheimer’s patients found that visual medial-temporal atrophy ratings have AUC equal to 0.88 [13]. A large multicenter diagnostic study of 1767 patients found that an automated plasma p-tau217 assay discriminated Alzheimer Disease pathology with AUC equal to 0.94 [14]. Despite their diagnostic value, current screening tools face practical barriers. Cognitive tests are time-consuming and culturally biased, and imaging and CSF biomarkers are costly and invasive [15–17]. These methods’ limitations making large-scale primary care screening of NCDs challenging. There is therefore an urgent need for new screening approaches that are accurate, scalable, and cost-effective for early detection of NCDs in the community setting [18, 19].

In recent years, machine learning (ML) applied to electronic health records (EHRs) has emerged as a promising approach to predict the risk of NCDs before clinical onset. A study using gradient-boosted trees in over one million US patients achieved an AUC of 0.85 for current Alzheimer’s detection [11]. A primary care study at Stanford Health Care used random forest models to predict one-year incident mild cognitive impairment, yielding AUC of 0.68 [20]. In the Cache County cohort, a population-based random forest model predicted dementia with an AUC of 0.67 [21]. Although these studies demonstrate the potential of ML-EHR approaches across diverse settings, most ML approaches often remain “black boxes”, may not generalize well beyond the training data, and are sensitive to missing data, which limits clinical translation.

In this context, Bayesian network (BN) modeling offers a promising approach to address these challenges [22]. A Bayesian network is a probabilistic graphical model that encodes dependencies among variables in a directed acyclic graph (DAG) [23]. It can represent the causal relationships between risk factors and an outcome (for instance, linking age, gender, medical history and other factors to NCD) and compute the likelihood of the outcome given only partial evidence [24, 25]. BNs are inherently interpretable, allowing clinicians to visualize how individual risk factors contribute to predicted outcomes [26, 27]. Bayesian inference involves updating prior beliefs with observed data to estimate the probability of outcomes under uncertainty. BNs also accommodate missing data through probabilistic inference, as they can estimate the posterior distribution of unknown variables conditioned on available observations. This property is particularly valuable in EHR settings, where missingness is common due to incomplete clinical documentation. By enabling model-based inference without requiring complete-case datasets or imputation, BNs offer a practical degree of robustness when applied to real-world healthcare data [28]. Despite these strengths, BN models remain underutilized for large-scale NCD screening in primary care, particularly within the Chinese healthcare system.

In the present study, we developed and validated a Bayesian network based digital screening model for neurocognitive disorders using a large EHR dataset, Cheeloo Whole Lifecycle eHealth Research-based Database (Cheeloo LEAD). We focus on the primary health care context in China and target adult population who have not yet been diagnosed with an NCD. We evaluated the proposed BN model’s performance and compared it against a multivariable logistic regression model to assess its added value. Our goal is to create an accessible, low-cost toll capable of estimating an adult individual’s NCD risk during routine healthcare encounters and flagging high-risk individuals before clinical diagnosis.

Methods

Study population

The data used for this study were obtained from the Cheeloo Whole Lifecycle eHealth Research-based Database (Cheeloo LEAD), a large-scale longitudinal electronic health record (EHR) system covering multiple regions in Shandong Province, China. This database includes a randomly sampled cohort of 5 million individuals (4,912,928) from 39 counties (districts) out of a population of 101 million in 136 counties (districts) in Shandong Province, using the National Institute of Healthcare Big Data collection model to establish a longitudinal cohort. This study is a cross-sectional evaluation of specific moments in participants’ timelines. All raw EHR data were subjected to a standardized cleaning process. Duplicate entries were removed, and missing value and outliers were evaluated for each variable. Diagnostic information was mapped to ICD-10 codes, and laboratory indicators were converted to uniform units across districts where necessary. Variable names and formats were harmonized across regions to ensure consistency. All data preprocessing and quality control procedures were centrally performed at Shandong University before modeling. A total of 1,626,817 participants who had records in the database from January 1, 2015, to October 31, 2017, were included based on the following exclusion criteria: (1) participants diagnosed with neurocognitive disorders at baseline were excluded, (2) participants younger than 18 years old were excluded, and (3) participants without a risk event before October 31, 2017, were excluded. Individuals diagnosed with NCDs at baseline were excluded to ensure that the model was trained on individuals without known disease at the time of risk prediction, reflecting a screening context. We also excluded individuals without any recorded risk event prior to the end of the observation period. Among the 1,626,817 participants, 4,518 were diagnosed with neurocognitive disorders. The data were extracted from the EHR system, comprising demographic characteristics, laboratory results and medical history. The matching was conducted using the ID number and seat unique identifier. The data were subsequently aggregated and collated at the University of Shandong.

This study was performed in accordance with the Declaration of Helsinki and was approved by the Institutional Review Board of the Shandong University School of Public Health, China (Approval No. LL20240308). The research involved secondary analysis of fully anonymized electronic health records, and informed consent was not required, as determined by the Institutional Review Board of the Shandong University School of Public Health, in accordance with the Measures for the Ethical Review of Life Science and Medical Research Involving Humans (2023), issued by the National Health Commission of China.

Outcome definitions

In this study, we coded the diagnosis of neurocognitive disorders as F00-F09 according to the International Classification of Diseases-10 (ICD-10). The details of this classification are outlined in Supplement S1. Patients who were assigned any of these codes were considered to have neurocognitive disorders. To comprehensively assess the impact of neurocognitive disorders, this study included not only typical NCDs but also ICD-10 codes F07 and F09. These conditions primarily present with behavioral and personality problems but may also involve changes in cognitive functioning due to their etiology involving brain disease or injury. Including these codes provides a more complete understanding of all mental and behavioral changes due to brain disease or injury.

Statistical analysis

Grouping and feature selection

Figure 1 illustrates the flowchart of the entire study. The population was divided into an internal training set (n = 1,248,960) and an validation set (n = 377,857) based on their recording location. Samples from Qingdao city, Yantai city, and Weihai city were assigned to the validation set, while samples from other cities in Shandong Province were used as the training set. This grouping allows for the assessment of the model’s performance across different regions and its generalizability, as the validation set population differs significantly from the training set population in terms of environmental factors and lifestyle habits. This approach also helps to avoid overfitting in the training set. Within the internal training set, we further divided it into a training set (n = 874,272) and a testing set (n = 374,688) based on a 7:3 ratio.

Fig. 1.

Flowchart of the study

In order to select the most appropriate features, a number of risk factors were taken into consideration. Candidate predictors included demographic characteristics, diagnostic codes, and medication use. Initially, variables that were statistically significant in univariable logistic regression analysis were included for further feature selection. We used p < 0.001 (Bonferroni correction) as the statistically significant threshold to avoid type I error inflation. Subsequently, we sorted all the statistically significant variables by their R² values in logistic regressions, selecting the top 30 variables for further analysis.

To justify the adequacy of sample size for model development, we followed the framework proposed by Riley et al. [29], which provides criteria for minimum required sample size in prediction models with binary outcomes. This approach considers the number of candidate predictor parameters, the anticipated outcome prevalence, and the expected model discrimination (C-statistic). We used the pmsamplesize R package [30] to estimate the minimum required sample size to satisfy three criteria: (1) a global shrinkage factor ≥ 0.9, (2) small absolute difference of ≤ 0.05 in adjust Nagelkerke’s R2, and (3) precise estimation of the overall risk in the population. To ensure adequate statistical power for model performance evaluation, we assessed the minimum required sample size for validating a binary outcome prediction model, following the framework proposed by Riley et al. [31] Sample size required of validation set were estimated using pmvalsampsize R package. We specified an outcome prevalence of 0.250% for training set, 0.385% for validation set and an expected C-statistic of 0.75.

Bayesian network

A Bayesian network (BN) model is a graphical representation used to describe uncertain causal relationships between variables. It is structured as a directed acyclic graph (DAG), where nodes represent variables, and directed edges indicate causal dependencies between them. For two nodes 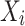and 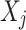in a BN 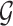, if there is a directed edge 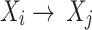in 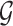, 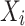is a parent of 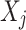. Under causal Markov conditions, the joint probability P of a Bayesian network can be expressed by the product of the conditional dependencies between all variables:

where 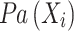represents the set of parent nodes of .

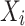Bayesian network analysis using data involves two main steps: structure learning and parameter learning [32]. Structure learning aims to identify the causal dependencies between variables from data. Methods for Bayesian network structure learning include score-based algorithms, constraint-based learning algorithms, and hybrid algorithms combining both approaches. Score-based algorithms use a scoring function to search the space of all possible structures [33], while constraint-based methods rely on the conditional independence of variables to derive Bayesian network structures [34, 35]. Parameter learning aims to determine the conditional probability distributions of all variables once the network structure is established. Common methods for parameter learning include the maximum likelihood estimate and the maximum posterior probability methods [36]. Additionally, prior knowledge about the structure or parameters can be incorporated into the learning process.

In our analysis, we included neurocognitive disorders and 31 other variables (gender, and the top 30 selected variables) in constructing the initial network. Gender was included a priori due to its established role in NCD epidemiology and its importance as a demographic stratification variable in public health models. In the first step of constructing Bayesian network model, we used the Incremental Association Markov Blanket (IAMB) algorithm [35] to identify variables directly related to NCDs among all 31 variables. Next, we implemented Tabu Search algorithm using the bnlearn R package, with default parameters and Bayesian Information Criterion (BIC) scoring function [37]. Tabu Search algorithm [33] is a metaheuristic optimization score-based structure learning approach that iteratively explores network structures by adding, removing, or reversing arcs. To avoid local optima, the algorithm maintains a tabu list of recently visited structures that are temporarily forbidden from revisiting. For parameter learning, we used the maximum likelihood estimate method [36] to determine the network’s parameters. The BN analyses were conducted using the bnlearn package in R 4.0.3 [38].

To enhance model robustness and reduce overfitting, 5-fold cross-validation was conducted within the training set for Bayesian network model [39]. In each fold, the training data were partitioned into five subsets. For each fold, we identified the optimal classification threshold that optimized both sensitivity and specificity simultaneously determined by the Youden index. The optimal thresholds obtained across the five folds were averaged and then applied to compute AUC-ROC, sensitivity, and specificity for each fold. We then reported the mean and standard deviation of these performance metrics across the folds as measures of internal performance consistency.

Model comparison

In this study, a multivariable logistic regression model was used as a benchmark to compare its discrimination performance with the Bayesian network model. The multivariable logistic regression model was fit using maximum likelihood estimation. The variables directly associated with neurocognitive disorders (obtained from the IAMB algorithm) were utilized for model construction. Multivariable logistic regression model was trained on training set (randomly selected 70% subset of the internal dataset). For samples with missing data, missing values were imputed using Random Forest method separately within each data split. Imputation in the testing and validation sets was performed independently, without access to outcome variable (NCD), to prevent data leakage. The multivariable logistic regression model was subjected to the same 5-fold cross-validation approach as the Bayesian network to evaluate model robustness estimate internally validated performance metrics.

Sensitivity analysis

To assess the generalizability of the model, we conducted a sensitivity analysis, simulating randomly missing data in the validation dataset. Given the large amount of missing data in real-world applications, 30% of the data for each of the 30 variables used to construct the network model was made randomly missing. The Bayesian network model allows for the prediction of NCD probability directly from incomplete data. In contrast, the multivariate logistic regression model requires missing data to be imputed first. For the logistic regression model, missing data were imputed using random forests. Missing values were imputed using the random forest algorithm implemented in the randomForest package and missForest package in R [40, 41]. The default settings were used, with 100 trees. The algorithm iteratively performed imputation until convergence or a maximum of 10 iterations. Imputations was conducted separately within the training, testing and validation datasets to prevent information leakage.

Model evaluation

The performance of the model was evaluated using metrics, including the area under the receiver operating characteristic curve (AUC), sensitivity, specificity, calibration curves and decision curves analysis (DCA).

Sensitivity is the rate at which the test correctly identifies true positives and specificity is the rate at which the test correctly identifies true negatives. The ROC curve illustrates the trade-off between sensitivity and specificity at different thresholds, with the horizontal axis representing 1-specificity and the vertical axis representing sensitivity. AUC is a composite metric between 0 and 1 that indicates the ability of the model to correctly identify patients and non-patients, with a larger AUC indicating better accuracy. We selected the threshold that maximized the Youden Index on ROC curve. This threshold was used to compute sensitivity, specificity, and accuracy for each model in the respective datasets. To test whether differences in AUC between the Bayesian network model and the multivariable logistic regression model were statistically significant, we perform pairwise Delong’s tests [42] for correlated ROC curves using the pROC package in R [43].

Calibration curves, where the horizontal axis represents the predicted risk of disease and the vertical axis represents the actual risk of disease [44]. A linear regression model was fitted to the scatter plots in the calibration curves to obtain the slope (B) and intercept (A) of the calibration curves, such that the calibration ability of the model is better when B is closer to 1 and A is closer to 0. Calibration performance was additionally evaluated using the Integrated Calibration Index (ICI) [45] and Expected Calibration Error (ECE) [46], which provide global and local measures of calibration accuracy. ICI was calculated as the average absolute difference between observed and predicted probabilities across all patients. ECE was computed as the maximum absolute difference between observed and predicted probabilities across decile bins of predicted risk. DCA allows the assessment of clinical benefit, is able to combine true and false positive rates at different thresholds, and considers the practical value of predictive modelling in clinical decision making [47]. These evaluation metrics collectively help in understanding the performance and reliability of the models in predicting neurocognitive disorders.

Results

Descriptive analysis

This study was based on the Cheeloo LEAD database, with a cross-sectional data window from January 1, 2015, to October 31, 2017, including 1,626,817 individuals. A total of 4,518 patients with NCDs were identified according to the inclusion and exclusion criteria, resulting in a cumulative prevalence rate of NCDs of 0.277% in the population aged 18 years and above. The numbers of males and females with NCDs were similar, with 2,217 and 2,301 patients, respectively. However, the cumulative incidence rate was higher for women (0.345%) than for men (0.230%).

Following previous studies on age group division [48, 49], we categorized the study population into eight age groups: 18–24 years, 25–34 years, 35–44 years, 45–54 years, 55–64 years, 65–74 years, 75–84 years, and 85 years or older. The cumulative incidence rate increased with age. The number of cases in the eight age groups was 158, 533, 502, 684, 876, 875, 705, and 185, respectively. The cumulative incidence rate was highest in the older age groups (≥ 65 years), with rates of 0.517% in the 65–74 age group, 0.870% in the 75–84 age group, and 1.303% in the 85 + age group. The number of patients with neurocognitive disorders and the cumulative incidence rate of NCDs in the sample population by sex and age group are shown in Table S1&S2.

Sample size adequacy for model development was assessed using the pmsamplesize R package. Based on 31 predictor parameters, a target C-statistic of 0.75, and an outcome prevalence of 0.250%, the minimum required sample size was 126,664 individuals with at least 317 events. All datasets met the threshold. The training set (n = 874,272, event = 2,184) and testing set (n = 374,688, event = 883) each independently met the required event-per-parameter ratio (EPP ≥ 10.21), ensuring that model development and internal validation were conducted under adequately powered conditions. The minimum required sample size for validating model performance was estimated to be 99,784 individuals (with at least 384 events), based a target C-statistic of 0.75, and an outcome prevalence of 0.384% and implemented via the pmvalsampsize R package. The validation set in this study comprised 377,857 participants, including 1,451 NCD cases, thereby exceeding the minimum requirement.

Variables selection

One-way logistic regression analysis was used to screen the variables included in the model, excluding those unrelated to the prevalence of NCDs. This analysis identified 239 significant variables, which were ranked according to their R² values. The top 30 variables, along with gender, were selected to construct the Bayesian network for NCD (Supplement Table S3). Table S4 displays the baseline characteristics of the selected variables, grouped by individual NCD status.

Bayesian network

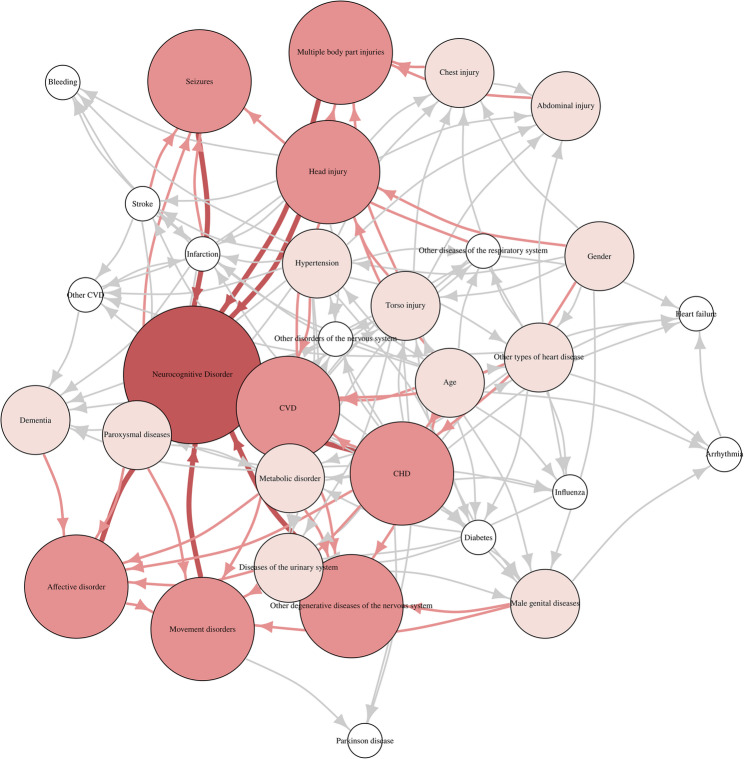
The final Bayesian network structure was learned using a tabu search algorithm optimized under the BIC score. The optimal model yielded a total BIC score of −4,431,200, reflecting the trade-off between model complexity and likelihood fit. The Bayesian network, including the selected variables, NCD and gender, is shown in Fig. 2.

Fig. 2.

The structure of Bayesian network model. Labeled ovals represent nodes; arrows (arcs) represent conditional-dependence relationships. Darker colors indicate nodes that are closer to the NCD

In the learned BN, Eight variables are directly associated with NCD: cerebrovascular disease, head injury, other degenerative diseases of the nervous system, affective disorder, multiple body part injuries, coronary heart disease, movement disorders, and seizures. The remaining 24 variables (75%) exhibited no directed edges toward the NCD node in the final Bayesian network. This indicates that, conditional on the eight directly connected variables, these remaining factors were rendered statistically independent of NCD under the learned structure. In the context of Bayesian inference, this reflects the conditional Markov property of the network: once the direct parents of NCD are accounted for, the non-parent variables contribute no additional predictive or probabilistic information regarding the presence of NCD.

Among the 31 variables included in the Bayesian network, 3 did not exhibit a directed path toward the NCD node. These variables were bleeding, heart failure, and Parkinson disease. The absence of a directed path to NCD indicates that any marginal association may be confounded by other variables. In the Bayesian reasoning framework, such variables still contribute indirectly by informing the joint probability distribution and influencing posterior inferences when included as part of the evidence set during probabilistic queries.

Multivariable logistic regression

Table 1 shows the results of the multivariable logistic regression. Seven of the eight variables were significantly associated (p < 0.001) with an increased risk of neurocognitive disorders, including cerebrovascular disease (OR = 7.11, 95% CI: 6.42–7.87), head injury (OR = 4.17, 95% CI: 3.65–4.76), other degenerative disease of the nervous system (OR = 4.38, 95% CI: 3.63–5.28), affective disorder (OR = 3.65, 95% CI: 3.09–4.31), multiple body part injuries (OR = 5.19, 95% CI: 4.30–6.27), coronary heart disease (OR = 2.25, 95% CI: 1.77–2.86), and seizures (OR = 1.22, 95% CI: 1.09–1.37). However, “movement disorders” (OR = 1.08, 95% CI: 0.84–1.39, p = 0.56) did not reach statistical significance in the multivariable logistic regression model, despite its presence as a direct parent in the Bayesian network. This divergence may reflect differences in modeling frameworks, as logistic regression evaluates marginal associations, whereas the Bayesian network considers conditional dependencies among variables.

Table 1.

Results of multivariable logistic regression

Variables	Beta	SE	OR (95% CI)	P value
Cerebrovascular disease	1.96	0.052	7.11 (6.42–7.87)	< 0.001
Head injury	1.43	0.068	4.17 (3.65–4.76)	< 0.001
Affective disorder	1.48	0.095	4.38 (3.63–5.28)	< 0.001
Other degenerative diseases of the nervous system	1.29	0.085	3.65 (3.09–4.31)	< 0.001
Multiple body part injuries	1.65	0.096	5.19 (4.30–6.27)	< 0.001
Seizures	0.81	0.122	2.25 (1.77–2.86)	< 0.001
Coronary heart disease	0.2	0.058	1.22 (1.09–1.37)	< 0.001
Movement disorders	0.07	0.129	1.08 (0.84–1.39)	0.560

Model performance

Discrimination performance

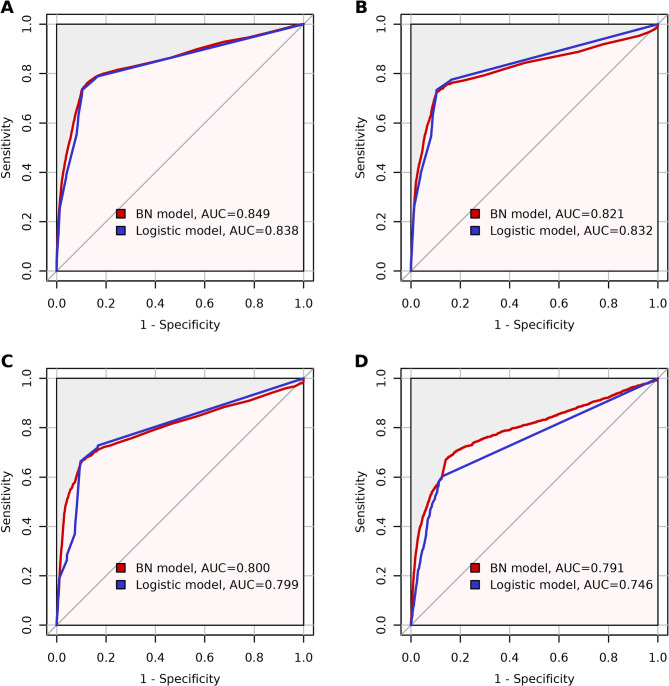
Figure 3 shows the discrimination performance of the Bayesian network model and the multivariable logistic regression model for the training set, testing set, validation data and sensitivity analysis. The Bayesian network model (red lines in Fig. 3) achieved an AUC of 0.849 (95% CI; 0.839-0.859) in the training set, 0.821 (95% CI; 0.803-0.840) in the testing set, and 0.800 (95% CI; 0.785-0.815) in the validation set. The multivariable logistic regression model (blue lines in Fig. 3) demonstrated an AUC of 0.838 (95% CI; 0.829-0.847) in the training set, 0.832 (95% CI; 0.817-0.847) in the testing set, and 0.799 (95% CI; 0.787-0.811) in the validation set. These results indicate that the predictive discriminative power of the Bayesian network model is comparable to that of the multivariable logistic regression model. In the sensitivity analysis with missing data (Fig. 3D), the Bayesian network model achieved an AUC of 0.791 (95% CI; 0.777-0.806), while the logistic regression model had an AUC of 0.746 (95% CI; 0.733-0.759). Table 2 presents the cross-validation results for both the Bayesian network and multivariable logistic regression models, including performance metrics from each fold as well as their averaged values. In the 5-fold cross-validation performed on the training set, the Bayesian network achieved a mean AUC of 0.849, a mean sensitivity of 0.896, and a mean specificity of 0.737 when using the averaged threshold derived from the Youden index. These results indicate good internal consistency and suggest that the model maintained stable performance across different subsamples within the training set. The logistic regression model yielded a mean AUC of 0.838, a mean sensitivity of 0.896, and a mean specificity of 0.733. Delong’s test revealed that there was no statistically difference in AUC between the two models in the training set (p = 0.1188), testing set (p = 0.3856), and validation set (p = 0.8869). However, in the sensitivity analysis under 30% missing data, the Bayesian network model significantly outperformed the multivariable logistic regression model (p < 0.0001). This suggests that the Bayesian network model retains similar discriminative power with incomplete data and performs significantly better than the logistic regression model, demonstrating superior generalization and reduced overfitting.

Fig. 3.

ROC curves of the BN model (red line) and the Logistic model (blue line) in (A) training set, (B) testing set, (C) validation set and (D) sensitivity analysis

Table 2.

Results of cross-validation

Metrics	Fold 1	Fold 2	Fold 3	Fold 4	Fold 5	Mean (SD)
Bayesian network model
Sensitivity	0.897	0.896	0.897	0.895	0.895	0.896 (0.001)
Specificity	0.725	0.736	0.748	0.725	0.753	0.737 (0.013)
AUC	0.848	0.846	0.854	0.834	0.863	0.849 (0.011)
Logistic regression model
Sensitivity	0.897	0.896	0.896	0.895	0.895	0.896 (0.001)
Specificity	0.722	0.731	0.742	0.722	0.749	0.733 (0.012)
AUC	0.832	0.839	0.844	0.826	0.847	0.838 (0.009)

Calibration performance

Figure 4 shows the calibration curves for the Bayesian network model and Logistic regression model in training set and testing set, and Figure S1 shows the calibration curves in validation set and sensitivity analysis. The horizontal axis represents the probability predicted by the model, and the vertical axis represents the observed probability of neurocognitive disorders. In the training set and testing set dataset, BN model shows slopes close to 1 and intercepts close to 0, indicating good calibration (Fig. 4A and B). In contrast, the logistic regression exhibits a larger discrepancy between the slope and 1 (Fig. 4C and D). In the validation set (Figure S1), the Bayesian network model had an intercept of 0 and a slope of 1.48, while the logistic regression model had a slope of 2.26, indicating significantly poorer calibration for the logistic regression model. In the sensitivity analysis, the Bayesian network model demonstrated better calibration (A = 0, B = 1.51) compared to the multivariable logistic regression model (A = 0, B = 0.18). A comprehensive summary of these results in both internal and validation datasets and in the sensitivity analysis can be found in Table 3.

Fig. 4.

Calibration curves of the BN model in the (A) training set, (B) testing set, and Logistic regression model in the (C) training set, (D) testing set. The A, B in the figures: A represents the intercept; B represents the slope

Table 3.

Comprehensive summary of model performance

Method	Dataset	AUC (95% CI)	Specificity	Sensitivity	Intercept of calibration curve*	Slope of calibration curve
Bayesian Network	Training Set	0.849 (0.839–0.859)	0.875	0.762	< 0.0001	0.99
	Testing Set	0.821 (0.803–0.840)	0.896	0.724	< 0.0001	0.94
	Validation Set	0.800 (0.785–0.815)	0.882	0.690	0.0003	1.48
	Sensitivity Analysis (30% missing)	0.791 (0.777–0.806)	0.849	0.681	0.0005	1.51
Logistic Regression Model	Training Set	0.838 (0.829–0.847)	0.899	0.734	0.0002	1.16
	Testing Set	0.832 (0.817–0.847)	0.899	0.734	0.0002	1.1
	Validation Set	0.799 (0.787–0.811)	0.903	0.664	0.0001	2.26
	Sensitivity Analysis (30% missing)	0.746 (0.733–0.759)	0.867	0.603	0.0013	0.18

* Represents the absolute value of the intercept of calibration curves

To supplement visual calibration curves and slope/intercept measures, we also report ICI and ECE values. For the Bayesian network model, the ICI was 0.00027 (training set), 0.00050 (testing set), 0.00307 (validation set), and 0.00271 (sensitivity analysis); the corresponding ECE values were 0.00014, 0.00037, 0.00148, and 0.00163. These results demonstrate good calibration consistency across datasets.

Decision curve

Decision curve analysis (DCA) was used to assess the clinical net benefit of the Bayesian network model across a range of risk thresholds. In the testing set, the BN model provided positive net benefit relative to both “treat-none” and “treat-all” strategies for threshold probabilities between 0 and 0.16. In the validation set, the model yielded positive net benefit within a narrower range, from 0 to 0.12. These threshold intervals represent realistic clinical decision points for initiating further screening or diagnostic evaluation in population-based settings. The results suggest the proposed BN model is suitable for identifying high-risk individuals when a low-to-moderate intervention threshold is adopted, thus supporting its potential utility in early-stage NCD screening workflows. The decision curves are shown in Supplement Figures S2.

Discussion

In this study, we developed and validated a Bayesian network model for screening neurocognitive disorders in adults using data from a comprehensive electronic health record database. Our BN model demonstrated robust discrimination across the development and validation cohorts. The AUC was approximately 0.85 in the training set, 0.82 in the testing set, and 0.80 in a validation dataset, indicating consistently high performance and generalizability in identifying individuals at risk of NCDs. Importantly, the BN maintained its predictive accuracy even when data were incomplete. When 30% of data were randomly removed, the BN model maintained robust performance (AUC = 0.79), outperforming the logistic regression model under the same conditions (AUC = 0.75). This robustness to missing information suggests that the BN approach is well-suited for large-scale screening in real-world settings, where EHR data are often incomplete or inconsistently recorded.

Beyond discrimination performance, the BN model provided insights into the factors most directly associated with NCDs risk. In the learned network, eight variables were identified as direct causes of neurocognitive disorders (parent nodes linked to the outcome), encompassing a range of known risk variables. The model proposed by the Lancet Commission on Dementia Prevention suggests that the improvement of 12 potentially modifiable risk factors across the life cycle could delay or prevent 40% of dementia cases [50]. Of the 12 risk factors for dementia, five were found to be similar to factors (hypertension, depression, physical inactivity, traumatic brain injury, social isolation) included in the risk factors directly associated with NCDs obtained in our established screening model. These findings support the variables incorporated in the established Bayesian network for predicting neurocognitive disorders, enhancing both predictive validity and interpretability. Notably, our BN model highlighted movement disorders as a direct cause influencing NCDs risk, despite its lack of statistical significance in the multivariable logistic regression model. Movement disorders and Parkinson’s disease are widely recognized as significant risk factors for NCDs. However, our findings suggest that movement disorders may serve as a confounder between Parkinson’s and NCDs; specifically, once movement disorders are accounted for within the BN structure, Parkinson’s disease becomes conditionally independent of NCDs. This indicates that the previously observed correlation between Parkinson’s disease [51] and NCDs may have been primarily driven by the broader presence of movement disorders. Further longitudinal and experimental studies are warranted to verify this relationship, exploring in greater depth the role of movement disorders as confounders between Parkinson’s disease and NCDs.

Multivariable logistic regression models and Bayesian network models are both widely employed tools for clinical prediction, yet they rely on distinct methodological assumptions, which influence their suitability in clinical practice. Logistic regression assumes linearity in the log-odds relationship between predictors and outcomes and absence of significant multicollinearity between variables. In contrast, Bayesian networks assume causal assumptions, including causal Markov assumption, causal faithfulness assumption, and causal sufficiency assumption [52]. Bayesian networks do not require a linear relationship assumption, explicitly model conditional dependencies among variables, and accommodate multicollinearity effectively by capturing the joint distribution structure of variables through directed acyclic graphs. In our analysis, both logistic regression and Bayesian network model demonstrated comparable discrimination in the testing and validation sets. However, logistic regression was notably less robust in scenarios involving missing data, as it mandates complete data or imputation methods [53], potentially introducing additional bias or inaccuracies. The BN model, by contrast, inherently accommodates missingness through probabilistic inference, which aligns better with the reality of electronic health records. Not only the graphic structure of the BN offers a visual representation of conditional dependencies, its interpretability also lies in its capacity for probabilistic reasoning. Rather than requiring clinicians to manually interpret the full network, the model produces individualized risk estimation through conditional inference. This enables clinicians to understand how different risk factors influence disease probability and how certain predictors may be conditionally independent of the outcome, thereby offering transparent and clinically meaningful insights. These outputs can be translated into simplified clinical interfaces, facilitating integration into electronic health record systems and potential scalability in low-resource primary care settings. This characteristic enhances usability in real-world screening contexts. Conversely, logistic regression models provide limited insight into complex variable interrelationships, potentially reducing their practical utility in personalized clinical decision-making.

There are also some limitations in this study. Although medication data were available and screened in the selection process, none of the treatment variables met the inclusion threshold. As a result, potential effects of treatment on NCDs risk were not captured in the final model, which may lead to residual confounding. The proposed Bayesian network assumed no unmeasured confounding variables [54]. However, our study utilized routinely collected electronic health records, which inherently lack certain domains of potential confounders, such as biological markers including genetic variables. The omission of these variables may result in residual confounding and consequently affect the inferred structure and causal interpretations derived from the Bayesian network. Thus, the potential for unmeasured confounding cannot be entirely ruled out. Better discrimination could be achieved by including more biological indicators, such as metabolites or genetic variables. Another key limitation of this study is the assumption of data completeness in the primary analysis. Individuals without recorded diagnoses were treated as negative for those conditions, which may not fully reflect real-world EHR documentation. While this approach ensured consistency between models, it could underestimate undiagnosed or unrecorded cases. To address this, we conducted sensitivity analyses by introducing random missingness, which showed that Bayesian network retained stable performance under incomplete data scenarios. Furthermore, the study population was primarily from different regions of Shandong Province, China, consisting mostly of East Asian individuals. The model’s effectiveness might decrease when applied to populations of different races [55]. Future research is warranted to explore how the developed Bayesian network model can be operationalized into a clinical decision support tool. Integrating the model into electronic health record systems with automated risk flagging may facilitate its adoption in primary care workflows. Prospective implementation studies will be needed to evaluate impact on early detection rates. Another key limitation of this study is the extreme class imbalance in the dataset, with only 0.28% of individuals diagnosed with NCDs. Although we used evaluation metrics that are robust to imbalance, we did not apply resampling or weighting strategies during model development. Future work should consider incorporating imbalance correction techniques to improve sensitivity and negative predictive value in rare-event settings [56]. Furthermore, we did not formally assess model stability or fairness. Further evaluation of subgroup-specific performance and algorithmic bias, particularly across demographic strata (e.g., age, gender), is warranted in future work [57, 58]. Additionally, the conversion of continuous variables to categorical variables for statistical analysis likely led to some information loss. Future research should extend the BN model to accommodate mixed data types. Another potential direction for future research involves addressing the heterogeneity of NCDs. Given the diverse diagnostic categories encompassed under ICD-10 codes F00-F09, future studies may consider adopting multi-task learning frameworks to simultaneously model shared and subtype-specific risk patterns. This approach may improve the specificity of risk profiling and facilitate more tailored clinical decision-making across different NCD subtypes.

Conclusions

This study developed a Bayesian network-based screening model for neurocognitive disorders using large-scale electronic health record data. The model effectively identified key risk factors and represented their dependencies through a directed acyclic graph. The proposed BN model demonstrated robust predictive performance across testing and validation sets, including under condition of missing data. These findings support the potential utility of the BN model as an effective tool for risk stratification in primary care settings, and as a foundation for future development of accessible screening platform.

Authors’ contributions

FX and HL conceived the study. YY and SZ contributed to the statistical analysis. SZ a contributed to figures. YY, HL and FX wrote and modified the manuscript. All authors reviewed and approved the final manuscript.

Funding

FX was supported by the National Natural Science Foundation of China (82330108) and Shandong Province Key R&D Program (2021SFGC0504).

Data availability

The EHR datasets used and/or analyzed in the current study can be made accessible by the corresponding author upon a justified request. Prior to utilizing the data, proposals need to be approved by all partners and a data sharing agreement will need to be signed. Full information on the screening model obtained in this study and the methodology used has been made publicly available via github (https://github.com/YuYF97/NCD_model).

Declarations

Ethics approval and consent to participate

This study was performed in accordance with the Declaration of Helsinki and was approved by the Institutional Review Board of the Shandong University School of Public Health, China (Approval No. LL20240308). The research involved secondary analysis of fully anonymized electronic health records, and informed consent was not required, as determined by the Institutional Review Board of the Shandong University School of Public Health, in accordance with the Measures for the Ethical Review of Life Science and Medical Research Involving Humans (2023), issued by the National Health Commission of China.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.