. 2025 Aug 28;201(13-14):911–918. doi: 10.1093/rpd/ncaf034

Table 1.

Variables included in the cost–benefit function, B(t), given in Fig. 1.

Variable (units)	Description
b(t) (Euro y⁻¹ km⁻²)	Net monetary flow for a specific km² in a geographical area.
d(t) (Sv y⁻¹)	External effective dose rate at time t in the affected area.
	The monetary value of a statistical healthy year (in prices at the year zero level) (Euro HEALTHy⁻¹). Swedish GDP per capita is ⁓50*10³ € y⁻¹, and may represent a coarse estimate of the monetary value of any healthy year lost due to cancer disease.
r (inh km⁻²)	Population density in the affected area.
P (y Sv⁻¹)	Loss of productive life years due to radiation induced cancer. This expression is fetched from Munro (2013), where P is the probability coefficient for fatal cancer per unit effective dose (case Sv⁻¹) as defined in IAEA 1994 [8]. P is the probability of fatal cancer induced by radiation and is set to 0.05 cases per Sv⁻¹. Factors β and δ account for non-fatal cancers and hereditary affects, which according to Munro is set at 0.01 and 0.013. The factor n_rad represents the average number of life years lost due fatal cancer and is set to 13 y per cancer case in IAEA [8]. Hence this product becomes P = 0.05(1 + 0.01 + 0.013) 13 = 0.66 cancer free y per Sv^-1, which is thus the estimated loss of cancer free year per Sv⁻¹. In Munro [9] this factor is simplified to P = 1.
f_s	Shielding factor of residential buildings in the area; default is set to 0.4.
r(t)	A time-dependent function describing the decay of the external effective dose rate. An expression for r(t) derived from Jönsson et al. [14] has been used here.
t_r (y)	Time from start of evacuation until resettlement. For simplicity it has been assumed that evacuation starts at t = 0.
S_evac (Euro inh⁻¹ y⁻¹)	Monetary loss rate of capital of real estate during evacuation. In this study which has an area representative of Swedish cities and towns in terms of population density, we have used a value of 5 million SEK (≈500 000 000 euros) when the value of different properties within the area are taken into consideration and is therefore proportional to the population density ρ. Typical household size per single residence is set at 2.4 members. S_evac(t) is in turn given by S_evac·(r/2.4)·(1-Exp(−(ln2/Ω)·t) where it is assumed that the buildings’ values are depreciated over a life-time given by the parameter Ω, (see below) in absence of service and renovation and that even after return, the costs of restoration and renovation will equal to that of the annual depreciation rate. In this model we assume that the value depreciation of a property stops when evacuated owners return. Hence, S_evac is multiplied by the return rate, R_ret(t) (See below).
Ω	Depreciation rate (y⁻¹) of real estate and infrastructural capital value. In this example we have set Ω = 2.31 y. This value will represent a situation where we assumed that the full capital value of a residential house has been completely depreciated after 15 y.
a_DRD (y inh⁻¹)	Cost of productive life years lost due to Disaster Related Deaths (DRDs). Yanovskyi et al. [10] estimate this number to be, on average, 11 years per DRD case. The likelihood of a DRD case in a population combined with the estimated life years lost due to evacuation in order of 10 years is set to 0.11 years per evacuated average person.
S_cleanup (Euro km⁻²)	Direct costs of decontamination per unit area in the affected region. For a typical Swedish semi-urban residential area, a sum of 100 MEuro in 2020 year price level has been assumed [15].
d (%)	The discount rate. In this study a value of 3.5% has been used in accordance with other economic assessments in Sweden, with the Transport Agency’s Analysis Method for Socioeconomic Calculation Values for Transportation Sector (ASEK), as the main reference point. In the latest version ASEK 8.1, it is recommended to use 3.5% as discount rate for future costs and benefits[16].
(t)	Time-dependent decontamination efficiency as elaborated in e.g. Rääf et al. [17].
b_r (I(t), R_ret(t), ) (Euro inh⁻¹)	Net monetary flow rate per returning inhabitant by restoring infrastructure and production in the affected region per unit evacuated area (Euro y⁻¹ km⁻¹). In this study we assume it is a function of average income from employment, I(t), fraction of evacuees returning to Lund, R_ret, and fraction of returnees being in employment upon return, s. It will hence be described by the following formulae: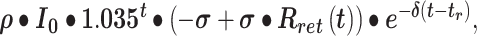 where we assumed an average annual income in the city of Lund at I₀ = 50 kEuro y⁻¹ per employed returned inhabitant at time of the accident (t = 0). We have also assumed an annual income increase of 3.5%, that is, I=I₀·1.035^t in the expression in Fig. 1. Furthermore, the first term in this expression represents the net loss rate from the fraction of the evacuated population who would be in employment if the accident had not taken place, assumed to be s = 50% of the city of Lund. The second term represents the annual net gain from the fraction of returnees who become actively employed (see below).
R_ret(t)	Fraction of evacuated population returning to the remediated region. This fraction can be as low as 50% in Sweden according to Rasmussen et al. [18]. In this study it is assumed that 15% of the evacuees will return within 1 y, of which s = 50% will be in employment (irrespective of age). The fraction of returned will then increase by 10% each year until reaching a maximum of 50% around t = 13 y.