Nonlinear system theory: Another look at dependence

Abstract

Based on the nonlinear system theory, we introduce previously undescribed dependence measures for stationary causal processes. Our physical and predictive dependence measures quantify the degree of dependence of outputs on inputs in physical systems. The proposed dependence measures provide a natural framework for a limit theory for stationary processes. In particular, under conditions with quite simple forms, we present limit theorems for partial sums, empirical processes, and kernel density estimates. The conditions are mild and easily verifiable because they are directly related to the data-generating mechanisms.

Let ε_i, 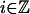, be independent and identically distributed (iid) random variables and g be a measurable function such that

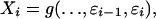[1]

is a properly defined random variable. Then (X_i) is a stationary process, and it is causal or nonanticipative in the sense that X_i does not depend on the future innovations ε_j, j > i. The causality assumption is quite reasonable in the study of time series. Wiener (1) considered the fundamental coding and decoding problem of representing stationary and ergodic processes in terms of the form Eq. 1. In particular, Wiener studied the construction of ε_i based on X_k, k ≤ i. The class of processes that Eq. 1 represents is huge and it includes linear processes, Volterra processes, and many time series models. In certain situations, Eq. 1 is also called the nonlinear Wold representation. See refs. 2-4 for other deep contributions of representing stationary and ergodic processes by Eq. 1. To conduct statistical inference of such processes, it is necessary to consider the asymptotic properties of the partial sum 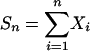and the empirical distribution function .

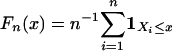In probability theory, many limit theorems have been established for independent random variables. Those limit theorems play an important role in the related statistical inference. In the study of stochastic processes, however, independence usually does not hold, and the dependence is an intrinsic feature. In an influential paper, Rosenblatt (5) introduced the strong mixing condition. For a stationary process (X_i), let the sigma algebra 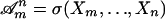, m ≤ n, and define the strong mixing coefficients

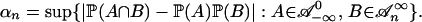[2]

If α_n → 0, then we say that (X_i) is strong mixing. Variants of the strong mixing condition include ρ, Ψ, and β-mixing conditions among others (6). A central limit theorem (CLT) based on the strong mixing condition is proved in ref. 5. Since then, as basic assumptions on the dependence structures, the strong mixing condition and its variants have been widely used and various limit theorems have been obtained; see the extensive treatment in ref. 6.

Since the quantity 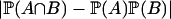in Eq. 2 measures the dependence between events A and B and it is zero if A and B are independent, it is sensible to call α_n and its variants “probabilistic dependence measures.” For stationary causal processes, the calculation of probabilistic dependence measures is generally not easy because it involves the complicated manipulation of taking the supremum over two sigma algebras (7-9). Additionally, many well-known processes are not strong mixing. A prominent example is the Bernoulli shift process. Consider the simple AR(1) process X_n = (X_n-1 + ε_n)/2, where ε_i are iid Bernoulli random variables with success probability 1/2 (see refs. 10 and 11). Then X_n is a causal process with the representation 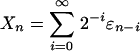and the innovations ε_n, ε_n-1,..., correspond to the dyadic expansion of X_n. The process X_n is not strong mixing since α_n ≡ 1/4 for all n (12). Some alternative ways have been proposed to overcome the disadvantages of strong mixing conditions (8, 9).

Dependence Measures

In this work, we shall provide another look at the fundamental issue of dependence. Our primary goal is to introduce “physical or functional” and “predictive dependence measures” a previously undescribed type of dependence measures that are quite different from strong mixing conditions. In particular, following refs. 1 and 13, we shall interpret Eq. 1 as an input/output system and then introduce dependence coefficients by measuring the degree of dependence of outputs on inputs. Specifically, we view Eq. 1 as a physical system

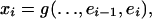[3]

where e_i, e_i-1,... are inputs, g is a filter or a transform, and x_i is the output. Then, the process X_i is the output of the physical system 3 with random inputs. It is clearly not a good way to assess the dependence just by taking the partial derivatives ∂g/∂e_j, which may not exist if g is not well-behaved. Nonetheless, because the inputs are random and iid, the dependence of the output on the inputs can be simply measured by applying the idea of coupling. Let (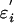) by an iid copy of (ε_i); let the shift process ξ_i = (..., ε_i-1, ε_i), 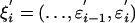. For a s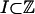et , let 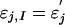if j ∈ I and ε_j,I = ε_j if j ∉ I; let ξ_i,I = (..., ε_i-1,I, ε_i,I) and 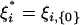. Then ξ_i,I is a coupled version of ξ_i with ε_j replaced by 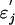if j ∈ I. For p > 0 write 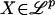if 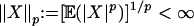and ∥X∥ = ∥X∥₂.

Definition 1 (Functional or physical dependence measure): For p > 0 and 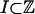let δ_p(I, n) = ∥g(ξ_n) - g(ξ_n,I)∥_p and 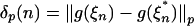. Write δ(n) = δ₂(n).

Definition 2 (Predictive dependence measure): Let p ≥ 1 and g_n be a Borel function on 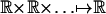such that 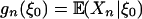, n ≥ 0. Let ω_p(I, n) = ∥g_n(ξ₀) - g_n(ξ_0,I)∥_p and 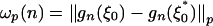. Write ω(n) = ω₂(n).

Definition 3 (p-stability): Let p ≥ 1. The process (X_n) is said to be p-stable if 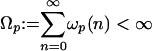, and p-strong stable if 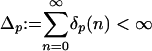. If Ω = Ω₂ < ∞, we say that (X_n) is stable.

By the causal representation in Eq. 1, if min{i: i ∈ I} > n, then δ_p(I, n) = 0. Apparently, δ_p(I, n) quantifies the dependence of X_n = g(ξ_n) on {ε_i, i ∈ I} by measuring the distance between g(ξ_n) and its coupled version g(ξ_n,I). In Definition 2, 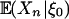is the n-step ahead predicated mean, and ω_p(n) measures the contribution of ε₀ in predicting future expected values. In the classical prediction theory (14), the conditional expectation of the form 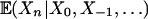is studied. The one 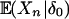used in Definition 2 has a different form. It turns out that, in studying asymptotic properties and moment inequalities of S_n, it is convenient to use 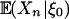and predictive dependence measure (cf. Theorems 2 and 3), while the other version 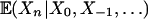is generally difficult to work with. In the special case in which X_n are martingale differences with respect to the filter σ(ξ_n), g_n = 0 almost surely and consequently ω(n) = 0, n ≥ 1.

Roughly speaking, since 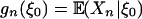, the p-stability in Definition 3 indicates that the cumulative contribution of ε₀ in predicting future expected values 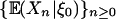is finite. Interestingly, the stability condition Ω₂ < ∞ implies invariance principles with 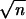-norming in a natural way (Theorem 3). By (i) of Theorem 1, p-strong stability implies p-stability since δ_p(n) ≥ ω_p(n).

Our dependence measures provide a very convenient and simple way for a large-sample theory for stationary causal processes (see Theorems 2-5 below). In many applications, functional and predictive dependence measures are easy to use because they are directly related to data-generating mechanisms and because the construction of the coupled process g(ξ_n,I) is simple and explicit. Additionally, limit theorems with those dependence measures have easily verifiable conditions and are often optimal or nearly optimal. On the other hand, however, our dependence measures rely on the representation 1, whereas the strong mixing coefficients can be defined in more general situations (6).

Theorem 1. (i) Let p ≥ 1 and n ≥ 0. Then δ_p(n) ≥ ω_p(n). (ii) Let p ≥ 1 and the projection operator 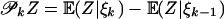, 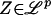. Then for n ≥ 0,

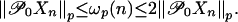[4]

(iii) Let p > 1, C_p = 18p^3/2(p - 1)^-1/2 if 1 < p < 2, C_p = 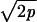if p ≥ 2; let 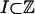. Then

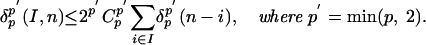[5]

Proof: (i) Since ,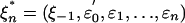

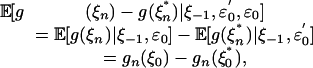which by Jensen's inequality implies δ_p(n) ≥ ω_p(n). (ii) Since 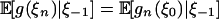and 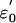and (ε_i) are independent, we have 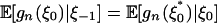and inequality 4 follows from

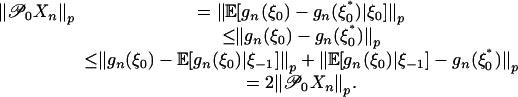(iii) For presentational clarity, let I = {..., -1, 0}. For i ≤ 0 let

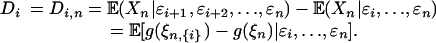Then D₀, D_-1,.. .are martingale differences with respect to the sigma algebras σ(ε_i,..., ε_n), i = 0, -1,.... By Jensen's inequality, ∥D_i∥_p ≤ δ_p(n - i). Let 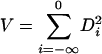, 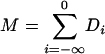and 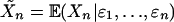. Then 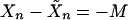and

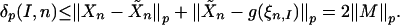To show Eq. 5, we shall deal with the two cases 1 < p < 2 and p ≥ 2 separately. If 1 < p < 2, then 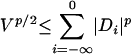. By Burkholder's inequality (15)

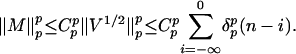If p ≥ 2, by proposition 4 in ref. 16, 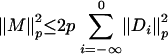. So Eq. 5 follows.

Inequality 5 suggests the interesting reduction property: the degree of dependence of X_n on 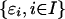can be bounded in an element-wise manner, and it suffices to consider the dependence of X_n on individual ε_i. Indeed, our limit theorems and moment inequalities in Theorems 2-5 involve conditions only on δ_p(n) and ω_p(n).

Linear Processes. Let ε_i be iid random variables with 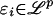, p ≥ 1; let (a_i) be real coefficients such that

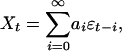[6]

is a proper random variable. The existence of X_t can be checked by Kolmogorov's three series theorem. The linear process (X_t) can be viewed as the output from a linear filter and the input (..., ε_t-1, ε_t) is a series of shocks that drive the system (ref. 17, pp. 8-9). Clearly, 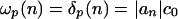, where 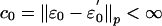. Let p = 2. If

[7]

then the filter is said to be stable (17) and the preceding inequality implies short-range dependence since the covariances are absolutely summable. Definition 3 extends the notion of stability to nonlinear processes.

Volterra Series. Analysis of nonlinear systems is a notoriously difficult problem, and the available tools are very limited (18). Oftentimes it would be unsatisfactory to linearize or approximate nonlinear systems by linear ones. The Volterra representation provides a reasonably simple and general way. The idea is to represent Eq. 3 as a power series of inputs. In particular, suppose that g in Eq. 3 is sufficiently well-behaved so that it has the stationary and causal representation

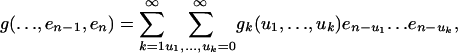[8]

where functions g_k are called the Volterra kernel. The right-hand side of Eq. 8 is generically called the Volterra expansion, and it plays an important role in the nonlinear system theory (13, 18-22). There is a continuous-time version of Eq. 8 with summations replaced by integrals. Because the series involved has infinitely many terms, to guarantee the meaningfulness of the representation, there is a convergence issue that is often difficult to deal with, and the imposed conditions can be quite restrictive (18). Fortunately, in our setting, the difficulty can be circumvented because we are dealing with iid random inputs. Indeed, assume that e_t are iid with mean 0, variance 1 and g_k(u₁,..., u_k) is symmetric in u₁,..., u_k and it equals zero if u_i = u_j for some 1 ≤ i < j ≤ k, and

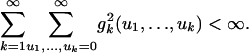Then X_n exists and is in 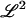. Simple calculations show that

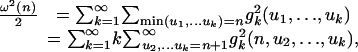and

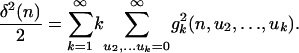The Volterra process is stable if .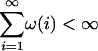

Nonlinear Transforms of Linear Processes. Let (X_t) be the linear process defined in Eq. 6 and consider the transformed process Y_t = K(X_t), where K is a possibly nonlinear filter. Let ω(n, Y) be the predictive dependence measure of (Y_t). Assume that ε_i have mean 0 and finite variance. Under mild conditions on K, we have 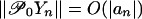(cf. theorem 2 in ref. 23). By Theorem 1, 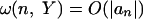. In this case, if (X_t) is stable, namely Eq. 7 holds, then (Y_t) is also stable.

Quite interesting phenomena happen if (X_n) is unstable. Under appropriate conditions on K, (Y_n) could possibly be stable. With a nonlinear transform, the dependence structure of (Y_t) can be quite different from that of (X_n) (24-27). The asymptotic problem of 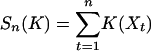has a long history (see refs. 23 and 27 and references therein). Let 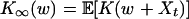and assume 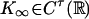for some 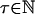. Consider the remainder of the τ-th order Volterra expansion of Y_n

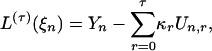[9]

where 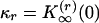r = 0,..., τ, and

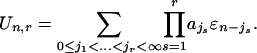Let 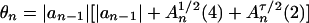and 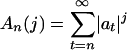. Under mild regularity conditions on K and ε_n, by theorem 5 in ref. 23, 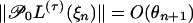. By Theorem 1, the predictive dependence measure ω^(τ)(n) of the remainder L^(τ)(ξ_n) satisfies

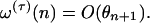[10]

It is possible that 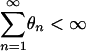while 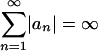. Consider the special case a = n^-βl(n), where 1/2 < β < 1 and l is a slowly varying function, namely, for any c > 0. l(cn)/l(n) → 1 as n → ∞. By Karamata's Theorem (28) for j ≥ 2, 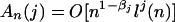. If τ > (2β - 1)^-1 - 1, then 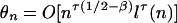is summable. Therefore, if the function K satisfies κ_r = 0 for r = 0,..., τ and (τ + 1)(2β - 1) > 1, then Y_t = K(X_t) is stable even though X_t is not. Appell polynomials (29) satisfy such conditions. For example, let 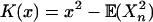, then K_∞(w) = w² and κ₁ = 0, κ₂ = 2. If β ∈ (3/4, 1), then the process 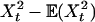is stable. If 1/2 < β < 3/4, then S_n(K)/∥S_n(K)∥ converges to the Rosenblatt distribution.

Uniform Volterra expansions for F_n(x) over 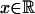are established in refs. 30 and 31. Wu (32) considered nonlinear transforms of linear processes with infinite variance innovations.

Nonlinear Time Series. Let ε_t be iid random variables and consider the recursion

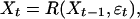[11]

where R is a measurable function. The framework 11 is quite general, and it includes many popular nonlinear time series models, such as threshold autoregressive models (33), exponential autoregressive models (34), bilinear autoregressive models, autoregressive models with conditional heteroscedasticity (35), among others. If there exists α > 0 and x₀ such that

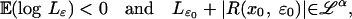[12]

where

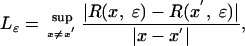then Eq. 11 admits a unique stationary distribution (36), and iterations of Eq. 11 give rise to Eq. 1. By theorem 2 in ref. 37, Eq. 12 implies that there exists p > 0 and r ∈ (0, 1) such that

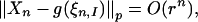[13]

where I = {..., -1, 0}. Recall 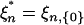. By stationarity, 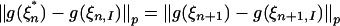. So Eq. 13 implies 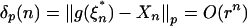. On the other hand, by Theorem 1 (iii), if 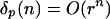holds for some p > 1 and for some r ∈ (0,1), then Eq. 13 also holds. So they are equivalent if p > 1. In refs. 37 and 38, the property 13 is called geometric-moment contraction, and it is very useful in studying asymptotic properties of nonlinear time series.

Inequalities and Limit Theorems

For (X_i) defined in Eq. 1, let S_u = S_n + (u - n)X_n+1, n ≤ u ≤ n + 1, n = 0, 1,..., be the partial sum process. Let R_n(s) = 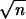[F_n(s) - F(s)], where 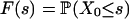is the distribution function of X₀. Primary goals in the limit theory of stationary processes include obtaining asymptotic properties of {S_u, 0 ≤ u ≤ n} and 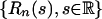. Such results are needed in the related statistical inference. The physical and predictive dependence measures provide a natural vehicle for an asymptotic theory for S_n and R_n.

Partial Sums. Let 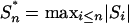, 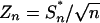and B_p = p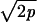/(p - 1), p > 1. Recall 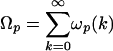and let

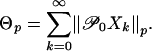By Theorem 1, Θ_p ≤ Ω_p ≤ 2Θ_p. Moment inequalities and limit theorems of S_n are given in Theorems 2 and 3, respectively. Denote by IB the standard Brownian motion. An interesting feature in the large deviation result in Theorem 2(ii) is that Ω_p and X_k do not need to be bounded.

Theorem 2. Let p ≥ 2. (i) We have ∥Z_n∥_p ≤ B_pΘ_p ≤ B_pΩ_p. (ii) Let 0 < α ≤ 2 and assume

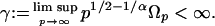[14]

Then 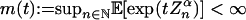for 0 ≤ t < t₀, where t₀ = (eαγ^α)^-12^-α/2. Consequently, for u > 0, .

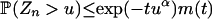Proof: (i) It follows from W.B.W. (unpublished results) and theorem 2.5 in ref. 39. For completeness we present the proof here. Let 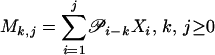and 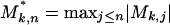. Then 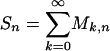. By Doob's maximal inequality and theorem 2.5 in ref. 39 (or proposition 4 in ref. 16),

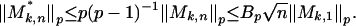Since 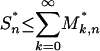, (i) follows. (ii) Let Z = Z_n and p₀ = [2/α] + 1. By Stirling's formula and Eq. 14

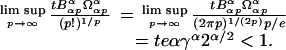By (i), since 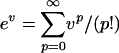, (ii) follows from

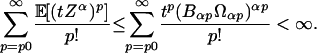Example 1: For the linear process 6, assume that

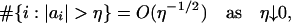[15]

and 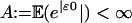. We now apply (ii)of Theorem 2 to the sum 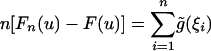, where g̃(ξ_i) = 1_Xi≤u - F(u). To this end, we need to calculate the predictive dependence measure ω_p(n, g̃) (say) of the process g̃(ξ_n). Without loss of generality let a₀ = 1. Let F_ε and f_ε be the distribution and density functions of ε₀ and assume c:= sup_uf_ε(u) < ∞. Then Eq. 14 holds with α = 1. To see this, let Y_n-1 = X_n - ε_n, Z_n-1 = Y_n-1 - a_nε₀ and 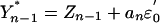. Let n ≥ 1. Then 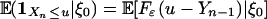and 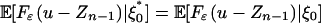. By the triangle inequality,

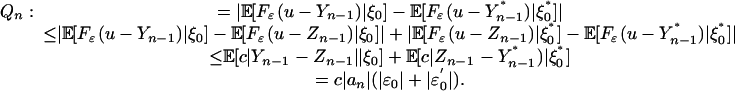Hence, 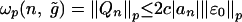. Since 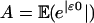, we have 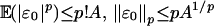. Clearly, 0 ≤ Q_n ≤ 1. So 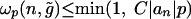, where C = 2cA. For η > 0 let the set 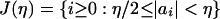. By Eq. 15

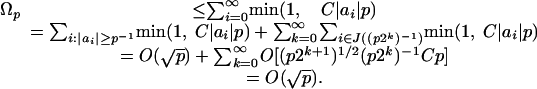Condition 15 holds if .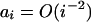

Theorem 3. (i) Assume that Ω₂ < ∞. Then

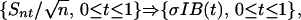[16]

where 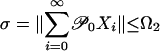. (ii) Let 2 < p ≤ 4 and assume that 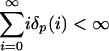. Then on a possibly richer probability space, there exists a Brownian motion IB such that

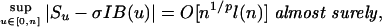[17]

where l(n) = (log n)^1/2+1/p(log log n)^2/p.

The proof of the strong invariance principle (ii) is given by W.B.W. (unpublished results). Theorem 3(i) follows from corollary 3 in ref. 40, and the expression 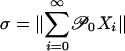is a consequence of the martingale approximation: let 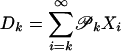and M_n = D₁ +... + D_n, then ∥S_n - M_n∥ = o(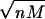) and ∥S_n∥/ 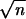= σ + o(1) (see theorem 6 in ref. 41). Theorem 3(i) also can be proved by using the argument in ref. 42. The invariance principle in the latter paper has a slightly different form. We omit the details. See refs. 43 and 44 for some related works.

Empirical Distribution Functions. Let 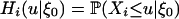, , 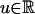be the conditional distribution function of X_i given ξ₀. By Definition 2, the predictive dependence measure for g̃(ξ_i) = 1_Xi≤u - F(u), at a fixed u,is 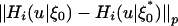. To study the asymptotic properties of R_n, it is certainly necessary to consider the whole range u ∈ (-∞, ∞). To this end, we introduce the integrated predictive dependence measure

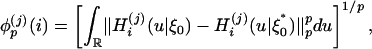[18]

and the uniform predictive dependence measure

[19]

where 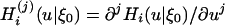, j = 0, 1,..., i ≥ 1. Let 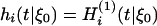. Theorem 4 below concerns the weak convergence of R_n based on 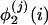. It follows from corollary 1 by W.B.W. (unpublished results).

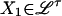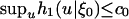Theorem 4. Assume that and for some positive constants τ, c₀ < ∞. Further assume that

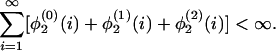[20]

Then 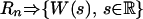, where W is a centered Gaussian process.

Kernel Density Estimation. An important problem in nonparametric inference of stochastic processes is to estimate the marginal density function f (say) given the data X₁,..., X_n. A popular method is the kernel density estimation (45, 46). Let K be a bounded kernel function for which 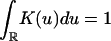and b_n > 1 be a sequence of bandwidths satisfying

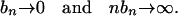[21]

Let K_b(x) = K(x/b). Then f can be estimated by

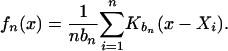[22]

If X_i are iid, Parzen (46) proved a central limit theorem for 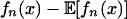under the natural condition 21. There has been a substantial literature on generalizing Parzen's result to time series (47, 48). Wu and Mielniczuk (49) solved the open problem that, for short-range dependent linear processes, Parzen's central limit theorem holds under Eq. 21. See references therein for historical developments. Here, we shall generalize the result in ref. 49 to nonlinear processes. To this end, we shall adopt the uniform predictive dependence measure 19. The asymptotic normality of f_n requires a summability condition of .

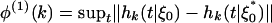Theorem 5. Assume that 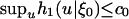for some constant c₀ < ∞ and that f = F′ is continuous. Let 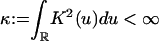. Then under Eq.21 and

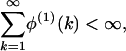[23]

we have 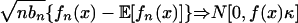for every .

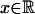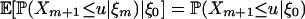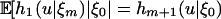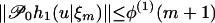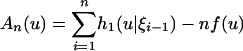Proof: Let m be a nonnegative integer. By the identity and the Lebesgue dominated convergence theorem, we have and h_m+1 is also bounded by c₀. By Theorem 1(ii), . Let . By Theorem 2(i) and Eq. 23

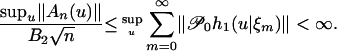Let 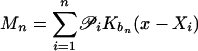and 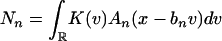. Observe that

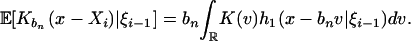Then 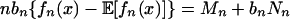. Following the argument of lemma 2 in ref. 49, M_n/ 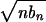⇒ N[0, f(x)κ], which finishes the proof since 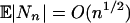and b_n → 0.