Kinematic simulation and trajectory planning of intelligent tunneling automatic mesh-laying robot

Abstract

China is the world’s largest producer and consumer of coal, with an increasing demand for coal resources. Improving coal mining efficiency and ensuring production safety have become key issues that urgently need to be addressed in the intelligent construction of coal mines. Tunnel excavation is one of the core processes in coal mine production, and anchor mesh anchoring support, as a key step in tunnel excavation, has become a focus of attention for researchers. Currently, in the process of coal mine roadway excavation in China, anchor mesh support mostly adopts manual operation, which has problems such as low operation efficiency, high safety risks, and difficult quality control. In response to these problems, this paper designs and develops an automatic mesh-laying robot system integrated into the body of the excavation anchor integrated machine. Through the optimization design of the mechanical arm structure, robot kinematic modeling, optimization of the operation path planning control algorithm, and virtual simulation experiment verification, the possibility of barrier free operation in the narrow space of the automatic mesh-laying robot system has been verified. Finally, a physical prototype of the automatic mesh-laying machine has been developed and the deployment experiment of the autonomous mesh-laying operation control algorithm physical prototype has been carried out. The results show that the trajectory planning algorithm based on polynomial interpolation can efficiently complete the trajectory tracking of the preset operation path. Compared with manual operation, The quality and efficiency of mesh-laying have improved significantly, effectively reducing the labor intensity of workers and enhancing operational safety.

Introduction

Coal, as the main energy source in China, accounts for over 60% of the primary energy mix and holds an important position in the country’s energy supply structure; Meanwhile, as the world’s largest producer and consumer of coal, China’s coal production accounts for over 50% of the world’s total output. In the foreseeable future, China’s socio-economic development will still be dominated by coal resources. In addition, as a crucial pillar industry in human economic and social development, coal mining intelligence is the core technological support and necessary path for the high-quality development of the industry^1,2.

In recent years, with the continuous increase in demand for coal resources, improving coal mining efficiency and ensuring production safety have become key issues that urgently need to be addressed in the development process of the coal industry³. For coal production, tunnels are necessary passages for underground coal mining. As the ‘blood vessels’ of mines, coal mine tunnels are indispensable in the production and construction of coal mines, playing a crucial role in the long-term safety and high-efficiency production of coal mines. According to existing data statistics, the total length of newly excavated tunnels in state-owned coal mines is 12000 km per year, with a huge engineering scale. However, the coal industry has long been plagued by the phenomenon of ‘heavy coal mining and light excavation’, and the level of excavation equipment lags behind that of intelligent coal mining. The main factors currently restricting excavation efficiency are the high dependence and low automation on manual support operations, low automation and intelligence levels of anchor mesh support processes, slow support speed, poor quality of mesh-laying, and difficulty in simultaneous excavation and support⁴.

Anchor mesh support, as one of the core technologies for controlling the surrounding rock of coal mine tunnels, directly affects the safety and mining efficiency of the mine in terms of construction efficiency and quality^5–8. With the advancement of intelligent mining construction, traditional manual mesh-laying urgently needs to be upgraded due to low efficiency and high risks. In recent years, automated mesh-laying technology centered around robot arms has become a research hotspot both domestically and internationally. Many researchers at home and abroad have conducted meaningful exploration and research on the transportation automation and laying automation technology of anchor mesh in response to the current low level of automation in laying mesh⁹. Zhang Ziling¹⁰ developed an intelligent mining anchor drilling vehicle automatic mesh-laying control system by combining the manual mesh-laying process, greatly improving the automation level of coal mine roadway anchor mesh support operations. Yang Zeyuan¹¹ proposed a method for controlling the posture of the rotating joint of a mesh-laying robot arm used for supporting equipment. Through theoretical design, system simulation, and semi physical simulation experiments, the posture control system of the robot arm was verified; Wang Chenglong¹² conducted research on the automatic mesh unit of coal mine anchor drilling robots and designed an automatic mesh device that uses mechanical claws and arms to grasp, move, and adjust the posture of the anchor mesh; Wang Fuqiang¹³ conducted research on a fully automatic mesh-laying device for anchor drilling vehicles. By studying the anchor protection mesh-laying operation process during coal mine tunnel excavation, he innovatively constructed a fully automatic mesh-laying device, which was matched with the anchor drilling vehicle to achieve automation of mesh-laying. This process not only greatly reduces the labor intensity of workers, improves mesh-laying efficiency, but also enhances the safety of mesh-laying. Our team conducted exploratory research on the independent laying process of rigid top mesh for excavation tunnels in the early stage¹⁴. By installing a sliding rail type laying mechanical arm on the side of the excavator anchor integrated machine body, the operation time of top mesh-laying was greatly reduced, and the defect of manually pulling the mesh with temporary support in the old process was overcome.

On the basis of previous research, this article further conducted relevant research on the flexible roll mesh-laying process of excavation roadway and roadway support. A design and development of an automatic mesh-laying robot system integrated into the body of the excavation anchor integrated machine were carried out. The system integrates functions such as automatic mesh-taking from the anchor mesh warehouse, autonomous transportation along the preset path, and automatic mesh-laying after lifting to the target point position. It simplifies the tedious processes of manual transportation and mesh lifting, reduces the risk of operation, and effectively improves the efficiency of mesh-laying. The innovation of this manuscript can be summarized as follows: (a) Structurally, it is integrated into the body of the anchor digging machine, which does not require additional occupation of tunnel space and solves the spatial conflict between traditional mesh-laying equipment and excavation equipment; (b) In terms of applicable mesh types, it is designed for the flexible roll mesh of roadway walls, while existing technologies mostly rely on temporary support and laying of top mesh on the integrated excavator anchor machine, which is suitable for rigid top mesh or sheet mesh; (c) In terms of efficiency, compared to the semi-automatic system researched by Zhang Ziling and others that requires manual assistance for positioning, this robot achieves fully autonomous operation, and the efficiency of laying nets is improved by about 2 times. Through the optimization design of the robot arm structure, kinematic modeling of the robot, optimization of the operation path planning control algorithm, and virtual simulation experiment verification, the possibility of barrier free operation in narrow spaces of the automatic mesh-laying robot system has been verified, providing strong technical support for the intelligent construction and intelligent rapid excavation of coal mines.

Design and D-H modeling of automatic Mesh-laying robot

Design of automatic Mesh-laying robot machine

The author’s team has designed and developed a flexible roll mesh automatic laying robot integrated into the body of the excavator anchor machine, as shown in Fig. 1. The automatic laying robot is installed on the left side of the excavator anchor machine’s travel side, and can grasp the flexible roll mesh located in the anchor mesh compartment directly below the mechanical arm through the end gripper, and transport it along the preset path to directly above the top anchor drilling machine, that is, in the tunnel section with dimensions of 6240 mm × 4550 mm, the automatic laying robot can achieve obstacle free operation within the range of length × width × height = 3460 mm × 1770 mm × 2450 mm.

Fig. 1.

Operating conditions and dimensional parameters of automatic mesh-laying robot.

The structural form of the automatic mesh-laying robot is borrowed from the KUKA industrial robot form, mainly including a robot arm rotating base, a robot arm, a robot arm forearm, wrist joints, swing joints, a mesh grabbing mechanical gripper, and 7 mining explosion-proof servo motors, as shown in Fig. 2. The robot forearm length L₃ = 1400 mm, the robot arm length L₅ = 2500 mm, the body weight is 1.5t, the load is 30 kg, the overall power is 17.4kw, the maximum single explosion-proof servo motor is 6kw, the working voltage is 127 V, the protection level is IP65, and the working temperature is 0–50 °C.

Fig. 2.

Structure composition and testing prototype of automatic mesh-laying robot.

Establishment of linkage coordinate system

The automatic mesh-laying robot developed in this article includes 7 degrees of freedom, namely the base rotation degree of freedom, the mechanical arm pitch degree of freedom, the mechanical forearm pitch degree of freedom, the wrist joint rotation degree of freedom, the swing joint rotation degree of freedom, the mechanical gripper opening and closing degree of freedom, and the mechanical gripper rotation degree of freedom, namely 6 rotational degrees of freedom and 1 telescopic degree of freedom. Among them, the opening, closing, and rotational degrees of freedom of the mechanical gripper do not participate in the multi-joint linkage control of the autonomous operation of the automatic mesh-laying robot, and are only used for the grasping and unwinding of flexible roll mesh. The Modified D-H parameter method¹⁵ is used to construct the linkage coordinate system of the automatic mesh-laying robot as shown in Fig. 3, and the corresponding Modified D-H parameter table is shown in Table 1.

Fig. 3.

Modified D-H coordinate system for automatic mesh-laying robot.

Table 1.

Modified D-H parameter table of cantilever roadheader.

i	di	ai−1	θi	αi−1
1	0	0	θ 1	0
2	L 2	0	θ 2	90°
3	0	L 3	θ 3	0
4	0	L 4	−90°	0
5	L 6	L 5	θ 4	180°
6	0	0	θ 5	90°
7	0	L 7	0	0

Figure 3 shows the posture and position of the rotation axis of the automatic mesh-laying robot’s rotary joint, and provides the corresponding link lengths L₁ ~ L₇ between different rotary joints. For the convenience of solving, the opening and closing of the mechanical gripper and the rotational degrees of freedom are included in the Modified D-H parameter table, as shown in Table 1. It should be noted that in Table 1, i = 4 represents the introduced virtual joint D-H parameters, and i = 7 represents the offset between the end of the automatic mesh-laying robot and the central axis of the mechanical gripper.

Kinematic analysis of robot

The main operating mechanism of the automatic mesh-laying robot is a multi-degree of freedom robot arm. During the mesh-laying process, a series of tasks such as end positioning and posture determination are performed by the joints of the robot arm. Therefore, studying the kinematics of the automatic mesh-laying robot is fundamental to achieving robot trajectory planning and motion control. In this section, the improved D-H parameter method is used to model the kinematics of the automatic mesh-laying robot studied in this paper, analyze its forward and inverse kinematics calculation methods, calculate the theoretical end position through forward solution, and generate control instructions for trajectory planning through inverse solution, thus achieving the transformation from mathematical model to physical implementation.

Forward kinematics analysis

Forward kinematics is the process of determining the specific pose of the end effector of a mesh-laying robot, given the initial joint angles of the robot arm, and ensuring that this pose is unique. In robotics, the pose transformation from one coordinate system to another is represented by a 4 × 4 matrix, which is called a homogeneous transformation matrix. The homogeneous transformation matrix includes the attitude matrix and position matrix of one coordinate system relative to another coordinate system. In the improved D-H parameter method, the homogeneous transformation matrix between two coordinate systems can be obtained using the four parameters of the improved D-H. The improved D-H parameters in this paper are shown in Table 1, where the definitions of the four parameters are as follows:

1. Link offset d_i: the distance between the two common normal lines a_i−1 and a_i on joint i. Expressed in the coordinate system as the distance from x_i−1 to x_i along the z_i axis.

2. Link length a_i−1: The length of the common normal line segment between joint axis i−1 and joint axis i. In the coordinate system, it is represented as the distance measured from z_i−1 to z_i along the x_i−1 axis.

3. Joint angle θ_i: The rotation angle of link i around axis i relative to link i−1. In the coordinate system, it is represented as the angle of rotation from x_i−1 to x_i around the z_i axis.

4. Connecting rod torsion angle α_i−1: The angle between joint axis i−1 and joint axis i, pointing from axis i−1 to axis i. In the coordinate system, it is expressed as the angle of rotation from z_i−1 to zi around the x_i−1 axis.

The homogeneous transformation matrix from coordinate system {i} to coordinate system {i−1} is represented by and calculated by the following equation:

1

The of 7-degree-of-freedom mesh-laying robot arm designed in this article needs to be solved, and the total transformation matrix of the end effector of the robot arm relative to the base coordinate¹⁶ is:

2

In the Eq. (2), R is the attitude matrix of the robot end coordinate system relative to the base coordinate system, which is a third-order square matrix, and P is the position matrix of the robot end coordinate system relative to the base coordinate system.

The homogeneous transformation matrix of adjacent coordinate systems can be obtained from Eq. (1) and Table 1, that is:

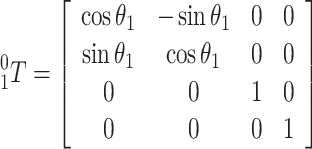3

4

5

6

7

8

9

Multiplying the homogeneous transformation matrices Eq. (3) to Eq. (9) in sequence yields the end pose description matrix of the automatic mesh-laying robot:

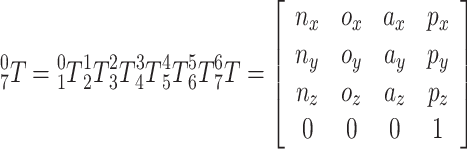10

The elements of the matrix in the equation are expressed as:

To simplify the equation, C3 = cos θ₃, S4 = sin θ₄, and so on in the above equation.

Inverse kinematics analysis

Given the pose of the end effector of the automatic mesh-laying robot, the calculation method for the angle θ_i of each joint of the reverse computing arm is called inverse kinematics solution¹⁷, which is the inverse process of forward kinematics solution and the calculation process is more complex than forward kinematics calculation. The angle result obtained from forward kinematics analysis is unique, while the joint angle result obtained from inverse kinematics analysis may have multiple solutions or even have no solution¹⁸.

Using analytical methods to solve inverse kinematics, Eq. (2) is left multiplied at both ends simultaneously :

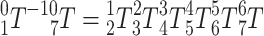11

Note that (i, j)_l represents the i rows and j columns of the matrix on the left side of the equation, and (i, j)_r represents the i rows and j columns of the matrix on the right side of the equation. According to (2, 4)_l = (2, 4)_r, the calculation on the left side of Eq. (11) yields:

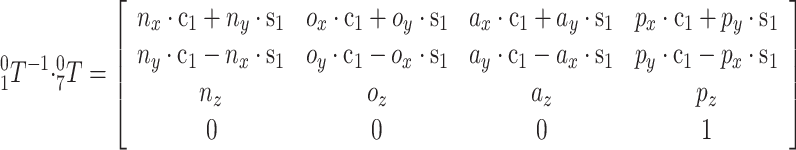12

In the Eq. (12), C₁ represents cos θ₁, S₁ represents sin θ₁.

The calculation on the right side of Eq. (11) yields:

13

In the Eq. (13), C₂₊₃₋₄ represents cos (θ₂ + θ₃-θ₄), S₂₊₃₋₄ represents sin (θ₂ + θ₃-θ₄), C₂₃ represents cos (θ₂ + θ₃), S₂₃ represents sin (θ₂ + θ₃).

From Eq. (12) and Eq. (13) where the elements of the matrix are equal and the geometric relationship between the positions of the robot arm in its initial state, the inverse equation of θ₁ ~ θ₅ can be derived as follows:

14

In the Eq. (14), , , , ,

,

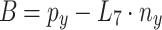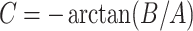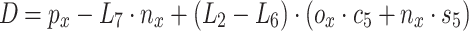Analysis of working space of robot arm

Monte Carlo method for workspace analysis

The workspace refers to the collection of all areas that the end effector of the robot arm can reach during the mesh-laying operation. The workspace is an important indicator for evaluating whether the mesh-laying robot arm can effectively complete the transfer and transportation of flexible roll mesh in narrow spaces. Therefore, analyzing the workspace of the mesh-laying robot arm is of great significance for practical applications. This article uses Monte Carlo simulation to analyze the workspace of a mesh-laying robot arm^19,20.

The steps to simulate and analyze the workspace using Monte Carlo method are as follows:

(1) The position vector of the end effector can be obtained by solving the forward kinematics as follows:

15

In the equation, L₁ = 640.5 mm, L₂ = 96 mm, L₃ = 1400 mm, L₄ = 240 mm, L₅ = 2507.85 mm, L₆ = 354.72 mm, L₇ = 510 mm.

(2) Call the function rand() in MATLAB to generate random numbers, multiply rand() by the difference between the maximum and minimum joint angles, and obtain the random step size for each joint angle, Therefore, the random variables of each joint angle are:

16

In the equation, Indicate the minimum value of joint rotation angle, Indicate the maximum value of joint rotation angle, i∈[1, 5].

(3) By substituting the 5 random variables of joint angles obtained in Eq. (16) into Eq. (15), the set of spatial points that can be reached by the end effector of the mesh-laying robot can be obtained. MATLAB software is used to calculate the position of the end effector and draw three-dimensional and two-dimensional workspace cloud maps.

Simulation of the working space of robot arm

Use the Robotics Toolbox in MATLAB software to simulate and analyze the workspace of the mesh-laying robot arm, output 50,000 random points to simulate the three-dimensional workspace of the robot arm, and call the plot3 and plot drawing commands to obtain the three-dimensional workspace cloud map of the seven degree of freedom mesh-laying robot as shown in Fig. 4. The core operation area of the roadway support mesh is within the range of 1.2–3.5 m from the bottom plate and 0–1.8 m from the roadway support, while the height of the robotic arm workspace is 2800 mm and the width is 1770 mm, which can fully cover this area. Through MATLAB simulation and physical testing verification, the positioning error of the robotic arm at the corner of the roadway is ≤ 50 mm, which meets the requirements of mesh alignment and has no unreachable dead corners for operation.

Fig. 4.

Cloud map of workspace for automatic mesh-laying robot.

Trajectory planning of robot arm

The Robotics Toolbox in MATLAB enable tasks such as robot arm modeling, workspace simulation analysis, trajectory planning, etc., and present simulation results in the form of images for easy observation of the motion state of the robot arm¹⁹. To ensure that the end effector of the mesh-laying robot arm reaches the installation position smoothly, it is necessary to plan the trajectory of the mesh-laying robot arm. During the transportation process, the mesh-laying robot arm adjusts its posture through 5 rotating joints, ensuring that the end effector accurately reaches the position directly above the top anchor drilling rig.

MATLAB 3D modeling of robot arm

In MATLAB, the Link () function and Serial Link () function can assist users in building robot arm models²⁰. Create a robot arm linkage model using the Link () function, with the call format L = Link ([a θ d offset], modified); jointtype; When jointtype=’P’, the joint is moving; Offset represents the offset of each joint angle variable; ‘modified ‘represents the use of improved D-H parameters. Use the Serial Link (L) function to connect the links generated by the Link () function to generate a robot arm model. Call the Teach () function to draw a mathematical 3D simulation model of the robot arm, as shown in Fig. 5. Use the plot () function to draw the model driver, and drag the slider in the model driver to control the motion of each joint of the robot arm.

Fig. 5.

MATLAB model diagram of automatic mesh-laying robot.

Simulation of robot arm trajectory planning

Use the jtraj function in the Robotics Toolbox for spatial planning of robot arms. The function call format is [q q_d q_dd] = jtraj (q₁, q₄, t), where q₁ is the initial position angle of the robot arm, q₄ is the endpoint position angle of the robot arm, t is the given simulation time, q is the joint space trajectory from q₁ to q₄, and q_d and q_dd are the joint velocity and joint acceleration planned for this trajectory²¹. Take the starting point position q₁ as (1640, 258, −1400), as shown in Fig. 6(a); Taking the termination point position q₄ as (1700, −3202, 1400), as shown in Fig. 6(d), two intermediate points were inserted between the starting and ending points, namely q₂ (1700, 258, −1400) and q₃ (1700, −3202,−1400), Among them, q₁ to q₂ simulate the process of the initial robot arm slightly moving towards the side of the tunnel, which moves by 60 mm. q₂ to q₃ simulate the process of the robot arm moving along the central axis of the tunnel to directly below the installation position of the side mesh, which moves by 3460 mm. q₃ to q₄ simulate the process of the robot arm finally delivering the rolled mesh to the installation position of the side mesh, which moves by 2800 mm. The motion time is set to 10 s, and the unit step size is 0.1s. Simulation analysis is conducted on 5 joints separately.

Fig. 6.

The positions of the automatic mesh-laying robot at q₁, q₂, q₃, and q₄ respectively.

Call the jtraj function to perform fifth degree polynomial interpolation on the joint space of the robot arm model²², and use the plot3() command to obtain the trajectory diagram of the end effector from the initial position q₁ to the endpoint position q₅, as shown in Fig. 7(a). The plot () command can be used to plot the variation curves of angular displacement, angular velocity, and angular acceleration of each joint, as shown in Fig. 7(b).

Fig. 7.

The end motion trajectory of the automatic mesh-laying robot arm and the temporal variation of each joint of the robot arm.

Observing Fig. 7, it can be seen that the curves of angular displacement, angular velocity, and angular acceleration of each joint during the movement of the robot arm are smooth and stable, and there are no interruptions or abrupt changes in the curves over time. This indicates that the design of each link of the robot arm is reasonable, and there will be no joint displacement during the movement of the robot arm. The changes in angular acceleration of each joint correspond to the trends in velocity changes of each joint, therefore the spatial trajectory planning of this joint is reasonable.

ADAMS kinematic simulation

In order to verify the correctness of MATLAB trajectory planning and provide reliable basis for selecting drive motors for each joint and studying the relationship between torque and motion, ADAMS was used for kinematic analysis of the automatic mesh-laying robot arm²³. Compare the obtained motion trajectory with the motion trajectory obtained in MATLAB to verify the correctness of MATLAB’s trajectory planning.

Import the 3D model of the mesh-laying robot arm into ADAMS, define the material of the parts, and set the direction of gravity acceleration; Then add motion pair constraints, fix the base and bottom of the robot arm first, set each joint as a rotating pair, and add rotation drives at each rotating pair. Export the data results of the simulated path of the robot arm obtained from MATLAB as external drivers to form SPLINE curves in ADAMS software, which contain the angle changes of the entire motion process of the robot arm. Call the CUBSPL function to set the rotation drive for each joint, and use the obtained SPLINE curve as the drive function for each joint. The drive function for the first joint is CUBSPL (time, 0, SPLINE_1, 0), and the drive functions for other joints are set sequentially.

After adding constraints and drivers, kinematic analysis is performed on the robot arm in an unloaded state to track the motion trajectory of the end effector in real-time, resulting in the motion trajectory of the robot arm shown in Fig. 8.

Fig. 8.

Real time tracking trajectory curve in ADAMS.

Physical prototype verification

Figure 9 shows the ADAMS kinematic simulation process of the mesh-laying robot arm operating according to the preset path planned in MATLAB in Fig. 6. Comparing Figs. 6 and 9, it can be seen that the robot arm can autonomously operate according to the path planned in MATLAB. After deploying the corresponding control algorithm in the ADAMS virtual prototype, the expected operation effect can also be achieved, proving that the fifth-degree polynomial interpolation trajectory planning algorithm can meet the accuracy requirements of on-site operation of the mesh-laying robot arm.

Fig. 9.

Kinematic simulation of autonomous operation of mesh-laying robot in ADAMS software.

Further carry out physical prototype verification experiments to transform the temporal variation of the rotation angles of each joint of the mesh-laying robot arm in the model into a language that can be recognized by servo motors and deployed on the physical prototype. After power on, control each servo motor to start moving according to the planned rotation angle law to verify the feasibility of the control code on the physical prototype.

Figure 10 shows the autonomous operation status of the physical prototype of the mesh-laying robot arm at different time nodes. Through test records, the mesh-laying robot can smoothly complete the process of grabbing, transporting, lifting, and releasing the mesh. The entire process takes 55 s, which is much lower than the 3 min of manual operation time. The manual operation testing conditions including the tunnel section with 6240 mm × 4550 mm, which is consistent with the actual working environment of the prototype. Two skilled workers cooperate with each other to work, and the mesh-laying specification is the same batch of flexible roll mesh. The manual operation requires completing steps such as handling the rolled mesh, temporary support fixation, and manual alignment of the mesh. The average of 10 tests is taken, and the average time is 3 min; The prototype operation is a fully autonomous process that does not require manual intervention, with an average time of 55 s for 10 consecutive tests. This indicates that the mesh-laying robot arm can significantly improve work efficiency while freeing up the high-intensity labor of on-site workers, reduce the probability of safety accidents, and meet the expected design goals. At present, the prototype has completed 50 consecutive mesh-laying tests, and key components such as servo motors and clamps have not malfunctioned. The average positioning error is stable within ± 30 mm, meeting the design requirements. More than 1000 long-term operation experiments will be conducted in the future to record component wear, energy consumption changes, and fault maintenance situations, in order to verify long-term reliability.

Fig. 10.

Deployment and testing of control algorithm for physical prototype of mesh-laying robot arm.

In addition, during the on-site experiment, the execution device of the automatic mesh-laying robot operated stably without significant shaking. The displacement of each joint was continuous and smooth during the motion, and there was no mechanical impact phenomenon, further verifying the effectiveness and feasibility of the algorithm. Figure 11 shows the comparison of the tracking situation between the measured data and the preset data during the lifting process of the mesh-laying robot’s large and small arms. Through comparison, it can be seen that each joint of the mesh-laying robot can complete real-time tracking of the preset path during the operation process, and has high tracking accuracy. This further proves the feasibility of the control algorithm and provides theoretical support and experimental data verification for the planning of complex operation paths and autonomous operations in the future.

Fig. 11.

Comparison of tracking between measured data and preset data during the lifting process of the mesh-laying robot’s large and small arms.

Conclusion

(1) In response to the problems of high labor intensity and high safety factor in manual mesh-laying in coal mine excavation tunnels, this paper designs and develops an automatic mesh-laying robot system integrated into the body of the excavation anchor integrated machine, which can complete the fully autonomous operation process of grabbing, transporting, lifting, and releasing the flexible roll mesh of the roadway.

(2) A kinematic model and linkage coordinate system of an automatic mesh-laying robot were constructed using an improved D-H method, and theoretical derivation and analysis of the forward and inverse kinematics of the mesh-laying robot arm were carried out. Based on the Monte Carlo method and combined with MATLAB, simulation analysis of the workspace of the robot arm was carried out, and the conclusion was drawn that the workspace of the robot arm can meet practical applications.

(3) A model of an automatic mesh-laying robot arm was established using the Robotics Toolbox in MATLAB, and joint space planning simulation was performed on the robot arm to obtain the kinematic curves of each joint. The curves showed no abrupt changes, indicating that the trajectory of the automatic mesh-laying robot arm is continuous, and the designed robot arm can smoothly reach the target welding position.

(4) The correctness of MATLAB trajectory planning was verified using ADAMS, laying the foundation for the selection, dynamic analysis, and control algorithm optimization of the subsequent mesh-laying robot arm motor. This has significant practical significance for reducing labor intensity and improving job safety for workers.

Author contributions

Chengjun HU: Complete the first draft of the paper; Kun ZHANG: Complete the Figures and the Table; Gege PAN: Simulation; Mingchao DU: Put forward the idea of this paper; Jinglong BI: Experiment; Liangsong Huang : Development of Robot Control System; Bo LI: Experiment; Shuo WANG: MATLAB simulation;

Data availability

The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.