Abstract
We have used the method of x-ray diffraction microscopy to image the complex-valued exit wave of an intact and unstained yeast cell. The images of the freeze-dried cell, obtained by using 750-eV x-rays from different angular orientations, portray several of the cell's major internal components to 30-nm resolution. The good agreement among the independently recovered structures demonstrates the accuracy of the imaging technique. To obtain the best possible reconstructions, we have implemented procedures for handling noisy and incomplete diffraction data, and we propose a method for determining the reconstructed resolution. This work represents a previously uncharacterized application of x-ray diffraction microscopy to a specimen of this complexity and provides confidence in the feasibility of the ultimate goal of imaging biological specimens at 10-nm resolution in three dimensions.
Keywords: coherent x-ray diffraction imaging, x-ray microscopy
X-ray diffraction microscopy is a recently developed method in which only the coherent diffraction pattern of the sample is measured. It provides a path to high resolution without the limitations imposed by an x-ray optical system. The idea to image a noncrystalline object by phasing and inverting its diffraction pattern goes back to a suggestion by Sayre (1, 2) and was first demonstrated with x-rays by Miao et al. (3). In this article, we report the imaging of the complex-valued exit wavefront (both phase and magnitude) of a whole freeze-dried and unstained yeast cell. The images, at 30-nm resolution from multiple angular orientations of the cell, required an exposure of approximately one minute each using 750-eV x-rays (1 eV = 1.602 × 10-19 J). This demonstration paves the way for the application of 3D x-ray diffraction microscopy (XDM) (4, 5) to frozen-hydrated samples in the future.
High-resolution 3D images of biological samples are currently made by at least three methods: zone-plate x-ray microscopy (6–9), transmission electron microscopy (10, 11), and x-ray crystallography. All three have particular strengths and limitations. Both water-window (7–9) and multi-keV (12) zone-plate microscopes are currently limited to ≈60-nm 3D resolution by details of zone-plate resolution, depth of field, and operation. On the other hand, high-resolution transmission electron microscopes, although capable of extraordinary resolution, are limited by multiple electron scattering to specimens thinner than 0.5–1 μm (10, 13). The third method, x-ray crystallography, traditionally yields the highest resolution structures and is the structural technique of choice, but it is limited to specimens that can be crystallized. In summary, the traditional structural techniques do not provide a capability for 3D imaging of an intact eukaryotic cell with resolution around 10 nm, and it is toward this end that our present efforts are directed.
Since its introduction, XDM has been demonstrated with metal test objects in two dimensions (3, 14) and three dimensions (4) and with stained biological specimens (15) and microcrystals (5). The method is conceptually simple. The specimen (in our case a single yeast cell) is mounted on a thin support film, such that it acts as the sole source of scattering. The specimen is illuminated by a coherent beam of x-rays, and the far-field diffraction pattern is recorded on a charge-coupled device (CCD) camera. The intensity measurements are converted to magnitudes and are submitted to an iterative algorithm (16) for retrieval of the phases. In our experiments, the phase retrieval was accomplished by the difference-map algorithm (17). This iterative method is well suited to problems where the object function sought has to satisfy two different constraints. In our particular case, the first constraint is that the magnitude of the Fourier transform of the object should be equal to the magnitude of the measured diffraction pattern. The second constraint is that the object must lie within the support boundary, which must be known or determined by the algorithm. In the current experiment, the sampling of the diffraction pattern is such that the object's “support” (the region within which it is known to be contained) is only 4% of the corresponding real space area, providing a very strong constraint on the recovered object.
The resolution of XDM, like crystallography, is limited both by the wavelength of the radiation and by the maximum angle to which scattered photons are adequately counted. Even though the diffraction-imaging method dispenses with all efficiency and contrast-transfer losses of lenses, we expect that the radiation dose required to record the faint continuous pattern will also pose a limitation to the resolution (18, 19), as we discuss further below.
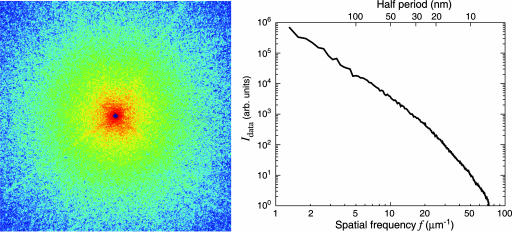
The yeast cell used in our experiment, Saccharomyces cerevisiae carrying the CLN3–1 mutation (20), was ≈2.5 μm in diameter and was prepared by rapid freezing in liquid ethane followed by drying in a commercial freeze dryer. The diffraction data were collected by using an apparatus (21) at beamline 9.0.1 of the Advanced Light Source at Lawrence Berkeley National Laboratory where the central cone of an undulator x-ray beam was focused by an off-axis zone-plate segment onto a 4-μm pinhole located 115 cm downstream. This combination (22) of zone plate and pinhole is equivalent to a monochromator with resolution of ≈0.2% at 750 eV. The specimen, mounted on a formvar-coated electron microscope grid 25 mm downstream of the pinhole, was illuminated by the central maximum of the pinhole's Airy pattern and scattered the x-ray photons onto the Roper Scientific (Trenton, NJ) MTE-2 in-vacuum CCD detector 15 cm downstream. The width of the coherence patch (determined by the pinhole-to-specimen distance) was 12.8 μm and was well matched to the specimen size. The CCD chip (EEV backside-thinned chip with direct illumination) had 1300 × 1340 pixels at 20 × 20 μm in size. A square aperture with beveled edges was arranged between pinhole and specimen with the beam passing through one corner; this protected the CCD from scatter by the pinhole in three quadrants simultaneously. The corner then was repositioned to allow collection of the missing quadrant. The CCD was protected from the intense beam at the center of the pattern by a beam stop that obscured ≈20 × 20 pixels, which means that information at spatial frequencies below ≈1 μm-1 was missing from the recording. It was necessary to acquire several patterns with varying exposure times, at each view direction, because the dynamic range of the CCD chip was not adequate for collecting the full range of intensities present in the diffraction patterns. Because of these strategies, each 2D data set was formed from a compilation of 26 exposures recorded with a total x-ray illumination time of 65 seconds and involving a dose of ≈108 Gy to the cell. The recorded data (a subset of which is shown in Fig. 1) extend to a collection angle corresponding to 78 inverse micrometers. In this experiment, we collected data in this manner for nine angular positions from -3 to + 5°; however, our apparatus is capable of tilting the specimen from to -80 to + 80°.
Fig. 1.
Soft x-ray diffraction pattern of a freeze-dried yeast cell. (Left) The assembled pattern shown represents the summation of several diffraction patterns, with a total exposure of 65 seconds to 750-eV x-rays. The assembled pattern covers 1200 × 1200 pixels of the 1340 × 1300 original array and extends to a spatial frequency, or diffraction angle divided by wavelength, of 48 inverse micrometers at the edges and 68 inverse micrometers at the corners. A spatial frequency of 48 inverse micrometers at the edges corresponds to a half-period pixel size in real space of 10 nm. The speckles in the diffraction pattern have a consistent size associated with the inverse of the size of the yeast cell. (Right) Power spectrum as a function of spatial frequency.
The yeast cell reconstructions reported here are made challenging by a combination of factors. First, the specimen is a strong phase/amplitude object with the consequence that the effective source of the far-field diffraction pattern is a complex-valued exit wave. Second, we used a central beam stop to protect the CCD from the most intense part of the pattern, which unfortunately prevents recording of the lowest spatial frequencies. The detrimental effect of this is exacerbated by the very round shape of the cell because of the existence of modes that are negligibly constrained, either by the available diffraction data or by the support of the object. Fig. 2 shows the two least constrained modes. The amplitudes of such modes can be varied enormously and still be consistent with the available information (the measured diffraction intensities and the object support). Our solution is to choose the amplitudes so as to minimize the variance of the object's values. This solution is easy to implement and delivers a smooth function that minimizes the introduction of image features not warranted by the data. To start the algorithm, a good approximation of the yeast cell's support initially was obtained from the autocorrelation as computed directly from the (incomplete) diffraction data. The shape of the support was then refined interactively to be very tight [progressive tightening of a support also may be achieved by the “shrinkwrap” algorithm (14)]. This refinement eliminates translations of the cell that could also compromise the averaging procedure discussed below. We did not apply any constraint on the values of the object, as is often done with real-valued objects (positivity constraint).
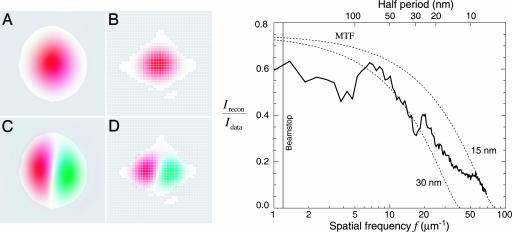
Fig. 2.
Technical details of the reconstruction of the diffraction data of Fig. 1. (Left) Because the very intense nondiffracted beam was blocked by a beamstop, no data were recorded at very low spatial frequencies. Shown here are two modes in the reconstruction superimposed on the missing data region of the detector (white pixels in the diffraction or Fourier space in B and D). We also show these modes in object space, superimposed on the support (allowed spatial region) of the yeast cell (A and C). The amplitudes of weakly constrained modes such as these are undetermined by our reconstruction. (Right) One measure of the quality of the reconstruction is the degree to which it reproduces the recorded data (diffraction intensities). The reconstructions of Fig. 3 are averages Irecon = | 〈Frecon 〉 | of many complex iterates Frecon of a phasing algorithm, each differing only in the values of their phases. Diffraction data that are reliably phased will add constructively, whereas data with phases that are inconsistent over many iterates will add randomly, leading to reduced intensity in the reconstruction compared to the recorded intensities Idata. The ratio Irecon/Idata is shown alongside the theoretical modulation transfer function (MTF) of conventional imaging optics with an efficiency of 75% and Rayleigh resolutions of 30 and 15 nm, respectively.
Iterative phasing algorithms are generally designed to reach a fixed point when all of the imposed constraints are satisfied. In actual applications, and primarily as a result of noise in the data, convergence to a fixed point is never perfect, and the algorithm arrives instead at a steady state with residual fluctuations. A single reconstruction, taken from the stream of fluctuating iterates, will convey more detail than is warranted because of fluctuations primarily in high spatial frequency features. To address this issue, we have adopted the procedure of averaging large numbers of these fluctuating reconstructions. The effect is that features present in all iterates (the sought-after signal) are maintained and those that vary from iterate to iterate (the noise) are reduced or eliminated. We believe that this approach delivers the most detailed image that is warranted by the data. For the reconstructions shown here, the difference map algorithm (17) was used with β = -1, although separate runs with Fienup's hybrid input–output algorithm (difference map with β = +1) gave indistinguishable results. The algorithm was first allowed to proceed for 1,000 iterations, and then a total of 981 iterates were averaged (every 50th iterate). The total reconstruction process of 50,000 iterations took ≈12 h on a desktop PC. Further details of the algorithm's implementation for the yeast cell work will be detailed in a separate publication.
Even in the Born approximation, the reconstruction of 2D diffraction data yields a partially defocused projection of the specimen if the x-rays used are overly soft because there will be some noticeable departure of the Ewald sphere from a principal plane in the full 3D reciprocal space. When the Born approximation applies, this effect can be corrected by collecting 3D diffraction data. Using our same apparatus, Chapman et al. (28) have obtained reconstructions of nonbiological objects by properly mapping diffraction intensities from planar CCD recordings into a 3D cube in reciprocal space (Movie 1, which is published as supporting information on the PNAS web site, displays their 3D reconstruction). Application of the iterative phasing algorithm to a 3D set of diffraction intensities can then yield true 3D information on the scattering strength of each voxel (4).
A key question in evaluating the reconstructions concerns their resolution. The diffraction data appear good out to each edge at a spatial half-period corresponding to a real-space pixel size of 10.3 nm (Fig. 1), but one must also consider the reliability of the recovered phases at different spatial frequencies. Because the reconstruction is based on the average of many iterates as described above, one measure can be obtained by comparing the magnitude of the Fourier transform of the averaged complex reconstruction, Irecon = | 〈Frecon 〉|2, with the magnitude of the recorded diffraction intensities, Idata, as a function of spatial frequency f. Spatial frequencies that are phased with less consistency will show a reduction in the ratio Irecon/Idata, as shown in Fig. 2. Although this spatial–frequency-dependent ratio provides a more complete indication of resolution than any single parameter does, it is nonetheless useful to compare it to the modulation transfer function (MTF) of conventional (incoherent brightfield) imaging with a lens. We therefore show the MTF of lenses with 75% efficiency and Raleigh resolutions of 15 nm and 30 nm on the same figure (see Fig. 2). The ratio Irecon/Idata for the reconstruction falls approximately between these two curves, suggesting an equivalent resolution of better than 30 nm. This resolution estimate is supported by the observation of features at this scale that are reproduced in independent reconstructions obtained from diffraction data acquired at different tilt angles (Fig. 3).
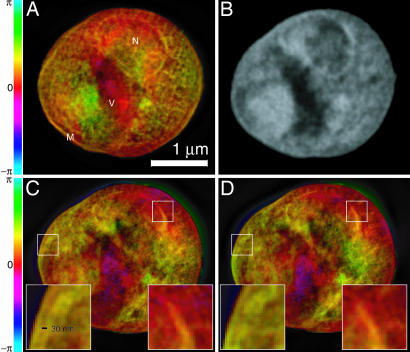
Fig. 3.
Images of a freeze-dried yeast cell. A was obtained by phasing the diffraction data in Fig. 1, whereas C and D were obtained from reconstructions of two separate, slightly lower exposure data sets acquired with the cell tilted by 3° (C) and 4° (D) relative to A (Movie 2, which is published as supporting information on the PNAS web site, displays reconstructed images at 1° intervals over a 7° range). Insets in C and D show ≈30-nm fine features at the cell and nuclear membrane regions that are reproduced consistently in these separate recordings and reconstructions, even though these 2D reconstructions are projections along the beam axis with some blurring as a result of defocus. The renderings of the complex-valued reconstructions use brightness to represent magnitude and hue to represent phase (the color scale indicates reconstructed phase values). A is labeled according to a provisional identification of the nucleus (N), a storage vacuole (V), and the cell membrane (M). B shows a National Synchrotron Light Source X1A2 STXM (27) image taken of the same cell using 540-eV x-rays and a zone plate with an estimated Rayleigh resolution of 42 nm; this image shows absorption effects only, so it is shown in grayscale. The STXM image is shown here for comparison purposes only; it was taken at a different photon energy and in a different contrast mode (incoherent brightfield) than applies to the reconstructed diffraction data. The information contained in the STXM image was not used in any way in obtaining the diffraction reconstruction.
Such reproduction of features also gives us confidence that the significant internal structures revealed in the reconstructed images, shown and explained in Fig. 3, are in fact real. Based on their characteristic shape and relative positions, structures that appear to be the nucleus and vacuole (N and V in Fig. 3A) can be identified, and similar structures are seen in a scanning transmission x-ray microscope (STXM) image of the same cell (Fig. 3B). It is expected that the reconstruction from diffraction data should show similarity but not perfect agreement with a STXM image of the same specimen because of the use of a different photon energy and imaging modality.
Radiation damage is an important consideration in life-science microscopy, so we (19), and others (18), have made efforts to understand its role in limiting the resolution of diffraction microscopy. The tentative conclusion of our calculations is that 3D XDM of frozen-hydrated samples should be possible to around 10-nm resolution. As noted, our 2D measurements (of dried cells) at 30-nm resolution required a dose of 108 Gy, whereas separate measurements on a frozen-hydrated cell revealed no sign of damage in 18-nm half-period structures after 5 × 109 Gy, which is in agreement with previous results (23, 24). According to the dose fractionation analysis (25, 26) of Hegerl and Hoppe, the dose required for 3D imaging at a given resolution and statistical accuracy should be nearly the same as for the 2D measurement.
We have reported a demonstration of the imaging of an intact and unstained biological cell by XDM. This experiment shows that such a microscope can be used to visualize yeast cells and their internal components. The 2.5-μm-wide cells in our experiment were imaged at 30-nm resolution, which is not far short of the calculated radiation-damage limit (19) of around 10 nm. In addition, our experiment is already capable of handling samples up to ≈10 μm in size and is beginning to deliver diffraction patterns of frozen-hydrated yeast cells. Moreover, the same microscope at the Advanced Light Source at Lawrence Berkeley National Laboratory also is being used to develop the next generation of XDM experiments, which will remove some of the limitations apparent in our current method by reducing the loss of low spatial frequency information and providing data suitable for iterative phasing in 3D. In particular, the microscope has been used by Chapman et al. (28) to produce a full 3D tomographic image of a gold test object. Overall, we may conclude that the results reported here, in combination with the work of Chapman et al. (28), open the way for the high resolution 3D imaging of frozen-hydrated biological cells.
Supplementary Material
Acknowledgments
We acknowledge support provided by the Advanced Light Source staff and Bruce Futcher of Stony Brook University's Department of Biochemistry and Cell Biology for providing the cell line imaged with our microscope. This project is supported by National Institutes of Health, National Science Foundation, and Department of Energy grants to the Stony Brook group. The Advanced Light Source at Lawrence Berkeley National Laboratory is supported by the Director, Office of Science, Office of Basic Energy Sciences, Materials Sciences Division, of the U.S. Department of Energy.
Author contributions: D. Shapiro, T.B., V.E., M.H., C.J., J.K., E.L., and D. Sayre designed research; D. Shapiro, P.T., T.B., V.E., M.H., C.J., J.K., E.L., H.M., and A.M.N. performed research; D. Shapiro, P.T., V.E., C.J., E.L., H.M., and A.M.N. analyzed data; D. Shapiro, P.T., T.B., V.E., M.H., C.J., and E.L. contributed new reagents/analytic tools; and D. Shapiro, V.E., M.H., C.J., J.K., and D. Sayre wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: XDM, x-ray diffraction microscopy; CCD, charge-coupled device; STXM, scanning transmission x-ray microscope.
References
- 1.Sayre, D. (1980) in Imaging Processes and Coherence in Physics, eds. Schlenker, J., Fink, M., Goedgebuer, J. P., Malgrange, C., Viénot, J. C. & Wade, R. H. (Springer, Berlin), Vol. 112, pp. 229-235. [Google Scholar]
- 2.Sayre, D., Chapman, H. N. & Miao, J. (1998) Acta Crystallogr. A 54, 232-239. [Google Scholar]
- 3.Miao, J., Charalambous, P., Kirz, J. & Sayre, D. (1999) Nature 400, 342-344. [Google Scholar]
- 4.Miao, J. W., Ishikawa, T., Johnson, B., Anderson, E. H., Lai, B. & Hodgson, K. O. (2002) Phys. Rev. Lett. 89, 088303. [DOI] [PubMed] [Google Scholar]
- 5.Williams, G. J., Pfeifer, M. A., Vartanyants, I. A. & Robinson, I. K. (2003) Phys. Rev. Lett. 90, 175501. [DOI] [PubMed] [Google Scholar]
- 6.Haddad, W. S., McNulty, I., Trebes, J. E., Anderson, E. H., Levesque, R. A. & Yang, L. (1994) Science 266, 1213-1215. [DOI] [PubMed] [Google Scholar]
- 7.Wang, Y., Jacobsen, C., Maser, J. & Osanna, A. (2000) J. Microsc. 197, 80-93. [DOI] [PubMed] [Google Scholar]
- 8.Weiß, D., Schneider, G., Niemann, B., Guttmann, P., Rudolph, D. & Schmahl, G. (2000) Ultramicroscopy 84, 185-197. [DOI] [PubMed] [Google Scholar]
- 9.Larabell, C. A. & Le Gros, M. A. (2004) Mol. Biol. Cell 115, 957-962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Grimm, R., Singh, H., Rachel, R., Typke, D., Zillig, W. & Baumeister, W. (1998) Biophys. J. 74, 1031-1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Medalia, O., Weber, I., Frangakis, A., Nicastro, D., Gerisch, G. & Baumeister, W. (2002) Science 298, 1209-1213. [DOI] [PubMed] [Google Scholar]
- 12.Wang, S., Duewer, F., Kamath, S., Kelly, C., Lyon, A., Nill, K., Pombo, P., Scott, D., Trapp, D., Yun, W., et al. (2002) in Proceedings of the 28th International Symposium for Testing and Failure Analysis, ed. Boit, C. (AMS International, Phoenix, AZ), pp. 227-233.
- 13.Jacobsen, C., Medenwaldt, R. & Williams, S. (1998) in X-Ray Microscopy and Spectromicroscopy, eds. Thieme, J., Schmahl, G., Umbach, E. & Rudolph, D. (Springer, Berlin), pp. II93-II102.
- 14.Marchesini, S., He, H., Chapman, H. N., Hau-Riege, S. P., Noy, A., Howells, M. R., Weierstall, U. & Spence, J. C. H. (2003) Phys. Rev. B 68, 140101. [DOI] [PubMed] [Google Scholar]
- 15.Miao, J. W., Hodgson, K. O., Ishikawa, T., Larabell, C. A., LeGros, M. A. & Nishino, Y. (2003) Proc. Natl. Acad. Sci. USA 100, 110-112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fienup, J. R. (1978) Optics Lett. 3, 27-29. [DOI] [PubMed] [Google Scholar]
- 17.Elser, V. (2003) J. Opt. Soc. Am. A 20, 40-55. [DOI] [PubMed] [Google Scholar]
- 18.Shen, Q., Bazarov, I. & Thibault, P. (2004) J. Synchrotron Rad. 11, 432-438. [DOI] [PubMed] [Google Scholar]
- 19.Howells, M. R., Beetz, T., Chapman, H. N., Cui, C., Holton, J. M., Jacobsen, C. J., Kirz, J., Lima, E., Marchesini, S., Miao, H., et al. (2005) J. Electron Spectrosc. Rel. Phenom., in press. [DOI] [PMC free article] [PubMed]
- 20.Tyers, M., Tokiwa, G. & Futcher, B. (1993) EMBO J. 12, 1955-1968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Beetz, T., Howells, M. R., Jacobsen, C., Kao, C.-C., Kirz, J., Lima, E., Mentes, T. O., Miao, H., Sanchez-Hanke, C., Sayre, D. & Shapiro, D. (2005) Nucl. Instrum. Methods Phys. Res. A 545, 459-468. [Google Scholar]
- 22.Howells, M. R., Charalambous, P., He, H., Marchesini, S. & Spence, J. C. H. (2002) in Design and Microfabrication of Novel X-Ray Optics, ed. Mancini, D. (SPIE, Bellingham, WA), Vol. 4783, pp. 65-73. [Google Scholar]
- 23.Schneider, G. (1998) Ultramicroscopy 75, 85-104. [DOI] [PubMed] [Google Scholar]
- 24.Maser, J., Osanna, A., Wang, Y., Jacobsen, C., Kirz, J., Spector, S., Winn, B. & Tennant, D. (2000) J. Microsc. 197, 68-79. [DOI] [PubMed] [Google Scholar]
- 25.Hegerl, R. & Hoppe, W. (1976) Z. Naturforsch. 31a, 1717-1721. [Google Scholar]
- 26.McEwen, B. F., Downing, K. H. & Glaeser, R. M. (1995) Ultramicroscopy 60, 357-373. [DOI] [PubMed] [Google Scholar]
- 27.Feser, M., Beetz, T., Jacobsen, C., Kirz, J., Wirick, S., Stein, A. & Schäfer, T. (2001) in Soft X-Ray and EUV Imaging Systems II, eds. Tichenor, D. A. & Folta, J. A. (SPIE, Bellingham, WA), Vol. 4506, pp. 146-153. [Google Scholar]
- 28.Chapman, H. N., Barty, A., Marchesini, S., Noy, A., Cui, C., Howells, M. R., Rosen, R., He, H., Spence, J. C. H., Weierstall, U., et al. (2005) arXiv: physics/0509066.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.