Investigation on the transition depth of open pit to underground mining in Sijiaying iron mine

Abstract

When the expansion of an open pit limit is restricted by the permanent facilities located near the boundary of the pit, the traditional economic evaluation method is insufficient to determine the ultimate transition depth of mining from open pit to underground. A new method needs to be constructed to determine the transition depth from open pit mining to underground. In the context of mining in the transition from open pit to the underground at Sijiaying Iron Mine located in North China, this study investigates the ultimate depth of the open pit mining under the conditions of the New Luan River located on the footwall and a Provincial Highway on the hanging wall near the open pit slope. Formulas for calculating the limiting depth of open pit mining when immovable permanent facilities exist on the hanging wall, footwall, and both sides of orebodies are established, respectively. Using these established formulas verifies the economic feasibility of the new method. The calculated transition depth of mining from the open pit to the underground for the case mine is 388 m. The result shows that the presented formulas achieve significance and usability in ascertaining transition depth from the open pit to the underground under the constraints of various permanent immovable facilities on the hanging wall and footwall of the ore body.

Introduction

Although open pit mining offers several advantages over underground mining—such as enhanced production capacity, improved recovery rates, reduced loss and dilution, greater flexibility, and increased safety¹—the challenges posed by the mining environment, deposit geometry, and increasing depth have rendered the transition from open pit to underground mining a necessary approach for developing many deposits². Over the years, determining the optimal depth for the transition from open pit to underground mining has become a vital issue, creating a challenge for mining operational decisions^2,3. With the gradual increase of the demand for mineral resources in social development, decreasing total resources determines the inevitable interaction between open pit mining and underground mining in time and space^4,5. In the process of open pit mining of metal deposits, the difference in deposit occurrence characteristics, the restriction of the mining environment, and the increase of open pit mining cost all constitute the constraint conditions that restrict the continuation of open pit mining². Under this condition, implementing open-pit to underground mining technology has become the first choice for open-pit mines to continue developing their deep resources and maintaining production continuity⁶. As mining transitions from open pit to underground, it is a comprehensive mining technology that integrates open pit and underground mining technologies⁷. The advantages and disadvantages of the two mining technologies must be inherited simultaneously in the implementation process. Therefore, it is essential to assess the possibility of mining transitioning from mining to underground mining⁸. In this context, the configuration of the underground mining model–particularly the excavation geometry and sequence–primarily depends on the selected access structure (e.g., declines, shafts, adits) and the chosen mining method. Their interaction significantly affects the efficiency, cost, and safety of deep mining operations^9,10.

Determining this limit depth impacts the total profit of mine operation and the decision to transform the mining mode, so it has attracted one of the hot topics in the mining industry. Many scholars have studied from different angles and proposed various methods to determine the open pit mining boundary of conversion to the underground mine. For example, Ordin and Vasil’ev¹¹ investigated the optimization of depth for the transition from open pit to underground coal mining of the Raspadsky Open Pit Mine with numerical calculation using the dynamic programming method. Considering the open pit mining safety, Zhizhang et al.¹² determined that the ultimate stable slope angle of Changshanhao mine is 38° through three-dimensional numerical calculation and determined that the safe mining depth of the mine is 1216 m according to this angle. Khaboushan et al.¹³ executed two optimization models with varying strategies of solution on the 3D profile of the actual orebody, providing a quantitative analysis method for determining the optimal transition depth between open pit mining and various underground mining methods. The integer programming model and its improved schedules are used widely in mining transition depth from open pit to underground^14,15. Bakhtavar¹⁶ established the geological and economic block model of Chah-Gaz iron ore deposit in Iran. He obtained the transition depth of the mine from open pit to underground mining of 450 m. MacNeil and Dimitrakopoulos¹⁷ determined the most favorable candidate transition depth from open pit to underground mining based on the comprehensive consideration of the total revenue of the open pit and underground mining parts. They proposed a stochastic integer programming optimization model integrating geological uncertainty and technical risk management. To maximize the profit of open pit mining and underground mining, Bakhtavar et al.¹⁸ established a model by introducing the block economic value of open pit and underground mining to study the transition problem using the (0–1) integer programming method. Chung et al.¹⁹ proposed a new integer programming formula for calculating the transition position from open pit mining to underground mining and verified the model’s validity by taking a two-dimensional gold deposit as an example. MacNeil et al.²⁰ explored the optimal mining depth in the transition from open pit to underground at AngloGold Ashanti’s Geita gold mine in Tanzania by evaluating the profits of candidate transition depths. Badakhshan et al.²¹ developed a mixed integer programming model that considered the negative environmental effects and investigated the transition depth of the Sungun large-scale copper deposit, determining it to be 887.5 m.

It faces many challenges to study the problem of the transition from open pit to underground mining from different respects and realize the smooth transition^20,21, e.g., the stability of the pit slope²², ground subsidence caused by the conversion from open pit to underground mining²³, a strategy selection for the sustainable development of the open pit mining and technical system^24,25, and the method on optimizing the design of an open pit mine²⁶ et al. Due to the influence of the open pit mining environment, some mines have the problem that the surface boundary of the open pit mining cannot be expanded, and the mining depth is difficult to reach the original design depth of the open pit. Here, there is another case that affects the determination of the transition depth of the mining from the open pit to underground, i.e., there are immovable permanent facilities near the sides of the open pit. In this case, the traditional economic evaluation method is insufficient to determine the ultimate depth of the open pit mining, a new method needs to be established to assess the maximum depth of open pit mining and determine the depth limit of open pit mining transited into underground.

Sijiaying Iron Mine, located in Hebei Province, North China, faces significant challenges in determining the optimal mining depth in the transition from open pit to underground. After more than ten years of high-efficiency open pit mining, the mine has entered a critical stage of planning and decision-making for the transition. According to the preliminary design for underground development, the mine is expected to adopt stage stoping with subsequent filling method and sublevel stoping with subsequent filling method as the primary mining methods. In terms of access, a vertical shaft developing system has been selected, based on a comprehensive assessment of technical feasibility and economic efficiency. Based on this mine, this paper applies formulas for calculating the limiting depth of open pit mining when immovable permanent facilities exist on the hanging wall, footwall, and both sides of orebodies. The transition depth from open pit to underground mining in Sijiaying Iron Mine is calculated, and the rationality of the new method is verified by traditional economic methods, which provides a new approach for estimating the transition depth from open pit to underground mining. The scientific novelty of this study lies primarily in the explicit mathematical formulation (formulas 1–5) of technical constraints imposed by immovable permanent surface structures to determine the transition depth. The practical application of these derived formulas using the Sijiaying Iron Mine example further demonstrates their practical significance and applicability for assessment.

Status of open pit mining in the case mine

After more than ten years of open pit mining, the Sijiaying open pit mine has formed a large, deep, and concave open pit stope with a length of 2980 m and a width of 1600 m on the surface, and an average depth of 311 m. The pit mining is divided into No. 1 and 2 mining areas, with the N18 exploration line as the boundary of the two mining areas, and the produced ores are supplied to the No.1 and 2 mineral processing plants, respectively. Figure 1 shows the mining environment of the case mine.

Fig. 1.

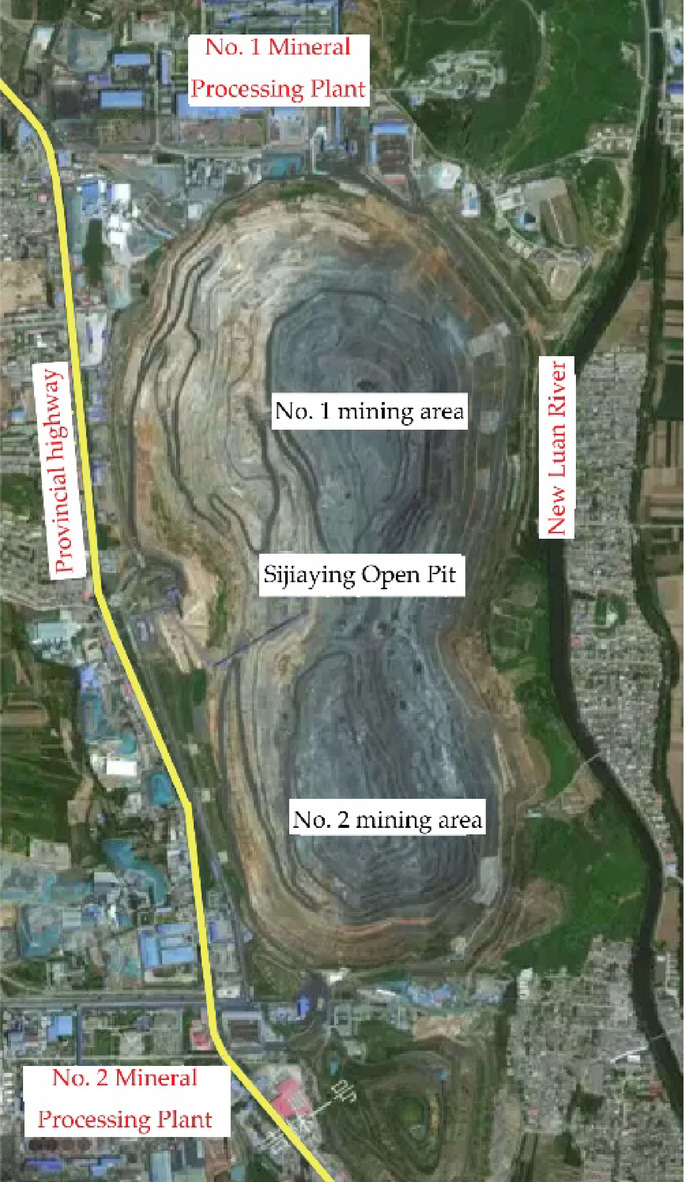
Mining environment of Sijiaying Iron Mine in North China. The yellow line on the left (west of the pit) is a provincial highway, and the black line on the right (east) is the New Luan River. The image is sourced from the publicly accessible Google Maps platform and all annotations in the image were created by Zengxiang Lu, the correspongding author of this paper, only for illustrating the surrounding environment of the case mine to the readers.

As can be seen from Fig. 1, there is an inter-provincial highway on the west side of the open pit(hanging wall of the deposit), and the New Luan River is adjacent to the east side of the pit (footwall of the deposit). The highway and the river constitute the technical constraints of expanding the pit limit, restricting further increases in the depth of open pit mining. Given these constraints, understanding the mechanical parameters of the ores and rocks is crucial for the subsequent design of the open-pit to underground mining transition. Relevant parameters are presented in Table 1.

Table 1.

The relevant mechanical parameters of ore and rock.

	Density/t·m−3	Compressive strength/MPa	Tensile strength/MPa	Cohesion/MPa	Angle of internal friction/(°)
Ore	3.16	124.2	2.0	8.0	34.3
Rock	2.70	150.0	2.1	6.0	34.5

The mining area has entered the deep concave open pit mining stage, and there is no condition to extend the pit boundary. According to the reserves of resources preserved and the actual production situation of the mine, relevant research on the open pit to underground mining of Sijiaying Iron Mine is also imminent.

Two constraints and their balance criterion for open pit mining of ore deposit

Economic constraint

It is essential to determine the maximum depth based on the profitability of the open pit operation. When the expansion of the open pit limit is not affected by the mining surrounding environment, the depth of open pit mining depends on the profitability of the mining operations²⁷, and the traditional economic evaluation method is sufficient to determine the ultimate transition depth of mining from open pit to underground.

Usually, with the increase of the open pit mining depth, there will be a threshold value of mining cost, and the corresponding open pit mining depth of this “cost threshold” will become the transition depth limit of the deposit mining from the open pit to the underground. The optimal depth of mining in the transition from the open pit to underground is defined by comparing the cost of mining using the open pit vs. underground methods^2,28, i.e., when the cost of the open pit mining is equal to that of underground, the open pit mining of the deposit has reached its maximum depth, it needs to be transferred to underground mining. Therefore, this “cost threshold” constitutes the problem of the economic constraint of one deposit mining in transitioning from open pit mining to underground.

The economic and rational stripping ratio is usually an essential economic index to determine the final boundary of open pit mining. It is the basis for comparing and calculating the best effect of realizing the cost and profit of ore mining. For the open pit mining transitioning to underground, the constraint conditions of comprehensive mining cost determined by the limiting depth of the open pit can also be used as the evaluation basis. Therefore, the comprehensive cost constraint conditions of mine mining constitute the economic constraints of the mine from open pit mining to underground.

The “cost threshold” is more related to the stripping ratio, the overall stripping ratio, the break-even, the operating (instantaneous), and the allowable or economic-rational stripping ratio are often used to solve the transition problem.

Technical constraint

The deposit continues using the open pit mining method, which can help the enterprise obtain greater profits²⁹. But sometimes, due to the influence of the surrounding environment of the mining area, the restrictions of the surface terrain conditions around the open pit, or the requirements of safety or environmental protection, e.g., the protection of the railway, main buildings or structures, rivers, and lakes around the mining pit et al., during the process of open pit mining, the pit limit of one or more sides of the open pit cannot be continued to expand. As a result, the mining depth of the open pit is restricted. Under this constraint, although the open pit mining cost has not reached or approached that of underground, it is necessary to consider the transition from open pit to underground mining in time. Therefore, the surface topography constraints constitute the technical constraints of transitioning from the open pit to underground mining. The constraints of surface terrain conditions on the expansion of the open pit mining limits may be manifested in one or more sides of the hanging wall, footwall, and the two ends of the strike of the ore body. The surface terrain constraint condition for determining the limiting depth of open pit mining is a kind of technical constraint condition.

Balance criterion between two constraints

Based on the above economic and technical constraints, the core criterion for determining the ultimate transition depth from open pit to underground mining can be summarized as follows:

Under economic constraints, the transition depth is defined as the point at which the total cost of extracting one additional unit of ore by open pit equals the cost of mining the same unit by underground methods. This depth represents the economic transition point and marks the optimal point for switching from open pit to underground mining. Under technical constraints, the final depth of open pit mining must satisfy both slope stability requirements and surface terrain limitations, and must not exceed the economically permissible depth. In such cases, even if the economic transition point has not been reached, a shift to underground mining must occur in advance due to technical or safety considerations.

Regardless of the technical constraints in calculating the limit depth of open pit mining, it is essential to evaluate whether the chosen method is economically viable, technically feasible, safe, and reliable. Additionally, it is crucial to determine the limit depth of open pit mining through a comprehensive assessment that considers specific research objectives and existing economic and technological policies.

Limiting depth of open-pit mining under technical constraints

Basic model

A new method must be constructed to determine the limiting depth of the open pit mining under technical constraints which influences the expansion of the open pit limit. Four cases reflect the technical constraints of open pit mining, they are:

1. There are immovable permanent facilities located on the hanging wall of the ore body near the boundary of the open pit;

2. There are immovable permanent facilities situated in the footwall of the ore body near the boundary of the open pit;

3. There are immovable permanent facilities on both the hanging wall and the footwall of the ore body;

4. There are immovable permanent facilities on one or two ends of the strike of the ore body near the boundary of the open pit.

Figure 2 shows a typical cross-section of open pit mining located in the exploration line profile. The yellow area presents the ore body with an average dip angle of γ₁ in the hanging wall, an average dip angle of γ₂ in the footwall, and a width of δ, and the gray area is the waste, i.e., the stripping area.

Fig. 2.

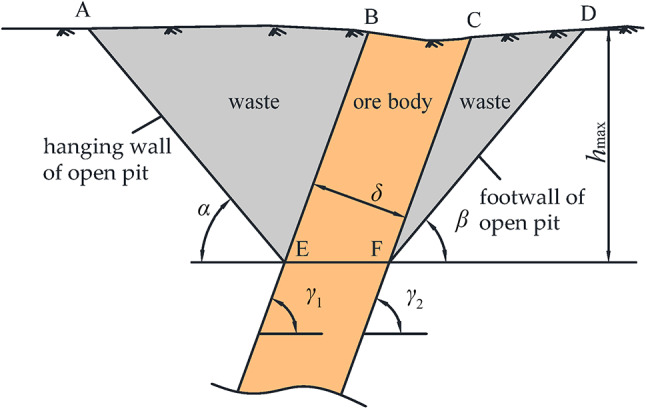
The cross-section of the open pit is perpendicular to the ore body strike, including the basic parameters of the open pit mining.

As shown in Fig. 2, the four points of A, E, F, and D constitute the current limit of open pit mining. h_max is the current depth of the pit, and α and β are the maximum allowable slope angle, i.e., the limiting angle of the pit side, along the hanging wall and the footwall of the pit side, respectively.

When there are immovable permanent facilities on one or both ends of the open pit on the strike of the ore body to be mined, unless the strike length of the ore body is small, it will generally only affect the strike length of the open pit so that the expansion of the surface boundary of the open pit is limited. Still, the limiting depth of the open pit is not affected. Thus, the case four is not discussed here.

Determination of open pit mining depth under technical constraint

Factors influencing the determination of open-pit mining depth

In addition to the geometric and spatial constraints imposed by immovable surface facilities, weather conditions significantly influence slope stability by altering the geomechanical and hydrogeological characteristics of the pit rock mass. These effects, in turn, constrain the maximum allowable slope angles (α and β in Fig. 2) used in the calculation of open pit mining depth. Prolonged exposure to rainfall, freeze–thaw cycles, and surface water infiltration leads to progressive degradation of shear strength and increased pore water pressure, accelerating the deterioration of the rock mass.

Moreover, the coupling effects of geological discontinuities, in-situ stress, and mining-induced disturbances further compromise slope stability, thereby affecting the determination of maximum mining depth under technical constraints. Therefore, the design of the maximum allowable slope angles must account for local climatic conditions to ensure safe mining operations and prevent slope failure. In regions subject to intense seasonal rainfall or severe freeze–thaw conditions, more conservative slope angles may be required, ultimately reducing the achievable mining depth under technical constraints.

Immovable permanent facilities located on the hanging wall

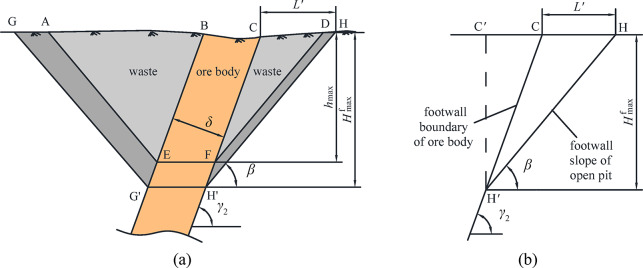
It is assumed that there are immovable permanent facilities at point G that cannot be moved and will affect the expansion of the width of the pit limit, as shown in Fig. 3, and that a safety berm (safe distance) from these facilities to the pit boundary is considered in the geometric analysis. Point A is the nearest position to the pit side boundary located on the hanging wall of the ore body when the safety berm is taken into account. Under this condition, the deposit’ s mining needs to be transferred to underground mining from the open pit.

Fig. 3.

Unmovable permanent facility located near the hanging wall slope of the open pit. (a) the cross-section of the open pit, including some related parameters of open pit mining; (b) extracted geometry for deriving the maximum depth for open pit mining under this case.

For the profile illustrated in Fig. 3, draw a line from point G according to the allowable angle α of the pit slope to establish intersection point G’ with the boundary of the hanging wall of the ore body. Subsequently, draw a horizontal line from point G’ to create an intersection point H’ with the boundary of the footwall of the ore body, and then draw a line from point H’ following the allowable angle β of the footwall of the pit side to form the intersection point H with the surface. Then, GG’H’H constitutes the pit limit when there is a permanent facility near the boundary of the pit on the hanging wall of the ore body. At this juncture, 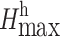represents the maximum depth for open pit mining under the condition of the permanent facility located on the pit side of the hanging wall.

We can extract a geometry from Fig. 3 (a) as shown in Fig. 3 (b) which is helpful to derive the formula for calculating 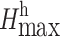. It denotes that L is the horizontal distance between points G and B, measured under the condition that the required safety berm from point G to the pit boundary is satisfied, and γ₁ is the average dip angle of the hanging wall of the ore body, according to the geometric relationship shown in Fig. 3 (b), it can be derived:

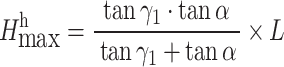1

where α is the maximum allowable angle along the hanging wall of the pit side; L is the distance between points G and B.

Permanent facilities located on the footwall

As shown in Fig. 4(a), it supposes that H is the nearest point of the unmovable permanent facility near the boundary of the pit on the footwall of the ore body, and that a safety berm from this facility to the pit boundary is considered in the geometric analysis, affecting the further expansion of the pit limit. In this case, we can refer again to Fig. 3 (a) and draw a line from point H according to the allowable slope angle β of the pit to form intersection point H’ with the boundary of the footwall of the ore body; next, draw a horizontal line starting from H’ to create an intersection point G’ with the hanging wall boundary of the ore body; finally, draw a line from G’ according to the allowable angle α of the pit side which intersects with the ground at point G. Then, HH’G’G constitutes the pit limit when the immovable permanent facility is on the footwall of the ore body. Also, 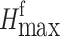denotes the maximum depth for open pit mining under the condition of the unmovable permanent facility located on the footwall slope of the open pit.

Fig. 4.

Unmovable permanent facility seated near the footwall slope of the open pit. (a) the cross-section of the open pit, including some related parameters of open pit mining; (b) extracted geometry for deriving the maximum depth for open pit mining under this case.

Similarly, a geometry is extracted from Fig. 4 (a), as shown in Fig. 4 (b). Let L’ signify the distance from points C to H, measured under the condition that the required safety berm from point H to the pit boundary is satisfied, and the formula for calculating 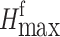can be derived as follows:

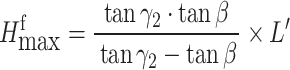2

where γ₂ is the average dip angle of the footwall of the ore body.

Permanent facilities located on both the hanging wall and footwall

Sometimes, there are unmovable permanent facilities on both sides of the deposit’s hanging wall and foot wall, i.e., points G and H(as shown in Fig. 3 or Fig. 4), which restrict the expansion of the pit limits. In this case, the maximum depth of open pit mining H_max could be determined according to the minimum values obtained from formulas (1) and (2), as formula (3).

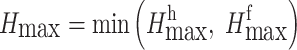3

Application of the method

Formulas (1) to (3) show the calculating method of the maximum depth of open pit mining in various cases of unmovable permanent facilities located on the pit sides, which only denote one pit profile based on the exploration line. Because an open pit has a long distance along the strike of the ore body, the result of the depth calculation of one section is not representative, and multiple sections are needed to determine the final depth.

Therefore, the calculating cross-section could be selected according to the exploration line of the deposit. Based on the maximum depth calculation results of each exploration line profile, the final depth of open pit mining could be determined by the following three formulas:

1. On the footwall:

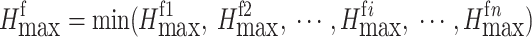4

where is the maximum mining depth of the open pit at exploration line i, and i is the exploration line’s number of 1 to n.

• 2.On the hanging wall:

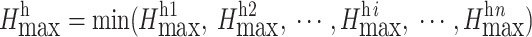5

where 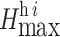is the maximum mining depth of the open pit at exploration line i, and i is the exploration line’s number of 1 to n.

• 3.On both the hanging wall and footwall, the maximum mining depth of the open pit is the same as formula (3).

Limiting depth of open pit mining under economic constraints

The cost comparison method for raw ore is one of the primary approaches to determining the economic limit depth of open pit mining. This method is grounded in the principle that the cost of extracting raw ore through open-pit mining should not exceed the cost of underground mining. By identifying the equilibrium point between the boundary stripping ratio and the economically viable stripping ratio, this approach has emerged as the preferred method for defining the optimal mining depth of open pit operations due to its simplicity and broad applicability.

Figure 5 illustrates a typical cross-section of open pit mining along the exploration line. Here, HH’G’G represents the boundary of open pit mining. To extract the ore dO within range EFG’H’, it is necessary to increase the amount of waste rock dW in the stripping areas AEG’G and DFH’H.

Fig. 5.

The cross-section method is employed to determine the limiting depth of open-pit mining. This method involves sections perpendicular to the ore body’s direction and incorporates the fundamental parameters required for open-pit mining operations.

As shown in Fig. 5, h_max represents the current pit depth, H’_max denotes the maximum economically constrained depth for open pit mining, α, and β are the maximum allowable slope angles of the pit walls, which correspond to the limiting angles of the top and bottom walls of the pit; γ is the average dip angle of the ore body.

Based on the primary economic design indicators, the pure mining cost (C_a) for open pit mining, the raw ore cost (C_u) for underground mining, and the stripping cost (C_b) for open pit mining are determined, respectively. According to the principle that the boundary stripping ratio must not exceed the economically reasonable stripping ratio, which indicates that the raw ore cost of open pit mining must not surpass that of underground mining, the critical condition for transitioning from open pit to underground mining can be determined as follows:

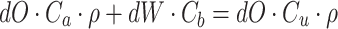6

where ρ denotes the bulk density of the ore.

When the average thickness of the ore body is δ, based on the geometric relationship, the limiting depth for transitioning from open pit to underground mining can be determined^[2].

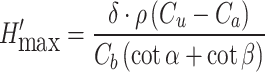7

As can be observed from formula (7), in the absence of surface topography constraints, the limiting depth of open pit mining is influenced by the average thickness of the ore body, the bulk density of the ore, the costs associated with mining and stripping in open pit operations, the cost of underground mining, and the final slope angles permitted by the hanging wall and footwall of the open pit; however, it is independent of the dip angle of the ore body.

Maximum mining depth of open pit in Sijiaying iron mine

The maximum mining depth of Sijiaying open pit iron mine under technical constraints

In the Sijiaying open pit mining operation, because of the restriction of the Inter-provincial Highway, the open pit limit cannot expand towards the hanging wall; meanwhile, the New Luan River restricts the expansion to the footwall of the pit limit, and the open pit mining has to transferred to the underground. Therefore, selecting the transition depth of mining from open pit to underground is one of the most critical decisions in the design stage of the mine.

There are 13 exploration lines named N8, N10, …, and N32 in the Sijiaying open pit, and only nine exploration lines, according to the pit geometry, affect the open pit mining depth and be used to calculate the maximum depth. According to the distances of the protection boundary of the Provincial highway to the ore deposit hanging wall and those of the New Luan River to the deposit of footwall, the maximum allowable angles of both pit sides and the dip angle of the ore body at each exploration line in situ, formulas (1) and (2) are used to calculate the maximum mining depth of open pit mining at each exploration line under the condition of the permanent facility located on both the pit sides of the hanging wall and the footwall, respectively. The orebody parameters are shown in Table 2.

Table 2.

Mining parameters of the orebody under the condition that permanent facilities are present on both the hanging wall and footwall sides in the case mine.

Exploration line No.	Dip angle of ore body		Hanging wall		Footwall
	γ1/(°)	γ2/(°)	L/m	α/(°)	m	β/(°)
N12	48	49	766	43	447	36
N14	43	55	874	41	388	38
N16	43	39	1022	41	220	34
N18	42	43	1123	42	356	34
N20	47	45	1043	43	363	34
N22	40	44	1094	41	243	35
N24	33	38	1203	43	108	35
N26	27	43	1384	43	126	36
N28	37	47	1000	43	204	36

Based on the parameters of the ore body and the open pit operation in situ, the calculated results of the maximum depth of open pit mining are shown in Fig. 6.

Fig. 6.

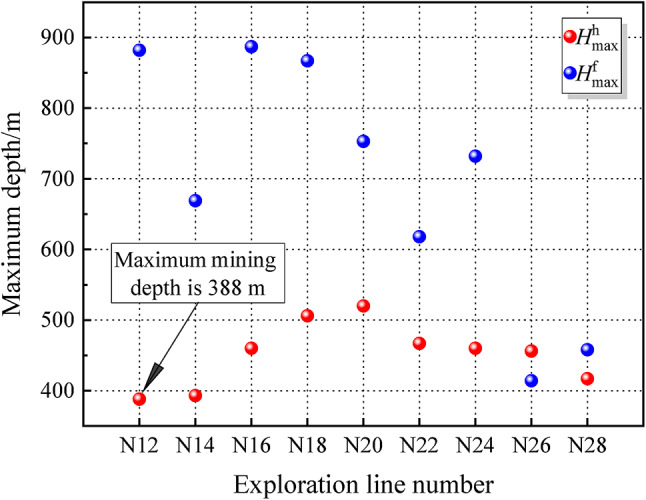
The maximum depth of open pit mining at each exploration line under the conditions of the permanent facilities located on both the pit sides of the hanging wall and the footwall in the case mine.

It can be seen from Fig. 6 that the minimum mining depth of the Sijiaying open pit under the constraint of the Inter-provincial Highway located on the hanging wall is 388 m based on formula (4). and that under the constraint of the New Luan River on the footwall is 414 m based on formula (5). Then, according to formula (3), the final transition depth of Sijiaying Iron Mine in transition from open pit to underground mining can be determined as 388 m.

The maximum mining depth of Sijiaying open pit iron mine under economic constraints

Based on the average values of the primary production, technical, and economic indicators for open pit mining and the average values of the production, technical, and economic indicators for underground mining design at Sijiaying Iron Mine over a 5-year period, the economically constrained limit mining depth for open pit operations at Sijiaying Iron Mine is calculated. Using the limiting angle of the hanging wall, the limiting angle of the footwall, the thickness, and the economic indicators for both open pit and underground mining of ore bodies along different exploration lines at Sijiaying Iron Mine, Formula (7) is applied to determine the maximum economically constrained mining depth for each exploration line. Table 3 presents the primary production indicators and technical-economic indicators for open pit mining at the Sijiaying Iron Mine, as well as the five-year average production and technical-economic indicators for the underground mining design.

Table 3.

Average production and technical-economic indicators for open pit and underground mining at the mine.

Exploration line No.	α/(°)	β/(°)	δ/(m)	ρ/(t∙m-3)	Ca(¥∙t-1)	Cb(¥∙t-1)	Cu(¥∙t-1)
N12	43	36	70	3.16	16.80	30.20	108.96
N14	41	38	72
N16	41	34	70
N18	42	34	70
N20	43	34	74
N22	41	35	74
N24	43	35	76
N26	43	36	80
N28	43	36	80

Based on the mine’s open pit production indicators, technical-economic indicators, and the five-year average production and technical-economic indicators from the underground mining design, the calculated maximum open pit mining depth is shown in Fig. 7.

Fig. 7.

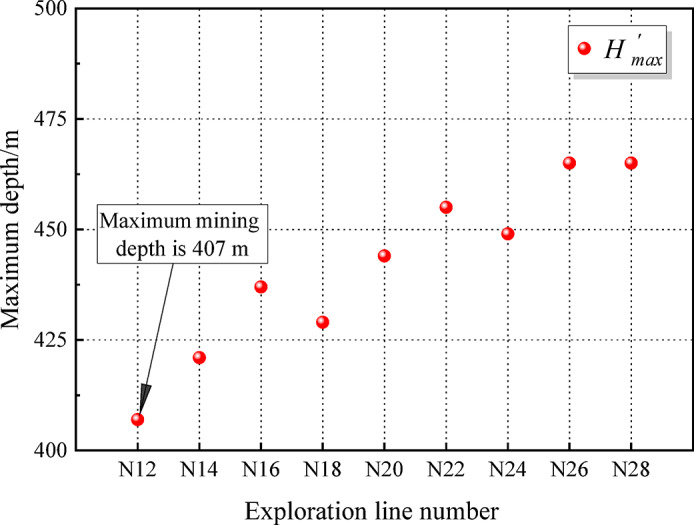
Under the specific conditions of the case mine, and by considering the average values of the indicators subject to economic constraints, the maximum feasible open pit mining depth for each exploration line is determined.

As shown in Fig. 7, under economic constraints, the minimum feasible mining depth of Sijiaying Open pit Mine is 407 m, excluding the limitations imposed by immovable permanent facilities near the top and bottom walls of the open pit mine.

Determination of the maximum mining depth for Sijiaying open pit iron mine

The final mining depth of the open pit mine, as determined using the traditional economic evaluation method, is 407 m. However, this depth is restricted by immovable permanent facilities near the boundaries of the hanging walls and footwall of the open pit mine. As a result, the technically feasible final mining depth is set at 388 m. The final mining depth established through the technical evaluation method is less than that calculated via the economic evaluation method, indicating that the transition limit depth from open pit to underground operations, as determined by the technical evaluation method, is economically viable and technically feasible.

The maximum mining depth of the Sijiaying open pit is determined based on a comprehensive assessment of key geological and mining factors. These include the orebody geometry, pit slope angles, as well as economic indicators from both open pit operations and underground mining design. These factors collectively constrain the maximum depth of open pit mining by influencing slope stability, operational safety, and the economic feasibility of transitioning to underground mining. The critical geological and mining parameters that define this depth are summarized in Table 4.

Table 4.

Key parameters and their values determining the maximum open pit mining depth of the Sijiaying iron mine.

Parameter	Value	Unit
Ore density	3.16	t∙m−3
Average dip angle of the hanging wall	40.00	(°)
Average dip angle of the footwall	44.78	(°)
Average orebody thickness	74.00	m
Maximum allowable slope angle on the hanging wall	43.00	(°)
Maximum allowable slope angle on the footwall	38.00	(°)
Open pit mining cost	16.80	¥∙t−1
Open pit stripping cost	30.20	¥∙t−1
Underground mining cost	108.96	¥∙t−1
Final economic depth	407.00	m
Final technical depth	388.00	m

The maximum open pit mining depth under current technical and economic conditions is determined to be 388 m, beyond which underground mining should be adopted to ensure safety, continuity, and profitability of resource extraction. In summary, when open pit mining is limited by surface permanent facilities and further extension is not feasible, the technical evaluation method provides an effective approach for determining the limit depth of open pit mining.

Conclusion

The traditional economic evaluation method can determine the limiting transition depth of ore deposits from open pit to underground mining. However, when the limit of open pit mining is restricted by the permanent facilities on the surface and cannot be expanded, even if the depth of open pit mining does not reach the limit depth determined by the economic evaluation method, the mining mode needs to be transferred to underground mining. Therefore, the traditional economic evaluation method is insufficient to determine the ultimate transition depth of mining from open pit to underground under this condition.

The open pit mining limits are sometimes constrained by the permanent facilities on the surface and cannot be expanded. Simple effectual formulas were developed to ascertain the transition depth of these cases from open pit to underground mining. Based on the established formulas, the determined transition depth for the case mine is 388 m.

The significance and usability of the presented formulas will be achieved by utilizing them to ascertain transition depth from open pit to underground under the technical constraints of various practical cases. In this way, when the width of the pit limit cannot be expanded due to the permanent facilities on the surface, the transition depth from open pit to underground can be easily determined by these simple formulas.

By enabling timely transitions to underground mining, they also contribute to reducing surface disturbance, preserving land use, and mitigating potential impacts on surrounding infrastructure and ecosystems—thereby promoting more environmentally sustainable mining practices.

Author contributions

Investigation, formal analysis, data curation, visualization, writing–original draft, C.M.; Investigation, resources, formal analysis, data curation, Q.M; Investigation, resources, formal analysis, data curation, W.Z; Methodology, formal analysis, writing–review and editing, project administration, P.W.; Data curation, formal analysis, writing–review and editing J.L; Conceptualization, methodology, writing–review and editing M.C; Conceptualization, methodology, writing–review and editing, supervision, project administration, funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Key Science and Technology Projects of Hebei Iron and Steel Group (Grant No. HG2023215).

Data availability

All relevant data are within the manuscript. If you have any questions, please don’t hesitate to contact Zengxiang Lu at the address below. Email: zengxiang_lu@sohu.com.

Declarations

Competing interests

The authors declare no competing interests.