Non-linear interactions between intraocular, intracranial pressure and the retinal vascular pulse amplitude in the Fourier domain

Abstract

The low explanatory power of a mixed effects linear model in evaluating interactions between retinal vascular pulse amplitude, intraocular pressure, and intracranial pressure suggests that these interactions are driven by non-linear dynamics. However, mathematical models inherently balance interpretability with predictive capability, and models explaining substantial variance may compromise interpretive clarity, a well-recognized limitation of artificial intelligence models, known as the black box problem. To explore these interactions, a generalized additive mixed model (GAMM) was applied to retinal venous and arterial pulse amplitude data in relation to intraocular and intracranial pressures. Each GAMM, constrained to prioritize interpretability, utilized 51 basis functions, and successfully achieved convergence. Partial effect plots and three-dimensional interaction visualizations were generated, revealing the geometric nature of these physiological relationships. The arterial and venous GAMMs explained 49.21 and 62.96% of the deviance respectively, describing a complex three-dimensional surface with pronounced curvature at intracranial pressures exceeding 25 cm water. Consistent with findings from a previously reported linear mixed-effects model, elevated intracranial pressure had an antipodal effect on the vascular pulse amplitude manifest as a reduction in venous and augmentation of the arterial pulse amplitudes.

Introduction

Several studies have established a strong linear interactions between retinal hemodynamic parameters and intracranial pressure^1–4. Paradoxically, linear models perform poorly in non-invasively predicting intracranial pressure^5–7. However, in our recent work we demonstrated that a linear model accounted for less than 9% of the variance in interactions between retinal vascular pulse amplitude, intracranial pressure, and intraocular pressure, highlighting the likelihood that these interactions are governed by non-linear dynamics⁸. Non-linear relationships in physiological phenomena often emerge from the interplay of multiple factors that interact in non-additive ways. These dynamics may arise from feedback loops, threshold effects, synergistic or antagonistic interactions, temporal and spatial heterogeneity, or other multivariate and emergent properties^9–11. At the level of the optic nerve, such interactions likely encompass several of these complex mechanisms. Moreover, non-linear correlations often manifest as skewness and heteroscedasticity in the dependent variable’s distribution. Non-linear transformations of data frequently result in asymmetry, such as skewed or log-normal distributions. In our recent work, we deployed an extreme gradient boosting algorithm to predict intracranial pressure using Fourier-decomposed retinal vascular pulse amplitudes. The resulting model converged on skewed, predominantly log-normal distributions, further underscoring the non-linear nature of these physiological relationships¹².

Additionally, non-linear correlations often contribute to heteroscedasticity, where the variability of the dependent variable changes across different levels of the independent variable. This non-constant variance reflects the non-linear nature of their interactions, due to the effect size of the independent variable which varies in magnitude depending on its level. Recognizing the presence of non-linearity, skewness, and heteroscedasticity is therefore essential for constructing accurate models and drawing reliable inferences¹³. This is particularly the case, in the context of predicting intracranial pressure.

Building on prior findings of asymmetrical distributions, non-linearity, and heteroscedasticity in the retinal vascular pulse and its interactions with intraocular and intracranial pressure^8,14, this study extends the analysis by quantifying the explanatory power of the non-linear components using a generalized additive mixed model (GAMM). This approach provides a unified framework that combines the strengths of three distinct models to handle complex, real-world data. It integrates the capacity of Generalized Linear Models to analyze non-normal distributions, the flexibility of Additive Models to model non-linear relationships through smooth functions, and the ability of Mixed Models to account for correlated data structures, such as repeated measurements on the same subject or hierarchical grouping. Beyond its core capability to simultaneously address non-normality, non-linearity, and correlation, this approach offers several key advantages. These include exceptional flexibility for representing complex phenomena and a data-driven nature that can uncover patterns without relying on strong prior assumptions. The geometry of these interactions is further characterized to provide a detailed understanding of their dynamics. Given the inherent trade-off between model predictability and interpretability, the model was deliberately constrained to preserve interpretability, ensuring that the insights gained remain clinically and physiologically meaningful.

Results

The age showed a bimodal Distribution with a mean of 30 years (range 17–47 years). There was a gender bias, 20 (95.2%) participants were females and there was one (4.8%) male. The parameters of the venous and arterial models (Table 1) indicated that both the linear terms (parametric coefficients) and the smooth terms were highly significant (p < 0.0001). Effective degrees of freedom (edf) represents the complexity, the closer the edf is to unity the more linear the term. All edfs were greater than one and therefore non-linear. The smooth terms (HRW_a-YJtV-A, V_Dist):IOP_i) showed a higher degree of non-linearity compared to the random effects (subject, laterality).

Table 1.

Parameters for the arterial and venous GAMMs.

Parametric coefficients	Estimate	Std. error	t-value	p-value
Venous model
Intercept	25.2981	0.0562	450.2909	< 0.0001
Smooth terms	edf	Ref.df	F-value	p-value
s(HRWa-YJtV, VDist):IOPi	29.7619	29.9964	1148.7706	< 0.0001
s(subject, laterality)	19.9978	20.0000	10663.3449	< 0.0001
Arterial model
Parametric coefficients	Estimate	Std. Error	t-value	p-value
Intercept	26.8629	0.0568	472.9291	< 0.0001
Smooth terms	edf	Ref.df	F-value	p-value
s(HRWa-YJtA, VDist):IOPi	29.3895	29.9758	199.6716	< 0.0001
s(subject, laterality)	19.9977	20.0000	7356.0616	< 0.0001

The parametric coefficients are the result of fitting the GAMM, they represent the linear component of the model and the smooth terms are the non-linear components. The table reports the significance of the model’s components using two different types of tests: (1) For Parametric Coefficients (Linear Terms): Approximate t-tests are used. (2) For Smooth Terms (Non-Linear Terms): Approximate F-tests are used. A statistically significant result for the parametric coefficients, is determined by a p-value 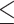0.05 derived from the t-value, while for the smooth terms it is indicated by an F-value > 1 and a p-value 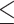0.05. It can be observed that both fixed and the random effects have an edf higher than unity and therefore non-linear. All terms were statistically significant (p 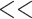0.0001). The venous model explained 62.96144% of the deviance and the arterial 49.2073%. HRW_a-YJtV, HRW_a-YJtA= Venous and arterial Yeo-Johnson transformed harmonic regression amplitude, V_Dist =Distance along the vessel, laterality = ocular laterality (right/left), edf = effective degrees of freedom, Ref.df =reference degrees of freedom.

Perspective surface plot

The perspective surface plot Fig. 1 defines the complex geometry of the interaction between the retinal vascular pulsation amplitude, intraocular, and intracranial pressure. The model captured 62.96% and 49.21% of the deviance for the venous and arterial models respectively. The surface representing the interaction of the retinal vascular pulse amplitude, intraocular, and intracranial pressures is formed from the contributions of the linear and non-linear model components. The most prominent observation is two asymmetrical folds inclined to the axial plane particularly at intracranial pressure >25 cm water in the venous model. Similarly the arterial model demonstrates a fold parallel to the IOP_i axis at an intracranial pressure >25 cm water. In addition to an antipodal effect where high intracranial pressure was correlated with a reduction in the venous and amplification of the arterial pulse amplitude, consistent with the linear mixed effects model described in previous work⁸. There is an approximately 150° rotational asymmetry which accounts for the need of rotating the perspective of the surface to allow comparisons in Figs. 1b and 1. Both the antipodal effect and further observations on these surfaces will be detailed in the partial effects and trellis plots below.

Figure 1.

Generalized additive mixed model for venous (a,b) and arterial (c,d) interactions between the retinal vascular pulsation amplitude, intraocular, and intracranial pressure. The arterial model accounts for 49.2073% and the venous model accounts for 62.96144% of the deviance. The surface defines the complex non-linear geometry of the interaction with deformity along three axes and prominent folds in the surfaces at intracranial pressure > 25 cm water, asymmetrical in the venous and symmetrical in the arterial model. The 330^o rotation is chosen to provide a comparison and maximize visibility of the surface. HRW = harmonic regression wave. Perspective plot generated in R: A Language and Environment for Statistical Computing.

Partial effects smooth line plots

Partial effects smooth line plots Fig. 2A–F highlight the relationship between intracranial pressure and the smooth terms (retinal vascular pulse, distance, and induced intraocular pressure). In this plot, a comparison is provided between the venous and arterial partial effects. The most prominent feature is the antipodal effect where the negative slope of regression with the venous and the positive with the arterial pulse amplitude can be observed in Fig. 2a,b. The effect of intracranial pressure on distance along the vessel Fig. 2c,d is similar in both vessel types where both plots demonstrate an impact of higher intracranial pressure on more peripheral points in the vessel. Both the pulse amplitude and distance correlated non-linearly with intracranial pressure. Although induced intraocular pressure had a linear contribution to both models, this was highly significant with a positive slope of regression in the venous model. In contrast, it was of low significance in the arterial model as indicated by the wide confidence intervals and the almost horizontal slope of regression as observed in Fig. 2e,f.

Figure 2.

Partial effects smooth line plots for the non-linear interactions between the retinal vascular pulse amplitude, intraocular, and intracranial pressure. (a,b) The relationship between intracranial pressure and the retinal vascular pulse demonstrated an antipodal effect where low venous and increased arterial pulse amplitudes are caused by elevated intracranial pressure. Pulse amplitude and distance had a non-linear contribution to the model, in contrast to that of IOP_i that was linear. All model terms were significant except the IOP_i response term in the arterial model. The effect of elevated intracranial pressure can therefore be summarised as to reduce venous and increase the arterial pulse amplitude, the effect increases a more peripheral locations in the vessel. Raised intracranial pressure was correlated with with higher IOP_i values in the venous model, the correlation of intracranial pressure with IOP_i is uninterpretable in the arterial model due to the low significance of this term at a p-value 0.05.

Partial effects surface contour plots

The partial effects surface contour plot of the fixed terms is demonstrated graphically in Fig. 3. The surface plot defines the quantitative features of the interactions between the intracranial pressure with a combination of smooth terms, which are the pulse amplitude as a function of distance (Fig. 3a,c) and pulse amplitude as a function of induced intraocular pressure (Fig. 3b,d). It should be emphasized that for the contour plots the color code represents intracranial pressure (cm water) at points of equal predicted values enclosed in the gradient boundaries. The area enclosed in between the contours shares characteristics, which indicate peaks or troughs within the range of the X and Y axes at the center of the contour area. The distance between the contour lines indicates the gradient of change in intracranial pressure, when lines are spaced close to each other, this indicates a steep gradient. In contrast, when contour lines are widely spaced the Z variable (intracranial pressure) alters over a shallow gradient. The multiple concentric lines within the figure represent the multi-modal nature of the distribution. Regions where lines straight indicate the linear component of the model. Figure 3a,c shows that the gradient of the retinal vascular pulse attenuates over an increased distance from the center of the optic disc in the retinal venous model, although this pattern was not as prominent in the arterial plot, a trend in the gradient of intracranial pressure from the lower right to the upper left indicated that the impact of elevated intracranial pressure is higher on the more peripheral and lower vascular pulsation points in both vascular systems. Hence, reduction in the venous and amplification of arterial pulse is expected to occur predominantly at more peripheral vascular locations. This was particularly the case at pathological intracranial pressure ( 30 cm water) in the arterial model. In Fig. 3b the pattern of the contour lines indicates that for venous pulsations to be sustained a proportionate increase in IOP_i needs to be applied, this relationship becomes non-linear with retinal venous pulse and intracranial pressure. In the region of HRW_a-YJtV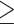1 the contour lines are close together indicating a higher and non-linear gradient of intracranial pressure change. In contrast, the lower venous pulse amplitude range HRW_a-YJtV < 1 the contour lines are further apart and almost equidistant. This indicated a shallower gradient and more linear intracranial pressure change at lower venous pulse amplitude: IOP_i range, in contrast to the higher venous pulse amplitude IOP_i range where the intracranial pressure gradient is steeper and non-linear. In the case of the arterial model in Fig. 3d the trend appears analogous to that of the venous IOP_i surface plot where there is a differential correlation of intracranial pressure with HRW_a-YJtA:IOP_i, which was dependent on the HRW_a-YJtA where a cut-off in the mid axis range distinguished a lower from a higher intracranial pressure influence region. However, the lower significance of induced intraocular pressure (IOP_i) on the arterial model compared to the venous limits its interpretive value.

Figure 3.

Partial effects contour surface plot for non-linear interactions between the retinal vascular pulse amplitude, intraocular, and intracranial pressure. Contour lines and color code represent intracranial pressure (cm water) at points of equal predicted values. (a) The surface plot defines the quantitative features of the interactions between intracranial pressure and the retinal venous pulse as a function of distance along the vessel and retinal venous pulse as a function of induced intraocular. Venous pulsation is high at distances close to the optic disc at physiological intracranial pressure (< 25 cm water). As both distance and intracranial pressure increase there is a reduction in venous pulsation amplitude. (b) In order for venous pulsations to be sustained a proportionate increase in induced intraocular pressure (IOP_i) needs to be applied, this relationship becomes highly non-linear with increased retinal venous pulse and intracranial pressure. (c) and (d) represent the arterial response, in (c) arterial pulsations are prominent in the peripapillary region particularly when ICP increases above 30cm water. (d) The arterial pulse response with IOP_i failed to achieve statistical significance at a p-value0.05. HRW_a = harmonic regression wave amplitude.

Trellis plots

The complex non-linear interactions can be demonstrated graphically in Figs. 4 and 5, which represent sections through the three-dimensional model orthogonal to the IOP_i axis observed in Fig. 1. The trellis graph of the generalized additive mixed model for venous pulsation data (Fig. 4) demonstrated a steeper slope of regression with higher induced intraocular pressure levels, and a reduction of venous pulsation amplitude can be observed with raised intracranial pressure. These features can be contrasted with the arterial model Fig. 5, which although demonstrates elevation of arterial pulsation amplitude there is an elevation of the arterial pulse amplitude with raised intracranial pressure. Both models show a steepening of the slope of regression, particularly at intracranial pressures exceeding 25 cm water at all ranges of IOP_i, with the regression line becoming steeper at higher IOP_i levels.

Figure 4.

Trellis graph of the generalized additive mixed model for venous pulsation data demonstrating changes in slope of regression with intracranial and induced intraocular pressure. A steeper slope of regression is generated at higher induced intraocular pressure levels. When combined with raised intracranial pressure, a steepening of the slope of regression particularly at induced intraocular pressures exceeding 40mmHg.

Figure 5.

Trellis graph of generalized additive mixed model for arterial pulsation data demonstrating changes in slope of regression with intracranial and induced intraocular pressure. By comparison with the venous model (Fig. 4) and antipodal effect where high intracranial pressure reduces the venous and amplifies the arterial pulse is observed. The is consistent with the linear mixed effects model described in previous work⁸.

Generalized additive mixed model fit parameters

The suitability of the model fit can be visualised in Fig. 6 QQ-plot that showed an adequate model fit for the majority of the data set. The histogram of the residuals converged on to a normal distribution in both cases. The venous model demonstrated full convergence after 9 iterations and the arterial model showed full convergence after 11 iterations. Model diagnostics indicate an adequate number of basis functions for the venous and arterial models, with p-values for the smooth terms being 0.38 and 0.68, respectively.

Figure 6.

Generalized additive mixed model fit for non-linear interactions between the retinal vascular pulse amplitude, intraocular, and intracranial pressure. Demonstrates the model fit as indicated by the QQ plot and the convergence of the residuals on to a right skewed distribution as indicated in the histogram of residuals.

Discussion

The GAMM highlights that the interactions between ICP, IOP, and retinal vascular pulse amplitude are governed predominantly by non-linear dynamics. This behavior may arise from several underlying mechanisms, including feedback loops and regulatory processes, threshold effects, multi-factorial interactions, saturation phenomena, plateaus, and emergent properties. These mechanisms are integral to the non-linear interactions observed in various physiological systems, such as enzyme kinetics modeled by the Michaelis-Menten equation¹⁵, neuronal action potential generation¹⁶, hormonal feedback regulation¹⁷, and the summation of signals in retinal ganglion cells¹⁸. The intricate physiological interactions at the optic disc encompass the opposing intracranial and intraocular pressures, hemodynamic parameters, and the biomechanical properties of the sclera, lamina cribrosa, and optic nerve. Among these factors, the derived Generalized Additive Mixed Model provides a simplified representation by considering static pressure values and the retinal vascular pulse amplitudes. It has also confirmed the antipodal mechanism of the retinal vascular pulse in response to raised ICP previously observed in a mixed effects linear model derived in our earlier work⁸.

The retinal vascular pulse amplitude as a function of distance along the vessels significantly contributed non-linear terms. Non-linearity in vascular wall dynamics originates from two primary sources. The first is elastic non-linearity, resulting from the curvature of the stress-strain curve, which is due to vessel wall heterogeneity. The second involves the interaction between the arterial pulse wave and the surrounding pressures, including intraocular and intracranial pressures, leading to non-linear wave propagation and reflection phenomena.

Although retinal vascular structural properties have been reported in the literature, compliance, distensibility and the elastic modulus of the vessel wall remain unreported. However, underlying mechanisms for non-linear vessel wall response to pressure can only be inferred from the systemic vessels. The walls of blood vessels consist of three layers: the intima, media, and adventitia. The wall is mainly composed of water (70%), which is inelastic and incompressible, and a mesh of fibers with elastic properties, including collagen, elastin, and smooth muscle cells. The mechanical properties of blood vessels depend on the connections between these structures and the size and orientation of the muscular layer^19,20. Elastin, with a Young’s modulus of approximately 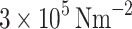, is flexible, while collagen, with a Young’s modulus of approximately , is stiffer. Smooth muscle contraction increases the apparent stiffness of the vessel by shifting the stress-strain curve to the left, whereas relaxation decreases stiffness by shifting the curve to the right²¹. Additionally, the geometrical arrangement of the fibrous components, particularly in the media layer, contributes to the anisotropic properties^20,22. Elastin governs the deformation response at low strains, whereas collagen and smooth muscle cells contribute to the stiff response at high strains, resulting in a two-phase nonlinear stress-strain curve²³.

There are unique retinal venous structural and physiological characteristics that likely contribute to the non-linear dynamics although not fully studied in the retinal circulation. Venous pressure and flow waveforms vary significantly due to the high wall compliance of veins, which is influenced by external factors such as respiration and extraluminal pressure²⁴. Veins exhibit low pulse pressure oscillations near zero transmural pressure, and the complex interplay between the venous wall, flow, and transmural pressure has been extensively studied. Holt’s experimental “flow regulator” model, analogous to the Starling resistor, provided key insights by altering input (P_I), output (P_O), and external pressures (P_E). He observed constant flow when P_I>P_O>P_E and partial collapse when P_I>P_E>P_O, with flow determined by P_I>P_E rather than P_O²⁵. Similarly, Conrad used a tunnel diode analogy to describe negative impedance between pressure drop and flow in collapsible tubes²⁶. Kresch and Noordergraaf further characterized collapsible vessels, computing tube cross-sectional shapes under varying transmural pressures, which Moreno et al. later confirmed experimentally^27,28.

Due to the collapsible nature of veins, measuring pulse transmission is challenging. Anliker et al. addressed this by using catheter-tip manometers in an experimental setup, ensuring system linearity to minimize wave reflection effects²⁹. They found that compliance and pulse wave velocity increase with transmural pressure, while attenuation is frequency-independent and attributed to blood viscosity, radial transmission to surrounding tissues, and wall viscoelasticity, the latter being predominant^29,30. This independence from strain rate supports energy dissipation consistency across frequencies. These findings align with systemic arterial behaviors but highlight the unique properties of venous dynamics.

The retinal vascular pulse wave emerges from pressure-flow interactions with the vessel wall. Retinal venous pulse waves propagate retrograde through the cerebrospinal fluid in the wall of the central retinal vein, attenuating before reaching the eye^31,32. Retinal veins act as Starling resistors, where intraocular pressure (IOP) externally compresses the veins. To avoid collapse, venous pressure near the eye must exceed IOP, making IOP a critical determinant of ocular perfusion pressure, defined as mean arterial pressure minus IOP³³. Differences in arterial and venous compliance curves reflect their unique mechanical properties; arterial compliance curves are curvilinear³⁴, while venous curves are sigmoidal²⁸. Systemic venous compliance exceeds arterial compliance by 19 to 24 times for equivalent transmural pressure and cross-sectional area^35–38. Increased venous transmural pressure leads to significant changes in cross-sectional geometry with minimal wall tension increase, transitioning from ribbon-shaped post-buckling modes under negative pressure to a circular shape with slight positive pressure^28,39,40. Taylor et al. noted retinal artery and vein cross-sectional differences, with venous constriction occurring at the lamina cribrosa⁴⁰. These findings emphasize the distinct mechanical and functional characteristics of venous and arterial vascular systems.

Ophthalmodyanmometry and cannulation studies have demonstrated a strong linear correlation between intracranial pressure and retinal venous pulsation pressure^{2,3,3,4,41–46}. Contrary to the assumption, these linear models did not achieve the high explanatory power that would be expected from the linear correlation, and to date, ophthalmodynamometric methods haven’t substituted invasive techniques for measuring intracranial pressure^5–7. Although insufficient as a sole factor for intracranial pressure prediction these results suggest that these predictive models require to either account for missing variables or techniques in data analysis are needed to overcome both non-linearity and heteroscedasticity.

Other parameters unaccounted-for in the GAMM model may have contributed to the observed non-linear dynamics. Non-linear biomechanical properties of the sclera, is likely a significant contribution due to the ophthalmodynamometric indentation of the globe during imaging. About 80% of the outer layer of the eye’s tunic is made up of the sclera. The extracellular matrix (ECM), which is rich in collagen, gives the sclera its mechanical characteristics. About 50% of the wet weight of human sclera is composed of collagen, of which 80–90% is type I collagen⁴⁷. Collagen fibrils also exhibit a crimped structure, forming a spring-like wave pattern axially along each fibril that imparts elasticity⁴⁸. In addition to collagen, the ECM of the human sclera also contains proteoglycans, free glycosaminoglycans, and elastin fibers, the latter of which are predominantly located in the peripapillary sclera⁴⁹. This anisotropic architecture and crimp response of scleral collagen fibrils constitute the most significant elements of the non-linear elastic response of the posterior human sclera. In a post-mortem study, Grytz et al. reported that the nonlinear stiffening of the sclera with increasing IOP was well reproduced by the uncrimping of scleral collagen fibrils, and a circumferentially-aligned ring of collagen fibrils around the scleral canal. They reported that elastic modulus of the sclera averages about 41.83±23.37 MPa (mean±standard deviation)⁵⁰.

Complex pressure and flow dynamics may have also played a role in the non-linear interactions. The flow of cerebrospinal fluid around the optic nerve is influenced by ICP⁵¹. Changes in ICP can alter the pressure gradient across the optic nerve head, affecting the IOP-ICP relationship. The retinal blood vessels respond to changes in IOP and ICP with autoregulatory mechanisms that are inherently non-linear. For example, vasoconstriction and vasodilation in response to pressure changes involve complex biochemical pathways that do not follow linear kinetics⁵².

The varying impact of induced intraocular pressure on the retinal vasculature, combined with the opposing effect of intracranial pressure on the retinal vascular pulse, presents a fascinating phenomenon. Observed in earlier work⁸ the mechanisms remain elusive. However, there are two possible explanations:

1. There is a cyclic change in vessel wall compliance during a pulsation event where intravascular pressure and compliance are at opposite ends of their range. As intravascular pressure increases during cardiac systole vessel wall compliance is reduced by increased intravascular pressure. During cardiac diastole, intravascular pressure is reduced, and hence vessel wall compliance increases⁵³. Transmural pressure (P_tm) is the difference between vascular input pressure (P_i) and intraocular pressure (IOP). Elevation of intraocular pressure reduces transmural pressure through this relationship⁵⁴:

   1

   As IOP increases, transmural pressure decreases, resulting in an increase in vessel wall compliance by reducing vessel wall tension. Allowing the vessel collapses partially or completely when the transmural pressure is between diastolic and systolic intravascular pressure (within the pulse pressure range). As input pressure exceeds the transmural pressure, the vessel re-fills, producing a vascular pulse cycle^55,56. When transmural pressure is negative, the vessel wall collapses, and pulsations in the vascular segment cease. Because the collapse pressure in the retinal veins is lower than in the retinal arteries, a higher transmural pressure range (and hence higher IOP) influences the thicker-walled arteries at a higher pressure compared to the veins, the differential influence of IOP_i in the retinal veins and arteries.
2. Reduction in retinal venous compliance by raised intracranial pressure through increased resistance in the venous circulation and vessel wall distension^28,57,58. Possible mechanisms for increased retinal arterial pulsations in this scenario include:

   1. Elevated IOP_i above central retinal arterial diastolic pressure^59,60 together with reduced venous compliance of the artery wall, may limit the damping of the vascular pulse pressure⁶¹.
   2. Augmentation of the vascular pressure wave through wave reflections and possibly widening of the retinal vascular pulse pressure^62–65.

An observation in Figs. 1,  2,  4, and  5 that the model demonstrates a zone of discontinuity (visualized as a fold or plateau) whose position shifts along the ICP (Y) axis as a function of distance (X) from the optic disc. This is coupled with a change in the slope of the pulsation-amplitude-to-distance relationship, and by an alteration in the model’s slope of regression. This finding could imply that the vascular autoregulatory breakdown point is not a single, fixed ICP value but is indeed variable across the retinal vascular tree. The retina’s arterioles and venules are structurally heterogenous^66,67 the role in autoregulation change as they branch away from the central retinal vessels (near the optic disc) into smaller precapillary arterioles and venules. Vessels closer to the optic disc are larger, have more smooth muscle, and are the primary contributors to vascular resistance. More peripheral vasculature are smaller in diameter and have less smooth muscle. The vascular the myogenic response, a key part of autoregulation is consequently non-uniform. Larger, more proximal vessels often have a stronger myogenic response than smaller, distal vascular segments. Additionally, the influence of local metabolic factors is stronger on the smaller, more distal arterioles closest to the neural tissue they supply.

We hypothesize that the GAMM is capturing this biological complexity, effectively generating a map of the spatial vulnerability of the retinal vasculature to elevated ICP . The zone of discontinuity represents the ICP level at which the vessels at a specific distance from the optic disc experience a failure of autoregulatory function. This concept of divergent arterial and venous behavior is supported by the work of Nagel et al., who described opposite changes in retinal vascular response to alterations in perfusion pressure, with the study describing an increase in arterial and reduction in retinal venous diameters⁶⁸.

The shift in the zone of discontinuity is likely to represent the variability of vascular response with a corresponding change in vascular dimension and consequently structure and function with the vessel segment closer to the optic disc being a larger resistance vessel. It may be able to maintain its tone and compensatory vessel wall tone up to a higher ICP threshold. This would place its “fold” at a higher ICP on the Y-axis. Whereas a vessel segment further from the optic disc (higher distance value) is a smaller, more metabolically sensitive vessel. It may be quicker to dilate maximally and reach its failure point at a lower ICP threshold. This would place its zone of discontinuity at a lower ICP on the model’s Y-axis.

The arterial model showed a single symmetrical fold this may be due to the fact that. The arterial system is an active, pressurized system. The failure of autoregulation likely follows a more consistent, predictable pattern based on hydrostatic and wall-stress principles along the vessel, leading to a “symmetrical” fold in the three dimensional surface. Whereas the venous model showed a double asymmetrical fold The venous system is a passive, low-pressure system where the venous compliance is more readily susceptible by rising ICP. The point at which a vein collapses or its pulsation changes dramatically may be influenced by a more complex interplay of local tissue pressure, the pressure inside the vein, and its specific anatomical location (e.g., crossing points with arteries), leading to a less uniform, “asymmetrical” pattern of failure.

Further studies that include continuous intracranial pressure measurement are needed to further shed light on these mechanisms. The predilection of peripheral vascular locations to raised intracranial pressure influences was demonstrated in both venous and arterial systems, which may reflect differences in vessel wall compliance and pulse wave attenuation characteristics. Centrifugal structural changes in the retinal venous system include reduction in the diameter and wall thickness secondary to ultrastructural changes⁶⁶. Both the direct low resistance of the venous part of the retinal circulation, centrifugal attenuation of the venous pulse, higher peripheral venous pressure gradient and venous distention that occurs with raised intracranial pressure may result in the susceptibility for peripheral compared to the central venous pulse amplitude. The peripheral involvement in turn may result in the predilection of the peripheral arteriolar circulation secondarily.

Significant non-linear terms and heteroscedasticity arising in the context of interactions between the retinal vascular pulse, intraocular and intracranial pressure require that these phenomena be taken into consideration in algorithms for non-invasive intracranial pressure prediction. Although research has established that gender differences in vascular auto-regulation favor enhanced endothelial function and vasodilation in females⁶⁹, the present study was limited by a gender bias. This was an inherent consequence of the higher referral rate for idiopathic intracranial hypertension among female subjects. Therefore, any conclusions regarding gender differences drawn from this specific modelling data remain uncertain.

Methods

Participants in the study included healthy adults who were related to patients treated at the Lions Eye Institute as well as medical students. All of the participants gave their written consent. The data was collected over a period of five years (2015–2020). The University of Western Australia Human Ethics Committee granted study approval in accordance with the principles of the Declaration of Helsinki. The dataset was the same as that used for the linear mixed effects model cited in previous work⁸ considering the additional constraints outlined below.. There were a total of 21 patients in the study group, an intracranial pressure of 25 cm water was considered the upper normal limit⁷⁰. Ten cases (20 eyes) were in the ICP_h>25cm water and 8 cases (13 eyes) in the ICP_n25cm water. Three cases (labelled A, B, R) overlapped between the two groups as a result of interchanging between the ICP_n to the ICP_h groups. Therefore there were a total of 19 eyes in the ICP_n group and 26 eyes in the ICP_h, giving a total of 45 eyes in the study as three eyes were excluded from the analysis due to poor image quality. Tables 2 and 3 demonstrate the number of subjects, eyes, and data points in each study group. Only data points that demonstrated a fit to the harmonic regression model with a p values0.05 were used in the analysis.

Table 2.

Number of subjects and eyes in the normal intracranial pressure (ICP_n) study group. In the column “Side” R= right,L=left.

	Case	ICP	Side	Data points
1	A	23	L	5607
2	A	23	R	4966
3	B	19	L	2604
4	B	19	R	2574
5	E	20.5	L	2502
6	E	20.5	R	1344
7	I	22.5	L	1276
8	I	22.5	R	3722
9	K	11	R	1121
10	L	18.5	L	3432
11	M	9.5	L	2007
12	M	9.5	R	1919
13	O	24	L	3214
14	O	24	R	3042
15	R	22	R	292
16	S	17	L	7472
17	S	17	R	8082
18	T	17	L	2721
19	T	17	R	8605
Total				66502

Table 3.

Number of subjects and eyes in the normal intracranial pressure (ICP_h) study group. In the column “Side” R = right, L = left.

	Case	ICP	Side	Data points
1	A	31	L	6008
2	A	31	R	6902
3	B	26	L	131
4	B	26	R	496
5	C	68	L	852
6	C	68	R	679
7	D	30	L	4262
8	D	30	R	2660
9	F	57	L	2005
10	F	57	R	1962
11	G	29	L	2501
12	G	29	R	2436
13	H	28.5	L	636
14	H	28.5	R	963
15	J	33	L	536
16	J	33	R	2663
17	N	40	L	3697
18	N	40	R	3702
19	P	29	L	114
20	P	29	R	493
21	Q	25.5	L	1924
22	Q	25.5	R	3155
23	R	34	L	5384
24	R	34	R	4529
25	U	42.5	L	2511
26	U	42.5	R	1897
Total				63098

Ophthalmodynamometry technique

Details of the technique of modified photoplethysmography are provided in our earlier publications^14,71. We have summarized the imaging methodology and mathematical model. Baseline intraocular pressure was measured, and the subjects’ pupils were dilated with 1% Tropicamide. A Meditron ophthalmodynamometer (Meditron GmbH, Poststrasse, Völklingen, Germany) was used for imaging the retinal vessels centered on the optic disc. The device comprises a three-mirror Goldmann contact lens fitted at the observer end with a ring-shaped force transducer. The sensor ring is connected to a liquid crystal display monitor. A foot pedal connected to the display monitor is used to finalize the ophthalmodynamometric force reading once the indentation force is stabilized. The examination commenced with the calibration step. The Goldmann contact lens of the ophthalmodynamometer was placed on the topically anesthetized corneal surface. The examination was performed by applying discrete increments in indentation force onto the globe. The aim was to induce observable central retinal vein pulsations in response to a constant force. The force measured by the sensor ring was set by depressing the foot pedal; the displayed reading was noted by a second observer. This served as each test run’s endpoint. At each discrete force level, the optic nerve was continuously imaged bio-microscopically through the central portion of the Goldmann contact lens. The examination was repeated 8 to 10 times for each subject to attain a range of force values for each eye. Videos with significant motion artifacts, optical media reflection, or optic nerve decentration in the image sequence for fewer than three sequential cardiac cycles were excluded from the analysis. The ophthalmodynamometric force (ODF), displayed as Meditron units (mu), was converted to grams of force, where 1 mu = 3.33 grams of force and induced IOP = 0.89 x ODF+Baseline IOP in mmHg⁷².

Retinal imaging was conducted using a digital camera (Canon 5D Mark III, Japan) mounted on an imaging slit lamp (Carl Zeiss, Germany). At least three cardiac cycle-duration sequences were captured, each at a rate of 25 frames per second. Image pre-processing was done in Adobe Photoshop (CS6), and individual video frames were imported as independent images in the (.tif) format. The audio signal from the pulse oximeter (Nellcor N65, Covidien, Mansfield, MA), applied to the right index finger and recorded simultaneously enabled synchronization of the retinal vascular pulse image sequence with the cardiac cycle. This enabled the mathematical analysis of the periodic component from the green channel transmittance of the video sequence.

Data processing

Images were scaled to a grid of x-coordinated pixels; the pixel at x has an associated triple intensity , I(x)=(R(x), G(x), B(x)), where R, G, and B represent the red, green, and blue levels, respectively. The intensity triples were converted to the standard [0, 255] scale. Following this procedure, data for any given video were represented as a sequence I₁(x),I₂(x) 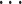I_M(x), where M is the total number of frames. Each sequence of images was rasterized and aligned. Image segmentation was performed manually, by creating four vessel templates to isolate portions of each image corresponding to two parts (A and B) of the lower and upper retinal vein, and artery. To account for both noise and the central vessel reflex, either pure white RGB intensity [I = (255, 255, 255)] or black RGB intensity [I = (0, 0, 0)] with RGB mean intensity values within 1% of either of these extremes were eliminated from the analysis. The mean color intensity over a template representing the aggregate vessel volume for any given template (T) was summarized by computing means for each of the RGB channels and plotting the time series of these values: [R(x): x 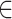T], [G(x): x 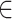T] and [B(x): x 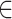T]. An array of values across the entire optic disk and peripapillary retina from either 2x2 or 5x5 pixel clusters was then used to generate false-color maps based upon the values of either the amplitudes, slopes, or timing information⁷³.

Generalized additive mixed model

For both arteries and veins, the periodic trend component was independently modeled using a harmonic regression waveform expansion. The Yeo-Johnson transformation was applied to normalize the pulsation data. At its core, a generalized additive mixed model (GAMM) extends a generalized linear model by incorporating a sum of smooth functions of covariates and random effects^74,75.

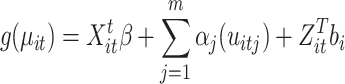where represents the link function, 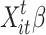is the linear parametric term with a parameter vector that includes the intercept, 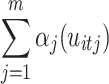represents the smooth and nonlinear function, and contains the cluster-specific random effects⁷⁶. The most common smooth used is the thin plate regression spline⁷⁷, which is an unspecified function estimated via a scatterplot smoother in an iterative procedure known as the local scoring algorithm⁷⁵. In this study, the GAMM included both linear (parametric coefficients) and nonlinear (smooth terms) components that modeled the interaction between harmonic regression amplitude (HRW_a), distance (V_Dist), defined as the distance along the retinal vessels measured from the center of the optic disc in millimeters (mm), and induced intraocular pressure (IOP_i), which constituted the smooth terms of the model. The random effects were composed of subject and ocular laterality. A Gaussian (normal) distribution was assumed for the errors. Both the arterial and venous GAMMs featured a smooth component with 51 basis functions, each with its own coefficient (30 for the smooth terms and 21 for the random effects). Model fit was assessed using the deviance, while a quantile plot was created to visually evaluate fit criteria and a histogram of the residuals was used to check for convergence toward a normal distribution.

Conclusions

A generalized additive mixed model accounted for approximately half of the deviance arising from interactions of the retinal vascular pulse, intraocular, and intracranial pressure. The complex geometry generated by the model supported the antipodal effect of raised intracranial pressure where venous pulsation amplitude decreases in contrast to the arterial pulsation amplitude which increases.

Author contributions

A.A.R wrote the draft manuscript, performed the analysis, and derived the mathematical models. W.M and D.Y.Y. conceived the experiment, A.V., W.M, and A.A.R, conducted the experiment(s). All authors reviewed the manuscript.

Data availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors Anmar Abdul-Rahman, William Morgan, and Dao-Yi Yu are co-inventors of the technique Modified Photoplethysmography. The author Aleksandar Vukmirovic has no competing financial and/or non-financial interests in relation to the work described.