Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1992 Mar;61(3):612–620. doi: 10.1016/S0006-3495(92)81866-0

Bioelectrorheological model of the cell. 3. Viscoelastic shear deformation of the membrane.

J Poznański 1, P Pawłowski 1, M Fikus 1
PMCID: PMC1260279  PMID: 1387010

Abstract

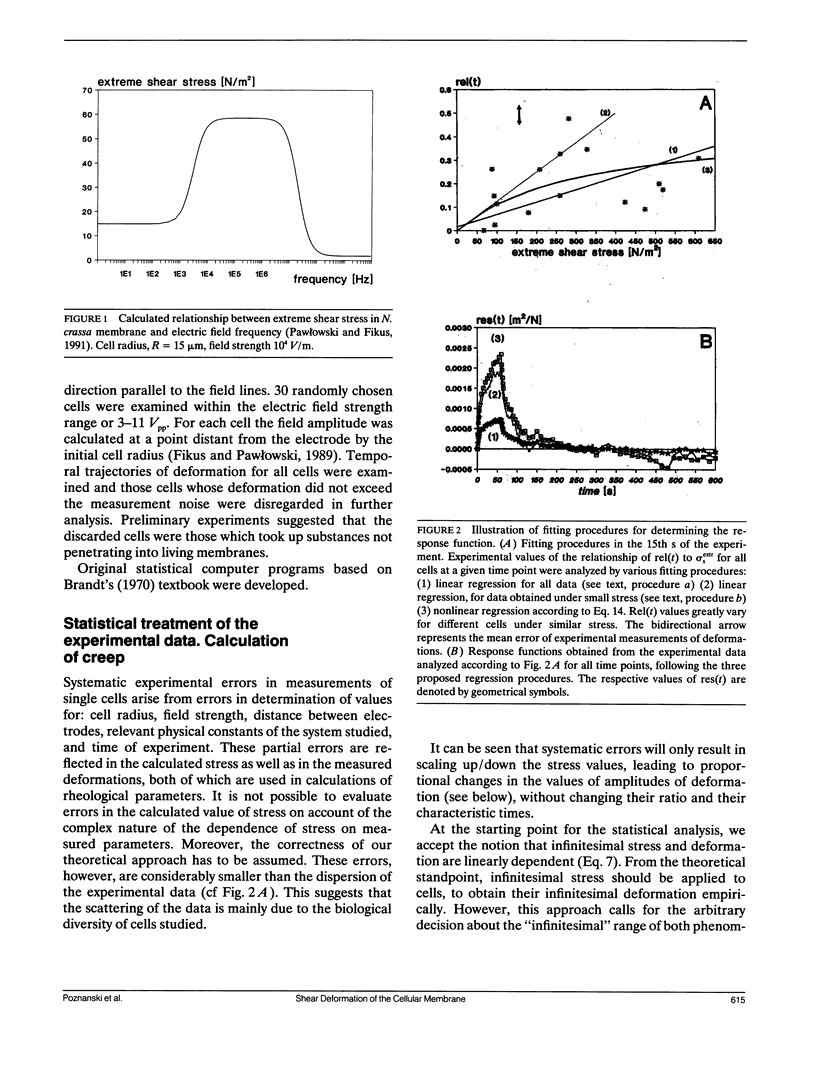
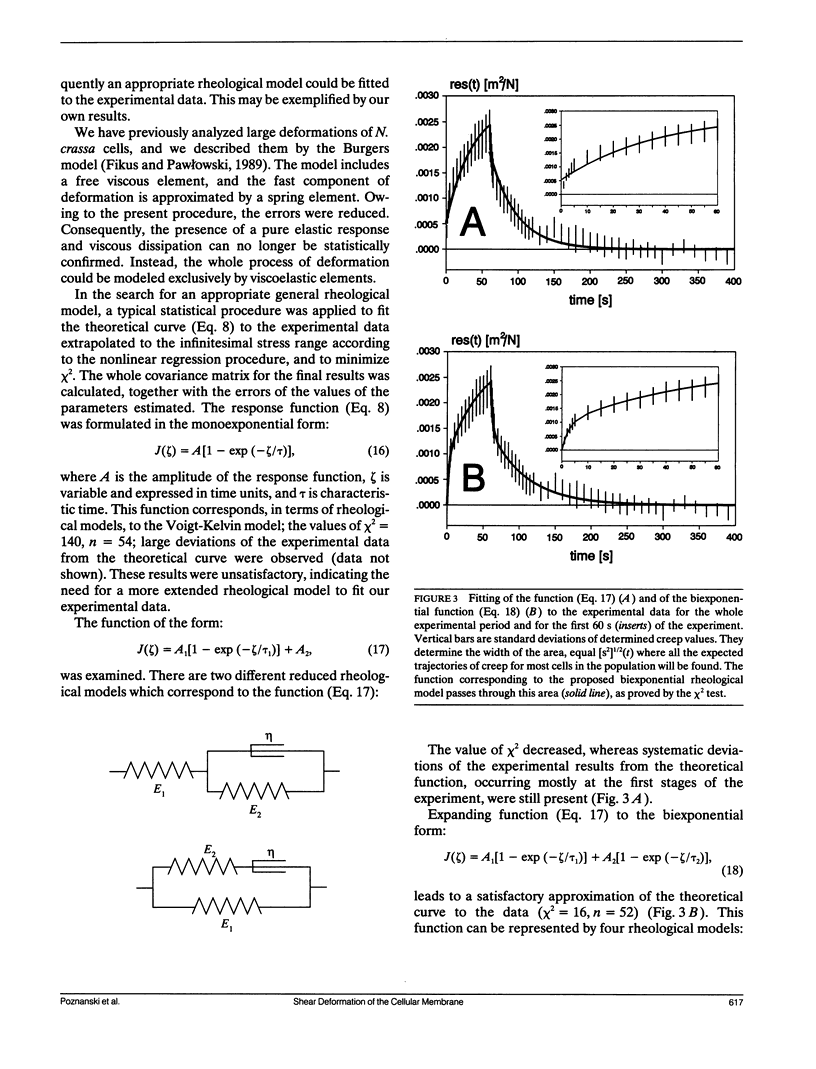
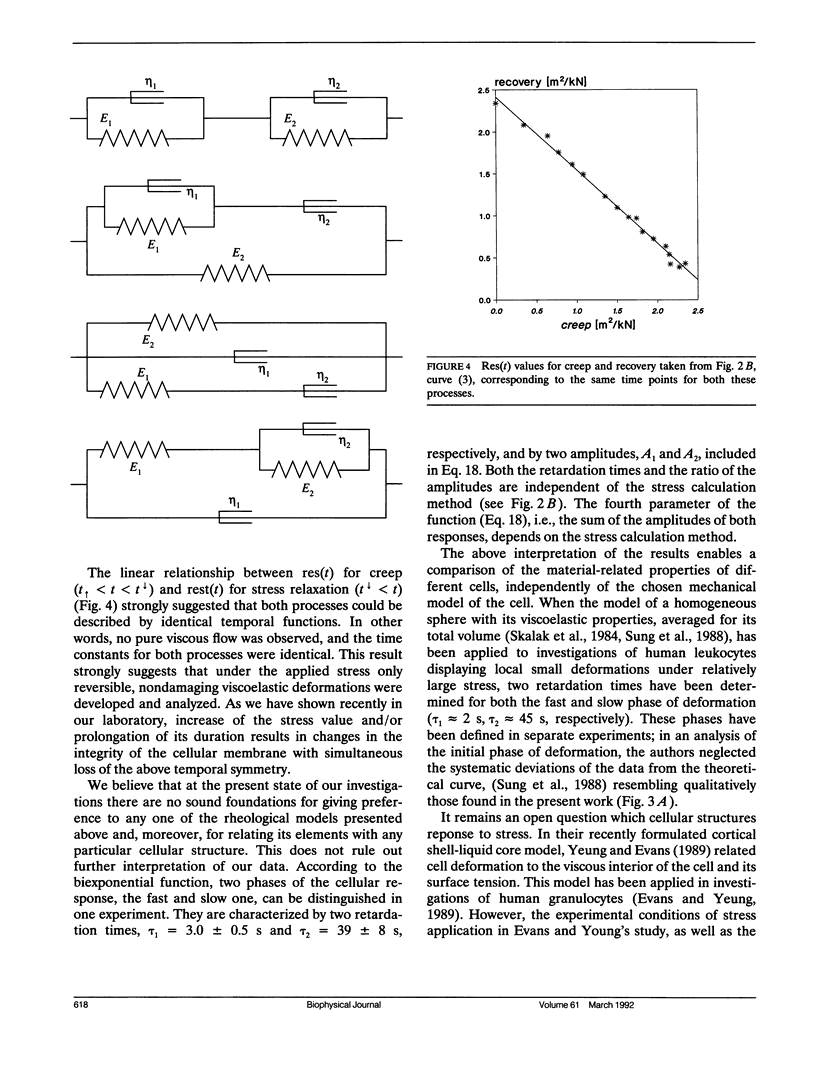
An analytical electromechanical model of a spherical cell exposed to an alternating electric field was used to calculate shear stress generated in the cellular membrane. Shape deformation of Neurospora crassa (slime) spheroplasts was measured. Statistical analysis permitted empirical evaluation of creep of the cellular membrane within the range of infinitesimal stress. Final results were discussed in terms of various rheological models.

Full text

PDF

Images in this article

615FIGURE 2
on p.615

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Aaronson L. R., Martin C. E. Temperature-induced modifications of glycosphingolipids in plasma membranes of Neurospora crassa. Biochim Biophys Acta. 1983 Nov 9;735(2):252–258. doi: 10.1016/0005-2736(83)90300-0. [DOI] [PubMed] [Google Scholar]
  2. Engelhardt H., Sackmann E. On the measurement of shear elastic moduli and viscosities of erythrocyte plasma membranes by transient deformation in high frequency electric fields. Biophys J. 1988 Sep;54(3):495–508. doi: 10.1016/S0006-3495(88)82982-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Evans E., Yeung A. Apparent viscosity and cortical tension of blood granulocytes determined by micropipet aspiration. Biophys J. 1989 Jul;56(1):151–160. doi: 10.1016/S0006-3495(89)82660-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Fikus M., Pawlowski P. Bioelectrorheological model of the cell. 2. Analysis of creep and its experimental verification. J Theor Biol. 1989 Apr 20;137(4):365–373. doi: 10.1016/s0022-5193(89)80035-9. [DOI] [PubMed] [Google Scholar]
  5. Marszalek P., Zielinsky J. J., Fikus M., Tsong T. Y. Determination of electric parameters of cell membranes by a dielectrophoresis method. Biophys J. 1991 May;59(5):982–987. doi: 10.1016/S0006-3495(91)82312-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Nash G. B., Meiselman H. J. Red cell and ghost viscoelasticity. Effects of hemoglobin concentration and in vivo aging. Biophys J. 1983 Jul;43(1):63–73. doi: 10.1016/S0006-3495(83)84324-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Pawlowski P., Fikus M. Bioelectrorheological model of the cell. 1. Analysis of stresses and deformations. J Theor Biol. 1989 Apr 6;137(3):321–337. doi: 10.1016/s0022-5193(89)80075-x. [DOI] [PubMed] [Google Scholar]
  8. Skalak R., Chien S., Schmid-Schönbein G. W. Viscoelastic deformation of white cells: theory and analysis. Kroc Found Ser. 1984;16:3–18. [PubMed] [Google Scholar]
  9. Sung K. L., Dong C., Schmid-Schönbein G. W., Chien S., Skalak R. Leukocyte relaxation properties. Biophys J. 1988 Aug;54(2):331–336. doi: 10.1016/S0006-3495(88)82963-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Waugh R. E., Agre P. Reductions of erythrocyte membrane viscoelastic coefficients reflect spectrin deficiencies in hereditary spherocytosis. J Clin Invest. 1988 Jan;81(1):133–141. doi: 10.1172/JCI113284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Waugh R. E. Effects of inherited membrane abnormalities on the viscoelastic properties of erythrocyte membrane. Biophys J. 1987 Mar;51(3):363–369. doi: 10.1016/S0006-3495(87)83358-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Yeung A., Evans E. Cortical shell-liquid core model for passive flow of liquid-like spherical cells into micropipets. Biophys J. 1989 Jul;56(1):139–149. doi: 10.1016/S0006-3495(89)82659-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES