Long-range protein electron transfer observed at the single-molecule level: In situ mapping of redox-gated tunneling resonance

Abstract

A biomimetic long-range electron transfer (ET) system consisting of the blue copper protein azurin, a tunneling barrier bridge, and a gold single-crystal electrode was designed on the basis of molecular wiring self-assembly principles. This system is sufficiently stable and sensitive in a quasi-biological environment, suitable for detailed observations of long-range protein interfacial ET at the nanoscale and single-molecule levels. Because azurin is located at clearly identifiable fixed sites in well controlled orientation, the ET configuration parallels biological ET. The ET is nonadiabatic, and the rate constants display tunneling features with distance-decay factors of 0.83 and 0.91 Å^–1 in H₂O and D₂O, respectively. Redox-gated tunneling resonance is observed in situ at the single-molecule level by using electrochemical scanning tunneling microscopy, exhibiting an asymmetric dependence on the redox potential. Maximum resonance appears around the equilibrium redox potential of azurin with an on/off current ratio of ≈9. Simulation analyses, based on a two-step interfacial ET model for the scanning tunneling microscopy redox process, were performed and provide quantitative information for rational understanding of the ET mechanism.

Charge transfer plays key roles in many chemical and biological processes as well as in molecular electronics (1–5). For example, long-range protein electron transfer (ET) is central in aerobic respiration and photosynthesis. The importance of long-range ET is illustrated by a recent special issue of PNAS on this topic (6–12). Several articles reflect broadly the current status of this subject. However, one of the major objectives in nanoscale science and technology is to fabricate molecular electronic devices with specified functions. Molecular electronics is rooted in the concept of molecular charge transfer (particularly, molecular conductivity) (13, 14). Two essential steps involved in bottom-up manipulations are (i) organizing molecules into nanoscale structures and (ii) interfacing such nanostructures with macroscopically addressable components (e.g., metal and semiconductor electrodes). Molecular electronic device function thus rests fundamentally on charge transfer through organic and/or biological molecules and across the interface between molecules and macroscopic electrodes (15, 16). Understanding of charge transfer mechanisms has mostly been based on average results of macroscopic measurements. The advent of scanning probe microscopies, along with other supersensitive techniques, has made it possible to characterize or directly observe charge transfer through organic molecules down to the nanoscale and single-molecule levels, as illustrated by measurements of single-molecule conductivity (17–21) and probing of molecular switching and resonant tunneling (22, 23). This, however, remains a daunting challenge for proteins, with difficulties arising from the assembly of suitable structures with sufficient stability, the retention of biological functions at interfaces, and the control of molecular orientations on solid surfaces. Possible solutions for these problems might be offered from the features of natural biological ET systems. In particular, charge transfer in respiration and photosynthesis is well controlled and highly efficient, because biological ET between the donor and acceptor centers proceeds through chemically defined and well oriented sites with optimal tunneling pathways engineered by mother nature (24, 25). Although challenging, biomimetic strategies to assemble protein ET systems on metal surfaces with efficient ET pathways are therefore of general interest. Such systems can be used for seeking fundamental understanding of long-range protein interfacial ET and for applications in nanoscale bioelectronics.

Azurin is a blue single-copper protein that functions as an electron carrier physiologically associated with oxidative stress responses in bacteria (e.g., Pseudomonas aeruginosa) (26) and is a long-standing model for exploring electron tunneling through protein molecules (27–32). Thanks to its intrinsic merits (e.g., high stability and excellent redox properties), azurin has recently emerged as a favorite target for nanoscale bioelectronics (33, 34). Two structural features (a surface disulfide Cys 3 Cys 26 group and a hydrophobic patch around the copper center located at the two opposite ends) can be exploited to confine azurin molecules on Au(111) surfaces with well controlled orientations. Direct self-assembly through the disulfide group orients the protein molecules with the copper center opposite to the electrode surface, with a 26-Å distance between the copper center and the electrode surface (35, 36). An interfacial ET rate constant of ≈30 s^–1 was observed, largely consistent with intramolecular ET between the copper center and the Cys 3 Cys 26 site measured by pulse radiolysis in homogeneous solution (44 s^–1) (29). Interfacial ET can be significantly facilitated by wiring azurin molecules onto the gold surface by variable-length alkanethiols through noncovalent interactions of the hydrophobic patch around the copper ion with the terminal methyl group (37, 38). In this work, we use azurin as an example for comprehensive observations of long-range interfacial ET properties and particularly for in situ mapping of redox-gated tunneling resonance at the single-molecule level. The results of a concerted experimental and theoretical effort have provided detailed information for the ET mechanisms.

Materials and Methods

Materials and Reagents. The Au(111) electrodes used in both electrochemical and scanning tunneling microscopy (STM) experiments were homemade from polycrystalline gold wires (≥99.99% in purity, Goodfellow, Cambridge, England) by using a hydrogen flame as described in ref. 35. The quality of the electrodes was checked regularly by voltammetry and/or STM imaging. All electrodes were subjected to annealing and quenching before use.

A series of straight-chain alkanethiols CH₃(CH₂)_n–1SH (n = 3, 4, 6, 8, 10, 12, 14, 16, 18, and 20) with the highest available purity (from Sigma-Aldrich) were used as received. Azurin from P. aeruginosa was purified, and its concentration was determined by UV-visible spectrometry as described in ref. 36. Azurin in D₂O (99.9%, Cambridge Isotope Laboratories, Cambridge, MA) was prepared by repeatedly concentrating buffered azurin solutions (39). The NH₄Ac buffer (20 mM, pH 4.6) was prepared from 5 M stock solution (ultrapure, Fluka), and the solution pH was adjusted with glacial acetic acid (99–100%, J.T. Baker). Milli-Q water (18.2 MΩ, Millipore) was used throughout for cleaning and preparation of solutions. In isotope effect experiments, D₂O was used instead of Milli-Q H₂O, and all clean glassware was dried completely before use.

Preparation of Protein Monolayers. The self-assembled monolayers of alkanethiols were obtained by immersing freshly quenched Au(111) electrodes overnight (20- to 24-h adsorption) in ultrapure ethanol (Merck) containing 1 mM or less alkanethiol. After thorough rinsing with ethanol and Milli-Q water, the electrodes were transferred to 50–100 μM azurin solutions and incubated at 4°C or room temperature for a necessary time span to form azurin submonolayers or monolayers. The resulting electrodes were carefully rinsed with Milli-Q H₂O or D₂O and NH₄Ac buffer before measurements. These azurin-containing electrodes are denoted as Az-CH₃(CH₂)_n–1S-Au(111) (n = 3, 4, 6, 8, 10, 12, 14, 16, 18, and 20).

Electrochemical Measurements. All measurements were carried out by using an Autolab system (Eco Chemie, Utrecht, The Netherlands) controlled by the general purpose electrochemical system software at room temperature (22 ± 2°C). A three-electrode system consisting of a platinum coiled wire as counter electrode, a reversible hydrogen electrode (RHE) as reference electrode, and a Au(111)-based working electrode (WE) was used with the WE in a hanging-meniscus configuration (35). The RHE was checked regularly against a saturated calomel electrode (SCE) after each measurement. All electrode potentials are reported vs. SCE. Purified argon (5 N, Chrompack, Varian) was applied to purge dioxygen from electrolyte solutions before the measurements, and the gas stream was maintained over the solution during the measurements.

Electrochemical STM Measurements. STM measurements were performed with a PicoSPM system (Molecular Imaging, Tempe, AZ) equipped with a bipotentiostat for potential control of both the substrate and the tip. Electrochemical control was conducted in a home-designed cell with a three-electrode system similar to normal electrochemical measurements. The tips were prepared from either tungsten or Pt/Ir wires (φ = 0.25 mm) by electrochemical etching and insulated with apiezon wax to reduce Faradaic currents to 10 pA or less.

Data Analysis and Computation. Electrochemical data were analyzed largely by using accessory software of the Autolab system. mathcad professional 2001 was used in the simulation of experimental STM data.

Results and Discussion

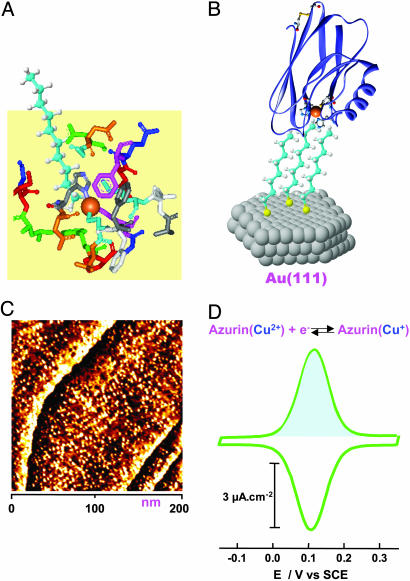
Fig. 1A shows a schematic representation in which the hydrophobic patch around the copper center in azurin is spatially and chemically suitable for coupling to the terminal methyl group of the alkanethiol. Mutagenesis experiments showed that the mutation of the tryptophan 48 (Trp 48) to other residues in azurin results in complete quenching of interfacial ET (38). Trp 48, which is not supposed to interact physically with the methyl group of the alkanethiol, thus appears still to play an important role in establishing the electronic coupling of azurin to the electrode surface (38). The wild-type protein molecules are confined well by hydrophobic interactions to form a monolayer with the copper center facing the electrode surface (Fig. 1B). Such a monolayer is structurally imaged by STM with molecular resolution in a buffer solution (Fig. 1C).

Fig. 1.

Assembly and characterization of azurin monolayers. (A) Schematic representation of noncovalent interactions between the methyl group of alkanethiol (octanethiol is represented here, and the thiol group is ignored) and the hydrophobic patch of azurin. The hydrophobic patch consisting of specific amino acid residues is extracted from the x-ray crystallographic structure according to ref. 43. (B) Schematic illustration of azurin molecules wired by the octanethiol monolayer self-assembled on the Au(111) surface, with a molecular orientation of the copper center facing the electrode surface. (C) A STM image of the azurin monolayer with molecular resolution obtained at the azurin/octanethiol/Au(111) system in NH₄Ac buffer (pH 4.6). Scan area is 200 × 200 nm, I_t = 0.1 nA, V_bias =–0.25 V, and substrate potential =+0.2 V vs. SCE. (D) A typical cyclic voltammogram of the azurin/octanethiol/Au(111) system in the same buffer as in STM imaging (C) with a scan rate of 2 V·s^–1. The shaded area shows the anodic Faradaic charge.

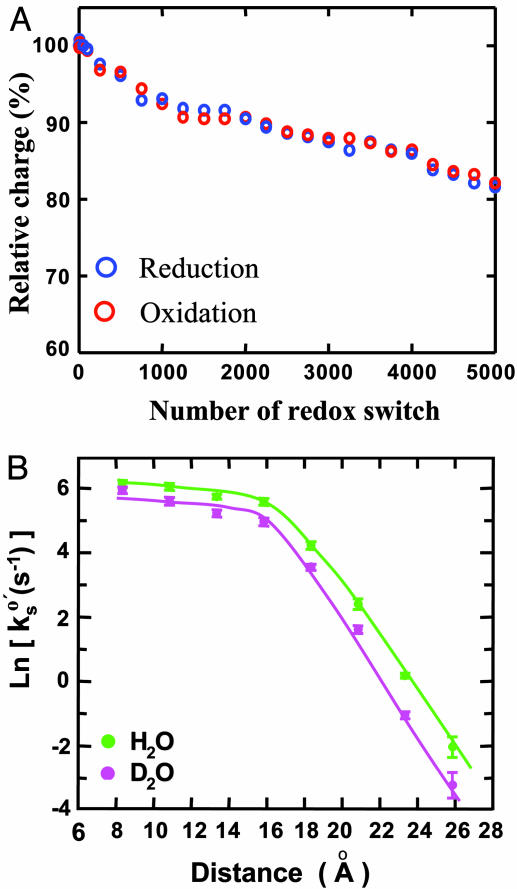
This molecular wiring assembly establishes effective electronic coupling between the copper center and the Au(111) surface, leading to fast and reversible interfacial ET detected by cyclic voltammetry (Fig. 1D). The azurin population can be estimated either from STM images or from the Faradaic charge (e.g., the shaded area in Fig. 1D). Notably, the values obtained by the two methods agree well, providing a convincing indication that azurin molecules immobilized in this orientation are fully active in ET function. A combination of electrochemical and STM measurements thus provides a way to quantify one of the fundamental and long-lasting questions in adsorption chemistry of redox proteins: What percentage of the protein molecules retain their biological activity in the immobilized state? In addition to fast ET, stability is another key factor determining reproducibility and operation in applications of the system to molecular electronics. We evaluated the stability of the present system by successive redox cycling at a frequency of 10 Hz. The result shows <20% decay in redox charge after 5,000 cycles (Fig. 2A). The stability, moreover, improves with increasing alkanethiol chain length. Long-term stability is also reasonably good, as evidenced by the fact that the system can be stored at 4°C for several months. This evaluation demonstrates high stability of this biomimetic system and could hold potential in molecular bioelectronics in addition to being a model ET system for fundamental approaches.

Fig. 2.

Stability evaluation and distant electron transfer. (A) Stability evaluation of the system represented by azurin/octanethiol/Au(111) subjected to successive cyclic voltammetry scans at 5 V·s^–1, equivalent to a redox switch frequency of ≈10 Hz. The relative charges were obtained by integrating the redox peaks and normalizing vs. the initial charge. (B) Distance-dependent ET kinetics shown by a plot of the rate constant (in natural logarithm) vs. the distance. The distance was estimated according to refs. 46 and 47 for the alkanethiolate lengths on the gold surface. The decay factors (defined as the rate decay per unit distance), obtained from the slopes (for long-chain alkanethiols, n > 8), were 0.83 and 0.91 Å^–1 in H₂O and D₂O media, respectively.

The interfacial ET properties of the system were comprehensively investigated in both H₂O and D₂O media. The equilibrium redox potential of immobilized azurin in H₂O is found to be in the range of 110–95 mV (vs. SCE), corresponding to the 4–18 methylene chain length. The redox potential is thus largely independent of the alkyl chain length, and all are close to the bulk equilibrium potential of this protein in homogeneous solutions (40). The ET kinetics is governed by the reorganization free energy, the bridge length, and configurational flexibility of the protein–bridge interface. The reorganization free energy (E_r), estimated from chronoamperometry (37), is in the range of 0.55–0.30 eV for alkane chain lengths with 4–18 methylene units; E_r thus increases with decreasing bridge length. The rate constant becomes independent of the distance in the range of four to eight methylene units, where the ET kinetics shows configuration-gating features. Configuration gating here means that the rate-limiting step of ET through short alkyl chains is a configurational rearrangement process of adsorbed azurin. Similar phenomena were found also for cytochrome c adsorbed electrostatically on carboxylic acid-terminated alkanethiol self-assembled monolayers (41). Configuration gating could thus play a significant role in determining the interfacial ET kinetics of such molecular wiring-based protein ET systems. Exponential distance decay is observed with longer bridges with a distance-decay factor (β) (defined as the rate decay per unit distance) of 0.83 Å^–1 (equivalent to 1.03 per methylene unit) (Fig. 2B, green curve). The β value is close to that for charge transfer through saturated hydrocarbons (43, 44), reflecting efficient electronic coupling between the copper center and the gold electrode. Interestingly, the ET rate constants at very short bridges (n < 4) are even smaller than those obtained at n = 4–8. This decay is attributed to further increase in the reorganization free energy, resulting from a more flexible protein–alkanethiol interfacial configuration caused by weaker hydrophobic interactions between the bridge methyl group and azurin.

Isotope effects can be an informative indication of the nature of elementary reactions, particularly in proton and hydrogen atom transfer processes. In the present case, both ET thermodynamics and kinetics show deuterium isotope effects, with the former being more pronounced. The redox potential of adsorbed azurin in D₂O is shifted positively relative to that in H₂O by 20–60 mV for the bridges with 4–18 methylene units. The shift increases with increasing bridge length, and the effect is clearly more significant than in homogeneous solution (39). The ET kinetics in D₂O has a similar overall distance-dependent pattern to that in H₂O (Fig. 2B). However, the rate at a given distance is clearly slower, and the distance-dependent decay is slightly faster as indicated by a larger β value of 0.91 Å^–1 (Fig. 2B, red curve). These apparent observations arise mainly from solvation and protein dynamic effects rather than from proton/deuteron tunneling. The bulk dielectric properties of H₂O and D₂O are similar, but structural and dynamic details of their solvation effects can be quite different. The solvation effects can result in differences in both intrinsic structures of azurin itself and local interactions between the azurin molecule and the terminal alkanethiol methyl group. The latter is less efficient in D₂O, which is clearly reflected by less stability of the azurin adlayer and smaller protein population at a given alkanethiol bridge. We therefore conclude that adsorbed azurin molecules are more dynamic in D₂O and, in turn, the configuration-gating effect is more significant. This configuration-gating effect is the main reason for the slowdown of the kinetics. More detailed theoretical modeling is desired but is beyond the main focus of the present report.

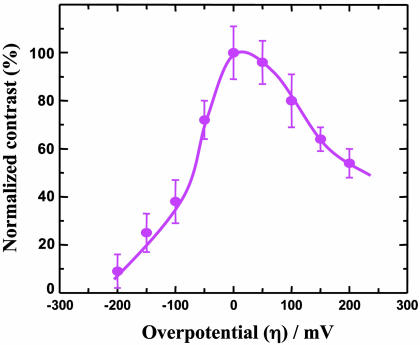
As a representative of the present system, azurin/CH₃(CH₂)₇S-Au(111) with the azurin population controlled at the submonolayer level was characterized by electrochemical STM (ECSTM) to observe single-molecule current–voltage relations by tuning the overpotential across the equilibrium redox potential. The energy state of both the substrate (i.e., the working electrode) and the tip (i.e., the scanning probe) in ECSTM is under control by electrochemical potentials relative to a common reference electrode in an aqueous buffer environment. This STM configuration is particularly suitable for in situ mapping of electronic properties of redox proteins during their biological action (e.g., ET or electrocatalysis), because the aqueous phase is essential for almost all biological processes in nature. STM observations were first performed with a large scan area (e.g., 200 × 200 nm²) to obtain molecule-resolved images of the azurin submonolayer and then focused on a few individual molecules by reducing the scan area. The high-resolution image where the ordered octanethiolate monolayer is clearly seen underneath the azurin molecules is notable and is indicative of a well organized assembly in both organic and protein adlayers. By keeping a constant bias voltage between the substrate and the tip, STM imaging started with the substrate potential set at the equilibrium redox potential of azurin (i.e., zero overpotential). Imaging was continued toward either positive or negative overpotentials by adjusting the substrate and tip potentials in parallel (i.e., at constant bias voltage) and finally was returned to the equilibrium potential. Both the octanethiolate monolayer and the azurin submonolayer are sufficiently robust to withstand repeated ECSTM scanning. As a result, a series of STM images was acquired at various overpotentials. Fig. 3 shows typical images in which three molecules were targeted. Focus is on the central molecule; two molecules in the upper left region serve as a positioning reference. The single-molecule contrast is clearly tuned by the redox state of azurin, with a maximum around the equilibrium redox potential (Fig. 3C). The contrast decreases upon applying either positive (Fig. 3 A and B) or negative (Fig. 3 D and E) overpotentials, but the effects are not symmetric, with the decay being stronger at negative overpotentials. The correlation between the normalized contrast and the overpotential is shown in Fig. 4 based on measurements of 50 individual molecules, with a maximum on/off current ratio of ≈9.

Fig. 3.

A series of STM images showing in situ observations of redox-gated electron-tunneling resonance arising from single azurin molecules. The images were obtained by using the azurin/octanethiol/Au(111) system in NH₄Ac buffer (pH 4.6) with a fixed bias voltage (defined as V_bias = E_T – E_S) of –0.2 V but variable substrate overpotentials (vs. the redox potential of azurin, +100 mV vs. SCE): +200 (A), +100 (B), 0 (C), –100 (D), and –200 mV (E). Scan area is 35 × 35 nm.

Fig. 4.

A correlation between the normalized contrast and the overpotential, showing an asymmetric dependence with a maximum on/off ratio of ≈9.

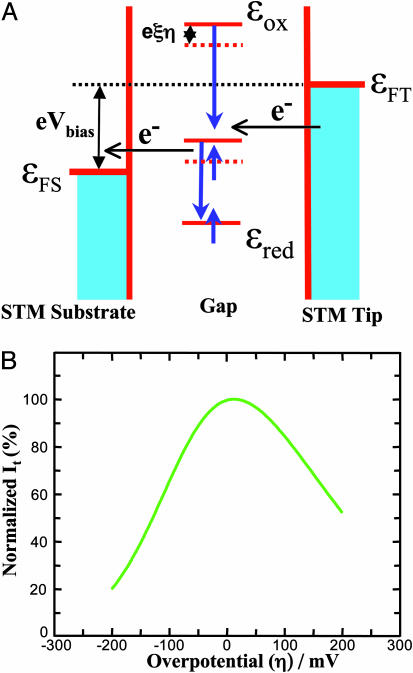
These observations can best be understood by a two-step ET mechanism at small bias voltages in the STM redox process. The theoretical notions have been developed over the past years (33, 48–50). Fig. 5A shows a schematic energy diagram to illustrate the relative energy levels of the substrate, the tip, and a redox molecule located in the substrate–tip gap. The energy levels may all be modified by changing the substrate potential, but the difference between the substrate and the tip levels remains constant if a fixed bias voltage is applied as in the present case. As a consequence, the redox level is shifted relative to the substrate and tip Fermi levels by the overpotential. The redox level is furthermore strongly coupled to the environment, with an initially oxidized (vacant) level above the tip Fermi level and an initially reduced (occupied) level below the substrate Fermi level (Fig. 5A), when the bias voltage (V_bias = E_T – E_S) is negative. Nuclear configurational fluctuations bring initial redox levels into the energy region close to the Fermi level of the electrodes, which in turn induces a two-step ET process. At negative bias voltage, ET proceeds first from the tip to the vacant redox level and then from the temporarily occupied redox level to the substrate (Fig. 5A). A corresponding ET sequence in the opposite direction would occur at positive bias voltage. The tunneling current (I_t) is thus gated by the redox level, which can be directly displayed by changes in the STM image contrast.

Fig. 5.

Theoretical analysis and computation. (A) Schematic energy diagram of the ECSTM showing the relative energy levels of the substrate, the tip, and the redox molecule. ε_FS and ε_FT denote the Fermi levels of the substrate and the tip, respectively; the energy levels of the redox molecule at the oxidized and reduced forms are represented by ε_ox and ε_red, respectively. (B) Dependence of STM tunneling current on the overpotential calculated by Eqs. 1-3 (see the text) with ρ_t = 0.42 and ρ_s = 0.29 number of states·eV^–1·atom^–1, α_t = α_s = 0.5, V_bias =–0.2 V, E_r = 0.45 eV, κ_S = 0.1, κ_t = 0.01, ξ = 0.7, γ = 0.20, θ = 5.6 eV^–1, ω_eff = 10¹³, T = 295 K, and other parameters with their normal values. The tunneling current is normalized relative to the maximum value.

The nonadiabatic limit of weak electronic coupling between the redox center and the enclosing electrodes applies for the present case. At finite bias voltages, the two-step tunneling current (I_t) dependence on the effective overpotential (eξη) and the bias voltage (eV_bias) is represented by two-step ET rate constants in the following combination (33):

[1]

where 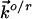and 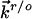refer to the rate constants for ET between the tip and azurin and between azurin and the substrate, respectively, and the arrow indicates the electron flow direction following the pathway shown in Fig. 5A. 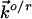and 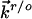have the following forms in the present case:

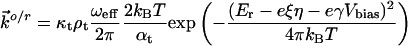[2]

[3]

where κ_t and κ_s are electronic transmission coefficients for ET between the tip and the protein and between the protein and the substrate, respectively; ρ_t and ρ_s are the electronic level densities of the tip and the substrate; ω_eff is the effective nuclear vibrational frequency; α_t and α_s are ET transfer coefficients between the tip and the protein and the protein and the substrate, respectively; ξ is the fraction of the substrate-solution potential drop; and γ is the fraction of the bias voltage drop at the molecular redox center. Other symbols have their usual meaning.

An exponential prefactor [exp(eθη)] (with θ in the range of 3–6 eV^–1) as a function of the overpotential in the expression form (Eq. 3) is necessary to account formally for asymmetric overpotential dependence observed experimentally (Fig. 4). The parameter θ represents either overpotential dependence of the tunneling barrier or electrochemical double-layer effects. By the introduction of this prefactor, we obtain the calculated tunneling current–overpotential relation (Fig. 5B) reasonably consistent with experimental observations (Fig. 4). The main parameters, reflecting the ET nature of this system in the ECSTM configuration, are extracted from such computations. The computations provide detailed information for rational understanding of the ET mechanism: (i) The position of the maximum resonance is comprehensively determined by all parameters; in the present case, it appears in a narrow positive overpotential region around the equilibrium redox potential, which could reflect the character of the nonadiabatic limit. (ii) The rate-limiting step is the ET between the tip and the azurin molecule [because at least an order of magnitude difference between the two transmission coefficients (e.g., κ_s = 0.1 and κ_t = 0.01) is required], in accordance with the fast interfacial ET between azurin and the substrate (≈500 s^–1 estimated from electrochemical measurements). (iii) The reorganization free energy is estimated as 0.35–0.45 eV, implying that E_r is not significantly different in STM and electrochemical ET (0.45 eV). (iv) The distribution of the bias voltage between the tunneling gap is asymmetric, with 0.15–0.20 as optimal values for the fraction of the bias voltage drop (γ) at the site of the redox center (i.e., the copper ion in azurin), reflecting asymmetric location of this center both physically and electronically. (v) The distribution of the overpotential in the tunneling gap also significantly affects the tunneling resonance, on which the asymmetric feature largely depends. However, the fraction of the substrate-solution potential drop (ξ = 0.7–0.75) deviates less from the ideal case (ξ = 1.0). In short, the two-step ET model offers a broad frame of the detailed ET mechanism in the STM redox process, even when a complicated ET process (like the present protein case) is involved.

We have provided a strategy suitable for in situ mapping of long-range protein interfacial ET at the single-molecule level. This strategy has been feasible by using a biomimetic assembly to achieve fast interfacial ET and high-resolution ECSTM. Although azurin is a large and structurally complicated molecule (vs. small redox molecules), ECSTM is sufficiently sensitive to observe directly redox-gated electron tunneling resonance of this protein. Experimental observations are supported by computations based on a two-step ET model. These results could lead to visible advances in fundamental understanding of long-range interfacial ET of proteins and hold general interest in nanoscale bioelectronics.