A Two-Compartment Model of Osmotic Lysis in Plasmodium falciparum-Infected Erythrocytes

Abstract

We recently identified a voltage-dependent anion channel on the surface of human red blood cells (RBCs) infected with the malaria parasite, Plasmodium falciparum. This channel, the plasmodial erythrocyte surface anion channel (PESAC), likely accounts for the increased permeability of infected RBCs to various small solutes, as assessed quantitatively with radioisotope flux and patch-clamp studies. Whereas this increased permeability has also been studied by following osmotic lysis of infected cells in permeant solutes, these experiments have been limited to qualitative comparisons of lysis rates. To permit more quantitative examination of lysis rates, we have developed a mathematical model for osmotic fragility of infected cells based on diffusional uptake via PESAC and the two-compartment geometry of infected RBCs. This model, combined with a simple light scattering assay designed to track osmotic lysis precisely, produced permeability coefficients that match both previous isotope flux and patch-clamp estimates. Our model and light scattering assay also revealed Michaelian kinetics for inhibition of PESAC by furosemide, suggesting a 1:1 stoichiometry for their interaction.

γ_Cl

Whole cell conductance of Cl⁻

A

Surface area of an infected RBC, a constant

b₀, b₁, b₂, b₃

Coefficients for the sigmoidal dependency of H versus T

c

RBC cytosolic sorbitol concentration; also c(t)

c_h

RBC cytosolic concentration of sorbitol at the time of cell lysis

c_e

Extracellular sorbitol concentration, a constant

d

Critical diameter of infected RBC, related to A by A = πd²

H

Hemoglobin release as a function of time

H_t

Total hemoglobin released after addition of saponin to lyse RBCs

K_d

Dissociation constant for furosemide in Hill equation

K_m

Michaelis dissociation constant for furosemide

L

Hill coefficient

M

Mean corpuscular hemoglobin concentration, a constant

N

Osmotically inactive volume of cell primarily consisting of the intracellular parasite, a constant

p

Fraction of RBCs that are infected in a lysis experiment (parasitemia)

P_Cl

Permeability of infected RBC plasma membrane to Cl⁻

P_S

Permeability of infected RBC plasma membrane to sorbitol

t

Time

t_h

Time required for a given infected RBC to lyse in sorbitol lysis solution

T

Transmittance of 700 nm light through suspension of RBCs

v

Pellet volume of infected RBCs used in a lysis experiment

V

Osmotically active volume of RBC cytosol; increases during experiment, also V(t)

V_i

Total volume of an infected RBC (including parasite volume) at t = 0

V_o,i

Osmotically active volume of RBC cytosol at t = 0

V_o,h

Osmotically active volume of RBC cytosol at t = t_h

INTRODUCTION

Within 18 h of infecting the human red blood cell (RBC), the malaria parasite, Plasmodium falciparum, dramatically alters the permeability of its host RBC to various solutes including anions (Kirk et al., 1994), sugars (Ginsburg et al., 1985), amino acids (Cabantchik, 1990), purines (Upston and Gero, 1995), and certain cations (Kirk and Horner, 1995b; Staines et al., 2000). These changes have been most extensively studied with either isotope flux or osmotic fragility experiments that measure the time to infected RBC lysis in isotonic solutions of a permeant solute. Evidence that these two methods study the same permeability mechanism is solid and based on 1), similarities in the spectrum and rank order of solutes with increased permeabilities, and 2), identical inhibitory effects of furosemide (Kirk et al., 1994), glybenclamide (Kirk et al., 1993), phloridzin (Kutner et al., 1987), NPPB (Kirk and Horner, 1995a), niflumic acid (Kirk et al., 1994), and DIDS (Breuer et al., 1987). Moreover, the inhibition dose-response for each blocker is independent of the permeant solute being tested, suggesting that a single transport mechanism is responsible for the increased permeability of all these solutes.

Recently, we used the whole-cell and on-cell patch-clamp methods to identify an unusual anion channel on the RBC membrane of trophozoite-stage infected cells (Desai et al., 2000). This channel, the plasmodial erythrocyte surface anion channel (PESAC), is present at 1000–2000 functional copies/cell and is absent from uninfected RBCs. It has a permeability sequence for anions of SCN⁻ > I⁻ > Br⁻ > Cl⁻ > Acetate⁻ > Lactate⁻ > Glutamate⁻. PESAC exhibits voltage-dependent single channel gating that correlates well with inward rectifying whole-cell currents. It has fast-flickering gating with mean open times of 0.5 ms, bursts of openings, and a 1/f power spectrum. Most importantly, PESAC's pharmacology and anion selectivity match those of tracer and osmotic lysis experiments; thus, it likely accounts for the increased permeability of infected RBCs to the broad range of solutes identified by those methods.

Of the three methods now available for studying permeation through PESAC—isotope flux, osmotic lysis, and patch-clamp—osmotic lysis experiments remain technically the easiest to perform. Previous osmotic lysis assays, however, have been limited to qualitative permeability measurements that could not be quantitatively compared to permeation rates estimated from isotope uptake or patch-clamp experiments. We now report two refinements to this simple assay that enable more quantitative interpretation of lysis data. First, we derived a mathematical model of osmotic lysis based on diffusional entry of sorbitol into infected RBCs via PESAC. Although similar models have been developed for uninfected RBCs (Saari and Beck, 1974; Beck and Saari, 1977), use with infected RBCs requires the additional incorporation of the intracellular parasite's volume into the derivation. Our second refinement is the use of spectrophotometric tracking of the lysis time course. Hemoglobin measurements at timed intervals, used previously, are somewhat cumbersome and produce a relatively small number of measurements during a lysis time course. In contrast, our spectrophotometric assay produced nearly continuous measurement of lysis kinetics, yielding more robust measurements with less effort.

These measured lysis time courses, in conjunction with our model, produce an estimate of the sorbitol permeability coefficient that, for the first time, matches those calculated from previous isotope uptake and patch-clamp experiments. Our experiments also reveal a 1:1 stoichiometry of PESAC inhibition by furosemide. Finally, these studies examine the relationship between the time to osmotic lysis and the population distributions of four infected RBC parameters: total RBC volume (V_i), RBC surface area (A), intracellular parasite volume (N), and sorbitol permeability (P_S).

MATERIALS AND METHODS

Parasite culture

P. falciparum (Indochina strain) was cultured according to standard methods in O⁺ human RBCs collected from healthy blood bank donors and separated from leukocytes with a Sepacell filter (Baxter Healthcare Corp., Memphis, TN). Parasite cultures were maintained at 5–10% parasitemia, synchronized by the sorbitol lysis method (Lambros and Vanderberg, 1979) 24 h before harvest, and enriched to 96–99% trophozoite- infected RBCs by the percoll-sorbitol method (Kutner et al., 1985; Aley et al., 1984).

Lysis of infected erythrocytes

Enriched infected RBCs were washed and kept in culture medium at 10% hematocrit on ice until used, typically within 30 min. Control experiments showed that storage on ice for up to 5 h does not alter the lysis time course (data not shown). Osmotic lysis was initiated by addition of 1.5 mL of prewarmed sorbitol lysis solution (280 mM sorbitol, 20 mM Na-HEPES, 0.1 mg/mL BSA, pH 7.4) to 30 μL of the RBC suspension in a cuvette maintained at 37°C by a peltier temperature controller (Beckman Coulter DU640 Spectrophotometer, Fullerton, CA). Osmotic lysis was monitored by measuring 700 nm light transmittance through the sample at 0.1- to 10-s intervals. RBCs were gently triturated with a pipetteman every 5 min to maintain a homogeneous suspension with negligible mechanical shearing, as verified in control experiments. To release residual hemoglobin trapped in unlysed or partially lysed cells, 30 μL of 10% w/v saponin was added at the end of the lysis time course.

Hemoglobin measurements

In parallel with each transmittance time course, hemoglobin release measurements were made with identical suspensions of infected RBCs at 37°C. Here, 80 μL aliquots of the RBC suspension in sorbitol lysis solution were harvested at timed intervals, centrifuged at 6000 × g for 20 s, and the supernatant harvested for subsequent determination of hemoglobin concentrations. These were measured with a modified protocol based on hemoglobin-dependent oxidation of 3,3′,5,5′-tetramethylbenzidine (plasma hemoglobin kit, Sigma-Aldrich, St. Louis, MO). Briefly, 50 μL of the hemoglobin-containing supernatant was mixed with 500 μL of tetramethylbenzidine (0.2 mg/mL in 90% Acetic Acid). 600 nm transmittance was then measured exactly 10 min after addition of 450 μL of 0.3% H₂O₂ and calibrated with hemoglobin standards (Sigma-Aldrich) for each experiment.

Measurement of N

We independently determined N for each lysis experiment by measuring total hemoglobin released by saponin (H_t), as described above. H_t includes hemoglobin released from both uninfected and infected RBCs. The contribution of uninfected RBCs to H_t is given by Mv(1 − p), where M is the mean hemoglobin concentration in uninfected RBC cytosol (340 mg/mL, measured as above, within normal clinical values (Eastham and Slade, 1992)). The volume of cells used in each lysis experiment (v) was precisely estimated from cell counts in a hemocytometer and a V_i of 100 fl. The parasitemia (p) after percoll-sorbitol enrichment was estimated by examination of Giemsa-stained slides.

Because the hemoglobin concentration in RBC cytosol after infection does not change (Lew and Hockaday, 1999), the contribution of infected RBCs to H_t is given by Mvp(V_i − N)/V_i. By recognizing that H_t is the sum of these uninfected and infected RBC contributions, we used simple rearrangement to derive an equation for N in terms of the above measured parameters:

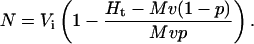(1)

Derivation of the two-compartment osmotic lysis model

We derived an equation describing the passive RBC membrane permeability of sorbitol, P_S, as a function of the time to hemolysis, t_h, and the geometric parameters of the infected RBC. For passive accumulation in the RBC cytosolic compartment, Fick's law of diffusion states that

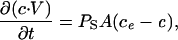(2)

where c = c(t) is the concentration of sorbitol in RBC cytosol at time, t ≥ 0. c_e, the concentration of sorbitol in the extracellular medium, is a constant in dilute cell suspensions. A is the surface area of the infected RBC; V = V(t) is the osmotically active volume of the RBC cytosol. With the chain rule, Eq. 2 becomes

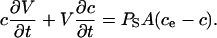(3)

Because the RBC membrane's permeability to water (Brahm, 1982) is much greater than that to sorbitol,

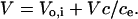(4)

This equation states that sorbitol entry into infected RBCs is isoosmotic and that V at any time, t, is the sum of V_o,i, the osmotically active volume of RBC cytosol at t = 0, and the extracellular volume containing the same amount of sorbitol. Rearranging Eq. 4 and substituting into Eq. 3 to eliminate V, we obtain

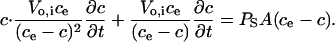(5)

Integration of Eq. 5 and subsequent addition of the boundary conditions—c = 0 at t = 0 and c = c_h at t = t_h, the time at which the cell lyses osmotically—produces

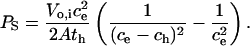(6)

At t = t_h, Eq. 4 becomes

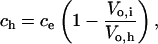(7)

where V_o,h is the osmotically active volume of the cell just before lysis. We assume that lysis occurs when the cell has expanded to a sphere because the RBC membrane is inelastic and cannot tolerate additional sorbitol entry without lysis. The RBC's membrane surface area, A, is a constant related to the critical diameter, d, of a spherical cell by A = πd². Thus,

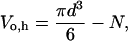(8)

where N represents the osmotically inactive volume of the cell. N is a constant determined largely by the intracellular parasite's volume, but also includes osmotically inactive components of RBC cytosol such as bound water (Kelemen et al., 2001). We introduce V_i as the total volume of the cell at t = 0 such that

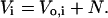(9)

Using Eqs. 7, 8, and 9 to eliminate c_h, V_o,h, and V_o,i from Eq. 6, we obtain the desired equation for P_S in terms of known or measurable parameters:

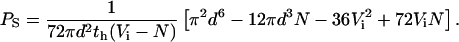(10)

RESULTS

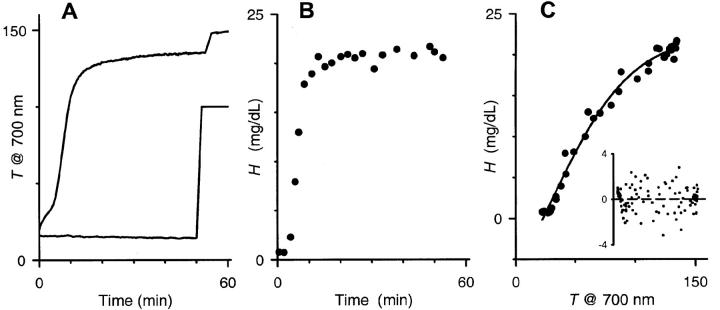
Osmotic lysis of human RBCs produces dramatic changes in light scattering, a phenomenon readily demonstrated by visual comparison of RBC suspensions in saline and in distilled water. When infected with P. falciparum trophozoites, RBCs are known to undergo osmotic lysis in isotonic sorbitol solutions within 15 min, which we attribute to sorbitol uptake via PESAC. We first examined whether this parasite-specific osmotic lysis can be tracked kinetically in a light scattering assay. Fig. 1 A shows a continuous recording of 700 nm transmittance through a suspension of infected RBCs in sorbitol. The large increase in transmittance reflects osmotic lysis of infected RBCs with a halftime of ∼7 min at 37°C (upper curve), a value that matches previous estimates obtained in typical hemoglobin release assays (Ginsburg et al., 1983). The shape of this profile reflects the population distribution of lysis times for infected cells. As discussed in detail below, the lysis time for each infected cell is a function of its two-compartment geometry and its sorbitol permeability coefficient.

FIGURE 1.

Time course of osmotic lysis measured with a light scattering assay. (A) Suspensions of trophozoite-stage infected RBCs (upper curve) or uninfected RBCs (lower curve) in sorbitol lysis solution were continuously monitored at 700 nm. The transmittance time courses are shown here in arbitrary units. The abrupt increases at ∼50 min correspond to the addition of saponin, which lyses both uninfected and infected RBCs and releases any trapped hemoglobin. (B) Hemoglobin release measurements with an equivalent aliquot of the infected RBC suspension used in (A), both performed at 37°C. Measurements with uninfected RBCs produced negligible hemoglobin release (not shown). (C) Relationship between % transmittance (T) and released hemoglobin (H) for this infected RBC experiment. Plot shows measurements pooled with another T-H pair from the same culture. Solid line represents the least-squares fit to H = b₀ +b₁/(1 + exp(−(T − b₂)/b₃)). Inset shows the residuals from three separate experiments for this fit. Notice the uniform distribution of these residuals about the x axis. Dashed line represents a least-squares fit to a straight line; it demonstrates an average residual of zero at all transmittances, indicating that the equation used in Fig. 3 B does not introduce bias.

Uninfected RBCs, measured under identical conditions, exhibited no transmittance change (lower curve, Fig. 1 A), consistent with their negligible sorbitol permeability (Bowman and Lwitt, 1977). Neither uninfected nor infected RBCs exhibited transmittance changes over 1 h in isotonic NaCl solutions (not shown).

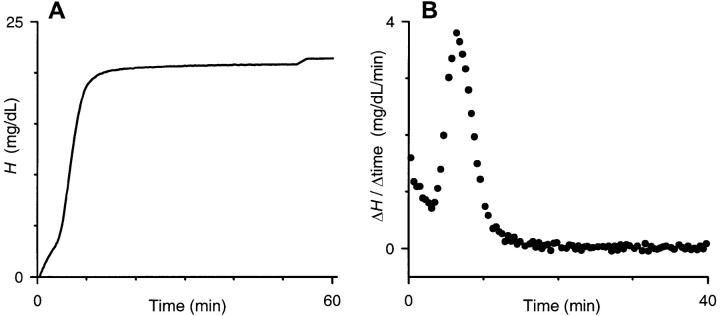
These transmittance measurements, although demonstrating the basic phenomenology of PESAC, are only an indirect marker of the biological process of osmotic lysis. Light transmittance through a suspension of cells is a complex function of cell shape and size, cellular debris and parasites liberated by lysis, aggregation of particles in suspension, and absorbance by protein and other solutes. To transform these measurements to more biologically relevant values, we made simultaneous hemoglobin release measurements, which more directly indicate cell lysis (Fig. 1 B). The complex relationship between transmittance and hemoglobin release was empirically fitted with a sigmoidal equation (see legend, Fig. 1 C). Examination of residuals confirmed that this equation was adequate and did not introduce bias in subsequent analyses (Fig. 1 C, inset). Least-squares estimates of the four sigmoidal parameters were then used to transform the transmittance lysis time courses to continuous hemoglobin release time courses (Fig. 2 A, transformed from data in Fig. 1, A and B).

FIGURE 2.

Continuous hemoglobin release time course obtained by combining light scattering and discrete hemoglobin measurements. (A) Hemoglobin release time course obtained by transformation of data in Fig. 1 A with hemoglobin measurements in Fig. 1 B. (B) Derivative of hemoglobin release time course in this experiment. Groups of four adjacent measurements in (A) were averaged; the instantaneous slope, plotted here, was then determined between each pair of neighboring averaged points. This method produces a weighted histogram of lysis times for the population of RBCs. The modal lysis time used in our permeability calculations corresponded to the peak of the bell-shaped distribution.

Although the general shape and time course of the transmittance curves (Fig. 1 A) and the hemoglobin release curves (Fig. 2 A) are similar, accurate statements about the population distribution of infected RBC parameters can only be made from the hemoglobin release curves. For example, we used the derivative of the hemoglobin release profiles to generate a population distribution of lysis times in sorbitol (Fig. 2 B). This distribution revealed a primary population of cells with a modal lysis time of 6.4 min and nearly symmetrical fall-off from this peak. Most experiments revealed a secondary population of cells that lysed in less than 3 min. This smaller population may reflect either RBCs infected with two or more parasites or a more mature stage of infection, e.g., schizont, both seen in small numbers in our cultures. We restricted our subsequent analyses to the primary bell-shaped population of RBCs and their osmotic lysis.

Previous hemoglobin release measurements using infected RBCs have been instrumental in defining both the pharmacology of PESAC and the relative permeabilities of uncharged solutes, but were limited to qualitative comparisons of rates. We derived an equation (Eq. 10), based on diffusional entry via PESAC that can be used to calculate solute permeability coefficients from the measured lysis time course. Using the modal lysis time, t_h, and the mean parasite volume, N, determined separately for each experiment, along with estimates of initial RBC volume (V_i = 100 fl; Nash et al., 1989) and RBC critical diameter (d = 6.6 μm; Canham and Burton, 1968; Jay, 1975), we calculated a sorbitol permeability coefficient of 1.95 ± 0.17 × 10⁻⁷ cm/sec (n = 12 separate experiments).

Micromolar concentrations of furosemide, a nonspecific blocker of various channels and carriers, block both ¹⁴C-sorbitol accumulation in infected RBCs and PESAC gating in single channel patch-clamp measurements. We examined the concentration dependence of furosemide blockade with our light scattering assay (Fig. 3 A) and Eq. 10. Fig. 3 B shows the resulting sorbitol permeability coefficients plotted as a function of furosemide concentration. The solid line represents the least-squares best fit to the Hill equation with a K_d of 2.8 μM and a Hill coefficient of 1.08 ± 0.06, suggesting a 1:1 stoichiometry for PESAC inhibition by furosemide.

FIGURE 3.

Dose response for inhibition of PESAC by furosemide. (A) Transmittance measurements with 0, 2, 12, and 200 μM furosemide added to the sorbitol lysis solution. Notice that the lysis time course is slowed by furosemide, but that the transmittance endpoint is not affected. (B) Calculated permeability as a function of furosemide concentration. For each furosemide concentration, P_S was calculated from transmittance and hemoglobin release experiments with Eq. 10 and then normalized with that of a control experiment (no added furosemide), performed simultaneously. The solid line represents a least-squares fit to the Hill equation, y = 1/(1 + (x/K_d)^∧L). A fit to the Michaelis-Menten equation produced a K_m of 2.7 μM and was essentially indistinguishable (not shown).

DISCUSSION

Osmotic lysis experiments have been used for many years to study changes in the permeability of P. falciparum-infected RBCs to a range of small solutes. We have improved this method with a light scattering assay that allows continuous tracking of the lysis time course, providing as much as a 100-fold improvement in temporal resolution over hemoglobin release measurements alone.

A second major achievement of this study is the development of a mathematical model that enables quantitative analysis of osmotic lysis time courses. According to this model, the time to lysis for a single infected RBC (t_h) is determined by four distinct parameters: V_i, d, N, and P_S. We used this model to estimate P_S by measuring modal t_h in our light scattering assay, calculating N by independent total hemoglobin measurements, and incorporating tabulated mean values of V_i and d (Eq. 10). We have tested this model by comparing our estimates of P_S to those obtained by other methods (see below) and by examining the effects of inhibition of PESAC by a range of furosemide concentrations.

For each osmotic lysis experiment, we used simultaneous light scattering and hemoglobin release measurements from identical sorbitol suspensions of infected RBCs. Although these two methods produce similar kinetic data, both are needed to obtain a high-resolution population distribution of lysis times (e.g., Fig. 2 B). Our light scattering method's main advantage is that it produces continuous kinetic data not practical with discrete hemoglobin measurements. Its main drawback is that transmittance measurements do not exclusively track the biologically important lysis phenomenon: they also reflect changes in cell shape, light scattering by subcellular components released upon lysis, and aggregation of particles. This complication is apparent in Fig. 1 C, which shows that the measured transmittances are not linearly related to the amount of hemoglobin released from RBC lysis. We overcame this limitation by transforming the light scattering data with discrete hemoglobin release measurements. Thus, the combination of the two parallel measurements produces continuous kinetic data without compromising biological relevance.

Mathematical model

Our mathematical model for osmotic lysis of infected RBCs is based on conservative diffusional considerations. Similar derivations have been carried out for uninfected human RBCs, yielding reasonable estimates for solute permeabilities (Saari and Beck, 1974; Beck and Saari, 1977). Our derivation for infected RBCs adds an intracellular compartment, N, which is constant and not osmotically active. N is assumed to consist primarily of the parasite's volume, but also includes other osmotically inactive intracellular components such as “bound water” (Kelemen et al., 2001).

In our model, the osmotic lysis time, t_h, for a single trophozoite-infected RBC depends on four parameters: the initial volume of the RBC (V_i), the RBC surface area (A = πd²), the osmotically inactive intracellular compartment (N), and the sorbitol permeability coefficient (P_S, which is proportional to the number of functional PESAC/cell). In a population of infected cells, each of these four parameters has a distribution of values. The extent of variation of these parameters in the population determines how gradually the transmittance changes in a lysis experiment. If all four parameters were invariant in the population, our measured lysis time courses would have been step functions rather than curvilinear as observed. For the same reason, the derivative of the hemoglobin release time course (Fig. 2 B) is a weighted distribution of cell lysis times and its shape reflects the population distributions of the four cellular parameters.

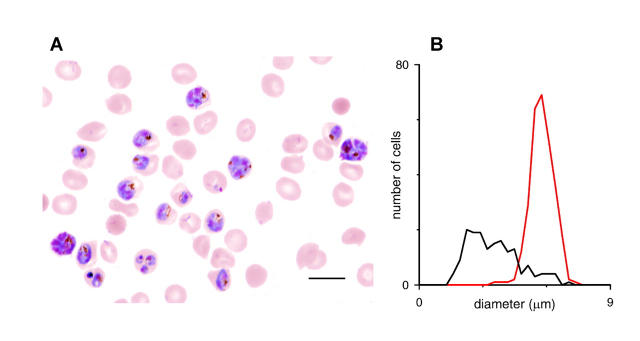
We wondered which, if any, of the four parameters had a controlling effect on the population distribution of lysis times. Three of the parameters appear to have relatively little variation. V_i and A, as determined by Coulter counter or microscopic methods, vary only ∼10–15% about their means for a given donor (Canham and Burton, 1968, and our Fig. 4 B, red curve). These variances do not appear to increase with infection by P. falciparum (Nash et al., 1989). Based on whole-cell conductances measured from small numbers of infected RBCs, cell-to-cell variability in P is also ≤10% (γ_Cl = 13.8 ± 1.2 ns in Desai et al., 2000; see discussion below on relationship between P and γ_Cl). The fourth parameter, N, appears to have a significantly greater population variation, which is clear upon microscopic examination of infected RBCs from our synchronized culture (Fig. 4). We examined what effect such variation in N might have on the distribution of t_h by plotting Eq. 10 after simple rearrangement (Fig. 5). Using physiological mean values for V_i, d, and P in this equation, t_h is only modestly dependent on N for values ≤70 fl. This, combined with the small population variations in V_i, A, and P, likely explain why the lysis time course is quite steep (Fig. 2 A) and the hemoglobin release distribution is rather narrow (Fig. 2 B). More quantitative examination of the shape of this distribution would be complicated, requiring addition of possible pairwise covariances among the four parameters. One example of such a nonzero covariance term would arise if large parasites (i.e., large N) induced larger numbers of PESAC on their host RBC membrane and thus a higher than average P_S.

FIGURE 4.

Size distributions of intracellular parasites and RBCs. (A) Light micrograph of a parasite culture grown to ∼30% parasitemia, fixed on a glass slide, and stained with Giemsa. With this stain, parasites appear as heterogeneous blue and red structures within a light-colored RBC cytosol. Scale bar, 10 μm. (B) Histogram of intracellular parasite and RBC diameters, black and red curves, respectively. Mean cell diameters were measured from light micrographs by eye with Photoshop (Adobe Systems, San Jose, CA). Notice that cell-to-cell variation in V_i (related to RBC diameter, red curve) is modest, but that variation is N (related to parasite diameter, black curve) is greater. Notice also that V_i for infected and uninfected RBCs are grossly identical.

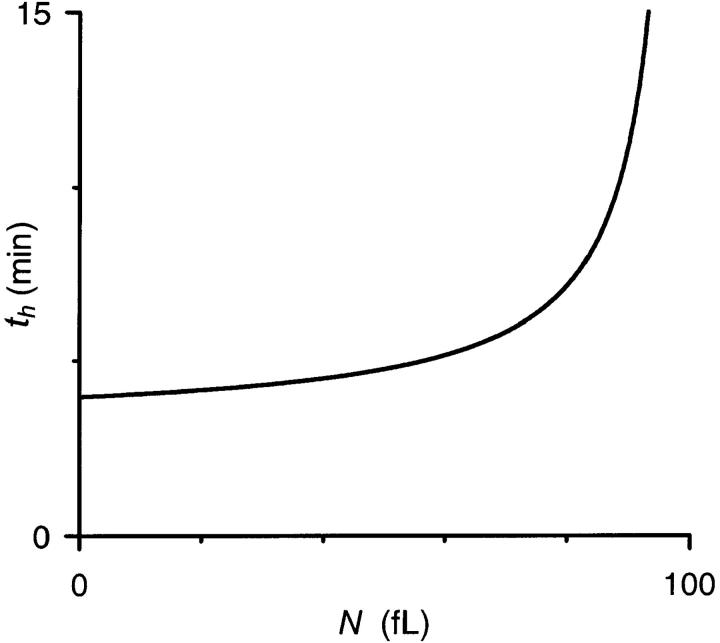
FIGURE 5.

Dependence of t_h on N. Plot shows calculated t_h for a range of N using Eq. 10 and physiological values of P_S, V_i, and d (1.95 × 10⁻⁷ cm/sec, 100 fl, and 6.6 μm, respectively). Notice that t_h is only modestly affected by physiological variations in N, the population mean of which varied between 39 and 71 fl in 12 separate experiments.

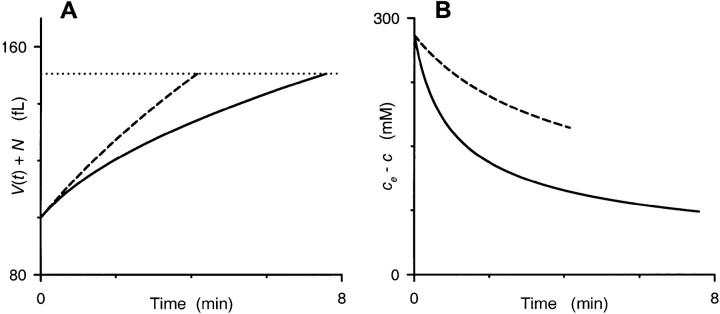
Fig. 5 reveals an interesting property of osmotic lysis that initially surprised us. It shows that, for fixed values of P_S, V_i, and A, infected RBCs with large parasites (larger N) will take longer to lyse than those with small parasites. Although this may seem counterintuitive, it becomes apparent upon consideration of absolute RBC cytosolic volumes, V(t), at t = 0 and t_h, respectively. Consider two hypothetical infected cells with identical P_S, V_i, and A, but parasites of extreme sizes, e.g., one with N = 20 and the other with N = 82 fl. For a V_i of 100 fl, the osmotically active RBC volumes will be 80 and 18 fl, respectively, at the start of our experiment. When suspended in our sorbitol lysis solution, both cells will endure the same absolute increase in volume to reach the critical volume (150.5 fl for A = 136.9 μm²) at which lysis occurs. To reach this volume, both cells will accumulate identical amounts of sorbitol, ∼14 fmol under our experimental conditions. The result of this entry will be a higher RBC cytosolic sorbitol concentration in the cell with larger N, c_h = 108 and 206 mM for N of 20 and 82 fl, respectively. This higher cytosolic concentration at the time of lysis (as well as at all t > 0) dissipates the gradient for sorbitol entry and explains why RBCs with large N take longer to lyse. We used numerical integration of Eq. 2 to demonstrate the time course of osmotic swelling and lysis (Fig. 6 A) and the dissipation of the sorbitol concentration gradient (Fig. 6 B) for these two extreme values of N.

FIGURE 6.

Our model's predicted time course for single RBC volumes. Numerical integration of Eq. 2 was performed with values of P_S, V_i, A, and c_e appropriate for our osmotic lysis experiments (1.95 × 10⁻⁷ cm/sec, 100 fl, 136.9 μm², and 280 mM, respectively). We used two extreme values of N, 20 fl (dashed curves) and 82 fl (solid curves), in iterative calculations of c(t) and V(t) in 0.001 min increments from 0 to 8 min. (A) shows the time course of total cell volume (given by V(t) + N) for these two RBCs. The volume of both RBCs increases monotonically, albeit at different rates, until a spherical shape is reached at a total cell volume of 150.5 fl, as indicated by the dotted horizontal line. Notice that the cell with a larger parasite (solid curve) takes significantly longer to reach this lysis threshold. (B) shows the time course of sorbitol accumulation in these two hypothetical RBCs, plotted as the difference between the constant extracellular sorbitol concentration (280 mM) and the numerically integrated intracellular concentration, c(t), to demonstrate the instantaneous gradient for sorbitol entry. Both curves are graphically terminated at the corresponding lysis times from (A). Notice that the RBC with a small parasite (dashed curve) maintains a larger gradient for t > 0, explaining why it reaches the lysis threshold sooner.

We restricted our study to osmotic lysis in sorbitol and did not explore other solutes known to have increased permeability in the infected RBC. A major reason was that sorbitol, a nonutilizable sugar alcohol, remains osmotically active in the infected RBC after entry via PESAC, simplifying the derivation of our model. In contrast, amino acids, physiological sugars, and purines, which also enter via PESAC and are known to produce osmotic lysis, are likely consumed by the parasite. Mathematical formulations for these solutes would require addition of rate constants for carrier-mediated entry into the parasite and for consumption or incorporation into protein or nucleic acid macromolecules. In most cases, these rate constants are not precisely known. Even if known, their addition to the model would complicate the derivation of Eq. 10 by producing a time variant N, here assumed constant.

Our derivation assumes that sorbitol can diffuse into RBC cytosol, but not into the intracellular parasite compartment defined by N. This is justified, in part, by the undetectable sorbitol permeability of the hexose transporter localized to the parasite plasma membrane (Woodrow et al., 2000). Furthermore, smears of infected RBCs osmotically lysed with sorbitol reveal intact parasites, suggesting a low sorbitol permeability of the parasite compartment (not shown). To the extent that sorbitol can enter the parasite compartment, our measured N would be an overestimate of the true osmotically inactive volume of the infected RBC. In the extreme case of infinite sorbitol permeability at the parasite plasma membrane, N would reduce to zero and our estimate of P_S would overestimate its true value by 30%.

Comparison to other methods

How do our permeability measurements compare to previous estimates? The initial rate of 1 mM ¹⁴C- sorbitol accumulation at 22°C has been measured at 600 μmol/10¹² cells/h (Kirk and Horner, 1995b). Using a Q₁₀ for permeation through PESAC of 1.3 (Ginsburg et al., 1983 and our data, not shown), this corresponds to 890 μmol/10¹² cells/h at 37°C, the temperature used in our study. With infected RBC volume, V_i = 100 fl, and surface area, A = 136.9 μm², this value converts to a P_S of 1.8 × 10⁻⁷ cm/s. The excellent concordance of our estimate, 1.95 ± 0.17 × 10⁻⁷ cm/s, with this value from tracer flux studies validates our approach.

It is also possible to compare these estimates to the whole-cell Cl⁻ conductance, measured with the whole-cell patch-clamp configuration (Desai et al., 2000). From previous data (Kirk and Horner, 1995b, and Kirk et al., 1994), we estimate a P_Cl/P_S of 120, which yields a P_Cl of 2.1–2.5 × 10⁻⁵ cm/s at 37°C for the tracer and lysis measurements. Using the constant field assumption and an estimate for intracellular free [Cl⁻] of 120 mmol/L cells (Hunter, 1977; Lin and Schroeder, 2001), this P_Cl corresponds to 10.5–12.5 nS/cell at 22°C, in good agreement with previous patch-clamp measurements of 13.8 ± 1.2 nS in isotonic saline (n = 12 cells, Desai et al., 2000). This agreement of the permeabilities calculated from measurements of hemolysis rates, radioisotope uptake rates, and whole-cell currents adds quantitative evidence to the hypothesis that a single transport mechanism, PESAC, adequately accounts for the parasite-induced increases in permeability to a range of solutes. PESAC can now be studied quantitatively with three methods: radioisotope uptake, patch-clamp, and osmotic lysis when combined with our Eq. 10.

There is now increasing information on how furosemide, a nonselective blocker of many channels and carriers, might act on PESAC at the molecular level. The concentration dependence of inhibition reveals a Hill coefficient of one, suggesting a 1:1 stoichiometry of interaction with PESAC. This interaction likely occurs somewhere on the extracellular face of the channel based on effects of furosemide added either to the bath in whole-cell patch-clamp experiments or to the pipette in single channel experiments (Desai et al., 2000). (An additional site on the intracellular face cannot be formally excluded yet.) Rare PESAC channel events of unchanged conductance seen with 200 μM furosemide in the pipette suggest that blockade occurs via an allosteric effect on channel gating rather than a direct pore-blocking effect (Hille, 2001).

We have chosen to refer to the voltage-dependent anion channel identified in our previous patch-clamp study as the plasmodial erythrocyte surface anion channel, or PESAC. This nomenclature is needed to distinguish this voltage-dependent channel from other transport mechanisms that might be induced in the RBC membrane by the parasite. Although PESAC remains the only anion channel we have seen on infected RBCs, other reports (Huber et al., 2002) and (Egee et al., 2002) suggest that there may be at least two other anion channels with properties distinct from those of PESAC. Some workers have used “new permeation pathway” or NPP to describe these parasite-induced permeability changes. This may have been adequate when the mechanism and location of the pathway were not precisely known, as well discussed (Kirk et al., 1994). Now, however, with single ion channel measurements of PESAC on the RBC membrane along with concordance of its selectivity, pharmacology, and rate with radioisotope and hemolysis measurements, a more descriptive name is warranted.