Slow Deactivation and U-Shaped Inactivation Properties in Cloned Ca_v1.2b Channels in Chinese Hamster Ovary Cells

Abstract

Whole-cell patch-clamp techniques were applied to Chinese hamster ovary cells stably expressing cloned smooth muscle Ca²⁺ channel α₁-subunits. In the presence of Ba²⁺ as a charge carrier, U-shaped inactivation was observed in the presence and absence of Ca²⁺ agonists. Also, tail currents deactivated slowly when conditioning steps of positive potential were applied. The deactivation time constant was decreased by hyperpolarizing the repolarization step. Application of ATP-γ-S or H-7 had little effect on the conditions necessary to induce slow tail, suggesting involvement of physical processes in the channel protein. In the presence of Bay K 8644, additional application of nifedipine decreased the amplitudes of the test and tail currents induced by a test step preceded by a conditioning step to +80 mV, but did not affect the decay time constant of the tail current. From these results and assumptions we have drawn up a kinetic scheme with one closed state, two open states (O₁, O₂) and two inactivated states linked to the closed state and open state O₁, respectively, i.e., open state O₂ protected from inactivation. Computer calculation reconstructed slow deactivation and U-shaped inactivation properties. A similar kinetic scheme with Ca²⁺-agonist-binding states accounted for the results in the presence of Ca²⁺ agonists.

INTRODUCTION

Voltage-sensitive Ca²⁺ channels are found in numerous excitable cells, contributing to the diverse functions of these tissues. It is known that some smooth muscles possess both low- and high-voltage-activated (HVA) Ca²⁺ channel currents, and that the HVA current component is predominant in all smooth muscles. The fact that nanomolar concentrations of dihydropyridine (DHP) Ca²⁺ antagonists block the HVA Ca²⁺ current in smooth muscles from numerous tissues and organs suggests that L-type Ca²⁺ channels play a central role. Mechanisms and factors modulating L-type Ca²⁺ channels are thus considered to play a critical role in controlling smooth muscle functions (Klöckner, 1996; Nakayama et al., 1996; Watanabe et al., 1996; Beech and McHugh, 1996).

In native smooth muscle cells, we have previously examined the properties of the L-type Ca²⁺ channel current using whole-cell recording (Nakayama and Brading, 1993a;b), and have shown that the degree of inactivation is consistently decreased by increasing the positivity of the conditioning potential to >+20 mV; the amplitude of test current was fully restored at around +80 to +100 mV (U-shaped inactivation), even though it was often necessary to use long duration conditioning step (5 s) to achieve steady state. Additionally, the restoration of test current amplitude was always accompanied by development of a slowly deactivating tail current upon repolarization from the test step. To explain the effects of highly positive conditioning steps on inactivation and deactivation, we have proposed a voltage-dependent conversion of the Ca²⁺ channel conformation from the normal open (O₁) to a second open state (O₂) in which Ca²⁺ channels do not, or only very slowly, inactivate during depolarization, and deactivate slowly upon repolarization. Further experiments with DHP Ca²⁺ agonists have suggested that the conversion of the Ca²⁺ channel conformation from O₁ to O₂ is distinct from the long channel opening mode (so-called mode 2 gating) induced by Ca²⁺ channel agonists, and that these two mechanisms operate separately. As a result, a combination of DHP Ca²⁺ channel agonists and depolarization produces at least four open states in native smooth muscle Ca²⁺ channels (Nakayama and Brading, 1995a).

Recently, evidence for depolarization-induced multiple open states has also been presented for L-type Ca²⁺ channels of other excitable cells, e.g., neurones (Kammermeier and Jones, 1998; Hivert et al., 1999), skeletal muscle (Fleig et al., 1996), and endocrine cells (Fass and Levitan, 1996). The amino acid structure of voltage-sensitive Na⁺ channels resembles that of Ca²⁺ channels. Interestingly, some time ago, the presence of a second open state resistant to inactivation was proposed in voltage-clamped squid axons, although alteration of the tail current deactivation time course was not observed (Chandler and Meves, 1970). Inasmuch as smooth muscle Ca²⁺ channels are resistant to voltage-dependent inactivation when preconditioned at +80 to +100 mV, these Ca²⁺ channels may be a good model to investigate the second open state.

In our latest study, using the cell-attached patch-clamp technique, to study Ca²⁺ channels formed from expression in Chinese hamster ovary (CHO ) cells of the smooth muscle α₁-subunit (Ca_v1.2b), we have shown the presence of a second open state, by comparing the deactivation time constant of summed unitary currents with and without conditioning at positive potentials (e.g., +80 mV for 4 s) (Nakayama et al., 2000). However, Ca²⁺ channels run down in this mode of the patch-clamp technique, and because it was only possible to record a few current traces from the same membrane patch, when conditioning steps of highly positive potentials were applied, it was necessary to accumulate current traces over many cells. Due to the limitation of this recording technique, it was difficult to address systematically whether multiple open states account for the characteristic deactivation and inactivation properties, i.e., to determine the correlation between slow deactivation and restoration from inactivation after conditioning by positive potentials, which will predict the voltage-dependent conversion of the (α₁-subunit) Ca²⁺ channel conformation from O₁ to O₂.

In the present study we carried out whole-cell patch-clamp experiments in CHO cells stably expressing Ca_v1.2b to address this issue more thoroughly. The whole-cell technique is more reliable and allows changes in Ca²⁺ current kinetics induced by numerous treatments to be compared in the same cell. We also examined whether voltage-dependent conversion of the Ca²⁺ channel open state occurs in the presence of DHP agonists, and how DHP antagonists affect the characteristic properties of inactivation and deactivation seen after highly positive conditioning steps. Such experiments are necessary to elucidate the relationship between the voltage-dependent second open state and mode gating. Further, we reconstructed the slow deactivation and U-shaped inactivation properties seen in cloned smooth muscle Ca²⁺ channels using computer calculation with multiple open state models.

METHODS

Cell preparation

CHO cells stably expressing cloned smooth muscle α₁-subunits (Ca_v1.2b: formerly referred to as α_1C-b) (CHOCa9: Bosse et al., 1992; Welling et al., 1993) were cultured in Dulbecco's modified Eagle's medium supplemented with 10% dialyzed fetal bovine serum, nonessential amino acids, streptomycin (30 μg/ml), and penicillin (30 units/ml). Cell passage was done before 80–90% confluence. For electrical recordings, the CHO cells were plated onto 22 mm coverslips, and were used upon 30–50% confluence.

Electrical recording

A standard patch-clamp technique (Hamill et al., 1981) was used to record macroscopic Ca²⁺ channel currents. A patch-clamp amplifier (Axopatch 200A, Axon, Foster City, CA) was operated through an AD/DA converter (TL-1, Axon). The measurements were carried out at room temperature (22–26°C). Ba²⁺ (10 mM) was used as a charge carrier. A cutoff frequency of 5 kHz was applied. The sampling interval was normally set to be 0.5 ms. In the experiments shown in Fig. 3 A (inset), the sampling interval was reduced to 0.1 ms. The pipette resistance was in the region of 5 MΩ, when a Cs⁺-rich pipette solution was used. Before establishment of the seal, the reference potential was set to be the zero current potential. Unless otherwise stated, the voltage of the cell membrane was clamped at −60 mV (holding potential). Capacitive transients were compensated electrically. Normally CHOCa9 cells tested had a membrane capacitance of 10–25 pF, and the series resistance was <15 MΩ after applying series resistance compensation by 20–50%. The time to clamped voltage was thus <0.3 ms. Also, as shown in Fig. 7, A and C, application of nifedipine reduced the amplitude of the tail current without significant change in the time to half decay (T_1/2), indicating that the voltage error was not significant. Deactivation of the tail current induced by simple rectangular pulse in normal bathing solution was, however, too fast to adequately analyze in the present experiments. (We dealt with this condition as a no slow tail current condition.) We thus compared decay time courses of more slowly deactivating tail currents (Fig. 3 B) induced by either or simultaneous application of the following two treatments: 1), conditioning at +80 mV; and 2), exposure to Bay K 8644.

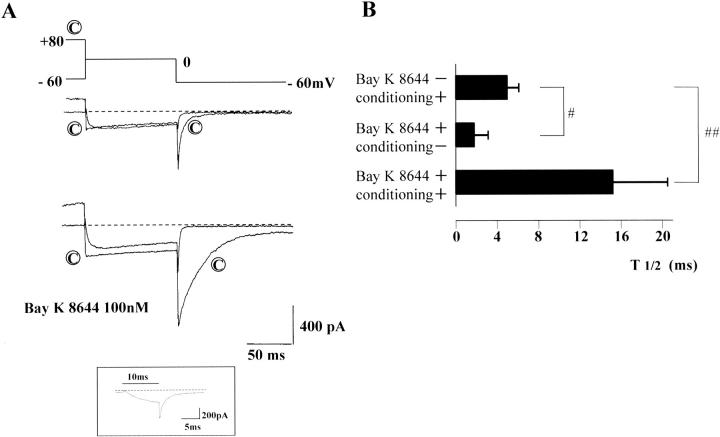
FIGURE 3.

Conditioned and unconditioned tail currents. In A, a pair of conditioned and unconditioned depolarizations were applied in the absence (upper) and presence of Bay K 8644 (100 nM) (lower current traces). The current traces indicated by © were preceded by a conditioning depolarization of +80 mV (4 sec). Only the last 25 ms are shown. Dotted lines indicate zero current level. (Series resistance ∼8 MΩ) Irrespective of the presence of Bay K 8644, the conditioning depolarization significantly slowed deactivation of the Ca²⁺ channel current upon repolarization to −60 mV. Because of fast deactivation, the sampling interval was shortened to 100 μs to precisely record the deactivation time course of the tail current without conditioning depolarization in the presence of Bay K 8644. The inset shows a representative current trace of such recordings (0 mV, 10 ms). T_1/2 of the tail current is summarized in B. The data are expressed by mean ± SD (n = 6). Single (#) or double sharps (##) indicate statistically significant differences of P < 0.05 or < 0.01, respectively (ANOVA).

FIGURE 7.

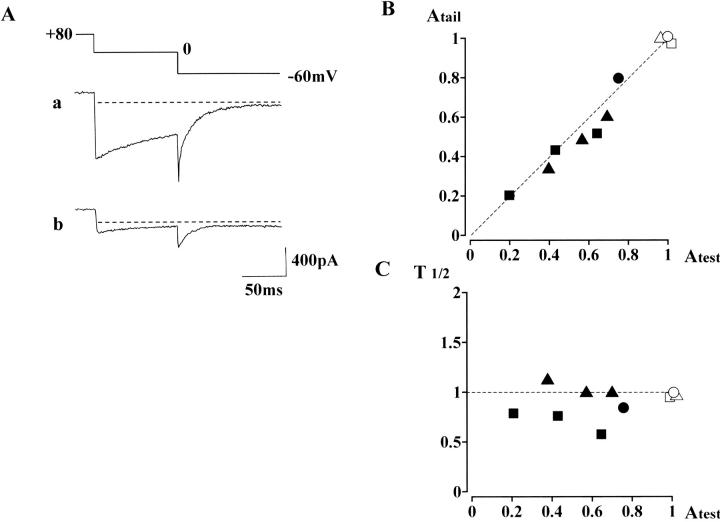
Inhibitory effects of nifedipine on the inward current evoked after large conditioning depolarization in the presence of Bay K 8644. In the presence of the Ca²⁺ agonist, a preconditioning depolarization (first step: +80 mV, 4 s; second step: 0 mV, 100 ms) was repeated at 60-s intervals. Subsequently, nifedipine was added to the extracellular solution. (A) A control current trace obtained in the presence of 100 nM Bay K 8644 is shown in a, whereas the current trace (b) is obtained 3 min after application of 1 μM nifedipine. (Series resistance, ∼8 MΩ) (B) Correlation between the peak amplitude of the tail current (−60 mV) and the current amplitude at the end of the 0 mV step. The current amplitudes were normalized by each control inward current obtained in the presence of only Bay K 8644. Open symbols correspond to the control data, whereas filled symbols are data obtained in the additional presence of nifedipine. Triangles are the data obtained in the cell shown in A. (The data obtained 1 and 2 min after addition of 1 μM nifedipine are also plotted.) Three filled squares represent the data obtained from another cell in which 1 μM nifedipine was added for 3 min in the presence of 100 nM Bay K 8644; i.e., three current traces were obtained. The filled circle represents a current trace obtained 2 min after addition of 100 nM nifedipine in the presence of 100 nM Bay K 8644. The dotted line in B has a correlation coefficient = 1. In C, the half decay time of the tail current, relative to that of the control value, is plotted against the peak amplitude of the tail current. The dotted line corresponds to the initial time to half decay (T_1/2).

Data analysis and statistics

Activation

The peak amplitude of the inward Ba²⁺ current (I_peak(E)) evoked by rectangular pulse (unconditioned depolarization step) was plotted against the voltage of the pulse (Fig. 1 B). Each data point was corrected by assuming the leak current to follow Ohm's law with zero current at 0 mV (Fig. 1 B). We used cells with the leak current at −60 mV < 10% of the maximal Ca²⁺ channel current (4% in average). The current traces are shown without leak subtraction (Fig. 1 A). The following equations were used to fit the current-voltage relationship:

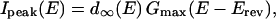(1a)

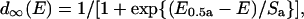(1b)

where G_max and E_rev are the maximum conductance and reversal potential of the Ca²⁺ channel (Ba²⁺) current. d_∞(E) indicates voltage dependence of the degree of activation based on the Boltzmann distribution, where E_0.5a is the half-maximal activation potential, and S_a is the slope factor for activation.

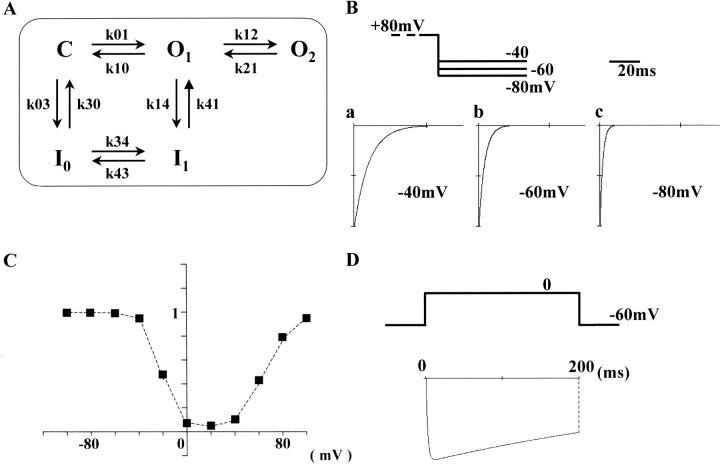
FIGURE 1.

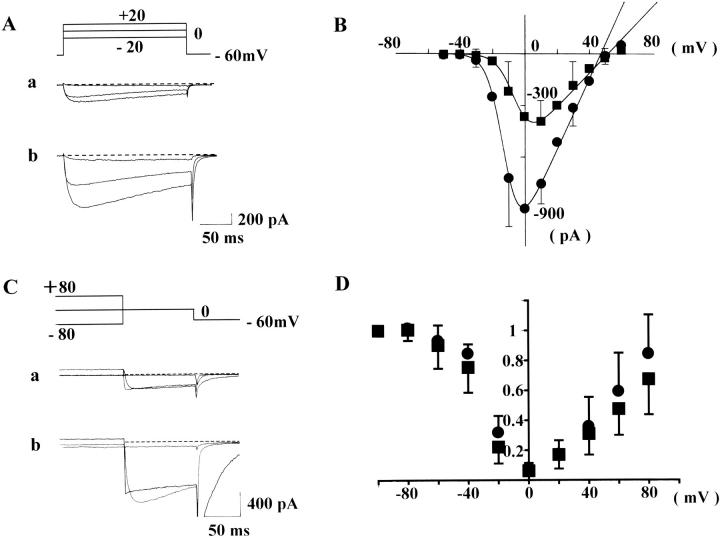
Activation curves (A and B). In the absence (current traces A a and squares in B) and presence of Bay K 8644 (100 nM) (current traces in A b and circles in B), rectangular pulses of various voltages (from −50 to +60 mV, 10-mV steps, 200-ms in duration)) were applied from the holding potential of −60 mV at 30-s intervals. In A, representative current traces, obtained from step pulses of −20, 0, and +20 mV are shown. The series resistance was ∼6–10 MΩ after series resistance compensation by 30–40%. Dotted lines indicate zero current level. In B, the peak amplitude of Ca²⁺ channel current is plotted against the rectangular pulse potential. Each current amplitude was linearly corrected by assuming the current recorded at −60 mV was only due to leak current. Each symbol in B indicates the mean value obtained from six cells. For clarity, the SD of means is only shown for some of the data points. The data points were fitted with Eqs. 1a and 1b defined in Methods. Fitting parameters are listed in Table 1. Inactivation curves (C and D). In the absence (current traces C a and squares in D) and presence of Bay K 8644 (100 nM) (current traces in C b and circles in D), a test step (0 mV, 100 ms) preceded by conditioning potentials of a wide range (between −100 and +80 mV, 20-mV steps, 4-s in duration) was applied at 60-s intervals. In C, representative test currents, obtained after preconditioning, depolarizations of −80, 0, and +80 mV are shown. Only the last 90 ms of conditioning step is shown. In D, the amplitude of test current relative to that conditioned by −100 mV is plotted against conditioning potentials. Each data point represents the mean value obtained from eight cells. Vertical bars, SD.

Decay time constant of the tail current

The discrete data points in some of the tail currents recorded (I(t)) were iteratively fitted with single (N = 1) or multiple (N ≥ 2) exponential terms:

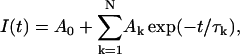(2)

using a modified simplex program (Nakayama and Brading, 1993a). (A and τ represent amplitude and time constant of an exponential term.) The total residual currents were used as a criterion for the convergence. This program was also used in curve fittings for activation and inactivation curves.

In the cells used in Fig. 3, we analyzed the deactivation time course of the tail current by fitting with single or two exponential terms described above. In the absence of Ca²⁺ agonist, deactivation at −60 mV without conditioning large depolarization was too fast to adequately analyze. Tail currents recorded after conditioning large depolarization in the absence of Bay K 8644 and without conditioning depolarization in the presence of Bay K 8644 were fitted well with a single exponential function, whereas tail currents recorded after large conditioning depolarization in the presence of Bay K 8644 were generally fitted well with two exponential terms. Using the SAS System software package (SAS Institute, Cary, NC), we confirmed the statistical significance (P < 0.05) of the additional two parameters (A₂ and τ₂) in the equation with two exponential terms. Because the number of exponential terms adequately fitting the deactivation time course was different under numerous conditions, in most experiments we simply used the time to half decay (T_1/2) to compare deactivation time courses.

The numerical data were expressed as mean ± SD. Differences between means were evaluated by paired t-tests or analysis of variance (ANOVA). P < 0.05 was normally taken as a statistically significant difference.

Computer modeling

Simulation of slow deactivating tail currents was performed using Mathcad 2000 (Mathsoft, Cambridge, MA). Numerical solutions of simultaneous differential equations were obtained using a Runge-Kutta procedure. We assessed a kinetic scheme in which one closed and two open states (C-O₁-O₂) are sequentially linked and the C and O₁ states have their corresponding inactivated states (I₀ and I₁). In this model, the transition rates between C and O₁ states were chosen to meet the activation curve (d_∞(E)) obtained by the method described above:

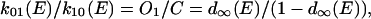(3)

where k₀₁(E) and k₁₀(E) are transition rates from C to O₁ and from O₁ to C, respectively, at E mV. On the other hand, the recovery from inactivation seen at conditioning potentials more positive than +20 mV was assumed to reflect the voltage dependence of transition between O₁ and O₂ states, i.e., the O₂ state was assumed to be noninactivating open state (Nakayama and Brading, 1995b). The transitions between C and I₀, and O₁ and I₁, were assumed to be voltage-independent, and that their equilibria were in different directions (favoring C over I₀, but O₁ over I₁).

We also drew a similar kinetic scheme with five states of channel conformation (C^*, O₁^*, O₂^*, I₀^*, and I₁^*) for the case of Ca²⁺ agonists. Asterisks indicate channel states with Ca²⁺ agonist bound.

Drugs and solutions

The composition of the normal pipette solution was (mM): CsCl, 141; MgCl₂, 1.4; EGTA N, N, N′, N′-tetraacetic acid), 2; ATP, 1; GTP, 0.1; TEA (tetraethylammonium), 7; and Hepes/Tris, 10 (pH 7.2). In some experiments examining possible involvement of phosphorylation process, ATP-γ-S (adenosine 5′-O-(3-thiotriphosphate)) was used instead of ATP. The extracellular solution used for whole-cell patch-clamp recordings had the following composition (mM): NaCl, 114; KCl, 5.9; BaCl₂, 10; MgCl₂, 1.2; glucose, 11.8; and Hepes, 11.8; pH was adjusted to 7.4 with Tris base. In some experiments, when 30 mM Ba²⁺ or 2.5 mM Ca²⁺ were used as charge carriers, the ionic composition was modified by isoosmotic substitution with Na⁺.

Bay K 8644 (±) and nifedipine were purchased from Calbiochem (San Diego, CA) and Sigma (St Louis, MO). Their stock solutions (dissolved in ethanol) were kept cool and protected from lights. ATP-γ-S and H-7 (1-(5-isoquinolinesulfonyl)-2-methylpiperazine dihydrochloride) were from Sigma; ATP (disodium salt) and GTP (trisodium salt) from Seikagaku (Tokyo, Japan); Dulbecco's modified Eagle's medium and other reagents for cell culture from Life Technologies (Tokyo, Japan).

RESULTS

Activation and inactivation properties

In the presence of 10 mM Ba²⁺ as a charge carrier, whole-cell Ca²⁺ channel currents were recorded from CHOCa9 cells, stably expressing the α₁-subunit of smooth muscle Ca channel Ca_v1.2 b. After disruption of the plasma membrane, a holding potential of −60 mV was applied.

In the absence or presence of Bay K 8644 (100 nM), a DHP Ca²⁺ agonist, rectangular pulses of various potentials (−50 to +60 mV) were applied to CHOCa9 cells to obtain activation parameters. Fig. 1 A shows representative current traces obtained from such experiments. In Fig. 1 B, the amplitude of the peak inward current was plotted against the membrane potential (n = 6 for each experiment). The instantaneous current-voltage (I-V) relationship was fitted with a Boltzmann equation (Eq.1 a) and linear maximum available Ca²⁺ channel (Ba²⁺) current (Eq. 1 b). All fitting parameters are listed in Table 1. This curve fitting revealed that Bay K 8644 1), increased the maximum conductance (G_max) (from 9.8 to 20.5 pA/pF), and 2), shifted the half-maximal activation potential (E_0.5a) toward hyperpolarization (from −5.6 to −12.4 mV). These effects of Bay K 8644 agree well with those seen in native smooth muscle Ca²⁺ channels (e.g., Nakayama and Brading, 1995a).

TABLE 1.

Fitting parameters for the instantaneous I-V relationship shown in Fig. 1 B (activation kinetics)

	E0.5a (mV)	Sa (mV)	Gmax (pA/mV)	Erev (mV)
Control	−5.6	5.4	9.8	51.4
+ Bay K 8644(100 nM)	−12.4	5.0	20.5	47.0

Inactivation properties were examined over a wide range of conditioning potential (between −100 and +80 mV), because this protocol had been useful to demonstrate characteristic features of Ca²⁺ channel inactivation in native smooth muscle (Nakayama and Brading, 1993b). After applying the conditioning potential for 4 s, the degree of inactivation was estimated by measuring the peak inward current after stepping directly to a test potential of 0 mV (100 ms). Fig. 1 C shows representative current traces obtained (a) in the absence or (b) in the presence of Bay K 8644. (Only the current traces obtained after conditioning potentials of +80, 0 and −80 mV are shown.) In Fig. 1 D, the relative amplitude of the peak inward current in the test step (I/I₋₁₀₀) was plotted against the conditioning potential (eight each for with or without Bay K 8644). The inactivation curves obtained from all cells were clearly U-shaped, whether Bay K 8644 was applied or not. This inactivation property also agrees well with that observed in native smooth muscles (Nakayama and Brading, 1993b; 1995a), suggesting that the α₁-subunit of smooth muscle preserves the U-shaped inactivation property. To minimize effects of the preceding voltage sequence in this inactivation experiment, the conditioning potential was applied in the following order: −60, +80, −80, −100, +60, −40, +40, +20, −20, and 0 mV. Preliminary inactivation experiments in which the conditioning potential was increased from −100 to +80 mV (by 20 mV steps) (n = 2), or decreased by the reversed order (n = 2), however, also produced U-shaped inactivation.

Two mechanisms are known to inactivate L-type Ca²⁺ channels, i.e., voltage-dependent and Ca²⁺-dependent inactivation. In the present study we mainly used 10 mM Ba²⁺ as a charge carrier to minimize the latter inactivation mechanism. However, it has been reported that Ba²⁺ also has a small inactivating effect (e.g., Markwardt and Nilius, 1988; Ferreira et al., 1997; Noceti et al., 1998). As shown in Fig. 1 B, the amplitude of current through the Ca²⁺ channels was maximal at around 0 mV, at which potential the degree of inactivation was also maximal. One would suspect that the divalent cation-dependent inactivation mechanism, despite the smaller effect with Ba²⁺ as a charge carrier, might be a primary cause in generating the U-shaped inactivation. To assess this possible contribution of divalent cation-dependent inactivation, we further examined inactivation of the current through the cloned Ca²⁺ channels in the presence of 2.5 mM Ca²⁺ or 30 mM Ba²⁺ (in 100 nM Bay K8644-containing solutions). (The current density of test inward current evoked by step depolarization to 0 mV (100 ms duration) was 9.0 ± 7.6, 41.0 ± 15.6, and 67.5 ± 17.3 pA/pF in the presence of 2.5 mM Ca²⁺, 10 mM Ba²⁺, and 30 mM Ba²⁺. For Ca²⁺ current recording, we used CHOCa9 cells showing particularly large inward currents.) Inactivation was produced by a conditioning step (4 s) to various potentials, and assessed by measuring the inward current induced by the following test depolarization to 0 mV (100 ms), and expressing it relative to the inward current evoked by the test potential after a conditioning step to −100 mV. In the presence of 2.5 mM Ca²⁺, the relative amplitudes of test current conditioned by 0 and +80 mV (I₀/I₋₁₀₀ and I₊₈₀/I₋₁₀₀) were 0.03 ± 0.02 and 0.67 ± 0.17 (n = 4), respectively, whereas they were 0.10 ± 0.06 and 0.79 ± 0.32 in the presence of 30 mM Ba²⁺ (n = 9). (0.08 ± 0.03 and 0.84 ± 0.26 in 10 mM Ba²⁺(n = 8)) The degree of inactivation at 0 mV was statistically significantly different between in the presence of 2.5 mM Ca²⁺ and 10 mM Ba²⁺, but did not differ between 10 mM and 30 mM Ba²⁺ (ANOVA, P < 0.05). These results suggested that ion-dependent inactivation did not largely contribute to U-shaped inactivation property seen in the presence of Ba²⁺, but there was some contribution when Ca²⁺ was used as a charge carrier.

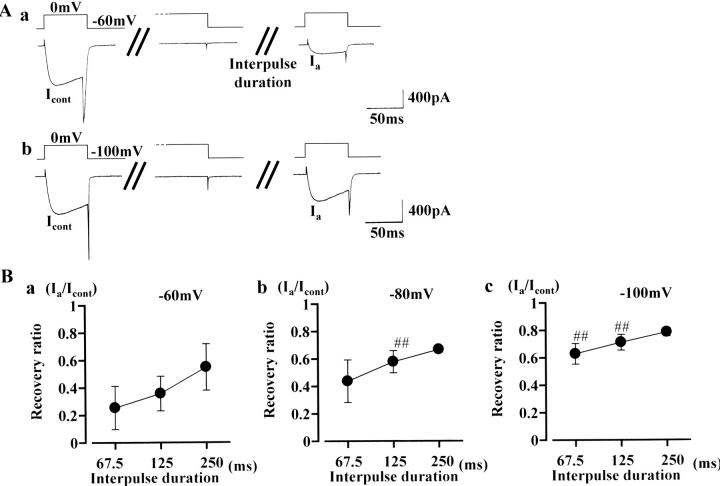
The experiments shown in Fig. 2 were designed to assess what mechanism, i.e., voltage- or Ca²⁺-dependent processes, underlies recovery of the inactivated Ca²⁺ channel current. After observing a control current (at 0 mV test step, in the presence of 10 mM Ba²⁺ and 100 nM Bay K 8644), a conditioning step to 0 mV (4 s) was applied. Subsequently, the same test step depolarization to 0 mV was applied after three different interpulse durations (Fig. 2 Aa shows the result with a 125 ms of interpulse duration). After 62.5, 125, or 250 ms interpulse duration was applied, the amplitude of the test current was restored to 25.4 ± 15.8%, 35.7 ± 12.6%, and 54.9 ± 16.9%, respectively (Fig. 2 Ba). The rate of recovery was much faster compared to a diffusion time constant calculated for Ba²⁺ (several tens of seconds, estimated using formulae described by Pusch and Neher, 1988), suggesting that a voltage-dependent inactivation process is the predominant mechanism to form the U-shaped inactivation curve (but that inactivation caused by an increase in bulk intracellular Ba²⁺ concentration is minor). In Fig. 2 Ab, recovery of Ca²⁺ channel current was measured after −100 mV interpulse potential (125 ms duration). The graphs in Fig. 2, Bb and Bc, summarize recovery with interpulse potentials of −80 and −100 mV, respectively. The rate of recovery was significantly accelerated by hyperpolarizing the interpulse potential.

FIGURE 2.

Recovery time course from inactivation caused by a conditioning depolarization at 0 mV. After observing a control test current (at 0 mV), the cell membrane was clamped at 0 mV for 4 s. Subsequently, the same test step was again applied after an interpulse duration of 62.5, 125, or 250 ms. Representative current traces (with an interpulse duration of 125 ms) are shown in A. The interpulse potential used was −60 mV in a and −100 mV in b. In B, each point represents the mean value of time-dependent recovery (n = 13): recovery is expressed as percentage of the control current amplitude recorded before the conditioning depolarization to 0 mV (4 s). Bars, SD. The interpulse potential was −60 mV in a, −80 mV in b, and −100 mV in c. Double sharps (##) indicate data points that differ significantly from those in a (ANOVA, P < 0.01).

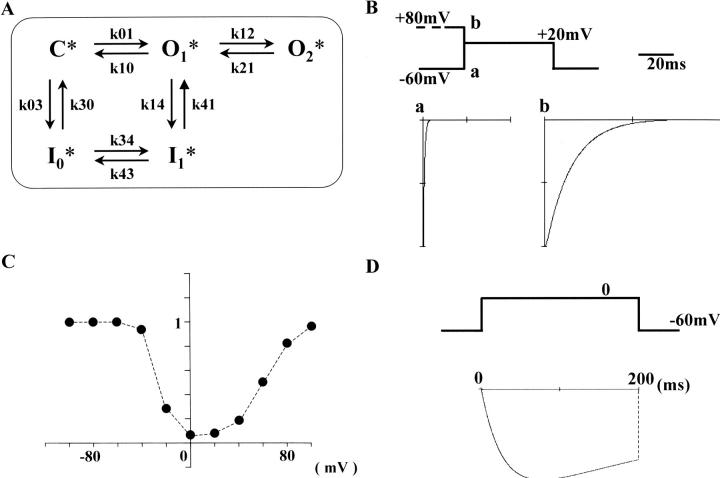
Slowly deactivating tail currents induced by conditioning depolarization and Ca²⁺ agonist

To clearly indicate how preceding positive conditioning steps alter Ca²⁺ channel kinetics, whole-cell currents obtained by a paired pulse protocol were superimposed in Fig. 3. Ca²⁺ channel currents seen after a positive conditioning step to +80 mV were labeled with ©. In the absence of Ca²⁺ agonist (upper traces in A), 100-ms test depolarizations to 0 mV (without a conditioning step) evoked inward currents, but inward tail currents deactivated rapidly upon subsequent repolarization to the holding potential (at −60 mV). When the cell membrane was conditioned at +80 mV for 4 s before the test step, slowly deactivating tail currents were observed upon repolarization to −60 mV. In the presence of Bay K 8644 (100 nM), the same paired pulse protocol was applied (lower traces in A). The simple step depolarization to 0 mV evoked inward currents, and slow tail currents were observed upon repolarization. The decay time course of this tail current was faster than that recorded after the positive conditioning step in the absence of Ca²⁺ agonist. In the presence of Bay K 8644, addition of the positive conditioning step (+80 mV, 4 s) increased the amplitude and further slowed the decay time course of the tail currents. Either in the absence or presence of Bay K 8644, inward currents of sizeable amplitude were recorded in the test step to 0 mV, being consistent with the U-shaped inactivation property shown in Fig. 1, C and D. It is also noteworthy that the induction of the slow tail current was reversible: i.e., when test depolarizations to 0 mV with or without a prior (conditioning) step at +80 mV were applied alternately, a slow tail current was observed only after the conditioning step.

The time to half decay (T_1/2) of the slow tail currents induced by either a conditioning step to +80 mV or Ca²⁺ agonist, or a combination of both is summarized in Fig. 3 B. T_1/2 values of the three slow tail currents were statistically significantly different from each other. When the conditioning step to +80 mV was applied in the presence of Bay K 8644, the tail currents were generally fitted well with two exponential terms. However, because a single exponential function was applicable to the tail currents in the absence of Ca²⁺ agonist, we used T_1/2 to roughly compare the deactivation time courses of the three types of tail currents.

In our previous studies we have proposed that the conformation of native Ca²⁺ channels in smooth muscle can be changed from normal (O₁) to a second open state (O₂) by large depolarizations in a voltage-dependent manner (Nakayama and Brading, 1993a), and that similar conversion of the channel conformation in the presence of Ca²⁺ agonist provides two more open states (Nakayama and Brading, 1995a): O₁^* and O₂^* (Asterisks indicate channel states with Ca²⁺ agonist bound). Because of the transition from the second to normal open state (from O₂ to O₁, or from O₂^* to O₁^*), Ca²⁺ channel current would deactivate more slowly after positive conditioning steps. This has been seen in the present study. Therefore, in Ca_v1.2b, the slow tail currents induced by conditioning at +80 mV are considered to correspond to the second open states (O₂ and O₂^*). Furthermore, test inward currents of sizeable amplitude were observed after positive conditioning steps (Fig. 1, C and D, and Fig. 3 A), and the duration of the conditioning step (4 s) can be adjusted to induce a steady state. These facts lead to the deduction of an additional hypothesis that the second open states are resistant to voltage-dependent inactivation (i.e., there is no corresponding inactivation state for the second open state in the models shown in Fig. 8 and Fig. 9). As shown later in Fig. 5, when conditioning potentials more positive than +20 mV was applied, the amplitudes of the test and tail inward currents increased in the same manner, supporting this hypothesis.

FIGURE 8.

Computer modeling of Ca²⁺ current deactivation and inactivation in the absence of Ca²⁺ agonist. The kinetic scheme used is shown in A. One closed (C) and two open states (O₁ and O₂) are sequentially linked. Only the C and O₁ states have their corresponding inactivated states, I₀ and I₁. The k_(s) represent the rate constants of transition (listed in Table 2). In B, simultaneous differential equations based on the scheme A were numerically solved to draw the deactivation time courses seen in the repolarization step at −40 (a), −60 (b), and −80 mV (c) after conditioning depolarization that can convert the conformation of all Ca²⁺ channels into O₂. To compare deactivation time courses at the three repolarizing potentials, the amplitude of the tail current was expressed relative to that at t = 0. In C, the voltage dependence of steady-state inactivation was calculated as the ratio of channel number in the C, O₁, and O₂ states to the total channel number after conditioning depolarization for 4 s (from −100 to +100 mV). The drawing in D is a computer calculation for Ca²⁺ channel current evoked by a step depolarization to 0 mV.

FIGURE 9.

Computer modeling of Ca²⁺ current deactivation and inactivation in the presence of Ca²⁺ agonist. The kinetic scheme is shown in A. This scheme is an analog to that used in the absence of Ca²⁺ agonists. The asterisks indicate channel states with Ca²⁺ agonist bound. The transition rate constants are listed in Table 3. In B, computer simulations of tail current decay time courses with (b) or without (a) preconditioning depolarization, which induces conversion of Ca²⁺ channel conformation from O₁^* to O₂^*. The voltage dependence of inactivation (C) and Ca²⁺ channel current evoked by depolarization to 0 mV was obtained by the same procedures used in Fig. 8, C and D.

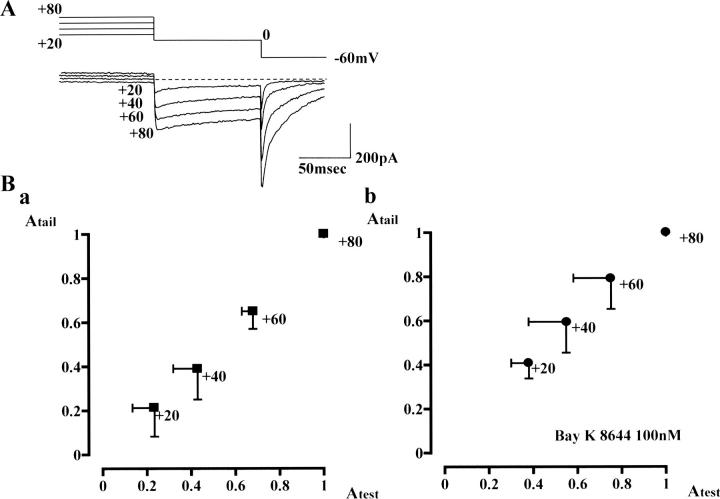
FIGURE 5.

Recovery of test current accompanied by development of slow deactivating tail current. A test step (0 mV, 100 ms) was preceded by conditioning potentials of +20, +40, +60, and +80 mV (4-s duration). Representative current traces (obtained in the absence of Ca²⁺ agonist) are shown in A. Correlation between the peak amplitude of tail current (y axis) and the current amplitude at the end of the test step (x axis) is plotted in B. The individual data points were normalized by the amplitudes of tail and test currents obtained by conditioning at +80 mV. Each data point represents the mean value obtained in the absence (n = 8) or presence of 100 nM Bay K 8644 (n = 8). Vertical and horizontal bars, SD.

Voltage dependence of deactivation time course

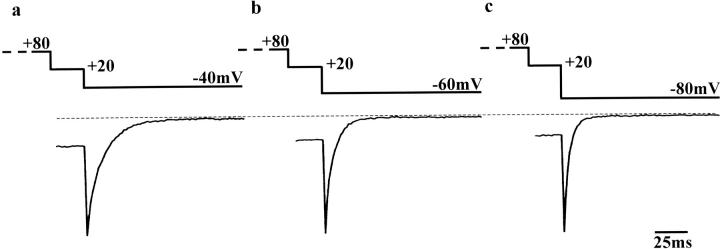
Provided that the conversion of Ca²⁺ channel conformation between normal (O₁ and O₁^*) and the second open states (O₂ and O₂^*) is a voltage-dependent process, the deactivation time constant would be affected by the voltage of the repolarization step. We thus examined the effect of changing the repolarization potential from −40 to −80 mV (Fig. 4; no Ca²⁺ agonist included in the bathing solution). A conditioning step to +80 mV (4 s) was applied before the test step (+20 mV). To record large tail currents, the duration of the test step was reduced to 25 ms. (From the model presented in the Discussion, it is considered that the number of Ca²⁺ channels in the second open state would decrease during the test step, and consequently the amplitude of slow tail current would be reduced upon repolarization.) The amplitude of the tail current increased by 27.3 ± 7.1% at −60 mV and by 47.7 ± 22.6% at −80 mV relative to that at −40 mV. In Fig. 4, the decay time courses are compared by separately expanding the tail currents recorded at −40 (a), −60 (b), and −80 mV (c). Also, the tail currents were normalized by each peak amplitude. The deactivation rate of the tail current was clearly accelerated by increasing the negativity of the repolarization potential. The T_1/2 at −40, −60, and −80 mV were 6.5 ± 0.5, 4.1 ± 1.2, and 2.0 ± 0.5 ms (n = 5), respectively. This tendency is essentially similar to previous results obtained from native smooth muscle (e.g., Fig. 9, in Nakayama and Brading, 1993a). In the presence of 100 nM Bay K 8644, the same protocol was also applied. The decay time course at each repolarization potential (from −40 to −80 mV) was slower in the presence of Bay K 8644, but as seen in the absence of Bay K 8644, deactivation was faster at more negative repolarization steps.

FIGURE 4.

Slowly deactivating tail currents obtained by changing the voltage of the repolarization step in the absence of Ca²⁺ agonist. The test step to +20 mV (25 ms) was preceded by a 4-s conditioning step to +80 mV. (Only the last 25 ms of the conditioning step are shown.) Subsequently, the cell membrane was repolarized to −40 (a), −60 (b), or −80 mV (c). (Series resistance ∼6 MΩ). To compare the deactivation time course, the tail currents were normalized by each peak amplitude. During experiments, Ca²⁺ channel current had small rundown. However, this does not affect the analysis in the normalized tail currents.

Slowly deactivating tail currents are attributable to Ca_v1.2b Ca²⁺ channels

Voltage-sensitive inward currents in nonexcitable cells, such as CHO cells, are in theory attributable to ion channels incorporated with expression vectors. The present study is based on this assumption. In this section, we describe evidence supporting the assumption that Ca_v1.2b Ca²⁺ channels are responsible for the voltage-sensitive inward currents. First of all, no slow tail currents like those in Fig. 1 C were observed when we applied largely positive conditioning steps in CHO cells without incorporated Ca²⁺ channels (data not shown).

Second, recovery of the test current at conditioning potentials more positive than +20 mV was accompanied by gradual development of slow tail current. Current traces shown in Fig. 5 A are representative test and tail currents recorded after conditioning at +20 to +80 mV (for 4 s, in the absence of Bay K 8644). These currents were recorded in one of the experiments shown in Fig. 1 D (squares). Irrespective of the presence of Ca²⁺ agonist, the peak amplitude of tail current (y axis) and the current amplitude at the end of the test step (x axis) were well correlated (Fig. 5 B). This result strongly suggests that the second open state induced by relatively large depolarization possesses two characteristic features: 1), resistance to inactivation, and 2), slow deactivation upon repolarization.

Third, we obtained pharmacological evidence with nifedipine, a DHP Ca²⁺ antagonist. In CHO cells, stably expressing Ca_v1.2b (CHOCa9), test depolarizations (0 mV, 100 ms) conditioned with a positive potential (+80 mV, 4 s) were repeated. Application of nifedipine (0.1–1 μM) decreased the amplitudes of test and tail currents in the same manner. Essentially similar results were obtained even in the presence of Bay K 8644. (This experiment was conducted mainly to examine the interaction of Ca²⁺ agonists and antagonists, and will be shown later in Fig. 7.)

L-type Ca²⁺ channels are known to run down during channel current recordings (Kameyama et al., 1988; Hao et al., 1999; Kepplinger et al., 2000). The run-down phenomenon seen in CHOCa9 cells also supported that Ca_v1.2b was responsible for the slow tail currents. In all current recordings of the present study with stable seal resistance, after rupture of the cell membrane, the amplitudes of the test current and subsequent tail current observed after positive conditioning steps gradually decreased by similar degrees (∼1–2%/min). This was true irrespective of the presence of Ca²⁺ agonists (data not shown).

To further reinforce that the slow deactivating tail currents were produced by cloned voltage-sensitive Ca²⁺ channels, we applied a transient repolarization protocol (Fig. 3 in Nakayama and Brading, 1993a). In the presence of Bay K 8644 (100 nM), the cell membrane was transiently (for 5 ms) repolarized to the holding potential after a conditioning step at +80 mV (4 s). Subsequently, the membrane was again clamped at +80 mV. The amplitude of the outward current evoked by the redepolarization to +80 mV was almost the same as that before the transient repolarization (data not shown), suggesting that ionic currents with E_rev close to 0 mV, e.g., nonselective cation currents and Cl⁻ currents, etc., did not significantly contribute to the slow tail current.

Effects of phosphorylation-related drugs

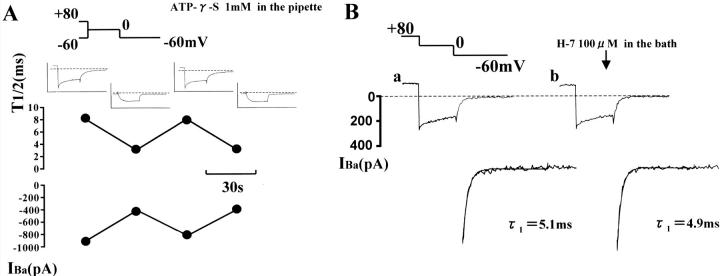
It has been shown that phosphorylation of channel protein is involved in voltage-dependent facilitation of L-type Ca²⁺ channels (e.g., Artalejo et al., 1992; Sculptoreanu et al., 1993). The experiments shown in Fig. 6 were designed to assess whether a phosphorylation process itself is required in the conversion of cloned Ca_v1.2b channel conformation from a normal (O₁ and O₁^*) to the second open state (O₂ and O₂^*). In Fig. 6 A, the pipette solution contained 1 mM ATP-γ-S, resistant to enzymatic hydrolysis (Gratecos and Fischer, 1974), and ATP was removed. In the presence of Bay K 8644 (100 nM) in the bathing medium, test depolarizations to 0 mV with or without conditioning at +80 mV (4 s) were alternately applied at 30-s intervals. If Ca²⁺ channels undergo transformation from normal to a second open state via a voltage-dependent phosphorylation process, once slow tail current is induced by a conditioning step to positive potentials in the presence of ATP-γ-S in the pipette, every test step subsequently applied is expected to produce a similar slow tail current upon repolarization. As shown in Fig. 6 A, slowly deactivating tail currents were, however, evoked only when the test step was preceded by the conditioning step to +80 mV. Essentially the same results were obtained from seven other cells.

FIGURE 6.

Effects of ATP-γ-S and H-7. In A, conditioned (+80 mV, 4 s) and unconditioned test steps (0 mV, 100 ms) were applied alternately at 30-s intervals. The patch pipette contained 1 mM ATP-γ-S instead of ATP, and the bathing solution contained 100 nM Bay K 8644. Changes in the half decay time (T_1/2) and amplitude of the tail current are plotted. Note that slow deactivating tail currents appeared only after conditioning depolarization to +80 mV. The insets in A show current traces obtained by the paired pulse protocol. Only the last 25 ms of conditioning step is shown. In B, conditioned (+80 mV, 4 s) test steps were repeated at 60-s intervals. The bathing solution did not contain any Ca²⁺ agonist. The current traces (a) and (b) were recorded just before and after application of 100 μM H-7 for 120 s, respectively. Tail currents are shown expanded at bottom. The decay time constants were obtained by fitting the tail currents with Eq. 2 (single exponential term). Dotted line indicates zero current level. (Series resistance, 11 MΩ in A and 10 MΩ in B).

In Fig. 6 B, depolarizations to 0 mV preceded by a conditioning step to 80 mV (4 s) were repeated at 60 s intervals. The currents shown in (a) and (b) were obtained just before and 120 s after application of a high concentration (100 μM) of H-7, which would inhibit both A- and C-kinases completely (Hidaka et al., 1984). This drug had little effect on the slow deactivating tail current.

Interaction of Ca²⁺ agonists and antagonists

Previously, we have assessed the relationship between the second open state and so-called mode gating in native smooth muscle L-type Ca²⁺ channels by examining the effects of Ca²⁺ channel agonists and antagonists on Ca²⁺ channel currents seen after positive conditioning steps (Nakayama and Brading, 1995b). In Fig. 7 A, we applied the same protocol to CHOCa9 cells to assess whether Ca_v1.2b, smooth muscle α₁-subunit further preserves this interaction seen in native Ca²⁺ channels. In the presence of 100 nM Bay K 8644, a test step (0 mV, 100 ms) conditioned at +80 mV for 4 s (the same sequence of the voltage steps used in Fig. 6 B) was repeated at 60 s intervals. After observing a control current (Fig. 7 Aa), 1 μM nifedipine was additionally applied to the bathing solution. The current trace shown in Fig. 7 Ab was recorded ∼3 min after application of nifedipine. The amplitudes of the test and tail currents were decreased by similar degrees (triangles in Fig. 7 B), whereas the outward current at +80 mV was unchanged. This result support that L-type Ca²⁺ channels are responsible for both test and tail currents, and that the outward current at +80 mV is due to other ion channels.

The correlation of inhibitory ratios between the inward currents is shown in Fig. 7 B: the amplitude of the test current (A_test, x axis) is plotted against that of the tail current at −60 mV (A_tail, y axis). The test and tail currents decreased by ∼60%, 3 min after the nifedipine application (filled triangle). The squares represent the data obtained from another cell using the same protocol. Also, in a CHOCa9 cell, 100 nM nifedipine was applied in the presence of 100 nM Bay K 8644. This application of nifedipine decreased the amplitudes of the test and tail currents (filled circle) by ∼20% after 2 min. All data points (triangles and circles) lie close to the line with a slope of unity (Fig. 7 B). In Fig. 7 C, the correlation of the amplitude (x axis) and the time to half decay of the tail currents (T_1/2, y axis) were plotted. The T_1/2 was relatively stable (ranged from +20 to −40%) after application of nifedipine in the presence of Bay K 8644, whereas the amplitude was greatly decreased. This fact suggests that this additional application of nifedipine transforms some of the Ca²⁺ channels to the unavailable mode by competitively displacing Bay K 8644 with nifedipine. (i.e., Ca²⁺ channels with Ca²⁺antagonist bound favor unavailable mode, like mode 0.) The remaining Ca²⁺ channels in O₂^* state keep the slow deactivation time course seen after positive conditioning steps.

DISCUSSION

A second open state can account for both slowtail current and U-shaped inactivation

In CHO cells expressing only α₁-subunits of smooth muscle Ca²⁺ channels (Ca_v1.2b), individual and simultaneous applications of Ca²⁺ agonist and preconditioning large depolarization significantly prolonged the deactivation time course of the tail currents upon repolarization (Fig. 1): The half decay time (T_1/2 ) at −60 mV was ∼2 ms in the presence of Bay K 8644 and ∼5 ms after conditioning depolarizations to +80 mV; T_1/2 was further prolonged to ∼15 ms by the combination of the two treatments.

Previously, in native smooth muscle cells, we have obtained evidence for multiple open states induced by the same two treatments: relatively large depolarizations cause transition of Ca²⁺ channel conformation from the normal (O₁) to a second open state (O₂ ), in which Ca²⁺ channels deactivate slowly upon repolarization due to the transition from O₁ to O₂. In the presence of Bay K 8644, a normal open state with Ca²⁺ agonist bound (O₁^*), whose deactivation time constant is longer than that of normal open state in the absence of Ca²⁺ agonist, is also converted into another long open state (O₂^*) by relatively large depolarizations. The deactivation time constant is longer in the following order: O₂^* > O₂ > O₁^* (Nakayama and Brading, 1993a; 1995a). In light of the previous studies, the three types of slow tail currents observed in the smooth muscle α₁-subunit (Ca_v1.2b) in the present study, correspond to the extra three open states (i.e., O₂, O₁^*, and O₂^*) in intact smooth muscle.

It has been shown that Ba²⁺, used in the present study as a charge carrier, produces some ion-dependent inactivation like Ca²⁺, although this effect of Ba²⁺ is much smaller (Markwardt and Nilius, 1988; Ferreira et al., 1997; Noceti et al., 1998). This mechanism may have made some contribution to the U-shaped inactivation curve obtained in the present study (Fig. 1 D). However, because we applied conditioning steps for 4 s, which are often used to achieve a steady state in voltage-sensitive Ca²⁺ channels, it is considered that recovery from inactivation by increasing the positivity of the conditioning potential to more than +20 mV cannot be ascribed solely to reduced Ba²⁺-dependent inactivation of the current. Alternatively, the U-shaped inactivation after 4 s conditioning step (Fig. 1 D) can be explained by the additional hypothesis that cloned smooth muscle Ca²⁺ channels (Ca_v1.2b) in the second open state do not (or only very slowly) inactivate during depolarization (Nakayama and Brading, 1993b, 1995a,b). The inactivation experiments using different concentrations of extracellular Ba²⁺ and acceleration of recovery from inactivation at more negative membrane potentials (Fig. 2) support the latter alternative explanation.

It is still difficult to determine what molecular mechanisms underlie voltage-dependent inactivation properties. Using chimaeras of two Ca²⁺ channel α₁-subunits, which show fast or slow inactivation during depolarization, it has been shown that segment 6 of the first repeat (IS6) is the molecular determinant (Zhang et al., 1994). Ca_v1.2a (cardiac clone) and Ca_v1.2b (smooth muscle clone) are splice variants of the same gene, and have differences in N-terminus and IS6. Therefore, the characteristic inactivation property seen in cloned smooth muscle Ca²⁺ channels might be attributed to the difference in IS6. On the other hand, point mutation studies have recently shown that Ca²⁺ channel inactivation is particularly sensitive to amino acid substitution in the inner channel mouth region of IIIS6 and IVS6 (Berjukow et al., 1999). It is also known that smooth muscle Ca²⁺ channels have higher affinity to DHP derivatives than cardiac Ca²⁺ channels (which differ from smooth muscle ones in IS6), and that IIIS5-IIIS6 and IVS5-IVS6 are critical for DHP sensitivity (Mitterdorfer et al., 1996; Grabner et al., 1996; Schuster et al., 1996; Adachi-Akahane et al., 2001). In analogy with the difference in DHP sensitivity, IS6 might affect voltage-dependent inactivation properties via other regions (IIIS6 and IV6) of Ca²⁺ channel protein. Further examinations are required for detailed understanding in this structure-function correlation issue.

Simulation of U-shaped inactivation and slow deactivation with a second open state

In an attempt to simulate U-shaped inactivation and slow deactivation of the Ca²⁺ channel current, we have constructed a minimum kinetic model with five conformational states of smooth muscle Ca²⁺ channel (Fig. 8 A). In this model we assume that the transitions of the channel conformation between C and O₁, and O₁ and O₂, are voltage-sensitive, and that only the C and O₁ states have their corresponding inactivated states (I₀ and I₁).

Fig. 8 B shows computer simulation of voltage-dependent changes in the deactivation time course of the tail current when a conditioning step is applied. The rate constants (in ms⁻¹) used from C to O₁ (k₀₁) and O₁ to C (k₁₀) were chosen to meet the activation kinetics (Table 1) estimated from the I-V relationship in Fig. 1 B:

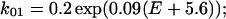(D1, 2)

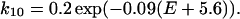On the other hand, the rate constants from O₁ to O₂ (k₁₂) and O₂ to O₁ (k₂₁) are as follows:

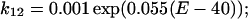(D3,4)

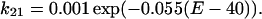These rate constants (k₁₂ and k₂₁) were chosen to reflect voltage dependence in the recovery phase of the U-shaped inactivation curve (Nakayama and Brading, 1995b). The rate constants used in this simulation are summarized in Table 2. (The rate constants in Table 2 are a set of examples that produce slow deactivation and U-shaped inactivation properties. Many other sets of the rate constants may be possible, especially when k₀₁ and k₁₀ are not limited by the activation parameters obtained in the present study.) The transitions between O₁ and I₁, and C and I₀, are assumed to be voltage-independent processes, and that their equilibria were in different directions (favoring C over I₀, but O₁ over I₁). The transition rate from O₁ to I₁ (k₁₄) was chosen to inactivate the Ca²⁺ channel current by ∼35% during depolarization to 0 mV for 200 ms (Fig. 8 D). Assuming complete microscopic reversibility of the C-O₁-I₁-I₀ cycle (Colquhoun and Hawkes, 1995; Rothberg and Magleby, 2001), the rate constants between I₀ and I₁ were chosen as follows:

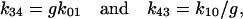(D5,6)

where g is the ratio of k₁₄/k₄₁ (= k₃₀/k₀₃ = 20). As shown in Fig. 8 B, the deactivation time course was slowed by reducing the negativity of the repolarization step, agreeing with the results obtained in the cloned smooth muscle Ca²⁺ channel (Fig. 4).

TABLE 2.

The rate constants (ms⁻¹) used in the kinetic scheme shown in Fig. 7

k01 = 0.2 exp(0.09(E + 5.6))	k10 = 0.2 exp(−0.09(E + 5.6))
k12 = 0.001 exp(0.055(E − 40))	k21 = 0.001 exp(−0.055(E − 40))
k03 = 0.00015	k30 = 0.003
k34 = 20 k01 = 4 exp(0.09(E + 5.6))	k43 = k10/20 = 0.01 exp(−0.09(E + 5.6))
k14 = 20 k03 = 0.003	k41 = k30/20 = 0.00015

E represents the membrane potential (mV).

Using the rate constants shown in Table 2, we have also reconstructed the voltage dependence of inactivation (f_∞(E)) as the ratio of the number of channels in C, O₁, and O₂ states to the total channel number after applying conditioning potentials (E) for 4 s. As shown in Fig. 8 C, f_∞(E) gradually increased as the positivity of the conditioning potential was increased to more positive than +20 mV, and became ∼85% at +80 mV. This U-shaped inactivation curve is similar to that seen in guinea-pig detrusor smooth muscle cells (Nakayama and Brading, 1993b; 1995b). It is noteworthy that when the transition rates between O₁ and O₂ were assumed to be voltage-independent (constant), no significant recovery was obtained at positive conditioning potentials (graph not shown).

In cloned smooth muscle Ca²⁺ channels expressed in CHO cells, the inactivation curves obtained were clearly U-shaped (the present study), however, the degree of inactivation at +80 mV ranged widely (Fig. 1 D). Incomplete recovery of f_∞(E) at the conditioning potential of +80 to +100 mV was also observed in several native smooth muscles: guinea-pig stomach and taenia caeci (L. M. Smith and S. Nakayama, unpublished observation), and pig and human detrusor (Kajioka et al., 2002). It is speculated that some mechanisms, not considered in the kinetic scheme shown in Fig. 8 A, may modulate recovery of f_∞(E) at positive conditioning potentials, e.g., a considerable transition from O₂ to its corresponding inactivated state (I₂). In addition, we examined possible effects of a smooth muscle β-subunit (β₃) (Klöckner et al., 1992; Murakami et al., 1994) on U-shaped inactivation property (and slow deactivation). This auxiliary subunit, however, did not alter the large variation in the degree of inactivation after large conditioning depolarizations (with no significant change in deactivation time course) (Communication to Japanese Physiological Society, Aoyama et al., 2001).

Simulation of results in the presence of Ca²⁺ agonists

To reconstruct the U-shaped inactivation and slow deactivation seen in the presence of DHP Ca²⁺ channel agonists, we applied a kinetic scheme (Fig. 9 A) analogous to that shown in Fig. 8 A. The asterisks indicate channel states with Ca²⁺ agonist bound. The kinetic schemes shown in Fig. 8 A and Fig. 9 A may correspond to mode 1 and mode 2 in the mode gating theory (Hess et al., 1984). Table 3 shows the transition rates used in the kinetic scheme in Fig. 9 A. The transition rate constants from O₁^* to C^* (k₁₀^*) and O₂^* to O₁^* (k₂₁^*) are smaller than those in the absence of Ca²⁺ agonists, causing slower decay of tail currents upon repolarization (Fig. 9 Bb). Despite use of rate constants chosen for slower deactivation, the kinetic scheme in Fig. 9 A produced a clearly U-shaped inactivation curve (Fig. 9 C). Because a small number of Ca²⁺ channels would take the kinetic scheme in Fig. 8 A even in the presence of Ca²⁺ agonists, the actual Ca²⁺ channel current would be the best fitted with a combination of the two kinetic schemes (Fig. 8 A and Fig. 9 A).

TABLE 3.

The rate constants (ms⁻¹) used in the kinetic scheme shown in Fig. 8

k01* = 0.01 exp(0.1(E + 12.4))	k10* = 0.01 exp(−0.1(E + 12.4))
k12* = 0.001 exp(0.045(E − 30))	k21* = 0.001 exp(−0.045(E – 30))
k03* = 0.00015	k30* = 0.003
k34* = 20 k01* = 0.2 exp(0.1(E + 12.4))	k43* = k10*/20 = 0.0005 exp(−0.1(E + 12.4))
k14* = 20 k03* = 0.003	k41* = k30*/20 = 0.00015

E represents the membrane potential (mV).

Application of Ca²⁺ agonists increased the amplitude of the Ca²⁺ channel current (Table 1). This is well understood with the presence of unavailable Ca²⁺ channels (like mode 0 in the mode gating theory, Hess et al., 1984) under normal conditions: i.e., in the absence of Ca²⁺ agonist, Ca²⁺ channels would take the normal kinetic scheme shown in Fig. 8 A (like mode 1), or stay as unavailable channels (like mode 0). On the other hand, Ca²⁺ channels bound to Ca²⁺ agonists would take the Ca²⁺-agonist-dependent kinetic scheme shown in Fig. 9 (like mode 2), where +80 mV conditioning produces a Ca²⁺ tail current with the slowest deactivation. Further, in the presence of Bay K 8644, additional application of a Ca²⁺ antagonist, nifedipine decreased the amplitude of the tail current evoked after the +80 mV conditioning step, but no significant change was observed in the decay time constant (Fig. 7). This phenomenon can be explained assuming that Ca²⁺ antagonists convert a significant number of Ca²⁺ channels from the Ca²⁺ agonist-dependent kinetic scheme (like mode 2) to an unavailable channel mode (like mode 0), (not to the normal kinetic scheme like mode 1). (We assume that the slow time course of the tail currents does not reflect dissociation and/or association of the DHP compounds during the decay time course.)

U-shaped inactivation and slow deactivation properties were reconstructed with a minimum model in the present study. It should be noted that the effect of Ca²⁺ agonists on the activation time course of the Ca²⁺ channel current would be more precisely expressed with complex kinetic schemes. For example, the transition between C to O₁ in the present study may be rewritten by incorporating multiple closed states sequentially linked to a normal open state (e.g., C₂-C₁-O₁) (Sanguinetti et al., 1986; Lacerda and Brown, 1989) or an allosteric model with four closed and four open states (C₄-O₄) (Marks and Jones, 1992).

In the present model, we did not incorporate a Ca²⁺- (or divalent cation-) dependent inactivation process, assuming that this mechanism was insignificant when Ba²⁺ was used as a charge carrier. However, several papers have reported relatively a small Ba²⁺-dependent inactivation, as described above (Markwardt and Nilius, 1988; Ferreira et al., 1997; Noceti et al., 1998). Ca²⁺ agonists would potentiate this inactivation mechanism. Although essentially similar U-shaped inactivation curves have been produced with the multiple open state model shown in Fig. 8 A, involvement of a Ca²⁺-dependent inactivation process (e.g., Vogalis et al., 1992; Beech, 1993; Nakayama, 1993) would be required in models applied in more general conditions. Furthermore, it should be noted again that complex modifications in the transition between closed and normal open states would make it possible to reconstruct the U-shaped inactivation curve more precisely, especially near −40 mV. For instance, models with multiple closed states linked to corresponding inactivated states (C₄-I₄) (Klemic et al., 1998; Patil et al., 1998; Jones et al., 1999), yield channel inactivation preferentially from partially activated closed states (shifting the down phase of U-shaped inactivation curve toward hyperpolarization), and voltage-dependent (hyperpolarization-induced fast) recovery from inactivation. The former mechanism itself can be used to reconstruct U-shaped inactivation. These models, however, do not provide slow deactivating tail currents after positive conditioning potentials, without incorporating a second open state.

Voltage-dependent facilitation

Voltage-dependent facilitation of L-type Ca²⁺ channels has been shown in numerous excitable cells. This mechanism may thus play an important role in many physiological processes. In this section we will compare features of voltage-dependent facilitation of L-type Ca²⁺ channels with those seen in other cells. In adrenal chromaffin cells, the potentiation of current amplitude after conditioning depolarization has been ascribed to voltage-dependent phosphorylation of channel protein (via kinases other than A-kinase) (Artalejo et al., 1992). In the present study, however, neither inclusion of ATP-γ-S in the pipette nor application of a high concentration H-7 to the bathing solution, which would inhibit both A- and C-kinases, altered the condition necessary to induce the second open states (O₂ and O₂^*) in the α₁-subunit of smooth muscle Ca²⁺ channel (Ca_v1.2b). The results obtained with phosphorylation inhibitors in the present study are consistent with those in native smooth muscle Ca²⁺ channels (Smith et al., 1999; Muraki et al., 1993), and also support the assumption of the model provided in Fig. 8, i.e., the transition between O₁ and O₂ is voltage-dependent. Furthermore, it has been reported that Ca_v1.2b has no consensus tyrosine phosphorylation site (Sunagawa et al., 2001).

In α₁-subunits of cardiac and neuronal L-type Ca²⁺ channel clones (Ca_v1.2a and c), voltage-dependent facilitation has also been examined. Many of these experiments have been carried out using Ba²⁺ as a charge carrier, although the pulse protocols used were different from those in the present study: An interpulse duration (transient repolarization step) was put between conditioning and test steps, and the duration of the conditioning depolarization was much shorter (<1 s) in most studies. To highlight variation in the under-lying mechanisms, it may also be noteworthy that voltage-dependent facilitation seen in cardiac and neuronal α₁-subunits usually requires β-subunits, (although there was some discrepancy on the subclass of the available β-subunit between studies (Cens et al., 1996; 1998; Dai et al., 1999)).

In many of the studies for Ca_v1.2a and c (coexpressed with β-subunits), conditioning pulses to large positive potentials increased the amplitude of the subsequent test current, and this amplification was often accompanied by acceleration of activation and inactivation time courses (e.g., Sculptoreanu et al., 1993; Bourinet et al., 1994; Dai et al., 1999). As in the case of the smooth muscle α₁-subunit (Ca_v1.2b), this type of voltage-dependent facilitation did not seem to be due to voltage-dependent phosphorylation itself, because some of the studies have shown that applications of ATP-γ-S or okadaic acid did not affect it (Bourinet et al., 1994; Dai et al., 1999). Basal activity of protein kinases has, however, been suggested to be critical, because prolonged exposures to phosphorylation inhibitors suppressed the voltage-dependent facilitation. On the other hand, facilitation with little alteration of current kinetics has been reported in rabbit cardiac α₁-subunit coexpressed with β1-subunit (Constantin et al., 1998). Unlike the present study, prepulses at positive potentials increase the amplitude of subsequent trains of test pulses for tens of seconds.

In the present study, we have shown that development of the second open states (O₂ and O₂^*) at positive potentials produces U-shaped inactivation and slows deactivation properties due to noninactivating (during depolarization) and slow deactivating (upon repolarization) features, respectively. Another unique facilitation linked with inactivation has been reported for Ca_v1.2 (Zühlke et al., 1999): Frequent applications of step depolarization increased the amplitude of the Ca²⁺ channel current. Either point mutation in the IQ motif or use of mutant calmodulin suppressed the frequency-dependent facilitation, being accompanied by slowing of the inactivation time course. Calmodulin has thus been suggested to play a pivotal role in the frequency-dependent facilitation and fast inactivation. However, unlike the transition into the second open states in the present study, these simultaneous changes occur only in the presence of Ca²⁺ as a charge carrier.

Taken together, it is suggested that numerous mechanisms underlie voltage-dependent facilitation of various types of Ca²⁺ channels, and that the second open states seen in smooth muscle Ca²⁺ channels are not due to voltage-dependent phosphorylation itself, but due to physical processes. Nevertheless, as was suggested in other types of voltage-dependent facilitation (Bourinet et al., 1994), it is possible that phosphorylation of smooth muscle Ca²⁺ channel protein could affect the basal conditions to induce the transitions between the normal and second open states (e.g., Ono and Fozzard, 1992; Groschner et al., 1996).

Overall, the present study on tail current analyses demonstrated that the α₁-subunit of Ca_v1.2b preserves multiple open states seen in native smooth muscle: Ca²⁺ channels in the second open state do not, or only very slowly, inactivate during depolarization, and deactivate slowly upon repolarization. Furthermore, the effects of large depolarization and Ca²⁺ channel agonists operate separately in the α₁-subunit of the smooth muscle Ca²⁺ channel. As a result, combination of the two treatments produces a total of four open states. Inasmuch as the second, long open state can be induced by large conditioning depolarizations even when intracellular phosphorylation processes is blocked, it is considered that some physical processes (voltage-dependent processes) underlie the conversion from the normal to the second open state. With this assumption, we have successfully reconstructed the slow deactivation and U-shaped inactivation of the channels using a minimum model.