FIGURE 2.

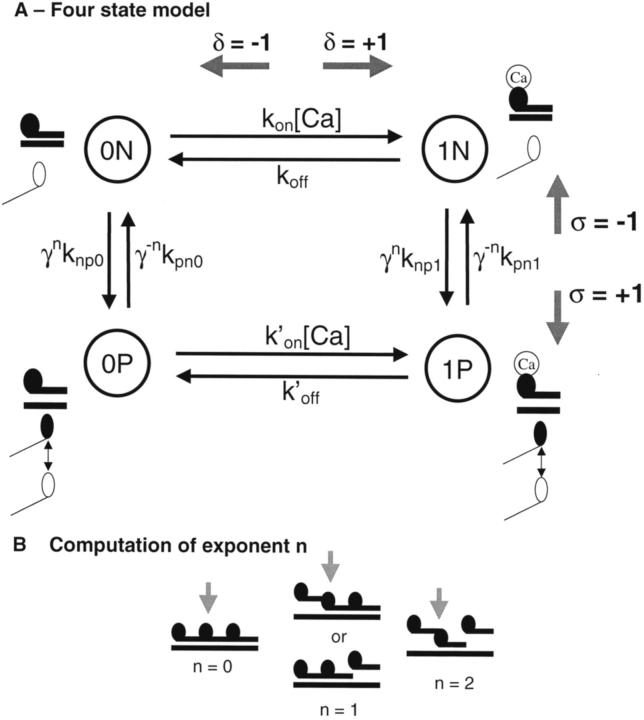
The model assumes 26 equivalent T/T units that are situated end-to-end along the thin filament. (A) Each T/T unit can be represented by a 4-state Markov model with transition rates between the states as shown. The states are coded with 0x or 1x to represent no Ca or Ca bound, respectively, to the single regulatory site on cardiac troponin. The units are coded with xN and xP to represent states that are in the nonpermissive and permissive conformations, respectively. Cross-bridges are not explicitly represented but are assumed to bind and generate force when units become permissive. The transition rates are shown for Ca binding are given by k_on[Ca] and k_off for the nonpermissive states and k′_on[Ca] and k′_off for the permissive states. The transition rate from a nonpermissive to a permissive state depends both on a base rate and a cooperativity term. The base rates are the k_npx and k_pnx where x is 0 or 1 depending on whether or not Ca is bound. The base rates are modified by cooperativity terms γⁿ and γ⁻ⁿ where n is the number of neighboring units in the permissive conformation (see B). The model can be solved in steady state using an Ising approach where each T/T unit is assumed to have two spins, δ and σ. The δ spin can take on values −1 for no Ca bound and +1 for Ca bound, and the σ spin can take on values −1 for nonpermissive and +1 for permissive. (B) The nearest-neighbor dependencies appear as exponents on γ terms that are computed on the number of neighboring units in the permissive conformation. The exponent n can take on the values of 0 for no permissive neighbors, 1 for a single permissive neighbor, and 2 when both neighbors are permissive. The whole model consists of 26 T/T units along the thin filament where the first and last units are assumed to be connected so that all units have two neighbors.