Probing the Cell Peripheral Movements by Optical Trapping Technique

Abstract

Swiss 3T3 fibroblasts cultured on a poly-L-lysine-coated coverslip was stimulated with 0.5 μM phorbol myristate acetate, and the movements of the peripheral membranes were probed with a 1-μm polystyrene bead held in an optical trap. The bead brought into contact with the cell edge occasionally moved away from and returned to the original position. The movement ranged over 100 nm and occurred mainly in one direction, suggesting that the protruding cell membrane pushed the bead. The maximum velocities derived from individual pairs of protrusive and withdrawal movements exhibited a correlation, which is consistent with the previous reports. Acceleration and deceleration occurred both in the protrusive and withdrawal phases, indicating that the movements were regulated. Movement of the membrane occurred frequently with an ensemble-averaged maximum speed of 23 nm/s at the trap stiffness of 0.024 pN/nm, but it was strongly suppressed when the trap stiffness was increased to 0.090 pN/nm. Correlation of the protrusive and withdrawal velocities and the acceleration and deceleration both in the protrusive and withdrawal phases can be explained by the involvement of myosin motor at least in the withdrawal process. However, the fact that the movements were suppressed at higher trap stiffness implies a stochastic nature in the creation of the gap between the peripheral cell membrane and the actin network underlying it.

INTRODUCTION

Cell migration is important in many cellular activities such as wound healing, morphogenesis, and in cell development (Stossel, 1993). In these phenomena, protrusion of the cell membrane at the leading edge is an indispensable step (Condeelis, 1993), and the mechanism that drives this movement has been a subject of intensive study (for reviews, see Mitchson and Cramer, 1996; Lauffenburger and Horwitz, 1996; Borisy and Svitkina, 2000). Electron microscopic studies have revealed that at the leading edge, actin filaments form a network adjacent to the cell membrane with their barbed end oriented toward the membrane (Small, 1988). Concomitant with the membrane protrusion, polymerization of actin occurs between the actin network and the cell membrane. Hence, it has been suggested that the elongating actin filaments make the membrane protrude (Cooper, 1991). Thermodynamic argument has demonstrated that growing polymer is capable of exerting a force on the membrane and performing a work against the load (Hill, 1981). Indeed, liposome membranes are deformed when actin polymerizes in the liposome (Miyata et al., 1999; Miyata and Hotani, 1992; Cortese et al., 1989), suggesting that the polymerization had performed a work to deform the elastic lipid membranes. Two mechanisms are postulated to explain the creation of a gap between the tip of a growing actin filament in the actin network and the membrane, which is necessary for a monomer to polymerize onto the tips of preexisting filaments in the cell (Stossel, 1993). One is the fluctuation of the membrane and/or the fluctuation of the filament tip (Peskin et al., 1993; Mogliner and Oster, 1996). A recent investigation on Ena/VASP function has provided a result that is consistent with the prediction of the latter type of fluctuation-driven membrane protrusion (Bear et al., 2002; Cramer, 2002). However, little experimental approach has been taken to evaluate the role of thermal fluctuation in cell membrane protrusion. Another mechanism is the forward movement of the cell membrane driven by the sliding of membrane-bound myosin over the actin filament network fixed to the substrate: the gap between the filaments and the cell membrane is immediately filled by the actin polymerization (Sheetz et al., 1992; Welch et al., 1997). To elucidate the mechanism of membrane protrusion, detailed analysis of the membrane motion is necessary. For this purpose, lamellipodial movement has been studied by many investigators. In the early studies, spatial resolution was limited to that of optical microscope. An atomic force microscope has been utilized for this purpose (Rotch et al., 1999) and the minute movements of the active edge of the cell have been revealed, but the time resolution was limited. We have measured movements of the leading edge of Swiss 3T3 fibroblasts spread on a poly-L-lysine-coated coverslip in the presence of phorbol myristate acetate (PMA), using a polystyrene bead held in an optical trap as a probe of the movement. The analysis of the bead motion demonstrated the protrusion and withdrawal of the cell edge occurred at nonuniform velocities, and the correlation between the two velocities. Interestingly, the protrusive and withdrawal activities depended on the trap stiffness.

MATERIALS

PMA and bovine serum albumin were from Sigma Chemical (St. Louis, MO). Polystyrene beads were from Polysciences (Warrington, PA). Dulbecco's modified Eagle's medium, minimum essential medium, L-glutamine, penicillin-streptomycin, and newborn bovine serum were from Gibco (Rockville, MD). Fetal bovine serum was from Nissui (Tokyo, Japan). HEPES was from Dojindo (Kumamoto, Japan).

METHODS

Cell culture

Swiss 3T3 fibroblasts were grown to subconfluent in Dulbecco's modified Eagle's medium containing 5% fetal bovine serum, 1% penicillin-streptomycin. A 24 × 24-mm coverslip, which had been washed in 0.1 N NaOH, subsequently in ethanol, and coated with 0.1 mg/ml poly-L-lysine, was secured to a polypropyrene hollow cylinder (inner diameter = 20 mm, height = 10 mm) with silicone grease to make an observation chamber. After cells were harvested with 1% trypsin-2.5 mM ethylenediamine tetraacetic acid, ∼10⁴ cells were plated into the observation chamber and were subcultured for 2 h at 37°C.

Measurements and analysis

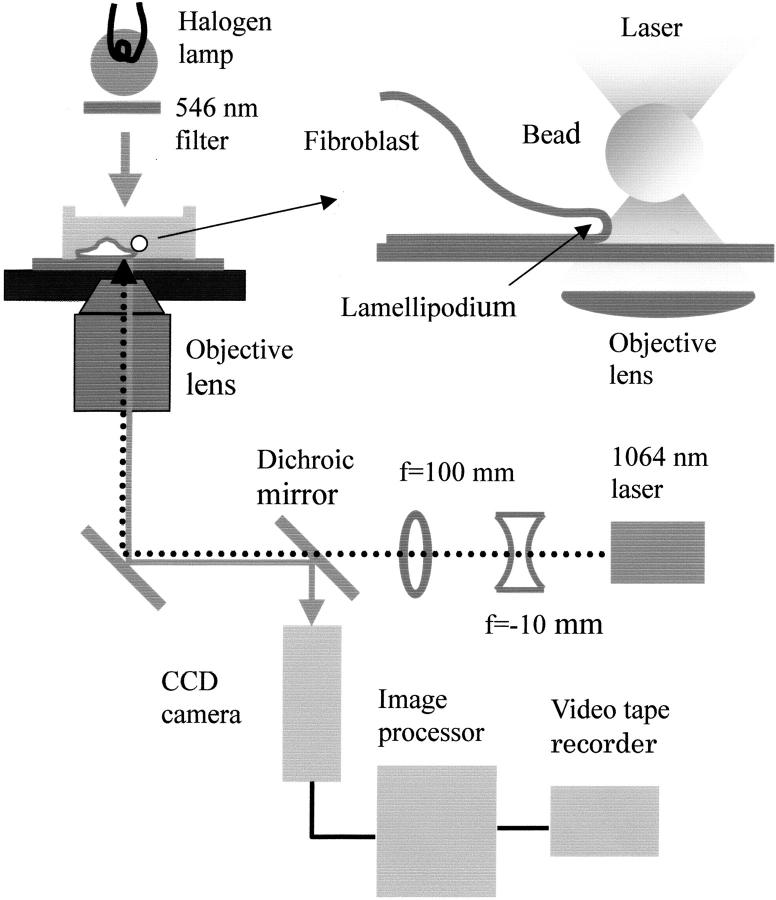
As depicted in Fig. 1, a 1064-nm infrared laser beam (0.6-mm diameter; CrystaLaser, Reno, NV), expanded 10 times with a combination of a concave lens (focal length = −10 mm; Melles Griot, Irvine CA) and a convex lens (f = 100 mm; Sigma Koki, Saitama, Japan) was steered into an inverted phase-contrast microscope (TMD, Nikon, Tokyo) through the laser scanner, (Sigma Koki), and overfilled the aperture of the objective lens (NA = 1.3, 100×, Ph4DL, Nikon) to generate an optical trap; the maximum laser power measured immediately before entering the objective was ∼150 mW. The trap stiffness was determined as previously described (Miyata et al., 1994; Svoboda and Block, 1994).

FIGURE 1.

The experimental system. For details, see text. Top right, the details of the sample chamber: a 1-μm polystyrene bead held in an optical trap (represented by a pair of shaded triangles) was made to contact with the lamellipodium of a fibroblast with movement of the stage. The figure is not drawn to scale.

After the cell culture medium was replaced with the experimental solution (minimum essential medium supplemented with L-glutamine and penicillin-streptomycin and 0.5 μM PMA, buffered with HEPES to pH 7.2), cells were observed by phase contrast microscopy. An appropriate bead, which had been coated with 1% bovine serum albumin for 5 h at room temperature to reduce nonspecific adhesion, was captured with the optical trap and placed near the cell edge. The phase-contrast image of the trap-held bead was recorded on a digital videotape for several seconds for later determination of the trap center. Then, the bead was manually brought into contact with the cell edge by moving the microscope stage, and its image was recorded for 1–2 min. This sequence (termed here run) was repeated with different cells several times within a period of 30 min. Experiments were done at three trap stiffness (0.024, 0.053, and 0.090 pN/nm).

Position of the bead was determined every 33 ms by calculating the centroid of the phase contrast image of the bead using a NIH-image-based program written by Dr. Akira Goto (Physics Department, Graduate School of Science, Tohoku University). Before the analysis, the coordinate system was rotated to make the x axis parallel to the major direction of the bead motion. The x-t and y-t traces were smoothed over 1 s, and x-y coordinate of the bead was determined using the smoothed data. Bead motions were categorized into three types. In the type I motion, beads moved forward relative to the cell center mainly in one direction (within 45° of the normal to cell edge); in the type II motion, beads moved almost parallel to the cell edge; in the type III motion, beads were pulled toward the cell center against the force from the optical trap, and were sometimes transported over 5 μm toward the cell center. At the end of each run, the trap was turned off to check if the bead was bound to the surface; if the bead was found to adhere to the cell surface, its motion was not analyzed. We did not analyze type II and III motion either. In Table 1, total number of the run and the number of each type of the motion at individual trap stiffness (0.024, 0.056, and 0.090 pN/nm) are indicated. Slippage of the bead on the cell surface might occur especially at higher trap stiffness, which could increase the withdrawal velocity. However, this effect was difficult to evaluate and was not analyzed.

TABLE 1.

Summary of the parameters characterizing the bead movements

		Frequency of each type of run
Stiffness pN/nm	Total*	Type I	Type II	Type III	〈vmax+〉	Rate†	〈vmax−〉	Rate†
0.024	20	9	6	5	23.3 ± 12.2	1.8 (16)	23.7 ± 15.5	1.8 (16)
0.056	30	13	3	14	17.6 ± 3.2	0.54 (7)	15.3 ± 2.4	0.38 (5)
0.090	26	13	3	10	12.0	0.08 (1)	<12.0	0
0.024‡	30	11	7	12	28.4 ± 24.6	0.82 (9§)	23.2 ± 13.6	0.82 (9§)

〈Bead velocities〉 are ensemble-averaged and in nm/s.

^*Total number of runs.

^†Protrusive or withdrawal movements (shown in parentheses) per run.

^‡Run with 200 nM cytochalasin D.

^§Eight events are from a single run.

The bead velocity (v_x, v_y) was determined from the smoothed traces by calculating the value Δx/2Δt and Δy/2Δt, respectively, where Δx and Δy are the differences of the bead coordinates corresponding to the time difference, 2Δt (=0.98 s). Apparent velocity of the adherent bead was determined in a similar manner. The force from the trap, f_x and f_y, were calculated as κ × x and κ × y, where κ is the trap stiffness.

RESULTS

Movement of the bead

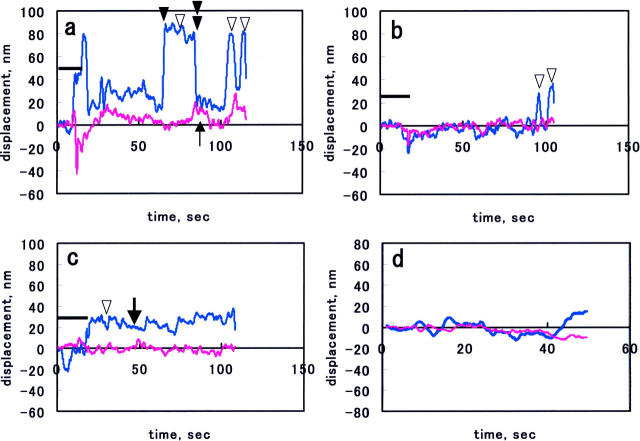
Fig. 2, a–c, shows representative x-t (cyan) and y-t (magenta) traces of beads exhibiting the type I motion (downward open arrowheads) at individual trap stiffness. As a result of the contact procedure in the beginning of each run, the bead was displaced from the trap center (bold bars in each graph indicate the period of the contact procedure). At the trap stiffness of 0.024 pN/nm, the bead exhibited movements away from the trap center mainly in one (x) direction, although movements in y direction were occasionally observed (Fig. 2 a, upward thin arrow). The latter movements were probably because of nonuniform advancement of the cell edge. After the movement away from the trap center (forward movement; black arrowhead), the bead returned to the trap center (rearward movement; black double arrowhead). Often, the bead once displaced from the trap center as a result of the contact procedure did not return to the original position, executing smaller movements (Fig. 2 c, bold arrow). This type of movement was probably due to the mechanical drift of the experimental system, because the beads adhered to the coverslip exhibited similar traces (Fig. 2 d). The x-t trace of type II motion, a movement parallel to the cell edge, was similar to the cyan trace in Fig. 2 a, and hence, this movement might be caused by the nonuniform advancement of cell edge and was driven by the same mechanism as the type I motion. The type III motion was characterized by occasional movements for relatively long distances toward the cell center. As described above, the bead was found to adhere to the cell plane in this case and its movement could not be stopped with the largest trap force (∼20 pN). Similar retrograde movements of the antiintegrin antibody- or fibronectin-coated bead bound to the surface of fibroblasts cells have been described (Choquet et al., 1997).

FIGURE 2.

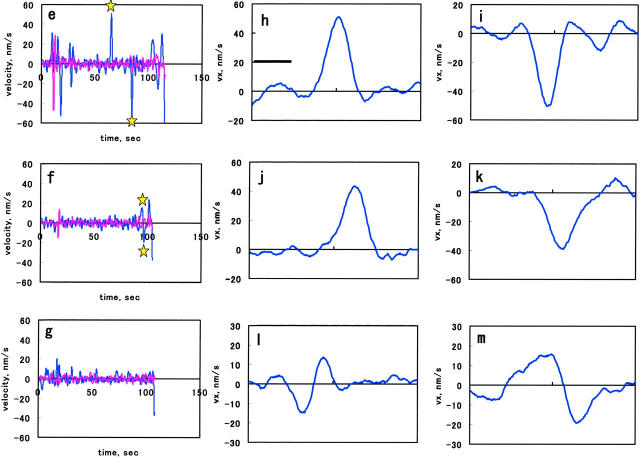
(a–c) Representative x-t (cyan) and y-t (magenta) traces of a bead obtained at the trap stiffness of 0.024, 0.056, and 0.090 pN/nm, respectively. The bold bar indicates the time period where bead contact procedure was performed. Downward arrowheads indicate the type I movement. In a, upward thin arrow indicates the bead motion in the y direction; black arrowhead and black double arrowhead indicate the forward and rearward movements. In b, the bead movements occurred toward the end of the record. In c, the bold arrow indicates the small random motion of the bead. In d, a representative x-t and y-t traces of an adherent bead. In e–g, the v_x-t (cyan) and v_y-t (magenta) traces derived from the displacement traces in a–c, respectively. Stars in e indicate the parts that are shown with an expanded time scale in h and i, and those in f show the part shown in m. In h–k, the v_x-t curves with an expanded timescale obtained at 0.024 pN/nm; l and m, at 0.056 pN/nm. Abscissa indicates time in seconds.

When the cells were observed under illumination of the laser at the highest power (∼150 mW), the protrusion and withdrawal of the cell edge occurred normally. Because the highest laser power used in the measurement was 45 mW, we concluded that no damage to the cell was caused by the laser illumination.

Analysis of the bead movements

Fig. 2, e–g, show v-t curves derived from the x-t and y-t traces shown in Fig. 2, a–c. As is evident from Fig. 2 e (cyan trace), the velocity of the forward motion, v_x, gradually increased, reached a maximum, and then decreased, indicating the acceleration and deceleration occurred during the outward motion. The v_x-t curves at the trap stiffness of 0.024 pN/nm are shown with an expanded time scale in Fig. 2, h–k. At the trap stiffness of 0.056 pN/nm, the bead movements were also seen (Fig. 2 f, arrows, and Fig. 2, l–m, for expanded timescale). At the highest trap stiffness, 0.090 pN/nm, the movement was significantly suppressed (Fig. 2 g). Because mechanical drift caused apparent movements as shown in Fig. 2 d, we analyzed the movement of the bead bound to coverslip. The distribution of apparent velocities of five adherent beads could be fitted with a Gaussian distribution function with a mean = 0.39 nm/s and an SD = 4.6 nm/s. This indicates that the occurrence of the events with apparent velocity >12 nm/s was negligible for adherent beads. Based on this, we adopted a value, 12 nm/s, as a cutoff value, below which the calculated values were rejected as those of the mechanical drift. By applying this cutoff value, we concluded that the v_y in Fig. 2, e and f, and v_x and v_y in Fig. 2 g, did not contain significant contribution from the movement of membrane.

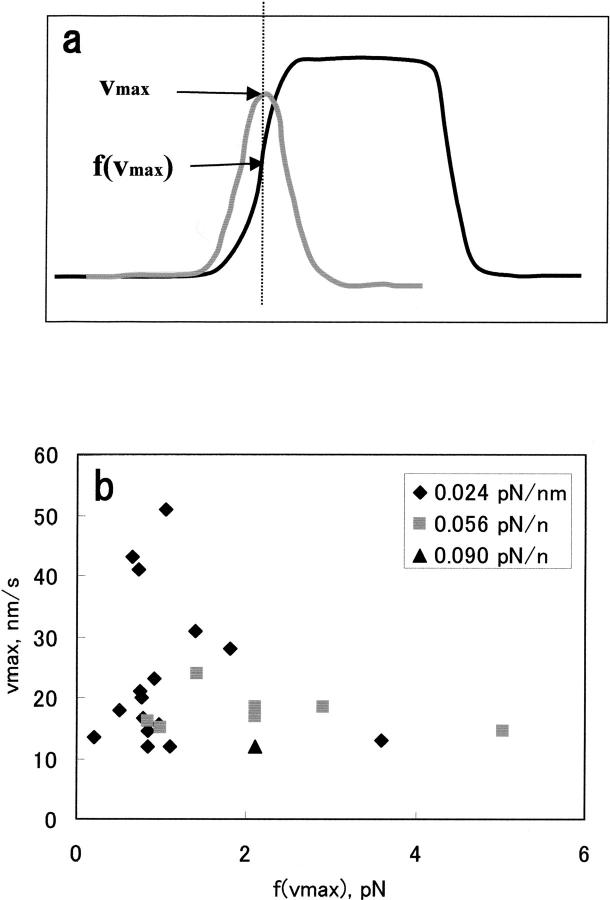
Because the theories have predicted that the velocity of the membrane protrusion decreases monotonously with increasing external force (Peskin et al., 1993; Mogliner and Oster, 1996), it is important to examine the force-velocity relation in the case studied here. In our case the protrusive velocity changed as described above. Hence, we plotted the maximum protruding velocity, v_max⁺, against the force that corresponds to the v_max⁺ as illustrated in Fig. 3 a. The actual plot is shown in Fig. 3 b. This plot demonstrates that the v_max⁺ rapidly decreased from 50 to 20 nm/s as f(v_max⁺) increased from ∼1 to ∼2 pN. This result is qualitatively consistent with the prediction, although the scattering of the data at 0.024 pN/nm precluded us from quantitative evaluation; we suspect that this scattering may reflect a stochastic nature of the system (see below). Also, due to the velocity cutoff set in the analysis, it was not possible to confirm the force dependence of the velocity on higher forces.

FIGURE 3.

(a) Schematic drawing of the method to determine f(v_max⁺). (b) The experimental v_max⁺-f(v_max⁺) plot obtained as shown in a. Filled diamonds, trap stiffness = 0.024 pN/nm; filled squares, 0.056 pN/nm; filled triangles, 0.090 pN/nm.

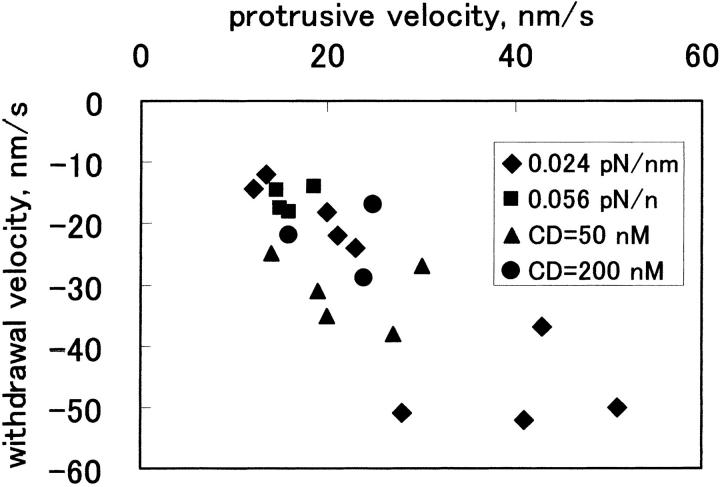
For comparison of the movements observed under different experimental conditions (e.g., trap stiffness), v_max⁺ and v_max⁻ of individual forward and rearward movements were determined and were ensemble-averaged for each experimental condition (〈v_max⁺〉 and 〈v_max⁻〉). Table 1 shows the 〈v_max⁺〉 and 〈v_max⁻〉 values, the frequency of each type of run, and the occurrence of the event per each run (termed rate). Table 1 demonstrates that the 〈v_max⁺〉 and 〈v_max⁻〉 values decreased with increasing trap stiffness: the 〈v_max⁺〉 value at 0.090 pN/nm was only marginally above the cutoff value. The rate also decreased with increasing trap stiffness. Thus, the bead in the stiffer trap moved less frequently at lower speed. It is also apparent that the standard deviation of 〈v_max⁺〉 and 〈v_max⁻〉 values at 0.024 pN/nm are larger than those at 0.056 pN/nm, which reflects the different degree of scattering of the plots shown in Fig. 3 b. Table 1 also demonstrates that at each trap stiffness, the averaged rearward velocities were similar to that of the forward velocities. This is a reflection of the correlation between the maximum velocities derived from individual pairs of forward and rearward movements, as demonstrated in Fig. 4, which shows the correlation coefficient of –0.79.

FIGURE 4.

A plot of withdrawal versus protrusive velocities. Results obtained under all conditions are plotted. Diamonds, trap stiffness = 0.024 pN/nm; filled squares, 0.056 pN/nm; filled triangles, data in the presence of 50 nM cytochalasin D; filled circles, in the presence of 200 nM cytochalasin D. In the presence of cytochalasin D, trap stiffness was 0.024 pN/nm.

The bead measurements were carried out in the presence of 50 and 200 nM cytochalasin D. At the higher drug concentration, actin polymerization in vitro (Cooper, 1987) or motility of the periphery of fibroblasts (Schafer et al., 1998) is inhibited. As summarized in Table 1, the event occurrence was significantly lower in the presence of 200 nM drug, although the averaged velocities were higher than the value obtained at the same trap stiffness in the absence of the drug. This was because in a single run, frequent movements occurred with velocities even higher than those in the absence of the drug. In other cases virtually no movement occurred. We suggest that the forward and rearward movements involved actin dynamics. In the presence of 50 nM cytochalasin D, the movements occurred more frequently than 200 nM drug, suggesting that the inhibition was incomplete.

DISCUSSION

In this work we attempted to measure the dynamic behavior of the cell membrane by optical trapping technique. A question arises if the probe bead exactly followed the membrane movement. Because the Reynolds number of 1 μm bead in an aqueous solution is calculated to be of the order of 10⁻⁷, its motion should be overdamped and acceleration or deceleration cannot be due to the inertia of the bead. Hence, we suggest that the bead strictly followed the membrane movement and that the observed bead movement reflected the membrane movement.

The fact that the membrane movements were suppressed by cytochalasin D suggested that actin polymerization played an important role in the membrane movement, which is consistent with the current notion of actin-based cellular protrusion (Borisy and Svitkina, 2000). The biophysical models of actin-based motility, a Brownian ratchet, or elastic Brownian ratchet mechanism of membrane protrusion (Peskin et al., 1993; Mogliner and Oster, 1996) quantitatively predict how the protruding velocity decreases with increasing external force. We have shown that the maximum protrusive velocity tended to decrease when the trap force increased. On the other hand, in each protrusive event, the velocity initially increased despite increasing trap force: this is also consistent with the theory, because it demonstrates that velocity increases with the increase in the concentration of actin monomer. Thus, in the acceleration phase, the monomer concentration increased, at the maximum velocity it was maximal, and it decreased during the deceleration.

One might argue that the change in the bead velocity was a result of a creeping motion of the membrane that was due to the viscoelastic property of the cell cytoplasm. Recent studies (Bausch et al., 1998; Thoumine and Ott, 1997) have demonstrated that the cell body can be approximated by a linear solid (Kelvin body). Bausch et al. have shown that NIH, 3T3 fibroblast cell behaves as a linear viscoelastic body in response to the external force up to 2 × 10³ pN with the relaxation time ∼0.1 s. Because in our measurements the trap force was at most 20 pN, well below the above limit, the relaxation due to the viscoelastic response should disappear within a fraction of a second. However, the change in the bead velocity continued for ∼1 s (Fig. 2, h–m). Thus, we presume that the viscoelastic behavior of the cell was not the major cause of the observed velocity change.

The measured bead velocity (up to 20 nm/s) was significantly lower than the speed of protrusion of the leading edge of mouse and chick fibroblasts in locomotion (100 nm/s; Abercrombie et al., 1970) and Rat2 cells (∼100 nm/s; Bear et al., 2002). The range of protrusion in our case (up to 100 nm) was also significantly smaller than the previous values (2–5 μm by Abercrombie et al.; ∼10 μm by Rotsch et al., 1999; 5 μm by Bear et al., 2002). These discrepancies may be in part due to the different experimental conditions: we subcultured the cells on the poly-L-lysine-coated glass and applied PMA to facilitate spreading and promote ruffling activity, whereas the previous studies used polarized, unstimulated cells spread on the extracellular matrix. Under our condition, PMA-stimulated cells were nonpolarized and the protrusive activity occurred all around the cell periphery. As a result of this, the protrusive activity at any one location was less pronounced as compared with the polarized cells in which the protrusive activity is more localized to limited location.

Our experiment has suggested an intimate relation between the protrusive and the withdrawal behavior: the acceleration and deceleration in the bead movement both in the protrusive and the withdrawal phases, and correlation existed between the protrusive and withdrawal velocities under various conditions. The change in the trap stiffness altered the velocity and the rate of occurrence of the movement not only in the protrusive phase, but also in the withdrawal phase. The similarity in the magnitudes of the protrusive and withdrawal velocities has been described (Abercrombie et al., 1970; Sheetz et al., 1992; Bear et al., 2002), which leads to a proposal of involvement of myosin in the protrusive as well as the withdrawal phases (Sheetz et al., 1992). Our result also invokes a mechanism that can explain the relation between the protrusive and withdrawal movement. Bear et al. (2002) have pointed out that the withdrawal of the peripheral membrane can occur as a result of collapse of relatively long actin filaments that bend or buckle easily. However, if it occurred in this experiment, the trapping force was at its maximum at the beginning of the failure, and hence the rearward motion of the bead would start with a maximum velocity, which was not the case here. We should consider other mechanisms to explain our experimental observations.

Potential mechanisms consistent with our experimental observations are 1), motor-assisted actin assembly in the protrusive phase and the motor-driven backward translocation of actin network in the withdrawal phase (Sheetz et al., 1992) with regulation of the motor activity both in the protrusive and the withdrawal phases, or 2), a combination of the polymerization-driven protrusive movement and the motor-driven withdrawal movement. In the second case, the polymerization activity and the motor activity are so regulated that the change in the velocity of the protrusive phase becomes similar to that of the withdrawal phase. It has been postulated that polymerizable actin monomer is provided by disassembly of actin filaments at the rear of lamellipodia (Cramer, 1999): the disassembly can be controlled through regulation of the activity of actin depolymerizing factor or cofilin and this may be a part of the presumed regulatory mechanism, because at least in the migrating cells the disassembly seems to be tightly coupled to the lamellipodial protrusion (Cramer et al., 2002). In addition, membrane tension, which acts as a load (Sheetz and Dai, 1996), might change and regulate the protrusive velocity.

The bead held in the stiffer trap moved less frequently with lower speed, indicating that the rate of filament elongation was lower perhaps due to the reduction of the on-rate of polymerization. One possibility to explain this is that the monomer concentration and/or myosin activity was lower when the trap stiffness was higher. However, we rather consider the possibility that the polymerization was physically blocked at higher trap stiffness by the bead placed immediately before the cell membrane. When the gap between the cell peripheral membrane and the underlying network is created, the cell membrane will become able to thermally fluctuate. For example, the flexibility of erythrocyte membranes, expressed as a bending modulus, is the order of 10⁻¹⁹ J (Evans, 1983; Scheffer et al., 2001). This value will yield an amplitude of out-of-plane thermal fluctuation of a tension-free (0.5 μm)² membrane as large as ∼10 nm (Helfrich and Servuss, 1984). Thermal fluctuation of the bead held in the trap as represented with the root-mean-square displacement is ∼2 nm at 0.090 pN/nm (Svoboda and Block, 1994). Hence, the bead contacting or placed near the membrane will physically confine the membrane movement. The confinement will be weaker at the lower trap stiffness: the root-mean-square displacement of the bead is ∼1.9 times larger at the trap stiffness of 0.024 pN/nm. Therefore, we speculate that the fluctuation of the cell membrane plays an important role in the final step of the membrane protrusion process, although the gap creation is likely to depend on myosin. The broad distribution of the maximum velocities at the lowest trap stiffness (diamonds in Fig. 3 b) may reflect the stochastic behavior of the membrane. Recent reports suggest that the elastic Brownian ratchet is a plausible mechanism operating in the protrusive process (Bear et al., 2002; Cramer, 2002), and the above argument should apply to this situation as well, although our experimental cannot distinguish the elastic Brownian ratchet from the Brownian ratchet model.

Previous studies have demonstrated that polymerization of actin inside the liposome was sufficient to deform the lipid membrane (Cortese et al., 1989; Miyata and Hotani, 1992; Miyata et al., 1999). Hence, if the motor-assisted mechanism operates in the protrusive phase, it would be a functional redundancy. However, at the leading edge of the cell, anchoring of actin filaments to the cell membrane has been suggested (Borisy and Svitkina, 2000). Therefore, it is conceivable that the motor-assisted detachment of the filaments from the membrane is a necessary mechanism for efficient lamellipodial protrusion.