Abstract
Leukocyte recruitment from the bloodstream to surrounding tissues is an essential component of the immune response. Capture of blood-borne leukocytes onto vascular endothelium proceeds via a two-step mechanism, with each step mediated by a distinct receptor-ligand pair. Cells first transiently adhere, or “roll” (via interactions between selectins and sialyl-Lewis-x), and then firmly adhere to the vascular wall (via interactions between integrins and ICAM-1). We have reported that a computational method called adhesive dynamics (AD) accurately reproduces the fine-scale dynamics of selectin-mediated rolling. This paper extends the use of AD simulations to model the dynamics of cell adhesion when two classes of receptors are simultaneously active: one class (selectins or selectin ligands) with weakly adhesive properties, and the other (integrins) with strongly adhesive properties. AD simulations predict synergistic functions of the two receptors in mediating adhesion. At a fixed density of surface ICAM-1, increasing selectin densities lead to greater pause times and an increased tendency toward firm adhesion; thus, selectins mechanistically facilitate firm adhesion mediated by integrins. Conversely, at a fixed density of surface selectin, increasing ICAM-1 densities lead to greater pause times and an increased tendency to firm adhesion. We present this relationship in a two-receptor state diagram, a map that relates the densities and properties of adhesion molecules to various adhesive behaviors that they code, such as rolling or firm adhesion. We also present a state diagram for neutrophil activation, which relates β2-integrin density and integrin-ICAM-1 kinetic on rate to neutrophil adhesive behavior. The predictions of two-receptor adhesive dynamics are validated by the ability of the model to reproduce in vivo neutrophil rolling velocities from the literature.
INTRODUCTION
Trafficking of blood-borne cells to tissues and organs is necessary for numerous immune functions, including inflammation, lymphocyte homing, and bone marrow replenishment after transplantation (Springer, 1994). Cellular trafficking depends on specific interactions between receptors on the cell surface and counterreceptors on the vascular wall. Leukocyte recruitment to the vessel wall proceeds via a multistep process, with each step mediated by distinct cell adhesion molecules. Initially, E- and P-selectin expressed on activated vascular endothelium interact with cell surface molecules bearing the carbohydrate sialyl-Lewis-x (sLex) (Rosen and Bertozzi, 1994). Selectin-sLex binding and force-driven unbinding generates transient adhesion, referred to as “rolling,” of leukocytes along the vessel wall. Once leukocytes have been slowed by selectin-mediated rolling, they become activated to firmly adhere to the vessel wall (Lawrence and Springer, 1991). Firm adhesion is mediated by interactions between cell surface β2-integrins and endothelial intercellular adhesion molecule-1 (ICAM-1). Different dynamic states of adhesion are thus mediated by different classes of adhesion molecules.
The dynamics of adhesion are ultimately determined by the physical chemistry of receptor-ligand interactions. For example, cell-free adhesion experiments from our laboratory (Brunk and Hammer, 1997; Rodgers et al., 2000; Greenberg et al., 2000) can successfully recreate leukocyte rolling. In such experiments, colloidal microspheres coated with selectin ligands, such as sLex or PSGL-1, are perfused over selectin-coated surfaces. We have demonstrated that these model leukocytes roll specifically over E-, P- and L-selectin substrates at velocities comparable to those of similarly sized real leukocytes (Brunk and Hammer, 1997; Rodgers et al., 2000; Greenberg et al., 2000). These results suggest that rolling adhesion is determined primarily by the physical chemistry of selectin-ligand binding, whereas features such as cell deformability, morphology, and signaling may act only to modulate behavior. Likewise, it is widely accepted that firm adhesion is controlled by integrin-ICAM-1 interactions, and that when pushed into an active state, integrins have functional properties that ensure firm binding (Stewart and Hogg, 1996). Indeed, experimental measurements of the physical properties of adhesion molecules have suggested that activated integrin-ICAM-1 bonds have an unstressed dissociation rate at least 25-fold lower than that of selectin-sLex bonds (Shimaoka et al., 2001; Smith et al., 1999), consistent with the role of activated integrin-ICAM-1 interactions in mediating firm adhesion as opposed to rolling.
Although the adhesive states that selectins and integrins support are known, the mechanism by which leukocytes go from rolling to firm adhesion, as well as the precise molecular requirements (i.e., the density of selectins and integrins) for leukocyte arrest, remain unclear. Further, the molecular requirements depend precisely on the type of leukocyte; the discussion here focuses on granulocytes. Studies in double knockout mice show that deficiency in E- and P-selectin can eliminate the granulocyte-mediated inflammatory response, even when integrins and ICAM-1 are available for firm adhesion (Bullard et al., 1996). Selectin-mediated rolling is thus necessary for integrin-mediated firm adhesion. However, granulocyte rolling velocities during inflammation are significantly increased in ICAM-1-deficient mice (Steeber et al., 1999), suggesting that ICAM-1 is also required for optimal selectin-mediated rolling. Moreover, the combined loss of both L-selectin and ICAM-1 dramatically reduces leukocyte migration into sites of inflammation beyond what is observed with loss of either receptor alone (Steeber et al., 1999). This result indicates synergistic roles for selectins and ICAM-1 in optimal leukocyte rolling and arrest. Tracking of individual leukocytes in the microcirculation by intravital microscopy demonstrates that rolling leukocytes exhibit a gradual, β2-integrin-dependent decrease in rolling velocity before arrest (Kunkel et al., 2000). This suggests a model of leukocyte recruitment in which β2-integrins play an essential role in stabilizing leukocyte rolling for a protracted period before arrest and firm adhesion.
The transition from rolling to firm adhesion may involve intracellular or extracellular mechanisms. Two mechanisms have been proposed for the cellular switch from rolling to firm adhesion. The first involves chemokines on the endothelial cell surface. In this model, chemokines transduce the signals that trigger integrin activity (Ebnet and Vestweber, 1999). Several chemokines, including stromal cell derived factor-1α (SDF-1α), secondary lymphoid tissue cytokine, and macrophage inflammatory protein-3β (MIP-3β), have been shown to trigger adhesion of lymphocytes to ICAM-1 in glass capillaries, and chemokines SDF-1β, MIP-3α, and macrophage chemoattractant protein-3 (MCP-3) induce adhesion of peripheral lymphocytes to ICAM-1 in static assays (Campbell et al., 1998). Under shear stress, the chemokine interleukin-8 (IL-8) induces strong neutrophil but not T-lymphocyte binding to ICAM-1, suggesting that IL-8 triggers firm adhesion of rolling neutrophils to endothelium at sites of inflammation (Tangemann et al., 1998).
A second possible mechanism for the transition from rolling to firm adhesion is that engagement of selectins leads to intracellular signaling and upregulation or activation of integrin receptors on the cell surface (Crockett-Torabi et al., 1995). L-selectin ligation has been shown to upregulate cell surface expression of β2-integrins (Crockett-Torabi et al., 1995). Binding of glycosylation-dependent cell adhesion molecule-1 (GlyCAM-1), a natural L-selectin ligand, to L-selectin on human lymphocytes activates integrin-mediated binding of these cells to ICAM-1, an integrin ligand (Hwang et al., 1996). In addition, binding of P-selectin-IgG to mouse neutrophils stimulates integrin-mediated binding to ICAM-1; PSGL-1 is necessary and sufficient for this process (Blanks et al, 1998). Despite studies showing upregulation of integrin activity by selectin ligation in static assays, it is unclear whether this effect can be demonstrated under hydrodynamic flow. Gopalan and co-workers (1997) have reported that neutrophils roll but do not arrest over monolayers expressing ICAM-1 and E-selectin, under shear stresses of 2 dynes/cm2. In a more recent study, Simon and co-workers (2000) demonstrated that neutrophil tethering on E-selectin under hydrodynamic flow leads to arrest via β2-integrins, through a mitogen-activated protein kinase (MAPK)-dependent signal transduction pathway. It is possible that the transition from rolling to firm arrest may require both chemokines and selectin-initiated signaling. However, the mechanism of this transition needs to be studied further.
To clarify the relationship between the molecular properties of adhesive molecules and the macroscopic behavior such as rolling or firm adhesion that they mediate, our laboratory has devised a direct numerical simulation of a spherical cell interacting with a reactive surface under flow (Hammer and Apte, 1992). Our computational model incorporates the hydrodynamics of a sphere rotating and translating near a plane under shear flow (Jeffrey, 1915; Brenner, 1961; Goldman et al., 1967a,b), and the force-dependent binding kinetics proposed by Bell (1978) and later modified by Dembo and co-workers (Dembo et al., 1988). A Monte Carlo simulation of the molecular binding and unbinding events is coupled with the deterministic solution of the equations of cell motion, which include hydrodynamics and wall effects. The resulting adhesive dynamics (AD) simulation accurately reproduces the fine scale dynamics of selectin-mediated rolling (Chang and Hammer, 2000). Given information on the physical chemistry of a receptor-ligand pair, the simulation can predict the dynamic behavior of cells contacting surfaces under shear flow (Chang et al., 2000).
AD simulations have demonstrated that the dynamic state of adhesion under flow is controlled by mechanochemical properties of adhesion molecules, as proposed by Bell (1978) and Chang et al. (2000). Different states of adhesion, including no adhesion, transient adhesion (rolling), and firm adhesion, emerge for different values of Bell model parameters. The unstressed dissociation rate and the bond interaction length are the most important molecular properties controlling the dynamics of adhesion. We have expressed the relationship between these receptor-ligand functional properties and the dynamics of adhesion in a state diagram, a one-to-one map between the biophysical properties of adhesion molecules and various adhesive behaviors (Chang et al., 2000). Experimental values from the literature for the unstressed dissociation rate and the bond interaction length, for molecules that are known to mediate rolling adhesion, fall within the rolling region of the state diagram. Thus, given the molecular properties of the receptor-ligand system of interest, AD simulations can accurately predict macroscopic adhesive behavior.
The current study extends the use of AD simulations to determine the dynamics of adhesion when two receptor-ligand systems are simultaneously active. One system is characterized by relatively weak adhesive properties, such as a low association rate and high unstressed dissociation rate, which suggest a propensity for rolling interactions, as are experimentally observed with the selectin-sLex system. The second system is characterized by relatively strong adhesive properties, such as a high association rate and low unstressed dissociation rate, as are experimentally observed with the activated integrin-ICAM-1 system. AD simulations predict that the two receptor-ligand systems have synergistic roles in promoting leukocyte adhesion and arrest. At low surface densities of ICAM-1 at which rolling is observed, addition of selectins causes a transition in adhesive behavior from rolling to firm adhesion. Conversely, at low surface densities of selectins at which rolling is observed, addition of ICAM-1 leads to a transition from rolling to firm adhesion. We present these results in a two-receptor state diagram, a map between the densities of the two receptor-ligand systems and the macroscopic adhesive behavior. The state diagram illustrates that selectin-sLex interactions and integrin-ICAM-1 interactions have synergistic functions in promoting cell adhesion and arrest. In addition, the two receptor-ligand systems have complementary functions: integrin-ICAM-1 bonds allow cell arrests of lengthened duration, whereas selectin-sLex bonds allow stable periods of rolling adhesion that transition the cell between durable arrests. The predictions of two-receptor adhesive dynamics are validated by the ability of the model to reproduce published in vivo neutrophil rolling velocities. Simulation parameters that independently reproduce neutrophil rolling velocities from E−/− and CD18−/− knockout mice can be combined to reproduce the two-receptor-mediated rolling of neutrophils in wild-type mice.
METHODS
Adhesive dynamics
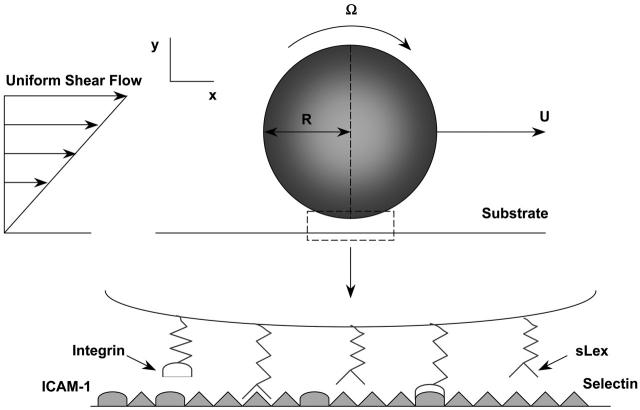
The adhesive dynamics method (shown schematically in Fig. 1) has been thoroughly described in several articles by Hammer and co-workers (Hammer and Apte, 1992; Chang and Hammer, 2000; Chang et al., 2000; King and Hammer, 2001). Essentially, a large number of adhesion molecules are randomly placed on the surface of a sphere and bounding wall. In the near-contact region between sphere and plane, adhesive receptor-ligand pairs are randomly tested for bond formation according to their deviation length-dependent binding kinetics. If a bond forms, over its lifetime it is represented by a linear spring whose endpoints remain fixed with respect to either surface. The orientation and length of each spring specifies the instantaneous force and torque exerted by that bond on the sphere, and also its probability for breakage per unit time. A summation of all external forces and torques enables a mobility calculation to determine the translational and rotational velocities of the sphere under flow. For a single particle in low Reynolds number Couette flow, the mobility function is available as a closed-form solution for all modes of motion (Hammer and Apte, 1992).
FIGURE 1.
Schematic diagram of adhesive dynamics. Adhesion molecules are randomly placed on the surface of a sphere and plane wall. Adhesive receptor-ligand pairs are tested for bond formation according to deviation length-dependent binding kinetics.
One model commonly used to describe the kinetics of single biomolecular bond failure is that of Bell (1978),
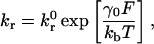 |
(1) |
which relates the rate of dissociation kr to the magnitude of the force on the bond F. The unstressed off rate kr0 and reactive compliance γ0 have been experimentally determined for the selectins with their respective ligands by observing pause-time distributions when perfusing cells or beads over sparsely populated surfaces (Alon et al., 1995; Smith et al., 1999). Initial estimates of the unstressed off rate for integrin-ICAM-1 bonds have been made using BIAcore measurements (Shimaoka et al., 2001). Other more sophisticated methods, collectively known as dynamic force microscopy (Evans and Ritchie, 1997; Tees et al., 2001), have been used to measure the force-driven dissociation of single bonds, demonstrating that the Bell equation is valid over some force-loading regimes (typically fast loading). Once the rate of dissociation is set by Eq. 1, the rate of formation directly follows from the Boltzmann distribution for affinity (Bell et al., 1984),
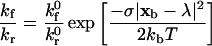 |
(2) |
and takes the form
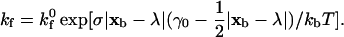 |
(3) |
In the above expressions, σ is the Hookean spring constant and |xb − λ| is the deviation bond length. The intrinsic on rate kf0 has not been experimentally measured; a kf0 value of 84 s−1 for selectin-ligand species has been shown to match simulations with experiment (Chang et al., 2000). For integrin-ICAM-1 species, the kf0 value is chosen to be one order of magnitude larger than that of selectin-ligand species. The expressions for the forward-binding rate must also incorporate the effect of the relative motion of the two surfaces. Chang and Hammer (1999) calculated the effective rate of collision of surface-tethered reactants in relative motion when the Peclet number (Pe = (radius of receptor)(relative velocity)/(lateral diffusivity)) is nonzero, and showed that the on rate exhibits a first-order dependence on Pe. The result is that the probability of bond formation is proportional to the slip velocity between the cell and plane, which has important implications to both commonly observed phenomena such as the shear-threshold effect (Finger et al., 1996; Greenberg et al., 2000) and the present study.
A very short-range repulsive force representing the contact force between surfaces is included, of the form
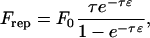 |
(4) |
where 1/τ is a length scale on the order of angstroms and ɛ is the surface-to-surface separation. Frep is directed normal to the plane in the case of cell-plane interactions. In the presence of particle-particle interactions, Eq. 4 is also used, directed along the line connecting cell centers. Although these two parameters have a physical significance when Eq. 4 is used as a model of the repulsion of an electronic double layer (Takamura et al., 1981), we use Eq. 4 as a generic short-range interaction and arbitrarily assign values of τ = 5 Å and F0 = 103 N. This force is of sufficiently short range to allow specific chemical adhesion while preventing cell overlap. Phenomenological expressions of this mathematical form have been used in other studies of cell adhesion, where ions in solution filter out the longer range van der Waals attraction (Bell et al., 1984). As a model of the roughness of the spherical and planar surfaces, it was assumed that both surfaces are covered with small bumps of sufficient coverage to support the particle, yet of a dilution that permits the flow disturbance caused by the bumps to be neglected. The contact interactions of adhesion and repulsion are exerted by the tips of these roughness elements. This simple model of surface roughness serves as a steric layer that prevents the hydrodynamic lubrication singularity that would be created by a mathematically smooth sphere contacting a mathematically smooth plane, a physically unrealistic situation. A value of surface roughness consistent with scanning electron micrographs of the beads was used, and, in practice, the results were found to be insensitive to the precise value of this parameter. Gravitational force is added, because beads and cells are typically denser than aqueous solution. This force promotes initial contact between the cell and the wall.
The solution algorithm for single-cell AD is as follows: 1), all unbound molecules in the contact area are tested for formation against the probability Pf = 1 − exp(−kfΔt), with kf given by Eq. 3; 2), all of the currently bound molecules are tested for breakage against the probability Pr = 1 − exp(−krΔt), with kr given by Eq. 1; 3), the external forces and torques on each cell are calculated by summing over adhesive forces and adding nonspecific interparticle and gravitational forces; 4), the mobility calculation is performed to determine the rigid body motions of the cells; and 5), cell and bond positions are updated according to the kinematics of cell motion. A MIPSpro Fortran 90 random number generator is used in steps 1 and 2; if the random number is greater that the probability, the bond is broken or formed in the time step.
An improvement over the original algorithm (Hammer and Apte, 1992) that was first implemented by King and Hammer (2001) is to only assign coordinates to molecules after they form a bond, and to cease to keep track of these coordinates after the bond has broken. This eliminates the need to continually update the coordinates of unbound molecules, relieving demands on storage and computational time. The contact area is defined as a circular area whose outer radius represents a surface-to-surface separation at which the probability for bond formation becomes vanishingly small. At each time step, the unbound molecules in the contact area are randomly assigned a bond length to perform the Monte Carlo test for bond formation. Note that the proper area weighted distribution of bond lengths is the square root of a uniform random variate ranging from 0 to 1. If the test for formation is successful, then the new bond is given three-dimensional coordinates on both surfaces. Bonds are assumed to be aligned vertically upon formation, a reasonable simplification because extensive calculations have shown that rolling behavior is insensitive to initial bond orientation, and given the small ratio of bond length to particle size. An additional random number, representing the polar angle of the bond in the circular contact area, fixes the coordinates on both surfaces.
For small particles (cells) suspended in a viscous fluid, one can neglect the particle's inertia, and the motion of the fluid is governed by the Stokes and continuity equations,
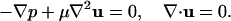 |
(5) |
The symbol p denotes the pressure, u is the velocity, and μ the fluid viscosity. No-slip conditions are enforced at the surface of the cell:
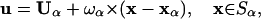 |
(6) |
where Uα and ωα are the translational and rotational velocities of cell α, xα its center of mass, and Sα its corresponding surface. The fluid velocity is also taken to be zero at the bounding planar wall (x3 = 0). The motion of an isolated cell is related to the forces acting on it by the 6 × 6 mobility matrix M:
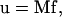 |
(7) |
where u is a six-element vector containing the sphere's translational and rotational velocities, and f is a vector containing the three components of net force and three components of the net torque acting on the sphere. For an isolated sphere near a plane in Stokes flow, all of the components of the mobility matrix M are known (Jeffrey, 1915; Brenner, 1961; Goldman et al., 1967a,b). Thus, after all of the external forces acting on the cell have been summed, the instantaneous sphere velocities can be evaluated directly from Eq. 7. The new positions of the sphere and tethers at t + dt are updated from their positions at t, using the translational and angular velocity of the cell. The process is repeated until 10 s of simulation time have elapsed.
RESULTS
Parameters used for the simulations are given in Table 1. All simulations in this paper are performed at a constant wall shear rate of 100 s−1, unless otherwise noted. This shear rate is in the center of the range for which leukocyte rolling is observed (Lawrence et al., 1987; Lawrence et al., 1990); the influence of shear rate on adhesive behavior is explored later in the results section. The particle size is chosen to match values from selectin-mediated rolling experiments (Brunk and Hammer, 1997). Cell surface densities of sLex and β2-integrin are set such that they are in excess of wall densities of selectin and ICAM-1, unless otherwise noted. Thus, selectin site density is the limiting reagent in selectin-sLex interactions, and ICAM-1 site density is the limiting reagent in integrin-ICAM-1 interactions.
TABLE 1.
Values of physical parameters used in simulations
| Parameter | Definition | Value | Reference |
|---|---|---|---|
| a | Particle radius | 5 μm | Brunk et al., 1996 |
| G | Shear rate | 100 s−1 | Lawrence et al., 1990 |
| μ | Viscosity | 0.01 P | |
| ρ | Fluid density | 1.0 g/cm3 | |
| Δρ | Density difference | 0.05 g/cm3 | |
| ɛs | Sphere roughness | 175 nm | King and Hammer, 2001 |
| ɛw | Wall roughness | 50 nm | King and Hammer, 2001 |
| σ | Spring constant | 100 dyn/cm | Morozov and Morozova, 1990 |
| λ | Equilibrium bond length | 20 nm | Bell, 1978 |
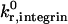 |
Unstressed off-rate for selectin-sLex | 2.4 s−1 | Smith et al., 1999 |
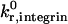 |
Unstressed off-rate for integrin-ICAM-1 | 0.1 s−1 | Shimaoka et al., 2001 |
| γ0,selectin | Reactive compliance for selectin-sLex | 0.39 Å | Smith et al., 1999 |
| γ0,integrin | Reactive compliance for integrin-ICAM-1 | 0.39 Å | |
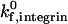 |
Intrinsic on-rate for selectin-sLex | 84 s−1 | Chang et al., 2000 |
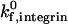 |
Intrinsic on-rate for integrin-ICAM-1 | 10–1000 s−1 | |
| T | Temperature | 298 K | |
| nr,selectin | Selectin surface density | 1–100 molc/μm2 | |
| nr,ICAM | ICAM-1 surface density | 1–100 molc/μm2 |
The unstressed off rate for selectin-sLex bonds, 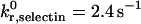 , and the reactive compliance for selectin-sLex bonds, γ0,selectin = 0.39 Å, are taken from experimental
, and the reactive compliance for selectin-sLex bonds, γ0,selectin = 0.39 Å, are taken from experimental 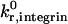 and γ0,selectin values measured for the P-selectin/PSGL-1 receptor-ligand pair (Smith et al., 1999). The intrinsic on rate for selectin-sLex bonds,
and γ0,selectin values measured for the P-selectin/PSGL-1 receptor-ligand pair (Smith et al., 1999). The intrinsic on rate for selectin-sLex bonds,  , has not been adequately measured. The chosen rate,
, has not been adequately measured. The chosen rate, 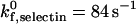 , is a reasonable value that extensive simulation shows can properly recreate experimental values for velocity and dynamics of rolling (Chang et al., 2000); this value was used in our previous one-receptor state diagram study (Chang et al., 2000).
, is a reasonable value that extensive simulation shows can properly recreate experimental values for velocity and dynamics of rolling (Chang et al., 2000); this value was used in our previous one-receptor state diagram study (Chang et al., 2000).
The kinetic parameters for integrin-ICAM-1 bonds are chosen to reflect the activated state of the β2-integrin. Although the mechanism by which β2-integrins become activated is unknown, and Bell model parameters for activated integrin-ICAM-1 bonds have not been experimentally determined, it has been proposed that integrin conformational change regulates adhesiveness (Stewart and Hogg, 1996). The Springer group has performed BIAcore measurements of the unstressed off rate for interactions between ICAM-1 and the integrin αL I domain, and demonstrated that the kinetics of interaction are conformation dependent (Shimaoka et al., 2001). Locking the αL I domain in an “open” conformation with disulfide bonds results in a 9000-fold increase in affinity to ICAM-1 (Shimaoka et al., 2001); the open conformation may represent the activated state of β2-integrin. The unstressed off rate for integrin-ICAM-1 bonds in our simulation, 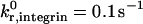 , matches the order of magnitude of the Springer group's off-rate measurement for interactions between ICAM-1 and open integrin αL I domains. The reactive compliance of activated integrin-ICAM-1 bonds is unknown. The initial value used in our simulations, γ0,integrin = 0.39 Å, is chosen to match that of selectin-sLex bonds; the influence of γ0,integrin on adhesive behavior is explored later in the results section.
, matches the order of magnitude of the Springer group's off-rate measurement for interactions between ICAM-1 and open integrin αL I domains. The reactive compliance of activated integrin-ICAM-1 bonds is unknown. The initial value used in our simulations, γ0,integrin = 0.39 Å, is chosen to match that of selectin-sLex bonds; the influence of γ0,integrin on adhesive behavior is explored later in the results section.
The intrinsic on rate for integrin-ICAM-1 bonds in our simulations, 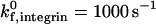 , is an order of magnitude larger that that for selectin-sLex bonds. This value is based upon BIAcore measurements of integrin-ICAM-1 bonds and selectin-ligand bonds from the literature, which suggest that the three-dimensional (3-D) on rate of activated integrin-ICAM-1 bonds may be an order of magnitude larger than that of selectin-ligand bonds. Specifically, two separate studies by the Springer group and Labadia and co-workers both demonstrate a kon for activated integrin-ICAM-1 bonds on the order of 105 M−1 s−1 at 25°C (Shimaoka et al., 2001; Labadia et al., 1998), whereas the Vestweber group reports a kon for E-selectin-ESL-1 bonds on the order of 104 M−1 s−1 at 25°C (Wild et al., 2001). Taken together, these studies suggest a higher association rate for integrin-ICAM-1 than selectin-ligand interactions. However, there is also evidence for higher kon values for selectin-ligand interactions; Mehta and co-workers report a kon for P-selectin-PSGL-1 interactions on the order of 106 M−1 s−1 at 25°C, and Nicholson and co-workers report a kon for L-selectin-GlyCAM-1 interactions of 105 M−1 s−1 at 25°C (Mehta et al., 1998; Nicholson et al., 1998). Thus, the on rate for activated integrin-ICAM-1 bonds may be equal to or lower than that of selectin-ligand interactions. Although the simulations in our study are primarily performed at an integrin-ICAM-1 association rate of
, is an order of magnitude larger that that for selectin-sLex bonds. This value is based upon BIAcore measurements of integrin-ICAM-1 bonds and selectin-ligand bonds from the literature, which suggest that the three-dimensional (3-D) on rate of activated integrin-ICAM-1 bonds may be an order of magnitude larger than that of selectin-ligand bonds. Specifically, two separate studies by the Springer group and Labadia and co-workers both demonstrate a kon for activated integrin-ICAM-1 bonds on the order of 105 M−1 s−1 at 25°C (Shimaoka et al., 2001; Labadia et al., 1998), whereas the Vestweber group reports a kon for E-selectin-ESL-1 bonds on the order of 104 M−1 s−1 at 25°C (Wild et al., 2001). Taken together, these studies suggest a higher association rate for integrin-ICAM-1 than selectin-ligand interactions. However, there is also evidence for higher kon values for selectin-ligand interactions; Mehta and co-workers report a kon for P-selectin-PSGL-1 interactions on the order of 106 M−1 s−1 at 25°C, and Nicholson and co-workers report a kon for L-selectin-GlyCAM-1 interactions of 105 M−1 s−1 at 25°C (Mehta et al., 1998; Nicholson et al., 1998). Thus, the on rate for activated integrin-ICAM-1 bonds may be equal to or lower than that of selectin-ligand interactions. Although the simulations in our study are primarily performed at an integrin-ICAM-1 association rate of 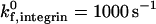 , the effect of
, the effect of 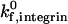 on adhesive behavior is explored extensively in the results section, using
on adhesive behavior is explored extensively in the results section, using 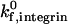 values of 100 s−1 and 10 s−1. This comprehensively represents values of
values of 100 s−1 and 10 s−1. This comprehensively represents values of 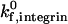 below, above, and roughly equal to the selectin-ligand on rate.
below, above, and roughly equal to the selectin-ligand on rate.
Adhesive behavior states
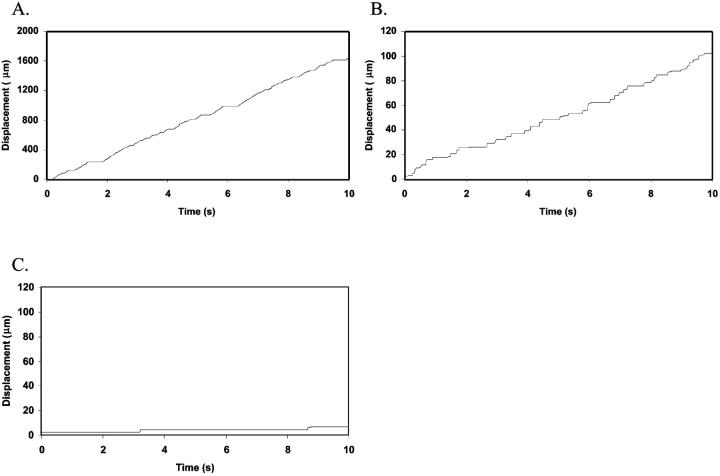
Similar to the previous, single-molecule state diagram paper, we define three distinct, observable dynamic states of adhesion (Chang et al., 2000). Sample trajectories that demonstrate these behaviors are shown in Fig. 2. The “no adhesion” state (Fig. 2 A) is characterized by a cell velocity greater than 50% of its hydrodynamic velocity, VH. In the “rolling adhesion” state (Fig. 2 B), cells translate at a mean velocity V < 0.5 VH, but do not remain permanently arrested. Leukocyte rolling typically falls within this regime, as it typically involves intermittent arrests and mean velocities below 0.5 VH (Brunk and Hammer, 1997; von Andrian et al., 1995; Goetz et al., 1994). In the cell biology literature, rolling is often defined as a significant decrease in velocity, perhaps to 50% or less of the hydrodynamic velocity for cells near a surface (Chen and Springer, 1999). In “firm adhesion” (Fig. 2 C), cells bind and remain motionless. An “arrested” cell is defined as one that translates at a mean velocity V < 0.02 VH. These criteria for defining rolling and firm adhesion are similar to those used in the previous single-molecule state diagram study (Chang et al., 2000), and provide a reasonable threshold for the perceptible transition to firm adhesion. In the examples shown in Fig. 2, A and B, differences in dynamic states are observed by changing the selectin surface density at constant ICAM-1 surface density. In Fig. 2, B and C, differences in dynamic states of adhesion are observed by varying the ICAM-1 surface density at a constant selectin surface density. Thus, depending on the relative densities of the two receptors, different adhesive behaviors may result.
FIGURE 2.
Representative cell trajectories for adhesive behavior states. (A) No adhesion is observed at a selectin density of 1 molecule/μm2 and an ICAM-1 density of 0 sites/μm2. The ratio of cell velocity to hydrodynamic velocity, V/VH, is 60%. (B) Rolling adhesion is observed at a selectin density of 10 molecules/μm2 and an ICAM-1 density of 0 sites/μm2. V/VH is 4%. (C) Firm adhesion is observed at a selectin density of 10 molecules/μm2 and an ICAM-1 density of 4 sites/μm2. V/VH is 0.3%. Calculations are performed with an integrin-ICAM-1 association rate of kf0,integrin = 1000 s−1.
State diagram for two-receptor adhesion
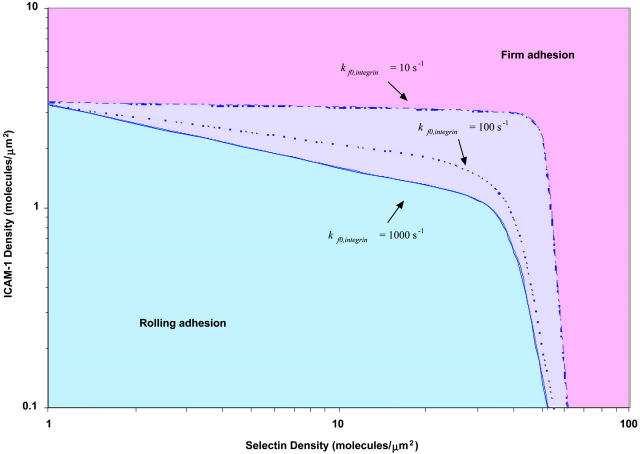
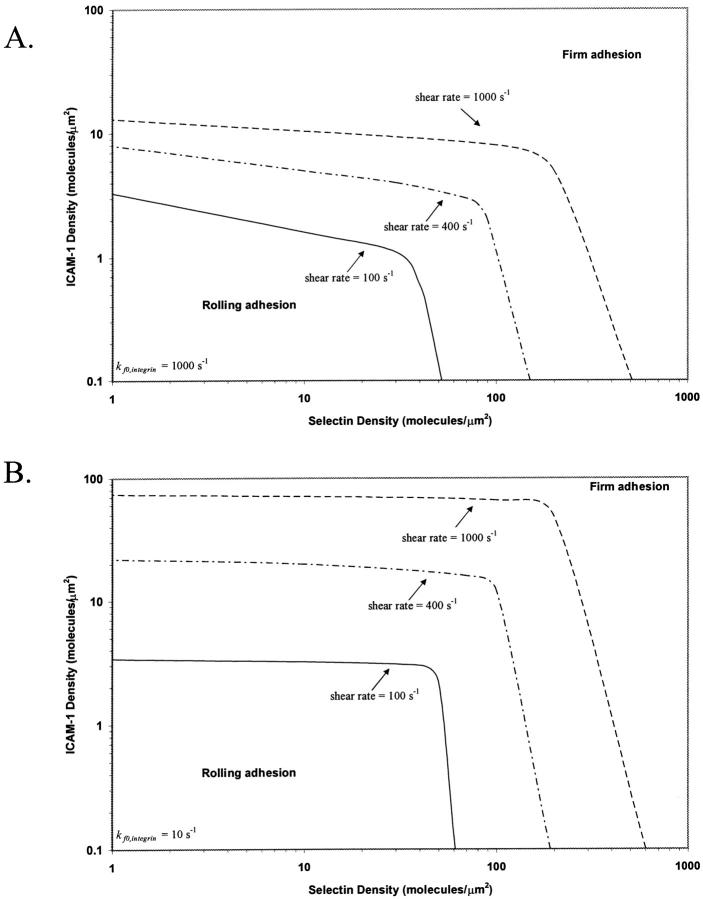
To determine the adhesive behavior expected for a given combination of receptor densities, we calculated a state diagram for two-receptor adhesion (Fig. 3), in which observed adhesive behaviors are plotted for a range of selectin and ICAM-1 surface densities. The boundary separating the states of rolling adhesion and firm adhesion is parametrized by a mean velocity of 0.02 VH. In this state diagram, the rate constants and mechanochemical properties are fixed. For integrin-ICAM-1 interactions, rate constants reflecting the activated state of the β2-integrin are used. The boundary separating rolling and firm adhesion is calculated for three different integrin-ICAM-1 association rates, 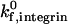 = 1000, 100, and 10 s−1.
= 1000, 100, and 10 s−1.
FIGURE 3.
The state diagram for adhesion mediated by two receptors. The boundary of rolling adhesion is shown for three different integrin-ICAM-1 association rates: kf0,integrin = 1000, 100, and 10 s−1. For each rolling state, the boundary represents a mean velocity of 0.02 VH.
The state diagram demonstrates synergistic functions of the two receptor-ligand systems in promoting cell adhesion and arrest. For example, at a selectin site density of 30 molecules/μm2, the state diagram predicts rolling adhesive behavior if no ICAM-1 is present on the surface. At an ICAM-1 site density of 3 molecules/μm2, the state diagram predicts rolling adhesion if no selectin is present on the surface. However, the combination of 30 molecules/μm2 selectin and 3 molecules/μm2 ICAM-1 results in firm adhesion, when 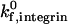 is greater than 100 s−1. As
is greater than 100 s−1. As 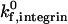 decreases, the location of the firm adhesion envelope shifts to slightly higher ICAM-1 densities, and the synergy between the two receptors is somewhat less pronounced though still present. Instead, at low
decreases, the location of the firm adhesion envelope shifts to slightly higher ICAM-1 densities, and the synergy between the two receptors is somewhat less pronounced though still present. Instead, at low 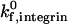 , there are critical values of both selectin and ICAM-1 density necessary for the transition to firm adhesion.
, there are critical values of both selectin and ICAM-1 density necessary for the transition to firm adhesion.
Above a threshold density of either receptor, the cell experiences firm adhesion. At selectin densities greater than 60 molecules/μm2, firm adhesion is predicted, regardless of ICAM-1 site density; this finding may be a result of our definition for firm adhesion, and only applies at the shear rate of 100 s−1 (in these simulations). Similarly, at ICAM-1 densities greater than 4 molecules/μm2, the state diagram predicts firm adhesion, regardless of selectin site density; the density of ICAM-1 required for firm adhesion is relatively insensitive to 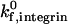 , for the parameter values used here. The density of ICAM-1 required to ensure firm adhesion is an order of magnitude lower than the density of selectin required to mediate firm adhesion; this result is not surprising given the strongly adhesive properties of integrin-ICAM-1 bonds as compared to selectin-sLex bonds. Therefore, addition of ICAM-1 on the surface for a cell rolling on a fixed level of selectin facilitates firm binding, and the presence of selectin facilitates firm binding at fixed levels of integrin and ICAM-1. Clearly, the two molecular pairs work synergistically to support firm binding.
, for the parameter values used here. The density of ICAM-1 required to ensure firm adhesion is an order of magnitude lower than the density of selectin required to mediate firm adhesion; this result is not surprising given the strongly adhesive properties of integrin-ICAM-1 bonds as compared to selectin-sLex bonds. Therefore, addition of ICAM-1 on the surface for a cell rolling on a fixed level of selectin facilitates firm binding, and the presence of selectin facilitates firm binding at fixed levels of integrin and ICAM-1. Clearly, the two molecular pairs work synergistically to support firm binding.
Effect of ICAM-1 site density on adhesive behavior
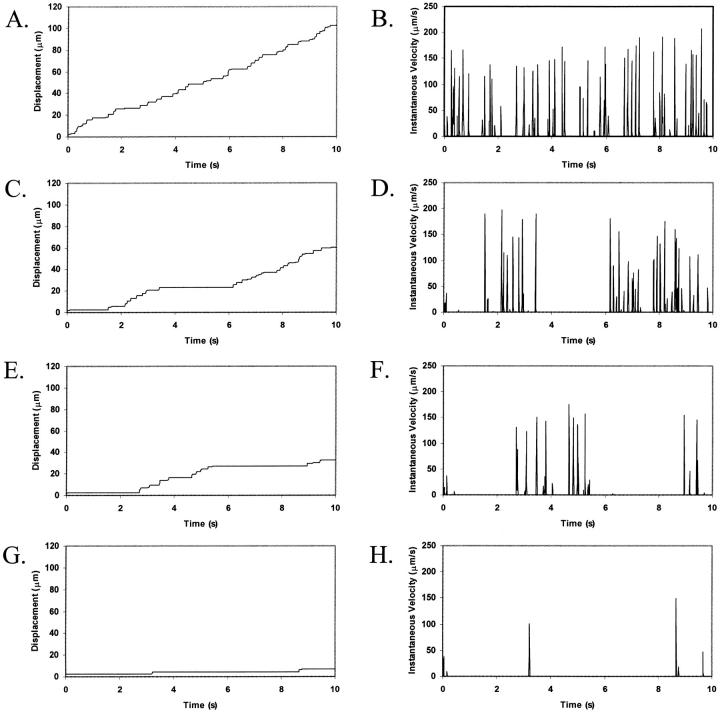
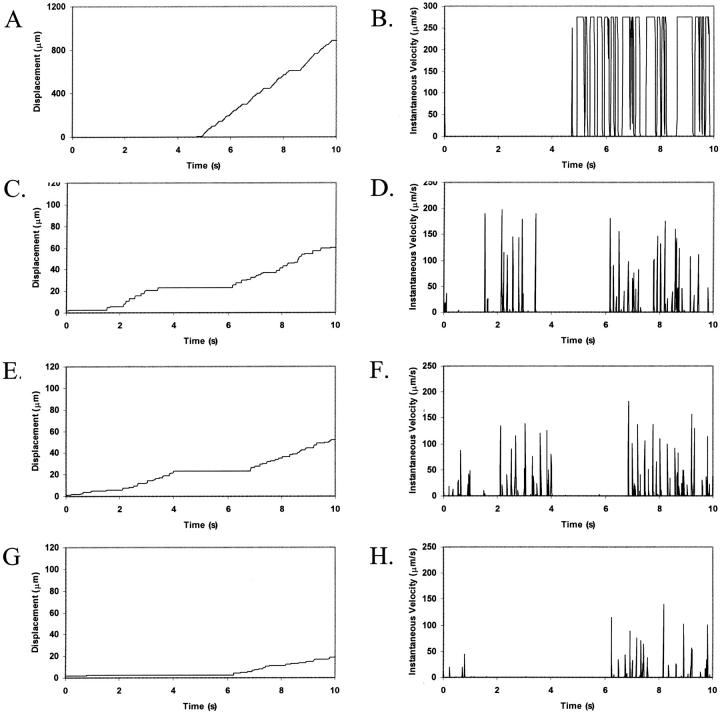
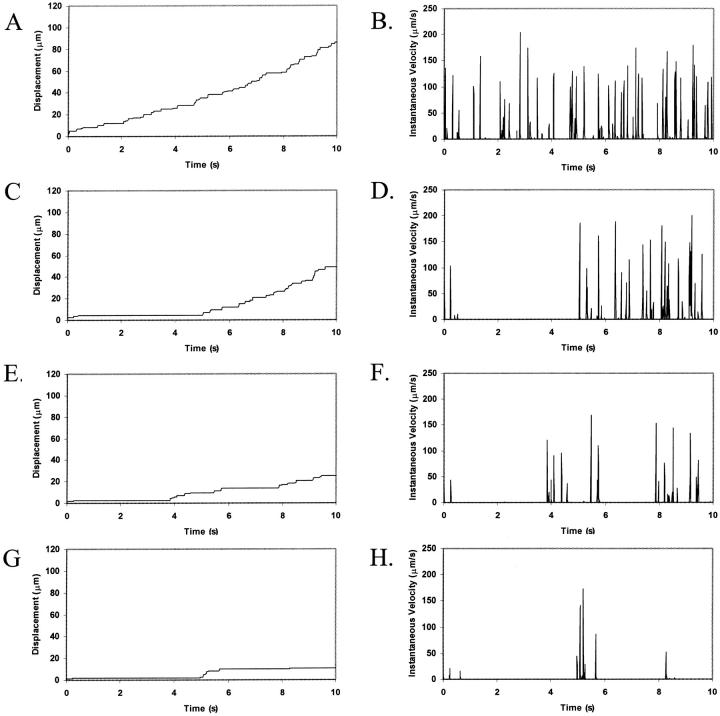
To determine the respective roles of selectin-sLex and integrin-ICAM-1 interactions in mediating cell adhesion, we examined the cell trajectories and instantaneous cell velocities resulting from various surface combinations of selectin and ICAM-1, at a 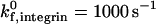 . The influence of ICAM-1 site density on adhesive behavior was determined by examining cell motion over surfaces with various ICAM-1 site densities (0, 1, 2, and 4 molecules/μm2) while keeping the selectin site density constant at 10 molecules/μm2. The dependence of cell trajectory and instantaneous velocities on ICAM-1 density is illustrated in Fig. 4. As ICAM-1 site density increases, the cell experiences more durable arrests. Pause times increase with greater ICAM-1 density, and adhesive behavior becomes saltatory at high ICAM-1 densities, with brief periods of firm arrest separated by periods of flow at VH (Fig. 4, G–H).
. The influence of ICAM-1 site density on adhesive behavior was determined by examining cell motion over surfaces with various ICAM-1 site densities (0, 1, 2, and 4 molecules/μm2) while keeping the selectin site density constant at 10 molecules/μm2. The dependence of cell trajectory and instantaneous velocities on ICAM-1 density is illustrated in Fig. 4. As ICAM-1 site density increases, the cell experiences more durable arrests. Pause times increase with greater ICAM-1 density, and adhesive behavior becomes saltatory at high ICAM-1 densities, with brief periods of firm arrest separated by periods of flow at VH (Fig. 4, G–H).
FIGURE 4.
Effect of ICAM-1 site density on cell trajectories and instantaneous velocity distributions. The surface density of selectin is 10 molecules/μm2. ICAM-1 surface density is (A and B) 0 molecules/μm2; (C and D) 1 molecule/μm2; (E and F) 2 molecules/μm2; and (G and H) 4 molecules/μm2. Calculations are performed with an integrin-ICAM-1 association rate of kf0,integrin = 1000 s−1.
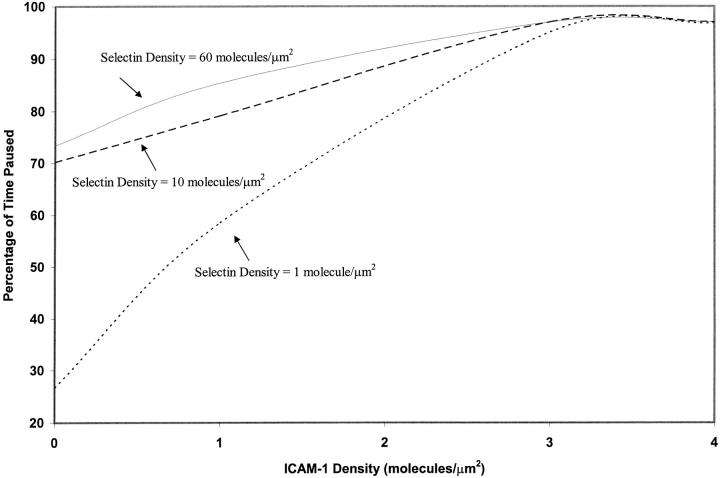
The percentage of time that the cell is paused increases with increasing ICAM-1 density, as shown in Fig. 5. This curve demonstrates that cell pause time rises with ICAM-1 density up to an ICAM-1 density of 3 molecules/μm2, at which concentration the cell is paused for 97% of its motion. The pause time then remains at 97% for ICAM-1 site densities greater than 3 molecules/μm2. These results suggest that the role of integrin-ICAM-1 interactions in cell adhesion is to allow cell arrests of lengthened duration, up until the cell is firmly bound.
FIGURE 5.
Percentage of time paused as a function of ICAM-1 site density and selectin site density, calculated at kf0,integrin = 1000 s−1.
Effect of selectin site density on adhesive behavior
The influence of selectin site density on adhesive behavior was determined by examining cell motion over surfaces with various selectin site densities (1, 10, 30, and 60 molecules/μm2) while keeping the ICAM-1 site density constant at 1 molecule/μm2, at a 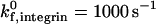 . The dependence of cell trajectory and instantaneous velocities on selectin density is illustrated in Fig. 6. In contrast to ICAM-1, increasing selectin densities do not increase the duration of arrests experienced by the cell. Rather, increasing selectin densities appear to decrease the instantaneous velocity of the cell when it is not arrested. The overall distance traveled by the cell decreases with increasing selectin density; cell arrests are interrupted by periods of progressively slower rolling as selectin site density increases.
. The dependence of cell trajectory and instantaneous velocities on selectin density is illustrated in Fig. 6. In contrast to ICAM-1, increasing selectin densities do not increase the duration of arrests experienced by the cell. Rather, increasing selectin densities appear to decrease the instantaneous velocity of the cell when it is not arrested. The overall distance traveled by the cell decreases with increasing selectin density; cell arrests are interrupted by periods of progressively slower rolling as selectin site density increases.
FIGURE 6.
Effect of selectin-site density on cell trajectories and instantaneous velocity distributions. The surface density of ICAM-1 is 1 molecule/μm2. Selectin surface density is (A and B) 1 molecule/μm2; (C and D) 10 molecules/μm2; (E and F) 30 molecules/μm2; and (G and H) 60 molecules/μm2. Calculations are performed with an integrin-ICAM-1 association rate of kf0,integrin = 1000 s−1.
The relationship between cell pause time and selectin density is illustrated in Fig. 5. This relationship is nonlinear, and dependent on ICAM-1 site density. For example, at a constant low ICAM-1 site density of 1 molecule/μm2, the percentage of time paused increases rapidly from 60 to 80% as selectin density increases from 1 to 10 molecules/μm2. The percent time paused remains relatively unchanged with further increases in selectin density, and increases from 80 to 85% as selectin density increases from 10 to 60 molecules/μm2, at a constant ICAM-1 site density of 1 molecule/μm2. In contrast, at a constant high ICAM-1 site density of 3 molecules/μm2, the percentage of time paused is greater than 95%, regardless of selectin density. Thus, selectin density alters the pause times at low ICAM-1 site densities, but selectin density does not affect pause times when ICAM-1 site densities are high. The relationship between pause times and receptor densities is similar at an integrin-ICAM-1 association rate of 10 s−1 (data not shown). These results suggest that the role of selectin-sLex interactions in cell adhesion is to allow stable periods of rolling adhesion that facilitate the transition between durable arrests; selectin-sLex interactions may play a more essential role when there are few active integrin-ICAM-1 interactions.
Wall shear rate
To determine the sensitivity of the synergy between selectins and integrins to shear rate, we calculated the state diagram at higher shear rates that span the physiological range for postcapillary venules. Fig. 7 shows the dynamics of adhesion for shear rates of 400 s−1 and 1000 s−1, calculated for integrin-ICAM-1 association rates of 1000 s−1 (Fig. 7 A) and 10 s−1 (Fig. 7 B). As shear rate increases, the location of the firm adhesion envelope shifts to higher ICAM-1 site densities. The effect of shear rate on adhesive behavior is moderate at a 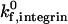 of 1000 s−1, but the effect is dramatic at a
of 1000 s−1, but the effect is dramatic at a 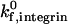 of 10 s−1. For example, an increase in shear rate from 100 s−1 to 1000 s−1 shifts the ICAM-1 density required for firm adhesion from ∼3 molecules/μm2 to 20 molecules/μm2 at a
of 10 s−1. For example, an increase in shear rate from 100 s−1 to 1000 s−1 shifts the ICAM-1 density required for firm adhesion from ∼3 molecules/μm2 to 20 molecules/μm2 at a 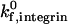 of 1000 s−1. In contrast, at a
of 1000 s−1. In contrast, at a 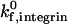 of 10 s−1, an increase in shear rate from 100 s−1 to 1000 s−1 shifts the ICAM-1 density required for firm adhesion from ∼3 molecules/μm2 to 80 molecules/μm2. Adhesive behavior is thus more sensitive to shear rate when the integrin-ICAM-1 association rate is low.
of 10 s−1, an increase in shear rate from 100 s−1 to 1000 s−1 shifts the ICAM-1 density required for firm adhesion from ∼3 molecules/μm2 to 80 molecules/μm2. Adhesive behavior is thus more sensitive to shear rate when the integrin-ICAM-1 association rate is low.
FIGURE 7.
The state diagram with shear rate ranging from 100 to 1000 s−1. The boundary of rolling adhesion is shown for three different shear rates (100, 400, and 1000 s−1), calculated at an integrin-ICAM-1 association rate of (A) kf0,integrin = 1000 s−1 and (B) kf0,integrin = 10 s−1. For each rolling state, the boundary represents a mean velocity of 0.02 VH.
As shear rate increases, rolling adhesion behavior dominates. In addition to shifting to higher ICAM-1 site densities, the firm adhesion envelope shifts to higher selectin site densities with increasing shear rate. The simulation thus predicts that high densities of selectins alone do not mediate firm adhesion at high-shear rates. Synergy between selectins and integrins in mediating firm adhesion is somewhat less pronounced at higher shear rates, as the firm adhesion envelope becomes more horizontal. Some synergy is still apparent though; even at a shear rate of 1000 s−1 and a 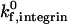 of 10 s−1, the envelope has a slight downward slope (Fig. 7 B).
of 10 s−1, the envelope has a slight downward slope (Fig. 7 B).
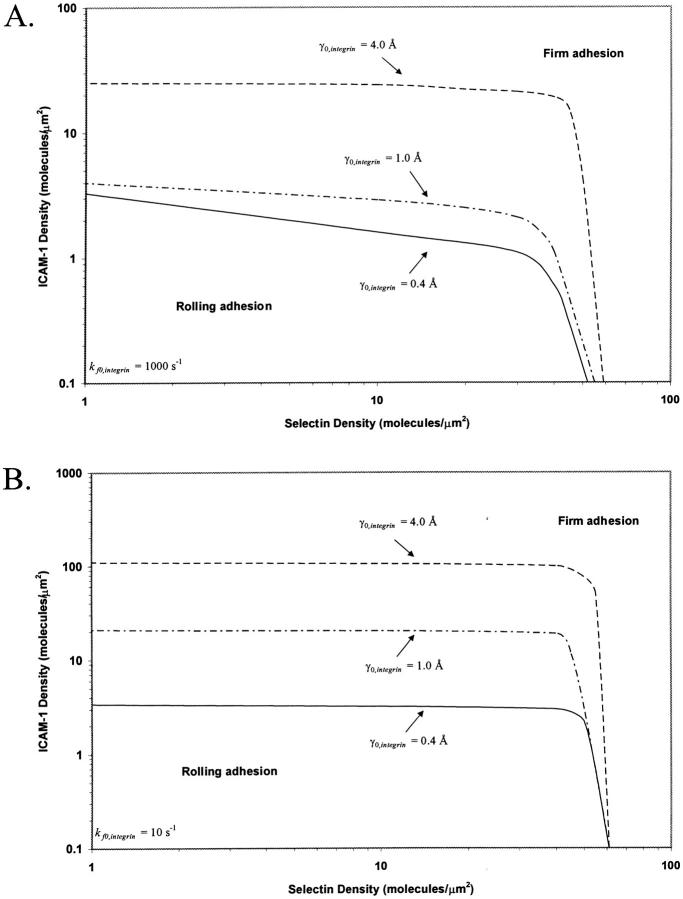
Integrin-ICAM-1 reactive compliance
Thus far, calculations have been for one value of γ0,integrin, 0.4 Å. The value of γ0,integrin has not been measured experimentally, although the value of γ0,selectin has been measured to be 0.4 Å for P-selectin/PSGL-1 interactions (Smith et al., 1999). We were thus interested in the effect of integrin-ICAM-1 reactive compliance on the two-receptor state diagram. Fig. 8 shows the dynamics of adhesion for γ0,integrin = 1.0 Å and 4.0 Å, higher values that make the integrins mechanically weaker, yet in combination with the values of their unstressed off rate, allow them to be capable of supporting firm adhesion. The effect of reactive compliance on the state diagram is calculated at integrin-ICAM-1 association rates of 1000 s−1 (Fig. 8 A) and 10 s−1 (Fig. 8 B). As γ0,integrin increases, the shape of the state diagram remains unchanged, but the location of the firm adhesion envelope shifts to higher ICAM-1 densities. Thus, higher surface densities of ICAM-1 are required to support firm adhesion as integrin-ICAM-1 reactive compliance increases. At values of γ0,integrin lower than 0.4 Å, we found that the firm adhesion envelope shifted to lower values of ICAM-1 density, such that very low ICAM-1 site densities (<1 molecule/μm2) would alone be capable of supporting firm adhesion.
FIGURE 8.
The boundary of rolling adhesion for three different integrin-ICAM-1 reactive compliances (γ0,integrin = 0.4, 1.0, and 4.0 Å), calculated at an integrin-ICAM-1 association rate of (A) kf0,integrin = 1000 s−1 and (B) kf0,integrin = 10 s−1. For each rolling state, the boundary represents a mean velocity of 0.02 VH.
Adhesive behavior is more sensitive to integrin-ICAM-1 reactive compliance when the integrin-ICAM-1 association rate is low. For example, an increase in reactive compliance from 0.4 Å to 4.0 Å shifts the ICAM-1 density required for firm adhesion from ∼3 molecules/μm2 to 30 molecules/μm2 at a 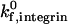 of 1000 s−1. In contrast, at a
of 1000 s−1. In contrast, at a 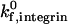 of 10 s−1, an increase in reactive compliance from 0.4 Å to 4.0 Å shifts the ICAM-1 density required for firm adhesion from ∼3 molecules/μm2 to 110 molecules/μm2.
of 10 s−1, an increase in reactive compliance from 0.4 Å to 4.0 Å shifts the ICAM-1 density required for firm adhesion from ∼3 molecules/μm2 to 110 molecules/μm2.
Effect of β2-integrin site density on adhesive behavior
Calculations to this point have focused on modulation of selectin and ICAM-1 surface densities, whereas the densities of sLex and activated β2-integrin on the cell have been assumed to be in excess; this would emulate how endothelial cell-surface changes might modulate the dynamics of adhesion. Alternatively, because leukocytes may regulate adhesive behavior by upregulating the density of activated β2-integrin on the cell surface (Stewart and Hogg, 1996), we were interested in determining the effect of activated β2-integrin site density on adhesive behavior. The influence of activated β2-integrin site density on adhesive behavior was determined by examining cell motion over surfaces with a constant ICAM-1 site density of 10 molecules/μm2 and a constant selectin site density of 15 molecules/μm2. Calculations were performed at a shear rate of 100 s−1 and a 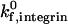 of 1000 s−1. The dependence of cell trajectory and instantaneous velocities on activated β2-integrin density is illustrated in Fig. 9. Similar to ICAM-1, as activated β2-integrin site density increases, the cell experiences more durable arrests. Pause times increase with greater activated β2-integrin density, and adhesive behavior becomes saltatory at high β2-integrin densities, with brief periods of firm arrest separated by periods of motion at VH (Fig. 9, G–H). Thus, activated β2-integrins and ICAM-1 work in conjunction to allow cell arrests of lengthened duration.
of 1000 s−1. The dependence of cell trajectory and instantaneous velocities on activated β2-integrin density is illustrated in Fig. 9. Similar to ICAM-1, as activated β2-integrin site density increases, the cell experiences more durable arrests. Pause times increase with greater activated β2-integrin density, and adhesive behavior becomes saltatory at high β2-integrin densities, with brief periods of firm arrest separated by periods of motion at VH (Fig. 9, G–H). Thus, activated β2-integrins and ICAM-1 work in conjunction to allow cell arrests of lengthened duration.
FIGURE 9.
Effect of β2-integrin cell surface density on cell trajectories and instantaneous velocity distributions. The surface density of ICAM-1 is 5 molecules/μm2, and the surface density of selectin is 15 molecules/μm2. β2-integrin site density is (A and B) 0 molecules/μm2; (C and D) 1 molecule/μm2; (E and F) 2 molecules/μm2; and (G and H) 4 molecules/μm2. Calculations are performed with an integrin-ICAM-1 association rate of kf0,integrin = 1000 s−1.
State diagram for neutrophil activation
To further investigate the mechanism by which neutrophils might modulate adhesive behavior, we calculated a state diagram for neutrophil activation, in which the β2-integrin density and the intrinsic on rate for integrin-ICAM-1 bonds are allowed to vary, whereas other parameters are fixed. This calculation emulates how neutrophil activation modulates the dynamics of adhesion, because neutrophils may regulate both integrin conformation and activated β2-integrin site density to modulate adhesive behavior (Stewart and Hogg, 1996). Calculations are performed with a fixed selectin surface density of 40 molecules/μm2 and a fixed ICAM-1 surface density of 1000 molecules/μm2. The state diagram is calculated at shear rates of 100 s−1 (Fig. 10 A) and 1000 s−1 (Fig. 10 B) to span the physiological range for postcapillary venules; curves are shown for integrin-ICAM-1 reactive compliances of 0.4, 1.0, and 4.0 Å. The boundary separating the states of rolling adhesion and firm adhesion is parametrized by a mean velocity of 0.02 VH.
FIGURE 10.
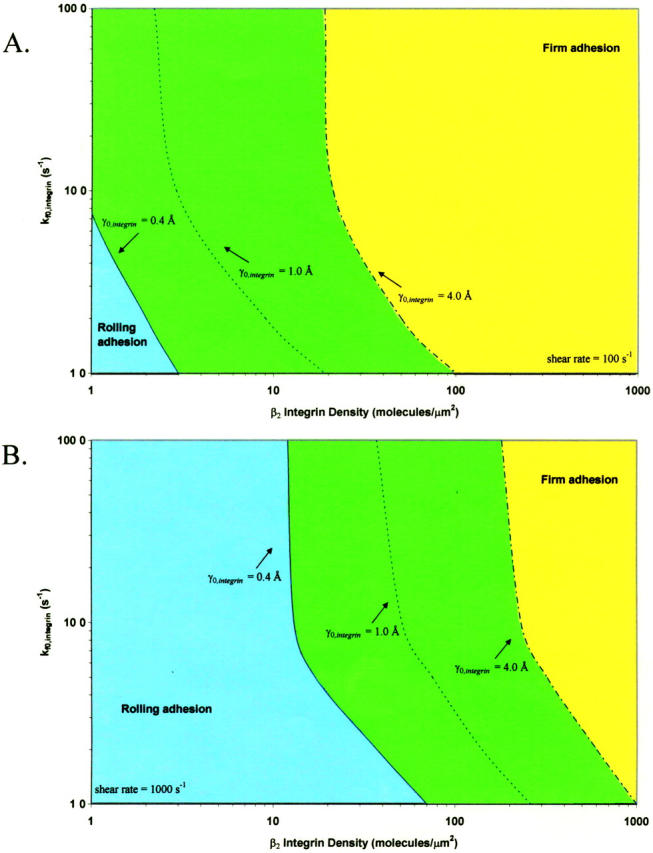
The state diagram for neutrophil activation. The boundary of rolling adhesion is shown for three different integrin-ICAM-1 reactive compliances (γ0,integrin = 0.4, 1.0, and 4.0 Å), calculated at a shear rate of (A) 100 s−1 and (B) 1000 s−1. The surface density of ICAM-1 is 1000 molecules/μm2, and the surface density of selectin is 40 molecules/μm2. For each rolling state, the boundary represents a mean velocity of 0.02 VH.
The state diagram demonstrates that neutrophil adhesive behavior is simultaneously influenced by 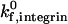 and β2-integrin density. The relative roles of
and β2-integrin density. The relative roles of 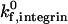 and β2-integrin density in modulating adhesion are dependent on integrin-ICAM-1 on rate. For example, at
and β2-integrin density in modulating adhesion are dependent on integrin-ICAM-1 on rate. For example, at 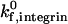 below 50 s−1, increases in either
below 50 s−1, increases in either 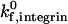 or β2-integrin density can result in a transition from rolling to firm adhesion. In contrast, at
or β2-integrin density can result in a transition from rolling to firm adhesion. In contrast, at 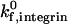 greater than 50 s−1, further increases in integrin-ICAM-1 on rate alone cannot result in a transition from rolling to firm adhesion. In this regime, a critical value of β2-integrin density is necessary for the transition to firm adhesion. Thus, neutrophil adhesion becomes more switchlike at higher values of
greater than 50 s−1, further increases in integrin-ICAM-1 on rate alone cannot result in a transition from rolling to firm adhesion. In this regime, a critical value of β2-integrin density is necessary for the transition to firm adhesion. Thus, neutrophil adhesion becomes more switchlike at higher values of 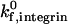 . The firm adhesion envelope shifts to higher β2-integrin site densities with increases in shear rate and integrin-ICAM-1 reactive compliance, but the shape of the state diagram remains unchanged.
. The firm adhesion envelope shifts to higher β2-integrin site densities with increases in shear rate and integrin-ICAM-1 reactive compliance, but the shape of the state diagram remains unchanged.
Comparison of model to published experimental data
Two-receptor adhesive dynamic simulations predict synergy between selectins and integrins in mediating leukocyte adhesion. We were interested in examining the validity of our adhesive dynamic model, by comparing simulation predictions to experimental results from the literature. We applied two-receptor adhesive dynamics to the simulation of in vivo neutrophil rolling. Kunkel et al. (2000) used intravital microscopy to track individual leukocytes in the microcirculation of wild-type mice, CD18 (β2-integrin) −/− knockout mice, and E-selectin −/− knockout mice after TNF-α induced inflammation. These investigators found that neutrophil rolling velocities in wild-type mice were significantly lower than rolling velocities in CD18−/− or E−/− mice. We used two-receptor adhesive dynamic simulations to recreate the cell trajectories and average rolling velocities reported (Kunkel et al., 2000).
Fig. 11 shows the data reported by Kunkel et al. (2000) with the corresponding simulation predictions. To simulate the in vivo system, we chose a shear rate of 1000 s−1, as the experiments were conducted in postcapillary venules with wall shear rates of 800–1400 s−1 (Kunkel et al., 2000). The biophysical parameters for E-selectin-ligand interactions were chosen to be γ0,selectin = 0.18 Å and 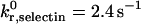 , and are taken from experimentally measured values (Smith et al., 1999). The
, and are taken from experimentally measured values (Smith et al., 1999). The 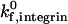 for E-selectin-ligand interactions was chosen to be 84 s−1 as in previous adhesive dynamic simulations (Chang et al., 2000). Using these parameters, we simulated the trajectory and average velocity of CD18−/− knockout mice neutrophils, interacting only with E-selectin (Fig. 11, B and E). We find that our simulated results most closely match both the experimental trajectory and the average rolling velocity of neutrophils from CD18−/− knockout mice when the E-selectin density in the simulations is 14 molecules/μm2 (Fig. 11, B and E).
for E-selectin-ligand interactions was chosen to be 84 s−1 as in previous adhesive dynamic simulations (Chang et al., 2000). Using these parameters, we simulated the trajectory and average velocity of CD18−/− knockout mice neutrophils, interacting only with E-selectin (Fig. 11, B and E). We find that our simulated results most closely match both the experimental trajectory and the average rolling velocity of neutrophils from CD18−/− knockout mice when the E-selectin density in the simulations is 14 molecules/μm2 (Fig. 11, B and E).
FIGURE 11.
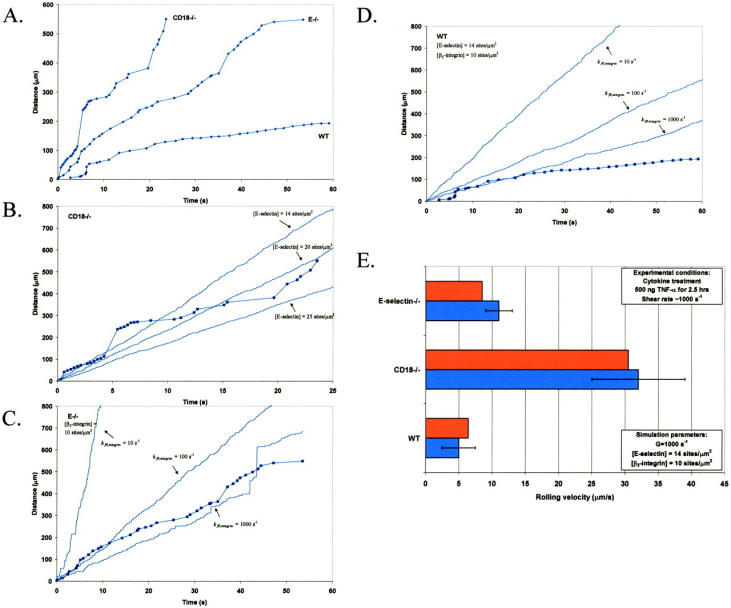
Comparison of two-receptor adhesive dynamic simulations to experiment. (A) Representative neutrophil rolling trajectories in wild-type, CD18−/−, and E−/− mice, as reported in Forlow et al. (2000). (B) Comparison of experimental CD18−/− neutrophil rolling trajectory to simulated cell motion; calculated results for three different selectin densities (14, 20, 25 sites/μm2) are shown. (C) Comparison of experimental E−/− neutrophil rolling trajectory to simulated cell motion; calculated results for three different integrin-ICAM-1 association rates (10, 100, 1000 s−1) are shown. (D) Comparison of experimental wild-type neutrophil rolling trajectory to simulated cell motion; calculated results for three different integrin-ICAM-1 association rates (10, 100, 1000 s−1) are shown. (E) Comparison of average neutrophil rolling velocities, as reported by Kunkel et al. (2000), to average rolling velocities predicted by simulations; this calculation is performed at kf0,integrin = 1000 s−1. Experimental velocities are represented by blue bars, and simulated results are represented by red bars.
To simulate the motion of neutrophils from E−/− knockout mice expressing only β2-integrin, we chose an activated β2-integrin site density of 10 molecules/μm2, to reflect a situation in which a small percentage of β2-integrins on the cell are activated. We chose a 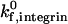 of 1000 s−1 (as justified earlier in the Results section) and a
of 1000 s−1 (as justified earlier in the Results section) and a 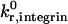 on the order of 0.1 s−1 (Shimaoka et al., 2001). Although the reactive compliance of integrin-ICAM-1 bonds is unknown, we found that γ0,integrin = 0.6 Å gave a reasonable match to experimental data. As shown in Fig. 11, C and E, the simulation with this set of parameters reproduces both the cell trajectory and average rolling velocity of neutrophils from E−/− knockout mice, reported by Kunkel et al. (2000). Lower integrin-ICAM-1 association rates of 100 s−1 and 10 s−1 predict an E−/− cell trajectory that is markedly different from the experimental trajectory (Fig. 11 C).
on the order of 0.1 s−1 (Shimaoka et al., 2001). Although the reactive compliance of integrin-ICAM-1 bonds is unknown, we found that γ0,integrin = 0.6 Å gave a reasonable match to experimental data. As shown in Fig. 11, C and E, the simulation with this set of parameters reproduces both the cell trajectory and average rolling velocity of neutrophils from E−/− knockout mice, reported by Kunkel et al. (2000). Lower integrin-ICAM-1 association rates of 100 s−1 and 10 s−1 predict an E−/− cell trajectory that is markedly different from the experimental trajectory (Fig. 11 C).
The parameters for E-selectin and β2-integrin receptors were combined to simulate the two-receptor-mediated motion of neutrophils from wild-type mice (Fig. 11, D and E). Simulations reproduce the finding that neutrophils in wild-type mice roll at slower speeds than in CD18−/− or E−/− knockout mice (Fig. 11 D). This simulation predicts a cell trajectory that is slightly faster than the representative wild-type neutrophil trajectory from experiments (Fig. 11 D); this may be the result of experimental heterogeneity in shear rate or receptor density. The predicted cell trajectory appears to deviate from the actual cell trajectory after ∼20 s of rolling; this may reflect a further extent of neutrophil activation or cell deformability not included in our model. However, the simulated average velocity of neutrophils in wild-type mice matches the reported average rolling velocity for neutrophils in wild-type mice (Fig. 11 E). Thus, parameters determined independently to simulate the rolling of neutrophils in CD18−/− and E−/− knockout mice can be combined in a two-receptor simulation to accurately reproduce the rolling of neutrophils in wild-type mice. Additionally, the ability of the chosen simulation parameters to recreate experimental data introduces the possibility that integrin-ICAM-1 bonds may have a higher reactive compliance than selectin-sLex bonds; this may lend a possible explanation for the necessity of selectin-mediated rolling before integrin-mediated firm adhesion of leukocytes.
DISCUSSION
This paper presents adhesive dynamic simulations of cell adhesion under conditions where two receptor-ligand systems are active, one system with strongly adhesive properties and the other with weakly adhesive properties. Using two-receptor adhesive dynamics, we have constructed a state diagram for two-receptor adhesion. The state diagram illustrates that selectin-sLex interactions and integrin-ICAM-1 interactions have synergistic functions in promoting cell adhesion and arrest. The combination of low surface densities of ICAM-1 and selectin mediates firm adhesion, whereas the presence of low densities of either receptor alone results in rolling adhesion. Examination of the individual roles of integrin-ICAM-1 bonds and selectin-sLex bonds in cell adhesion demonstrates that the two receptor-ligand systems also have complementary functions. Integrin-ICAM-1 bonds, which have strongly adhesive properties, allow cell arrests of lengthened duration. Selectin-sLex bonds, which have weakly adhesive properties, allow stable periods of rolling adhesion that support the cell between durable arrests. An increase in shear rate shifts the state diagram and results in the requirement of greater selectin densities and greater ICAM-1 densities to promote firm adhesion. An increase in integrin-ICAM-1 reactive compliance, a parameter that might be adjusted by the cell to modulate integrin activity, shifts the state diagram and results in the requirement of greater ICAM-1 densities to promote firm adhesion. Adhesive behavior is more sensitive to changes in shear rate and reactive compliance when the integrin-ICAM-1 association rate is low. To model neutrophil regulation of adhesive behavior, we constructed a state diagram for neutrophil activation, which demonstrates that neutrophil adhesive behavior is simultaneously influenced by 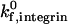 and β2-integrin density, with adhesion becoming more switchlike at higher values of
and β2-integrin density, with adhesion becoming more switchlike at higher values of 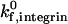 . The predictions of two-receptor adhesive dynamics are validated by the ability of the model to reproduce, both qualitatively and quantitatively, in vivo neutrophil rolling velocities. Simulation parameters that independently reproduce neutrophil rolling velocities from E−/− and CD18−/− knockout mice can be combined to reproduce the two-receptor-mediated rolling of neutrophils in wild-type mice (Kunkel et al., 2000).
. The predictions of two-receptor adhesive dynamics are validated by the ability of the model to reproduce, both qualitatively and quantitatively, in vivo neutrophil rolling velocities. Simulation parameters that independently reproduce neutrophil rolling velocities from E−/− and CD18−/− knockout mice can be combined to reproduce the two-receptor-mediated rolling of neutrophils in wild-type mice (Kunkel et al., 2000).
In our simulations, we have used a hard sphere uniformly coated with adhesive receptors, as a representative of a cell. Real cells are deformable and rough, and can undergo changes in receptor density, receptor distribution, cytoskeletal attachment, and membrane rigidity caused by signaling. These cellular features likely modulate the dynamics of adhesion in ways that we have not included. However, the primary determinant of adhesive behavior is the physical chemistry of receptor-ligand interactions. Deformation and receptor distribution on the cell may modulate when and where adhesion occurs, but they do not determine the type of adhesive behavior that will be observed. Support for this view comes from both partially and totally cell-free systems that can mimic leukocyte rolling. The Springer group has shown that formaldehyde-fixed cells can roll on selectin surfaces (Lawrence and Springer, 1993) and that leukocytes or selectin-expressing transfected cells can roll over carbohydrate substrates (Alon et al., 1995). Our lab has shown that cell-free experiments, in which colloidal microspheres coated with selectin ligands are perfused over selectin-coated surfaces, can successfully recreate leukocyte rolling (Brunk and Hammer, 1997; Rodgers et al., 2000; Greenberg et al., 2000). Finally, previous AD simulations from our laboratory have demonstrated that the dynamics of adhesion can be accurately predicted from the functional properties of receptor-ligand bonds, most importantly dissociation rate and bond interaction length (Chang et al., 2000). These studies emphasize that the physical chemistry of the adhesion molecules is the single most important factor controlling the dynamics of adhesion under flow.
In previous computational work, we used adhesive dynamics to simulate the adhesion of a cell to a surface as some of the biophysical parameters that govern receptor-ligand functional properties and the dynamics of adhesion were varied. Initial AD simulations demonstrated the ability of the model to recreate the entire range of expected and observed adhesive phenomena, and showed that AD simulations could recreate data on neutrophil rolling as a function of selectin surface density (Hammer and Apte, 1992). AD simulations were then used to model the overall rate of reaction of species that are bound to surfaces under relative motion (Chang and Hammer, 1999). This study showed that the rate of collision between receptor and ligand increases with shear rate, and the encounter duration decreases. Depending on the rate of bimolecular reaction, increases in shear rate can increase adhesion (by increasing the encounter frequency) or decrease adhesion (due to the decreased encounter time); this result may explain the requirement of a threshold level of shear for L-selectin-mediated adhesion (Finger et al., 1996). More recently, AD studies have shown that the biophysical parameters that are most important in determining adhesive behavior are the unstressed dissociation rate and the bond interaction length (Chang et al., 2000). The data can be summarized in a state diagram, a one-to-one map between the biophysical properties of adhesion molecules and different adhesive behaviors (Chang et al., 2000). The present study extends single-particle adhesive dynamics to model adhesive behavior of a particle when two receptor-ligand systems are active; our study demonstrates synergy between two receptor-ligand systems in mediating adhesion, as shown in a two-receptor state diagram.
Our simulation results corroborate the conclusions of numerous experimental studies that demonstrate cooperation between selectins and integrins in converting rolling to firm adhesion. Jung et al. (1998) found that leukocyte firm adhesion in inflamed mouse cremaster venules is most efficient in the presence of both β2-integrin and E-selectin. Blockade of either E-selectin or β2-integrin function leads to increased rolling velocities, suggesting that E-selectin and β2-integrin serve distinct functions in mediating slow rolling (Jung et al., 1998). Mice doubly deficient in β2-integrin and E-selectin have severely impaired viability, in contrast to mice singly deficient in either molecule, demonstrating synergy between E-selectin and β2-integrin (Forlow et al., 2000). Similarly, the presence of ICAM-1 in inflamed mouse cremaster venules is required for optimal P- and L-selectin mediated rolling; deficiency of ICAM-1 leads to significantly increased rolling velocities (Steeber et al., 1998). The combined loss of L-selectin and ICAM-1 dramatically reduces leukocyte migration into inflamed venules, beyond what is observed with loss of either molecule alone, indicating synergistic roles for L-selectin and ICAM-1 in promoting leukocyte rolling and arrest (Steeber et al., 1999). Direct observation by intravital microscopy of leukocyte migration in the microvasculature has shown that rolling leukocytes exhibit a gradual, β2-integrin-dependent decrease in rolling velocity before arrest (Kunkel et al., 2000). Taken together, the findings of both two-receptor simulations and experiments support a model of leukocyte adhesion in which a series of overlapping, synergistic interactions among adhesion molecules result in an adhesion cascade (Steeber and Tedder, 2000). Selectin-sLex interactions and integrin-ICAM-1 interactions work together to gradually transition the cell from rolling adhesion to firm adhesion.
A surprising result of our simulations is the importance of selectin-sLex interactions in facilitating the transition to firm adhesion. Although it has been suggested that selectins mediate the transition to firm adhesion by signaling the upregulation of β2-integrins (Crockett-Torabi et al., 1995), AD simulations demonstrate that the role of selectins goes beyond signaling. Selectin-sLex bonds may promote the transition to firm adhesion by virtue of their ability to capture the cell and mediate slow rolling, and thus make firm adhesion more likely. The mechanochemical properties of selectin-sLex bonds may thus contribute to the rolling-to-adhesion transition, independent of signaling activity by selectins.
Our simulations also highlight the importance of measuring the mechanical properties of β2-integrin-ICAM-1 bonds. BIAcore measurements of the unstressed off rate for interactions between soluble ICAM-1 and immobilized β2-integrin have been made (Labadia et al., 1998). In addition, BIAcore measurements of the unstressed off rate for interactions between ICAM-1 and the integrin αL I domain have been performed (Shimaoka et al., 2001). These measurements have demonstrated that the kinetics of interaction are conformation dependent; locking the I domain in an open conformation with disulfide bonds results in a 9000-fold increase in affinity to ICAM-1 (Shimaoka et al., 2001). Because adhesiveness of β2-integrins may be dynamically regulated by signals within the cell via inside-out signaling (Stewart and Hogg, 1996), it is essential to characterize the biophysical properties of integrin-ICAM-1 bonds in various affinity states of β2-integrins. Physical parameters, such as reactive compliance, have not yet been measured for integrin-ICAM-1 bonds, and will help in characterizing leukocyte adhesion mediated by both selectins and integrins.
The three-dimensional (3-D) on rate for integrin-ICAM-1 bonds has been directly measured using BIAcore (Shimaoka et al., 2001; Labadia et al., 1998); the value may be either above or below that of selectin-ligand bonds (Wild et al., 2001; Mehta et al., 1998; Nicholson et al., 1998). Our simulations are performed with integrin-ICAM-1 two-dimensional (2-D) intrinsic on rates of 10–1000 s−1. This comprehensively represents values above, below, and roughly equal to that of selectin-ligand bonds. Although the 3-D on rate of integrin-ICAM-1 bonds has been measured, there are known difficulties in converting 3-D on-rate measurements into 2-D values (reviewed in Zhu, 2000). Bell (1978) formulated a theory to allow for conversion of 3-D on rates to 2-D kinetic rates; however this calculation involves numerous assumptions, most notably the size of the reaction complex. The method is highly inaccurate, and the calculated 2-D on rates differ from the actual values by orders of magnitude (Zhu, 2000). It is thus difficult to calculate a priori the 2-D on rate from the 3-D value. Our approach to on-rate selection for integrin-ICAM-1 bonds has been to model adhesive behavior over a range of 2-D integrin-ICAM-1 on rates, and compare the predicted behavior to experimental data as a means of estimating the 2-D on rate. We have used this method previously (Chang et al., 2000; Chang and Hammer, 2000) to estimate the 2-D on rate for selectin-ligand bonds from adhesive-dynamic simulations.
An added intricacy to the problem of two-receptor adhesion is recent evidence that engagement of selectins with their ligands leads to intracellular signaling and upregulation of integrin receptors on the cell surface. Several studies have demonstrated signal transduction activity of both L-selectin and PSGL-1 on neutrophils (Crockett-Torabi et al., 1995; Hidari et al., 1997). Ligation of L-selectin on human neutrophils leads to increased tyrosine phosphorylation of multiple proteins involved in signal transduction cascades, including mitogen-activated protein kinase; a signaling cascade from L-selectin to the activation of MAPK has been established in T-lymphocytes (Waddell et al., 1995; Brenner et al., 1996). L-selectin ligation has been shown to upregulate cell-surface expression of β2-integrins (Crockett-Torabi et al., 1995), and binding of GlyCAM-1 to L-selectin on human lymphocytes activates integrin-mediated binding of these cells to ICAM-1 (Hwang et al., 1996). In the case of PSGL-1, a signal transduction cascade induced by PSGL-1 binding has been identified, with some of the phosphorylated proteins including MAPKs (Hidari et al., 1997). Binding of P-selectin-IgG to mouse neutrophils stimulates integrin-mediated binding to ICAM-1; PSGL-1 is necessary and sufficient for this process (Blanks et al., 1998). The most convincing evidence for intracellular signaling has been provided by Simon et al. (2000), who demonstrated that neutrophil tethering on E-selectin under hydrodynamic flow leads to arrest via β2-integrins, through a MAPK-dependent signal transduction pathway.
Although there is significant evidence for selectin-mediated signal transduction, the relative roles of selectin signaling and chemokine signaling in integrin upregulation remain unclear. Several experimental studies suggest that chemokine signaling may be considerably more important than selectin signaling in converting rolling to firm adhesion. For example, platelet activating factor and IL-8 induce the immobilization of rolling neutrophils, converting rolling to stationary adhesion in a median response time of 240 ms in vitro (Rainger et al., 1997). Immobilized IL-8 can stimulate neutrophils to firmly adhere in vitro; neutrophils introduced over a surface of P-selectin, ICAM-1, and IL-8 roll an average of 200 μm before firmly adhering, under a shear stress of 2 dynes/cm2 (DiVietro et al., 2001). Increasing the density of IL-8 on the surface decreases the average distance and time that neutrophils roll before becoming firmly adherent (DiVietro et al., 2001). There is also evidence that chemokines play an important role in converting rolling to firm adhesion of monocytes, T-lymphocytes, and B-lymphocytes (Campbell et al., 1996; Stein et al., 2000; Palframan et al., 2001). However, our simulations apply to either selectin-mediated or chemokine-mediated integrin activation; the calculations only address the consequences of integrin activation on rolling and firm adhesion, and are independent of how integrins become activated.
We plan to extend two-receptor adhesive dynamics in the future to include intracellular signaling cascades, to determine the influence of various intracellular signaling mechanisms on microscopic and macroscopic adhesive behavior. We will test the hypothesis that signal transduction by selectins and subsequent upregulation of integrin activity can alone bring about a switch in cellular motion, independent of chemokine effects. In addition, we hope to modify adhesive dynamics to include the location and distribution of integrins, to develop a more accurate model for neutrophil adhesion. One should view the calculations presented here as the necessary prerequisite for this investigation. In such a model, it is likely we will characterize the transition of β2-integrins between passive and active states. The calculation presented in the current paper shows how the state of adhesion and rolling dynamics is controlled by the integrin properties, including density.
Acknowledgments
The authors acknowledge the support of National Institutes of Health (GM59100 and HL18208) and the Whitaker foundation.
References
- Alon, R., D. A. Hammer, and T. A. Springer. 1995. Lifetime of the P-selectin-carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 374:539–542. [DOI] [PubMed] [Google Scholar]
- Bell, G. I. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- Bell, G. I., M. Dembo, and P. Bongrand. 1984. Competition between non-specific repulsion and specific bonding. Biophys. J. 45:1051–1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanks, J. E., T. Moll, R. Eytner, and D. Vestweber. 1998. Stimulation of P-selectin glycoprotein ligand-1 on mouse neutrophils activates beta 2-integrin mediated cell attachment to ICAM-1. Eur. J. Immunol. 28:433–443. [DOI] [PubMed] [Google Scholar]
- Brenner, B., E. Gulbins, K. Schlottmann, U. Koppenhoefer, G. L. Busch, B. Walzog, M. Steinhausen, K. M. Coggeshall, O. Linderkamp, and F. Lang. 1996. L-selectin activates the Ras pathway via the tyrosine kinase p56lck. Proc. Natl. Acad. Sci. USA. 93:15376–15381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner, H. 1961. The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Eng. Sci. 16:242–251. [Google Scholar]
- Brunk, D. K., and D. A. Hammer. 1997. Quantifying rolling adhesion with a cell-free assay: E-selectin and its carbohydrate ligands. Biophys. J. 72:2820–2833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullard, D. C., E. J. Kunkel, H. Kubo, M. J. Hicks, I. Lorenzo, N. A. Doyle, C. M. Doerschuk, K. Ley, and A. L. Beaudet. 1996. Infectious susceptibility and severe deficiency of leukocyte rolling and recruitment in E-selectin and P-selectin double mutant mice. J. Exp. Med. 183:2329–2336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell, J. J., S. Qin, K. B. Bacon, C. R. Mackay, and E. C. Butcher. 1996. Biology of chemokine and classical chemoattractant receptors: differential requirements for adhesion-triggering versus chemotactic responses in lymphoid cells. J. Cell Biol. 134:255–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell, J. J., J. Hedrick, A. Zlotnik, M. A. Siani, D. A. Thompson, and E. C. Butcher. 1998. Chemokines and the arrest of lymphocytes rolling under flow conditions. Science. 279:381–384. [DOI] [PubMed] [Google Scholar]
- Chang, K.-C., and D. A. Hammer. 1999. The forward rate of binding of surface-tethered reactants: effect of relative motion between two surfaces. Biophys. J. 76:1280–1292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, K.-C., and D. A. Hammer. 2000. Adhesive dynamics simulations of sialyl-Lewisx/E-selectin-mediated rolling in a cell-free system. Biophys. J. 79:1891–1902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, K.-C., D. F. Tees, and D. A. Hammer. 2000. The state diagram for cell adhesion under flow: leukocyte rolling and firm adhesion. Proc. Natl. Acad. Sci. USA. 97:11262–11267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, S., and T. A. Springer. 1999. An automatic braking system that stabilizes leukocyte rolling by an increase in selectin bond number with shear. J. Cell Biol. 144:185–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crockett-Torabi, E., B. Sulenbarger, C. W. Smith, and J. C. Fantone. 1995. Activation of human neutrophils through L-selectin and Mac-1 molecules. J. Immunol. 154:2291–2302. [PubMed] [Google Scholar]
- Dembo, M., D. C. Torney, K. Saxman, and D. A. Hammer. 1988. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. B Biol. Sci. 234:55–83. [DOI] [PubMed] [Google Scholar]
- DiVietro, J. A., M. J. Smith, B. R. Smith, L. Petruzzelli, R. S. Larson, and M. B. Lawrence. 2001. Immobilized IL-8 triggers progressive activation of neutrophils rolling in vitro on P-selectin and intercellular adhesion molecule-1. J. Immunol. 167:4017–4025. [DOI] [PubMed] [Google Scholar]
- Ebnet, K., and D. Vestweber. 1999. Molecular mechanisms that control leukocyte extravasation: the selectins and the chemokines. Histochem. Cell Biol. 112:1–23. [DOI] [PubMed] [Google Scholar]
- Evans, E., and K. Ritchie. 1997. Dynamic strength of molecular adhesion bonds. Biophys. J. 72:1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finger, E. B., K. D. Puri, R. Alon, M. B. Lawrence, U. H. von Andrian, and T. A. Springer. 1996. Adhesion through L-selectin requires a threshold hydrodynamic shear. Nature. 379:266–269. [DOI] [PubMed] [Google Scholar]
- Forlow, S. B., E. J. White, S. C. Barlow, S. H. Feldman, H. Lu, G. J. Bagby, A. L. Beaudet, D. C. Bullard, and K. Ley. 2000. Severe inflammatory defect and reduced viability in CD18 and E-selectin double-mutant mice. J. Clin. Invest. 106:1457–1466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goetz, D. J., M. E. El-Sabban, B. U. Pauli, and D. A. Hammer. 1994. Dynamics of neutrophil rolling over stimulated endothelium in vitro. Biophys. J. 66:2202–2209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman, A. J., R. G. Cox, and H. Brenner. 1967a. Slow viscous motion of a sphere parallel to a plane wall. I. Motion through a quiescent fluid. Chem. Eng. Sci. 22:637–652. [Google Scholar]
- Goldman, A. J., R. G. Cox, and H. Brenner. 1967b. Slow viscous motion of a sphere parallel to a plane wall. II. Couette flow. Chem. Eng. Sci. 22:653–660. [Google Scholar]
- Gopalan, P. K., C. W. Smith, H. Lu, E. L. Berg, L. V. McIntire, and S. I. Simon. 1997. Neutrophil CD18-dependent arrest on intercellular adhesion molecule 1 (ICAM-1) in shear flow can be activated through L-selectin. J. Immunol. 158:367–375. [PubMed] [Google Scholar]
- Greenberg, A. W., D. K. Brunk, and D. A. Hammer. 2000. Cell-free rolling mediated by L-selectin and sialyl Lewis(x) reveals the shear threshold effect. Biophys. J. 79:2391–2402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammer, D. A., and S. M. Apte. 1992. Simulation of cell rolling and adhesion on surfaces in shear flow: general results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 62:35–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hidari, K. I., A. S. Weyrich, G. A. Zimmerman, and R. P. McEver. 1997. Engagement of P-selectin glycoprotein ligand-1 enhances tyrosine phosphorylation and activates mitogen-activated protein kinases in human neutrophils. J. Biol. Chem. 272:28750–28756. [DOI] [PubMed] [Google Scholar]
- Hwang, S. T., M. S. Singer, P. A. Giblin, T. A. Yednock, K. B. Bacon, S. I. Simon, and S. D. Rosen. 1996. GlyCAM-1, a physiologic ligand for L-selectin, activates beta 2 integrins on naive peripheral lymphocytes. J. Exp. Med. 184:1343–1348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffrey, G. B. 1915. On the steady rotation of a solid of revolution in a viscous fluid. Proc. Lond. Math. Soc. 14:327–338. [Google Scholar]
- Jung, U., K. E. Norman, K. Scharffetter-Kochanek, A. L. Beaudet, and K. Ley. 1998. Transit time of leukocytes rolling through venules controls cytokine-induced inflammatory cell recruitment in vivo. J. Clin. Invest. 102:1526–1533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King, M. R., and D. A. Hammer. 2001. Multiparticle adhesive dynamics. Interactions between stably rolling cells. Biophys. J. 81:799–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunkel, E. J., J. L. Dunne, and K. Ley. 2000. Leukocyte arrest during cytokine-dependent inflammation in vivo. J. Immunol. 164:3301–3308. [DOI] [PubMed] [Google Scholar]
- Labadia, M. E., D. D. Jeanfavre, G. O. Caviness, and M. M. Morelock. 1998. Molecular regulation of the interaction between leukocyte function-associated antigen-1 and soluble ICAM-1 by divalent metal cations. J. Immunol. 161:836–842. [PubMed] [Google Scholar]
- Lawrence, M. B., L. V. McIntire, and S. G. Eskin. 1987. Effect of flow on polymorphonuclear leukocyte/endothelial cell adhesion. Blood. 70:1284–1290. [PubMed] [Google Scholar]
- Lawrence, M. B., C. W. Smith, S. G. Eskin, and L. V. McIntire. 1990. Effect of venous shear stress on CD18-mediated neutrophil adhesion to cultured endothelium. Blood. 75:227–237. [PubMed] [Google Scholar]
- Lawrence, M. B., and T. A. Springer. 1991. Leukocytes roll on a selectin at physiologic flow rates: distinction from and prerequisite for adhesion through integrins. Cell. 65:859–873. [DOI] [PubMed] [Google Scholar]
- Lawrence, M. B., and T. A. Springer. 1993. Neutrophils roll on E-selectin. J. Immunol. 151:6338–6346. [PubMed] [Google Scholar]
- Mehta, P., R. D. Cummings, and R. P. McEver. 1998. Affinity and kinetic analysis of P-selectin binding to P-selectin glycoprotein ligand-1. J. Biol. Chem. 273:32506–32513. [DOI] [PubMed] [Google Scholar]
- Morozov, V. N., and T. Y. Morozova. 1990. What does a protein molecule look like? Commun. Mol. Cell. Biophys. 6:249–270. [Google Scholar]
- Nicholson, M. W., A. N. Barclay, M. S. Singer, S. D. Rosen, and P. A. van der Merwe. 1998. Affinity and kinetic analysis of L-selectin (CD62L) binding to glycosylation-dependent cell-adhesion molecule-1. J. Biol. Chem. 273:763–770. [DOI] [PubMed] [Google Scholar]
- Palframan, R. T., S. Jung, G. Cheng, W. Weninger, Y. Luo, M. Dorf, D. R. Littman, B. J. Rollins, H. Zweerink, A. Rot, and U. H. von Andrian. 2001. Inflammatory chemokine transport and presentation in HEV: a remote control mechanism for monocyte recruitment to lymph nodes in inflamed tissues. J. Exp. Med. 194:1361–1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rainger, G. E., A. C. Fisher, and G. B. Nash. 1997. Endothelial-borne platelet-activating factor and interleukin-8 rapidly immobilize rolling neutrophils. Am. J. Physiol. 272:H114–H122. [DOI] [PubMed] [Google Scholar]
- Rodgers, S. D., R. T. Camphausen, and D. A. Hammer. 2000. Sialyl Lewis(x)-mediated, PSGL-1 independent rolling. Biophys. J. 79:694–706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosen, S. D., and C. R. Bertozzi. 1994. The selectins and their ligands. Curr. Opin. Cell Biol. 6:663–673. [DOI] [PubMed] [Google Scholar]
- Shimaoka, M., C. Lu, R. T. Palframan, U. H. von Andrian, A. McCormack, J. Takagi, and T. A. Springer. 2001. Reversibly locking a protein fold in an active conformation with a disulfide bond: integrin alphaL I domains with high affinity and antagonist activity in vivo. Proc. Natl. Acad. Sci. USA. 98:6009–6014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon, S. I., Y. Hu, D. Vestweber, and C. W. Smith. 2000. Neutrophil tethering on E-selectin activates beta 2 integrin binding to ICAM-1 through a mitogen-activated protein kinase signal transduction pathway. J. Immunol. 164:4348–4358. [DOI] [PubMed] [Google Scholar]
- Smith, M. J., E. L. Berg, and M. B. Lawrence. 1999. A direct comparison of selectin-mediated transient, adhesive events using high temporal resolution. Biophys. J. 77:3371–3383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Springer, T. A. 1994. Traffic signals for lymphocyte recirculation and leukocyte emigration: the multistep paradigm. Cell. 76:301–314. [DOI] [PubMed] [Google Scholar]
- Steeber, D. A., M. L. Tang, X. Q. Zhang, W. Muller, N. Wagner, and T. F. Tedder. 1998. Efficient lymphocyte migration across high endothelial venules of mouse Peyer's patches requires overlapping expression of L-selectin and beta7 integrin. J. Immunol. 161:6638–6647. [PubMed] [Google Scholar]
- Steeber, D. A., M. L. Tang, N. E. Green, X. Q. Zhang, J. E. Sloane, and T. F. Tedder. 1999. Leukocyte entry into sites of inflammation requires overlapping interactions between the L-selectin and ICAM-1 pathways. J. Immunol. 163:2176–2186. [PubMed] [Google Scholar]
- Steeber, D. A., and T. F. Tedder. 2000. Adhesion molecule cascades direct lymphocyte recirculation and leukocyte migration during inflammation. Immunol. Res. 22:299–317. [DOI] [PubMed] [Google Scholar]
- Stein, J. V., A. Rot, Y. Luo, M. Narasimhaswamy, H. Nakano, M. D. Gunn, A. Matsuzawa, E. J. Quackenbush, M. E. Dorf, and U. H. von Andrian. 2000. The CC chemokine thymus-derived chemotactic agent 4 (TCA-4, secondary lymphoid tissue chemokine, 6Ckine, exodus-2) triggers lymphocyte function-associated antigen 1-mediated arrest of rolling T lymphocytes in peripheral lymph node high endothelial venules. J. Exp. Med. 191:61–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart, M., and N. Hogg. 1996. Regulation of leukocyte integrin function: affinity vs. avidity. J. Cell. Biochem. 61:554–561. [DOI] [PubMed] [Google Scholar]
- Takamura, K., H. L. Goldsmith, and S. G. Mason. 1981. The microrheology of colloidal dispersions. XII. Trajectories of orthokinetic pair-collisions of latex spheres in a simple electrolyte. J. Colloid Interf. Sci. 82:175–189. [Google Scholar]
- Tangemann, K., M. D. Gunn, P. Giblin, and S. D. Rosen. 1998. A high endothelial cell-derived chemokine induces rapid, efficient, and subset-selective arrest of rolling T lymphocytes on a reconstituted endothelial substrate. J. Immunol. 161:6330–6337. [PubMed] [Google Scholar]
- Tees, D. F., R. E. Waugh, and D. A. Hammer. 2001. A microcantilever device to assess the effect of force on the lifetime of selectin-carbohydrate bonds. Biophys. J. 80:668–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Andrian, U. H., S. R. Hasslen, R. D. Nelson, S. L. Erlandsen, and E. C. Butcher. 1995. A central role for microvillous receptor presentation in leukocyte adhesion under flow. Cell. 83:989–999. [DOI] [PubMed] [Google Scholar]
- Waddell, T. K., L. Fialkow, C. K. Chan, T. K. Kishimoto, and G. P. Downey. 1995. Signaling functions of L-selectin. Enhancement of tyrosine phosphorylation and activation of MAP kinase. J. Biol. Chem. 270:15403–15411. [DOI] [PubMed] [Google Scholar]
- Wild, M. K., M.-C. Huang, U. Schulze-Horsel, P. A. van der Merwe, and D. Vestweber. 2001. Affinity, kinetics, and thermodynamics of E-selectin binding to E-selectin ligand-1. J. Biol. Chem. 276:31602–31612. [DOI] [PubMed] [Google Scholar]
- Zhu, C. 2000. Kinetics and mechanics of cell adhesion. J. Biomech. 33:23–33. [DOI] [PubMed] [Google Scholar]