The Ca²⁺ Dynamics of Isolated Mouse β-Cells and Islets: Implications for Mathematical Models

Abstract

[Ca²⁺]_i and electrical activity were compared in isolated β-cells and islets using standard techniques. In islets, raising glucose caused a decrease in [Ca²⁺]_i followed by a plateau and then fast (2−3 min⁻¹), slow (0.2–0.8 min⁻¹), or a mixture of fast and slow [Ca²⁺]_i oscillations. In β-cells, glucose transiently decreased and then increased [Ca²⁺]_i, but no islet-like oscillations occurred. Simultaneous recordings of [Ca²⁺]_i and electrical activity suggested that differences in [Ca²⁺]_i signaling are due to differences in islet versus β-cell electrical activity. Whereas islets exhibited bursts of spikes on medium/slow plateaus, isolated β-cells were depolarized and exhibited spiking, fast-bursting, or spikeless plateaus. These electrical patterns in turn produced distinct [Ca²⁺]_i patterns. Thus, although isolated β-cells display several key features of islets, their oscillations were faster and more irregular. β-cells could display islet-like [Ca²⁺]_i oscillations if their electrical activity was converted to a slower islet-like pattern using dynamic clamp. Islet and β-cell [Ca²⁺]_i changes followed membrane potential, suggesting that electrical activity is mainly responsible for the [Ca²⁺] dynamics of β-cells and islets. A recent model consisting of two slow feedback processes and passive endoplasmic reticulum Ca²⁺ release was able to account for islet [Ca²⁺]_i responses to glucose, islet oscillations, and conversion of single cell to islet-like [Ca²⁺]_i oscillations. With minimal parameter variation, the model could also account for the diverse behaviors of isolated β-cells, suggesting that these behaviors reflect natural cell heterogeneity. These results support our recent model and point to the important role of β-cell electrical events in controlling [Ca²⁺]_i over diverse time scales in islets.

INTRODUCTION

Although numerous studies have examined glucose-induced [Ca²⁺]_i signaling in isolated mouse or rat β-cells (Gylfe, 1988; Wang and McDaniel, 1990; Herchuelz et al., 1991; Yada et al., 1992; Hellman et al., 1992; Dryselius et al., 1994; Larsson et al., 1996; Smith et al., 1997; Jonkers et al., 1999; Salgado et al., 2000) and islets (Jonkers et al., 1999; Valdeolmillos et al., 1989; Santos et al., 1991; Valdeolmillos et al., 1993; Gilon et al., 1994; Worley et al., 1994; Bergsten et al., 1994; Gilon and Henquin, 1995; Bergsten, 1995; Martin et al., 1995; Liu et al., 1998; Henquin et al., 1998; Barbosa et al., 1998), few have systematically compared [Ca²⁺]_i signaling in single β-cells and intact islets under the same experimental conditions and in the same laboratory (Jonkers et al., 1999). In addition, most of what is currently known about [Ca²⁺]_i signaling in single β-cells comes from studies of ob/ob mouse islets, which likely differ from those of normal mice. Furthermore, although the role of islet and β-cell electrical activity in glucose-dependent [Ca²⁺]_i signaling and insulin secretion is relatively well established (Henquin et al., 1998; Satin, 2000; Ashcroft and Rorsman, 1989; Henquin, 1987), only a few studies have used simultaneous measurements of [Ca²⁺]_i and electrical activity to determine the specific role of β-cell electrical events in the magnitude and timing of glucose-dependent [Ca²⁺]_i oscillations (Dryselius et al., 1994; Santos et al., 1991; Worley et al., 1994; Leech et al., 1994; Rorsman et al., 1992). Understanding detailed aspects of the [Ca²⁺]_i signaling of single mouse β-cells and islets is important, since these characteristics can be used as constraints on existing as well as future theoretical models of islet bursting and [Ca²⁺]_i oscillations (e.g., Sherman, 1996; Satin and Smolen, 1994; Bertram et al., 2000; Goforth et al., 2002; Göpel et al., 1999; Kuznetsov et al., 2002).

In the present study, we compared [Ca²⁺]_i and electrical signaling in intact mouse islets and isolated β-cells. Our aim was to test whether glucose-induced changes in [Ca²⁺]_i are primarily determined by the electrical firing patterns of β-cells and islets, and to compare the experimental results with the predictions of a new model of islet bursting and [Ca²⁺]_i (Goforth et al., 2002; Bertram et al., 2000). In addition, as we recently showed that dispersed β-cells exposed to 11.1 mM glucose exhibit heterogeneous electrical firing patterns that can be subdivided into three classes (Classes I–III) (Kinard et al., 1999), we examined whether these distinct electrical patterns in turn produce three corresponding patterns of [Ca²⁺]_i. If so, these different [Ca²⁺]_i signaling patterns could differentially support insulin secretion, since β-cells release insulin in response to elevated [Ca²⁺]_i (Henquin et al., 1998; Satin, 2000; Henquin, 1987; Ämmälä et al., 1993).

MATERIALS AND METHODS

Culture of islets and islet β-cells

Mouse islets were isolated from the pancreases of Swiss-Webster mice by collagenase digestion, as previously described (Khan et al., 2001; Hopkins et al., 1991). Islets were dispersed into single cells by shaking them in a low-calcium medium (Lernmark, 1974). Islets or β-cells were placed on glass coverslips in 35-mm petri plates and cultured in RPMI-1640 medium with fetal bovine serum, L-glutamine, and penicillin/streptomycin (Gibco, Grand Island, NY). All cultures were kept at 37°C in an air/CO² incubator. Cells were fed every 2–3 days, and were kept in vitro for up to five days. In contrast, islets were cultured for 1–2 days. We did not see any systematic differences in the Ca²⁺ signaling of isolated β-cells with time in culture, in contrast to previous reports (Gilon et al., 1994; Bergsten, 1995).

[Ca²⁺]_i measurements

Cultured islets or single β-cells were loaded with the Ca²⁺-sensitive dye, fura-2/AM (Molecular Probes, Eugene, OR). 2 μmol/l fura-2-AM and 1 μl of 2.5% pluronic acid were added to cells in 35-mm culture dishes containing 1 ml of medium, and cells were incubated for 30 min at 37°C in the incubator. After loading, cells were washed once and then incubated in standard external solution for 20 min. [Ca²⁺]_i was measured by placing cells or islets in a small recording chamber mounted on the stage of an Olympus IX-50 inverted epifluorescence microscope (Olympus, Tokyo, Japan). Fura-2 was excited at 340/380 nm using a galvanometer-driven mirror that alternated light originating from a xenon light source between two prisms (HyperSwitch, IonOptix, Milton, MA). A photomultiplier and photon counting were used to quantify fura-2 emission at 510 nm (IonOptix). Fluorescence data were acquired and analyzed using IonWizard software (IonOptix).

[Ca²⁺]_i values were determined from the fluorescence ratio (R) of Ca²⁺-bound fura-2 (excited at 340 nm) to unbound fura-2 (excited at 380 nM). An in vitro calibration kit was used to convert R values to [Ca²⁺]_i levels in single β-cell recordings (Molecular Probes). However, because of islet autofluorescence, the [Ca²⁺]_i levels of individual islets were determined using a standard equation (Grynkiewicz et al., 1985). To convert R to [Ca²⁺]_i using this equation, R_max and R_min were obtained by exposing islets to 10 μM ionomycin plus 3 mM Ca²⁺ or 1 mM EGTA plus 0 mM Ca, respectively, at the end of each experiment. The equilibrium constant for Ca²⁺ binding to fura-2 (K_d) was assumed to be 224 nM (Grynkiewicz et al., 1985). Due to uncertainties inherent in converting fura-2 ratios to [Ca²⁺]_i concentrations, the latter should be considered as estimates of [Ca²⁺]_i.

Electrophysiology

Cells or islets were superfused with a standard external solution containing (in mM): 115 NaCl, 3 CaCl₂, 5 KCl, 2 MgCl₂, 10 HEPES, 11.1 glucose (pH 7.2). The perforated patch-clamp technique was used to record islet or cell membrane potentials or ion currents. Pipettes were pulled from borosilicate glass using a two-stage horizontal puller (Sutter Instruments' P-97, Novato, CA). Pipette tips were then filled with a solution containing (in mM) 28.4 K₂SO₄, 63.7 KCl, 11.8 NaCl, 1 MgCl₂, 20.8 HEPES, 0.5 EGTA (pH 7.2), and 0.1 mg/ml amphotericin B. An Axopatch 200B patch-clamp amplifier (Axon Instruments, Union City, CA) was used in the standard tight-seal perforated patch-clamp mode to record membrane potentials or ion currents in current-clamp or voltage-clamp mode, respectively (Hamill et al., 1981). Pipette resistances ranged from 5 to 8 MΩ using our internal solutions, whereas seal resistances ranged from 2 to 10 GΩ.

Dynamic clamping was used to titrate artificial conductances into single cells to determine their effects on membrane electrical activity and [Ca²⁺]_i (Kinard et al., 1999; O'Neil et al., 1995). To implement dynamic clamp, membrane potential (V) was rapidly sampled via a 12-bit A/D-D/A board (Digidata 1200; Axon Instruments) in current clamp and then scaled appropriately. Artificial currents based on measured V were then calculated in software (DClamp; Dyna-Quest Technologies, Sudbury, MA) and scaled, and were sent out in real time to a patch-clamped cell. Membrane potential was then rapidly resampled and the process continued. See Eqs. 11–13 below.

Solutions were applied to cells or islets using a gravity-driven perfusion system that allowed switching between multiple reservoirs and flow rates in excess of 1 ml/min. The experimental bath was exchanged within 30 s. All experiments were carried out at 32–35°C using a feedback controlled temperature regulation system (Cell Micro Controls, Virginia Beach, VA). All drugs were made up fresh daily from frozen stock solutions. Drugs and chemicals were obtained from Sigma Chemical (St. Louis, MO).

Data analysis and graphics were implemented using IGOR Pro software (WaveMetrics, Lake Oswego, OR) and statistics were performed using GraphPad Pro (GraphPad, San Diego, CA).

Classification of single β-cell electrical patterns

The heterogeneous electrical activity of single β-cells was sorted into three broad categories consisting of plateau cells, bursters, and spikers, based on characteristics such as spike amplitude, period, and the existence of plateau depolarizations. As we have previously found (Kinard et al., 1999), cell patterns could be sorted based on “activity fraction”, the fraction of time the cell spent above a threshold level. Cell behaviors and thresholds in particular were very variable, however, so we used a related measure, “delta peak”, determined as follows: all point histograms of voltage traces were constructed and fit by nonlinear least squares to a sum of two Gaussians (see Fig. 4 of Kinard et al., 1999, for examples). The delta peak was defined as the difference of the amplitudes of the two Gaussians, normalized by the larger peak: Δp = 100(L_a − R_a)/max(L_a, R_a), where L_a and R_a are the heights of the left and right peaks, reflecting the total duration of repolarized and depolarized periods, respectively. This procedure yielded scores varying from −100 to +100.

Modeling

Islet [Ca²⁺]_i oscillations were simulated using standard techniques and the recently published “calcium subspace” model (Goforth et al., 2002). This model is a member of the class of models we call “phantom bursters”, where the interaction between two slow variables (S₁ and S₂) produces intermediate (and hence “phantom”) kinetic behavior (Bertram et al., 2000). Electrical bursting in the subspace model results from the cyclic activation of a novel Ca²⁺-activated K⁺ current called K_slow (Göpel et al., 1999). As described in Goforth et al. (2002), K_slow is postulated to be activated by Ca²⁺ accumulation in a submembrane space (subspace) located between the endoplasmic reticulum (ER) and the plasma membrane. We assume that the submembrane portion of the ER and the plasma membrane are in close enough proximity to hinder the diffusion of Ca²⁺ between the subspace and the bulk cytosol and create a standing gradient of Ca²⁺ concentration. Although such a partially membrane-delimited compartment has not been identified in β-cells, similar structures have been described in cardiac myocytes (Blaustein and Golovina, 2001) and in neurons (Bootman et al., 2001). The existence of a subspace thus remains a prediction of the model for the time being.

The faster phantom variable S₁ in this case is cytosolic [Ca²⁺], denoted c in the model equations, which mediates rapid changes in subspace [Ca²⁺], denoted c_SS, whereas the slower variable S₂ represents the [Ca²⁺] in the ER, denoted c_ER, which slowly accumulates and is passively released into the subspace. This model can reproduce the experimentally observed biphasic modulation of K_slow under voltage-clamp conditions by thapsigargin or insulin, which decrease ER Ca²⁺ pumping, as well as islet bursting in current clamp (Goforth et al., 2002). Although the specific parameters of the Ca²⁺ subspace model were chosen to highlight certain features of the observed data, the results obtained are general features of the model over a range of parameter values.

As the model is only slightly modified from that in Fig. 8 of Goforth et al. (2002), we describe here only changes in the model. The equation for membrane potential is

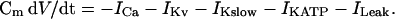(1)

The three Ca²⁺ compartments are described by linear flux exchange equations:

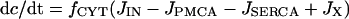(2)

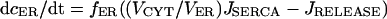(3)

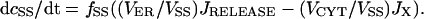(4)

The quantity that corresponds most closely to experimentally measured [Ca²⁺]_i is a weighted average of c and c_SS:

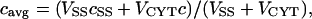(5)

where V_SS is 40% of V_CYT.

To increase c_ER to the experimental range of 200–500 μM (Varadi and Rutter, 2002; Maechler et al., 1999; Tengholm et al., 2001), we have reduced the ER leak rate p_ER to 0.001 ms⁻¹ and increased the ER uptake rate k_SERCA to 0.2 ms⁻¹. The plasma membrane pump rate k_PMCA was adjusted to 0.2 ms⁻¹ to keep plateau fraction near 50%. In all other respects, the Ca²⁺ handling is identical to that in Fig. 8, Goforth et al. (2002).

FIGURE 8.

Stochastic simulation of single-cell behavior (Eqs. 1–9). Parameters as in Fig. 2 and Modeling except g_KATP, which is 42 pS, and g_Ca, which is 1500 pS for Class I firing (A), 1400 pS for Class II (B), and 1050 pS for Class III (C).

For the deterministic simulations (Figs. 2 and 5), all the ionic currents are also unchanged, including I_KATP, which is again treated as a fixed conductance,

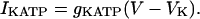(6)

One consequence of this assumption is that inhibition of the SERCA pump eliminates medium and slow bursting in favor of fast spiking because it eliminates the only very slow negative feedback mechanism, K_slow. This is in agreement with experimental observations of Worley et al. (1994), Bertram et al. (1995), and Gilon et al. (1999), but does not account for the observations of Liu et al. (1998) and Miura et al. (1997) that slow oscillations can persist in thapsigargin. If g_KATP is treated as a slow negative feedback process (Magnus and Keizer, 1998; Miwa and Imai, 1999; Rolland et al., 2002) so that there are two S₂ variables, both sets of observations can be accommodated (Bertram and Sherman, unpublished simulations). Here, we have used the simpler model with very slow negative feedback only through K_slow, which is adequate to interpret the experimental data presented in this study.

FIGURE 2.

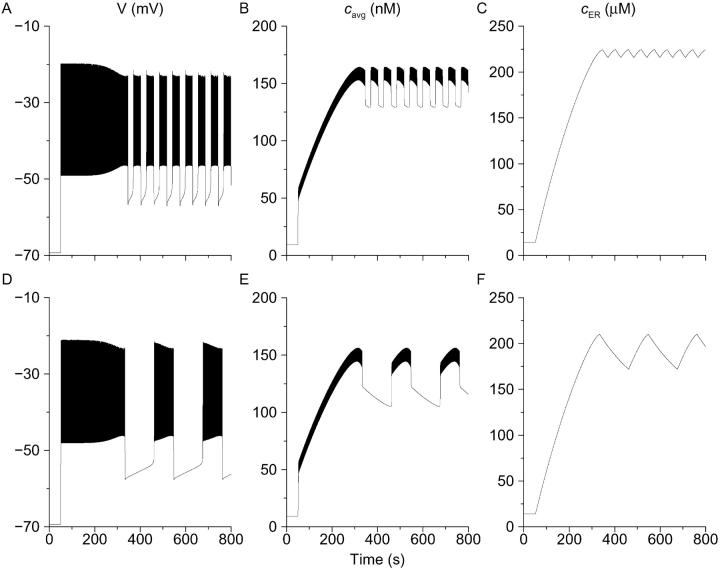
Deterministic simulation of first phase transient and oscillations after addition of glucose (Eqs. 1–6, Methods). (A–C) A medium cell, representing a medium islet. Parameters are as in Modeling section, except g_KATP, which is initially 1 nS and stepped down to 55 pS at T = 50 s to simulate the addition of glucose. For simplicity, no attempt is made to model the latency period or the phase 0 decrease of calcium. (D–F) A slow cell, representing a slow islet. Parameters as in A–C, except g_KATP is stepped to 62 pS.

FIGURE 5.

Deterministic simulation of steady-state bursting in the presence of glucose showing the three Ca²⁺ compartments (Eqs. 1–6, Methods). Parameters are as in Fig. 2 except g_KATP, which is 60 pS throughout, and k_PMCA, which is 0.18 ms⁻¹. (A) Membrane potential. (B) Weighted average of [Ca²⁺]_i and [Ca²⁺]_SS, corresponding to measured cytosolic [Ca²⁺], which declines throughout the active phase. (C) Subspace [Ca²⁺], which rises throughout active phase and activates K_slow to terminate the burst. (D) Store [Ca²⁺], which rises slowly in active phase and falls slowly in silent phase.

For the stochastic simulations (Figs. 8 and 10), I_KATP is rewritten as

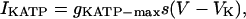(7)

where s satisfies the stochastic differential equation (Higham, 2001):

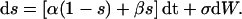(8)

The intensity of the noise, σ, decreases as the square root of the number of ion channels (Fox, 1997):

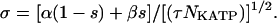(9)

We chose N_KATP = 500 and τ = 100 ms, values that produce reasonable visual agreement with experimental records. For simplicity, we present simulations in which noise was added only to the K_ATP channels; similar results were obtained by applying a similar approach to other channels. In the deterministic limit (large N_KATP), s approaches its mean value s₀ = α/(α + β). For comparison with deterministic simulations, the mean value of g_KATP, g_KATP-max s₀, is reported in the figure legends.

FIGURE 10.

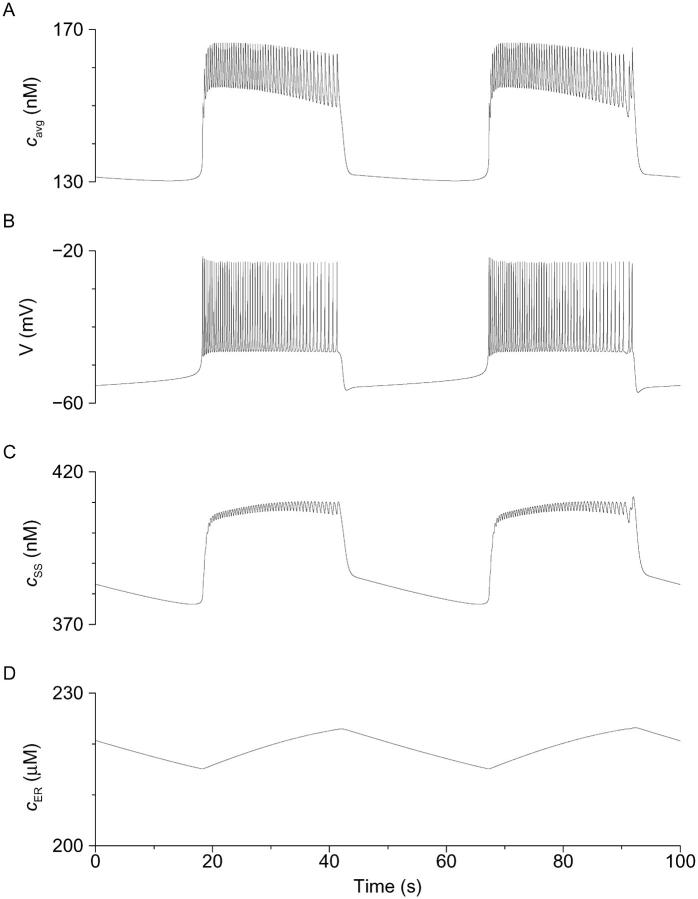
Stochastic simulation of dynamic-clamp conversion (Eqs. 1–9). Deterministic parameters as in Fig. 5, except k_PMCA = 0.2 ms⁻¹. Stochastic parameters and dynamic-clamp parameters are as in Methods. Dynamic-clamp conductance is turned on at T = 20 s and maintained thereafter.

Both deterministic and stochastic simulations are carried out using the stochastic Euler algorithm as implemented in the program XPP (Ermentrout, 2002). Briefly,

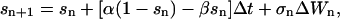(10)

where ΔW_n is a Gaussian random variable with mean 0 and variance Δt.

Deterministic simulations were carried out using the Gear-type algorithm CVODE. Source files for use with XPP or reimplementation of the simulations with other software are available at http://mrb.niddk.nih.gov/sherman.

Dynamic clamping

Dynamic-clamp current was applied using the same formulation as previously (Bertram et al., 2000):

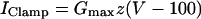(11)

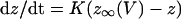(12)

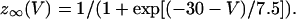(13)

We used K = 2 ms⁻¹ and G_max as indicated in the figure legends. In the experiments, an auxiliary computer read the instantaneous value of V from the cell and calculated the corresponding values of z and I_Clamp using Eqs. 12 and 13, and I_Clamp was injected into the cell in real time. In the simulations, I_Clamp was added to the right side of Eq. 1.

RESULTS

Glucose induces transient changes in islet [Ca²⁺]_i

In glucose-free solution, islet [Ca²⁺]_i was 72.3 ± 5.5 nM (n = 19). In 63% of the islets examined, increasing glucose to 10 mM produced an initial decrease in [Ca²⁺]_i to 66.5 ± 5.1 nM. The mean latency of this phase was 145 ± 36 s (n = 12; Fig. 1, A and B). A similar transient reduction in [Ca²⁺]_i has been reported for mouse (Valdeolmillos et al., 1989, 1993; Gilon et al., 1994; Worley et al., 1994; Bergsten et al., 1994; Bergsten, 1995; Liu et al., 1998; Henquin et al., 1998; Barbosa et al., 1998), rat (Antunes et al., 2000), pig (Bertuzzi et al., 1996), and human islets (Martin and Soria, 1996), and has been attributed to increased Ca²⁺ sequestration into the endoplasmic reticulum as the ratio of ATP/ADP increases (Yada et al., 1992; Hellman and Gylfe, 1984; Roe et al., 1994).

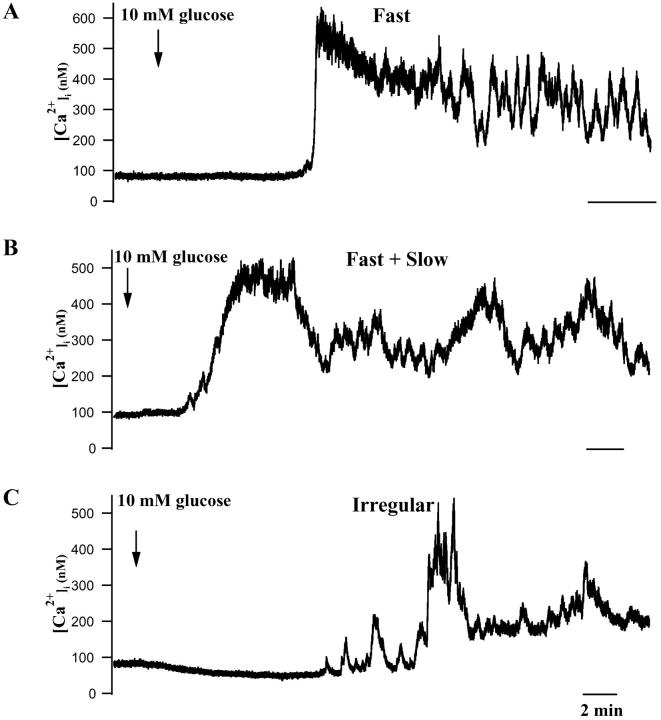
FIGURE 1.

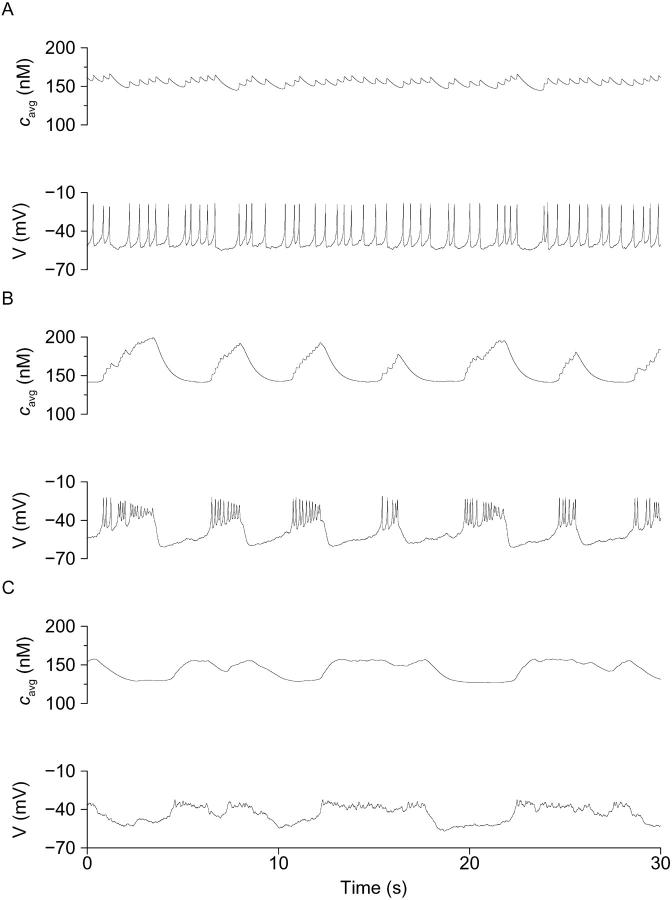
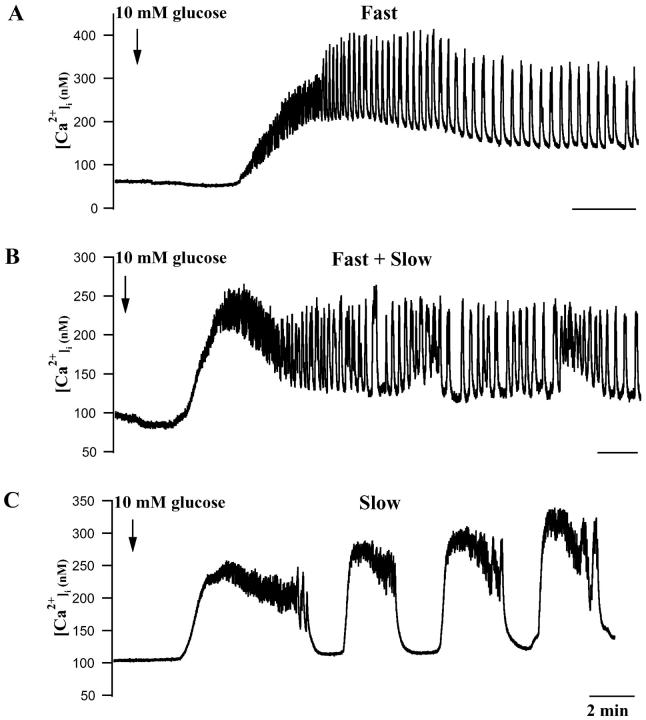
[Ca²⁺]_i responses of individual mouse islets to changing glucose from 0 to 10 mM. (A) Representative islet exhibiting mainly fast phase 2 oscillations. (B) Islet showing a mixture of fast and slow [Ca²⁺]_i oscillations. (C) Islet showing primarily slow [Ca²⁺]_i oscillations. Initial islet [Ca²⁺]_i changes often included initial decreases, a plateau phase, and then oscillations (see text). All time bars represent 2 min.

After the transient decrease, [Ca²⁺]_i increased to a mean plateau level of 310.5 ± 22.7 nM (n = 19), a greater than fourfold increase over resting [Ca²⁺]_i. The mean latency for reaching the peak of this plateau was 281 ± 27.7 s, and its mean duration was 233.2 ± 25.1 s (n = 19). After the plateau phase, [Ca²⁺]_i typically declined over tens of seconds, with most islets then exhibiting regular [Ca²⁺]_i oscillations. These oscillations ranged between a minimum of 89.4 ± 7.5 nM (n = 19) and a maximum of 236.1 ± 20 nM [Ca²⁺]_i. The basic characteristics of islet [Ca²⁺]_i signaling are summarized in Table 1. (The comparative data for single cells will be discussed below). Similar data were obtained in mouse islets by Gylfe et al. (1998), Jonkers et al. (1999), Liu et al. (1998), Gilon et al. (1994), and Bergsten (1995). The [Ca²⁺]_i oscillations we observed in mouse islets were heterogeneous in terms of their frequency, with 47.4% of the islets exhibiting fast oscillations of 2–3 min⁻¹, 10.5% exhibiting slow oscillations of 0.2–0.8 min⁻¹, and the remainder exhibiting a mixture of fast and slow oscillations (Jonkers et al., 1999; Valdeolmillos et al., 1989; Bergsten et al., 1994; Bergsten, 1995; Liu et al., 1998; Henquin et al., 1998). Although we use the terms “fast” and “slow” here to be consistent with the islet Ca²⁺ literature (Henquin et al., 1998), these “fast” [Ca²⁺]_i oscillations occur at the same frequency as glucose-dependent oscillatory electrical activity. They are slower than the oscillations seen in islets exposed to muscarinic agonists (Bertram et al., 1995; Sánchez-Andrés et al., 1988; Santos et al., 1991) or those often seen in isolated β-cells (Kinard et al., 1999; Rorsman and Trube, 1986; Misler et al., 1989, Pressel and Misler, 1991; Barnett et al., 1995). On the other hand, they are faster than the oscillations seen in islets exposed to epinephrine (Cook and Perara, 1982; Debuyser et al., 1991), the slower oscillations seen in glucose alone (Gilon et al., 1994; see also Figs. 3 and 4 B below), or those reported in single β-cells and small clusters by others (Gylfe et al., 1991; Smith et al., 1997; Jonkers et al., 1999). Therefore, we have termed this intermediate pattern with a period ranging from 10 to 60 s “medium bursting” (Bertram et al., 2000).

TABLE 1.

[Ca²⁺]_i handling of islets and isolated β-cells

Groups	Resting [Ca2+]i(nM)	Latency to initial decrease(s)	[Ca2+]i in phase 0(nM)	Latency to phase I(s)	Peak [Ca2+]i in phase I(nM)	Phase I duration(s)	Silent phase [Ca2+]i in phase II(nM)	Active phase [Ca2+]i in phase II(nM)
Islets N = 19	72.3 ± 5.4	145.0 ± 36.0	66.5 ± 5.1	281.1 ± 27.7	310.5 ± 22.7*	233.2 ± 25.1	138.5 ± 7.8*	284.7 ± 20.6
Isolated β-cells N = 37	65.2 ± 2.7	160.1 ± 27.6	54.1 ± 3.5	301.2 ± 42.1	437.5 ± 20.1	239.0 ± 16.6	176.1 ± 12.3	319.7 ± 14.4

Mean ± SE.

^*P < 0.05 versus isolated β-cells.

FIGURE 3.

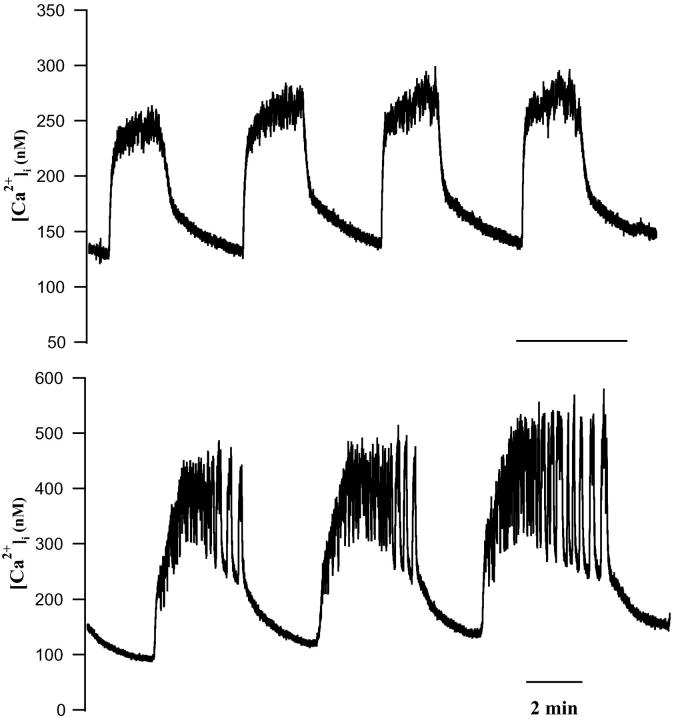
Slow [Ca²⁺]_i oscillations with prominent interburst decaying phases. (Top) Islet where calcium slowly rose for the entire duration of the active phase, and slowly decayed during the interburst phase. (Bottom) Another islet where faster oscillations occurred on the slower oscillations as “bursts of bursts” (see text). All time bars represent 2 min.

FIGURE 4.

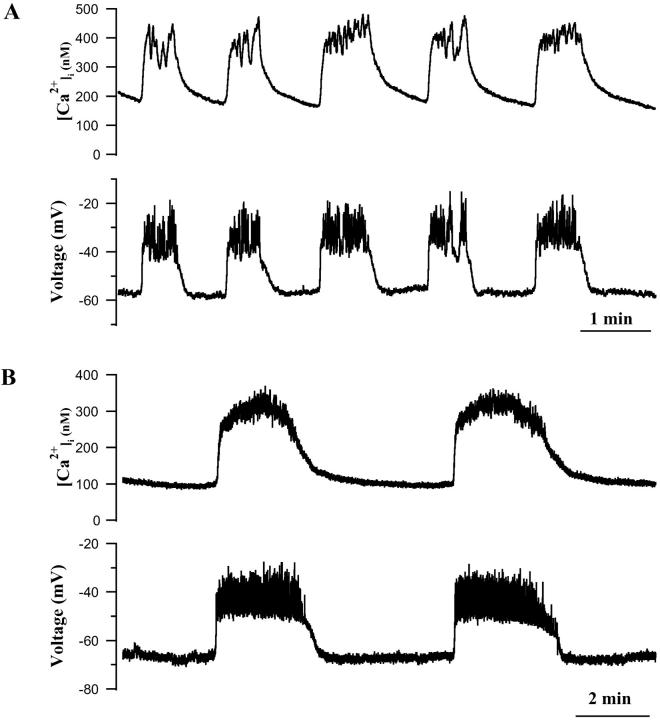
Simultaneous recordings of [Ca²⁺]_i oscillations (top) and electrical activity (bottom) in two slow islets. (A) Islet where faster electrical bursts occurred on slower bursts and triggered concomitant fast [Ca²⁺]_i oscillations. (B) An islet having very slow electrical activity and the [Ca²⁺]_i oscillations, indicating that electrical activity can account for the slow as well as medium [Ca²⁺]_i oscillations.

Examples of fast and slow [Ca²⁺]_i oscillations are shown in Fig. 1. Fig. 1 A shows an islet that had large amplitude, fast oscillations that occurred at a frequency of 3.5 min⁻¹ (Valdeolmillos et al., 1989; Worley et al., 1994; Barbosa et al., 1998). In contrast, the islet shown in Fig. 1 C mainly had slow [Ca²⁺]_i oscillations that occurred at 0.25 min⁻¹. Fig. 1 B shows an islet that exhibited a mixture of fast (≈3 min⁻¹) and slow (0.2 min⁻¹) oscillations, where the fast oscillations occur during the [Ca²⁺]_i oscillations and the troughs in between them. Several groups have reported that mouse islets can display fast or slow [Ca²⁺]_i oscillations or both simultaneously (Jonkers et al., 1999; Valdeolmillos et al., 1989; Santos et al., 1991; Bergsten et al., 1994; Liu et al., 1998; Henquin et al., 1998).

One consistent feature of the data, which is apparent from Fig. 1, is that the kinetics of the [Ca²⁺]_i oscillations are independent of the duration of the initial [Ca²⁺]_i plateau seen when glucose is raised. We further observed that the duration of the initial transient was always greater than the duration of succeeding plateaus, with the latter approaching the duration of the transients in the slowest cases. Based on past experience with the phantom-bursting model (Bertram et al., 2000), we hypothesized that the kinetics of both the transients and the slow oscillations reflect the timescale of the slower negative feedback variable, S₂, (here, c_ER, Fig. 2, C and F; see Methods and Goforth et al., 2002) and thus would always be on the order of a few minutes. The succeeding oscillations, in contrast, would represent the “phantom” interactions between S₂ and S₁ (here, c, which is not shown but is reflected in the fast component of c_avg), and could thus occur on a timescale anywhere between those of S₁ and S₂, or from minutes to seconds. To test this hypothesis, we simulated the [Ca²⁺] and electrical responses of islets to a step change in glucose concentration. As shown in Fig. 2, the model successfully reproduces an initial plateau in c_avg after glucose exposure, as well as the electrical and [Ca²⁺]_i oscillations that follow. In Fig. 2, A–C, oscillations of membrane potential, free cytosolic [Ca²⁺] (c_avg), and ER [Ca²⁺] (c_ER) are shown. The oscillations occur on the “medium” timescale (≈2 min⁻¹) because of the relatively large contribution from S₁. In Fig. 2, D−F, “slow” oscillations (≈0.7 min⁻¹) are seen because the oscillation frequency is dominated by the timescale of c_ER. In both cases, the slow loading of the ER due to Ca influx determines the initial c_avg plateau, which lasts ∼2 min.

Thus, by adjusting parameters, medium or slow oscillations could be produced in two model islets having identical plateau phases, in agreement with our experimental observation that the period of the [Ca²⁺]_i oscillations is not correlated to the duration of the initial plateau. In addition, the model predicted that in slower islets, [Ca²⁺]_i would decay more slowly after each period of Ca²⁺ influx. A representative example of the slow tails during steady-state oscillations is shown in Fig. 3 (top). In the model, this slow decay is due to the slow, passive release of Ca²⁺ from the ER after each burst of action potential-mediated Ca²⁺ influx, as anticipated by Gilon et al. (1999), who noted that the slow tails have kinetics similar to the dissipation phase of [Ca²⁺]_ER. The model also suggests that, other things being equal, the slow tails will be more prominent in cases where [Ca²⁺]_i rises throughout the active phase of the oscillation, i.e., when the filling of the ER dominates over the slowing of Ca²⁺ entry (compare Figs. 3, top and 4 A with Fig. 4 B). Such slow tails of [Ca²⁺]_i were a conspicuous feature not only of islet [Ca²⁺]_i recordings (Figs. 3 and 4), but of single cells when artificially induced to oscillate on timescales comparable to those of islets (Fig. 9).

FIGURE 9.

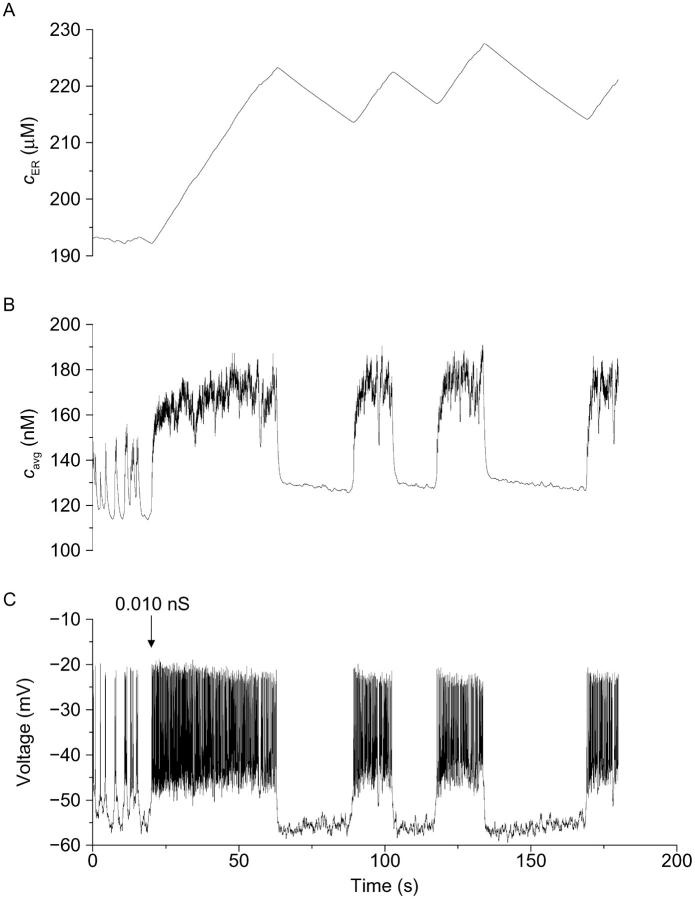
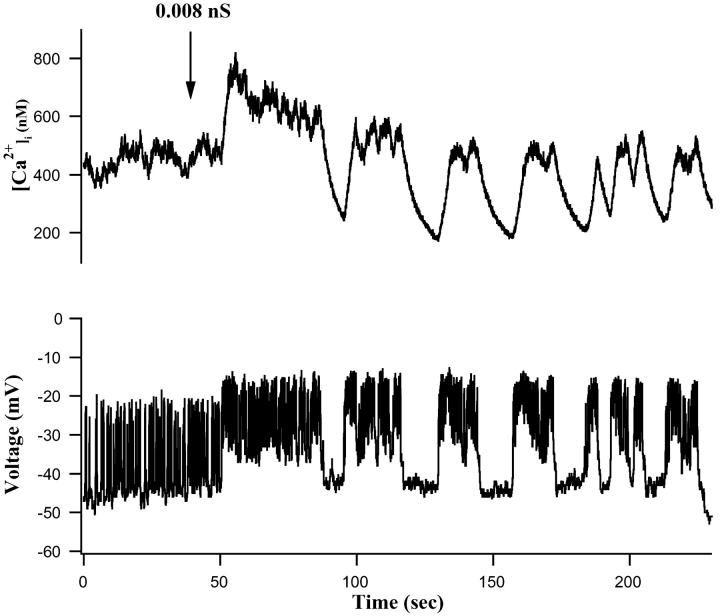
Converting fast single-cell electrical activity to an isletlike pattern with dynamic clamp resulted in corresponding [Ca²⁺]_i oscillations that resembled those of islets. Starting at the arrow, 0.008 nS of maintained exogenous conductance were added in accordance with Eqs. 11–13. Calcium changes are shown at the top; membrane potential changes at the bottom.

We also observed many islets with more complex [Ca²⁺]_i rhythms. In some cases, oscillations clustered together in time, whereas in others, fast oscillations were superimposed on top of slow ones. These two types of “bursts of bursts” were apparent in recordings both of islet calcium and of islet electrical activity. An example of the first type, in which medium or slow bursts were clustered together and separated by longer silent phases is shown in Fig. 3 (bottom), in an islet exposed to 15 mM glucose. “Bursts of bursts” of this type were recently simulated by Arredouani et al. (2002), who exposed islets to clustered pulses of KCl to increase [Ca²⁺]_i. Examples of the second type of superimposed bursting consisting of slow plateaus with superimposed fast bursts are shown in Figs. 4 A and 9. In some islets, 1–3 short period oscillations were seen to regularly trail each slow wave (Fig. 1 C).

Fast and slow [Ca²⁺]_i oscillations are due to fast and slow forms of islet electrical activity

Using the perforated patch technique to record from β-cells on the surface of intact islets (Göpel et al., 1999), and a fast photomultiplier and fura-2 fluorescence to monitor simultaneous changes in islet [Ca²⁺]_i, we determined the extent to which the various patterns of [Ca²⁺]_i oscillations we observed were determined by the electrical activity of individual islets. We were especially interested in determining whether islets displaying slow [Ca²⁺]_i oscillations (0.2 min⁻¹ or less) had correspondingly slow electrical activity, as a variety of nonelectrical mechanisms have been proposed to account for the slow [Ca²⁺]_i oscillations in islets and single β-cells (Hellman et al., 1992; Dryselius et al., 1994; Liu et al., 1998; Leech et al., 1994; Gylfe et al., 1991; Tornheim, 1997; Porterfield et al., 2000; Jung et al., 2000).

Fig. 4 shows data obtained from two representative islets where [Ca²⁺]_i and membrane potential were recorded simultaneously. As expected from previous recordings of mouse islet electrical activity, islet silent phase potential was between −55 and −65 mV, plateau potential was near −40 mV, and the peaks of the voltage spikes approached −20 mV (Henquin, 1987). Summary results for the islets studied are given in Table 2; comparison of islets with single cells will be discussed below. There was a high degree of synchrony between [Ca²⁺]_i and the membrane potential, with changes in membrane potential leading the changes in [Ca²⁺]_i (cf. Valdeolmillos et al., 1989; Santos et al., 1991; Barbosa et al., 1998). The islet shown in Fig. 4 A had 50-s duration slow waves that occurred at a frequency of 0.8 min⁻¹. The bursts of bursts of electrical activity mentioned above are apparent here, with the faster electrical events driving the faster [Ca²⁺]_i oscillations within the slower plateaus. The close synchrony between [Ca²⁺]_i and membrane potential is even more impressive in this case, considering that the electrical activity was recorded in a superficial β-cell whereas the fura-2 signal represented the average fluorescence of many β-cells within the islet syncytium. This suggests that the extensive gap junctional coupling known to exist within the islet is very effective in synchronizing the activity of the islet cells (Mears et al., 1995; Serre-Beinier et al., 2000). In contrast, the islet shown in Fig. 4 B displayed much slower [Ca²⁺]_i oscillations, which occurred at 0.2 min⁻¹. These slow [Ca²⁺]_i oscillations were also highly synchronized with islet bursting electrical activity (Valdeolmillos et al., 1989). This suggests that electrical activity is likely to be a critical mediator of all the islet [Ca²⁺]_i oscillations we observe, fast, medium, and slow (Dryselius et al., 1994; Valdeolmillos et al., 1989). Consistent with this, the application of Ca²⁺-free saline, diazoxide, or the L-type Ca²⁺ channel blocker nimodipine abolished all the [Ca²⁺]_i oscillations of islets (data not shown).

TABLE 2.

Steady-state electrical properties of islets and isolated β-cells

Groups		Resting membrane potential (mV)	Plateau potential (mV)	Action potential peak (mV)	Action potential amplitude (mV)	Frequency (min−1)	δ-peak
Islets N = 9		−58.6 ± 3.3*†	−43.1 ± 2.6	−19.1 ± 3.1	33.7 ± 3.5*‡	0.54 ± 0.11*‡	N/A
Isolated β-cells	Class I N = 10	−46.1 ± 2.5	N/A	−23.6 ± 4.3	21.3 ± 2.2	94.0 ± 12.9	66.7 ± 10.6
	Class II N = 23	−44.0 ± 1.0	−36.0 ± 1.7	−19.0 ± 1.6	17.8 ± 1.0	35.8 ± 6.2	50.1 ± 9.9
	Class III N = 3	−45.3 ± 7.3	−32.0 ± 7.57	−22.0 ± 4.6	6.7 ± 1.3	12.3 ± 2.8	−28.0 ± 14.5

Mean ± SE.

^*P < 0.05 versus Class I.

^†P < 0.05 versus Class II.

^‡P < 0.05 versus Class III.

The relationship between electrical activity and Ca²⁺ dynamics postulated in the Ca²⁺ subspace model is shown in Fig. 5. Fig. 5, A and B, show c_avg and V, respectively, corresponding to the experimentally measured [Ca²⁺]_i membrane potential, and Figs. 5, C and D, show the predicted underlying response of subspace [Ca²⁺] (c_SS) and ER [Ca²⁺] (c_ER). During the active phase of bursting, Ca²⁺ enters the cytosol through L-type channels. Much of this is transported into the ER by SERCA pumps, causing c_ER to rise (Fig. 5 D). The influx into the cytosol also elevates c_SS (Fig. 5 C). During the silent phase, there is little influx feeding the ER, so there is a net release of Ca²⁺ into the subspace compartment. This release is reflected in the slow tail in c_SS (Fig. 5 C). We suggest that dyes such as fura-2 measure the weighted average of Ca²⁺ concentration in the bulk cytosol and the subspace, c_avg (Fig. 5 A), where the weights are the volumes of the two compartments (Goforth et al., 2002). Thus, the fluorescence records capture features of the [Ca²⁺] in the bulk cytosol, the subspace, and (indirectly) the ER. Experimentally, there was considerable variation in the kinetics of individual [Ca²⁺]_i oscillations in islets having bursts that lasted minutes or more. In some of these islets, [Ca²⁺]_i progressively increased for the duration of each plateau wave (Figs. 3, top and 4 A), whereas in others, [Ca²⁺]_i either declined during the plateau (Fig. 1 C) or increased first and then declined (Fig. 4 B). All of these behaviors could be reproduced by the model depending on the parameter values used. Thus, a decline in c_avg is shown in Figs. 2 B and 5 A (see also Goforth et al., 2002), whereas an increase followed by a decrease is shown in Fig. 2 E. In the subspace model, these dynamics reflect competition between the ER as a Ca²⁺ source and influx through Ca²⁺ channels. As the ER fills, it releases progressively more Ca²⁺, causing the plateau to rise. However, spike frequency slows down near the end of the burst, reducing Ca²⁺ influx and causing the plateau to decline. The rise is seen when bursts are slower or when the rate of flux both in and out of the ER is larger, i.e., when the ER is more labile. Note, however, that in this model, the K_slow channels sense only Ca²⁺ in the subspace, which continues to rise throughout the active phase (Fig. 5 C). It is this rise that is responsible for the termination of the active phase.

Glucose induces multiple transient changes in [Ca²⁺]_i in single mouse β-cells as in islets, but single β-cells typically lack robust slow [Ca²⁺]_i oscillations

As we found with intact islets, exposing single mouse β-cells to 10 mM glucose resulted in three phases of activity, although there were both qualitative and quantitative differences between the [Ca²⁺]_i changes of isolated β-cells and islets. The [Ca²⁺]_i properties of single β-cells are summarized in Table 1. In glucose-free saline, single β-cells had a mean basal [Ca²⁺]_i of 65.2 ± 2.7 nM (n = 37), as in islets (p > 0.05), and was similar to previous reports (Gylfe, 1988; Wang and McDaniel, 1990; Yada et al., 1992; Gilon et al., 1994; Krippeit-Drews et al., 2000). Upon exposure to 10 mM glucose, [Ca²⁺]_i decreased to 54.1 ± 3.5 nM (in 23/37 cells, or 62.2%), which was not significantly different from that of islets (Fig. 4; Table 1). This suggests that ER Ca²⁺ sequestration is likely to be similar in single β-cells and islets. Decreases in [Ca²⁺]_i levels upon glucose stimulation have been reported previously in single rodent β-cells by others (Gylfe, 1988; Wang and McDaniel, 1990; Yada et al., 1992).

After the initial decrease, [Ca²⁺]_i then increased to reach a plateau of 437.5 ± 20.1 nM (n = 37). The mean latency measured from the time of glucose addition was 301.2 ± 42.1 s. As with islets, the [Ca²⁺]_i plateau usually decreased over several minutes time. Only the peak Phase I [Ca²⁺]_i (437.5 ± 20.1 nM) and silent phase [Ca²⁺]_i (176.1 ± 12.3 nM) differed significantly between islets and single cells, suggesting that there is no gross difference in the Ca²⁺ handling capabilities of single cells and islets. Despite this, there were striking differences in oscillatory behavior. Whereas single β-cells on occasion exhibited one or more [Ca²⁺]_i transients after the plateau phase (Fig. 6 A), it was more often the case that irregular [Ca²⁺]_i changes were seen (Fig. 6 C). The paucity of slow [Ca²⁺]_i oscillations in the isolated β-cells stands in sharp contrast to previous reports of others (Gylfe, 1988; Hellman et al., 1992; Larsson et al., 1996; Smith et al., 1997; Jonkers et al., 1999; Leech et al., 1994). Also absent were oscillations corresponding to medium islet bursting.

FIGURE 6.

[Ca²⁺]_i responses of individual mouse β-cells to changing glucose from 0 to 10 mM. (A) Representative β-cell exhibiting mainly fast and stochastic [Ca²⁺]_i changes, including some near oscillations. (B) β-cell showing a mixture of fast and vestigial slow [Ca²⁺]_i changes. (C) β-cell showing very irregular [Ca²⁺]_i transients after glucose addition. Initial β-cell [Ca²⁺]_i changes often included initial decreases, a plateau phase (see text). All time bars represent 2 min.

Simultaneous recordings of electrical activity and [Ca²⁺]_i in isolated β-cells

We had previously reported that the electrical activity of single β-cells is heterogeneous and can be sorted into three classes: fast spiking cells (Class I), fast bursters (Class II), and plateau cells (Class III) (Kinard et al., 1999). The fast spiking or bursting we observed in isolated cells was similar to many reports of fast and heterogeneous electrical spiking or fast bursting (Rorsman and Trube, 1986; Misler et al., 1989, Pressel and Misler, 1991; Barnett et al., 1995). We found the same three classes of firing behavior in the present study and summarized their properties in Table 2. Unlike the properties of Ca²⁺ handling (Table 1), the properties of membrane potential were much different in single cells compared to islets. As detailed below, all three classes of single cells were much faster than islets. They were also more depolarized (compare “Resting membrane potential”, Table 2), which likely accounts for the increased silent phase [Ca²⁺]_i in isolated cells described above (see also Table 1).

Given that the [Ca²⁺]_i signaling patterns that were associated with these three electrical patterns might differentially support insulin secretion, we measured the electrical activity of single β-cells from each class using perforated patch, while simultaneously monitoring [Ca²⁺]_i with fura-2. As in our previous study of single β-cell electrical activity (Kinard et al., 1999), we used the weighted percent time that cells were depolarized, or delta peak, to differentiate among the three classes (see Methods). Our aim was to determine whether the three electrical classes I–III in turn produced distinct [Ca²⁺]_i patterns.

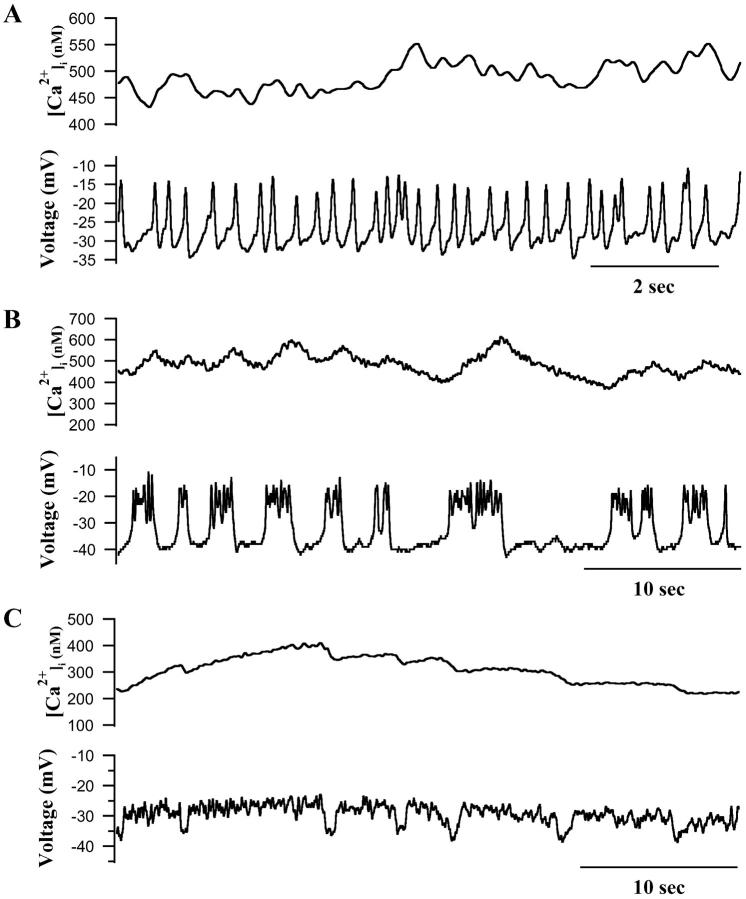
As shown in Fig. 7, β-cells of the three classes indeed had characteristic [Ca²⁺]_i patterns in 10 mM glucose. Thus, Class I cells, which were continuously spiking from a threshold of near −40 mV, and had a mean delta peak value of 66.7 ± 10.6, were associated with a sustained [Ca²⁺]_i level that was either nonoscillatory or exhibited very small oscillations that were in phase with the sharp electrical spikes. The peak [Ca²⁺]_i measured in these cells was 328.3 ± 23.2 nM. Interestingly, [Ca²⁺]_i and membrane spiking activity appeared to be most clearly synchronized in Class I β-cells when spike frequency either abruptly increased or decreased (Fig. 7 A), resulting in either increased or decreased [Ca²⁺]_i. Thus, in these cells the frequency of electrical spiking appeared to be a major determinant of [Ca²⁺]_i.

FIGURE 7.

The electrical activity and [Ca²⁺]_i changes of single β-cells exposed to 11.1 mM glucose. (A) Class I continuously spiking β-cell having sustained [Ca²⁺]_i and small oscillations. (B) Class II β-cell having fast bursts of electrical activity and corresponding oscillations in [Ca²⁺]_i. (C) Class III plateau cell with close synchrony between calcium and electrical activity and negligible electrical voltage spikes.

In Class II cells, which had a mean delta peak value of 50.1 ± 9.9 and typically displayed bursts of spikes lasting 5 s or less (Bertram et al., 2000; Kinard et al., 1999), we found that electrical activity and [Ca²⁺]_i were clearly synchronized (Fig. 7 B). Thus, the very fast [Ca²⁺]_i oscillations observed in these cells closely resembled the electrical changes recorded in parallel. Similarly, Class III plateau cells (delta peak of −28.0 ± 14.5) also exhibited close synchrony between changes in [Ca²⁺]_i and electrical activity, and their electrical and [Ca²⁺]_i plateaus were very similar in terms of their kinetics (Fig. 7 C).

Thus, in single β-cells, individual voltage spikes tended to produce only small increases in [Ca²⁺]_i, whereas trains of spikes maintained [Ca²⁺]_i at a steady elevated level. In contrast, larger and more pulsatile changes in [Ca²⁺]_i were associated with more defined episodes of electrical bursting. The [Ca²⁺]_i oscillations associated with Class II and III type electrical patterns, although more burstlike, were also much faster (i.e., 12–35 min⁻¹) than even the fastest [Ca²⁺]_i oscillations of intact islets, but were close to the rate of spiking seen during bursts in islets (Fig. 4 A; Bertram et al., 2000; Kinard et al., 1999). Overall, it appeared that electrical activity was an important determinant of [Ca²⁺]_i signaling in single β-cells as well as in islets. Whereas the highly ordered electrical activity of islets produced very regular [Ca²⁺]_i oscillations, the more stochastic electrical activity of isolated β-cells correspondingly produced faster and less regular [Ca²⁺]_i oscillations. Given that single cells in our hands are almost exclusively fast, with oscillations lasting <5 s, it is particularly striking that our islets are so slow.

We next tested whether the subspace model could simulate the behavior of isolated β-cells as well as islets. Beginning with a medium-bursting islet, we reduced the conductance of the KATP channels to make the bursting fast. We also added simulated stochastic channel noise, as noise was very apparent in the single-cell recordings (Sherman et al., 1988). The result was a pattern much like our Class II cells (Fig. 8 B). Note that this fast-bursting pattern is primarily a consequence of the changed conductance; the noise changes the pattern quantitatively, not qualitatively, so as to enhance agreement with the experiments. When in addition to the above changes we increased the conductance of the L-type Ca²⁺ channels, spike amplitude also increased, resulting in a pattern much like our Class I cells (Fig. 8 A). In contrast, decreasing the Ca²⁺ conductance reduced spike amplitude, resulting in a pattern like our Class III cells (Fig. 8 C). In addition to simulating reasonably well the three observed patterns, the features of the fast oscillations also resembled the experimental observations in three respects. Going from Class I to Class II to Class III, oscillation frequency decreases, spike amplitude decreases, activity fraction increases, and delta peak decreases (compare Table 2). The pattern of [Ca²⁺]_i also adjusts much as seen in the experiments, with longer electrical events producing more pronounced fluctuations in [Ca²⁺]_i.

These simulations suggest that the marked differences in behavior between islets and isolated cells may be due to modest variation of cellular parameters, such as conductances. To determine whether single β-cells were intrinsically capable of producing isletlike [Ca²⁺]_i oscillations, we took advantage of our earlier observation that single β-cells can be induced to exhibit isletlike electrical bursting if an appropriate artificial conductance is introduced with dynamic clamp (Bertram et al., 2000; Kinard et al., 1999; Sharp et al., 1993).

As shown in Fig. 9 (top), a single β-cell showing characteristic fast, irregular electrical activity in 10 mM glucose produced correspondingly irregular changes in [Ca²⁺]_i under control conditions. However, the application of 8 pS of an artificial, voltage-dependent Ca²⁺ conductance (Bertram et al., 2000; Kinard et al., 1999) resulted in slow bursts lasting 20–30 s (bottom) and more pronounced, isletlike [Ca²⁺]_i oscillations (compare with Fig. 4 A). Similar results were seen after application of dynamic-clamp conductances to 15/20 isolated β-cells. In the representative cell shown in Fig. 9 (top), the application of dynamic clamp resulted in a drop in [Ca²⁺]_i from around 400 nM to <200 nM once bursting commenced. We attribute this effect to the very strong influence of the interburst period in lowering [Ca²⁺]_i. Thus, the termination of spiking consistently decreased [Ca²⁺]_i presumably by suppressing Ca²⁺ influx at a more hyperpolarized potential. Results from our dynamic-clamp studies thus show that single β-cells are capable of producing isletlike changes in [Ca²⁺]_i once islet electrical bursting is enabled. The implication is that isolated β-cells can produce more regular and more pronounced [Ca²⁺]_i oscillations, but that this does not normally occur in the absence of cell-cell coupling by gap junctions.

Single cells may be fast because of heterogeneity or noise

We have shown that the fast [Ca²⁺]_i patterns of single cells result from the fast electrical pattern, but the question remains: Why is the electrical activity fast? Two main hypotheses have been considered: one, that isolated β-cells differ in their properties from cells in islets (Smolen et al., 1993), and the other, that isolated cells have the same properties as cells in islets, but are more susceptible to stochastic channel fluctuations, which are averaged out when cells are electrically coupled (Sherman et al., 1988). These are in fact not mutually exclusive possibilities, but let us consider the two hypotheses separately.

One possibility is that there are small, but systematic, quantitative differences in the mixture of ionic conductances of single β-cells compared to islets. For example, Göpel et al. (1999) proposed that single β-cells have less g_Ca and hence less K_slow than cells in islets. Alternatively, single cells may possess the right mix of conductances on average when coupled, but not individually when isolated. It is clear that in the former case, the cells can be “corrected” (i.e., made to behave like islets) by using dynamic clamp to augment an inadequate conductance or subtract a conductance present in excess. However, more subtle forms of correction are also possible. We applied the same type of exogenous conductance used in the experiments depicted in Fig. 9 to both our Class I (Fig. 8 A) and Class II (Fig. 8 B) model cells. Both of these cell types were fast because of reduced outward g_KATP, yet adding an inward current readily converted them to isletlike bursters (not shown). Furthermore, this was true despite the fact that the Class I cells also had excess g_Ca whereas the Class II cells had insufficient g_Ca compared to our standard slow islet model cells (Figs. 2 and 5). We conclude that the success of experimental dynamic-clamp conversion in cases such as Fig. 9 is compatible with either systematic parameter deviation or random parameter heterogeneity being the source of fast single β-cell behavior.

We went on to confirm that we could also produce cells with Class II patterns by the addition of channel noise, even when the cell parameters were appropriate for isletlike (medium) bursting. As shown in Fig. 10, such a cell could also be converted to a regular islet burster having pronounced medium period [Ca²⁺]_i oscillations by the addition of voltage-dependent conductance with the same characteristics (see Methods) and nearly the same magnitude as that used in the experimental case. The response of the model in particular captures two key elements of the experiments. Immediately after initiation of dynamic clamp, the cell goes into continuous firing followed by slower bursting (compare Figs. 8 and 10); this was invariably observed in all successful conversions in both experiments and simulations. Also, the conversion to slower bursting results in the appearance of slow tails in the [Ca²⁺]_avg time course, though not as dramatically as in the experiments. The most significant discrepancy between the experiment and the model is that interburst cytosolic [Ca²⁺] falls in the former but rises in the latter. Overall, the simulation of Fig. 10 supports the hypothesis that experimental dynamic-clamp conversion succeeds because it overcomes channel noise.

We will return to the issue of noise versus heterogeneity in the Discussion, but first make some final comments about Fig. 10. The model suggests that the transient firing period is a miniature version of the first phase transient seen when bursting is initiated by a step increase in glucose (Fig. 2): First the ER fills, then bursting commences when [Ca²⁺]_ER begins to oscillate. Before initiation of dynamic clamp, [Ca²⁺]_ER was noisy but flat. As in our previous simulations, which first predicted dynamic-clamp conversion (see Fig. 8 in Bertram et al., 2000), the effect of the added inward conductance is to prevent S₁ (here, [Ca²⁺]_i) from driving fast bursts and allow S₂ (here, [Ca²⁺]_ER) to vary, initiating the slower rhythm.

DISCUSSION

The goal of the present study was to systematically compare [Ca²⁺]_i signaling and electrical activity in mouse islets and isolated β-cells under similar experimental conditions to help refine and constrain current models of islet dynamics, as well as newer models that we and others are currently developing. Our long-range goal is to construct a model that can reproduce the entire spectrum of behaviors observed in single β-cells and in islets and to account for the modulation of these behaviors under varying conditions. A hindrance to this objective has been the fact that few studies have appeared in which both single β-cells and islets from the same preparation have been studied under identical conditions by the same investigators. We began this investigation with the hypothesis that the single β-cell, which is the basic building block of the islet, intrinsically has most or all of the machinery needed to reproduce islet bursting and its concomitant [Ca²⁺]_i oscillations.

Although both single β-cells and islets were found to be glucose responsive, there were very clear differences in terms of their [Ca²⁺]_i signaling and their electrical activity. Thus, whereas intact islets and isolated β-cells showed similar initial decreases in [Ca²⁺]_i followed by plateaus when challenged with glucose, isolated cells typically exhibited faster, less pronounced, and much less regular [Ca²⁺]_i oscillations than islets. This difference reflects the very different electrophysiological properties of islets and isolated β-cells, since the latter in our hands only spike repetitively or show fast (<5 s) bursting in 11 mM glucose, rather than medium or slow electrical bursting (Kinard et al., 1999). The three electrical patterns were indeed associated with distinct changes in [Ca²⁺]_i, ranging from elevated steady levels (Class I cells), to fast oscillations lasting either a few seconds (Class II cells) or up to 10 s (Class III cells). Thus, despite marked quantitative differences between the stochastic electrical activity of isolated β-cells, and the more regular and more oscillatory electrical activity of islets, in both preparations we found that [Ca²⁺]_i closely tracked the electrical activity. Most notably, when single cells were induced by exogenous current injection to behave electrically like islets, the [Ca²⁺]_i pattern followed suit (Fig. 9).

We found that single voltage spikes were not very effective in raising [Ca²⁺]_i above baseline, whereas bursts of spikes were. This is because the timescale of [Ca²⁺]_i accumulation is slow compared to the duration of a spike (Rorsman et al., 1992). Continuous spiking nonetheless resulted in a high average level of [Ca²⁺]_i because the interspike potential in single β-cells was very depolarized, comparable to the plateau potential seen in bursting islets. As oscillations in β-cells [Ca²⁺]_i are believed to be responsible for triggering oscillations in insulin secretion (Henquin, 1987, 1992; Rosario et al., 1986; Kinard and Satin, 1996), these differences in [Ca²⁺]_i oscillations would likely be reflected in different secretion patterns, though we did not measure secretion in this study.

Why don't single β-cells exhibit islet-like bursting?

Unlike other workers, we rarely observed either pronounced slow [Ca²⁺]_i or membrane potential oscillations in our single β-cells (Hellman et al., 1992; Jonkers et al., 1999). A number of explanations have been put forth to explain why single β-cells do not exhibit the slower bursting that is characteristic of intact islets. Most recently, Göpel and colleagues have proposed that the amplitudes of voltage-gated L-type Ca²⁺ currents, and concomitantly, a novel Ca²⁺-activated K⁺ current called K_slow, are smaller in isolated β-cells compared to islets, resulting in abnormal bursting (Göpel et al., 1999). However, the K_slow current we observed in isolated β-cells is in fact comparable in size to islet K_slow (Goforth et al., 2002). Thus, it is unlikely that differences in K_slow amplitude alone are sufficient to explain the different bursting patterns of islets and isolated β-cells.

We consistently found that single β-cells were more depolarized than islets, namely near −40 mV, and that their electrical activity resembled the fast spiking seen at the tops of the plateaus of bursting islets (also see Fig. 3, A and B, in Lebrun and Atwater, 1985). Intriguingly, the resting membrane potential of isolated β-cells is also near −40 mV. This observation led us to hyperpolarize single β-cells with direct injected current or with excess artificial K_ATP conductance with dynamic clamp; these maneuvers did not result in medium bursting (Kinard et al., 1999). Nonetheless, we cannot rule out the possibility that single β-cells have insufficient K⁺ conductance or systematically differ in some other current compared to islets. Interestingly, we were able to convert fast bursters and spikers to medium bursters by adding an inward, voltage-dependent conductance (Fig. 10), as suggested by previous mathematical modeling (Bertram et al., 2000). The ability of single cells to be converted in this manner strongly suggests that single β-cells possess the slow negative feedback process required for isletlike bursting. The data are also consistent with this being the S₂ variable postulated by the phantom-bursting model (Bertram et al., 2000).

Numerous studies have examined the role of paracrine interactions within islets and the importance of gap junctions to islet stimulus-secretion coupling (Mears et al., 1995; Meda, 1996; Serre-Beinier et al., 2000). It is known that electrical bursting is well synchronized across the islet, and that this results in synchronized [Ca²⁺]_i signaling in different parts of the islet (Jonkers et al., 1999; Valdeolmillos et al., 1993; Bergsten et al., 1994; Gylfe et al., 1991; Nadal et al., 1999). We recently reported that reducing gap junctional conductance using specific antisense oligonucleotides to islet connexin proteins results in much faster islet electrical activity resembling that of isolated cells (Zhang et al., 2002). This suggests that part of the observed differences between isolated β-cells and islets can be attributed to the absence of cell-cell coupling. It is possible that changes in protein or gene expression patterns or other parameters may also account for some or all of the differences between isolated β-cells and islets. The question remains, how does electrical coupling modify the electrical activity pattern? Even if isolated β-cells do not differ systematically from cells in situ, their properties may individually vary from the average properties of cells in islets. Coupling would then effectively average the properties of the cells in the population, bringing them into the narrow range needed for isletlike bursting (Smolen et al., 1993). The electrical activity of our single mouse β-cells was also markedly stochastic (Kinard et al., 1999), and theoretical studies have shown that excess noise due to the opening and closing of small numbers of ion channels tends to disrupt the formation of islet bursting (Sherman et al., 1988). However, when we used dynamic clamp to convert the electrical activity of spiking or fast-bursting β-cells to a more isletlike electrical pattern, more regular and isletlike [Ca²⁺]_i oscillations resulted (Fig. 9; see also Bertram et al., 2000; Kinard et al., 1999). This shows that isolated β-cells are indeed capable of rhythmical, isletlike [Ca²⁺]_i oscillations if their electrical activity is suitably modified. Since the conversion was accomplished by introducing very small changes in conductance, in the pS range, only a very small number of active channels might be needed to account for the different electrical properties of fast-bursting β-cells and slower-bursting islets. This also suggests that the differences in single-cell burst frequencies reported in different laboratories or using different mouse strains may stem from very small differences in ion channel or Ca²⁺ handling properties.

Our simulations have shown that dynamic clamp can convert fast single β-cells to medium or slow oscillations whether the cells are fast because of heterogeneity of cell properties (Bertram et al., 2000) or because of noise (Fig. 10). In both cases, the added inward current opposed the repolarizing effect of S₁, allowing time for the dormant S₂ to become manifest. In the Ca²⁺ subspace model, this means that [Ca²⁺]_ER and [Ca²⁺]_avg rise, activating more K_slow, and begin to oscillate. We note that the oscillations in measured calcium after conversion shown in Fig. 9 are larger than those seen even in very slow islets (compare with Figs. 1, 3, and 4). In the model, it is this increase in [Ca²⁺]_avg amplitude that defeats noise: The smaller the noise-induced conductance fluctuations are relative to the range of variation of the negative feedback conductance, the less effective they are in impeding oscillations (Sherman et al., 1988). We note also that the slow calcium oscillations reported in single cells tend to have very large amplitude (Gylfe, 1988; Hellman et al., 1992; Larsson et al., 1996; Smith et al., 1997; Jonkers et al., 1999; Leech et al., 1994). It may be that in those preparations, the range of the negative feedback variable is sufficiently large that noise is relatively ineffective.

Though we cannot give a complete answer yet as to their precise contributions, we believe that both heterogeneity and noise play a role in explaining the differences between islets and single cells. Isolated β-cells do not occur in nature, and there is thus no selective pressure for individual cells to obey exacting constraints on their properties, provided the islets in aggregate behave as needed.

Progress and challenges in modeling islets and islet cells

We have shown that the recently developed Ca²⁺ subspace model (Goforth et al., 2002) can account for a variety of additional features of the [Ca²⁺]_i oscillations of whole islets and single β-cells with minimal modification. First, the model readily accounts for the wide range of oscillation periods found in islets (Fig. 2) by changing a single-channel conductance. In the examples chosen for illustration here, reducing K_ATP conductance made the oscillations faster. One study has found that increasing K_ATP conductance by adding diazoxide, but not by reducing glucose concentration, dramatically decreased burst frequency (Henquin, 1992). It is important to note that our results do not depend on this response to g_KATP. Similar results, including the three classes of single-cell firing and conversion of fast cells to medium bursting with dynamic clamp, could be achieved (not shown) when we made the cells fast by increasing the ER leak rate or by increasing g_KCa. In the simulations reported here, further reduction in g_KATP increased oscillation frequency to the level we observed in isolated β-cells (Fig. 8). Varying a second conductance, here g_Ca, was able to reproduce the diverse behaviors of single cells, continuous spiking, fast-bursting, and plateaus (Fig. 8, A–C). Again, any other parameter change that results in variation in spike amplitude could have similar effects on the fast electrical patterns. The most pertinent conclusion to draw is that these diverse behaviors are likely not random artifacts, but the consequences of natural variation of cellular properties. We had previously demonstrated that the three classes of single-cell behavior could be parameterized by any of several phenomenological features: delta peak, activity fraction, cycle duration, or spike amplitude (Kinard et al., 1999). The fundamental new finding is that variation of a single biophysical parameter is sufficient to account for all of those changes.

Second, the modeling showed that the transient first phase of electrical activity seen when glucose is elevated from subthreshold to stimulatory levels could result from the filling of internal stores. During the filling phase, the K_slow current is inhibited because the ER acts as a sink, reducing [Ca²⁺] in the Ca²⁺ subspace. A connection between the first-phase transient and ER filling has been previously proposed (Bertram et al., 1995; Mears et al., 1997). In the present model, however, the state of the ER is transmitted to the plasma membrane by K_slow, which depends on release of store Ca²⁺ to a submembrane compartment rather than by a store-operated cation channel (I_CRAN or I_CRAC). In both the experiments and the simulations, we observed that first phase duration is independent of subsequent burst period and also that it is comparable to the active-phase duration in the slowest bursting islets and cells that we and others have measured. Both of these observations can be explained by postulating that the first phase is mediated by the S₂ process, which in the present model is unleashed by the reduced inhibition of K_slow as the ER fills. Despite these successes, a number of significant challenges remain for future modeling efforts. Most critical is the need to demonstrate that model cells that behave in detail like our single cells when uncoupled behave like islets when coupled. It may be possible to accomplish this using only electrical coupling through gap junctions, but we are also considering an alternative model based on autocrine and paracrine feedback of insulin onto β-cells via activation of K_ATP channels (Bertram et al., 2002).

The models also need to account for the complex bursts of bursts pattern, which appears to be characteristic of islets. Preliminary studies (R. Bertram, unpublished simulations) have shown that the clustering of fast or medium bursts within slower bursts can be simulated by the Ca²⁺ subspace model if an additional slow negative feedback variable representing a glycolytic oscillator is incorporated into the model. So modified, the phantom-bursting model then predicts accordionlike bursts resembling those we found in this study (Fig. 3 bottom). The other bursts of bursts pattern we observed, in which fast oscillations occur on top of the slow plateaus (Figs. 4 A and 9 bottom), can also be seen in phantom-type models under some conditions. It has been proposed both that bursts of bursts are a feature of single cells (Arredouani et al., 2002; Jonkers et al., 1999), and that they represent interaction of fast and slow cells within an islet (Liu et al., 1998). We are not in a position to settle this question, especially since there are at least two varieties of bursts of bursts, but we reiterate that we observed the top-of-the-plateau variety in single cells when they were induced to burst on an isletlike timescale (Fig. 9 bottom).

Finally, for simplicity we have neglected the possible role of the KATP channel as an alternate or additional S₂ process through indirect effects of [Ca²⁺]_i (Rolland et al., 2002). The interactions of this negative feedback modality with the ER and K_slow are of significant potential interest but make the behavior of the model much more complex and are deferred to future work.

In conclusion, we have demonstrated here the importance of organizing mouse β-cells into islets for normal oscillatory (bursting) electrical activity. At the same time, we have shown that isolated β-cells possess the machinery needed to oscillate like cells in islets, which can be realized by stimulation with appropriate, but small, exogenous currents. In Zhang et al. (2002), we demonstrate the converse, that cells in islets behave like single β-cells when gap junctions are inhibited. Oscillatory electrical activity is in turn both necessary and sufficient for normal [Ca²⁺]_i oscillations. Although pleiotropic effects of gap junction inhibition cannot be ruled out, we believe that bursting electrical activity underlies normal pulsatile insulin secretion in mice. A key task for the future is to determine the relative contributions of disordered kinetics and loss of β-cell mass to the impaired insulin secretion of human Type II diabetes.