The Effect of Lipid Demixing on the Electrostatic Interaction of Planar Membranes across a Salt Solution

Abstract

We study the effect of lipid demixing on the electrostatic interaction of two oppositely-charged membranes in solution, modeled here as an incompressible two-dimensional fluid mixture of neutral and charged mobile lipids. We calculate, within linear and nonlinear Poisson-Boltzmann theory, the membrane separation at which the net electrostatic force between the membranes vanishes, for a variety of different system parameters. According to Parsegian and Gingell, contact between oppositely-charged surfaces in an electrolyte is possible only if the two surfaces have exactly the same charge density (σ₁ = −σ₂). If this condition is not fulfilled, the surfaces can repel each other, even though they are oppositely charged. In our model of a membrane, the lipidic charge distribution on the membrane surface is not homogeneous and frozen, but the lipids are allowed to freely move within the plane of the membrane. We show that lipid demixing allows contact between membranes even if there is a certain charge mismatch, |σ₁| ≠ |σ₂|, and that in certain limiting cases, contact is always possible, regardless of the value of σ₁/σ₂ (if σ₁/σ₂ < 0). We furthermore find that of the two interacting membranes, only one membrane shows a major rearrangement of lipids, whereas the other remains in exactly the same state it has in isolation and that, at zero-disjoining pressure, the electrostatic mean-field potential between the membranes follows a Gouy-Chapman potential from the more strongly charged membrane up to the point of the other, more weakly charged membrane.

INTRODUCTION

Adhesion between biological membranes is governed by a manifold of interactions, which include specific binding and unspecific repulsion by macromolecules (Guttenberg et al., 2001), as well as bending undulations of the membrane (Helfrich, 1978). A further important contribution originates from electrostatics, which is the key issue of this article. On average, ∼10% of all lipids in biomembranes carry a negative charge. The actual charged lipid fraction depends strongly on cell type and the organelles. Due to its high cardiolipin content the average lipid charge density of mitochondrial membranes is ∼4× larger than that of plasma membranes (Sackmann, 1995). There are essentially no positively-charged lipids in biomembranes. In contrast, many membrane-associated proteins carry a net positive charge, as, for example, the eight net positive charges of cytochrome c, which is associated to the negatively-charged mitochondrial membranes.

Although positively-charged lipids are not abundant in biomembranes, liposomes of artificially synthesized cationic lipids play an important role as putative nonviral gene carriers (vectors) for therapeutic purposes (Felgner et al., 1987; Li and Huang, 2000). They serve as targets for negatively-charged nucleic acids (Wetzer et al., 2001; Safinya, 2001; Chesnoy and Huang, 2000). The likely reason for the high efficiency of gene transfer is the electrostatic interaction of the positively-charged carrier liposomes with the biological cell membranes, which, on average, are negatively charged (Safinya, 2001). In artificial systems DNA binds to positively-charged liposomes in a multilayer arrangement, where negatively-charged DNA layers and positively-charged membranes stack in an alternating manner (Rädler et al., 1997; Koltover et al., 1999). It has been demonstrated that the release of counterions is an important factor for the electrostatic free energy of such lamellar complexes (Wagner et al., 2000).

In general, lipids do not mix ideally, but instead form domains, sometimes called rafts (Brown and London, 1998; Simons and Ikonen, 1997). These domains exist on nanoscopic and mesoscopic length scale and there is a yet-ongoing discussion concerning their lifetimes and length scales. In biomembranes, rafts display a distinct lipid and protein composition, and it is likely that the formation of these domains depends on the nonideal mixing properties of the membrane components (Rietveld and Simons, 1998). Such domains have also been identified in artificial membranes by confocal microscopy (Korlach et al., 1999). The physical chemistry of such demixing processes is based on interactions between adjacent lipids (Sugar et al., 1999). The diffusion behavior of lipids can well be altered by domain boundaries which serve as diffusion barriers (Almeida and Vaz, 1995) The finding that membranes containing anionic lipids and basic proteins form domains is an indication that biomembranes may contain positively- and negatively-charged regions.

The analysis of membrane electrostatics is, however, significantly complicated by the fact that lipids may not mix ideally. For this reason the theoretical treatment has so far been restricted to systems with ideally mixing components, e.g., diacyl phosphatidylcholine mixtures with diacylphosphytidylglycerols (Cutsforth et al., 1989; Mosior and McLaughlin, 1992; Montich et al., 1993; Heimburg et al., 1999). In these experimental systems unfavorable mixing properties of membrane components can be neglected. Likewise, in the following we focus on membranes containing ideal mixtures of negatively- and positively-charged molecules.

Charged biomembranes interact with other charged objects like soluble proteins via Coulomb forces. These forces are screened by the microions of the electrolyte solution, but for membranes this is not the only screening mechanism possible. As mentioned, biomembranes consist of many different types of lipids with a rich variety of attached alkane chains and a variety of headgroup areas, some of which are charged (Sackmann and Lipowsky, 1995; Safran, 1994).

According to our present knowledge, membranes are predominantly in a fluid state in which the individual membrane components are free to move within the plane of the membrane. In ideal mixtures the lateral diffusion is not hindered by domain boundaries. If another charged object approaches the surface of such a multicomponent (mixed) membrane, charged lipids are allowed to migrate toward, or away from, the interaction zone. This demixing of charged and neutral lipids results in a locally varying lipid composition profile on the membrane. One may consider the demixing as a kind of two-dimensional screening of the electrostatic forces by charged lipids confined within the plane of the membrane, which supplements the more familiar screening that is due to the electrolyte ions in the three-dimensional space of the solution. Such local demixing has been observed for several peripherals such as prothrombin (Cutsforth et al., 1989) and cytochrome c (Heimburg et al., 1999), as well as for integral proteins using electron spin resonance methods (Marsh, 1987), e.g., for Na⁺,K⁺-ATPase (Esmann et al., 1988; Arora et al., 1989), bacteriophage M13 coat protein (Wolfs et al., 1989), and myelin basic protein (Sankaram et al., 2002).

That membrane demixing can have an enormous impact on the electrostatic adsorption free energy has been recognized and emphasized mainly in the literature on protein and DNA binding on membranes (May et al., 2000; Fleck and von Grünberg, 2002; Menes et al., 1998; Denisov et al., 1998; Heimburg and Marsh, 1995; Heimburg et al., 1999; Takamoto et al., 2001; Last et al., 2001; Huster et al., 2000). For example, it has been shown that protein-induced lipid demixing is responsible for the formation of huge lipid-protein domains in membranes (Denisov et al., 1998); these are regions with a large lateral density of adsorbed proteins, coexisting with other regions of lower protein density. A similar partitioning phenomenon has recently been observed in systems consisting of negatively-charged latex spheres and positively-charged mixed bilayer vesicles (Aranda-Espinoza et al., 1999; Ramos et al., 1999). Whereas initially the spheres adsorb without preference everywhere onto the vesicles, adhesion saturation has been found at a later stage and the membrane partitioned into attractive and repulsive zones where additional incoming spheres were attracted to, or repelled from, respectively. Again, lipid demixing has turned out to be crucial for the understanding of the underlying mechanism (Chen and Nelson, 2000). It should be noted that similar lipid reorganization phenomena may occur close to the tips of atomic force microscopes close to charge surfaces (Butt, 1991; Xu et al., 1997; Müller et al., 1999). Another recent experiment that must be mentioned in this context is that of Nardi et al. (1998, 1997) who have studied the adhesion process between a cationic vesicle and an anionic membrane, both simple binary mixtures of neutral and charged lipids serving as model systems for cationic gene delivery vectors. Measurements of the membrane tension have revealed that due to the adhesion-induced reorganization (or demixing) of the membranes, adhesion of multi-component membranes is fundamentally different from that of single-component membranes.

The aforementioned experiments have motivated the present theoretical study. The article addresses the rather general question of how lipid demixing affects the interaction between two oppositely-charged membranes, modeled here as two planar and parallel surfaces. That this is an interesting nontrivial physical question can be seen already from the case of two membranes with a frozen lipid composition, that is, if the two membranes are considered as two uniformly-charged planar surfaces immersed in an electrolyte solution. If the two surfaces are oppositely charged with exactly the same charge density, then their interaction is always attractive. This is, however, not the case if they are oppositely charged but with surface charge densities that are not equal. Then, the interaction is attractive at large surface separations only and becomes repulsive at close approach. That oppositely-charged surfaces can interact repulsively is a surprising and counterintuitive effect which has first been discovered and analyzed by Parsegian and Gingell (1972). These authors have shown that the observed repulsion is due to the osmotic pressure of counterions that must remain within the gap between the surfaces to ensure the electroneutrality of the system. Parsegian and Gingell, starting from the linearized Poisson-Boltzmann (PB) equation, have systematically calculated that distance separation between the charged surfaces where attraction changes over to repulsion, i.e., where the disjoining pressure between the surfaces is zero.

In the present article we elaborate and extend the study of Parsegian and Gingell by examining if and how their ideas apply to mixed membranes consisting of laterally mobile lipids. We thus consider the interaction of two oppositely-charged planar surfaces hosting a two-dimensional system of screening of lipidic charges. Two-dimensional lipid screening here competes with three-dimensional screening by microions belonging to the salt solution between the surfaces. We will show that lipid demixing increases the region in parameter space where oppositely-charged membranes attract each other; that, in particular, it allows oppositely-charged membranes to make touching contact even if there is a certain charge mismatch between the surfaces; that a switching between contact/noncontact situations can be regulated via the salt concentration of the solution; and, finally, that the results obtained in linear PB theory remain qualitatively correct if the calculation is based on the full nonlinear PB equation.

The effect of demixing on the interaction of oppositely-charged membranes has previously been studied by Lau and Pincus (1999) for the case of no added salt, a restrictive assumption that allowed them to obtain exact solutions to the nonlinear PB equation. A brief theoretical discussion of the thermodynamic and kinetic aspects of adhesion between oppositely-charged binary membranes is also given in Nardi et al. (1998). The phenomenon of repulsion between oppositely-charged surfaces has recently been discussed by Ben-Tal (1995). Related free energy expressions can be found in Stahlberg et al. (1991), Jönsson and Stahlberg (1999), and Oshima (1975), derived in linear but also in nonlinear PB theory (Jönsson and Stahlberg, 1999). A theoretical discussion of adhesion processes of multicomponent membranes, also related to our problem, is given in Weikl and Lipowski (2001). Here the interplay between membrane reorganization and adhesion is considered for a system of two interacting model membranes, with one membrane having components that are attracted by the second membrane, thus acting as local stickers; see also Bell (1988) and Lipowski (1996a).

The validity of the PB theory, upon which our calculations are based, for treating the interaction between charged surfaces in aqueous salt solutions has been examined by various authors by comparison to computer simulation studies; for reviews see Andelman (1995) and Vlachy (1999). In essence, these studies confirm that PB theory is adequate for monovalent salt ions and salt concentrations not exceeding ≈ 0.1 M.

The article is organized as follows. We first introduce our model and formulate the problem (Model and Notation). Following Parsegian and Gingell (1972), the main theoretical task is to calculate the intermembrane distance where the force between the membranes vanishes. This is first done in Effective Interaction in Linear Theory, resorting to the simpler linear PB theory to uncover the underlying physics, and then repeated in Effective Interaction in Nonlinear Theory, now starting from the full nonlinear PB equation.

MODEL AND NOTATION

We consider the interaction between two charged membranes embedded in an aqueous electrolyte solution. We model the membrane surface as an incompressible two-dimensional fluid mixture composed of different types of lipidic surface groups. In principle our treatment also applies to charged or uncharged membrane peptides or proteins. However, in the following we restrict our notation to lipids. The membranes are assumed to interact with each other only locally; that is, the interaction is governed by a membrane area A_int, which is small compared to the total surface A_tot of the membrane, A_int « A_tot. This small area, the interaction region, is treated here as the system, whereas those parts of the membranes that are not involved in the interaction are treated as the reservoir for the surface groups. These groups can freely move between the interaction region and the reservoir. The interaction regions are furthermore taken to be planar stiff sheets, oriented parallel to each other and separated by a relative distance l. Thus, we assume that surface undulation forces can be neglected. These planar interaction regions, though being small compared to A_tot, are still large enough that one can safely ignore effects, which might occur due to the finite size of the interaction zone. The first membrane (i = 1) is located at x = 0 and the other (i = 2) at x = l. Fig. 1 shows a schematic view of the whole arrangement.

FIGURE 1.

Schematic view of our model of two membranes. The membranes interact only locally via interaction zones, assumed to be planar and parallel surfaces, located at x = 0 (membrane 1) and x = l (membrane 2). We consider only electrostatic interactions. Outside the interaction zones, the membranes are characterized by their surface potentials (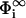), their surface-charge densities (σ_i), the valency of the lipidic charges (q_i), and the surface fraction of charged lipids (η_i) (i = 1,2). In our model, we allow lipids to freely flow between the interaction zones and those parts of the membrane not involved in the interaction (reservoir), so the surface potentials in the interaction zone (Φ(0) for membrane 1 and Φ(l) for membrane 2) as well as the surface charge densities ( and ) can be different from their corresponding values in the reservoir.

Let us first introduce the notation for those parts of the membranes whose surface properties are not affected by the presence of the other membrane, i.e., whose surface groups belong to the reservoir. For simplicity we consider here membranes composed of just two types of mobile surface groups; one type is neutral, the other charged. η_i denotes the surface fraction of the charged lipids on both membranes (i = 1,2). With q_i being the valency of the charged lipid, the surface charge density (given in units of the elementary charge e) becomes 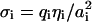(i = 1,2), where 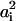is the headgroup area per charged lipid on membrane i = 1,2. Through this relation, the quantities σ_i, 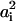, q_i, and η_i are linked, and we thus have three independent variables to characterize the surface properties of the membranes which, in the following, we choose to be σ_i, q_i, and η_i. Finally, the surface potentials and are related to the ratio between σ_i and the screening constant to be introduced below (Eqs. 7 and 11). We remark that η_i can be tuned via the pH of the solution. If φ_i is the total surface fraction of those lipids that are allowed to dissociate, then

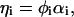(1)

where α_i is the degree of dissociation, which is determined by the appropriate dissociation constants and the pH value of the solution via the law of mass action (Fleck and von Grünberg, 2002). Since the pK_A of charged lipids depends on the electrostatics of the environment, we assume in the following that the pH of the aqueous medium is far away from the pK_A of the lipids.

The first quantity to be calculated is the reduced electrostatic potential Φ (i.e., the potential multiplied by e and the inverse temperature β = 1/kT) on and between the two membranes. If the interaction zones of the two membranes are separated by a finite distance l, small enough for them to start interacting with each other, charged lipids will either come into or escape from the interaction region, depending on what is energetically more favorable. This redistribution of charges results in a difference of potential between the membrane surface potentials in the interaction region and those in the reservoir ,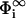

(2)

It can be shown (May et al., 2000; Fleck and von Grünberg, 2002) that the lipid distribution minimizing the total free energy follows the relation

(3)

where (i = 1,2) is now the surface charge density in the interaction region, to be distinguished from σ_i, the surface charge density on the noninteracting parts of the membranes in the reservoir. Eq. 3 results from the balance of two terms in the free energy functional (Fleck and von Grünberg, 2002), the electrostatic energy and the mixing entropy of lipids. In our case where the difference ΔΦ_i is caused by the interaction of oppositely-charged objects, this specifically means that an entropy penalty in the total free energy prevents too strong an accumulation of lipidic charges in the interaction zone, which, from the electrostatic point of view, would be rather favorable. The nominator of Eq. 3 is recognized as the Boltzmann factor, while the denominator takes account of the finite size of the lipidic groups, preventing that the local surface density of lipids in the interaction zone exceeds the maximum packing value 1/η_i (close packing). We observe that reduces to its reservoir value, σ_i, (i) if the difference of potential is zero as it is the case for immobile lipids, or (ii) if all lipids are fully charged (η_i = 1), in which case lipid mobility is, of course, of no consequence to our problem.

The electrostatic potential can be calculated from the PB equation, which for a 1:1 electrolyte takes the form

(4)

where the prime denotes differentiation with respect to x. κ² = 8πλ_Bc_s is the screening constant with λ_B = e²β/ɛ the Bjerrum length and c_s the salt concentration in the reservoir. λ_B is the distance where the interaction energy of two elementary point charges in the solvent under consideration equals kT, and can thus be regarded as a measure for the relative significance of electrostatic forces in this specific solvent. The potential is taken to be zero deep in the bulk of the electrolyte, far away from any charged surface. The solution to Eq. 4 for the case of one planar membrane with a charge density σ, is the famous Gouy-Chapman potential (Evans and Wennerström, 1994),

(5)

with the first derivative

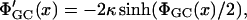(6)

where . Therefore the relationship between σ_i and 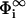is given by

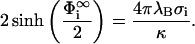(7)

Returning now to our problem of two interacting planar membranes, we formulate a complete boundary value problem by specifying the boundary conditions for solving for Φ,

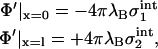(8)

with the effective surface charge densities from Eq. 3. At this point, it becomes clear that the principal problem of our calculation lies in the fact that the potential to be calculated not only appears in Eq. 4, but via Eqs. 2 and 3, also on the right-hand side of the boundary conditions. In fact, the boundary conditions mark the point where the two-dimensional system of screening lipid charges is coupled to the three-dimensional system of screening electrolyte ions.

Once Φ(x) is known for a given membrane-membrane distance l, one can eventually turn to the quantity that is of central interest in this article, the pressure, which at a given point in the electrolyte solution relative to the bulk pressure, is (Evans and Wennerström, 1994):

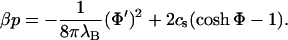(9)

Negative values for p at a given distance l indicate an effective attraction between the membranes; positive values, a repulsive interaction.

EFFECTIVE INTERACTION IN LINEAR THEORY

We first restrict ourselves to the condition Φ < 1, which allows linearization of the sinh Φ in Eq. 4 and of the exponentials in Eq. 3. This greatly simplifies our problem while still preserving its qualitative features. The boundary value problem introduced above now reads,

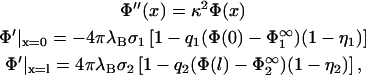(10)

where the surface potentials in the reservoir 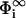follow from Eq. 7,

(11)

The Gouy-Chapman potential, Eq. 5, simplifies in linear theory to

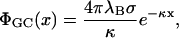(12)

and the equation for the pressure, Eq. 9, to

(13)

The general solution to the PB equation in Eq. 10 is

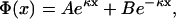(14)

so that Eq. 13 reduces to just

(15)

Case of immobile lipids

To set the stage, we start by considering the limiting case of immobile lipids when 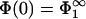and . This important case is discussed by Parsegian and Gingell (1972), the major points of which we now briefly repeat to lay the ground for our considerations further below. As in Parsegian and Gingell (1972), we wish to determine that specific distance l_min where the effective intermembrane force changes its sign, i.e., we seek to find the distance where p in Eq. 15 becomes zero. Obviously, this is the case if either A = 0 or B = 0. If A = 0, then the boundary conditions in Eq. 10 together with Eq. 14 lead to

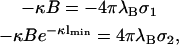(16)

from which we conclude that

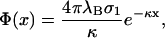(17)

and

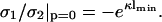(18)

The last equation specifies the distance l_min at which the pressure vanishes. Clearly, this equation cannot be satisfied for like-charged surfaces, but only for oppositely-charged surfaces. One recognizes that for σ₁ = −σ₂, the point of zero force is at contact. If, however, σ₁ differs slightly from −σ₂, then the point of zero pressure is at some finite distance l_min, meaning that even oppositely-charged membranes can repel each other at distances l < l_min. This is due to the electroneutrality condition which, in cases where σ₁ ≠ −σ₂, requires a few counterions to stay in the slab between the two membranes, thus leading to a repulsive osmotic pressure if l < l_min. We furthermore observe from Eq. 18 that |σ₁| ≥ |σ₂| since 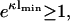that is, the case A = 0 corresponds to the situation where the magnitude of the surface charge density of the first membrane located at x = 0 is higher than that of the other membrane at x = l_min. The potential, Eq. 17, is the linearized Gouy-Chapman potential for a single, isolated membrane, Eq. 12, as if the second membrane were nonexistent. In other words, the effective intermembrane force vanishes if the less charged membrane is at a distance l_min where its surface charge density just equals the net surface charge density one would obtain by integrating the Gouy-Chapman profile in front of an isolated membrane from l_min to ∞. The surface charge density of the second membrane thus replaces the missing tail of the Gouy-Chapman density profile of an isolated membrane. This has been pointed out by Jönsson and Stahlberg (1999) in another context.

It is readily seen that the other case leading to zero pressure, B = 0, corresponds to the situation where |σ₂| ≥ |σ₁|. Then for l = l_min there is an unperturbed Gouy-Chapman layer in front of the second membrane and the surface charge density of the membrane at x = 0 takes the role of simulating the cut tail of the Gouy-Chapman profile. The condition for l_min becomes

(19)

Fig. 2 a shows the two curves and 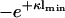plotted against κl_min. These curves divide the parameter space spanned by σ₁/σ₂ and κl into regions of attractive and repulsive intermembrane interaction. Fig. 2 a represents the central finding of Parsegian and Gingell (1972). It is obvious from the preceding considerations that the plot contains redundant information. The case |σ₁|/|σ₂| < 1 is simply a repetition of the case |σ₁|/|σ₂| > 1 with interchanged membranes, which is verified by the fact that by swapping the labels of the membranes in Eq. 19 one indeed recovers Eq. 18. Demanding that the membrane with the higher magnitude of the surface charge density is located at x = 0, one could, without loss of generality, concentrate on the case A = 0 and the part |σ₁|/|σ₂| > 1 in parameter space. Nevertheless, in the following discussion we will consider the whole parameter space, mainly to keep close contact with the familiar plot of Parsegian and Gingell.

FIGURE 2.

Regions of attraction and repulsion between two oppositely-charged membranes consisting of immobile lipids (a) and mobile lipids (b and c), as a function of the intermembrane distance and the ratio of surface charge densities. Fig. 2, b and c show the line of zero net force for four different values of the surface fraction of charged lipids η₂ (η₂ = 1, 0.75, 0.5, and 0.25, from top to bottom for the curves in the un-hatched region). The sign of the effective intermembrane force in the hatched region of the parameter space can be inferred from a corresponding point in the un-hatched region.

Case of mobile lipids

We return to the boundary value problem, Eq. 10, seeking to determine again the zero pressure line in the parameter space, but now for the case of mobile lipids. From now on, we focus on oppositely-charged membranes, because the case of like-charged membranes leads always to repulsion, be the lipids mobile or not (Parsegian and Gingell, 1972). Therefore, we demand that q₁/q₂ < 0 and σ₁/σ₂ = . In addition, 0 < η₁ ≤ 1 and 0 < η₂ ≤ 1. Note that both and must be positive quantities. Again we start from the expression for the pressure, Eq. 15, which is zero if either A or B is zero. Assuming A to be zero, the first boundary condition in Eq. 10 results in

(20)

This equation is solved by

(21)

leading us to the potential 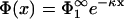, which is again the familiar Gouy-Chapman potential. So, like in the case of immobile lipids, the potential (and thus the ion distribution) in the slab 0 < x < l_min between the membranes is identical to that be found if membrane 1 were alone, provided of course that the two membranes are separated just by the zero-pressure distance l_min. We note that, due to this property, two of the parameters specifying the surface properties of membrane 1, namely q₁ and η₁, are now immaterial for the following considerations.

Inserting the potential 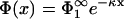into the second boundary condition of Eq. 10 and using Eq. 11, yields

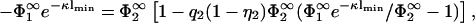(22)

and hence

(23)

If η₂ = 1, the right-hand side of this equation reduces to 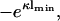and we recover Eq. 18. It is clear from our previous discussion that the case B = 0 cannot provide new information; one can check this by redoing the calculation with B = 0, which leads to a potential 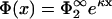and again to Eq. 23 but with the label ‘1’ replacing the label ‘2’. Fig. 2, b and c, show the zero-pressure line in the parameter space calculated from Eq. 23 for four different values of η₂, for 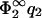= 0.05 (Fig. 2 b) and for 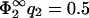(Fig. 2 c). For completeness, we have also added the curves for the case B = 0 (|σ₁| < |σ₂|, hatched region). Via Eq. 11, 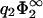is related to the two quantities characterizing the electrolyte solution, λ_B and κ, and can thus be experimentally changed through variation of temperature, salt concentration, or the choice of the solvent (ɛ). In particular, increases (with σ₂ remaining constant) on increasing λ_B, that is, if the significance of electrostatic forces relative to thermal forces increases.

We now discuss the findings of Fig. 2. We have seen that the surface properties of the membrane having the higher surface density of charged lipids remain completely unaffected by the presence of the other membrane; that is, if, for example, |σ₁| > |σ₂|, then 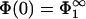and 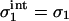, so that there is no difference between the lipid distribution on those parts of the membrane belonging to the interaction region and those belonging to the reservoir. However, on the other membrane having the lower density of charged lipids (membrane 2, if |σ₁| > |σ₂|), the lipid surface density in the interaction region changes in response to the presence of membrane 1. Assuming that membrane 1 is positively charged (q₁ > 0, q₂ < 0) and recalling that , we see that 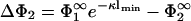must be positive. Consequently, the surface charge density in the interaction zone of membrane 2,

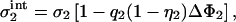(24)

must be larger in magnitude than its reservoir value, σ₂. In other words, at l = l_min additional lipids must have flowed from the reservoir into the interaction zone of membrane 2. One may say that the membrane with the higher density of charged lipids, while itself remaining inert, attracts charged lipids on the other membrane out of the reservoir into the interaction zone. The other conceivable mechanism—that one membrane expels charged lipids from the interaction region of the other membrane—is not observed. That, of two interacting membranes, only one membrane shows a major rearrangement of lipids, is a surprising result. Lipid mobility is thus completely irrelevant for the membrane with the higher surface density of charged lipids; it suffices to model this membrane just by a planar wall with a homogeneous surface charge density.

To understand the implication that the observed lipid redistribution has on the effective interaction, let us return for a moment to the case of immobile lipids (η₂ = 1) and assume that the system of two membranes are at a state point in parameter space where there is zero pressure (solid thick curves in the |σ₁| > |σ₂| regions of Fig. 2, b and c). If now the lipid mobility is switched on (η₂ < 1), additional charged lipids are allowed to flow into the interaction zone of membrane 2. This results in a change from zero pressure to negative pressure at this particular point in parameter space; the effective interaction between the membranes will now be attractive. In other words, lipid mobility is responsible for an additional attractive contribution to the effective intermembrane interaction potential, the latter being nothing but the total free energy of the system as a function of κl. We see from Fig. 2 that, as a result of this additional attractive component in the free energy, the region in parameter space where the two membranes attract each other increases with decreasing η₂ and/or increasing . This statement, of course, applies to the part of the parameter space where |σ₁| > |σ₂|; in the |σ₁| < |σ₂| part (hatched region) the relevant quantities to look at are η₁ and .

Lipid mobility allows contact in cases where σ₁ ≠ −σ₂

The consequences of the fact that lipid mobility produces some extra attraction can best be illustrated by plotting those regions of parameter space where touching contact (i.e., κl = 0) between the membranes is energetically possible. Fig. 3 shows the zero-pressure line calculated from Eq. 23 for κl = 0, now in the parameter space spanned, on the one hand, by σ₁/σ₂ and, on the other hand, by η₂ for |σ₁| > |σ₂| and η₁ for |σ₁| < |σ₂|. For state points located to the left of this line, contact between the membranes is possible; for those lying on the right-hand side, two membranes at κl = 0 would repel each other and contact is not possible. Again, we consider the case = 0.5 and restrict the following discussion of Fig. 3 to the |σ₁| > |σ₂| part of the parameter space (i.e., we assume the more strongly charged membrane to be membrane 1 at x = 0).

FIGURE 3.

Regions in parameter space where touching contact (κl = 0) between two oppositely-charged membranes corresponds to the equilibrium configuration, as a function of σ₁/σ₂ and the surface fraction η₂ of mobile lipids on the membrane with the lower surface densities of lipids. The dashed line is the function −1/η₂. See text for details.

In case of immobile lipids (η₂ = 1), two oppositely-charged membranes can come to contact without an additional external force only if they have exactly the same number of lipids per unit area, i.e., if, and only if, σ₁ is equal to −σ₂. For membranes consisting of mobile lipids (η₂ < 1), we find, however, that there is a whole range of possible values for σ₁/σ₂ over which touching contact between membranes is possible. This means that a certain mismatch between σ₁ and σ₂ is now allowed; it can be compensated by charged lipids flowing in from the reservoir into the interaction zone of membrane 2. Combining Eqs. 23 and 24, one recognizes that everywhere on the zero-pressure line in a plot (σ₁/σ₂ versus η₂) the surface charge density σ₂^int just equals −σ₁. For state points to the right of the line, the mismatch between σ₁ and −σ₂ becomes too large, and contact is impossible, even if allowance is made for lipid mobility. Entropy then prevents a further flow of lipidic charges into the interaction zone, so that here < |σ₁|. Then, electroneutrality again requires counterions to stay in the slab between the membranes, resulting in an effective repulsion between the membranes at those state points. The highest surface charge density possible in the interaction zone of membrane 2 is σ₂/η₂ when close packing of lipids in the interaction region is reached. Therefore, the zero-pressure line must be located always to the left of the curve −1/η₂ (dashed line in Fig. 3), regardless of the value of . We observe that for the case , considered in Fig. 3, close packing is the mechanism delimiting the contact region only at rather high values of η₂, where the zero pressure is seen to approach the line −1/η₂.

The range in σ₁/σ₂, over which a lipid redistribution can compensate a mismatch, increases with decreasing η₂ (see Fig. 3) until, for η₂ → 0, the largest allowed mismatch is reached,

(25)

The limit η₂ → 0 for finite values of 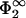implies that the area per lipid headgroup goes to zero, and that one is thus approaching the limit of pointlike lipids. Close packing then ceases to work as a mechanism against the infinite accumulation of charges in the interaction zone; entropy alone is responsible for the fact that the largest possible charge mismatch in Eq. 25 remains still finite. Only if , i.e., on approaching the limits of the range of validity for linearization, Eq. 25 shows a divergence.

These findings have an interesting implication. We recall that the surface fraction of charged lipids is linked to the degree of dissociation of the lipids (Eq. 1). Hence,

(26)

Suppose the lipids on the second membrane have a rate of dissociation α₂ ≈ 1 which depends only weakly on the pH of the solution, whereas the charge state of the lipids on the first membrane (i.e., the membrane with the higher surface charge density) depends strongly on the pH via α₁. Then, by changing the pH of the solution, one can regulate the state of charge of the first membrane, while η₂ and thus σ₂ is kept approximately fixed. Varying the pH, one is then moving in vertical direction through the plot of Fig. 3. This means that systems are conceivable where, by changing the pH of the solution, one can switch between a contact and no-contact situation of two membranes.

A similar effect has the variation of the salt content of the electrolyte solution. Fig. 4 is meant to illustrate this point. The zero-pressure line is shown now in the (σ₁/σ₂ versus ) plane of the parameter space; the curves are again computed from Eq. 23 with κl = 0 for various values of η₂. The quantity is linked through Eq. 11 to the screening length 1/κ which shrinks on increasing the salt concentration in the electrolyte. To the right of the curves in Fig. 4, contact between the membranes is possible while state points on the left-hand side of the curves correspond to a situation of net repulsion between the membranes at contact. For a given pair of oppositely-charged membranes, characterized by the value of σ₁/σ₂ and η₂, increasing the salt concentration in the system means moving from the right to the left on horizontal lines in the plot. The state point where this horizontal line crosses the corresponding zero-pressure curve (labeled by η₂) marks the point where the net intermembrane force at contact switches from attraction to repulsion. Therefore, increasing salt causes membranes, initially at touching contact, to separate from each other; and vice versa, decreasing the salt concentration in the electrolyte can induce membranes to make contact. The salt concentration necessary for inducing this change can be directly read off from Fig. 4.

FIGURE 4.

Regions in parameter space where touching contact between oppositely-charged membranes is energetically allowed. Plot is similar to that in Fig. 3, but now the parameter space is spanned by σ₁/σ₂ and , while η₂ is fixed to 0.1, 0.3, 0.5, 0.7, and 0.9. Variation of 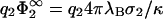can be experimentally realized by controlling the salt concentration in the electrolyte solution. State points to the left of the curves correspond to systems where touching contact between the membranes is energetically impossible; those to the right, energetically possible. Reducing the salt concentration in the electrolyte can cause membranes to make contact.

Effective interaction in nonlinear theory

We are now in the position to return to our initial nonlinear boundary value problem, formulated in Eqs. 1–9. Again, we want to calculate the distance l_min where the pressure p in Eq. 9 vanishes. Hence, from Eq. 9,

(27)

It is crucial for the following to realize that this equation is nothing but the square of Eq. 6, which means that the differential Eq. 27 is satisfied by the Gouy-Chapman potential, Eq. 5. This result confirms our expectation based on the results of the previous sections that at zero pressure, i.e., if l = l_min, the potential between the membranes follows a Gouy-Chapman potential up to the point of the other membrane, as if only one membrane in isolation were present.

Eq. 27 must be satisfied everywhere in the region between the membranes, also at the boundaries. Inserting the first boundary condition of Eq. 8 in conjunction with Eq. 3 into Eq. 27, taken at x = 0, and using Eq. 7, results in

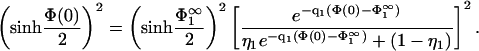(28)

Evidently, one of two possible solutions to this equation is 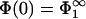; this is the solution we first focus on. Eq. 3 shows that the surface charge density in the interaction zone is the same as in the reservoir, and the microionic distribution and the potential between the membranes looks as if only membrane 1 were present. It follows that for this case, the potential at x = l_min is, from Eq. 5,

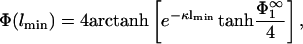(29)

which one can use in the second boundary condition of Eq. 8 to obtain (using again Eq. 7)

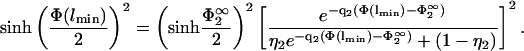(30)

Now, fixing the input parameters q₂, η₂, , and 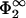, one can solve Eqs. 29 and 30 for the only remaining unknown, the zero-pressure distance l_min. A solution can be found provided 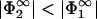. Then σ₂ is lower in magnitude than σ₁. If this were not the case, then the Gouy-Chapman profile in the region between the membranes would be governed by the second membrane; that is, (i), Eq. 30 would be satisfied with Φ(l_min) = 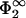; (ii), Eq. 29 would change to

and (iii), one would have to search for the second solution of Eq. 28 which then determines the equilibrium distance l_min. It is obvious that, as in the previous sections, the two solutions expected from Eqs. 28 and 30 reflect the fact that either the first or the second membrane can have a higher density of charged lipids. Without loss of generality we can place the more strongly charged lipid at x = 0; i.e., we assume |σ₁| > |σ₂|, allowing us to concentrate on just one of two possible solutions in Eqs. 28 and 30. Then, 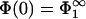, and l_min follows from the two Eqs. 29 and 30.

If lipid mobility were not allowed for, then l_min would be that distance where the surface charge density of membrane 2 just equals the net surface charge density of the Gouy-Chapman profile integrated between x = l_min and ∞ (see Jönsson and Stahlberg, 1999). Here, the two-dimensional system of mobile lipids offers another possibility to reduce the total free energy. From this and the discussion of the linear case treated in the previous section, one expects again the equilibrium intermembrane distance to be shifted toward smaller distances when lipids are allowed to move. In the linear case we had to make a choice for two parameters only, and η₂. Due to the nonlinearity in Eq. 3, we now need to specify three parameters, q₂, 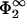, and η₂, to be able to calculate the zero-pressure line in the space spanned by σ₁/σ₂ and κl. In the following, we assume for simplicity that each charged lipid on the second membrane carries just one elementary charge. Fig. 5 then shows the zero-pressure line for various combinations of and η₂, calculated from numerically solving Eq. 30 for l_min for given values of σ₁/σ₂ (i.e., through Eq. 7). Only the part of the parameter space is shown where |σ₁| > |σ₂|.

FIGURE 5.

Regions of attraction and repulsion between oppositely-charged lipid membranes, for various combinations of η₂ and . Plots are similar to Fig. 2, but now with the zero-pressure line determined from the nonlinear Poisson-Boltzmann equation. The order of the values of the varied quantity corresponds to the order of the curves from top to bottom. The thin solid line is the function 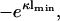giving the zero-pressure state line for η₂ = 1.0 in linear theory (see Eq. 18).

With Fig. 5 a we first explore the effect of the nonlinearity alone, without making allowance for the demixing of the membrane (that is, we set η₂ = 1). We recall that in linear theory for η₂ = 1 the zero-pressure line is given by Eq. 18, and that there is thus no dependence on . By contrast, we observe that nonlinear theory predicts the region of attractive interactions in parameter space to considerably expand with increasing values of . Whereas the curve for = 0.01 is practically identical to −e^κl from Eq. 18, a small difference between the zero-pressure lines predicted by linear theory/nonlinear theory is already observable at = 0.5 for high values of σ₁/σ₂. Although for = 0.5 linear theory is still supposed to be valid for the second membrane, this is not necessarily the case for the first membrane, where at high values of σ₁ the surface potential can become considerably >1. Note that if the surface charge densities of both membranes are equal in magnitude, |σ₁| = |σ₂|, the membranes will be always in contact at equilibrium, regardless of the value of 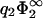. Note, on the other hand, how dramatically the predictions of linear theory fail for 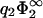= 5.0.

Fig. 5, b and c, illustrate the effect of lipid demixing on the interaction: for fixed values of ( = 0.5 in Fig. 5 b and = 1.0 in Fig. 5 c), we have calculated zero-pressure lines for various values of η₂. Fig. 5 b can be directly compared to the results of linear theory depicted in Fig. 2 c. One recognizes at a glance that for this value of , linear theory makes qualitatively correct predictions, with only minor corrections at high values of σ₁ necessary to account for nonlinear effects. The thin solid line in Fig. 5, b and c, give the results of linear theory for η₂ = 1. The huge difference between the results of linear/nonlinear theory for η₂ = 1 (thin and thick solid line, respectively) in Fig. 5 c indicate that linear theory becomes questionable for highly charged membranes, something we have already noticed in Fig. 5 a. Fig. 5 c demonstrates that, in this highly nonlinear parameter regime, demixing has a marked effect on the effective interaction between the membranes. For the lowest value of η₂ and the highest value of 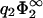, the interaction between the membranes is attractive almost over the whole region in parameter space investigated here (0 < κl < 1.5 and −5 < σ₁ / σ₂ < 0).

Fig. 6 shows again various zero-pressure state lines for κl = 0 in the plane spanned by and η₂, obtained now from Eqs. 28–30. The state line for of Fig. 3, calculated in linear theory, is also shown (thin solid line). A major result of the previous section has been that due to lipid demixing, membrane contact is possible even in cases of a certain charge mismatch. Comparison of the thin solid curve of linear theory with the corresponding curve of nonlinear theory (thick solid line) now reveals that the nonlinearity of the problem tends to even enhance this effect: the contact region in parameter space becomes much larger. Notice that the curve for 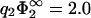lies on top of the curve −1/η₂, indicating close packing. So, here, close packing is really limiting the contact region in parameter space. Indeed, inspection of Eq. 30 reveals that for 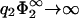the zero-pressure state line tends to −1/η₂, for finite η₂. Another interesting limit is η₂ → 0 for finite . As can be seen from Fig. 6, the zero-pressure line for η₂ → 0 terminates at finite values of σ₁/σ₂ for low values of 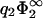. However, Eq. 30 predicts that this termination point goes exponentially to −∞ if .

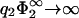FIGURE 6.

Same as in Fig. 3, but now the zero-pressure state lines are calculated within the nonlinear Poisson-Boltzmann theory. For comparison, the state line depicted in Fig. 3 is given as a thin solid line. The other curves (from top to bottom) correspond to values of 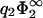= 0.2, 0.4, 0.5, 1.0, and 2.0. Pairs of membranes with state points lying to the right of the curves will repel each other at contact. The dashed line is the function −1/η₂ which the zero-pressure lines approach in the limit .

This implies that if the more weakly charged membrane exceeds a certain surface potential , and if the surface fraction of charged lipids on this membrane vanishes (η₂ → 0), then the two membranes will always make contact, regardless of the charge mismatch between the membranes. This important result should be contrasted to the behavior one finds ignoring lipid demixing, i.e., for a membrane model consisting of two planar surfaces with homogeneous surface charge densities, where contact requires σ₁ = −σ₂.

CONCLUSION

We have studied the effect of lipid demixing on the electrostatic interaction of two oppositely-charged membranes, modeled here as two planar and parallel planes, hosting a two-dimensional binary mixture of neutral and charged mobile lipids. The lipids in the interaction zone are assumed to be in contact with a reservoir of lipids from those parts of the membrane not involved in the interaction. We have been guided by the classical article of Parsegian and Gingell in our search for state points in the parameter space wherein the two membranes neither repel nor attract each other.

This is a summary of our main results:

1. Demixing adds an attractive component to the effective interaction between the membranes.

2. Therefore, the distance separation where there is a zero net force between the membranes is generally reduced when compared to calculations ignoring lipid demixing. For separations smaller than this zero-pressure distance, the osmotic pressure of counterions, remaining between the membranes, leads to repulsion, even though the membranes are oppositely-charged.

3. According to Parsegian and Gingell, oppositely-charged membranes are in contact at equilibrium only if σ₁ = −σ₂. Lipid demixing, however, allows contact between membranes even if there is a certain charge mismatch, |σ₁| ≠ |σ₂|.

4. In certain limiting cases, contact is always possible, regardless of the value of σ₁/σ₂ (if σ₁/σ₂ < 0).

5. Provided the surface potentials of both membranes are low enough, linear theory produces qualitatively correct results. We give analytical expressions, based on the linear theory, for the zero-pressure state line in parameter space.

6. The predictions of linear theory has been compared to those of nonlinear theory. The main effect of the nonlinearity of the underlying Poisson-Boltzmann equation is that it further expands the region of attractive interactions in parameter space, compared to the predictions of linear theory.

7. The nonlinearity of our problem has an enhancing effect also with respect to our main finding that lipid demixing considerably increases the region in parameter space where contact between unequally-charged membranes is possible.

8. Of the two interacting membranes, only one membrane shows a major rearrangement of lipids while the other remains in exactly the same state it would have in isolation. It is the membrane with the lower surface density of charged lipids which charges up and which thus adapts to the presence of the other membrane. Lipid mobility is therefore completely irrelevant for the membrane with the higher surface density of charged lipids; it suffices to model this membrane just by a planar surface with a homogeneous surface charge density, identical to that which the membrane has if it is well-separated from any other charged object.

9. At zero disjoining pressure, i.e., if the two membranes are at a distance where the net force is zero, the potential between the membranes follows a Gouy-Chapman potential from the more strongly charged membrane up to the point of the other, more weakly charged membrane (characterized by η₂ = 1, q₂, 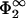) as if only the more strongly charged membrane in isolation were present.

10. In cases where demixing cannot occur (η₂ = 1), linear theory predicts a zero-pressure line in the σ₁/σ₂ – κl plane that is independent of , whereas nonlinear theory shows a rather strong dependence on this quantity.

The results shown here add to the understanding of adhesion phenomena between charged membranes. Many important interactions are at least partially mediated by the electrostatics of layered systems. As described in the Introduction, this includes the fusion of positively-charged liposomes with cell membranes in nonviral gene delivery systems (Felgner et al., 1987; Li and Huang, 2000; Wetzer et al., 2001; Safinya, 2001). The concepts outline here may also be applicable to multilayered DNA-cationic lipid systems (Rädler et al., 1997; Koltover et al., 1999), which serve as model systems for problems related to gene delivery.

It has been pointed out by several authors that reorganization of charged compounds in (bio)membranes can occur close to electrodes (Gingell and Fornes, 1976) and atomic force microscopy (AFM) tips. Actually, this experimental problem is very similar to that described in Fig. 1 In this context it is interesting to note that it has been observed that electrostatic forces on AFM tips are strongly dependent on the ionic strength of the aqueous buffer (Müller et al., 1999), which has been attributed to osmotic forces (Xu et al., 1997). A very similar effect occurs when a polarized electrode approaches a biological surface.

In the present article, several simplifications were made. Membranes are considered to be planar and the charged components of membranes are allowed to diffuse freely. This neglects the possibility of domain formation, of specific molecular interactions via stickers and repellers, and of membrane undulations. Domain formation due to complex mixing properties of multicomponent systems leads to complications when describing the local arrangement of charged molecules. It has been found in both artificial and biological membrane systems that domains may form on nanoscopic to microscopic length scales (Korlach et al., 1999; Rietveld and Simons, 1998; Simons and Ikonen, 1997). Unfavorable lipid mixing properties will affect the segregation of charged lipids and proteins.

Furthermore, in many studies it is pointed out that adhesion may be partially controlled by specific molecular interactions, which is in contrast to the nonspecific electrostatic interactions described in this article. Membranes may be crosslinked by macromolecules like integrin (stickers; see Guttenberg et al., 2001; Lipowski, 1996b) or be repelled by lipids with polymeric headgroups (repellers; see Weikl and Lipowski, 2001; Weikl et al., 2002; Bruinsma et al., 2000; Guttenberg et al., 2001). A further important repulsive feature of opposing membranes are the undulation forces, which are a consequence of surface bending fluctuations (Helfrich, 1978; Honger et al., 1994). The interplay of attractive and repulsive molecular interactions with surface undulations and local electrostatic interactions has been reviewed by Sackmann and Bruinsma (2002).

To combine electrostatics with specific molecular interactions, undulations, and domain formations remains a goal for future studies.