Ca²⁺ Regulation in the Near-Membrane Microenvironment in Smooth Muscle Cells

Abstract

The microenvironment between the plasma membrane and the near-membrane sarcoplasmic reticulum (SR) may play an important role in Ca²⁺ regulation in smooth muscle cells. We used a three-dimensional mathematical model of Ca²⁺ diffusion and regulation and experimental measurements of SR Ca²⁺ uptake and the distribution of the SR in isolated smooth muscle cells to predict the extent that the near-membrane SR could load Ca²⁺ after the opening of single plasma membrane Ca²⁺ channels. We also modeled the effect of SR uptake on 1), single-channel Ca²⁺ transients in the near-membrane space; 2), the association of Ca²⁺ with Ca²⁺ buffers in this space; and 3), the amount of Ca²⁺ reaching the central cytoplasm of the cell. Our results indicate that, although single-channel Ca²⁺ transients could increase SR Ca²⁺ to a certain extent, SR Ca²⁺ uptake is not rapid enough to greatly affect the magnitude of these transients or their spread to the central cytoplasm unless the Ca²⁺ uptake rate of the peripheral SR is an order-of-magnitude higher than the mean rate derived from our experiments. Immunofluorescence imaging, however, did not reveal obvious differences in the density of SR Ca²⁺ pumps or phospholamban between the peripheral and central SR in smooth muscle cells.

INTRODUCTION

The sarcoplasmic reticulum (SR) plays an important role in regulating intracellular Ca²⁺ concentration ([Ca²⁺]_i) in all types of muscle. In striated muscle, release of Ca²⁺ from the SR and its re-uptake into the SR by sarcoplasmic/endoplasmic reticulum Ca²⁺ pumps is essential for contractile regulation. In smooth muscle, the role of the SR is less well-defined and may vary depending upon the smooth muscle cell type and upon the nature of a contractile stimulus. Both SR Ca²⁺ release and Ca²⁺ influx through the plasma membrane may contribute to the change in [Ca²⁺]_i required to initiate or maintain contraction in smooth muscle cells. Normal resting [Ca²⁺]_i in smooth muscle is 50–150 nM. During contractile activation, [Ca²⁺]_i rises to 500–1000 nM (see Becker et al., 1989; Sanders, 2001). During relaxation, three mechanisms are thought to be responsible for bringing [Ca²⁺]_i back to its resting level (Sanders, 2001). The sarcoplasmic/endoplasmic reticulum Ca²⁺ pump (SERCA) actively transports Ca²⁺ back into the SR whereas an ATP-dependent plasma membrane Ca²⁺ pump and a plasma membrane Na⁺/Ca²⁺ exchanger move Ca²⁺ out of the cell and into the extracellular space. Because both Ca²⁺ influx and SR release can occur during activation and both Ca²⁺ extrusion and SR uptake can occur during relaxation, the SR has the potential to either gain or lose net Ca²⁺ during any contraction/relaxation cycle. It is important, therefore, to understand mechanisms that regulate the Ca²⁺ content of the SR. Refilling of a depleted SR may occur through the opening of store-operated Ca²⁺ channels in the plasma membrane, resulting in the influx of a substantial amount of Ca²⁺ and the uptake of all or a portion of this Ca²⁺ into the SR (see Sanders, 2001; Sturek et al., 1992). A second mechanism for maintaining the SR Ca²⁺ content when the SR is only partially depleted could involve coupling between single plasma membrane Ca²⁺ channels and the SR at sites where the SR and plasma membranes are in close apposition. At these sites, Ca²⁺ entering the cell after the opening of single plasma membrane Ca²⁺ channels could be taken up into near-membrane SR stores to partially refill these stores without significantly increasing [Ca²⁺]_i near the contractile proteins to a high enough level to trigger contraction.

Electron micrographs reveal the presence of peripheral SR elements in close proximity (10–25 nm) to the plasma membrane in smooth muscle cells (see Devine et al., 1972; Somlyo, 1980; Gabella, 1983; Somlyo and Franzini-Armstrong, 1985). This close apposition may extend for considerable distances (>1 μm) along the cell length and is thought to form a restricted diffusion space between the two membranes (discussed in Kargacin, 1994). Thus, the superficial SR in smooth muscle cells is distributed in a way that would favor localized interactions between single plasma membrane ion channels and the SR proteins involved in Ca²⁺ regulation. This could facilitate coupling between localized Ca²⁺ influx events and the filling of peripheral SR Ca²⁺ stores in smooth muscle cells.

In previous work (Kargacin and Kargacin, 1995), we estimated that the SR in smooth muscle is capable of taking up Ca²⁺ at a rate that is 50–75% of the rate at which Ca²⁺ is removed from the cytoplasm after a contractile stimulus. Thus, a substantial portion of the Ca²⁺ entering a cell after the opening of a single plasma membrane Ca²⁺ channel could be taken up into the SR; however, the rate at which this occurs relative to the rate at which Ca²⁺ diffuses away from an influx site would be an important determinant of how fast and efficiently an SR store located near a site of Ca²⁺ influx could be replenished. It is also important to understand how uptake of Ca²⁺ by the SR influences the amplitude and time course of single-channel Ca²⁺ transients and the interaction of these transients with Ca²⁺-binding molecules. To better understand the coupling between events at the plasma membrane and SR function, we developed a three-dimensional mathematical model of Ca²⁺ diffusion and regulation in smooth muscle cells derived from the one- and two-dimensional models that we utilized in previous studies (Kargacin and Fay, 1991; Kargacin, 1994, 2003; Kargacin and Kargacin, 1997). We also carried out experiments to determine the maximum rate of SR Ca²⁺ uptake in saponin-permeabilized smooth muscle cells and used immunofluorescence microscopy to study the distribution of SR Ca²⁺ pumps in these cells. The three-dimensional models simulated a cell segment in which a portion of the SR was in close apposition to the plasma membrane. This allowed us to examine the influence of the density and localization of SR Ca²⁺ pumps on the magnitude and spatial and temporal characteristics of the Ca²⁺ transients resulting from the opening of single plasma membrane Ca²⁺ channels and the extent and time course of SR loading during these transients. We also examined the role that Ca²⁺ buffering is likely to play in coupling SR Ca²⁺ uptake to single-channel Ca²⁺ transients in the microenvironment between the plasma membrane and the SR.

MATERIALS AND METHODS

Materials

To keep Ca²⁺ contamination to a minimum, uptake buffer was made with AnalaR grade KCl and HCl and Aristar grade KOH from BDH (Toronto, Canada), microselect MgCl₂-6H₂O and HEPES-K⁺ salt from Fluka (Ronkonkoma, NY). Fura-2 free acid was purchased from Molecular Probes (Eugene, OR). Indocarbocyanine Cy3-conjugated secondary antibodies were purchased from Bio/Can Scientific (Mississauga, Canada); AlexaFluor 488-conjugated secondary antibodies were purchased from Molecular Probes (Eugene, OR). All other chemicals were purchased from Sigma (St. Louis, MO). Polyclonal anti-SERCA2 was kindly provided by Dr. Jonathan Lytton at the University of Calgary. This antibody recognizes both SERCA2 and SERCA3 and was prepared in Dr. Lytton's laboratory by immunizing rabbits with a purified recombinant fragment of rat SERCA2 encompassing amino acids 362–704. Monoclonal anti-phospholamban (Suzuki and Wang, 1986) was kindly provided by Dr. Jerry Wang at the University of Calgary.

Three-dimensional model of Ca²⁺ diffusion and regulation in smooth muscle cells

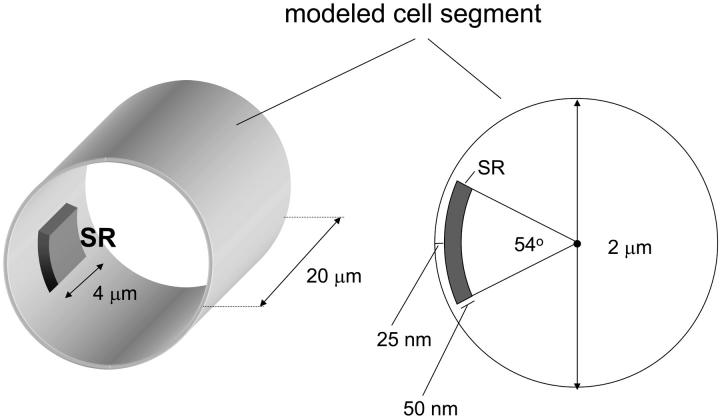
The three-dimensional model of Ca²⁺ diffusion and regulation in a smooth muscle cell segment that was used in our simulations is shown diagrammatically in Fig. 1. The cell segment was cylindrical in shape (diameter = 2 μm; length = 10 or 20 μm). Diffusion and regulatory processes were modeled using the explicit finite-differences method described by Crank (1975) to numerically solve the following partial differential equation:

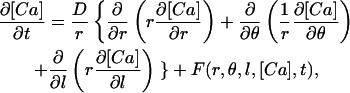(1)

where r, θ, and l are the radial, angular, and length dimensions in a cylindrical coordinate system, D is the diffusion coefficient, and F(r,θ,l,[Ca],t) is a function describing the position, concentration, and time-dependent regulatory processes included in the model (see Eqs. 2–4 below). (Note that in this and the following equations, [Ca] refers to [Ca²⁺]_i.) The modeled cell segment was divided into 40 radial elements (each one extending 25 nm in the radial direction), 20 or 40 length elements (each 500-nm long), and 20 (18°) angular elements. Near-membrane SR was represented by a segment of a cylindrical volume located 25 nm from the plasma membrane with a thickness in the radial direction of 50 nm, a length of 4 μm and spanning 54° in the angular direction (see Fig. 1). These dimensions are in keeping with those reported in the literature for segments of the near-membrane SR (see Devine et al., 1972; Somlyo, 1980; Gabella, 1983; Somlyo and Franzini-Armstrong, 1985) and were chosen so that uptake of Ca²⁺ by the SR element in the model was not limited by the size of the element. At the start of the simulations, extracellular [Ca²⁺] was assumed to be 1.5 mM; resting cytoplasmic [Ca²⁺] was assumed to be 150 nM. The diffusion coefficient was assumed to be the same in all directions and was equal to 2.2 × 10⁻⁶ cm² s⁻¹ as in our previous work (Kargacin and Fay, 1991; Kargacin, 1994). In the model, radial diffusion was not able to occur through the SR segment (i.e., Ca²⁺ could only reach the volume elements central to the SR by diffusing around the SR segment). The finite-differences method of solution of Eq. 1 requires that diffusion be computed into one element at each longitudinal position beyond the ends of the modeled cell segment. In the simulations described below, this was done by setting [Ca²⁺] in the length elements beyond the boundary equal to the value at the boundary (i.e., Ca(r, θ, 0) = Ca(r, θ, 1) and Ca(r, θ, L + 1) = Ca(r, θ, L) where L is the total length of the cell segment). These boundary conditions did not affect the outcome of simulations reported here because the localized Ca²⁺ signals that were modeled did not reach the longitudinal boundaries of the cell segment (Kargacin, 2003; also discussed in Zou et al., 1999). This was confirmed by comparing the results of simulations done when the length of the segment in the model was 10 μm with those obtained when the length of the segment was increased to 20 μm. The Ca²⁺ regulatory processes included in the model were described in previous publications (Kargacin and Fay, 1991; Kargacin, 1994; Kargacin and Kargacin, 1997) and will only be briefly outlined in the following paragraphs.

FIGURE 1.

Smooth muscle cell model. The smooth muscle cell segment modeled was cylindrical in shape with a diameter of 2 μm and a length of 20 μm. An element of SR near the plasma membrane was included in the model. The SR element extended 4 μm in the longitudinal direction, 50 nm in the radial direction, and spanned an angle of 54° (∼0.94 μm of arc). To solve the diffusion equation for a cylinder the modeled cell segment was divided into 20 or 40 length elements, 40 radial elements, and 20 angular elements. The physical presence of the SR element in the model prevented direct radial diffusion between the near membrane space and the central cytoplasm of the cell. In addition to diffusion, the model also incorporated plasma membrane extrusion mechanisms and SR Ca²⁺ uptake, Ca²⁺ buffers in the cytoplasm, and leak channels for Ca²⁺ in the plasma membrane and the SR. The Ca²⁺ affinities used in the model for the cytoplasmic Ca²⁺ buffer, the SR Ca²⁺ pump, and the plasma membrane Ca²⁺ pump were 1 μM, 0.22 μM, and 0.2 μM, respectively. Single channel Ca²⁺ currents representing the opening of plasma membrane Ca²⁺ channels were also included in the model. Ca²⁺ influx into the cell from these channels occurred into the near-membrane space between the plasma membrane and the SR opposite the center of the SR element (see Fig. 2 B). Resting [Ca²⁺] in the modeled segment was 150 nM; extracellular [Ca²⁺] was 1.5 mM. Additional details of the model are given in Materials and Methods and in previous publications (see Kargacin and Fay, 1991; Kargacin, 1994; Kargacin, 2003).

To model localized Ca²⁺ influx into the space between the plasma membrane and the SR membrane in the model, 0.1-pA or 1-pA single channel Ca²⁺ currents lasting 4 ms were assumed to flow into a single near-membrane volume element (0.025 μm in the radial × 0.5 μm in the longitudinal × ∼0.3 μm in the angular direction) located between the plasma membrane and the SR membrane, immediately in front of the center of the SR segment (see Fig. 2 B). Ca²⁺ buffering in the cell segment was the same at all locations and was described by the equation

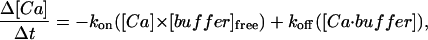(2)

where k_on (=10⁷ M⁻¹ s⁻¹) and k_off (=10 s⁻¹) are the on- and off-rates for Ca²⁺ binding to the buffer, and [Ca · buffer] is the concentration of the Ca²⁺-bound form of the buffer. The buffer was assumed to be immobile; total [buffer] in the cell was varied in some of the simulations. The values for the kinetic parameters of the buffer are in keeping with other work in the literature and represent mean parameters for the overall kinetics for Ca²⁺ buffering in smooth muscle cells (see Kargacin and Fay, 1991; Kargacin, 1994, 2003).

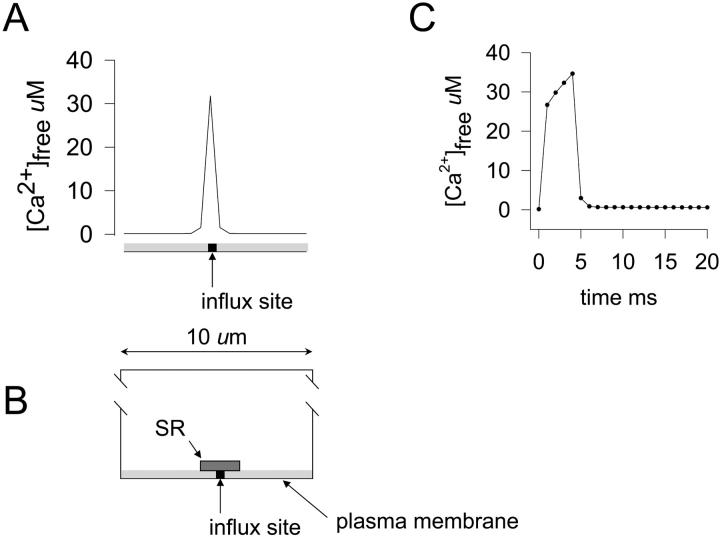
FIGURE 2.

Near-membrane [Ca²⁺] profile and time course of the [Ca²⁺] change in the near-membrane space of the modeled cell segment. (A) Ca²⁺ concentration profile in the near-membrane along the length of the modeled cell segment 3 ms after the opening of a single plasma membrane Ca²⁺ channel carrying a current of 0.1 pA. The bar at the bottom of the plot shows the position of the channel in the near-membrane space according to the diagram in B. The total length of the cell segment modeled was 10 μm; the width of the Ca²⁺ transient at half-maximum amplitude was ∼500 nm. (B) Two-dimensional diagram of the modeled cell segment in the central longitudinal plane showing the relative positions of the near-membrane space where the [Ca²⁺] profile shown in A was measured (light shading), the SR (darker shaded rectangle), and the cytoplasmic element into which Ca²⁺ influx occurred (black square). (C) Time course of the [Ca²⁺] change in the near-membrane element underlying the Ca²⁺ influx site after the opening of the channel (channel open time = 4 ms). For the simulations shown in A and C, SR Ca²⁺ uptake was not included in the model; however, the SR element was included as a physical barrier. Cytoplasmic [buffer]_free was 200 μM at the beginning of the simulations.

Ca²⁺ uptake into the SR was described by the Hill equation,

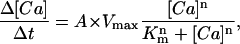(3)

where A is the ratio of the surface area of the SR element to the volume of the element; V_max is the maximum uptake velocity (=3.5 × 10⁻¹² mol cm⁻² s⁻¹; discussed below, also see Kargacin and Fay, 1991); K_m is the [Ca²⁺] at half-maximal velocity ([Ca²⁺]_50% = 219 nM); and n is the Hill coefficient for uptake (=2), as discussed previously (Kargacin and Fay, 1991). In the simulations described below, SR Ca²⁺ uptake occurred at various sites on the SR membrane (Results and Discussion). A Hill equation was also used to describe Ca²⁺ extrusion from the modeled cell segment. As discussed previously (Kargacin and Fay, 1991; Kargacin, 1994), values for V_max, K_m, and n of 3.2 × 10⁻¹³ mol cm⁻¹ s⁻¹, 200 nM and 1, respectively, were used for the plasma membrane Ca²⁺ pump. In the simulations, V_max for the plasma membrane Ca²⁺ pump was doubled to take into account the possible contribution of the Na⁺/Ca²⁺ exchanger to Ca²⁺ extrusion in the model (see discussion in Kargacin and Fay, 1991; also see Lucchesi et al., 1988; Cooney et al., 1991). Ca²⁺ extrusion from the modeled cell segment took place at all sites on the plasma membrane. Equations were also included in the model to account for the passive leak of Ca²⁺ into the cytoplasm from the SR and from the extracellular space. Equations of the form

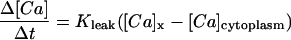(4)

were used to described the SR and plasma membrane Ca²⁺ leaks. In equations of the form of Eq. 4, [Ca]_x is the [Ca²⁺]_free in the SR lumen or the extracellular space; the constants (K_leak) were adjusted so that the Ca²⁺ leaks into the cytoplasm from the SR and from the extracellular space balanced SR Ca²⁺ uptake and plasma membrane extrusion under resting conditions (when [Ca]_x = 1.5 mM in both the extracellular space and the lumen of the SR; [Ca]_cytoplasm = 150 nM).

Measurement of SR Ca²⁺ uptake in suspensions of isolated smooth muscle cells

Ca²⁺ uptake into the SR of saponin-permeabilized isolated rabbit stomach smooth muscle cells was measured using fura-2 as described previously (Pollock et al., 1998; also see Kargacin and Kargacin, 1995). Briefly, enzymatically dispersed cells were saponin-permeabilized in a rigor buffer (150 mM K-methanesulfonate, 1 mM Mg-methanesulfonate, 5 mM EGTA, 20 mM piperazine-n,n′-bis(2-ethanesulfonic acid; pH 7.0), centrifuged (10 × g), resuspended in uptake buffer (100 mM KCl, 10 mM MgCl₂, and 20 mM HEPES at pH 7.0), and then centrifuged and resuspended three more times in uptake buffer. Suspensions of cells (50 μl) in uptake buffer (see below) were pipetted into a small (∼75 μl) chamber on the stage of an inverted microscope. After measuring background fluorescence and light scatter at 340- and 380-nm excitation and 510-nm emission, fura-2 (7.5 μM, final concentration) was added to the chamber and SR Ca²⁺ uptake was initiated by the addition of MgATP (12 mM, final concentration) and an ATP regenerating system consisting of creatine phosphate and creatine phosphokinase (final concentrations of 12 mM and 19 U/ml, respectively). Solutions in the chamber were constantly stirred and fluorescence was measured at 510 nm with a photomultiplier through the side port of the microscope. Excitation light (alternating 340 nm and 380 nm), was provided by a fluorometer (SPEX CMX model; Edison, NJ) through the epifluorescence port of the microscope. 340:380 fluorescence ratios were obtained at 1-s intervals. Experiments were conducted at 22°C.

Raw 340:380 fluorescence ratios were corrected for light scatter and background fluorescence and converted first into [Ca²⁺]_free using the equation of Grynkiewicz et al. (1985) and then into [Ca²⁺]_total by solving a set of simultaneous equations to account for Ca²⁺ binding to the various components in the uptake buffer (see Kargacin and Kargacin, 1995; Pollock et al., 1998). Uptake velocities were determined from the negative slopes of the [Ca²⁺]_total vs. time curves during the time of most rapid Ca²⁺ uptake according to the equation

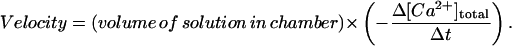(5)

After each experiment, the cell suspension in the chamber was saved and analyzed for its protein content using the BCA protein assay according to the instructions provided by the manufacturer (Pierce, Rockford, IL). Maximum uptake velocities were expressed as nmol g-protein⁻¹ s⁻¹. Experimental results are given as mean ± SE.

Immunofluorescence labeling

Freshly isolated rabbit stomach smooth muscle cells were fixed (20 min) in 1% paraformaldehyde added to the isolation medium, washed 3× in phosphate buffered saline (PBS; 150 mM NaCl, 2.1 mM NaH₂PO₄, and 8.4 mM Na₂HPO₄ at pH 7.3), permeabilized for 45 min with 0.1% Triton X-100 in PBS, washed 2× in PBS and once in incubation buffer (PBS with 3% BSA and 0.05% Tween). Cells were incubated with anti-SERCA2 or anti-phospholamban overnight at 4°C in incubation buffer, washed 3× in incubation buffer and incubated 1–1.5 h at room temperature with a Cy3- or AlexaFluor 488-conjugated secondary antibodies in incubation buffer. Labeled cells were washed 3× in PBS and pipetted (6 μl aliquots) into drops of 95% glycerol on glass slides. For the dual-label experiments, the cells were incubated with one primary antibody overnight at 4°C, washed 3× in incubation buffer and incubated with the second primary antibody for 1–1.5 h at room temperature. After washing 3× with incubation buffer, the cells were then incubated with secondary antibodies (added together) and treated as described above. Immunofluorescence images were either recorded on 35-mm film and digitized later with a scanner, or directly collected with a digital camera.

RESULTS AND DISCUSSION

Ca²⁺ transients resulting from the opening of single plasma membrane Ca²⁺ channels

A number of different plasma membrane Ca²⁺ channels have been identified in smooth muscle cells (reviewed by Sanders, 2001). The current carried by these channels is generally very low at physiological Ca²⁺ concentrations; consequently, it has been very difficult to characterize these channels using single channel recording techniques unless Ba²⁺ is used as a current carrier and Bay K 8644 is used to increase channel open times (see Benham et al., 1987; Yatani et al., 1987). Recordings in Ba²⁺ have yielded single channel currents ranging from ∼0.1 to 5 pA with open times ranging from ∼1 to 5 ms (see Benham et al., 1987; Yatani et al., 1987; Ganitkevich and Isenberg, 1990; Klöckner and Isenberg, 1994a,b; Ohya et al., 1998). Rubart and co-workers (Rubart et al., 1996) recorded single L-type Ca²⁺ channel currents from rat cerebral artery smooth muscle cells in physiological Ca²⁺. These channels had mean unitary currents of ∼0.2 pA (at −40 mV in 2 mM extracellular Ca²⁺). Zou and co-workers (Zou et al., 1999) studied single caffeine-activated Ca²⁺ channels in single toad stomach smooth muscle cells and reported mean unitary currents of ∼1 pA (at −80 mV in 2 mM extracellular Ca²⁺). Fig. 2 A shows the predicted [Ca²⁺] as a function of position along the length of the segment in the near-membrane space of the central plane of the modeled cell segment 3 ms after the opening of a single plasma membrane Ca²⁺ channel carrying a current of 0.1 pA. The relative positions of the influx site and the SR element in the model are shown diagrammatically in Fig. 2 B. Fig. 2 C shows the time course of a predicted Ca²⁺ transient in the volume element immediately adjacent to the plasma membrane in the model for the simulation shown in Fig. 2 A (open time for the channel was 4 ms). The [Ca²⁺]_i in this volume element reached a maximum value of ∼35 μM. After the closing of the channel, [Ca²⁺]_i, declined rapidly due to diffusion away from the influx site and binding to the Ca²⁺ buffer included in the model. For the simulation shown in Fig. 2, A and C, [buffer]_free in the cytoplasm was 200 μM before the channel opened ([buffer]_total = 230 μM); for this simulation, although the SR element was present in the model as a diffusion barrier, Ca²⁺ uptake into the SR was not included.

Influence of SR Ca²⁺ uptake on near-membrane [Ca²⁺]_i in response to the opening of a single plasma membrane Ca²⁺ channel

To determine the extent to which SR Ca²⁺ uptake is likely to influence the [Ca²⁺]_i reached in the restricted diffusion space between the plasma membrane and a near-membrane SR element, simulations were carried out with SR Ca²⁺ uptake included in the model. In the simulations, SR uptake was assumed to occur at all points on the surface of the SR facing the plasma membrane. To our knowledge, the density of Ca²⁺ pumps on the SR membrane of smooth muscle cells is not known. In previous work (Kargacin and Fay, 1991; also see discussion in Kargacin and Kargacin, 1995), however, based on 1), determinations of the rate at which Ca²⁺ is removed from the cytosol of smooth muscle cells after contractile stimulations (Becker et al., 1989); 2), the Ca²⁺ extrusion rate per unit area of the smooth muscle plasma membrane surface (determined by Lucchesi et al., 1988; also see Kargacin and Fay, 1991); 3), the relative contributions of plasma membrane extrusion mechanisms and SR Ca²⁺ uptake to the Ca²⁺ removal process (Kargacin and Kargacin, 1995; also see Kargacin and Fay, 1991); and 4), the volume of the SR in smooth muscle cells (determined by Devine et al., 1972), we computed an SR Ca²⁺ uptake rate per cm² of SR surface area of ∼3 × 10⁻¹² mol-Ca²⁺ cm⁻² s⁻¹.

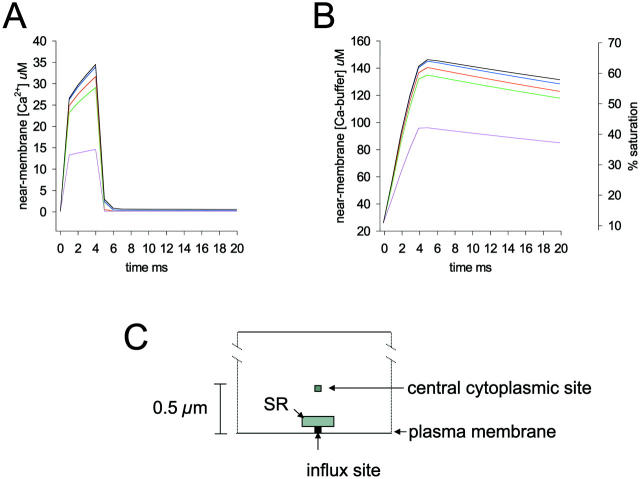
For the following simulations, we used this value as a starting point and varied the uptake rate into the near-membrane SR element in the model about this value. The results in Fig. 3 A show the near-membrane Ca²⁺ transients predicted by the model after the opening of a single plasma membrane Ca²⁺ channel (4 ms open time; 0.1 pA Ca²⁺ current) when SR uptake was not included in the model (black trace) and when SR uptake was included and the maximum uptake velocity was 3, 15, 30, or 150 × 10⁻¹² mol-Ca²⁺ cm⁻² s⁻¹. The amplitude of the near-membrane Ca²⁺ transient was not greatly affected by SR Ca²⁺ uptake except at the highest SR Ca²⁺ uptake velocity. Furthermore, the amount of Ca²⁺ reaching the central cytoplasm of the cell was not greatly influenced by the SR uptake except in the case of the highest uptake rate. After the opening of the plasma membrane Ca²⁺ channel, maximum [Ca²⁺]_i in the same plane and longitudinal position as the Ca²⁺ channel but at a central cytoplasmic position (at a position 0.5 μm from the plasma membrane; see Fig. 3 C) increased from a resting level of 150 to 215 nM when SR uptake was not included in the model. When SR uptake was included, [Ca²⁺]_i at this same cytoplasmic point reached levels of 213, 204, 195, and 152 nM, respectively, when simulations were run with SR uptake rates of 3, 15, 30, and 150 × 10⁻¹² mol-Ca²⁺ cm⁻² s⁻¹.

FIGURE 3.

Near-membrane [Ca²⁺] and Ca²⁺-bound buffer as a function of time for different SR Ca²⁺ uptake rates. (A) [Ca²⁺] in the near-membrane space at the site of Ca²⁺ influx after the opening of a single plasma membrane Ca²⁺ channel carrying a current of 0.1 pA (open time = 4 ms). [Ca²⁺] values as a function of time in the near-membrane space are shown for SR uptake rates of 0 (black trace), 3 × 10⁻¹² (blue trace), 15 × 10⁻¹² (red trace), 30 × 10⁻¹² (green trace), and 150 × 10⁻¹² (magenta trace) mol-Ca²⁺ cm⁻² s⁻¹. SR Ca²⁺ pumps were located on the side of the SR element facing the influx site. (B) Concentration of the Ca²⁺-bound form of the cytosolic Ca²⁺ buffer in the near-membrane space at the site of Ca²⁺ influx for the simulations in A; [buffer]_free was 200 μM ([buffer]_total = 230 μM) at the start of the simulations. The right vertical axes in B gives the % saturation of the Ca²⁺ buffer; SR Ca²⁺ uptake rates were 0 (black trace), 3 × 10⁻¹² (blue trace), 15 × 10⁻¹² (red trace), 30 × 10⁻¹² (green trace), and 150 × 10⁻¹² (magenta trace) mol-Ca²⁺ cm⁻² s⁻¹. (C) Diagram showing the relative positions of the SR the Ca²⁺ influx site and the central cytoplasmic site at which Ca²⁺ was monitored for the simulations described in the text.

Fig. 3 B shows the changes in the concentration of the Ca²⁺-bound form of the buffer in the volume element between the plasma membrane Ca²⁺ channel and the SR membrane for the simulations shown in Fig. 3 A. Association of Ca²⁺ with the buffer continued to increase for the 4-ms duration of the channel opening and then declined after the channel closure. Comparison of the results for the simulation in which there was no SR Ca²⁺ uptake with those in which SR had uptake rates of 3, 15, and 30 × 10⁻¹² mol-Ca²⁺ cm⁻² s⁻¹ indicates that SR Ca²⁺ uptake did not have a major influence on the binding of Ca²⁺ to the buffer. When the SR Ca²⁺ uptake rate was 150 × 10⁻¹² mol-Ca²⁺ cm⁻² s⁻¹, however, competition between SR Ca²⁺ uptake and Ca²⁺ binding to the buffer reduced the relative contribution of the buffer. When one examines the Ca²⁺ transients shown in Fig. 3 A and the time course of the buffering process shown in Fig. 3 B, it is clear that the steep decline in [Ca²⁺]_i in the near-membrane space after the closing of the plasma membrane Ca²⁺ channel still occurred when there was no SR Ca²⁺ uptake included in the model and when loading of the buffer reached its maximum extent. This indicates that the decline in [Ca²⁺]_i seen when the channel closes is due primarily to the diffusion of Ca²⁺ away from the influx site rather than to SR Ca²⁺ uptake or to the association of Ca²⁺ with the buffer in the near-membrane space. Thus, even in the presence of a physical barrier, the model predicts that diffusion of Ca²⁺ away from a Ca²⁺ channel influx site remains a major factor for determining the shape of the Ca²⁺ transient in the neighborhood of the channel.

Measurement of SR Ca²⁺ uptake in saponin-permeabilized isolated smooth muscle cells

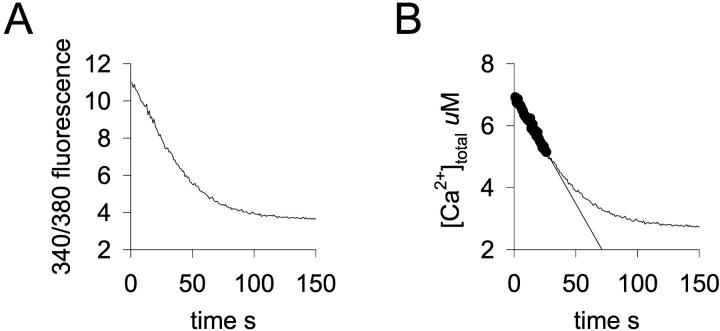
Only the highest SR Ca²⁺ uptake rate used in the model (which would require an SR Ca²⁺ uptake velocity 50× greater than that computed in our previous studies; see Kargacin and Fay, 1991) had a significant impact on 1) the predicted magnitude of the single channel Ca²⁺ transient, 2) the amount of Ca²⁺ reaching the central cytoplasm of the cell, and 3) the association of Ca²⁺ with the Ca²⁺ buffer in the modeled cell segment. The estimate of the SR uptake rate (3 × 10⁻¹² mol cm⁻² s⁻¹) that we used as a starting point for the simulations discussed above was determined indirectly from the rate at which Ca²⁺ declines in smooth muscle cells during contractile signaling and the likely contribution of plasma membrane extrusion processes to this decline (see Kargacin and Fay, 1991; Lucchesi et al., 1988; Cooney et al., 1991). To determine if this estimate was accurate, we measured Ca²⁺ uptake into the SR of saponin-permeabilized isolated rabbit stomach smooth muscle cells and computed a Ca²⁺ uptake rate per unit surface area of SR from these measurements. Fig. 4 A shows the raw fura-2 fluorescence data and a corresponding uptake curve showing the change in [Ca²⁺]_total in the uptake buffer (Fig. 4 B) for a typical SR uptake Ca²⁺ experiment . The maximum rate of uptake for the curve shown (computed from the points on the curve shown by the filled circles in Fig. 4 B) was 22.6 nmol g-cell-protein⁻¹ s⁻¹. The mean uptake rate measured at 22°C for 76 such experiments from nine different isolated rabbit stomach smooth muscle cell preparations was 28 ± 2 nmol g-cell-protein⁻¹ s⁻¹. The highest mean uptake rate of the nine different isolated cell preparations we used for the experiments was 57 nmol g-protein⁻¹ s⁻¹. Assuming a specific gravity of 1 g ml⁻¹, a Q₁₀ for SERCA2 SR Ca²⁺ pumps of 2.5 (see Lundblad et al., 1986), and a weight ratio of cell protein:cell water of 1:4, a mean uptake rate of 26 × 10⁻⁶ mol l-cell volume⁻¹ s⁻¹ at 37°C can be calculated from the measured mean uptake rate of 28 nmol g-cell-protein⁻¹ s⁻¹. Although Devine and co-workers (Devine et al., 1972) did not determine the percentage of cell volume occupied by the SR for rabbit stomach smooth muscle cells, they did determine a value of ∼2% for rabbit Taenia coli. Using an SR volume:cell volume ratio of 0.02, a mean Ca²⁺ uptake rate per unit volume of SR of 13 × 10⁻⁴ mol l-SR⁻¹ s⁻¹ can be computed. The volume of the near-membrane SR segment in the model cell is 18 × 10⁻¹⁷ l and the surface area is ∼7 × 10⁻⁸ cm². Therefore, the expected Ca²⁺ uptake rate of the SR element in the model per unit surface area, based on our uptake experiments (see Fig. 4), is 3.3 × 10⁻¹² mol cm⁻² s⁻¹. The SR volume:cell volume estimates for smooth muscle by Devine and co-workers (Devine et al., 1972) ranged from 2% to 6% for all of the smooth muscle cell types examined. If one uses the highest SR volume:cell volume estimate, a mean uptake rate of 1.1 × 10⁻¹² mol cm⁻² s⁻¹ can be computed. If we use the highest mean uptake rate measured for our different cell preparations (57 nmol g-protein⁻¹ s⁻¹), our estimates of the uptake rate range between 2.2 × 10⁻¹² and 6.6 × 10⁻¹² mol cm⁻² s⁻¹ for the SR element in our simulations when the total SR volume ranged between 2% and 6% of the cell volume. Permeabilized toad stomach smooth muscle cells lose ∼30% of their soluble protein during isolation and permeabilization (see Kargacin and Fay, 1987). A similar protein loss from the rabbit stomach smooth muscle cell preparations would result in an overestimate of Ca²⁺ uptake rates of ∼30%. Our measured mean SR Ca²⁺ uptake rates (ranging between 1.1 and 6.6 × 10⁻¹² mol cm⁻² s⁻¹) are consistent with the uptake rate per unit area of SR membrane that we estimated indirectly in our previous work (Kargacin and Fay, 1991). Thus it is unlikely that uptake rate per unit area of SR membrane (3 × 10⁻¹² mol cm⁻² s⁻¹) that was used as a starting value in our simulations could be an order-of-magnitude lower than the mean SR Ca²⁺ uptake rate in smooth muscle cells in vivo. If the peripheral SR plays a major role in shaping Ca²⁺ transients in smooth muscle cells, flux of Ca²⁺ into the near-membrane SR would have to be much greater than the cellular average.

FIGURE 4.

SR Ca²⁺ uptake in isolated rabbit stomach smooth muscle cells. (A) Fura-2 340:380 fluorescence ratio as a function of time after the addition of Ca²⁺ and ATP to a 50 μl suspension of saponin-permeabilized isolated smooth muscle cells. The trace shown was corrected for background fluorescence and light scatter as described in Materials and Methods. Uptake of Ca²⁺ into the SR of the permeabilized cells results in a decrease in [Ca²⁺] in the buffer and a decrease in fluorescence ratio. (B) [Ca²⁺]_total in the chamber as a function of time for the experiment shown in A. [Ca²⁺]_total determined as described in Materials and Methods after 340/360 fluorescence was converted into [Ca²⁺]_free using the equation of Grynkiewicz and co-workers (Grynkiewicz et al, 1985) and binding of Ca²⁺ to the components in the buffer was taken into account. Maximum rate of uptake (22.6 nmol g-cell-protein⁻¹ s⁻¹) for the cells in the suspension was determined from the initial steepest part of the curve (filled circles) using Eq. 5.

Immunofluorescence imaging of SR Ca²⁺ pumps and phospholamban in isolated smooth muscle cells

From the measurements described above, it appears unlikely that we greatly underestimated the mean SR Ca²⁺ uptake rate that was used as a starting point for the simulations. It is possible, however, that there is a higher density of SR Ca²⁺ pumps on the peripheral SR than there is on the deeper SR in smooth muscle cells. This would allow the superficial SR to be more effectively coupled to plasma membrane proteins involved in Ca²⁺ regulation. To test this possibility, we labeled freshly isolated rabbit stomach smooth muscle cells with an antibody to the smooth muscle SR Ca²⁺ pump or with an antibody to phospholamban, a protein involved in regulating Ca²⁺ uptake by the pump in cardiac and smooth muscle (see Sanders, 2001) . Immunofluorescent images of rabbit stomach smooth muscle cells labeled with either antibody (Fig. 5) did not reveal any obvious differences in the intensity of labeling localized near the plasma membrane relative to that associated with the deeper SR in these cells. From these results, we cannot rule out the possibility that there are some SR elements within these cells with Ca²⁺ pump densities too low to detect with our antibodies or that there are more modest differences in Ca²⁺ pump density and uptake rates between the peripheral and central SR in smooth muscle cells. However, to our knowledge, there is no other evidence from morphological studies employing either electron or fluorescence microscopy that would support the hypothesis that there is a measurable difference in the distribution of SR Ca²⁺ pumps between the near-membrane and the more central SR in smooth muscle cells.

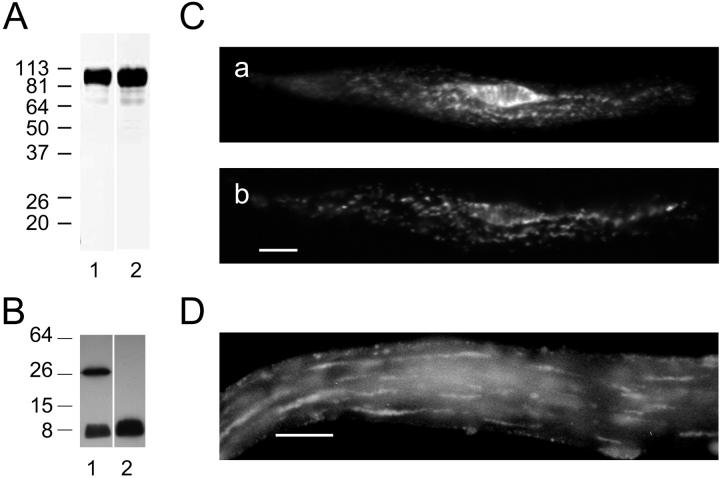
FIGURE 5.

Localization of SERCA2 and phospholamban in single isolated rabbit stomach smooth muscle cells. (A) Western blot of rabbit stomach homogenate labeled with anti-SERCA2; 20 μg of protein was loaded onto lane 1, and 40 μg onto lane 2; proteins were separated on a 10% gel; molecular weights are shown to the left of lane 1. (B) Western blot of phospholamban in a canine cardiac muscle homogenate. Lane 1 shows both pentameric (∼30 kDa) and monomeric (∼6 kDa) phospholamban in the homogenate. Lane 2 shows only the monomeric form of phospholamban after the homogenate sample was boiled. Molecular weights are shown to the left of lane 1; 5 μg of protein were loaded onto lanes 1 and 2; and proteins were separated on a 15% gel. (C) (a) Immunofluorescence image of SERCA2 in an isolated rabbit stomach smooth muscle cell; (b) immunofluorescence image of phospholamban in the cell shown in a. Control experiments (not shown) in which the primary antibodies were not present did not reveal any nonspecific labeling by the secondary antibodies. (Scale bar = 10 μm.) (D) Higher power immunofluorescence image of phospholamban in an isolated rabbit stomach smooth muscle cell. (Scale bar = 10 μm.)

Uptake of Ca²⁺ by the SR after the opening of single plasma membrane Ca²⁺ channels

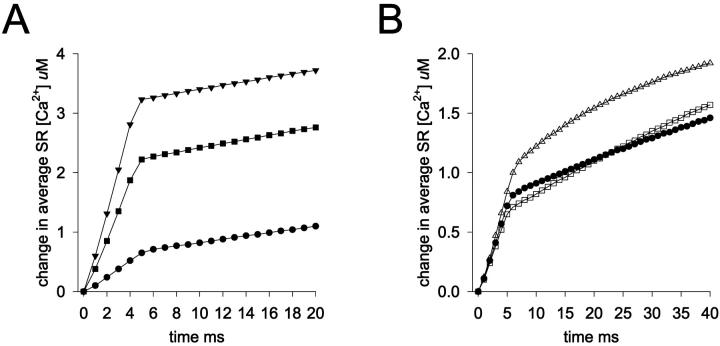
The results in Fig. 6 A show the changes in the Ca²⁺ content of the near-membrane SR after the opening of a single Ca²⁺ channel (at t = 0; 4 ms open time, 0.1 pA current) for different SR uptake rates. As in the simulations described above, the SR Ca²⁺ pumps were assumed to be present on the surface of the SR facing the plasma membrane. Uptake velocities of 3, 15, and 30 × 10⁻¹² mol-Ca²⁺ cm⁻² s⁻¹ were examined in the simulations; the results show the overall change in [Ca²⁺]_SR for the entire near-membrane SR segment present in the model. After the opening of the plasma membrane Ca²⁺ channel, SR [Ca²⁺] increased rapidly during the time the channel was open and then continued to increase at a more modest rate during the remainder of the time period of the simulations.

FIGURE 6.

Change in SR [Ca²⁺] in the modeled cell segment as a function of time for different Ca²⁺ uptake rates and for different cytoplasmic Ca²⁺ buffer concentrations. (A) Change in [Ca²⁺] as a function of time in the near-membrane SR element of the modeled cell segment for SR uptake rates of three (filled circles), 15 (filled squares), and 30 (filled triangles) × 10⁻¹² mol-Ca²⁺ cm⁻² s⁻¹ after the opening of a single plasma membrane Ca²⁺ channel carrying a 0.1-pA Ca²⁺ current (open time = 4 ms). Concentration of free cytoplasmic Ca²⁺ buffer was 200 μM at the start of the simulation. (B) Change in SR [Ca²⁺] as a function of time in the near-membrane SR element in the model for different concentrations of the cytoplasmic Ca²⁺ buffer. Cytoplasmic [buffer]_free at the start of the simulations was 200 μM (filled circles), 100 μM (open squares), and 0 (open triangles).

The results discussed above indicating that diffusion plays a major role in determining the [Ca²⁺]_i in the vicinity of a Ca²⁺ channel once the channel closes suggests that Ca²⁺ buffering in this region could facilitate near-membrane SR Ca²⁺ uptake by retaining Ca²⁺ near the SR membrane. When the concentration of the Ca²⁺ buffer in the model cell was altered, however, it was apparent that the presence of a buffer in the near-membrane space impeded rather than facilitated the rapid uptake of Ca²⁺ by the near-membrane SR. As shown in Fig. 6 B, reducing the free buffer concentration from 200 μM to 100 μM in the resting cell did not greatly affect SR Ca²⁺ loading. Reducing the buffer concentration increased the secondary rate of rise of Ca²⁺ after the closing of the channel; however, the initial uptake rate was slightly lower at the lower buffer concentration. When the buffer was completely removed in the model, the most efficient initial uptake of Ca²⁺ by the SR occurred. The reason for this becomes apparent when one considers the Ca²⁺ gradient that develops in the near-membrane space after the opening of a single plasma membrane Ca²⁺ channel. With a starting [buffer]_free of 200 μM, the simulations discussed above predict a maximum [Ca²⁺]_i of ∼35 μM immediately adjacent to a plasma membrane Ca²⁺ channel carrying a current of 0.1 pA during the 4-ms time period that the channel is open (see Fig. 2). A Ca²⁺ concentration of this magnitude (>100× the [Ca²⁺]_50% of the smooth muscle SR Ca²⁺ pump ≈ 200 nM; see Materials and Methods) would be expected to saturate the SR Ca²⁺ pumps immediately facing the influx site. The Ca²⁺ gradient in the near-membrane space is predicted to be very steep; however (see Fig. 2 A), when cytoplasmic Ca²⁺ buffering is reduced, the higher [Ca²⁺] and the ability of Ca²⁺ to spread longitudinally and in the angular direction beyond the site of influx would allow the SR to take up additional Ca²⁺ at sites away from those opposing the channel. Thus reduced Ca²⁺ buffering in the near-membrane diffusion space would allow Ca²⁺ to more quickly reach SR pumps more distant from the influx site. For a channel carrying a 0.1 pA current with an open time of 4 ms the model predicted a maximum [Ca²⁺]_i of 0.47 μM in the near-membrane space 2 ms after the channel closed when the starting cytoplasmic free buffer concentration was 200 μM. When the cytoplasmic buffer concentration was 100 μM, the predicted maximum [Ca²⁺]_i was 0.62 μM and, when the cytoplasmic buffer concentration was 0, the predicted maximum [Ca²⁺]_i was 1.56 μM. At this same time point, the widths of the Ca²⁺ signals at half-maximal Ca²⁺ concentration were ∼600 nm, 700 nm, and 800 nm, respectively, for starting free buffer concentrations of 200, 100, and 0 μM.

The Ca²⁺ buffers incorporated into the model were assumed to be immobile. This assumption may not hold for all Ca²⁺-binding molecules, however. Of the endogenous mobile Ca²⁺ buffers, most are likely to be proteins (e.g., calmodulin) which have cytoplasmic diffusion coefficients an order-of-magnitude less than the diffusion coefficient for Ca²⁺ (see Smith et al., 1996). Thus, for the time periods considered in our simulations, the impact of assuming that these buffers are immobile would be minimal. Highly mobile Ca²⁺ buffers, on the other hand, could increase the apparent diffusion coefficient for Ca²⁺ in cells. Studies with small Ca²⁺-binding molecules introduced into cells exogenously (e.g., fluorescent Ca²⁺ indicators) suggest that such buffers can increase the apparent cytoplasmic Ca²⁺ diffusion coefficient by a factor of 2 or more (see Zhou and Neher, 1993). Endogenous buffers of this type could facilitate SR Ca²⁺ loading by allowing Ca²⁺ to more rapidly move away from sites where the SR Ca²⁺ pumps are saturated. Whether endogenous highly mobile Ca²⁺ buffers are present in smooth muscle cells is unknown, however. In adrenal chromaffin cells, Zhou and Neher (1993) were unable to obtain evidence of the presence of highly mobile endogenous buffers suggesting that these buffers did not contribute significantly to the Ca²⁺ binding capacity in these cells.

SR loading after Ca²⁺ influx through a single plasma membrane Ca²⁺ channel carrying a current of 1 pA

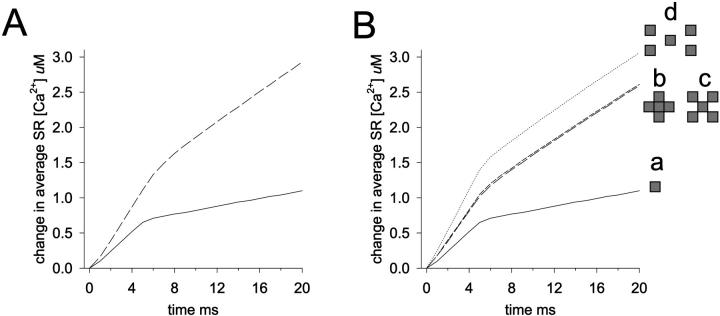
Although the SR Ca²⁺ pumps facing a plasma membrane Ca²⁺ channel are predicted to saturate after the single channel openings discussed above, spreading of Ca²⁺ in the near membrane space longitudinally and in the angular dimension would allow additional uptake to occur by pumps at more distal sites even if the SR pumps nearest the channel were saturated. The simulations shown in Fig. 7 A compare SR Ca²⁺ loading after 4-ms openings of single channels passing 0.1 and 1 pA Ca²⁺ currents. Although the amplitude of the predicted Ca²⁺ transient was an order-of -magnitude greater for the 1 pA current (not shown), the amount of Ca²⁺ taken up into the near-membrane SR element was only increased by a factor of 2 during the 4-ms time period that the channel was open (Fig. 7 A). This indicates that the SR Ca²⁺ pumps proximal to the influx site were working at maximum velocity, limiting the ability of the SR to take up additional Ca²⁺ at this site. During the following 15 ms of the simulation shown in Fig. 7 A, the rate of SR uptake continued to remain high, however, for the simulations that included the 1-pA channel as more distal uptake sites contributed to the SR loading.

FIGURE 7.

Change in [Ca²⁺] in the SR of the modeled cell segment after the opening of a single Ca²⁺ channel carrying a current of 1 pA or after the opening of a cluster of five channels. (A) Change in SR [Ca²⁺] as a function of time is shown after the opening of a Ca²⁺ channel carrying a current of 0.1 pA (solid line) or 1 pA (dashed line). (B) Change in SR [Ca²⁺] as a function of time after the opening of a single channel (solid line) or five channels in three different configurations (dashed and dotted lines). The configurations of the clustered channels about the central channel are shown by the diagrams and letters to the right of the figure. The solid line shows the results for a single channel (a); the long dashes show the results for channels in configuration (b); the shorter dashes the results for channels in configuration (c); and the dotted line, the results for channels in configuration (d). All of the channels in B carried currents of 0.1 pA. Open times for the channels for the simulations shown in A and B were 4 ms; SR uptake rate was 3 × 10⁻¹² mol-Ca²⁺ cm⁻² s⁻¹; and cytoplasmic [buffer]_free was 200 μM.

SR loading after influx into the near-membrane space from a cluster of open Ca²⁺ channels

To this point, we have assumed that there was only one Ca²⁺ channel open on the plasma membrane overlying the SR element in the model. Estimates of the number of Ca²⁺ channels in smooth muscle cells range from <1000 to ∼5000 channels per cell (Yatani et al., 1987; Ganitekvich and Isenberg, 1990; Rubart et al., 1996). Reported values for the average cell capacitance of isolated canine saphenous vein and rat cerebral artery smooth muscle cells are 20 pF and 13.7 pF, respectively (Yatani et al., 1987; Rubart et al., 1996). Determination of surface area from these measurements (assuming a specific capacitance of 1 μF/cm²) and the above estimates of the number of channels per cell (1000–5000), yields channel densities ranging from ∼0.5–4 channels per μm² of surface area. The area of the membrane overlying the SR element in our model was 3.8 μm². Thus, one could expect 2–14 channels in this area if the channels in the cell are distributed uniformly. Although there is evidence for Ca²⁺ channel-mediated influx of Ca²⁺ into smooth muscle cells at rest (Ganitekvich and Isenberg, 1990; Rubart et al., 1996), given a low open channel probability under resting conditions (steady-state open probability ∼0.0003 at −40 mV, and ∼0.002 at −20 mV; Rubart et al., 1996), it is unlikely that more than one channel would be open at any given time in the membrane overlying the SR element in the model if one assumes a uniform distribution of channels on the plasma membrane.

It has been suggested that L-type Ca²⁺ channels in vascular smooth muscle cells may be found in clusters (Klöckner and Isenberg, 1994a,b). If this is the case, the probability that more than one channel in a 4-μm² area of plasma membrane could be open in a resting smooth muscle cell could be increased especially if localized changes in membrane potential due to the opening of one channel results in the opening of other nearby voltage-dependent channels. The probability of having more than one channel open would also increase during contractile activation (Quayle et al., 1993, estimated a smooth muscle Ca²⁺ channel open probability of 0.44 under depolarizing conditions suggesting that, even under these conditions, based on the channel densities discussed above, 1–6 channels would be the maximum number of channels expected to be open in the membrane overlying the SR in our model). The results in Fig. 7 A for a single channel current of 1 pA are equivalent to those that would be obtained if there were 10 channels each carrying a current of 0.1 pA opening at the same time at a point on the plasma membrane overlying the center of the SR element in the model. As also noted above, the efficiency with which the near-membrane SR was able to take up Ca²⁺ after the influx event was limited by saturation of the SR pumps underlying the influx site. We also examine the effect of having a number of channels organized in a cluster about a central channel so that the transient signal was distributed over a wider area overlying the near-membrane SR. Fig. 7 B shows the results of simulations in which four channels were arranged in three different configurations about a central channel. As the mean distance from the central channel to the four other channels was increased, SR uptake was also increased. The most spacious configuration of five channels resulted in SR uptake that was approximately the same as that seen when 10 channels were confined to an area overlying the center of the SR element (compare Fig. 7, A and B).

SUMMARY AND CONCLUSIONS

The simulations reported in this study focused primarily on the effects of three processes (diffusion, Ca²⁺ buffering by intracellular Ca²⁺-binding molecules, and uptake of Ca²⁺ by the SR) on Ca²⁺ signaling in smooth muscle cells in cellular regions where the SR is in close apposition to the plasma membrane. During the first few ms after the opening of a plasma membrane Ca²⁺ channel, the model predicted that SR Ca²⁺ uptake would have relatively little influence on the amplitude of single channel Ca²⁺ transients in the near-membrane space unless SR Ca²⁺ uptake rates were considerably higher than the value (3.5 × 10⁻¹² mol cm_{SR surface area}⁻² s⁻¹) we used in our previous work (discussed above Kargacin and Fay, 1991). The latter value is in excellent agreement with that determined experimentally in the present study (3.3 × 10⁻¹² mol cm_{SR surface area}⁻² s⁻¹). These experimental results therefore support our conclusion that SR uptake near the plasma membrane is unlikely to greatly influence near-membrane Ca²⁺ transients or the amount of Ca²⁺ reaching the central cytoplasm of a cell. Furthermore, our immunofluorescence results (Fig. 5) do not support the hypothesis that the near-membrane SR has a higher mean density of Ca²⁺ pumps than does the deeper SR in smooth muscle. Our present results suggest that, for the peripheral SR to have a major influence on Ca²⁺ transients arising from the opening of plasma membrane Ca²⁺ channels, the SR Ca²⁺ pumps would have to be clustered at high densities on the SR membrane at sites in close proximity to the channels. To our knowledge, however, evidence for such clustering has not been obtained from electron microscopic or other studies of smooth muscle cells. Although our results indicate that SR Ca²⁺ uptake is unlikely to play a major role in modulating localized, transient Ca²⁺ signals, our simulations do predict that near-membrane SR elements can take up a significant amount of Ca²⁺ during a transient signaling event. Thus, coupling between single plasma membrane Ca²⁺ channel openings and near-membrane SR Ca²⁺ uptake could provide a mechanism for rapidly replenishing local, peripheral Ca²⁺ stores in smooth muscle cells. This does not appear to be a mechanism that could rapidly reload the entire cellular SR, however. A typical vascular smooth muscle cell is spindle shaped, ∼100 μm in length and 1–2 μm in diameter. Assuming a cylindrical central portion 50 μm in length and two conical shaped ends, the cell volume of a 2-μm diameter cell is ∼0.2 pl. Devine et al. (1972) estimated the volume occupied by the SR in a number of different smooth muscle cell types and obtained values ranging between 2 and 6% of the cell volume. Thus, the volume of the SR for the typical cell under consideration would be expected to be between 4 × 10⁻³ and 1 × 10⁻² pl. The volume of the near-membrane SR element in our simulations is ∼8 × 10⁻⁵ pl (see Methods). This volume represents at most 2% of the total SR volume expected to be present in a 100-μm-long, spindle-shaped smooth muscle cell with a radius of 2 μm. Based on these considerations, it would require a considerable number of single channel openings to significantly increase the overall SR Ca²⁺ content in a smooth muscle cell. This is unlikely to occur on a millisecond timescale, but could conceivably occur over several seconds or minutes.

There is considerable variation in the size of, the function of, and the mechanisms thought to regulate various types of smooth muscle cells. For this study, we developed a model that was general enough to allow us to make broadly applicable predictions. The results we obtained could be modified in specific smooth muscle cell types or for specific cellular morphologies, however. In the present model, for example, because relatively little is known about the role of the Na⁺/Ca²⁺ exchanger in smooth muscle Ca²⁺ regulation (discussed in Sanders, 2001), we included Na⁺/Ca²⁺ exchange as part of a plasma membrane Ca²⁺ extrusion mechanism that also included the contribution of the plasma membrane Ca²⁺ ATPase. Arnon and co-workers (Arnon et al., 2000) have proposed that Na⁺/Ca²⁺ exchangers are clustered as sites overlaying the SR in cultured arterial myocytes, however. If this is the case, Na⁺/Ca²⁺ exchange might play a role in modulating single channel Ca²⁺ transients depending upon the relative location of Ca²⁺ channels and these clusters on the plasma membrane. Exchangers located within a few nm of an influx site would experience a high Ca²⁺-dependent driving force. This could reduce the amplitude of intracellular Ca²⁺ transients arising at such sites. Although the role of calcium-induced calcium release in regulating smooth muscle contraction has not been well determined, ryanodine receptors are known to be present in the SR membrane in smooth muscle cells. If these receptors are located in close proximity to overlying plasma membrane Ca²⁺ channels, net SR Ca²⁺ release (as the result of calcium-induced calcium release) rather than SR uptake could result from the opening of single plasma membrane Ca²⁺ channels. Evidence both for and against the coupling of plasma membrane Ca²⁺ channel activity to SR Ca²⁺ release has appeared in the literature (reviewed by Sanders, 2001). The steep Ca²⁺ gradient that develops near a site of Ca²⁺ influx would limit the spatial range over which coupling could occur between single channel events and Na⁺/Ca²⁺ exchange or ryanodine receptor-mediated SR Ca²⁺ release. One would also expect the plasma membrane to depolarize near a Ca²⁺ influx site. This would decrease the driving force for Ca²⁺ entry through the membrane and reduce the amplitude of localized Ca²⁺ transients and, consequently, the amount of Ca²⁺ taken up into the near-membrane SR at such sites. On the other hand, estimates of single channel currents from L-type Ca²⁺ channels in smooth muscle cells range over an order of magnitude (from ∼0.1 to ∼1 pA) and currents at the higher end of this range would be expected to result in higher SR uptake amounts (see Fig. 7 B).

Our experimental results, when incorporated into our model, predict that uptake of Ca²⁺ by the near-membrane SR in smooth muscle is unlikely to greatly influence either the magnitude of the Ca²⁺ transients arising from the opening of single plasma membrane Ca²⁺ channels or diffusion of Ca²⁺ away from these channels even when diffusion is restricted by the physical presence of the SR. These results appear to contradict the buffer-barrier hypothesis that has been proposed for smooth muscle cells. This hypothesis (reviewed recently by Sanders, 2001) suggests that the close proximity of the SR to the plasma membrane at some locations allows the SR to take up a substantial amount of the Ca²⁺ entering a cell through the plasma membrane, thereby reducing the amount of Ca²⁺ that is able to reach the central cytoplasm of the cell unless the SR is fully loaded or SR Ca²⁺ uptake is inhibited. The results of our simulations suggest that, for such a mechanism to be operative, additional regulatory processes or structural entities that are presently not known (and were, therefore, not included in the model) would have to be present in cells. More comprehensive experimentally-derived knowledge of the microenvironments that exist between the plasma membrane and the SR membrane at sites where these two membranes are in close apposition in smooth muscle cells is required to further evaluate or model the signaling that is likely to occur in these regions. In addition to more precise knowledge of single-channel Ca²⁺ currents and the localization and the functioning of the Na⁺/Ca²⁺ exchanger and the plasma membrane Ca²⁺ pump, information about the possible clustering of SR Ca²⁺ pumps, about other mechanisms that could couple plasma membrane ion channel activity to SR function, and about structural proteins or cytoskeletal elements that could further limit diffusion in the near-membrane microenvironment is required for understanding the mechanisms involved in locally regulating Ca²⁺ in smooth muscle cells.