Protein Dynamics, Thermal Stability, and Free-Energy Landscapes: A Molecular Dynamics Investigation

Abstract

Proteins have a complex free-energy landscape because of their rich topology and the nature of their nonbonded interaction potential. This has important consequences because the roughness of the landscape affects the ease with which a chain folds and also determines the dynamic behavior of the folded structure, thus influencing its functional and stability properties. A detailed description of the free-energy landscape is therefore of paramount importance for a quantitative understanding of the relationships between structure, dynamics, stability, and functional behavior of proteins. The free-energy landscape of a protein is a high-dimensional hypersurface, difficult to rationalize. Therefore, achieving its detailed graphical representation in a way that goes beyond the familiar funnel-like free-energy model is still a big challenge. We describe here an approach based on global structural parameters that allows a two-dimensional representation of the free-energy landscape from simulated atomic trajectories. As shown in this and in the accompanying article, our representation of the landscape, combined with other conformational analyses, provides valuable information on its roughness and on how atomic trajectories evolve with time.

INTRODUCTION

The thermodynamic stability of a protein in its native state is of paramount importance, but certainly not the only crucial parameter. Every protein has to fulfill a specific physiological function at the most appropriate velocity and the structural flexibility of the native fold is certainly an essential element for the modulation of the functional properties. Indeed it is well established that proteins with the same fold can have widely different dynamic properties and, in turn, display distinct functional behaviors (Di Iorio et al., 1997; Szilágyi and Závodszky, 2000).

The capability of adapting a given protein fold to different dynamic properties is related to the complexity of proteins. They are composed in many cases by several subunits, each consisting of a polypeptide chain with a well-defined amino acid sequence. Even when constituted by a single and relatively short chain, the level of complexity of proteins is very high and it is difficult to describe, in comprehensive and quantitative terms, the relationships between their stability, dynamic, and functional properties. This situation is intrinsically determined by the unique structural organization of proteins, which leads to a marked anisotropy of cohesion forces between its constituent atoms and to a conformational space with many potential energy minima arranged in a hierarchical fashion (Ansari et al., 1985). Each valley in this hypersurface pertains to a particular spatial arrangement of the protein. The minima in higher tiers correspond to different conformations, e.g., substrate free or substrate bound, whereas those in lower tiers pertain to taxonomic states and conformational substates. The probability for the system to undergo a conformational transition through equilibrium fluctuations is low due to the complexity of the paths connecting different regions of the phase space. However, substrate binding or dissociation originate a “proteinquake”, which involves nonequilibrium fluctuations that allow the protein to rapidly change its conformational state (Ansari et al., 1985).

Certainly, the need for undergoing conformational changes to accomplish biological functions suggests that proteins must conserve, in their native state, a considerable degree of structural flexibility. On the other hand, if one considers that some proteins have in vivo lifetimes of several months, it is also obvious that considerable restraints to their conformational freedom must be operative. The segregation of the hydrophobic residues within the core and the presence of secondary and tertiary structure are typical restrains operative in the native state. A fundamental question is to what extent such restraints hamper the exercise of the liquid-like degrees of freedom at temperatures below the folding temperature T_F.

The free-energy landscape (FEL) of proteins is necessarily rugged because, as in the general case of one-dimensional connected objects in the three-dimensional space, the chain can sample many different conformations and may even display repulsive and therefore energetically unfavorable contacts between residues. Nevertheless, native interactions are designed to provide stabilizing energetic contributions, thus generating what is referred to as stability gap. Therefore, the FEL displays an overall slope, which directs the nascent chain toward the locally stable and kinetically accessible native conformation. In other words, the landscape of proteins is not globally flat, but has a preferred direction of flow toward the native fold, commonly represented as a rugged funnel, the so-called folding funnel (Bryngelson and Wolynes, 1987; Leopold et al., 1992; Onuchic et al., 1995). In such a landscape the folding time is approximately given by τ = τ₀ exp(βF^#), where τ₀ is the reconfiguration time of a protein in the rugged landscape, whereas F^# is the free-energy barrier for the folding transition starting from a set of random coil configurations. The reconfiguration time τ₀ increases with the ruggedness of the landscape and depends on the degree of collapse of the chain. This is strongly related to the proximity to the glass transition temperature, at which also smaller traps become kinetically competitive with the global minimum in free energy. The free-energy barrier F^# is also temperature dependent and below T_F, at which the global minimum that represents the native state becomes thermodynamically stable, it decreases with the ground state energy itself (Plotkin et al., 1997).

The folding of the polypeptide chain, be it spontaneous or mediated by the interaction with chaperons, is thought to be driven by the search for a minimal frustration (Bryngelson et al., 1995; Wolynes and Eaton, 1999; Wolynes et al., 1996). In turn, the dynamic properties of small globular proteins, like the rubredoxin fold, have been shown to depend significantly on the frustration level of nonbonded interactions (Tavernelli and Di Iorio, 2001).

From what was just stated, it is clear that our capability of explaining in quantitative terms the interplay between folding, stability, and dynamic properties of a native protein is conditional to a detailed knowledge of its FEL.

Here we report an approach for the computation of a two-dimensional representation of the FEL of a protein based on suited global parameters derived from molecular dynamics (MD) simulations.

This approach is used to analyze previously reported (Tavernelli and Di Iorio, 2001) and further extended atomic trajectories obtained by classical molecular dynamics simulations on two rubredoxins (Rd) respectively from the mesophile Clostridium pasteurianum and the hyperthermophile Pyrococcus furiosus. The simulations have been carried out at 308 K and 373 K, corresponding to the optimal growth temperatures for the two bacteria. The two rubredoxins are characterized by the same fold, but have totally different dynamic and functional properties (Eidsness et al., 1997; Tavernelli and Di Iorio, 2001 and references therein).

In the accompanying article we have used our representation of the FEL to characterize the folding state of bovine ribonuclease A and of its S-protein (Cotesta et al., 2003).

METHODS

Simulation details

Simulations were done with GROMOS96 (van Gunsteren et al., 1996) as formerly described (Tavernelli and Di Iorio, 2001). Here we only provide details not given or that no longer apply to what was reported previously.

Starting velocities were randomly assigned from a Maxwell distribution at 70 K below the final temperature. Heating to the final T was done within 50 ps, while imposing a positional restrain on all protein atoms with a force constant that was gradually decreased from 2500 kJ mol⁻¹ nm⁻² to zero. After the first 50 ps of thermalization, we simulated each protein at each of the two temperatures considered (308 K and 373 K) for an additional 10 ns. The simulations were carried out at constant temperature and constant atmospheric pressure, removing the translation of the center of mass every 10 ps. Storage of the coordinates, velocities, and energy terms was done every 50 fs.

Radius of gyration

We compute this shape parameter using the following equation

(1)

considering only the coordinates of the C_α-atoms of all N residues. The radius of gyration gives an estimate of the characteristic volume of a globular polymer, which is inversely related to its compactness.

Backbone dihedral configurational distance

To analyze the backbone configurational difference between two sampled structures A and B along the trajectory we consider the distance based on their backbone dihedral angles (φ,ψ)

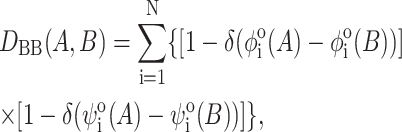(2)

where δ is the Kronecker delta-function. In computing D_BB we take into account only proper dihedral angle transitions, i.e., connecting two potential energy minima, as defined in the GROMOS96 43A1 force field, neglecting vibrational fluctuations within a minimum. Therefore, for each angle , the reference value is that of the corresponding minimum in the potential well, namely .

In our analyses we have considered every fifth configuration in each trajectory and computed maps relative to a length of at most 7 ns. This combination is the best possible compromise, which leads to plots with a good enough resolution, while keeping the data sets within size limits that can be handled.

Configurational shape distance

Another type of configurational distance between two structures A and B used in our analyses of the trajectories rests on the following equation (Pliska and Marinari, 1993)

(3)

with

(4)

representing the distance, within a given configuration, between the i^th and the j^th C_α-atoms, whose coordinates are given respectively by and . Therefore, D₄(A,B) compares all possible intramolecular backbone distances between pairs of C_α-atoms in A with all corresponding distances in B, thus providing a measure of the conformational distance more responsive to overall structural changes compared to more commonly used global parameters like root mean square deviation (RMSD) of the C_α-atoms or radius of gyration.

Free-energy landscapes

To achieve a two-dimensional representation of the FEL, we define the probability of finding the system in a given valley α characterized by the value Q_α of some quantity of interest, as proportional to exp(−βF_α), where F_α is the free energy characterizing that state. Because the system is thought to reach quasiequilibrium within the valley, one can obtain a picture of the FEL computing the probability P(Q) and plotting the quantity −ln P(Q). Thus, to obtain a two-dimensional map we compute the joint probability P(Q_α,E) of finding the system in a state characterized by Q_α and a value E for the total nonbonded interaction energy, each probability P(Q_α) and P(E) being obtained from the corresponding histograms computed from the atomic trajectories.

The distance between two contour lines a and b can easily be converted into a free-energy difference using the following equation

(5)

where p_A and p_B represent the probability of being, respectively, in state A or B. Any global parameter can be used to describe the FEL such as the percentage of native contacts, atomic RMSD, radius of gyration, configurational distance D₄ (Eqs. 3 and 4), backbone dihedral configurational distance D_BB (Eq. 2), or fluctuations along principal components (Amadei et al., 1996).

Characteristic path length

Generally speaking, the characteristic path length (CPL) (Watts and Strogatz, 1998) is defined as the average number of contacts needed to connect, along the shortest possible path, two randomly chosen C_α-atoms. We consider two residues to form a contact if they interact attractively and are within a given cut-off distance. The assignment is discrete, namely 1 if both conditions are fulfilled and 0 otherwise. Therefore, for any two residues in a given configuration, the path length corresponds to the number of attractive electrostatic contacts separating them, including also H-bonds between side chains and backbone. If averaged over all possible residue pairs, the CPL measures the degree of electrostatic connectivity of the fold and inversely relates to its thermodynamic stability. In the extreme case of a fully unfolded structure, the CPL has a value of the order of the chain length.

Dihedral-angle structural-distance maps

A convenient way to obtain information on the backbone configurations explored during a simulation is to represent in two-dimensional plots the dihedral angle conformational distances. The map relative to a given distance range, defined by values of D_BB (Eq. 2) between two integers m and n, is obtained by reporting on both axes the simulation time and marking with a dot all corresponding configuration pairs that lie within that distance interval.

The regions away from the main diagonal provide information on the diffusion of the system in the configurational space, indicating if it tends to return at later times in the vicinity of a previously visited configuration. Instead, the pattern that the maps display along the diagonal gives a measure of the roughness of the landscape. More precisely, the appearance of triangular spots in this region marks the presence of free-energy troughs that the system has visited during the simulation and in which it has thermalized for a while, before jumping to another configurational substate. Measuring the time τ spent in a particular well, one can estimate the height of the activation barrier B that the system has to overcome to leave it. This can be done using Arrhenius' law

(6)

where τ₀ is the microscopic time step used in the simulation.

RESULTS AND DISCUSSION

The energy of a protein is a function of the topological arrangement of its N atoms. In exact terms, it is described by a hypersurface in the 3N-dimensional configurational space, with a very large number of minima separated by activation barriers and saddle points. Each valley in this hypersurface pertains to a particular conformation of the protein. This situation closely resembles that found in finite spin glasses (Kirkpatrick and Thirumalai, 1988).

Free-energy landscapes

Due to the high dimensionality of the configurational space of a protein, it is impossible to give a representative picture of its FEL as a function of the entire phase space. To overcome this problem, we introduce here an approach that allows the representation of the landscape in a lower dimensional subspace. To do this we use few simple collective entities, also referred to as global parameters, which allow the identification of ensembles of subconformations belonging to a given structural state (e.g., native or molten globular). The basic concepts underlying this approach are given in the Methods section. Here we wish to stress that a two-dimensional representation of a high-dimensional hypersurface, as the FEL of a protein, is certainly highly degenerate. This means that what appears as a well-defined minimum, in reality is the result of the superposition of a series of minima that cannot be resolved by the chosen pair of parameters. In other words, we have to take into account the stratification of the landscape arising from the low dimensionality of the representation. One way to partially overcome this difficulty is to report, on the same graph, the contour plot of the free energy and the projection of the simulated trajectory onto the same plane. This approach allows the identification of valleys that correspond to temporally and possibly structurally distinct subsets of structures visited during the simulation.

Before analyzing protein- and temperature-specific features of our FEL representations, we wish to discuss the advantages deriving from the use of the conformational distance D₄ (Eqs. 3 and 4) compared to other, more conventional, global parameters. Comparing the graphs shown in Figs. 1 and 2, it is clear that the contour plots based on the conformational distance D₄ (Fig. 1) resolve a larger number of local minima compared to those obtained using the radius of gyration (Eq. 1, Fig. 2). Other global parameters have been tested, such as RMSD, fraction of native contacts, or dihedral angle conformational distance D_BB (Eq. 2), but they give comparably low-resolution representations of the FEL. The projection of the trajectories onto the contour plots depicted in Fig. 3 provides additional evidence for the adequacy of D₄ in resolving single potential wells visited during the simulation, as discussed below.

FIGURE 1.

Free-energy landscape representations computed from the 10-ns simulations on meso-Rd (left panels) and thermo-Rd (right panels) at 308 K (top panels) and 373 K (bottom panels). On the abscissas we plot the conformational distance D₄ from the structure at time zero (Eqs. 3 and 4) and on the ordinates the total nonbonded interaction energy E. According to the bar codes, the different colors of the contour lines refer to distinct values of the negative natural logarithm of the joint probability P(D₄,E) of finding the system in a state characterized by a given pair of values of D₄ and E (see Methods for more details).

FIGURE 2.

Representations of the free-energy landscapes for meso-Rd (left panels) and thermo-Rd (right panels) calculated from the 10-ns trajectories at 308 K (top panels) and 373 K (bottom panels). The contour plots were computed from the radius of gyration based only on the C_α-atoms (abscissas) and the total nonbonded interaction energy (ordinates). Other details are given in the legend to Fig. 1 and under Methods.

FIGURE 3.

Projection of the 373-K atomic trajectories onto the FEL representations depicted in the bottom panels of Fig. 1 (top panels in this figure) and Fig. 2 (bottom panels in this figure). To reduce the crowding of the graphs, the trajectories have been averaged in blocks of 50 frames, corresponding to 2.5 ps, and splined. In the graphs on the left (meso-Rd) the entire trajectory is divided into three major time frames 0.05–1.6 ns (red), 1.6–3.35 ns (cyan), and 3.35–10.05 ns (magenta). Furthermore, we outline segments of the trajectory that insist on local minima of the landscape based on D₄ and the total nonbonded interaction energy. They are 0.43–0.835 ns (green), 0.975–1.025 ns (blue), 1.2–1.35 ns (yellow), 1.425–1.5 ns (black). In the graphs referring to thermo-Rd (right panels the different colors used for the projection of the trajectories correspond to the four contiguous segments 0.05–1.3 ns (red), 1.3–1.55 ns (cyan), 1.55–2.125 ns (yellow), and 2.125–10.05 ns (magenta). More details are given in Table 1.

The low-dimensional representations of the FEL reported in Figs. 1 and 2 show that, in the case of thermo-Rd (right panels), increasing the temperature from 308 K (top) to 373 K (bottom) leads to a more structured landscape and to a larger area within the outmost contour lines. The latter difference underlies a modest increase in entropy, consistent with a greater flexibility of the molecule, which allows it to sample new configurations not visited at 308 K. For meso-Rd the changes brought about by temperature on the FEL are definitely more pronounced (Figs. 1 and 2, left panels). The surface within the outmost contour lines clearly increases with heating, thus implying that during the simulation the system explores a larger volume of the configurational space, thanks to an augmented thermal energy. As already underlined, the FEL representations based on D₄ are far more structured than those resting on the radius of gyration. We therefore concentrate on the former. At 308 K (top left graph in Fig. 1) the trajectory of meso-Rd is confined within a small conformational region displaying a single valley, centered around (0.1,−2270) and a shallow well around (0.25,−2150). During the first 3 ns of the simulation at this temperature, the trajectory jumps several times between them (data not shown) and thereafter stabilizes itself in the deeper valley. Compared to that at 308 K, the FEL at 373 K (bottom left panel in Fig. 1) is much rougher and extends toward higher conformational distances from the reference structure. We postulate that the configuration corresponding to the 308 K free-energy minimum becomes unstable when the temperature increases above a critical value, thus initiating the transition toward a looser globular state reported previously (Lazaridis et al., 1995; Tavernelli and Di Iorio, 2001).

More detailed information about the time evolution of the systems is obtained from the projection of the trajectories onto the FEL representations depicted in Fig. 3, where we use different colors for various time windows. First of all, it is quite clear that the trajectory projections onto the contour plots based on the radius of gyration (bottom panels of Fig. 3) do not provide much information about the time evolution of the protein conformation. Instead, the trajectory projections onto the D₄-FEL representations (top panels in Fig. 3) are quite informative. We start from thermo-Rd (top right panel in Fig. 3). The first 1.3 ns of the trajectory are depicted in red. Within 85 ps thermo-Rd finds the first shallow minimum centered around (0.06,−2515), but leaves it quite rapidly to start exploring the nearby space until, at t ≅ 0.5 ns, it finds the second trough, centered around (0.13,−2550). Between 1.3 ns and 1.55 ns (cyan) there is a diffusion toward large values of D₄, followed by a return to the second well for almost 0.5 ns (yellow). The final part of the trajectory (magenta) is confined within the deepest minimum around (0.24,−2335). As already stated, the return to the same trough during distinct time frames does not necessarily imply a return to the same subset of structures, but we will come again to this point.

The time evolution of meso-Rd at 373 K is definitely more tortuous, as shown in the upper left panel of Fig. 3. The system needs >0.4 ns to reach the first minimum centered around (0.22,−2260) where it remains for ∼0.4 ns (green). Thereafter it finds an escape path toward other regions of the phase space characterized by higher values of the distance D₄. A new basin of attraction for the trajectory develops, which is divided into two subminima centered respectively around (0.61,−2585) and (0.64,−2245). From all the structural parameters computed from our trajectories, including those previously reported (Tavernelli and Di Iorio, 2001), we can exclude that this basin corresponds to an unfolded state of the molecule. However, it is reasonable to assume that it represents an intermediate step toward unfolding. The actual transition between the minimum centered around (0.22,−2260) and the rightmost basin is quite tortuous, with several local minima (blue, yellow, black) along a path that involves structures with high values of the total nonbonded interaction energy, up to roughly −1200 kJ/mol compared to an average of ∼−2300 kJ/mol. This indicates that, within the trajectory being considered, the activation barrier for this transition should be of the order of a few hundreds kJ/mol.

Because most of the simulation time is spent within the final wells found by the two systems (roughly 78% and 67%, respectively, for thermo-Rd and meso-Rd) the relative weight of the first 30–40% of the trajectories in the FEL representations depicted in Fig. 1 is somewhat limited. To gain more details about the transition from the starting to the final states, we have computed—from D₄ and the total nonbonded interaction energy—FEL contour plots using only the first 4 ns of our simulations at 373 K. From the segments of the projected trajectories confined within the three innermost contour lines of these plots (not shown), we could get rough estimates for the time spent in the various wells. The results of this analysis are reported in Table 1 and show that, even when the trajectory is confined within a minimum in the FEL, meso-Rd tends to escape from it quite frequently. In the best case, i.e., the double deep around (0.61,−2585) and (0.64,−2245), the projection of the trajectory onto the FEL of meso-Rd is confined within the three innermost contour lines for only 50% of the time, in 19 frames lasting on average only 18.3 ps. The escapes from the minimum involve also quite remote regions of the FEL, as shown by the magenta line in the top left panel of Fig. 3, thus indicating that the system is still diffusing through the configurational space. The situation for thermo-Rd is completely different. Here, except for the time span between 1.3 and 1.55 ns, where the system explores structures characterized by large values of D₄ (cyan traces in the top right panel of Fig. 3), the projection of the trajectory onto the D₄-FEL representation is mostly confined within the central region of each valley.

TABLE 1.

Evolution of the 373 K trajectories based on their projection onto D₄-FEL representations computed from the first 4 ns of our simulations

	Segment no. & color	From	To	Center of region	Visited	For a total of	Segment fraction
Thermo	1 red	0.050 ns	1.300 ns	0.13,−2550	6 times	0.415 ns	0.33
	2 cyan	1.300 ns	1.550 ns
	3 yellow	1.550 ns	2.125 ns	0.13,−2550	1 time	0.453 ns	0.79
	4 magenta	2.125 ns	4.050 ns	0.24,−2335	11 times	1.903 ns	0.99
Meso	1 red	0.050 ns	1.600 ns
	1a green	0.430 ns	0.835 ns	0.22,−2260	3 times	0.130 ns	0.32
	1b blue	0.975 ns	1.025 ns	0.28,−2470	1 time	0.050 ns	1.00
	1c yellow	1.200 ns	1.350 ns	0.36,−1895	1 time	0.150 ns	1.00
	1d black	1.425 ns	1.500 ns	0.43,−1970	1 time	0.075 ns	1.00
	2 cyan	1.600 ns	3.350 ns	0.64,−2245	13 times	0.555 ns	0.32
	3 magenta	3.350 ns	4.050 ns	0.61,−2585	19 times	0.349 ns	0.50

For each segment we give the total span and the time spent by the system in a specific region of the landscape centered roughly at the given coordinates, along with its fractional duration relative to the segment length. For thermo-Rd such regions correspond always to well-defined minima in the landscape, for meso-Rd this applies only to the regions around coordinates (0.22,−2260), (0.64,−2245), and (0.61,−2585). In such cases, the fractional time spent in a deep is computed considering the trajectory segments whose projection lies within the three innermost contour lines. Colors correspond to those used in Fig. 3.

Characteristic path length

As described in the Methods section, the characteristic path length is a parameter that describes the overall degree of electrostatic connectivity among the various residues in a protein. Its value increases as the thermodynamic stability of the system decreases. Fig. 4 illustrates the distributions of the CPLs calculated from the trajectories (0.05–10.05 ns) of both rubredoxins at 308 K and 373 K.

FIGURE 4.

Distributions of the characteristic path length computed from the atomic trajectories at 308 K (dashed) and 373 K (solid) of meso-Rd (top) and thermo-Rd (bottom) in the time range 0.05–10.05 ns. The insert in the top graph shows an enlargement of the distribution in the CPL range between 4 and 8.

Clear differences between the two proteins emerge also from this analysis. Although thermo-Rd reacts to the increase in temperature by decreasing its CPL, the contrary is true for meso-Rd, at least for the major peak of its bimodal distribution curve. In addition, meso-Rd at 373 K shows a nonzero probability for configurations with very high CPL (see insert in the upper panel of Fig. 4), which are never observed along the thermo-Rd trajectories. We think that they correspond to unstable spatial arrangements, which can eventually initiate an unfolding process. Within the mainframe of the “proteinquake” model (Ansari et al., 1985) described in the Introduction, this would imply that during the simulation at 373 K meso-Rd visits structural substates that—although rare—increase substantially the probability of a conformational transition.

Dihedral-angle structural distance maps

To analyze the dynamics of the backbone we have monitored changes of the dihedral angle pairs (φ,ψ). The distance maps shown in Fig. 5 rest on the backbone dihedral configurational distance D_BB (Eq. 2) computed on all configuration pairs that can be made considering every fifth configuration in our trajectories between 0.05 and 7.05 ns, as already stated under Methods. The last 3 ns have been analyzed separately and do not add any additional information. The graphs in Fig. 5 refer to distances in the ranges 5–7, 8–9, and 10–11, the richest in information.

FIGURE 5.

Backbone structural-distance maps based on differences in the dihedral angles (φ,ψ) computed with Eq. 2 from the simulations at 308 K (left panels) and 373 K (right panels). The top row of the figure refers to meso-Rd, the lower to thermo-Rd. In the 308 K graphs, the gray and black halves correspond respectively to configurations that differ by 5–7 and 8–9 backbone dihedral transitions. In the plots computed from the 373-K trajectories, gray refers to the distance range 8–9 and black to 10–11. A dot in the graph implies that the configurations at the corresponding simulation times are characterized by a value of the distance D_BB in the selected range. In the bottom right graph the lines mark the following times: 0.25 ns, 0.55 ns, 1.1 ns, 1.3 ns, 1.55 ns, 2.1 ns, 2.4 ns, 3.4 ns, 4.05 ns, 4.4 ns, and 5.6 ns.

The triangular patterns present along the diagonal in both halves of the bottom left map of Fig. 5 indicate that thermo-Rd at 308 K attempts repeatedly a trapping into a region of the conformational space characterized by a high self-similarity between structures. To a moderate extent it even manages to do so after the first 2.6 ns, as delineated by the large triangular region barely visible in the 8–9 distance map (black). It seems, however, that the low temperature hampers this process. In the case of meso-Rd the 308 K trajectory evolves with frequent jumps among regions of the conformational space, delineated by the numerous triangular areas along the diagonal of the maps and by the presence of frequent rectangular spots away from the diagonal (top left graph in Fig. 5). In general, the map indicates that meso-Rd at 308 K stays throughout the simulation within a region of the conformational space characterized by a fairly high self-similarity. This suggests a rather smooth, broad, and well-defined free-energy minimum.

Increasing the temperature to 373 K produces opposite effects in the two proteins. There is a sensible decrease in the number of similar structures within the trajectories of meso-Rd, as suggested by an almost complete lack of patterns in the maps referring to this protein (top right plot in Fig. 5). Clearly, at higher temperature the increased thermal energy allows a more efficient sampling of the phase space, which leads to a lower probability of encountering similar structures along the atomic trajectories. This is related to the overall change of the FEL upon heating the system to 373 K that, in the case of meso-Rd, brings about the formation of a new global minimum different from the one pertaining to the native structure at low temperature. This picture is fully consistent with the results discussed so far and previously reported in the literature (Eidsness et al., 1997; Tavernelli and Di Iorio, 2001 and references therein). Instead, the large triangular regions at longer simulation times in the distance maps of thermo-Rd at 373 K (bottom right plot Fig. 5) point to a “funneling” toward a subset of increasingly self-similar configurations.

It is important to note that some of the maps reported in Fig. 5 display small triangles along the diagonal that are comprised within bigger ones. This is a proof for the presence of small energetic deeps within large ones, consistent with a hierarchical organization of the configurational space.

A comparison of the distance maps depicted in Fig. 5 with the projections of the trajectories onto the low-dimensional representations of the FEL shown in Fig. 3 should help in finding out how much the return to a minimum in the landscape corresponds also to a revisiting of the same conformational subspace described by the distance D_BB. The low-temperature distance maps (left panels of Fig. 5) are fully consistent with the low structure displayed by the FEL shown in the top row of Fig. 1. The opposite applies to meso-Rd at 373 K, whose FEL is rather complex (bottom left panel in Fig. 1). Accordingly, the D_BB distance maps display very little structure (top right panel of Fig. 5). A comparison between the data of Fig. 3 and those of Fig. 5 is most informative in the case of thermo-Rd at 373 K because: i), its distance maps display a trend toward a conformational space characterized by a high degree of self-similarity in the number of backbone dihedral transitions; and ii), there are several well-defined triangular patterns along the diagonal that appear to correspond to conformational subspaces visited in different trajectory frames. The bottom right graph of Fig. 5 allows us to identify the following trajectory frames: 0.25–0.55 ns, 1.1–1.3 ns, 1.55–2.1 ns, 2.1–2.4 ns, 3.4–4.05 ns, and 4.4–5.6 ns. In Fig. 6 we show the projection of these trajectory segments onto the FEL computed from the conformational distance D₄ and the total nonbonded interaction energy. From the D_BB-distance map (bottom right plot in Fig. 5) one expects the trajectory frames 0.25–0.55 ns and 1.1–1.3 ns to belong to different regions of the conformational space. Accordingly, the projection of these frames onto the FEL representation (respectively black and cyan traces in Fig. 6) does not display any significant overlapping even though they insist on the same local minimum. The whole time range between 1.1 ns and 2.1 ns forms a structured triangular pattern in the D_BB-distance map and indeed the cyan (1.1–1.3 ns) and magenta (1.55–2.1 ns) traces overlap to a considerable extent. However, in Fig. 6 the magenta trace (1.55–2.1 ns) partially overlaps also with the black trace (0.25–0.56 ns), in disagreement with what can be inferred from Fig. 5. From 2.1 ns onwards the distance map based on the number of backbone dihedral transitions points to a funneling toward the same region of the conformational space. This is in full agreement with the data depicted in Fig. 6 and in the top right panel of Fig. 3 because the entire trajectory segment between 2.1 ns and 10.05 ns insists on the potential well centered around (0.24,−2380). Combining the information given by the D_BB distance maps with the projection of the trajectories on the FEL it is therefore possible to estimate to what extent a minimum in our low-dimensional representation of the landscape corresponds to temporally and structurally distinct subset of structures. Analyzing the whole body of our simulations we must conclude that the correlation between the distance maps based on D_BB and the low-dimensional representations of the FEL shown in Fig. 1 is good only when the system thermalizes within a free-energy minimum for long trajectory segments. To the contrary, the distance maps based on D_BB lose structure whenever the system continuously jumps in and out of a deep in our representation of the FEL, as pointed out by the data on meso-Rd at 373 K. This is easy to rationalize because the thermalization time is related to the height of the activation barrier that the system has to overcome to escape from a minimum. Therefore, the diffusion through a highly corrugated FEL, with its many shallow minima separated by small barriers, must be characterized by short thermalization times within a deep, leading to a lower degree of similarity in the D_BB distance maps.

FIGURE 6.

Projection of trajectory segments from the simulation on thermo-Rd at 373 K selected on the base of the distance map depicted in the lower right panel of Fig. 5 and corresponding to 0.25–0.55 ns (black), 1.1–1.3 ns (cyan), 1.55–2.1 ns (magenta), 2.1–2.4 ns (red), 3.4–4.05 ns (blue), and 4.4–5.6 ns (yellow). Other details are as in Fig. 3.

Concluding remarks

Our low-dimensional representation of the FEL of a protein based on the conformational distance D₄ and the total nonbonded interaction energy, combined with other analyses of global structural parameters, allows a fairly detailed description of three fundamental features, namely: a), the roughness of the landscape; b), the diffusion profile of MD trajectories through the FEL; and c), the hierarchical organization of conformational substates. Based on this information, the differences in the dynamic properties between the two rubredoxins investigated here and in previous reports (Lazaridis et al., 1995; Tavernelli and Di Iorio, 2001) can be better rationalized. Particularly interesting is the comparison of the 373 K FEL of meso- and thermo-Rd, the former highly corrugated and the latter with deep minima. The new findings presented here and the link between structural flexibility and frustration that we have proposed previously (Tavernelli and Di Iorio, 2001) substantiate the connection between roughness of the FEL and frustration (Bryngelson et al., 1995; Wolynes and Eaton, 1999; Wolynes et al., 1996).