A Mesoscopic Model for Protein-Protein Interactions in Solution

Abstract

Protein self-association may be detrimental in biological systems, but can be utilized in a controlled fashion for protein crystallization. It is hence of considerable interest to understand how factors like solution conditions prevent or promote aggregation. Here we present a computational model describing interactions between protein molecules in solution. The calculations are based on a molecular description capturing the detailed structure of the protein molecule using x-ray or nuclear magnetic resonance structural data. Both electrostatic and van der Waals interactions are included and the salt particles are explicitly treated allowing investigations of systems containing mono-, di-, and trivalent ions. For three different proteins—lysozyme, α-chymotrypsinogen, and calbindin D_9k—we have investigated under which conditions (salt concentration, ion valency, pH, and/or solvent) the proteins are expected to aggregate via evaluation of the second virial coefficient. Good agreement is found with experimental data where available. Calbindin is investigated in more detail, and it is demonstrated how changes in solvent and/or counterion valency lead to attractive ion-ion correlation effects. For high valency counterions we have found abnormal trends in the second virial coefficient. With trivalent counterions, attraction of two negatively charged protein molecules can be favored because the repulsive term is decreased for entropic reasons due to the low number of particles present.

INTRODUCTION

Protein-protein interactions in aqueous solution are of fundamental biological interest and a complete description of the forces acting between proteins and other biomolecules is necessary in an attempt to understand the processes taking place in the living cell. Many of these processes involve weak noncovalent interactions causing the formation of both temporary and more permanent supramolecular structures. The list of examples can be made long: the binding of atomic ions or small molecule cofactors, signal peptides binding to receptor proteins, formation of biological membranes, protein-protein aggregation, etc. In a crystallographic context it is of particular interest to investigate under which conditions the proteins associate to form crystals suitable for diffraction experiments. It is well-known that aggregation can be induced by changes in pH, the salt concentration, valency of ions, or the polarity of the solvent. Presently these matters largely rely on experimental findings but as shall be shown here, valuable information can be derived using computational methods.

The second virial coefficient, B₂, is a useful indicator of the overall interaction between two molecules and its importance in describing protein aggregation has been stressed by several workers (Neal et al., 1999; George and Wilson, 1994). George and Wilson have shown that B₂, to form crystals suitable for diffraction studies, must lie within a narrow interval—the so-called crystallization slot. Second virial coefficients for large molecules can be measured using light- and/or neutron scattering, but is also readily obtained from Monte Carlo or molecular dynamics simulations (Allahyarov et al., 2002). During the years more and more computing power has become available and simulations of a single protein in solution has become a standard approach in theoretical biochemistry. However, to perform a Monte Carlo or molecular dynamics simulation based on an atomistic representation of, say, two proteins in a salt solution, in an attempt to calculate the second virial coefficient, is still beyond reach. The problem comes from the fact that B₂ requires a sampling of all protein separations and orientations, which is a time-consuming process compared to the simulation of one single protein molecule. Thus, to make any progress one has to resort to more coarse-grained models.

A significant simplification is obtained if the water molecules are replaced by a structureless dielectric continuum. This means that the only remaining molecules of the solvent are salt particles. However, systems with high salt concentration still require substantial computation times and to overcome this, screened Coulomb potentials are often utilized (Carlsson et al., 2001). The screened Coulomb approximation usually works well for weakly charged macromolecules in monovalent salt solution, but in solutions with multivalent salt and/or low dielectric permittivity it becomes less applicable. In such cases, salt particles must explicitly be taken into account to correctly reflect the electrostatic interactions in the system.

As for the protein description, it is crucial to capture the discrete charge distribution originating from (de-)protonated amino acids. Specific angular orientations are not without importance for the electrostatic interactions and treating the protein as an object with a central net charge only has been shown to fail (Allahyarov et al., 2002). Several workers have incorporated discreteness by placing point charges within or on the surface of a large sphere (Carlsson et al., 2001; Allahyarov et al., 2002). This approach assumes that the excluded volume of the protein possesses spherical symmetry which, even for globular proteins, may be a too-crude approximation considering that, at short protein-protein separations, attractive van der Waals interactions can be highly angular-dependent (Asthagiri et al., 1999). With van der Waals interactions we mean the sum of quantum mechanical dispersion forces, thermally averaged dipole-dipole, and dipole-induced dipole terms (Israelachvili, 1991). Between atoms or small molecules, the van der Waals term is relatively short-ranged, with a potential proportional to 1/r⁶. However, when integrated for large (spherical) molecules it becomes appreciably more long-ranged, scaling by ∼1/r at short and intermediate separations (Israelachvili, 1991). Thus, when incorporating van der Waals interactions it is necessary to either include the integrated term assuming spherical symmetry or explicitly evaluate the 1/r⁶ term for all atomic components in the two proteins.

In this work, we have chosen the latter approach, which captures the detailed structural properties of the protein but at the same time is more computationally demanding. The electrostatic interactions have been evaluated with discrete charges on all titratable amino acids and explicit salt particles and counterions in the solution. Three proteins have been studied: lysozyme, chymotrypsinogen, and calbindin. All three are structurally well-defined, and for lysozyme and chymotrypsinogen, experimental data is readily available in the literature. Calbindin is included as a good representative of a highly charged protein, and in addition, there exists a wealth of experimental data for its calcium binding properties (Linse et al., 1988, 1991; Svensson et al., 1991) and its ionization behavior is also well-documented (Kesvatera et al., 1999).

METHODOLOGY

Interactions

We use a dielectric continuum model for the solution assuming that all charges are uniformly screened by a constant relative permittivity with a value equal to that of pure water. The protein is modeled as a collection of hard spheres representing either single atoms or whole amino acids. A sphere in this model will carry an average charge determined by the pH and pK_a of the particular amino acid. The average charges on the titratable sites have been determined in separate Monte Carlo (MC) simulations of a single protein, in which the amino acids are allowed to titrate. Furthermore, attractive van der Waals interactions between all amino acids are explicitly taken into account.

The choice of a uniform relative permittivity has been and still is very much debated (Antosiewicz et al., 1994, 1996), the main argument being that the charges, at least within the same protein, should be scaled with a much lower value than that of water. This is in principle true but since most charges are located in the outer polar regions of the protein, the effect might be smaller than at first anticipated. Recent experimental and theoretical studies of the ionization behavior of calbindin does not seem to support the idea of a low dielectric permittivity of the protein interior (Spassov and Bashford, 1998; Kesvatera et al., 2001), and the best agreement between experiment and theory is obtained with a high uniform dielectric permittivity.

The objective of the MC simulations is to calculate the free energy change associated with bringing two protein molecules together in an aqueous salt solution. This free energy of interaction or potential of mean force, w(r), must take into account changes in energy and entropy originating from the solvent, the ions, and the proteins. The energy of interaction can be split into contributions from short-range repulsion (hs), electrostatics (el), and van der Waals (vdW) terms, and the interaction between any two sites can be written as

(1)

The hard-sphere (hs) term accounts for the repulsion arising when the electron clouds from two atoms or molecules come into contact. An exact description of this contribution requires a complex quantum mechanical treatment, and hence the simpler hard-sphere term is usually applied as

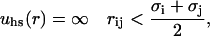(2)

where σ_i is the diameter of site i. The electrostatic term includes Coulombic interactions between charged sites, and in the dielectric continuum approximation it can be written as

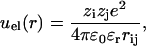(3)

where ɛ_r is the relative dielectric permittivity, z_i the valency of site i, r_ij the site-site distance, e the electron charge, and ɛ₀ the permittivity of vacuum.

To describe the short-range interaction between two protein molecules we invoke a van der Waals-type interaction,

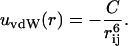(4)

Here C determines the magnitude of the attraction and is related to the Hamaker constant, A (Israelachvili, 1991),

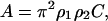(5)

where the ρ_i values are particle densities. As a first approximation, we have decided to use the same C for all amino-acid-to-amino-acid interactions. A straightforward improvement would be to let the amino-acid size affect the interaction, hence one would have a different C_ij for each pair of amino acids. Calculation of Hamaker constants can be done using the Lifshitz theory (Israelachvili, 1991), but detailed knowledge of the electronic properties is required and as a consequence, A is often treated as an adjustable parameter. Fortunately, Hamaker constants are not subject to large variations and for proteins in water, A is ∼3–10 kT (Farnum and Zukoski, 1999) (1 kT = 4.11 × 10⁻²⁷ J at 298.15 K).

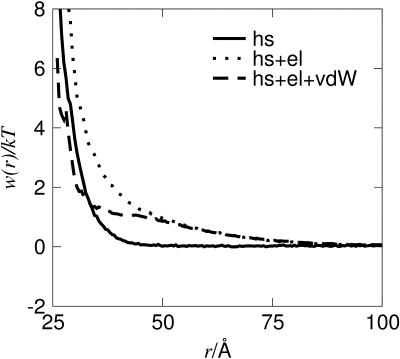
The effects of the described interactions are shown in Fig. 1 and it is to be noted that the effective hard-sphere contribution, reflecting the nonspherical shape of the protein, is surprisingly long-ranged. Including the electrostatic interaction makes the free energy of interaction even more repulsive, whereas the van der Waals term decreases the repulsion at short separation. Unless stated otherwise, the calculations presented in this work include all of the three terms discussed here.

FIGURE 1.

Contributions to the interaction free energy, w(r) from hard-sphere (hs), electrostatic (el), and van der Waals (vdW) interactions for lysozyme at pH 9.0.

One effect not taken into account here is the hydrophobic attraction arising at very short separation. As the two protein molecules approach, the water interactions in between become unfavorable and eventually the solvent seeks to the bulk. This results in a free energy gain and effectively creates an attraction. One can view the hydrophobic effect as a correction to the van der Waals term (Forsman et al., 1997) and the effect can be partially incorporated into the van der Waals term by adjusting the C coefficient. A more stringent alternative would be to include another short-range attractive term into Eq. 1. The argument against these refinements is that the proteins treated here are hydrophilic, and the hydrophobic effect is thus less important.

Model

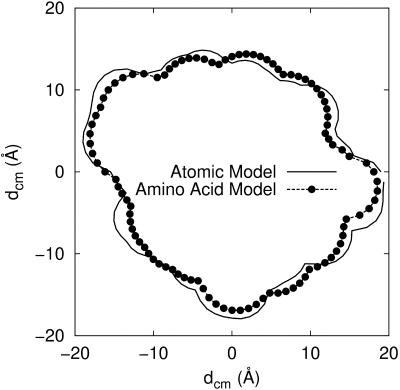
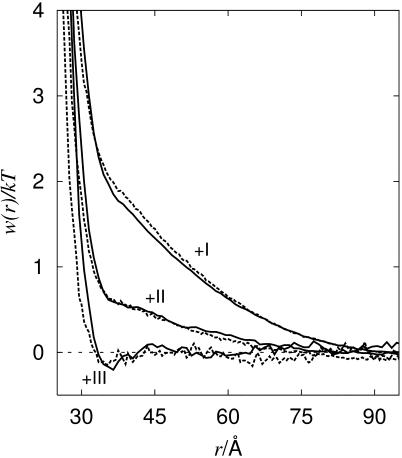
The simulated model system consists of two protein molecules built from spheres immersed in a spherical cell (Fig. 2). To maintain electroneutrality and the desired salt concentration, mobile salt particles with hard-sphere diameters, σ = 4 Å, are added. As for the protein shape, two models have been utilized—both based on structural data obtained from the Brookhaven Protein Databank (PDB). In the first (atomic) model, the protein molecules are mimicked by replacing each nonhydrogen atom in the protein by a hard sphere with diameter σ = 4 Å, which, for chymotrypsinogen, results in >1800 particles per protein molecule. In addition, one has to include the salt particles and in a dilute protein solution with high salt concentration, the total number of interacting particles can add up to many thousands, which leads to lengthy simulations. To improve the simulation efficiency, a slightly simplified mesoscopic model has been developed. Here the atoms in each amino acid are replaced by a single sphere located at the amino-acid center of mass. The size of these spheres are set equal for all residues and adjusted so that the total excluded volume of the protein is equal to that of the atomic model. This amounts to a diameter for the amino-acid spheres of σ = 6.8 Å. Average charges are assigned to the center of each sphere according to the actual pH. Despite this seemingly coarse description, the geometry of the surface is found to be remarkably similar to that of the atomic model (Fig. 3). More important, the simulated potentials of mean force for mono-, di-, and trivalent counterions are virtually identical to the more detailed model as shown in Fig. 4. In the mesoscopic model, the van der Waals term, −C/r_ij⁶, is evaluated for amino-acid pairs and the parameter C must reflect this. With a Hamaker constant of 9 kT, C/kT can be estimated to 25,000 Å⁻⁶ for amino-acid pairs.

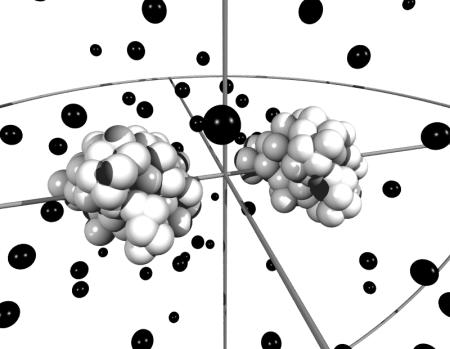
FIGURE 2.

Snapshot from a Monte Carlo simulation of calbindin using the amino-acid model. The black spheres illustrate ions whereas amino acids are depicted by white spheres, clustered to form the two proteins. In the simulations, the proteins are displaced along the z-axis and rotated independently. Ions are displaced in all three directions.

FIGURE 3.

Cross-sections of calbindin using the atomic and amino-acid models. A small ion (diameter 4 Å) is rolled on the surface so as to define the minimum distance to the center of mass.

FIGURE 4.

Free energy of interaction for calbindin (c_p = 0.79 mM) with different counterion valencies (+I, +III, and +III) simulated using the atomic (solid lines) and amino-acid (dashed lines) models. The van der Waals interactions are not included.

The actual charge on an amino-acid residue is pH-dependent, since acidic and basic amino acids can titrate. To specify the average charge on an amino acid at a particular pH, the relevant pK_a values must be known—either from experiment or simulations. The theoretical approach has been shown to be in good agreement with nuclear magnetic resonance studies (Kesvatera et al., 1999, 2001). Hence, we shall use this method to obtain pH-dependent average charges on titratable residues in the proteins. The average net charge of lysozyme, chymotrypsinogen, and calbindin as a function of pH is shown in Table 1.

TABLE 1.

Average net charges, Z on calbindin, lysozyme, and α-chymotrypsinogen at different pH values obtained from Monte Carlo simulation

Calbindin		Lysozyme		Chymotrypsinogen
pH	Z	pH	Z	pH	Z
3.5	3.7	4.5	9.0	3.0	12.9
4.0	1.6	6.0	8.0	4.0	9.2
5.0	−2.2	7.5	6.9	5.3	6.7
6.0	−5.0	9.0	4.9	6.8	5.2
7.0	−6.6	10.0	2.8
8.0	−7.4	10.5	1.5
9.0	−8.0
10.0	−8.8
11.0	−10.6

Monte Carlo simulations

Most simulations were performed in the canonical ensemble using the traditional Metropolis Monte Carlo algorithm (Allen and Tildesley, 1989) supplemented with a few semicanonical simulations of a single protein allowed to titrate (Kesvatera et al., 1999). The energy evaluation for each configuration includes all pair interactions,

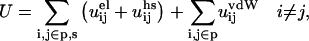(6)

where s and p mean salt and protein particles, respectively. During the MC simulation the proteins are allowed to translate symmetrically along the z-axis and individually rotate around vectors going through their center-of-mass. Mobile ions may translate in any direction. By these random displacements and rotations all possible configurations are explored; if a move leads to an energy decrease, the new state is accepted. If the energy increases, the state is accepted with the probability exp (−ΔU/kT). Proceeding this way, the system eventually reaches equilibrium and its properties can be sampled. The distribution function, ρ(r), is readily obtained by sampling the probability of finding the two proteins at a certain separation. This is directly related to the change in free energy of interaction,

(7)

where the ρ(∞) is determined from the asymptote of ρ(r) and the constant is set to 0. To represent this in a more convenient manner, w(r) can be integrated to yield the second virial coefficient,

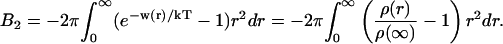(8)

The second virial coefficient comprises the predominant effect of the interaction between two proteins molecules; if B₂ is positive, then there is a net repulsion; and if negative, the net interaction is attractive. B₂ has some interesting properties; it is, in general, rather easy to fit experimental data with a variety of w(r) values with adjustable parameters. At the same time, the virial coefficient will be very sensitive to these parameters. This means that if one is able to produce a potential of mean force without adjusting parameters and if this w(r) reproduces experimental B₂ values, then the underlying physics is probably correct.

RESULTS AND DISCUSSION

Lysozyme

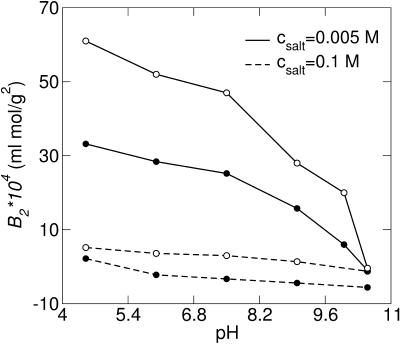
To verify our model we have simulated virial coefficients of lysozyme and compared with experimental data from Velev et al. (1998), who measured B₂ for lysozyme as a function of pH at 5 mM NaCl concentration. We have used an x-ray structure of egg-white lysozyme (Ramanadham et al., 1990) to determine the positions of the amino-acid spheres as explained above. Monovalent counterions are included to maintain electroneutrality and an appropriate amount of 1:1 salt to yield 5 mM is added. The amino-acid charges are assigned for each pH according to simulated pK_a values (Table 1). Each calculation includes 430 million configurations corresponding to a simulation time of ∼20 h on a standard PC. As seen in Fig. 5, reasonable agreement is found considering that we have made no efforts to adjust our parameters to fit the experimental data. At low pH the calculated B₂ values are found to be somewhat higher than those obtained from experiments. One possible explanation is that the ionic strength in the experiment is >5 mM due to residual salt from the protein preparation or from pH-adjusting agents. A higher salt content gives rise to a higher screening of the repulsive protein interactions, which in turn diminishes B₂. This agrees with the observed trend that the simulated data fits better at high pH values. At pH 10.5 the electrostatic repulsion is of minor importance and the van der Waals attraction dominates. Since at this point we perfectly match the experimental data, it can be concluded that the chosen C parameter is indeed reasonable. In fact, the virial coefficient is very sensitive to the C parameter at high pH whereas at low pH it is essentially negligible. For example, doubling the C parameter at pH 4.5 changes B₂ from 61 to 60 ml × mol/g², whereas at pH 10.5, B₂ is decreased from −0.4 to −149 ml × mol/g². This behavior is also evident from Eq. 8, where long-range interactions in general have a larger impact on B₂ than those of short-range.

FIGURE 5.

Measured (solid symbols) and simulated (open symbols) second virial coefficients, B₂, for lysozyme as a function of pH at two different NaCl concentrations—monovalent counterions.

Another possible explanation for the overestimated virial coefficient at low pH is that the charge distribution on the two protein molecules is fixed independently of their separation. It seems reasonable to assume that two positively charged proteins coming in close contact will release protons to reduce their net charge. This is, of course, not possible at all pH values, but if pH is close to the pK_a of some amino acids in the protein, it is certainly a mechanism that will lower the repulsive interaction leading to a reduction of the B₂ (André et al., 2003, unpublished results).

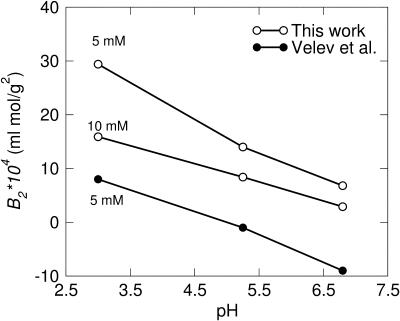
Chymotrypsinogen

Also measured by Velev et al. (1998) are second virial coefficients for α-chymotrypsinogen. This protein is—in a computational context—fairly large, containing 245 residues. The three-dimensional structure (PDB Id: 1CHG) used in the calculations is obtained by x-ray diffraction by Freer et al. (1970). Comparing with measured virial coefficients at 5 mM salt concentration (Fig. 6) shows that our calculations follow the experimental trend, but are more repulsive. However, the system is very sensitive to the ionic strength as illustrated by doubling the salt concentration from 5 mM to 10 mM, effectively decreasing the repulsion. This indicates that at low salt concentrations even trace amounts of residual ions may lower the experimental B₂, making direct comparison with theoretical calculations less accurate. Another explanation of the difference between theory and experiment could be that the protein average charge is set too high. When the two macro molecules come into close contact the titratable sites are perturbed, effectively lowering the net charge. This can be remedied by allowing both proteins to titrate during simulation so as to adjust charges as a function of protein-protein separation.

FIGURE 6.

Measured (solid symbols) and simulated (open symbols) second virial coefficients, B₂, for chymotrypsinogen as a function of pH at 5 mM/10 mM NaCl concentration.

It is to be noted that the chymotrypsinogen interactions are, in general, less repulsive than those between lysozyme, as also observed by Velev and co-workers. One explanation could be the high dipole moment of chymotrypsinogen leading to angular correlations (Velev et al., 1998), but the importance of such dipole-dipole interactions remain left for further study.

Calbindin

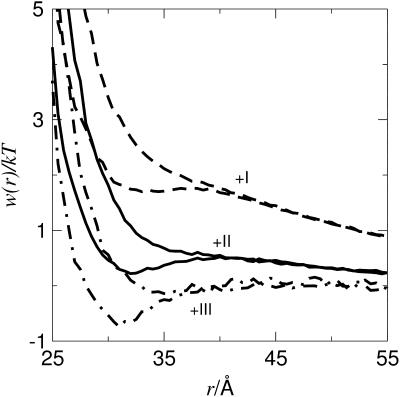
Currently there is no experimental data available for calbindin, but we hope to obtain second virial coefficients for calbindin under a variety of conditions in the near future. Calbindin is considerably smaller than lysozyme and chymotrypsinogen and is thus suitable for more exploratory simulations. The structure of calbindin used in the simulations derives from an x-ray determination of the calcium-free protein (Szebenyi and Moffat, 1986) and the overall charge is −7 at neutral pH; compare to Table 1. In a salt-free environment with only counterions present, we note that B₂ is strongly dependent on the counterion valency. Fig. 7 demonstrates that an increasing valency significantly decreases the repulsion between the proteins. This is qualitatively in accordance with mean field theories (Derjaguin and Landau, 1941; Verwey and Overbeek, 1948), and is a consequence of an increased electrostatic screening from multivalent ions. Note that in the case of trivalent counterions the electrostatics are completely screened and the van der Waals term hence leads to an attractive minimum. This qualitatively explains why proteins are found to precipitate upon addition of even small amounts of multivalent salts.

FIGURE 7.

Free energy of interaction for two calbindin molecules, c_p = 0.79 mM, with various counterions. Graphs both with and without short-range van der Waals interactions are shown.

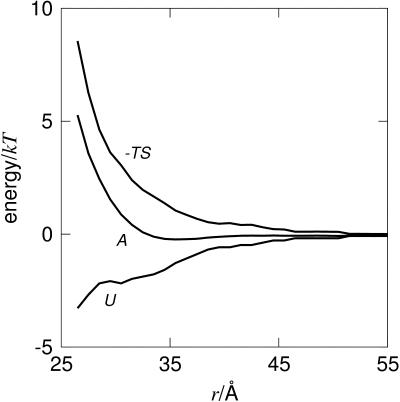
It is illustrative to split the free energy, A(r) = U(r) – TS(r), into the individual contributions from energy and entropy as shown in Fig. 8. The derivatives of these terms give the force acting between the two proteins, that is

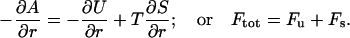(9)

The energetic force component, F_u, is attractive between the two negatively charged proteins, which at first sight might seem counterintuitive. However, this is a general result; for an overall neutral system of charges, the energy will always favor a compaction. Hence, the origin of repulsion is the entropy, and not the energy. This means that the reduced repulsion seen with trivalent compared to monovalent counterions (see Fig. 7) is a direct consequence of the fact that the number of particles has been reduced by a factor of three. Thus, one can favor attractive interactions by decreasing the entropic term. Similarly, one can also strengthen the attraction by favoring the energy term. One simple way to do this is by lowering the solvent polarity and hence the dielectric constant, which substantially enhances the energy term. From an experimental point of view, a gradual change of the dielectric constant can be achieved by addition of methanol which is miscible with water in all proportions. As a matter of fact, this is a well-known method for precipitating proteins, although the underlying mechanism has not been fully understood. Fig. 9 shows how the potential of mean force for a system containing trivalent counterions can display a net attraction, even though no van der Waals forces are included. Thus, a moderate reduction of the solvent polarity leads to a free energy minimum and eventually to a precipitation of the protein. This is a well-known phenomenon in colloid chemistry and is usually discussed in terms of ion-ion correlations (Guldbrand et al., 1984; Jönsson and Wennerström, 2001). When the electrostatic coupling strength is increased by increasing the valency or lowering the dielectric permittivity, it is accompanied by a strong accumulation of counterions close to the protein. In particular, trivalent counterions will be found very near the protein surface; however, they will not be bound in a chemical sense.

FIGURE 8.

The interaction free energy (A), energy (U), and entropy (−TS) for a solution of calbindin with trivalent counterions. The van der Waals interactions are not included.

FIGURE 9.

Interaction free energy for two calbindin molecules, 0.79 mM, with trivalent counterions at different dielectric constants, ɛ_r. The van der Waals interactions are not included.

Increasing the salt concentration is also known to induce protein aggregation and in the case of monovalent ions a relatively high amount is required to effectively reduce the repulsion. As expected, divalent counterions more readily support salt-induced aggregation as is illustrated in Fig. 10. In the monovalent case, a minimum in w(r) occurs at a salt concentration of ∼0.1 M, whereas for divalent counterions, this minimum is already found at ∼0.005 M salt. From the second virial coefficient, Fig. 11, one can note that even though an attractive minimum occurs in w(r), B₂ still remains positive.

FIGURE 10.

Free energy of interaction for two calbindin molecules, 0.79 mM with mono- (top) and divalent (bottom) counterions at various 1:1 salt concentrations (mM).

FIGURE 11.

Second virial coefficient, B₂ for calbindin, c_p = 0.79 mM, as a function of counterion valency (+II/+III) and 1:1 salt concentration.

Proteins with trivalent counterions, however, show a different behavior. Here the second virial coefficient is increased when 1:1 salt is added, which is in direct conflict with predictions from the DLVO theory (Derjaguin and Landau, 1941; Verwey and Overbeek, 1948). The origin of this effect stems from a competition of mono- and trivalent counterions. The latter accumulate close to the charged protein and give rise to an efficient screening. However, when more salt is gradually added, the monovalent counterions will replace the trivalent ones with a concomitant reduction of the protein screening. A similar behavior has been seen in DNA solutions (Khan et al., 1999).

It is to be noted that in these calbindin simulations a cell radius of 100 Å is used, which is adequate for systems where the protein-protein interactions are screened. However, in cases with no or very low 1:1 salt concentration, an artificial boundary effect may interfere and change the numerical results. This can be remedied by increasing the cell radius, but unfortunately this drastically increases the computation time. However, the general trends are preserved, and in cases with di- and trivalent ions, this effect is of no importance.

CONCLUSION

The protein model presented in this article includes electrostatic and van der Waals interactions, while at the same time it takes the specific protein structure into account. Considering the experimental uncertainties, calculated second virial coefficients for lysozyme and chymotrypsinogen are in good agreement with measurements. In the case of low protein net charge the agreement is actually very good, indicating that the magnitude of the attractive van der Waals term is reasonably chosen. The agreement with experiment can be improved by, for example, including an additional short-range attraction mimicking the hydrophobic interaction. Also, letting the proteins titrate during simulation allows the net-charge to vary as a function of protein-protein separation, effectively decreasing the electrostatic repulsion.

Calbindin has been simulated more intensively and the effect of salt concentration and salt valency have been investigated. Addition of multivalent counterions causes a dramatic reduction of the electrostatic repulsion between two proteins. Preliminary scattering experiments indicate that calbindin self-associates upon addition of small amounts of lanthane (III) ions. The present simulations predict this effect to be due to ion-ion correlation and it can be depleted by addition of monovalent salt. Correlation effects can be invoked by lowering the solvent polarity, effectively increasing the electrostatic interactions.