Gating Gramicidin Channels in Lipid Bilayers: Reaction Coordinates and the Mechanism of Dissociation

Abstract

The dissociation of gramicidin A (gA) channels into monomers is the simplest example of a channel gating process. The initial steps in this process are studied via a computational model that simulates the reaction coordinate for dimer-monomer dissociation. The nonbonded interaction energy between the monomers is determined, allowing for their free relative translational and rotational motion. Lowest energy pathways and reaction coordinates of the gating process are determined. Partial rupture of the six hydrogen bonds (6HB) at the dimer junction takes place by coupling monomer rotation and lateral displacement. Coupling rotation with axial separation is far more expensive energetically. The transition state for channel dissociation occurs when monomers are displaced laterally by ∼4–6 Å, separated by ∼1.6–2 Å, and rotated by ∼120°, breaking two hydrogen bonds. In membranes with significant hydrophobic mismatch there is a much greater likelihood of forming 4HB and possibly even 2HB states. In the 4HB state the pore remains fully open and conductive. However, transitions from the 6HB to 4HB and 4HB to 2HB states take place via intermediates in which the gA pore is closed and nonconductive. These lateral monomer displacements give rise to transitory pore occlusion at the dimer junction, which provides a rationale for fast closure events (flickers). Local dynamics of gA monomers also leads to lateral and rotational diffusion of the whole gA dimer, giving rise to diffusional rotation of the dimer about the channel axis.

INTRODUCTION

Ion channel function is characterized by three basic properties: permeability, selectivity, and gating (Hille, 2001). Permeability and selectivity are determined by specific interactions between the channel forming protein (or peptide) and the ion(s) and water(s) occupying its open transmembrane pore. With the availability of atomic level structures for an ever-increasing number of such proteins (Doyle et al., 1998; Murata et al., 2000; Sui et al., 2002; Fu et al., 2000; Dutzler et al., 2002, 2003; Kuo et al., 2003), theoretical study of these processes has become a major research focus (see Kuyucak et al., 2001, for a recent review of various approaches). Even though the rates of ion flow are typically 10⁶–10⁷ s⁻¹, too slow to be directly simulated, considerable atomic level insight into these processes has been gained by molecular dynamics or Monte Carlo (MC) simulations that establish, with greater or lesser precision, the energetics of permeation. The simplification that permits such analyses to be successful is the existence of (relatively) simple reaction coordinates for permeation, ones that can be (more or less) determined by inspection of the channel structure.

Gating, the process that controls ionic flow across a membrane, is a far more difficult nut to crack. Gating displacements (leading to channel opening and closing) are much slower, typically requiring milliseconds or longer. Unlike protein folding, in which the assembly seeks the minimum of the energy landscape funnel, these conformational changes must involve specific transitions over saddles, for which the corresponding “reaction coordinates” may be far from obvious. Concerted movements of substantial segments of the protein are presumably involved during opening, closing, or inactivation. Cartoon models for such processes pervade channel biophysics (see Hille, 2001), but to date no theoretical study has provided a molecular level analysis of gating in even the simplest system, although recent studies on potassium channels (Jiang et al., 2002, 2003) and the mechanosensitive MscL channel (Martinac and Perozo, 2002) provide data that will surely form the basis of such investigations. Gramicidin A (gA), in its conducting head-to-head conformation, provides a sufficiently tractable system that permits undertaking such a study. But even here there are significant complications. The “reaction coordinate” involves coupled complex relative motion of the gA monomers and membrane influences, mainly due to hydrophobic mismatch, that affect the overall channel dissociation process.

The gA channel is formed by head-to-head association of two monomers at their amino termini, one from each bilayer leaflet (Urry et al., 1971; Andersen, 1984). Upon association the assembly is stabilized by six junctional hydrogen bonds (O'Connell et al., 1990). Cifu et al. (1992) showed that the elementary conducting unit is a dimer; in the absence of intermonomer linkers, supramolecular association (the formation of coupled channels) is unlikely. There is an enormous body of experimental and theoretical work investigating the structure, selectivity, and conductance of gA channels (Neher et al., 1978; Urban et al., 1980; Andersen, 1983; Arseniev et al., 1986; Becker et al., 1992; Partenskii and Jordan, 1992; Roux and Karplus, 1994; Ketchem et al., 1997; Wallace, 1998; Townsley et al., 2001). Less attention has been paid to channel gating: the energetics and the “reaction coordinate” for dissociation and formation of the gA dimer. A number of studies have demonstrated the dependence of the formation and dissociation rates of gA channels on voltage (Bamberg and Benz, 1976; Sandblom et al., 2001), membrane thickness (Kolb and Bamberg, 1977; Elliot et al., 1983), ion concentration (Ring and Sandblom, 1988; Ring, 1992), and elastic properties of lipid bilayers (Neher and Eibl, 1977; Ring, 1996; Goulian et al., 1998; Lundbæk and Andersen, 1999). To understand the origin of these various phenomena, a molecular mechanism for dimer formation and dissociation in lipid bilayer membranes is needed.

Gating presumably occurs via dissociation and association of the monomers with the closing transition triggered by breaking the dimer's stabilizing hydrogen bonds (Durkin et al., 1993; Lundbæk and Andersen, 1999). The deletion of a single hydrogen bond (HB) at the junction between the monomers destabilizes the gA dimer (by ∼10 kJ mol⁻¹) and reduces its conductance (Durkin et al., 1993). As the monomers can rotate relative to each other, formation of 4HB or 2HB dimers is conceivably possible (Lundbæk and Andersen, 1999). The transition state in dissociation of the normal (6HB) dimer is believed to be reached when two hydrogen bonds are broken and the monomers separate by ∼1.6 Å (Lundbæk and Andersen, 1999). The average lifetime of the conducting state in native gA channels is on the order of milliseconds to seconds (Elliot et al., 1983; Sigworth and Shenkel, 1988; Ring and Sandblom, 1988).

Although many aspects of gA structure and function can be studied using all-atom molecular dynamics simulations aimed at determining the exact microscopic details of channel behavior, determination of transition states and reaction pathways requires special methods. To do this we attempt to capture essential features of gA dynamics by simplifying the model system. Our approach is based on kinetic MC methodologies widely used in statistical and condensed matter physics to study phase transitions, polymer systems, and critical phenomena in alloys and magnets (Binder, 1992; Landau and Binder, 2000). To investigate gA dissociation in detail we present a new computational model, previously described in preliminary fashion (Miloshevsky and Jordan, 2003), to simulate reaction coordinates for the dissociation process. We calculate the nonbonded interaction energy between the monomers, which are permitted to undergo free translational and rotational motion, and determine the lowest energy pathways and the reaction coordinates for the initial steps in the process D(imer) ⇔ 2M(onomer). The effects that the relative monomer rotation angle, the intermonomer separation distance, the lateral intermonomer displacement, and the monomer-monomer tilt angle have on the intermonomer interaction energy are analyzed. The potential of mean force (PMF) along the minimum energy pathway for dimer dissociation is calculated using the free energy perturbation method. We find that partial rupture of the hydrogen bonds at the dimer junction takes place via coupled monomer rotation and lateral displacement. Coupling rotation with axial separation is energetically far more expensive. Hydrophobic mismatch, due to differences between the length of the nonpolar portion of gA and the membrane bilayer's acyl chains, greatly aids formation of 4HB and possibly even 2HB states. Finally, we discuss rotational diffusion of the gA dimer around its channel axis, observed in MC runs.

COMPUTATIONAL MODEL

Nonbonded interaction energy between gA monomers is calculated using our Monte Carlo ion channel proteins code as follows. We use partial charges and van der Waals parameters from the CHARMM22 all-hydrogen force field (MacKerell et al., 1998), treat bulk water regions as continua with ɛ = 80, and immerse the gA monomers in a low dielectric (ɛ = 1) membrane slab. The choice of ɛ = 1, used for consistency with the CHARMM22 force field, where polarization effects are not explicitly included, somewhat overestimates electrostatic effects; consequently representative computations with a slab ɛ of 2, 4, and 10 were also carried out. The reaction field is treated by the method of images (Dorman et al., 1996). Van der Waals and electrostatic interactions are computed with no cutoff. Most simulations were based on two crystallographic structures (Ketchem et al., 1996; Townsley et al., 2001) (pdb entries 1MAG and 1JNO, resolved by solid-state and micellar NMR, respectively). At each MC step the full intermonomer interaction energy is computed directly. Calculating the image charge reaction field energy is time-consuming (with the 552 real gA charges; 10 generations of images yield 11,040 image charges). The total interaction energy arises from the direct interaction of the partially charged atoms of the two monomers (both electrostatic and van der Waals) and the interaction between real and image charges. To accelerate calculation we separate the dimer into monomers. We introduce a crucial simplification, to be justified later, holding atoms within each monomer fixed while the monomers are relatively mobile; thus the interaction energy of atoms in the individual monomers is invariant and need not be computed. Excluding these contributions greatly reduces the computational cost. Although the monomers are held rigid, they undergo free three-dimensional relative rotation and translation. The bulk water-low ɛ slab interfaces are chosen to be ∼13 Å from the center of the coordinate frame along the Z axis. Image planes are perpendicular to the Z axis and the outermost protein atoms, including their van der Waals radii, are included in the low ɛ membrane slab. The image planes move along the Z axis together with monomers as they separate axially, but their separation is always kept symmetric relative to the membrane slab.

When gramicidin is inserted in a membrane, its hydrophobic length typically differs from that of the lipid bilayer (Elliot et al, 1983). We compute the deformational energy associated with this “hydrophobic mismatch” in an harmonic approximation (Nielsen et al., 1998; Lundbæk and Andersen, 1999; Neustadt and Partenskii, 2002; Partenskii et al., 2003) as E_elst = cu², where c is an elastic constant, specific to a particular membrane, and u is the vertical displacement of the membrane from its nondeformed (channel free) state. The vertical displacement is related to the monomer-monomer separation distance d, where u = u₀ − 0.5 × d, and u₀ is the deformation depth (the hydrophobic mismatch) of each monolayer when the channel is in its native (6HB) conformation. The membrane's deformational energy depends not only on d, but also on the contact angle between lipid and channel, conventionally expressed in terms of the contact slope s. The effect that the membrane's elastic deformation has on channel energetics is effectively described by the constrained boundary condition s = 0 (Huang, 1986; Lundbæk and Andersen, 1999; Partenskii et al., 2003). The appropriate effective elastic constants are c = 1.7 kT/Ų for a dimyristoyl phosphatidylcholine (DMPC) membrane (u₀ = 1.65 Å) and c = 0.95 kT/Ų for a glyceryl monooleate (GMO) membrane (u₀ = 3.4 Å) (Partenskii et al., 2003).

The influence that this elastic energy has on monomer reorientation is implemented using the Metropolis Monte Carlo technique (Metropolis et al., 1953), in which transition to a new state depends upon the energy change, ΔE; the acceptance criterion is that exp(−ΔE/kT) is greater than a randomly chosen number between 0 and 1. The elastic energy 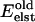is added to the total (electrostatic + vdW) interaction energy 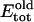between gA monomers. The elastic energy is only a function of their separation distance. Possible effects of monomer tilt or lateral motion on the elastic energy are neglected. As the relative monomer orientation and separation is changed, the intermonomer energy becomes 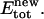The elastic energy 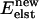is cu²; the total energy change is 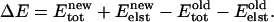We use the Metropolis criterion, with T = 300 K, to determine if the new configuration is accepted. As monomers separate the membrane's elastic energy decreases and the direct monomer-monomer interaction energy increases. Dimer behavior is determined by the competition.

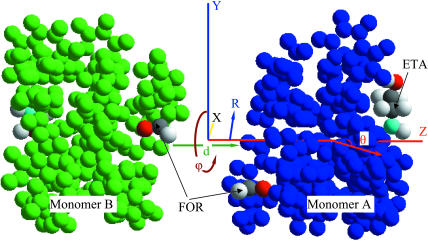
Simulation of complex gating motions in proteins with standard Monte Carlo or molecular dynamics fails to sample conformations separated by high energy barriers. These cannot be overcome by direct methods since they describe very low probability configuration space domains. Special computational techniques such as umbrella sampling (Torrie and Valleau, 1974, 1977), constrained reaction coordinate dynamics for the simulation of rare events (Carter et al., 1989), or high temperature molecular dynamics (Rosso et al., 2002) are required to sample reactive trajectories, the rare but important dynamical pathways that bridge long-lived stable states, for example, native and excited states of the gA channel. In these techniques the reaction coordinate is constrained within narrow windows or fixed at certain values and individual simulations performed for each window or at each fixed coordinate value, a computationally expensive approach. The novelty of our Kinetic Monte Carlo Reaction Path Following technique is its efficiency for following structural evolution unidirectionally along the reaction coordinate, determining the lowest energy pathways and the reaction coordinates for the initial steps of dissociating the dimer into monomers. Monomer B is held fixed and monomer A (see Fig. 1) is allowed both translational (three Cartesian degrees of freedom) and rotational (rotation ϕ and tilt θ angles) motion. As long as tilt is small, ϕ, and the third Euler angle, ψ, are almost equal; thus, if ψ were freely variable, motion in that direction would immediately counter the rotation about ϕ and it would be impossible to monitor reaction. Consequently it was forbidden. The Metropolis method (Metropolis et al., 1953) allows moves to states of higher energy. The smaller the energy difference the greater the probability of an acceptable uphill move. Thus the rotation angle ϕ is only allowed to increase. Other degrees of freedom are unconstrained. The reaction coordinate (angle ϕ) evolves slowly relative to the other degrees of freedom. As monomer A approaches a saddle point with rapidly increasing energy, only small changes in ϕ are likely to be accepted. This describes a major aspect of the motion along the reaction pathway. However, it is incomplete since the energy fluctuates around the lowest-energy groove. A large set of closely related paths may be sampled within a minimum energy pathway. At the peak of the energy barriers separating the stable states the reaction pathway may bifurcate. For accepted configurations several MC trials are used to relax monomer A with the new angle ϕ fixed. The remaining degrees of freedom then relax fully in response to movement along the reaction coordinate, an especially important feature as monomer A evolves downhill, since any new configuration with lower energy is always accepted.

FIGURE 1.

Two gA monomers (A and B) of the 1MAG structure are illustrated as separate mobile structural elements. The helices are shown in blue and green. Atoms of the FOR and ETA residues are displayed in their conventional colors. Arrows demonstrate the monomers' separation distance, lateral displacement, tilt angle, and rotation direction.

We validated this technique against results of a grid search (Leach, 2001). Since grid searching must be restricted to a very few degrees of freedom, comparisons were made with monomer A that only permitted two degrees of freedom, Z and ϕ. Z was unrestricted and only increases in ϕ were permitted; other degrees of freedom (lateral motion and tilt) were frozen. The two approaches yielded identical energy profiles over the whole ϕ-range.

RESULTS

The molecular model of Fig. 1 depicts the 1MAG gA structure derived by Ketchem et al. (1996). The lowest energy pathway was determined by ϕ rotation of monomer A by 360° from the 6HB state to the 4HB state, then to the 2HB state, finally returning to the 6HB state. The 6HB state is one where all the Os and Hs of each monomer's six junctional COs and NHs are all (roughly) equidistant from the complementary Hs and Os of the other monomer (essentially, ϕ ≤ 75°). In the 4HB state only four of the O-H and H-O pairs are equivalent; intermonomer rotation has separated the other two pairs (essentially 75° ≤ ϕ ≤ 200°). Other degrees of freedom (the three Cartesian coordinates and the tilt angle θ) for monomer A were freely variable. The reaction coordinates (separation distance d and lateral displacement R between the monomers, tilt angle θ of monomer A) corresponding to the lowest energy path were determined simultaneously.

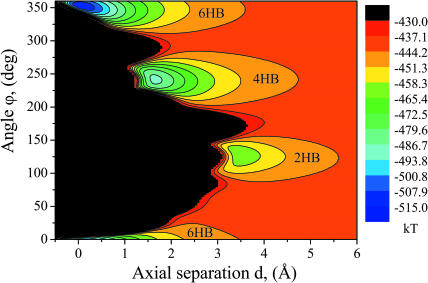
Fig. 2 presents an energy map for the 1MAG structure (the d,ϕ-map) as a function of the separation distance d and rotation angle ϕ. Lateral displacement and tilt are forbidden. The map, calculated by grid search (Leach, 2001), with d and ϕ steps of 0.05 Å and 0.5° respectively, describes this two-dimensional energy surface away from the reaction path. The black parts of the energy map are regions sterically inaccessible to monomer A. There are three clear energy wells corresponding to 6HB, 4HB, and 2HB states; these are uncoupled in d,ϕ-space. Large energy barriers separate transition between the wells. For the 1MAG and 1JNO structures used here, the energy, separation distance, and rotation angle differences between the three states determined from d,ϕ-maps are presented in Table 1.

FIGURE 2.

Contour map of the total (electrostatic + vdW) energy as a function of the separation distance d and rotation angle ϕ between gA monomers of the 1MAG structure. The energy wells corresponding to the states with 6HB, 4HB, and 2HB hydrogen bonds are illustrated.

TABLE 1.

Energy, separation distance, and rotation angle differences between 6HB, 4HB, and 2HB states for the 1MAG and 1JNO conformers

	ΔE [kT] 6HB–4HB	ΔE [kT] 4HB–2HB	Δd [Å] 6HB–4HB	Δd [Å] 4HB–2HB	Δϕ [deg] 6HB–4HB	Δϕ [deg] 4HB–2HB
1MAG	26.37	25.45	1.6	1.85	112	112.5
1JNO	33.72	20.92	1.45	1.3	131	107

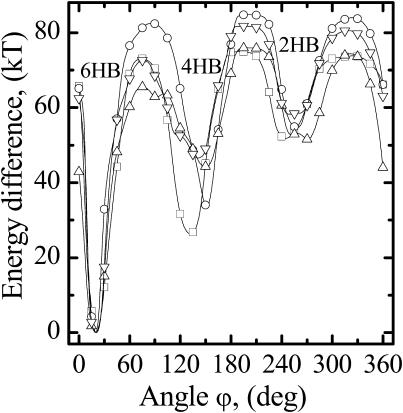
In our approach, the monomers are treated as rigid bodies; effects due to their flexibility are suppressed. To justify this, we rely on solid-state NMR observations (Tian et al., 1996; Tian and Cross, 1999) demonstrating no significant change in polypeptide gA structure even at the highest cation loading of the channel. The hydrogen-bonded COs and NHs in the polypeptide skeleton are not noticeably perturbed (Tian et al., 1996), suggesting that the monomers move as nearly rigid bodies. We considered all four experimental head-to-head dimer structures, corresponding to different conformations and peptide sequences. Fig. 3 shows the lowest energy contours on the d,ϕ-map as a function of ϕ; the monomer axes are coincident with both lateral motion and tilt suppressed. 1MAG (Ketchem et al., 1996) and 1JNO (Townsley et al., 2001) are for gramicidin A; 1JO3 (Townsley et al., 2001) is for gramicidin B, and 1JO4 (Townsley et al., 2001) is for gramicidin C. All exhibit qualitatively similar lowest energy pathways for dissociation; the basic profile is conserved. Differences most likely reflect conformational differences at TRP9 and sequence differences at residue 11, regions quite distant from the dimer junction. These profiles suggest that major aspects of gramicidin dissociation are basically independent of the structural details of the monomer. These observations are unaltered if all backbone carbonyl oxygens (COs) and amino hydrogens (NHs) are mobile. Calculations, not shown here, performed for the 1MAG structure, demonstrated that allowing backbone COs and NHs to librate and stretch has no significant effect on the intermonomer interaction energy. The three wells are still separated by huge energy barriers, and the monomers must undergo large (>4 Å) axial separations to migrate from one well to another. As rotation occurs, Os and Hs from the separate strands come into opposition, with strong consequent repulsion, a point discussed at length in what follows.

FIGURE 3.

The energy profiles corresponding to the lowest energy path on the d,ϕ-map between 6HB, 4HB, and 2HB states as a function of the rotation angle ϕ between monomers. Profiles are shown for four experimental gramicidin structures: □, 1MAG; ○, 1JNO; Δ, 1JO3; and ∇, 1JO4.

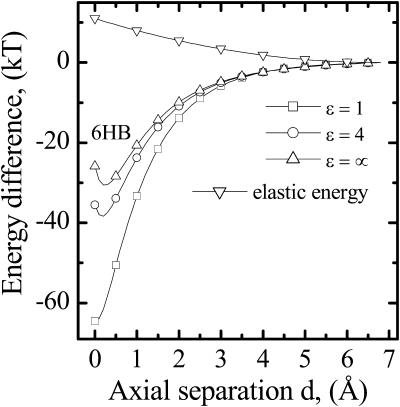
Fig. 4 illustrates the effect of the membrane dielectric constant, ɛ, on the 1MAG energy profile for axial displacement of monomer A along the Z axis, starting from the 6HB state. The rotation angle ϕ is fixed at zero. Increasing ɛ greatly alters the 6HB energy-well depth, with saturation at ɛ ∼ 10. This well (∼30 kT) is conserved even when electrostatics is suppressed and all partial charges on the protein atoms are turned off. The well remains deep and the profile is steep; at Z ∼ 0 Å the interaction is repulsive, but becomes attractive at Z > ∼0.5 Å. Thus, in equilibrium the strong electrostatic attraction between the monomers is counterbalanced by van der Waals repulsion. When the monomers separate >0.5 Å, van der Waals forces aid intermonomer binding. To estimate the importance of interaction with explicit waters, we augmented the model with two cylindrical regions containing ∼300 waters each, with the bulk continuum regions moved appropriately outwards. In the 6HB state the net solvent contribution (both electrostatic and van der Waals) to the intermonomer binding force is very small (∼1 kT/Å), far less than the ∼15 kT/Å intermonomer van der Waals force. The elastic energy of a GMO membrane as a function of the intermonomer separation distance, d, is also shown in Fig. 4. In the 6HB state it is ∼11 kT, gradually decreasing to zero with increasing d. The magnitude of the slope of the elastic and the intermonomer energies differ greatly in the separation range, d ≤ 2 Å. The intermonomer energy varies much more rapidly even in an artificial case where electrostatics is turned off.

FIGURE 4.

Energy profiles as a function of the axial monomer separation distance (movement along the Z axis directly from the 6HB state, ϕ ≡ 0). Profiles are shown for ɛ = 1 and 4, and when all partial charges on the protein atoms are excluded (ɛ ≡ ∞). The elastic energy profile as a function of the separation distance is illustrated for a GMO membrane.

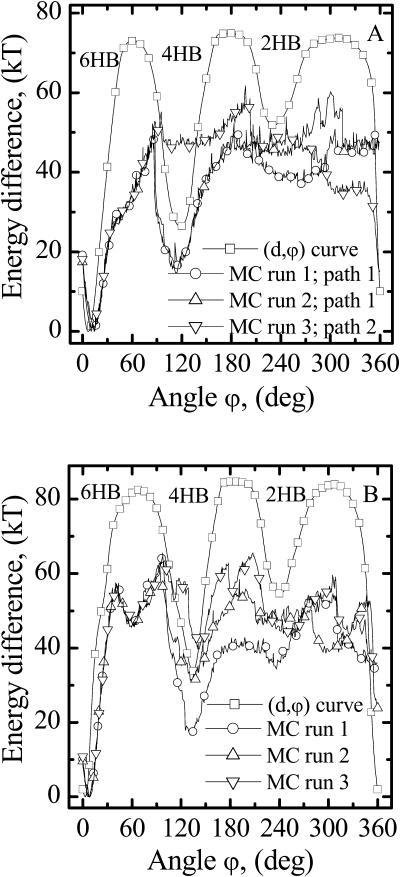
Fig. 5, A and B, illustrate the lowest energy profiles for the 1MAG and 1JNO structures, corresponding to the reaction coordinate for dimer dissociation. A large number of MC runs were followed to determine the behavior of monomer A and characteristic results are presented. Here monomer A is permitted lateral displacement and tilt. Only reaction coordinates, representing a trajectory in five-dimensional space, were determined. Maps of energy surface topology away from these pathways were not determined; thus energetics away from the lowest energy path remains unknown. The profiles, although different in detail, exhibit substantial qualitative similarities. The importance of the additional degrees of freedom (lateral displacement and tilt) is evident from the difference between the MC curves and the d,ϕ-curves of Fig. 3. Energy barriers decreased significantly. The data shown incorporate hydrophobic mismatch; similar behavior is found with no mismatch. In 1MAG (Fig. 5 A) the barrier separating the 6HB and 4HB wells is ∼50 kT; the well depth difference is ∼18 kT. Intermonomer hydrogen bonds break much more easily if monomer A undergoes rotary motion with simultaneous lateral displacement rather than with direct axial separation. At the peak of the 6HB–4HB barrier the reaction pathway bifurcates. Path 1 leads to the 4HB state. There is switching between hydrogen bonds at the intermonomer junction (a rotational shift and the breaking of two hydrogen bonds) with an abrupt discontinuity in the separation distance (∼1.6 Å, see Fig. 6 A). Along path 2 the monomers dissociate directly from the native 6HB state by coupled rotary and lateral motion with neither a separation distance discontinuity nor a rotational shift between hydrogen bonds. In 1JNO (Fig. 5 B) the picture is less sharply drawn. The 6HB–4HB barrier is now ∼60 kT, and the well-depth difference is in the range of ∼20–40 kT. For both structures the probability of realizing the different paths depends on the tilt permitted to monomer A, the membrane thickness, etc. However, in both the 1MAG and 1JNO structures, for ϕ > 150° (escape from the 4HB state) the energy fluctuates between 40 and 60 kT and the barriers between the 4HB and 2HB wells and 2HB and 6HB wells disappear (compare the MC curves with the d,ϕ-curve). Increasing the membrane ɛ to as much as 4 naturally lowers the energy differences; however, it has no qualitative effect on the results. In what follows, we only present results for which ɛ = 1.

FIGURE 5.

Energy profiles corresponding to the lowest energy pathways for (A) 1MAG and (B) 1JNO dimer dissociation. For 1MAG the two paths illustrated are typical. Path 1 corresponds to formation of the 4HB state. Along path 2 monomers dissociate directly from the 6HB state by lateral displacement. For 1JNO the distinctions are less sharply drawn; even though energy decreases in the 75° ≤ ϕ ≤ 120° range, not all paths lead to a 4HB state. The energy profiles in d,ϕ-space (tilt and lateral motion excluded) are also illustrated.

FIGURE 6.

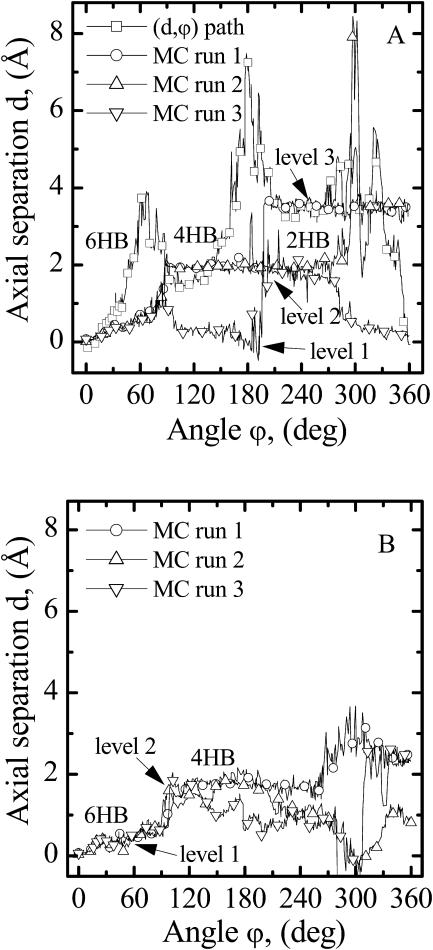
Axial separation distance, d, between gA monomers along the lowest energy pathways in GMO membranes (mismatch, u₀ = 3.4 Å). (A) Results from three representative MC runs and the d,ϕ-path are illustrated for the 1MAG structure. There are three levels in the separation distance corresponding to the 6HB, 4HB, and 2HB states. The separation distance discontinuity occurs at 75° on the path to the 4HB state and at 210° on the path to the 2HB state. The sharp peak at 300° (MC run 2) is a dimer dissociation event from level 2. (B) Results from three MC runs are illustrated for the 1JNO structure. In MC run 1, the 1JNO monomers dissociate laterally directly from the 6HB state. The formation of the 2HB state (level 3) was never observed.

Fig. 6, A and B, illustrate the angular dependence of the axial separation distance between monomers for the 1MAG and 1JNO structures, respectively. Zero separation corresponds to the native state, i.e., the fully open conducting channel. In the 6HB state the hydrogen-bonding pattern is 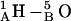(where 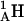is the amino hydrogen of residue 1A, and 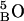is the carbonyl oxygen of residue 5B, etc.), 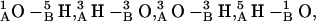and 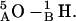For the d,ϕ-path (neither lateral displacement nor tilt allowed) 1MAG monomers separate ∼4 Å in transiting from the 6HB to the 4HB state (Fig. 6 A), due to a large electrostatic barrier. At ϕ ∼ 60° five COs and NHs from the individual monomers are in opposition: 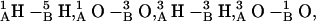and 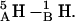This barrier is unaltered even if H-atom and O-atom motions (libration and stretching of the NH and CO bonds) are permitted. The ϕ-dependence of the axial separation distance is very different when lateral displacement and tilt are allowed (MC curves).

For 1MAG in a GMO membrane depicted in MC runs 1 and 2 of Fig. 6 A (mismatch u₀ = 3.4 Å) the axial separation exhibits three distinct levels, ∼0 Å, ∼1.6 Å, and ∼3.4 Å corresponding to 6HB, 4HB, and 2HB states, respectively. For both the 1MAG and 1JNO structures, the monomers' axial separation is insignificant for ϕ ≤ 75°; the separation distance gradually increases with ϕ up to ∼1 Å (level 1). Even an extremely large channel-bilayer hydrophobic mismatch does not alter this behavior. The dimer is in an intermediate state, with between six and four hydrogen bonds and no significant axial separation of the monomers. This reflects strong intermonomer interaction arising from the six native (original) intermonomer hydrogen bonds. Dissociation occasionally occurs from the native 6HB state (Fig. 6 A) with no rotational shift between hydrogen bonds (MC run 3). This pathway is especially probable when there is no mismatch, i.e., bilayer thickness matches the channel's hydrophobic length.

Fig. 6 B presents data for 1JNO in a GMO membrane (hydrophobic mismatch 3.4 Å). Usually in GMO, 1JNO undergoes a transition to the 4HB state with an abrupt separation distance discontinuity at ϕ ∼ 90°. However, direct dissociation from the 6HB state is observed in MC run 1. The crucial determinant is the lateral displacement (see Fig. 7 B), which is ∼2 Å (MC run 1); the permeation pathway, once displaced, never reformed. In the absence of a hydrophobic mismatch, direct dissociation of 1JNO from the 6HB state was also observed (results not shown).

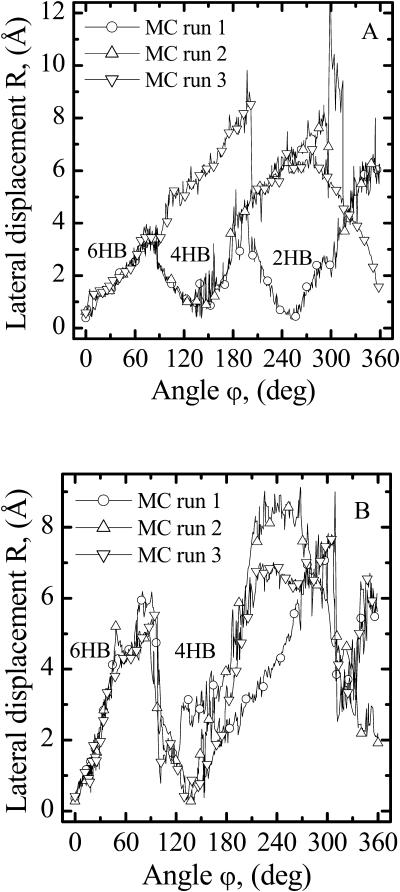
FIGURE 7.

The lateral displacement, R, at the intermonomer junction on the various pathways presented in Fig. 6. (A) For 1MAG, in MC run 3 the monomers may dissociate directly from the 6HB state. When the 4HB state forms (MC runs 1 and 2) a conductive gA dimer reforms (R near zero). Due to the large hydrophobic mismatch in GMO (u₀ = 3.4 Å) an open pore forms even in the 2HB state (MC run 1). (B) 1JNO monomers usually reform an open pore in the 4HB state; however, in MC run 1, there is direct dissociation. An open pore 2HB state never forms.

Hydrophobic mismatch aids formation of the 4HB state in both structures and the 2HB state in the 1MAG structure. When hydrophobic mismatch is taken into account, the axial separation abruptly increases by ∼1.6–2.0 Å (level 2), corresponding to formation of the 4HB state. There is a corresponding rotational shift of junctional hydrogen bonds; residues 5A and 5B no longer contribute to junctional stability. The new bonding pattern is 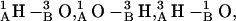and 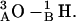This pathway (level 2) is also observed at low probability when there is no mismatch. For a large mismatch (GMO), formation of a 2HB state was also observed for 1MAG with an axial intermonomer separation of ∼3.4 Å (level 3) at ϕ ∼ 210°. There is a further rotational shift and breakage of junctional hydrogen bonds. The residual bonding pattern is 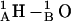and 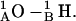For 1MAG the 2HB state was not observed in modeling behavior in a DMPC membrane, as the hydrophobic mismatch (u₀ = 1.65 Å) is too small. For GMO the 2HB state did not form in the 1JNO structure (Fig. 6 B). Transient dissociation events from levels 2 and 3 were observed in some MC runs (MC run 2 illustrates dissociation from level 2) where the 1MAG monomers separate by ∼6.8 Å. In sum, channel behavior is sensitive to bilayer deformation for monomers separated by ∼1.6 Å, in agreement with the assumption of Lundbæk and Andersen (1999).

Fig. 7, A and B, illustrate the lateral displacement between the monomers along the dissociative pathways for the 1MAG and 1JNO structures, respectively. The intermonomer junction is displaced sideways by ∼3.5 Å (1MAG) and ∼5 Å (1JNO) at the peak of the barrier separating the 6HB and 4HB wells; here ϕ ∼ 75° and the dimer pore is fully occluded. In the absence of any hydrophobic mismatch, dissociation takes place laterally for 1MAG with a high probability (MC run 3). Along this pathway, for ϕ > ∼75°, separation occurs laterally without the open pore reforming. With increasing hydrophobic mismatch, there is a greatly increased probability that the monomers' lateral displacement again approaches zero (forming the 4HB state) with a correspondingly fully reopened pore. In 1JNO the open pore (the 4HB state) reformed in all but one MC run (MC run 1 of Fig. 7 B, where the lateral separation is ∼2 Å at the “4HB angle” of ∼120°). For GMO the formation of 2HB state with a fully open pore in the 1MAG structure is observed (Fig. 7 A, MC run 1). The transition between the 4HB and 2HB states again involves sideways displacement of the intermonomer junction by ∼4 Å (Fig. 7 A). Three COs and NHs from the individual monomers are in opposition: 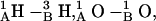and 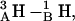producing an electrostatic barrier. Thus, in 1MAG transitions between the 6HB, 4HB, and 2HB states occur with intermediate pore closures. In 1JNO behavior is similar, but without formation of a 2HB state (Fig. 7 B). The 2HB state of 1JNO was observed if the tilt angle was fixed at zero.

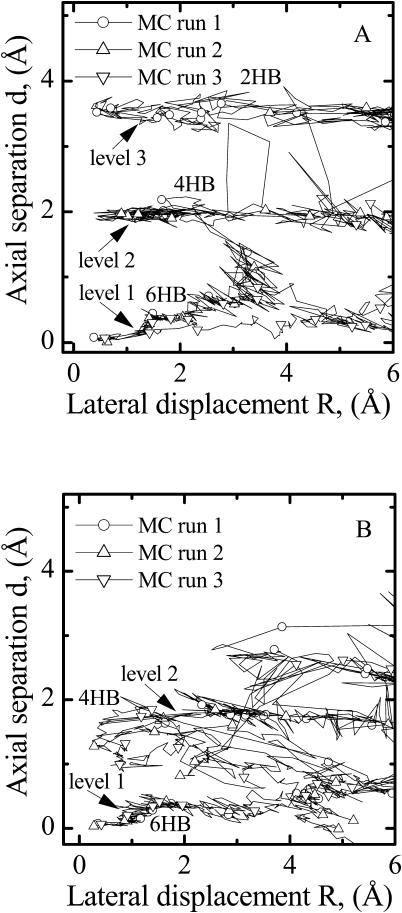
Fig. 8, A and B, illustrate axial intermonomer displacement along the dissociative pathways as a function of the lateral separation distance for the two structures. For 1MAG, at lateral displacements <∼3 Å there are three distinct axial separation levels with no direct transitions (Fig. 8 A); only if the lateral separation exceeds 3 Å is it energetically possible to transit among the three states. For the 1JNO structure there are only two such levels (Fig. 8 B). The 2HB state (level 3) is never observed and level 2 (the 4HB state) is quite diffuse (Fig. 8 B). In both structures, transition between the various axial separation levels only occurs for lateral displacements >3 Å.

FIGURE 8.

The axial separation distance, d, at the intermonomer junction as a function of the lateral separation, R, between gA monomers along the lowest energy pathways. (A) The three levels in the separation distance corresponding to the 6HB, 4HB, and 2HB states are clearly indicated for the 1MAG structure. Transition between the levels occurs when monomers are laterally displaced >3 Å. (B) The two separation distance levels corresponding to the 6HB and 4HB states are indicated for the 1JNO structure. Level 2 is much more diffuse than that seen for the 1MAG structure. Level 3 (the 2HB state) is never observed.

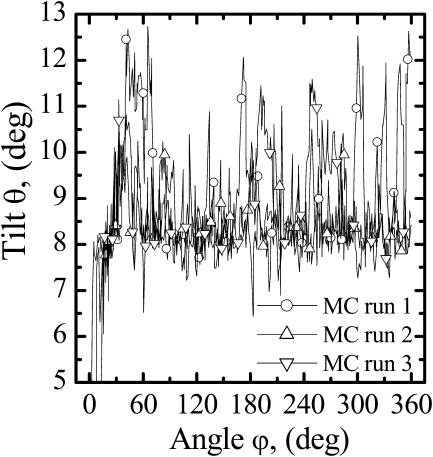
Fig. 9 illustrates the tilt angle θ for monomer A of 1MAG. It fluctuates between 7° and 10°. In the absence of hydrophobic mismatch either path 1 or 2 (Fig. 5) can occur depending on the tilt angle constraints. If tilt is forbidden or near zero, path 1 is followed frequently (9 out of 10 MC runs). When tilt is freely variable direct dissociation from the 6HB state (path 2) is most probable. For the 1JNO structure, tilt angle fluctuations are substantially larger, fluctuating as much as 25° (results not shown).

FIGURE 9.

Tilt angle, θ, of monomer A in the 1MAG structure. It fluctuates ∼8.5°.

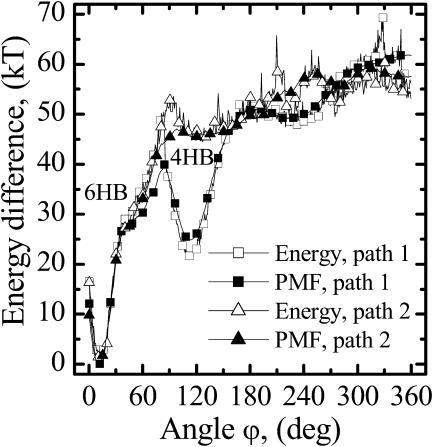
The potential of mean force (PMF) for dimer dissociation was calculated via free energy perturbation (Leach, 2001). With ϕ as reaction coordinate, varied from ϕ₀ = 0° to ϕ₁ = 360°, intermediate angular states were described by a coupling parameter λ ranging from 0 to 1. The intermediate angle ϕ, corresponding to λ_i, is ϕ(λ_i) = λ_iϕ₁ + (1 − λ_i)ϕ₀. In each MC simulation ϕ was fixed at ϕ(λ_i). The free energy differences ΔA(λ_i→l_i+1) and ΔA(λ_i→l_i−1) were obtained from a single MC simulation. Three configurations, ϕ(λ_i−1), ϕ(λ_i), and ϕ(λ_i+1), are treated simultaneously by calculating the energy difference between the configuration ϕ(λ_i) and its δλ-incremented neighbors ϕ(λ_I − δλ) and ϕ(λ_I + δλ) at each perturbation step. Fig. 10 illustrates the potential of mean force along the reaction coordinate for dissociation of 1MAG. The reaction coordinate ϕ was varied in 0.3° steps. In the main the PMF mimics the total energy profiles along reaction pathways. In the 6HB region there is no difference between the PMF and total energy profiles. The PMF barriers separating the 6HB and 4HB states are lower than the total energy barriers.

FIGURE 10.

Total energy and potential of mean force profiles along the reaction coordinate (rotation angle ϕ) for the dimer to monomer reaction in the 1MAG structure. Profiles are illustrated for paths 1 and 2.

DISCUSSION

Our results demonstrate that rupture of the six very strong hydrogen bonds between the monomers is not immediately dissociative. The monomers undergo rotary motion with simultaneous relative lateral displacement rather than direct axial separation. The reaction paths are five-dimensional trajectories that cannot be summarized in a single picture. Movies (viewed from within the membrane slab and along the channel axis) showing the monomers' dissociation behavior in a GMO membrane (mismatch 3.4 Å) are available at the URL (http://people.brandeis.edu/gennady/gA.html). The hydrogen bonds break slowly as the monomers undergo rotational and lateral shifts. Only after substantial rupture is the transition state reached, at which point there is the abrupt shift leading to hydrogen-bond reduction. After the first transition state is reached, the ϕ-dependence of the hydrogen-bonding pattern depends upon the path followed, i.e., upon the channel-bilayer hydrophobic mismatch. When two hydrogen bonds are broken, membrane elasticity greatly aids the transition from the native 6HB state to the 4HB state. This switching between hydrogen bonds at the intermonomer junction (a rotational shift by two hydrogen bonds) occurs abruptly with an axial separation distance discontinuity of ∼1.6 Å, a model prediction in excellent agreement with the conclusion of Lundbæk and Andersen (1999).

Hydrophobic mismatch has no discernable effect on dimer behavior in the 6HB state as the d-dependence of the intermonomer energy is much larger than that of the elastic energy (see Fig. 4). Changes in the intermonomer interaction energy and the elastic energy of the membrane deformation do not counterbalance one another. For a 3.4 Å mismatch in 1MAG the intermonomer energy increases by ∼31 kT and the elastic energy decreases by ∼3 kT as d increases from 0 to 1 Å. Consequently the probability of observing transient dissociation events originating from the 6HB state is too low to be sampled. Even for the artificial case with electrostatics ignored (ɛ ≡ ∞), the intermonomer energy varies much more rapidly than the elastic energy; the 6HB energy well remains deep and steep. Thus, in the 6HB state, relative monomer motion behavior is overwhelmingly likely to be governed by the intermonomer interaction energy. We calculated PDFs in 1MAG for intermonomer separation distances d, lateral displacements R, rotation angles ϕ, and tilt angles θ for both monomers. Both monomers were totally mobile, permitted free translational and rotational motion. The PDFs determined the most probable values of d, R, ϕ, and θ, and their fluctuation range in the 6HB state. We studied the 1MAG dimer's 6HB state in three cases: 1), no mismatch; 2), mismatch, u₀ = 1.6 Å, DMPC-like; and 3), mismatch, u₀ = 3.4 Å, GMO-like. The channel-bilayer hydrophobic mismatch had no noticeable effect on the PDFs in the 6HB state. Accounting for membrane deformation (mismatches of 1.6 or 3.4 Å) all fluctuations in the PDFs are within the MC error. This suggests that the gA channels prefer to remain dimeric (if initially dimeric) in membranes of reasonable thickness.

In the PDF determinations with both monomers freely mobile, direct fluctuations leading to the transition state (two broken hydrogen bonds and monomers separated by ∼1.6 Å) were never observed. This contrasts sharply with the transitory dissociative event seen in Fig. 6 A from level 2 (the 4HB state); nothing similar is seen originating from level 1 in either 1MAG or 1JNO. We conclude that direct dissociation (or attaining the transition state) from the 6HB state is a very rare event, too improbable to be observed by standard MC sampling of PDFs; thus the average lifetime of the open state of the gA dimer corresponds to the 6HB state transiting to unbound monomers. Thermally driven relative motion of the monomers coupled to the hydrophobic mismatch is not directly dissociative. Possibly the local concentration of bilayer's undulatory fluctuations that are eventually released leading to the gA transition state play a role in this process. Other factors encouraging fluctuations leading to instability might be the presence of ions in the channel, the transmembrane potential, etc. The channel-bilayer hydrophobic mismatch clearly affects the dissociation pathway when two hydrogen bonds are broken and the monomers separated at ∼1.6–2.0 Å. Full dissociation events were observed in a GMO-like membrane when the 1MAG monomers are no longer in the 6HB energy well (Fig. 6 A). However, instantaneous dimerization follows these dissociation events, which suggests that transition states with two broken hydrogen bonds are very short-lived compared to the 6HB state.

For a gA dimer inserted into GMO, hydrophobic mismatch greatly aids the formation of 4HB and even 2HB (in 1MAG) states. At the transition between the 6HB and 4HB states the monomers are laterally and rotationally shifted relative to each other by ∼4–6 Å and ∼75°–90°, respectively. Their axial separation gradually increases above zero. In the absence of a mismatch, there would be a high probability for either the 1MAG or 1JNO dimers to dissociate laterally (without forming a 4HB state). When there is mismatch just the opposite happens; 4HB state formation is highly probable in both cases. In the 4HB state the monomers are rotationally shifted by ∼140° and the corresponding axial separation distance is ∼1.6 Å. However, there is now no lateral displacement. The pore is perfectly open, as in the 6HB state. During the 6HB-to-4HB transition the pore is closed fleetingly due to lateral displacement (Fig. 8, A and B). There is experimental evidence (Mobashery et al., 1997) that increased membrane-channel mismatch leads to a new conducting state involving the same pair of monomers. We concluded, after discussion with O. S. Andersen (private communication), that this new conducting state could well be the 4HB state. Our analysis predicts similar behavior leading to formation of a 2HB state in a thick membrane; the pore would again be fully open at an axial separation distance of ∼3.4 Å. Again in the 4HB-to-2HB transition in 1MAG there is intermediate pore closure due to lateral displacement (Fig. 8 A). Thus, there can be three levels in the monomers' axial separation distance: ∼0 Å, ∼1.6 Å, and ∼3.4 Å. Direct dissociation due to the membrane contribution was observed only from the two last levels, not from the first level. Any differences between the results for 1MAG and 1JNO, seen in Figs. 5–8, probably reflect the latter conformer's less “stressed” backbone (Allen et al, 2003).

There is experimental evidence (Lee et al., 1993) that gA dimers undergo rotational diffusion around the bilayer normal. Our MC results demonstrate that rotational diffusion of the dimers is a consequence of local monomer dynamics. Movies of MC simulations performed for a 1MAG dimer inserted into a GMO membrane (mismatch 3.4 Å) are available at the URL (http://people.brandeis.edu/gennady/gARotation.html). Each monomer rotates and translates freely in three-dimensional space. These degrees of freedom (local dynamics) represent possible large amplitude motions of the rigid monomers. In the 6HB state the monomers only undergo rotary and sliding motion, with negligible fluctuations in axial separation. Rotational diffusion of the dimer arises naturally from local monomer dynamics. There is no preferred clockwise or anticlockwise rotation; dimer rotation occurs randomly in either direction. However, during this process the channel can make a full 360° turn around its axis, equivalent to rotational diffusion of the dimer as a whole. In addition to this uniaxial rotational diffusion, the dimer diffuses laterally as a unit. A recent solid-state NMR study (Mo et. al., 2004) of the monomeric gA closed state shows that the free monomer does not exhibit global axial rotation about the bilayer normal. This is consistent with our study; each monomer needs a partner for rotational diffusion to occur. For rotation axial angular momentum is required. Unless the membrane (or an external field) applies a torque, an isolated monomer will not rotate. However, in the dimer, the monomer motions are coupled. Their relative translational and rotational motions are highly restricted, manifesting themselves in fluctuations of the rotational angle ϕ and the lateral displacement R. Both dimer rotation around its axis and its translational diffusion in the membrane plane arise from the restricted translational and rotational monomer motions.

Our results provide a natural explanation for flickering during disappearance of double-barreled gA channels (Goforth et al., 2003; Rokitskaya et al., 2003). Lateral motion of either the 1MAG or 1JNO monomers along the dissociation pathway leads naturally to fluctuations in the pore cross-section at the dimer junction; this may rationalize abrupt transitions (flickers) on the sub-ms timescale. In going from the 6HB to the 4HB state, ionic conduction is partially interrupted and restored as the monomers undergo lateral fluctuations at the intermonomer junction. Armstrong and Cukierman (2002) have observed fast closure flickers, promoted by greater hydrophobic mismatch, for dioxolane-linked gramicidins. As these channels cannot separate, flickering was viewed as arising from bilayer undulations blocking the mouths of the channels. However, the dioxolane linkage does not preclude flicker due to rotation, lateral motion, and tilt; the membrane thickness effect is consistent with our observation of increased probability of occlusion with increased mismatch.

In our study both membrane and bulk water were treated as dielectric continua. For bulk water this is a good approximation. We carried out a series of MC runs and investigated the effect that explicit water molecules within the gA pore have on dissociation behavior for the d,ϕ-path (no lateral motion and tilt). The explicit water molecules reduce the energy difference between the wells and barriers; however, they do not alter the profile's basic shape. We also considered the possible influence of a permeant cation. A K⁺ ion located at mid-dimer increases the intermonomer attraction in agreement with numerical estimates and experimental results demonstrating channel stabilization by ion occupancy (Ring and Sandblom, 1988; Ring, 1992). With two K⁺ ions located at Z = 9 Å and Z = −9 Å (the binding sites close to the channel mouths) the intermonomer energy profile is slightly altered but its basic shape is conserved. In addition, the energy profile is sensitive to the value chosen for the dielectric constant of the membrane slab. However, in all the cases the shape of the intermonomer energy profile is conserved.

The effect that explicit water molecules and ions located within the pore had on the dissociation pathways, accounting for the monomer's lateral motion and tilt, could not be studied in full detail due to various technical problems. However, we monitored the initial stages of the dissociation process permitting both lateral motion and tilt while incorporating two K⁺ ions and seven water molecules in the gA pore, for 6HB, 4HB, and 2HB states, using the 1MAG structure. In the 6HB state, for ϕ up to ∼75° the most favorable pathways are identical; with the pore empty or occupied, monomers separate laterally, not axially. By ϕ ∼ 75°, the lateral separation, whether or not water is present, is almost 4 Å (data not shown), so that here too the conductance pathway is occluded at the junction. For ϕ > ∼75°, two or three water molecules leak into the membrane slab through the gap formed by the rotational shift and corresponding lateral displacement of the monomers, but the ions stay at their binding sites with the remaining water molecules. We found similar behavior for the 4HB and 2HB states, constructed with ϕ ∼ 120° and ϕ ∼ 240°, respectively. In both cases as ϕ increases from these initial values, the monomers again separate laterally, not axially; the conductance pathways become occluded at the junction as the lateral separations are again ∼4 Å. Although it is not possible to fully track the dissociative process, these studies confirmed the results presented in Figs. 6–8 for the empty channel. Even with an occupied pore, the initial steps in the dissociation mechanism are essentially the same, involving rotation and lateral displacement of the monomers. Neither the presence of water or ions favors dissociation via rotation and direct axial displacement. These results complement the study of Durkin et al. (1993) indicating that the gA monomers cannot be stabilized by the water molecules located in a defect at the monomer's junction and forming a hydrogen-bonded bridge between the free amide and carbonyl groups.

Interaction between the dissociating gA monomers and the surrounding explicit lipid molecules, not included in our study, may affect the dissociation pathways. The gA dimer dissociating by lateral monomer displacement shifts the lipids adjacent to the channel. The monomers may experience a lateral resistance from the surrounding lipid. However, experimental results (Tank et al., 1982; Borisenko et al., 2003) indicate that lateral diffusion of gramicidin monomers in the plane of the membrane is quite fast (D ∼ 3 × 10⁻⁸ cm² s⁻¹). This suggests that the monomers are relatively free to move sideways in the lipid bilayer (during 1 μs a gA monomer would travel ∼35 Å) so that the influence that the lipids adjacent to the channel have on the reaction pathways is likely insignificant.

Our fundamental observation, from which all results flow, is that for both 1MAG and 1JNO the initial step in the dissociation process involves lateral, not axial, separation of the monomers. The choice of the slab ɛ is unimportant; qualitative behavior is the same for all ɛ ≤ 4, so choosing the value dictated by the use of the CHARMM (MacKerell et al, 1998) parameter set is not a limitation. Our analysis has been based on one important simplification: that the monomer is effectively rigid in the initial steps of dissociation. This assumption is rationalized by experimental evidence that the monomeric gA channel closed state is a half-dimer state in the bilayer leaflet (He et al., 1994). However, recent results (Mo et al., 2004) suggest that the monomeric closed state may be a hybrid, somewhat between half the open state dimer and a structure restricted to the bilayer surface. Both C- and N-terminal domains remain well structured, but relative to the bilayer normal the orientation of the N-terminal region fluctuates noticeably (Mo et al., 2004). Although the structural differences between 1MAG and 1JNO are small in the all-important junctional region, our results demonstrate that they have an effect on possible reaction pathways. Both conformers can form a 4HB intermediate along the dissociation pathway. Both can also dissociate directly from the 6HB state. However, only for 1MAG does it seem possible that a 2HB state might form. These results illustrate possible ways in which the gA dimer may dissociate. The ability of our model to account for flickery block provides a justification for the rigid monomer approximation. Flickers, which we identify as 6HB–4HB interconversions, occur on a sub-ms timescale, far faster than overall channel dissociation rates. If full dissociation involves significant backbone rearrangement, this is then a much slower process, and unlikely to affect the initial steps. Nonetheless, large amplitude monomer deformations could conceivably promote direct dissociation from the 6HB state, a possibility that should be investigated. The influence of this additional flexibility on dissociation could be studied by combining our Monte Carlo approach with normal mode analysis techniques (Tirion, 1996; Tama et al., 2000; Li and Cui, 2002), a development presently being pursued.

CONCLUSIONS

We have presented a Monte Carlo study of the simplest channel gating process: the mechanism of the gA dimer to monomer dissociation reaction. By using a simplified model capturing essential features of the monomer's kinetics we have found the reaction pathways for gA dimer dissociation and investigated the effect of hydrophobic mismatch on these lowest energy paths. Our results reveal numerous important mechanistic features that are likely to be generally characteristic of the dimer dissociation process. Our predictions are in good agreement with much experimental data.

A large electrostatic barrier, separating the 6HB and 4HB states, arises as the monomers rotate and the interjunctional H-bonding scheme is dephased. To reduce this barrier, the monomers are displaced laterally. Axial separation is energetically far more expensive than this lateral motion. The transition state for channel dissociation is reached when the monomers are displaced laterally ∼4–6 Å and separated by ∼1.6–2.0 Å with a rotational shift by two hydrogen bonds. This prediction is supported by the study of Lundbæk and Andersen (1999). Lateral displacement fluctuations in the 6HB state provide a rationale for closure events (flickers) at sub-ms times.

Hydrophobic mismatch substantially stabilizes formation of 4HB and even possibly 2HB states. In transiting between the 6HB, 4HB, and 2HB states ionic conductance is interrupted as the monomers undergo a relative lateral shift at the intermonomer junction by ∼4–6 Å. However, when the 4HB state forms the pore is fully open and ionic conductance is restored. This prediction of our model is also supported by experimental evidence (Mobashery et al., 1997).

The dimer undergoes uniaxial rotational and lateral diffusion due to local monomer dynamics. This local dynamics represents possible large amplitude motions of the gA monomers leading to global axial rotation of the gA dimer. Experimental evidence for a uniaxial global gA dimer rotation has been demonstrated by Lee et al. (1993).