Temperature Dependency of Molecular Mobility in Preserved Seeds

Abstract

Although cryogenic storage is presumed to provide nearly infinite longevity to cells, the actual timescale for changes in viability has not been addressed theoretically or empirically. Molecular mobility within preserved biological materials provides a first approximation of the rate of deteriorative reactions that ultimately affect shelf-life. Here, temperature effects on molecular mobility in partially dried seeds are calculated from heat capacities, measured using differential scanning calorimetry, and models for relaxation of glasses based on configurational entropy. Based on these analyses, glassy behavior in seeds containing 0.07 g H₂O/g dm followed strict Vogel-Tamman-Fulcher (VTF) behavior at temperatures above and just below the glass transition temperature (Tg) at 28°C. Temperature dependency of relaxation times followed Arrhenius kinetics as temperatures decreased well below Tg. The transition from VTF to Arrhenius kinetics occurred between ∼5 and −10°C. Overall, relaxation times calculated for seeds containing 0.07 g H₂O/g dm decreased by approximately eight orders of magnitude when seeds were cooled from 60 to −60°C, comparable to the magnitude of change in aging kinetics reported for seeds and pollen stored at a similar temperature range. The Kauzmann temperature (T_K), often considered the point at which molecular mobility of glasses is practically nil, was calculated as −42°C. Calculated relaxation times, temperature coefficients lower than expected from VTF kinetics, and T_K that is 70°C below Tg suggest there is molecular mobility, albeit limited, at cryogenic temperatures.

INTRODUCTION

The actual timescale for biological change at low temperatures (<−10°C) is of practical and fundamental interest because it relates to questions of the most economically efficient way to bank biological materials as well as the nature and kinetics of reactions that occur under ultracold conditions. Shelf-life of biological materials is dependent on temperature because the physical and chemical reactions that cause aging result from molecular motion in amorphous (noncrystalline) matrices. Relaxation times describe the structural mobility of amorphous systems (how rapidly the structure of the glass reverts to that of the supercooled liquid in equilibrium) and can give a first approximation of the molecular mobility that may be associated with degradation of biological materials stored in the glassy state. The temperature dependency of relaxation is described by the fragility of the glass (Angell, 1991). In strong (i.e., nonfragile) glasses, molecular mobility follows Arrhenius behavior such that relaxation time is exponentially related to 1/temperature. Alternatively, mobility in fragile glasses have a larger temperature dependency, and models such as Vogel-Tamman-Fulcher (VTF) predict almost a double-exponential relationship between relaxation times and 1/temperature until viscosity (the reciprocal of mobility) approaches infinity at T₀ (Angell, 1991, 2002),

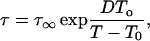(1)

where τ and τ_∞ are relaxation times at temperature T and the high temperature limit and D is a coefficient inversely proportional to glass fragility (i.e., low for fragile glasses). The value of D typically ranges from ∼5 to 12 for glasses of intermediate fragility and is often approximated from the relationship

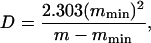(2)

where m is the glass fragility, describable by the slope of an Arrhenius plot of relaxation times at the glass transition temperature (Tg) and m_min = log (τ_Tg/τ_∞). When Arrhenius plots are not available, m can be approximated by m_min/(1–T₀/Tg) (Angell, 1991; Hodge, 1996; Andronis and Zografi, 1998). The ratio T₀/Tg approaches 1 for fragile glasses and theoretically approaches 0 for strong glasses, although 0.5 is the smallest value reported (Angell, 1991; Hodge, 1996). The value of τ_∞ is commonly assigned 10⁻¹⁴ s, the order of vibrational lifetimes (Angell, 1991). The values for Tg and τ at Tg (τ_Tg,) must be measured directly using calorimetry or various assessments of mobility. For the present study, we used electron paramagnetic resonance (EPR) measurements of cellular viscosity in seeds containing 0.07 g H₂O/g dm to approximate τ_Tg as 10⁻⁴ s (Buitink et al., 1999, 2000).

The physical significance of T₀ has been equated to the Kauzmann temperature (T_K, first reported in 1948), where the thermodynamic properties of the supercooled liquid (i.e., enthalpy, entropy, and volume) are extrapolated to a temperature that intersects with the properties of the crystal, and molecular motion is reduced to levels found in the crystalline state (Angell, 1991; Andronis and Zografi, 1998; Shamblin et al., 1999). Although impossible to measure directly, T_K can be calculated from the melting enthalpy and the temperature dependency of the heat capacity of crystalline and supercooled liquid states (Shamblin et al., 1999),

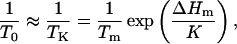(3)

where T_m is the melting temperature and K is proportional to the configurational heat capacity (Cp_config), the difference between Cp in the crystalline and liquid states (Angell, 1991; Shamblin et al., 1999). When these values are not available, K can be approximated by the heat capacity change during a glass transition (ΔCp) × the temperature (in K) of the glass transition (Shamblin et al., 1999). As with T₀/Tg ratios, a large ΔCp, observed in typical scanning experiments during glass transitions, may indicate fragile glass behavior (Angell, 1991), although it has also been attributed to high hydrogen bonding with few implications about glass fragility (Hodge, 1996; Shamblin et al., 1999).

Actual measurements of molecular mobility in glasses near T₀ (or T_K) are often precluded because of the long timescales or the limited temperature range of various instrumentation. Timescales at low temperatures can be approximated assuming Arrhenius or VTF behavior, although interpretation of the VTF model is limited to temperatures near Tg and Arrhenius behavior is assumed with T ≪ Tg. Consideration of the fictive temperature, T_f (a parameter that describes how closely the structure of the glass resembles the structure of the supercooled liquid in equilibrium), allows a quantitative expression of the temperature dependency of amorphous relaxation at temperatures below Tg using the Adam and Gibbs model (Adam and Gibbs, 1965; Scherer, 1984; Hodge, 1987; and later applied by Andronis and Zografi, 1998; Shamblin et al., 1999),

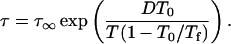(4)

Fictive temperature, T_f, is a measure of the configurational entropy of the glass relative to equilibrium conditions, and allows the temperature dependency of relaxation time to be expressed as a temperature dependency of entropy, which is a function of the heat capacity difference between the liquid and glassy states. According to Shamblin et al. (1999),

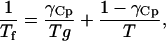(5)

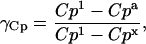(6)

where Tg is the glass transition temperature, Cp^l, Cp^x, and Cp^a are heat capacities of the supercooled liquid, crystal, and amorphous matrices, and γ_Cp ranges from 0 to 1 depending on whether relaxation follows VTF or Arrhenius kinetics.

The model described by Eq. 4 allows relaxation times in amorphous systems to be calculated with parameters measured using differential scanning calorimetry for a range of temperatures (Shamblin et al., 1999; Hancock and Shamblin, 2001; Zhou et al., 2002). This model is currently used to measure relaxation times of sugars and pharmaceuticals (Andronis and Zografi, 1998; Shamblin et al., 1999; Hancock and Shamblin, 2001; Zhou et al., 2002), but has yet to be applied to multicomponent systems. Application of this model to preserved cells would provide alternative methods to estimate intracellular viscosity at low temperatures, and hence allow better prediction of storage stability of cryopreserved materials. Depending on the water content of cells, “glass formers” have been variously attributed to solutes (dry cells, i.e., Leopold et al., 1994; Leprince and Walters-Vertucci, 1995) or water (dilute systems, i.e., Franks, 1985; Angell, 2002), making it unclear which pure substance provides an appropriate basis for comparison. Since water concentration is a common and easily measured feature of cells, thermodynamic measurements in this article are expressed in terms of water, rather than other components of the glass, namely solutes. Thus the heat capacity of the crystalline state (Cp^x in Eq. 6) and T_m and ΔH_m for water (Eq. 3) are well-known. In partially dried systems, the heat capacity of liquid water is quite different from pure water (Vertucci, 1990; Buitink et al., 1996), and values of Cp^l (Eq. 5) for materials with water contents between 0.05 and 0.15 g H₂O/g dm were calculated from the slopes of the linear relationships between water content (g H₂O/g dm) and heat capacity (J/g dm/°C) published for seeds and pollen at temperatures between 45 and −60°C (Vertucci, 1990; Buitink et al., 1996). At the homogenous nucleation temperature, estimates of Cp^l are similar for partially dried systems and pure liquid water (Angell et al., 1973).

In this article, various parameters reflecting the molecular mobility within the amorphous aqueous matrix are calculated for seeds containing 0.07 g H₂O/g dm in an attempt to correlate deterioration rates with physical parameters and to predict best-storage practices for biological materials. Calorimetric measurements of phase transitions and heat capacity are used to calculate the fictive temperature, Kauzmann temperature, rate of structural relaxation of the aqueous glass, and the temperature dependency of relaxation times. Demonstration of relaxation within the aqueous domain at temperatures well below Tg or T_f suggests that temperatures currently deemed safe for storage may be unreliable, and that preservation practices and assessments of longevity should be evaluated in the context of measurable molecular mobility.

METHODS AND MATERIALS

Calorimetric parameters needed to calculate τ in Eq. 4 were taken from differential scanning calorimetry measurements of soybean (Glycine max) and pea (Pisum sativum) seeds and cattail (Typha latifolia) pollen that have been previously published by this lab (Vertucci, 1990; Vertucci and Roos, 1993; Leprince and Walters-Vertucci, 1995; Buitink et al., 1996). Briefly, stepwise shifts in power when heating at 10°C/min from −100 to +100°C were used to detect glass transitions, and power displacement when warming 4°C at 4°C/min after a 2-min isothermal equilibration was used to measure heat capacity. Heat capacity was measured between −150 and 60°C in 10–30°C increments. Data reported for materials containing 0.07 g/g H₂O were used to ensure comparable conditions for relaxation time measurements and seed and pollen longevity experiments (Vertucci et al., 1994; Buitink et al., 1998). The heat capacity attributed to the aqueous glass (Cp^a in Eq. 6) in seeds and pollen containing 0.07 g/g H₂O was calculated by subtracting the heat capacity of comparable materials that were completely dry.

Values for the heat capacity of the supercooled liquid (Cp^l) and the crystal (Cp^x) as a function of temperature were taken from the literature. The heat capacity of water in partially dried systems at specific temperatures (Buitink et al., 1996) was interpreted as Cp^l (see Introduction), inasmuch as published values for pure water at those temperatures (Angell et al., 1973; Ginnings and Furukawa, 1953) gave nonsensical results. The heat capacity of ice (Cp^x) was taken from the linear increase of the Cp of ice with temperature (Angell et al., 1973). To approximate Cp^x near Tg, the linear relationship was extrapolated above 0°C.

Constants used to calculate parameters in Eqs. 1–5 are listed in Table 1. Enthalpy and temperature of water melting transitions have been reported for seeds (e.g., Vertucci, 1990) at ∼−5°C and 330 J/g H₂O for water-saturated seeds, and ∼−25°C and 150 J/g for drier seeds (∼0.25 g H₂O/g dm) where freezing and melting transitions are just detectable using standard calorimetric procedures. Glass transitions are measured between 20 and 40°C for seeds and pollen at the study water content of 0.07 g H₂O/g dm (Leopold et al., 1994; Leprince and Walters-Vertucci, 1995; Buitink et al., 1996, 1999) and an average value of 28°C is used for the purposes of this article.

TABLE 1.

Constants used to calculate relaxation times for seeds and pollen containing 0.07 g H₂O/g dm

Constant	Equation	Value	Reference
Tg	5	28°C	Leopold et al. (1994); Leprince and Walters-Vertucci (1995); Buitink et al. (1996, 1999, 2000).
TK (∼T0)	1, 3, 4	−44 to −41°C	Calculated
Tm	3	−5°C or −25°C	Vertucci. (1990)
Tf	4, 5	∼17°C	Fig. 3
ΔHm	3	330 J/g or 150 J/g	Vertucci (1990)
K	3	2135 J/g	Fig. 1
τ∞	1, 4	10−14 s	Hodge (1996); Andronis and Zografi (1998)
τTg	for mmin	10−4 s	Buitink et al. (1999, 2000)
mmin	2	10 (dimensionless)	Calculated
m	2	43 (dimensionless)	Calculated
D	1, 2, 4	7 (dimensionless)	Calculated

RESULTS AND DISCUSSION

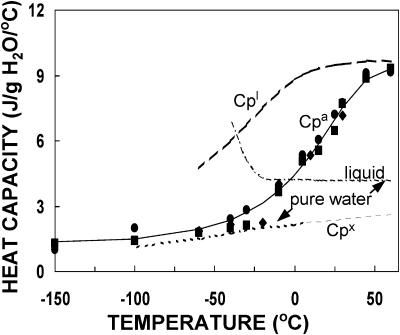
The relationship between heat capacity and temperature for the supercooled liquid, crystalline, and glassy states in soybean and pea seeds and cattail pollen containing 0.07 g H₂O/g dm are provided in Fig. 1. Heat capacity increased linearly with temperature for ice and hyperbolically for supercooled water. The heat capacity of amorphous water (Cp^a in Eq. 6) was calculated from the difference in published heat capacities of pea, soybean, and pollen at water contents of 0.07 and 0.0 g/g (Vertucci and Roos, 1993; Buitink et al., 1996). These values decreased from 2.5 to 0.4 J/g dm/°C with temperatures ranging from 60 to −150°C and gave Cp^a values between 9.3 and 1.3 J/g H₂O/°C when expressed in terms of water (Fig. 1). The large change in Cp^a at temperatures flanking the glass transition temperature, consistent with values of ΔCp at Tg measured during scanning experiments (Leprince and Walters-Vertucci, 1995), probably reflects high hydrogen bonding attributed to polyhydroxyl substances (Angell, 1991; Andronis and Zografi, 1998; Shamblin et al., 1999). Large changes in Cp^a were observed over a 50°C temperature range, which contrasts with a 25°C difference observed between onset and finish temperatures of glass melting transition recorded during typical scanning experiments at 10°C/min. Based on Cp^a data in Fig. 1, the midpoint of the glass transition occurs at ∼5°C, rather than at 28°C more typically observed when scanning experiments (10°C/min) are conducted. The lower value for Tg is expected with longer observation times. However, for the sake of consistency with past work using seeds, a Tg = 28°C is used in calculations presented here.

FIGURE 1.

Heat capacity of ice (Cp^x), supercooled water (Cp^l), and amorphous matrices (Cp^a) in pea (solid squares), soybean (solid circles), and cattail pollen (solid diamonds) containing 0.07–0.075 g H₂O/g dry mass as a function of temperature. Data are calculated from heat capacity values reported previously: seeds and pollen (Vertucci and Roos, 1993; Buitink et al., 1996), supercooled liquid water (Buitink et al., 1996), supercooled pure water and ice (Angell et al., 1973), and pure liquid water (Ginnings and Furukawa, 1953). Hypothetical values for heat capacity of the crystalline phase were calculated by extrapolating the linear relationship beyond 0°C (light dashed lines). Other curves are drawn from sigmoidal equations fit to data using SigmaPlot software. Data for pea, soybean, and pollen were pooled for the curve-fitting analysis and points on the curve provided Cp^a values used to calculate γ_Cp and T_f in Fig. 3.

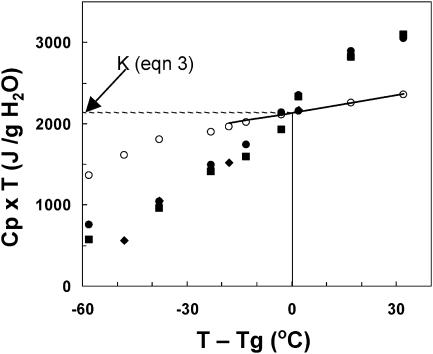
The constant K (Eq. 3), used to calculate the Kauzmann temperature, T_K, was calculated from the configurational heat capacity (Cp^l−Cp^x) at Tg according to Shamblin et al. (1999). As with many materials, the plot of (Cp^l−Cp^x) × T versus T−Tg for seeds and pollen gives a near-horizontal line, and K, approximated by the value of the curve at Tg, is assigned a value of 2135 J/g H₂O (open symbols in Fig. 2, Table 1). This calculation of K relies on extrapolation of the temperature dependency of Cp^x above 0°C. A similar value of K (2185 J/g H₂O) was approximated from the value of Cp^a (difference in heat capacity of seeds containing 0.07 and 0 g H₂O/g dm) × T at Tg (solid circles in Fig. 2), although this latter method is likely to introduce some error (Shamblin et al., 1999). Values of K for sugars and pharmaceuticals ranged from 100 to 350 J/g solute (Shamblin et al., 1999; Zhou et al., 2002), which are slightly larger than calculated here for water when expressed on a molar basis. The Kauzmann temperature was calculated according to Eq. 3 and ranged from −41 to −44°C, regardless of whether K = 2135 or 2185 or T_m and ΔH_m values were assigned as −5°C and 330 J/g or −25°C and 150 J/g (Table 1). Using constants listed in Table 1, an entropy-based T_K was calculated as −41°C according to Shamblin et al. (1999). The value T_K = −42°C was used in all subsequent calculations to approximate T₀. Based on this value, the ratio T_K/Tg ≈ T₀/Tg for seeds containing 0.07 g H₂O/g dm is 0.77 (T_K/Tg = 231/301), a value comparable to ethanol, glycerol, and some pharmaceuticals (Angell, 1991; Shamblin et al., 1999; Hancock and Shamblin, 2001), but considerably lower than sucrose, sorbitol, and trehalose (T_K/Tg ≥ 0.88) (Shamblin et al., 1999). From these data, glasses in partially dried seeds are interpreted to behave with intermediate fragility, and sugar glasses, often deemed protective in anhydrous organisms, are fragile. The value 1−T_K/Tg (≈0.23 for seeds containing 0.07 g H₂O/g dm) corresponds to the ratio of Ea below and above Tg (Hodge, 1996), and this is consistent with a 4.3-fold difference in slope of relaxation times described in Fig. 5.

FIGURE 2.

The relationship between temperature and configurational heat capacity multiplied by temperature. Configurational heat capacity (Cp^l−Cp^x) (open circles) was calculated from the difference between heat capacities of the crystalline and supercooled liquid states given in Fig. 1. The value of Tg used to scale the abscissa is 28°C. At Tg, the value of Cp_config × T is 2135 J/g H₂O, the value subsequently assigned for K (Table 1). Also given are heat capacity data points for the amorphous phase in seeds and pollen taken from Fig. 1.

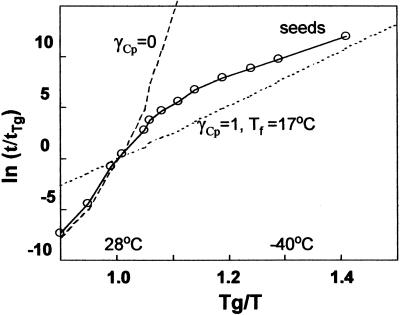
FIGURE 5.

Arrhenius plot, scaled by Tg (x axis) and τ_Tg (y axis), of relaxation time (τ) in molecular glasses of seeds and pollen containing 0.07 g H₂O/g dm (open circles). Dashed lines represent relaxation times when γ_Cp is constrained to constant values of 0 (VTF behavior) or 1 (Arrhenius behavior, T_f = 17°C), representing the two extremes of temperature dependency for molecular mobility of glasses.

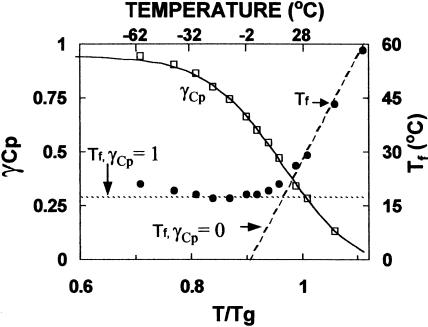
Based on values of Cp^l, Cp^x, and Cp^a (Fig. 1), the relative differences of heat capacities as a function of temperature in seeds and pollen at 0.07 g/g, expressed by γCp (Eqs. 5 and 6), can be calculated (Fig. 3, open circles). As with all glasses, Cp of the seed glass near Tg is intermediate between Cp^l and Cp^x (Fig. 1), and for seeds, γCp ranged from 0.3 to 0.5 near Tg. The difference in γCp between seeds and sugars (γCp ranged from 0.6 to 0.8; Shamblin et al., 1999) suggests that glasses may be more fragile in seeds, contrasting with conclusions based on T₀/Tg ratios. This discrepancy can be explained by examining the temperature dependency of γCp in seeds containing 0.07 g H₂O/g dm. Values for γCp in seeds ranged from <0.2 (indicative of fragile glasses) at temperatures above Tg to >0.8 (indicative of strong glasses) at temperatures below Tg. The observed temperature dependency of γCp resulted in a change in fictive temperature (T_f) (Eqs. 4 and 5) from values equivalent to T near and above Tg to values of ∼17°C when T ≪ Tg (Fig. 3, solid circles). Conceptually, the value of T_f at T < Tg reflects the temperature at which the thermodynamic properties (i.e., entropy, enthalpy, and volume) of the amorphous matrix were “frozen” into the glass and it has been suggested that T_f is a better indicator of glassy behavior than Tg (Hodge, 1996). Constant T_f indicates that the timescale for relaxation is short compared with the average relaxation time of the glass, and reflects the conversion of relaxation to Arrhenius kinetics. The temperature dependency of γCp shows that this change occurs at temperatures intermediate between T_f and T_K, an observation that has been reported previously for aqueous glasses (Andronis and Zografi, 1998; Angell, 2002).

FIGURE 3.

The relationship between temperature and the ratio of excess heat capacity to configurational heat capacity (γ_Cp) (left axis, open squares) and fictive temperature (T_f) (right axis, solid circles). Values for γ_Cp were calculated from points derived from fitted curves for Cp^x, Cp^l, and Cp^a in Fig. 1 according to Eq. 6, and T_f was calculated according to Eq. 5. Also given are T_f versus temperature relationships assuming γ_Cp = 0 (VTF behavior) and γ_Cp = 1 (Arrhenius behavior) (dashed lines).

Relaxation times within the aqueous amorphous matrix were calculated for seeds at 0.07 g/g using calculated values for T_f (Fig. 3), T_K, and other constants listed in Table 1 (Fig. 4, solid squares). Relaxation times calculated for seeds at Tg are 10–100 times shorter than those determined for sucrose or indomethacin at Tg (Andronis and Zografi, 1998; Shamblin et al., 1999), and this probably results from different measures of τ_Tg (Table 1). Relaxation times calculated for seeds changed by approximately eight orders of magnitude over a 100°C temperature range (Fig. 4). This order of change is intermediate between direct measurements of rotational correlation times in seeds and pollen using EPR (a 10-fold change according to Buitink et al., 1999, 2000; Fig. 4, solid diamonds) and measures in sucrose and indomethacin using other direct methods or application of the theoretical considerations used here (10–12 orders of magnitude according to Shamblin et al., 1999; Andronis and Zografi, 1998). Because of differences in temperature dependency, seed glasses are calculated to have greater molecular mobility than sucrose glasses at T ≪ Tg.

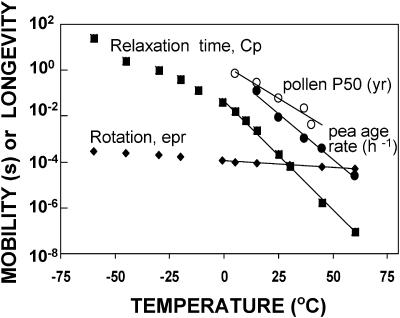
FIGURE 4.

Calculated values of relaxation time (τ) in molecular glasses of seeds and pollen as a function of temperature. Values are calculated according to Eq. 4 using constants in Table 1 and T_f (solid circles in Fig. 3). Also given are rotation correlation times measured for pea using EPR (solid diamonds; see also Buitink et al. (1999, 2000) and shelf-life parameters for pea seeds and pollen containing 0.07 g H₂O/g dry mass stored at temperatures between 5 and 60°C (Vertucci et al., 1994; Buitink et al., 1996). Linear regressions of log (mobility or shelf-life parameters) versus temperature (r² > 0.94, lines in figure) at temperatures >0°C gave slopes of 0.09 (τ), 0.006 (EPR measurements), 0.08 (pea age rate), and 0.06 (pollen half-life).

Molecular mobility within seeds and pollen is hypothetically related to the rate at which they deteriorate in storage (e.g., Vertucci and Roos, 1990; Buitink et al., 2000). To test this supposed relationship, aging rates reported for pea seeds and cattail pollen containing 0.07 g H₂O/g dm were plotted against storage temperature ranging from 0 to 60°C (Vertucci et al., 1994; Buitink et al., 1996) (Fig. 4, circles), and the slopes of the linear relationship between log age rate or P50 versus storage temperature (−0.08 and −0.06 for pea seeds and cattail pollen, respectively) were compared to the slopes of log τ or rotational correlation time versus temperature (−0.09 and −0.006, respectively). Although the temperature dependency of τ is greater than the temperature dependency of seed or pollen deterioration, changes in τ with temperature are more reflective of aging rates than measured rotation correlation times reported earlier (Buitink et al., 2000).

Temperature coefficients for relaxation times are described by Arrhenius plots scaled by Tg and τ at Tg (Fig. 5). For comparison, relaxation times for strict VTF behavior (fragile glass, γCp = 0, T_f = T) and Arrhenius behavior (strong glass, γCp = 1, T_f = 17°C) are also given. In seeds, τ followed VTF kinetics as temperature decreased through Tg, as is typical for most glasses. At temperatures <5°C (Tg/T = 1.1), τ deviated from VTF behavior, giving shorter relaxation times than predicted, as has been observed previously in other systems (Hodge, 1995; Andronis and Zografi, 1998). Activation energies calculated for seeds, assuming variable γCp with temperature, were 185 and 55 KJ/mol at and below Tg, compared to 246 and 660 KJ/mol when γCp = 0 (VTF behavior) and 66 KJ/mol if γCp = 1 (Arrhenius behavior). The tendency to deviate from VTF toward Arrhenius-like behavior as the glass was progressively cooled was noted for indomethacin (Andronis and Zografi, 1998) and resulted in lower temperature dependency of τ and greater molecular mobility at low temperatures than is usually predicted for glasses. Measurable relaxation at temperatures below T_K attests to the remaining molecular mobility in amorphous solids.

CONCLUSIONS

Theoretical considerations of differences in thermodynamic parameters among crystalline, supercooled liquid, and glassy states were applied here as a first estimate of molecular mobility within partially dried seeds. Changes in relaxation times with temperature, calculated in seeds using concepts of configurational entropy and measurements of heat capacity, are of similar order as the changes in seed and pollen aging rates with temperature, supporting the previously-hypothesized relationship between intracellular viscosity and storage stability and providing better correlations than techniques currently used for seeds. Based on the correlation between relaxation times and aging rates in seeds at temperatures >0°C, a lower temperature dependency of relaxation time at temperatures <0°C, and measurable relaxation at temperatures as low as −60°C, one can predict detectable aging and a shift in the temperature coefficient of storage stability in seeds held cryogenically. A test of these predictions will be presented in a subsequent article (C. Walters, L. Wheeler, and P. Stanwood, unpublished).

The results presented in this article show that the glasses formed when seeds dry have intermediate fragility near the glass transition, and that relaxation follows Arrhenius kinetics when temperature is between the fictive temperature (T_f) and the Kauzmann temperature (T_K). The physical basis for glass fragility is still poorly understood, although strong glasses are found in multicomponent aqueous systems and appear to have molecular constraints because of the large number of bonds that need to be broken to allow molecular rearrangements (Angell, 2002). It is believed that cooperative rearrangements among molecules are required to confer mobility and the number of molecules in cooperative groups increases with decreasing temperature (Adam and Gibbs, 1965 as cited by Angell, 1991 and Andronis and Zografi, 1998). Reversion to Arrhenius behavior at T < Tg implies that there is residual capacity for relaxation in glasses even at low temperature. The results reported here only consider the special case of seeds containing 0.07 g H₂O/g dry mass. Past studies have predicted temperature-water content interactions on intracellular viscosity (Vertucci and Roos, 1990; Buitink et al., 1999, 2000), and those effects, in combination with interactions with cellular constituents, are yet to be explored for diverse complex systems. The general results, that cooling 90°C below Tg results in a six-order change in relaxation time and even still there is evidence for relaxation at supercold temperatures (Figs. 4 and 5), has important implications for stability of cryogenically stored materials.

Therefore, molecular motion must be regarded as unavoidable in vitrified biological materials. Certainly, Tg marks the temperature at which limitations of molecular mobility are initiated; however, there is still sufficient motion in seeds at Tg to allow substantial degradation in a short time. Temperatures at which molecular motion are severely limited may be a better benchmark for “safe storage,” and so T_K rather than Tg may be a more appropriate standard. For the most part, gene banks are working toward new standards: conventional storage temperatures for seeds and hydrated materials are −18 and −196°C (liquid nitrogen), respectively, which are roughly comparable to T_K calculated for these materials at −28 and −150°C, assuming a T_K/Tg ratio of 0.76 and Tg = 50°C for seeds stored at 0.05 g H₂O/g dm and Tg = −110°C for hydrated cells. Nevertheless, molecular motion is still allowable at temperatures <T_K, meaning that indefinite shelf-life may not be possible using current cryogenic technologies. If this is true, the desired or achievable shelf-life for preserved materials must be more concretely defined by the user and gene bank operator and timescales for biological change must be determined for an array of materials and preservation strategies.