Abstract
A new method of analysis is described that begins to explore the relationship between the phases of ion channel desensitization and the underlying states of the channel. The method, referred to as covariance fitting (CVF), couples Q-matrix calculations with a maximum likelihood algorithm to fit macroscopic desensitization data directly to kinetic models. Unlike conventional sum-of-squares minimization, CVF fits both the magnitude of the recorded current and the strength of the correlations between different time points. When applied to simulated data generated using various kinetic models with up to 11 free parameters, CVF leads to reasonable parameter estimates. Coupled with the likelihood ratio test, it accurately discriminates between models with different numbers of states, discriminates between most models with the same number but a different arrangement of states, and extracts meaningful information on the relationship between the desensitized states and the phases of macroscopic desensitization. When applied to GABAA receptor traces (outside out patches, α1β2γ2S, 1 mM GABA, >2.5 s), a model with two open states and three desensitized states is favored. When applied to simulated data generated using a consensus model, CVF leads to reasonable parameter estimates and accurately discriminates between this and other models.
INTRODUCTION
GABA is the major inhibitory neurotransmitter in the vertebrate central nervous system. The GABAA receptor (GABAR) mediates fast inhibitory synaptic input and alteration of its properties has significant neurological and behavioral effects. It is the site of action of many neuroactive agents, including sedative/hypnotics such as benzodiazepines and barbiturates, endogenous steroids, alcohols, and multivalent cations. The study of the GABAR is hindered by the lack of a comprehensive kinetic model of its function. Although it may never be possible to identify a single model that accurately reproduces every observed behavior of the receptor, a model or family of models that reliably describes the biologically relevant functions (activation, desensitization, deactivation, and recovery) would be of great value. In particular, such a model or models would act as a much-needed framework for better understanding the growing body of evidence on the effects of structural and pharmacological manipulations.
To date, most studies have focused on measuring surrogate parameters such as relaxation time constants or mean sojourn times. From this work, several general features of GABAR function have become apparent. Open and closed time distributions of single-channel events under steady-state conditions are best fit by multiple components (Macdonald et al., 1989; Weiss and Magleby, 1989). From this, it is clear that the receptor is capable of visiting multiple distinct open and closed states. Because these distributions are derived from binned data, however, a great deal of information about the time correlations is lost. Studies examining the correlations between adjacent events (Ball and Sansom, 1989; Horn and Lange, 1983; Magleby and Weiss, 1990; Qin et al., 1996, 1997; Sakman and Neher, 1995; Weiss and Magleby, 1989) as well as the hidden Markov (Qin et al., 2000a,b) and the HJCFIT (Colquhoun et al., 2003) methods begin to take advantage of this type of information. The most comprehensive kinetic model, based on single-channel and macroscopic GABAR data, has a total of three open states, nine closed states, and three desensitized states (Haas and Macdonald, 1999). Two fundamental questions remain at least partially unanswered: how many of theses states are relevant to the description of synaptic function and what is the exact arrangement (i.e., connectivity) of the relevant states?
Perturbation studies using agonist concentration jumps examine the response of a population of GABARs to large and rapid changes in agonist concentration. This experimental paradigm more closely mimics synaptic events and the resulting traces are typically fit to exponential functions by sum-of-squares minimization. This method also ignores time correlations (see Appendix I) and generates surrogate values (time constants and magnitudes) whose relationship to the underlying molecular mechanisms is unclear. The recent application of first latency analysis to perturbation results begins to examine the arrangement of states and suggests that desensitization can precede channel opening (Burkat et al., 2001).
What is needed is a method that can fit macroscopic perturbation data directly to a particular kinetic model by taking into account both the magnitude of the current at each time point as well as the correlations among the different points. The method described here, referred to as covariance fitting (CVF), accomplishes this by using the Q-matrix technique to calculate the correlations predicted by various kinetic models. Coupled with the general multivariate likelihood function and likelihood maximization using a variable metric algorithm, this method accurately estimates kinetic parameters and reliably discriminates between models with up to 11 free parameters.
METHODS
Model nomenclature
A wide variety of kinetic models are discussed in this article. The agonist binding step has been omitted and all receptors are in the closed state (C) at time zero. Each model contains a single C state and all other nonconducting states are referred to as desensitized states (D). The distinction between the C and D states is otherwise arbitrary.
For models with a single open state: 1D, 2D, 3D, 4D indicate 1, 2, 3, or 4, desensitized states, respectively. The number of desensitized states on each side of the gating isomerization has a powerful influence on CVF results. To illustrate this feature of each model, a Roman numeral is used to indicate the number of desensitized states on the closed side of the gating isomerization. Thus, model 3D-I has a total of three desensitized states with one connected to the closed state and two connected to the open state. The arrangement of two or more desensitized states on the same side of the gating isomerization can be either linear (ln) or branched (br). Unless otherwise stated, all such models are branched, meaning all desensitized states are connected directly to either the open or closed state. 1D-C refers to a cyclic model in which the D state is connected to both the closed and open states. 3D-C refers to a cyclic variation of 3D-I in which a transition is allowed between the D state connected to the closed state and one of the D states connected to the open state. This nomenclature is not meant to be comprehensive, but uniquely describes the single open-state models studied here.
No systematic approach is used for naming the limited number of two and three open-state models studied here. Unless otherwise indicated, all multiopen-state models have three desensitized states. See legend to Fig. 7 for the abbreviations used to describe multiopen-state models.
FIGURE 7.
GABAR and simulated COO data, number and arrangement of states. Sum of L[LH]s from fitting GABAR and COO data to 12 different kinetic models. Solid lines connect models with a similar number of kinetic parameters. Dashed lines connect simple and complex models. See Tables 2 and 3 for summary of L[LR]s comparing selected models. (A) Sum of six L[LH]s for the six GABAR traces. (B) Sum of 10 L[LH]s for the 10 COO data sets (see Table 7 for simulation parameters). Single and double open-state models favored by GABAR data are emphasized (*). Abbreviations used in the text are: 2D-OO, refers collectively to the three left-most models; 3D-II-OO and OCO, respectively, refer to the models to the left and right of COO; OCOO, refers to the model with a third open state; 4D-OO, refers collectively to the three models with a total of 4D states and a direct connection between the open states; OCDO, refers to the right-most model.
Desensitized states are numbered beginning with those connected to the closed state (proximal) followed by those connected to open states (distal). Parameters associated with entry into a desensitized state are designated Kf, and parameters associated with leaving a desensitized state are designated Kr. Alpha (α) and beta (β) refer, respectively, to leaving or entering an open state from either the closed state or from a more proximal open state.
Generation of simulated data
Simulated stochastic data are generated using various kinetic models. The agonist binding step has been omitted and simulations are done as if GABA association is instantaneous. At time zero, all receptors start in the closed liganded state (C). Two different methods are used to choose subsequent dwell times. The bulk of the simulated data sets are generated using the QUB software (Research Foundation, State University of New York, Buffalo, NY) (Qin et al., 1996, 1997) that determines dwell times directly from the results of a random number generator with an exponential distribution and an average equal to the inverse of the exiting rate constant. A limited number of simulated data sets are generated using the results of a random number generator with a uniform distribution. Here, a random number between 0 and 1 is generated for each 0.01-ms time interval. The dwell time ends and a transition occurs when the random number falls within a critical region. The size of the critical region is proportional to the probability that a transition will occur during a 0.01-ms period. The fastest rate constant used (3000 s−1) has a transition probability of only 0.03 during any given interval. No differences are observed between the two methods in any subsequent analysis.
Smooth simulations are done either by numerically solving the differential equations using the Runge-Kutta method, or by using the Q-matrix technique (Eq. 3, Appendix I). The values generated by the two different methods for the same model differ by <0.3%.
Zero-time determination
Because the concentration jump in an actual experiment is not instantaneous, the most appropriate time point to be used as time 0 must be determined empirically. This is done by fitting the rising phase (beginning when the current reaches half the maximum) and the initial decay phase to the following formula using sum-of-squares minimization (Prizm, GraphPad, San Diego, CA):
 |
where It is the current associated with the time measured from the beginning of the recording trace (t), τr is the time constant of the rising phase, τd is the time constant of the fast phase of desensitization, Id is the magnitude of the fast phase of desensitization, Iss is the magnitude of the subsequent phases of desensitization plus the steady state, and Δt is adjusted as a free parameter. For subsequent analysis, each time point is adjusted by the value of Δt arrived at using the above fit.
Data point selection
Because CVF requires generation of a covariance matrix (see Appendix I), it is typically impossible to analyze an entire data set. A 3000-point data set, for example, would require a matrix with 9,000,000 elements. Data sets of 100–200 points are, therefore, selected from the raw sets. Selecting points evenly spaced in time (every 30 ms for a 3-s trace) would sacrifice a great deal of information during the steep initial phase of desensitization. Here, points are selected so that there is a roughly even distribution along the idealized path of desensitization (Fig. 1).
FIGURE 1.
Data point selection. (Top left) Sample of raw simulated data generated using model 1D-I, 0.1 ms per point, 300-ms duration. See Table 1 for simulation parameters. (Bottom left) Illustration of how the normalized distance along the idealized path of desensitization is calculated. Smooth curve from fit of raw data to a single exponential. Value of 1.72 is for tsf = 1 (see Methods). (Top right) Results of selecting 100 points evenly along the path of desensitization. (Bottom right) Results of fitting selected data to the correct model (1D-I) using CVF (solid line) and by minimizing sum of squares (dashed line). Insets show expanded time.
First, the raw set is fit to an exponential decay function by sum-of-squares minimization. The resulting exponential equation is then used to determine the extent of desensitization during the recording period (ΔInorm = I0 − If), where I0 is the current extrapolated to t = 0, and If is the current predicted by the exponential equation at the final time point. ΔInorm is used to normalize each current value. Time is normalized by dividing each value by Δtnorm × tsf, where Δtnorm is the final time point and tsf is a timescale factor that can be adjusted to favor earlier or later points. Unless stated otherwise, selection is done evenly along the path of desensitization by setting tsf = 1. When tsf > 1, earlier time points are favored and when tsf < 1, later time points are favored.
The normalized distance along the idealized path of desensitization is calculated in segments (Si) using the Pythagorean theorem (see Fig. 1). ΔIi is determined by evaluating the exponential equation for each time point associated with the raw data and Δti is the interval between each time point. As the segments are added, each time point is associated with a distance along the path of desensitization. The total distance is calculated by summing the normalized segments. The total distance along the idealized path is divided by the number of points desired (100–200) minus 1, giving a step distance. Finally, the selected data set is created using the relationship between the time and the distance along the path.
The first point in the raw data set with a current greater than one-half the peak current is included as the first point in the selected data set. Each subsequent point included is the first point past the next step distance. If a step distance is not associated with a point, the next point is included and the step distance recalculated based on the remaining distance and the number of points yet to be included.
Parameter estimation
CVF estimates kinetic parameters using the principals of maximum likelihood (ML) (see Appendix I) and a variable metric algorithm. A clear description of the variable metric algorithm can be found in Acton (1970), however the formula for calculating the Hessian matrix differs from that shown in Press et al. (1992). This study uses the formula presented in Press et al. (1992). First and second derivatives of the likelihood with respect to each parameter are calculated numerically. Maximization along a chosen trajectory is done by parabolic interpolation (Press et al., 1992). Convergence is reached when subsequent iterations change the parameters by a factor of <0.0005. This allows CVF to routinely identify differences in L[LH] as small as 0.001 (see Fig. 5 B). A detailed description is given in Appendix II of the different methods used to generate initial values for CVF. When performed using a Pentium IV 2.4 GHz processor (Intel, Santa Clara, CA), fitting a single data set with 200 points to a model with 11 free parameters typically requires between 12 and 36 h.
FIGURE 5.
Simulated 3D data, arrangement of states. (A) Sum of 10 L[LH]s from fitting 10 3D-I,pdd data sets (see Table 6 for simulation parameters) to eight different kinetic models. Solid lines connect models with a similar number of states. Dashed lines connect complex and submodels. No difference in L[LH] is detected between linear and branched model. Among the 3D models, the correct model (large symbol) and its linear counterpart have the highest total L[LH]. (B) Fitting results shown in A are used to calculate L[LR]s comparing 3D models that differ in the position of a single desensitized state. A log scale is used here to illustrate the differences in the distribution of L[LR]s observed when making different types of comparisons. Results of comparing branched and linear models for both 3D-I and 3D-II are combined.
Unless stated otherwise, all fitting is done using CVF. A limited amount of fitting is done using variance-weighted sum-of-squares minimization (wSS). This method is identical to CVF, except that the covariance matrix is limited to the diagonal elements. Each diagonal element contains the variance for a given time calculated using the covariance formula (see Appendix I). Fitting referred to simply as sum-of-squares minimization is done without weighting.
Model discrimination
In addition to identifying parameter estimates, the ML method generates a maximum likelihood estimate (MLE) that is used to discriminate between different kinetic models. Two models are compared by fitting the same data set to each model and calculating the ratio of their respective MLEs, the likelihood ratio (LR). As a test of statistical significance, it is well established that no test has a higher power than the LR test (Mood et al., 1974; Rao, 1973). To apply the LR test, it is necessary to know the expected distribution of the natural logarithm of the LR (L[LR]) when one of the two models (the null model) is correct. Highly improbable values of L[LR] lead to rejection of the null model.
When comparing models with the same number of free parameters, the model with the higher MLE is generally favored. When comparing models with a different number of free parameters, the more complex model often has a higher MLE simply by virtue of its greater flexibility. To legitimately reject the simple model, it is necessary to show that the higher MLE is significantly greater than that predicted by random chance while taking into account the extra free parameters. This requires knowing the distribution of the L[LR] when the simple model is correct.
If two models are identical except for the existence of an additional state, the simple model is said to be a submodel of the more complex model. The two are identical when the value of the forward rate constant is 0 or the value of the reverse rate constant is infinite (i.e., the receptor never enters or remains in the additional state). When comparing a complex model and a submodel, it is well known that, under specific conditions, 2 × L[LR] has a χ2-distribution with the number of degrees of freedom (df) equal to the number of unnecessary free parameters (Bishop et al., 1975; Horn, 1987; Knight, 2000; Shao, 1999). This relationship holds when the submodel is the correct model, the parameter estimates are approximately normally distributed, and there are no constraints on the free parameters in the neighborhood of their correct values (Chernoff, 1954; Feder, 1968; Kudo and Arbor, 1963; Nuesch, 1965; Perlman, 1969; Self and Liang, 1987; Shapiro, 1985). Kinetic parameters, however, can only be ≥0, which leads to a violation of this last condition. The correct value for the parameter associated with entry into the unnecessary state is 0 when the simple model is correct. As a result, 2 × L[LR] when comparing a simple model to one containing an additional unnecessary state will not necessarily follow a χ2-distribution. In this study, the results of fitting simulated data sets to different kinetic models is used to empirically describe the L[LR] distribution when a correct model is compared to various alternate models. Because L[LR]s are not normally distributed and different comparisons have different L[LR] distributions, tables reporting L[LR]s give the median values as well as the average and range of the values.
Statistics and p-values
Pairs of kinetic models (A and B) are compared using the LR test. Model A is rejected in favor of B if it can be shown that the probability of the observed L[LR] distribution is <0.05 when model A is known to be correct. In cases where A and B have the same number of states and free parameters, this will be done using a simple binomial distribution. If the null hypothesis is that the two models cannot be distinguished, meaning the L[LR] is distributed evenly around 0, the probability of observing 10 out of 10 sets favoring model B, for example, would be (1/2)10, corresponding to p < 0.001. The probability of observing <10 out of 10 sets is calculated using the general binomial equation (Bevington and Robinson, 1992).
Calculation of p-values using a binomial distribution is nonparametric and does not take into account the actual magnitude of the L[LR]s. In some cases where A and B have the same number of free parameters, the p-value does not favor rejection of one model over the other. In these cases the sum of the natural logarithm of the MLEs (L[LH]s) can sometimes be used to decide which model is favored (see below). No attempt is made here to determine a p-value based on the magnitude of the sum of the L[LH]s. Models supported by the L[LR] distribution and a p < 0.05 are referred to as “heavily” favored, and models supported by the sum of the L[LH]s alone are referred to as “slightly” favored.
Simulated data are analyzed to determine the effect on L[LR] of the inclusion of an unnecessary desensitized state. Results indicate that when comparing the correct model to one with an unnecessary state, the median L[LR] is ∼0.1 meaning ∼50% of the L[LR]s are between 0.0 and 0.1 and 50% are >0.1. Simple models can therefore be rejected based on a p-value calculated using a simple binomial distribution. Unless otherwise stated, all p-values reported here are calculated using the binomial equation. For comparisons between complex and submodels, the null hypothesis is that the probability of L[LR] being >0.1 is 50%. When >50% of the L[LR]s are <0.1, the p-value is reported as greater than the value when exactly 50% are <0.1. For comparisons between models with the same number of states, the null hypothesis is that the median L[LR] is 0 meaning the probability of L[LR] being >0 is 50%. When the median falls within 0.001 of 0, the p-value is reported as greater than the value when exactly 50% are <0.
Unless stated otherwise, all averages are expressed mean ± SE (σ/N1/2). All logarithms are natural logarithms.
Recombinant receptors
HEK 293 cells are grown in MEM supplemented with 10% fetal bovine serum. Transfection with DNA coding for the α1β2γ2s subunits of the GABAA receptor (1:1:1.2) is done by CaPO4 precipitation (Chen and Okayama, 1987). To facilitate the identification of transfected cells, DNA coding for the CD8 antigen is included. Transfected cells are identified using conventional light microscopy as those that bind anti-CD8 coated beads (Jurman et al., 1994).
Electrophysiology
Recordings are done at room temperature (20–22°C) in standard recording buffer (in mM, 150 NaCl, 4 KCl, 1 MgCl2, 1 CaCl2, 10 HEPES, pH 7.2 with NaOH) on the stage of an inverted phase contrast microscope enclosed in a Faraday cage. Patch electrodes (8–13 MΩ) pulled from thin-walled borosilicate glass are filled with electrode buffer (in mM, 3 NaCl, 140 KCl, 11 EGTA, 10 HEPES, 4 MgATP, pH 7.2 with KOH).
GABA (1 mM) is applied to voltage-clamped (from −50 to −70 mV) outside-out patches (2.5–3 s) using a θ-tube driven by a piezoelectric translator. The 10–90% exchange rate is <1 ms. Currents are recorded using a Dagan 3900A integrating patch-clamp amplifier (Minneapolis, MN), low-pass filtered (2 kHz) and digitized at 0.25 ms per point, and stored on disk for further analysis offline. Because the rise time of the filter (0.17 ms) is shorter that the sampling interval, no correction of the covariance matrix is made for the effects of the filter.
RESULTS
Model discrimination with simulated data
To demonstrate the capabilities and limitations of CVF, a series of simulated data sets are generated using different kinetic models. Each set is fit to both the kinetic model used to generate it (the correct model) as well as to alternate models. Fitting to the correct model tests the ability of CVF to estimate kinetic parameters, whereas fitting to alternate models and calculating the corresponding L[LR]s tests the ability of CVF to discriminate between models.
The LR test is used to make three general types of model comparisons: models with a different number of states (or free parameters), models with the same number but a different arrangement of states, and models with the same number and arrangement of states but with parameter values corresponding to different patterns of desensitization (see below). Unless otherwise stated, the following conventions are followed. When comparing models with a different number of states, the LR will be the MLE associated with the complex model divided by the MLE associated with the simple model. When comparing models with the same number of states but with a different arrangement of states or a different pattern of desensitization, the LR will be the MLE associated with the correct model divided by the MLE associated with the alternate model. Scatter plots showing the L[LR] distributions are labeled “Number”, “Arrangement”, or “Pattern” to indicate the type of comparison being made.
Simulated 1D data
The simple model 1D-I is used to generate a total of 80 data sets of 100 channels each 300 ms in duration and 0.1 ms per point (see Fig. 1 for a sample plot; see Table 1 for simulation parameters). The kinetic parameters are chosen to give a desensitization time constant of ∼30 ms.
TABLE 1.
Simulated 1D data, parameter estimation
| 1D-I
|
|||||
|---|---|---|---|---|---|
| Average ± SE
|
1D-0
|
||||
| Simulation Parameters | CVF | wSS | Simulation Parameters | Average ± SE | |
| α | 333 | 340 ± 10 | 453 ± 26 | 429.8 | 375 ± 35 |
| β | 3000 | 3177 ± 46 | 3504 ± 61 | 3062 | 3160 ± 137 |
| Kf | 314.8 | 334 ± 11 | 315 ± 17 | 35.52 | 36.8 ± 1.7 |
| Kr | 1.85 | 1.81 ± 0.06 | 1.84 ± 0.06 | 1.91 | 2.27 ± 0.18 |
| τ Desensitization | 32.6 ms | 30.3 ms | |||
| % Desensitization | 94.0% | 94.3% | |||
Simulation parameters are used to generate each data set. For both models: 100 channels are simulated per set, 300 ms duration, 0.1 ms/point, and 100 points selected evenly along the path of desensitization (tsf = 1, see Methods). No Gaussian noise is added. Averages determined by fitting each data set to the correct model using either CVF or by variance-weighted sum-of-squares minimization (wSS). 1D-I: average of 80 data sets, 1D-0: average of 10 data sets. Desensitization parameters are determined by fitting the smooth curve (generated using the simulation parameters) to a single exponential equation by sum-of-squares minimization.
The first 40 data sets were originally generated to determine the distribution of exponential parameters derived from fitting by sum-of-squares minimization. When the raw data were fit to single and double exponential equations, however, the F-test incorrectly favored the latter equation for 11 of the 40 sets. Furthermore, the p-value for 8 of the 11 is <0.0001. An accurate method for discriminating between the two equations should favor the incorrect equation, on average, in only two of the 40 sets (p-value <0.05). The F-test and sum-of-squares minimization assume the variance is uniform and uncorrelated. CVF was developed both to overcome the shortfalls of sum-of-squares minimization and to take advantage of the information contained in the covariance of ion channel data.
For each of the 80 simulated data sets, 100 points are selected evenly along the idealized path of desensitization (Fig. 1) and fit using CVF to the correct model (1D-I). The resulting kinetic parameters are approximately normally distributed (Fig. 2 A) as predicted by ML theory. For three of four parameters, the parameter estimate is within two standard errors (SEs) of the true value and all four estimates are within 10% of the true value (Table 1). The L[LH]s are also approximately normally distributed, as predicted by ML theory (Fig. 2 B). When the same 80 data sets are fit to the same model using wSS (see Methods), the SEs are larger and only two of the four estimates are within 10% of the true value (Table 1).
FIGURE 2.
Simulated 1D data, parameter estimation. (A) Frequency distribution histograms of kinetic parameters. Smooth curves are the results of fitting histograms to a Gaussian distribution. A total of 80 simulated data sets generated from kinetic model 1D-I, shown at top, are fit to the same model using CVF. All parameter values are s−1. Vertical axis is the number of data sets. See Table 1 for model values, parameter estimates, and SEs. All four kinetic parameters are approximately normally distributed. (B) (Top) Frequency distribution histograms of MLEs from the 80 fits to 1D-I shown in A. (Middle) Distribution of MLEs from fitting the same 80 data sets to 2D-II. Smooth curves are the results of fitting histograms to a Gaussian distribution. (Bottom) Distribution of 2 ×L[LR] comparing fit to 2D-II and 1D-I. Despite the additional free parameters, almost half the sets fit to both models with almost the same L[LH]. Smooth curve is a χ2-distribution, with 2 df.
To demonstrate the ability of CVF to discriminate between models with a different number of free parameters, the 80 data sets are each fit to an alternate model with an additional desensitized state also connected to the closed state (2D-II). This model contains two unnecessary free parameters. Because the two models would be identical if the unnecessary forward rate constant is zero (i.e., if the receptor never enters the second desensitized state), 1D-I is a submodel of 2D-II. The MLE associated with 2D-II can, therefore, never be less than that associated with 1D-I, and the L[LR] can never be <0.
When each of the 80 data sets generated using 1D-I are fit to 2D-II, the L[LH]s are approximately normally distributed (Fig. 2 B). The L[LR] associated with comparing 2D-II and 1D-I is determined for each set. Thirty-seven sets have a L[LR] of <0.1, including 25 with a L[LR] of <0.001. The distribution of 2 × L[LR] values differs substantially from that of a χ2-distribution with 2 df (degrees of freedom) (Fig. 2 B). Fig. 3 A shows a scatter plot of the individual determinations of L[LR] and the values are summarized in Table 2. The average L[LR] value is 0.546, which differs from 1, which is the value expected if 2 × L[LR] has a χ2-distribution with 2 df.
FIGURE 3.
Simulated 1D data, number and arrangement of states. Scatter plots of L[LR]s from results of fitting 1D data to different kinetic models. Throughout this article, the model used to generate the data is shown along the top, and the models used in fitting are shown along the bottom. Symbols plotted as 0 represent L[LR] of <0.001. Symbol plotted just above 0 represent L[LR] between 0.001 and 0.1. Adjacent symbols otherwise represent the average of L[LR] when multiple values are separated by less than the width of a symbol. (A) L[LR]s from results of fitting 1D-I data to models with additional free parameters. Same 80 data sets shown in Fig. 2. (Left) Results of fitting to 2D-II, which has one additional desensitized state and two additional free parameters. (Middle) Results of fitting to 1D-OCO, which has one additional open state connected to the closed state and two additional free parameters. (Right) Results of fitting to 2D-IC, which is a cyclic model with a single desensitized state connected to both the open and closed states and only one additional free parameter. (B) L[LR]s from results of fitting 30 of the 80 1D-I data sets and 10 1D-0 data sets to both 1D-I and 1D-0 models. Results are summarized in Tables 2 and 3.
TABLE 2.
Model discrimination, number of parameters
| LR | Data | Median | Average (range) | No. of Sets | p-value |
|---|---|---|---|---|---|
| 1D-C/1D-I | 1D-I | 0.0488 | 0.433 (0.0000–5.14) | 80 | >0.089 |
| 1D-OCO/1D-I | 1D-I | 0.0673 | 0.544 (0.0000–3.69) | 80 | >0.089 |
| 2D-II/1D-I | 1D-1 | 0.123 | 0.546 (0.0000–5.06) | 80 | 0.071 |
| 2D-II,10-40 | 6.37 | 6.32 (1.46–12.5) | 10 | <0.001 | |
| 2D-II,10-90 | 11.9 | 12.2 (2.67–22.8) | 10 | <0.001 | |
| 3D-III/2D-II | 2D-II,10-40 | 0.0000 | 0.0422 (0.0000–0.422) | 10 | >0.246 |
| 2D-II,10-90 | 0.0000 | 0.064 (0.0000–0.585) | 10 | >0.246 | |
| 3D-I/2D-I | 3D-I,pdd | 2.90 | 2.84 (0.089–5.85) | 10 | <0.01 |
| 3D-I,ddp | 14.9 | 14.3 (7.18–21.1) | 10 | <0.001 | |
| 4D-II/3D-I | 3D-I,pdd | 0.003 | 0.234 (0.0000–0.15) | 10 | >0.246 |
| 3D-I,ddp | 0.017 | 0.114 (0.0000–0.40) | 9 | >0.246 | |
| 4D-II | 0.637 | 0.621 (0.045–1.22) | 8 | 0.031 | |
| 3D-C/3D-I | 3D-I,pdd | 0.018 | 0.133 (0.0000–1.13) | 10 | >0.246 |
| COO/3D-I | 3D-I,ddp | −0.137 | 0.366 (−0.275–1.70) | 10 | >0.246 |
| COO | 2.11 | 3.00 (0.30–6.31) | 10 | <0.001 | |
| GABAR | 2.28 | 2.76 (1.32–5.57) | 6 | 0.016 | |
| COO/2D-OO | COO | 12.8 | 13.3 (5.53–24.2) | 30 | <0.001* |
| GABAR | 6.09 | 6.09 (0.295–11.7) | 18 | 0.016* | |
| 4D-OO/COO | COO | 0.0014 | 0.320 (0.0000–2.23) | 30 | >0.246* |
| GABAR | 0.032 | 0.423 (0.0000–3.50) | 18 | >0.286* | |
| OCDO/COO | COO | 0.185 | 0.109 (−1.20–0.84) | 10 | 0.246 |
| GABAR | 0.112 | 0.063 (−0.45–0.88) | 6 | 0.313 | |
| OCOO/COO | COO | 0.710 | 0.698 (0.0000–1.97) | 10 | 0.044 |
| GABAR | 0.546 | 1.17 (0.0000–3.51) | 6 | 0.234 |
Summary of L[LR]s discriminating between models (LR column) with a different number of free parameters. Fitting simulated and experimental data using CVF only. p-Values calculated using binomial distribution with null hypothesis that the median L[LR] is 0.1 (see Methods). Asterisk (*) indicates the average of three p-values calculated separately for each of the three models. See Figs. 3 A and 4 A for illustration of L[LR] distributions for 1D and 2D data, respectively. See Tables 1, 4, 6, and 7 for simulation parameters, number of channels, and number of points selected.
All 80 data sets are also fit to a model with an extra open state connected to the closed state (1D-OCO). The distribution of L[LR] associated with this comparison is similar though not identical to that observed when comparing 2D-II to 1D-1 (Fig. 3 A, Table 2). Finally, all 80 data sets are fit to a cyclic model (1D-C) with the single desensitized state connected to both the open and closed states. This model has only one unnecessary free parameter compared to the correct model. The reverse rate constant of the additional transition is constrained by microscopic reversibility. The distribution of L[LR] associated with this comparison is also similar but not identical to that observed when comparing 2D-II to 1D-1 (Fig. 3 A, Table 2). In all three cases, close to 50% of the L[LR]s are <0.1.
To test the ability of CVF to discriminate between models with the same number but a different arrangement of states, 30 of the 80 sets generated using 1D-I are fit to a model with the desensitized state connected to the open state (1D-0). All but three have positive L[LR]s (Fig. 3 B). Compared to a null hypothesis in which CVF has no discriminatory power and L[LR] is distributed evenly around 0, 27 out of 30 values above 0 are associated with a p-value of <10−5, based on the binomial distribution (see Methods). The values illustrated in Fig. 3 B are summarized in Table 3.
TABLE 3.
Model discrimination, arrangement of states
| LR | Data | Median | Average (range) | No. of Sets | p-value |
|---|---|---|---|---|---|
| 1D-1/1D-0 | 1D-I | 2.35 | 2.42 (0.94–6.98) | 30 | <10−5 |
| −0.138* | −2.10 (−16.4–0.0001) | 30 | 0.051 | ||
| 1D-0/1D-1 | 1D-0 | 1.11 | 1.36 (−1.38–3.49) | 10 | <0.01 |
| 4.22* | 4.61 (0.29–11.0) | 10 | <0.001 | ||
| 2D-II/2D-I | 2D-II,10-40 | -0.61 | −0.376 (−1.37–1.94) | 10 | 0.044 |
| 2D-II,10-90 | −0.42 | −0.61 (−2.16–0.54) | 10 | 0.044 | |
| 2D-I/2D-II | 2D-I,10-40 | 0.14 | 0.21 (−1.16–1.60) | 10 | 0.205 |
| 2D-I,3-700 | 3.06 | 2.50 (−0.49 − 5.50) | 10 | 0.117 | |
| 3D-I-br/ln | 3D-I,pdd | 0.0000 | 0.0002 (−0.0013 − 0.0042) | 10 | >0.246 |
| 3D-I/3D-III | 3D-I,pdd | 1.27 | 1.22 (−0.51–3.38) | 10 | <0.01 |
| 3D-I/3D-0 | 3D-I,pdd | 2.84 | 2.76 (0.29–5.43) | 10 | <0.001 |
| 0.0002* | 0.0094 (0.0000–0.82) | 10 | >0.246 | ||
| 3D-I/3D-II | 3D-I,pdd | 0.016 | 0.043 (−0.020–0.215) | 10 | 0.205 |
| COO | 0.623 | 0.586 (0.06–1.43) | 10 | <0.001 | |
| GABAR | 0.68 | 1.01 (0.093–2.51) | 6 | 0.016 | |
| COO/3D-II-OO | COO | 1.70 | 1.95 (−0.081–3.89) | 10 | <0.001 |
| GABAR | 1.76 | 2.22(1.15–4.05) | 6 | 0.016 | |
| COO/OCO | COO | 0.135 | 0.272 (−0.69–1.31) | 10 | 0.246 |
| GABAR | 0.11 | 0.223 (−0.21–1.01) | 6 | 0.234 |
Summary of L[LR]s discriminating between models (LR column) with the same number of free parameters, but a different arrangement of states. Fitting simulated and experimental data using CVF or wSS(*). p-Values calculated using binomial distribution with null hypothesis that the median L[LR] is 0.0 (see Methods). See Figs. 3 B, 4 B, and 5 B for illustration of L[LR] distributions for 1D, 2D, and some 3D data, respectively. See Tables 1, 4, 6, and 7 for simulation parameters, number of channels, and number of points selected.
Ten data sets are generated using model 1D-0 and fit to both models. Nine of 10 sets had positive L[LR]s, favoring the correct model (Fig. 3 B, Table 3). Compared to a null hypothesis in which L[LR] is distributed around zero, this is associated with a p-value of <0.01. Despite having equal numbers of free parameters, models 1D-I and 1D-0 result in data sets that can be reliably distinguished using CVF and the LR test. In both cases, the correct model is heavily favored over the incorrect model.
When 1D-I and 1D-0 data sets are fit to both models using wSS, 1D-0 is favored in both cases (Table 3), suggesting that the ability of CVF to accurately discriminate between models with a different arrangement of states comes from its ability to extract correlation information from the data.
Simulated 2D data
When simulated data sets generated using four different 2D models (10 sets each) are analyzed by CVF, similar results are observed as with 1D data sets. Twenty-one of 24 parameter estimates are within two SEs of the correct value (Table 4). For all four models, 10 of 10 L[LR]s are >0.1 when fitting to 1D-I and well over half of the L[LR]s are <0.1 when fitting to 3D models (Fig. 4 A, Table 2).
TABLE 4.
Simulated 2D data, parameter estimation
| 2D-II,10-40
|
2D-II,10-90
|
2D-I,10-40
|
2D-I,3-700
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| Simulation Parameters | Average ± SE | Simulation Parameters | Average ± SE | Simulation Parameters | Average ± SE | Simulation Parameters | Average ± SE | ||
| α | 333 | 381 ± 33 | 333 | 373 ± 53 | 164 | 149 ± 12 | 399 | 385 ± 64 | |
| β | 3000 | 3539 ± 133 | 3000 | 3380 ± 127 | 2977 | 2971 ± 194 | 3336 | 3494 ± 164 | |
| Kf1 | 389.2 | 607 ± 89 | 389.2 | 532 ± 107 | 1016 | 1109 ± 87 | 25.32 | 47 ± 18 | |
| Kr1 | 61.08 | 85 ± 19 | 61.08 | 76 ± 13 | 2.99 | 2.93 ± 0.40 | 0.1014 | 0.094 ± 0.018 | |
| Kf2 | 496.8 | 547 ± 43 | 183.3 | 203 ± 20 | 26.5 | 31.9 ± 6.8 | 224.7 | 242 ± 33 | |
| Kr2 | 3.005 | 2.62 ± 0.24 | 1.109 | 1.1 ± 36 | 61.0 | 121 ± 50 | 185.5 | 201 ± 28 | |
| τD1 | 9.65 ms | 10.6 ms | 9.75 ms | 2.63 ms | |||||
| %D1 | 53.6% | 42.2% | 53.9% | 53.9% | |||||
| τD2 | 38.8 ms | 89.2 ms | 39.0 ms | 722 ms | |||||
| %D2 | 39.6% | 53.4% | 39.4% | 42.8% | |||||
For each model, 10 data sets are generated using the simulation parameters. For all data sets, 100 channels are simulated per set and 100 points selected evenly along the path of desensitization (tsf = 1). No Gaussian noise is added. 2D-II,10-40; 2D-II,10-90; and 2D-I,10-40: 300-ms duration, 0.1 ms per point. 2D-I,3-700: 3-s duration, 0.25 ms per point. Averages determined by fitting all 10 data sets to the correct model by CVF. Desensitization parameters are determined by fitting the smooth curve (generated using simulation parameters) to a double exponential equation by sum-of-squares minimization.
FIGURE 4.
Simulated 2D data, number and arrangement of states and pattern of desensitization. Scatter plots of L[LR]s from results of fitting 2D data. Numbers below model names represent approximate time constants of desensitization (see Table 4 for simulation parameters). (A) L[LR]s from fits to models with one, two, and three desensitized states. (Left pair) Correct model is favored over a model with one less desensitized state. (Middle pair) Fitting to a model containing an unnecessary state gives L[LR]s similar to those observed for 1D data, reproduced from Fig. 3 for comparison on right. (B) L[LR]s from results of fitting 2D-I and 2D-II data to both 2D-I and 2D-II models. The correct model is only favored for the data set generated using 2D-I,3-700. (C) L[LR]s from results of fitting 2D-I data to the same model comparing dp and pd patterns of desensitization (see text). The correct model is only favored for the data set generated using 2D-I,3-700.
When comparing models with the same number but a different arrangement of the states, it is only possible to identify the correct model if the rates of the two phases of desensitization are sufficiently different (Fig. 4 B, Table 3). In the case of the data generated from model 2D-I,3-700, only seven of the 10 L[LR]s are clearly above 0 (p = 0.117). When the total of all 10 L[LH]s is calculated for both models, the correct model exceeds 2D-II by 25 log units. For this reason, the results are regarded as slightly favoring the correct model based on the magnitude of the L[LH]s rather than on the distribution of the L[LR]s. No attempt is made to discriminate between linear and branched forms of 2D-II data because of an inability to make such distinctions when studying 3D data (see below).
Because the two desensitized states are indistinguishable, data generated using model 2D-I (D1==C==O==D2) fit to the correct model with at least two distinct local maxima depending on which of the two desensitized states is responsible for each of the two phases of desensitization. To define their positions in relation to the gating isomerization, desensitized states connected to the closed state (such as D1 above) will be referred to as “proximal” states (p) and states connected to the open state (such as D2 above) will be referred to as “distal” states (d). 2D-I models can then be divided into 2D-I,pd and 2D-I,dp to indicate the pattern of desensitization. The former term refers to models in which the proximal state is responsible for the fast phase and the latter refers to models in which the distal state is responsible for the fast phase. CVF can identify the local maximum associated with the correct pattern of desensitization, when the rates of the two phases of desensitization are sufficiently different (Fig. 4 C, Table 5). As above, only seven of the 10 L[LR]s for 2D-I,3-700,dp are clearly above 0 when comparing the dp and pd patterns. The results are also said to slightly favor the correct model based on the magnitude rather than the distribution of the L[LR]s (p = 0.117). The total of all 10 L[LH]s for the correct model exceeds that for the pd pattern by 24.8 log units.
TABLE 5.
Model discrimination, pattern of desensitization
| LR | Data | Median | Average (range) | No. of Sets | p-value |
|---|---|---|---|---|---|
| 2D-I,dp/pd | 2D-I,10-40,dp | 0.27 | 0.38 (−1.45–2.61) | 10 | 0.205 |
| 2D-I,3-700,dp | 3.14 | 2.48 (−0.11–5.40) | 10 | 0.117 | |
| 3D-I,pdd/ddp | 3D-I,pdd | 0.59 | 0.62 (−0.99–1.64) | 10 | <0.01 |
| 0.0000* | 0.069 (−0.0091–0.71) | 10 | >0.246 | ||
| 3D-I,ddp/pdd | 3D-I,ddp | 2.68 | 2.50 (−0.50–5.40) | 10 | 0.044 |
| COO | 1.94 | 1.54 (−1.92–3.89) | 10 | <0.01 | |
| GABAR | 0.71 | 2.17 (0.147–9.49) | 6 | 0.016 | |
| COO,ddp/pdd | COO | 1.56 | 1.74 (−0.26–3.74) | 10 | <0.01 |
| GABAR | 1.12 | 1.44 (−0.07–3.78) | 6 | 0.094 |
Summary of L[LR]s discriminating between models (LR column) with the same number and arrangement of states, but a different pattern of desensitization (see text). Fitting simulated and experimental data using CVF or wSS (*). p-Values calculated using binomial distribution with null hypothesis that the median L[LR] is 0.0 (see Methods). See Fig. 4 C for illustration of L[LR] distributions for 2D data. See Tables 4, 6, and 7 for simulation parameters, number of channels, and number of points selected.
Simulated 3D data
Fitting GABAR data to 3D models with a single open state favors the 3D-I arrangement (see below). For this reason only 3D-I models are used to generate simulated data. Two different groups of data sets are generated using 3D-I models with parameters derived from those observed when fitting GABAR data (see Table 6 for simulation parameters). Similar results are observed as with 1D and 2D data. All 16 parameter estimates are within two SEs of the true values (Table 6). One of the two groups is fit to the correct model using wSS, which gives results comparable to CVF (Table 6).
TABLE 6.
Simulated 3D and 4D data, parameter estimation
| 3D-I,pdd
|
||||||||
|---|---|---|---|---|---|---|---|---|
| Average ± SE
|
3D-I,ddp
|
4D-II
|
||||||
| Simulation Parameters | CVF | wSS | Simulation Parameters | Average ± SE | Simulation Parameters | Average ± SE | ||
| α | 223.6 | 254 ± 43 | 277 ± 40 | 31.12 | 32.3 ± 2.1 | 603.6 | 641 ± 87 | |
| β | 3967 | 4009 ± 243 | 3949 ± 240 | 4466 | 4458 ± 135 | 3691 | 3867 ± 271 | |
| Kf1 | 1368 | 1182 ± 131 | 1131 ± 149 | 1365 | 1372 ± 105 | 864.8 | 917 ± 134 | |
| Kr1 | 23.22 | 24.2 ± 5.2 | 25.0 ± 3.7 | 0.2354 | 0.23 ± 0.03 | 210.8 | 298 ± 47 | |
| Kf2 | 160 | 194 ± 41 | 197 ± 36 | 229.6 | 217 ± 18 | 19.15 | 21.7 ± 2.8 | |
| Kr2 | 196.8 | 201 ± 39 | 216 ± 40 | 440.9 | 535 ± 78 | 0.1174 | 0.116 ± 0.025 | |
| Kf3 | 7.459 | 7.52 ± 0.45 | 7.75 ± 0.50 | 68.28 | 72.0 ± 5.0 | 44.83 | 58.1 ± 14.1 | |
| Kr3 | 0.1521 | 0.149 ± 0.04 | 0.166 ± 0.039 | 29.46 | 29.4 ± 2.6 | 29.39 | 42.4 ± 8.1 | |
| Kf4 | 6.27 | 10.2 ± 1.7 | ||||||
| Kr4 | 3.46 | 4.75 ± 1.00 | ||||||
| τD1 | 2.67 ms | 1.50 ms | 3.26 ms | |||||
| %D1 | 53.6% | 41.5% | 34.7% | |||||
| τD2 | 21.4 ms | 13.7 ms | 19.1 ms | |||||
| %D2 | 22.6% | 35.2% | 28.8% | |||||
| τD3 | 665 ms | 502 ms | 183 ms | |||||
| %D3 | 21.3% | 20.5% | 14.1% | |||||
| τD4 | 1494 ms | |||||||
| %D4 | 18.2% | |||||||
Simulation parameters are used to generate data sets 3 s in duration, 0.25 ms per point. After selection of points evenly along the path of desensitization (tsf = 1), Gaussian noise (σ = 0.564 channels) is added to each point. 3D-I,pdd: 100 channels, 100 points selected, 10 sets generated. 3D-I,ddp: 200 channels, 200 points selected, 10 sets generated. 4D-II: 200 channels, 200 points selected, eight sets generated. Desensitization parameters are determined by fitting the smooth curve (generated using simulation parameters) to a three- or four-component exponential equation by sum-of-squares minimization. See text for the meaning of pdd and ddp.
When fitting both groups to 2D-I, all but one of the L[LR]s are >0.1 and more than half of the L[LR]s are <0.1 when fitting to 4D-II (Table 2). Comparing results from the two groups suggests that, when fitting to a complex model and a submodel, simultaneously increasing the number of channels from 100 to 200 and the number of points selected from 100 to 200 increases the observed L[LR]s when the complex model is correct (3D-I/2D-I) but not when the submodel is correct (4D-II/3D-I, Table 2). When fitting to 3D-C, which is identical to 3D-I except for the addition of a transition between the proximal D state and one of the distal D states, more than half of the L[LR]s are <0.1 (Table 2). Compared to 3D-I, 3D-C has one additional free parameter.
To confirm that CVF can identify four desensitized states, the model 4D-II is used to generate a series of data sets with 100 channels each (see Table 6 for parameters). Initial results from data sets of 100 evenly selected points give very small values for L[LR] when comparing 4D-II and 3D-I (not shown). A series of eight data sets are then generated with 200 channels each and 200 points are evenly selected. When these data are fit to 4D-II and 3D-I, only one set had a L[LR] of <0.1 (Table 2). The magnitudes of the L[LR]s are, however, not as great as those observed when 3D data are fit to 3D and 2D models.
To test the ability of CVF to discriminate between different arrangements of states, one of the two groups of 3D-I data sets is fit to a series of 3D models (Fig. 5, Table 3). When compared to the correct model, 3D-II is slightly disfavored (based on total L[LH] alone), whereas both of the entirely asymmetric models (3D-III and 3D-0) are heavily disfavored (p < 0.01 and p < 0.001, respectively). Fitting using wSS fails to discriminate between 3D-I and 3D-0 (Table 3).
In fitting to either 3D-I or 3D-II, it is impossible to discriminate between branched and linear forms. The value of the L[LR]s for these comparisons are rarely >0.001 above or below 0. This is surprising given that, in the case of 3D-I, the comparison involves models with differing numbers of gateway states (states connected directly to an open state). The number of gateway states dramatically affects the correlations observed when fitting adjacent events recorded from single-channel data (Ball et al., 1989; Colquhoun and Hawkes, 1987). Fig. 5 B illustrates the distribution of L[LR]s when it is impossible to discriminate between models, when one model is slightly favored, and when one model is heavily favored over another. This figure also shows that CVF can regularly identify differences in L[LH] as small as 0.001.
The 3D-I models used to generate the two groups of simulated data sets differ from one another in the pattern of desensitization. One has parameters that give a pattern of desensitization in which the proximal state is responsible for the fast phase and the two distal states are responsible for the intermediate and slow phases (pdd). The other group has parameters that give a pattern of desensitization in which the distal states are responsible for the fast and intermediate phases and the proximal state is responsible for the slow phase (ddp). CVF heavily favors the correct pattern for both 3D-I,pdd and 3D-I,ddp data sets (Table 5). When applied to 3D-I,pdd, wSS fails to discriminate between the two patterns of desensitization (Table 5). Taken together, these results demonstrate that CVF can reliably extract kinetic parameters and discriminate between a variety of kinetic models with a single open state and up to three desensitized states.
Model discrimination with experimental data
GABAR data are recorded from six different outside-out patches as described in Methods (see Fig. 6 for sample trace) and analysis proceeds in several phases. The standard deviation of the baseline current is squared and used as an estimate of the background variance. For CVF, this value is added to the diagonal elements of the covariance matrix. The baseline current noise has an average covariance of 0.45 pA2 for an interval of 0.25 ms. No effort is made to correct for this degree of correlation because the predicted covariance from channel activity for the same time interval is 21 pA2 based on the final consensus model (see below). No effort is made to correct for open-channel noise, which is expected to have a standard deviation of ∼3% of the single-channel current (Sigworth, 1985). The standard deviation of the background current has an average of ∼56% of a single-channel current.
FIGURE 6.
GABAR trace response to 2.5-s application of 1 mM GABA (outside-out patch, symmetrical chloride, holding potential −70 mV). (Top) Raw data 0.25 ms per point. (Middle) Results of selecting 200 points along the path of desensitization with tsf = 3 (see Methods). (Bottom) Results of fitting selected data sets to COO model using CVF. Traces are inverted for display purposes. Inset shows expanded timescale. Scale bar, 100 pA, 1 s, 6.5 ms.
Each raw trace is fit by sum-of-squares minimization to an exponential function with three components and the extrapolated current at t = 0 is used to estimate the number of channels (assuming 28 pS per channel and 0.8 maximum probability of opening). When both the number of channels and the conductance per channel are allowed to vary as free parameters in the analysis of simulated data, the latter is underestimated by ∼15–20%, with a compensatory increase in the former. For this reason, the conductance per channel is fixed at 28 pS in the analysis of GABAR data.
Optimization of point selection
The results of each exponential fit are also used in selecting points along the idealized path of desensitization, as described in Methods, and to generate initial starting values for CVF (see Appendix II). Initial CVF results are used to create consensus models that are then used to generate simulated data. Analysis of the simulated data leads to refinement of the point selection process, CVF is reapplied to the six reselected GABAR data sets and the entire process repeated. The intermediate results from the first two selected GABAR data sets are described briefly, followed by a detailed description of the final analysis using the optimally selected points.
The process begins by selecting from each of the six raw traces 100 points distributed evenly along the path of desensitization and fitting each set to 11 different single open-state models (as shown for 3D-I data in Fig. 5). The number of channels is constrained to the estimate made as described above. Results on the number and arrangement of states are similar to those observed when 3D-I,pdd data are analyzed. 3D models are heavily favored over 2D models whereas at least half the 4D models had L[LR]s <0.1. 3D-I is slightly favored over 3D-II whereas the fully asymmetric models, 3D-0 and 3D-III, are heavily disfavored. For both 3D-I and 3D-II, most comparisons between branched and linear forms have L[LR]s within 0.001 of zero. The ddp pattern of desensitization is favored over pdd.
A key feature of the ddp pattern of desensitization is a high value for the forward rate constant associated with the proximal desensitized state and a low value for the corresponding reverse rate constant (see Table 6). This predicts that a fraction of the receptors desensitize by entering the proximal state without ever opening. Entry of the remaining receptors into the proximal desensitized state, which is thermodynamically favored, is slow because so few receptors (<5%) are in the closed state once the first gating isomerization has reached equilibrium (<1 ms). The fast and intermediate phases of desensitization reflect equilibration with the two distal states.
The estimate of channel number based on fitting to exponential equations may be unreliable if a significant proportion of the channels desensitize without opening, as predicted by the ddp pattern of desensitization. For this reason, the number of channels is allowed to vary as a free parameter in all subsequent analysis. When 23 of the 80 1D-I data sets described above (100 channels per set) are fit to the correct model with the number of channels allowed to vary as a free parameter, the estimate of the number of channels is 100.8 ± 1.1. This suggests that CVF can accurately estimate the number of channels in simulated data generated using a simple model.
Analysis of simulated data suggests that at least 200 points are needed to reliably identify the presence of a fourth desensitized state (see above). For this reason, six GABAR data sets of 200 points are evenly selected from the six raw traces. Reapplication of CVF to these six sets with the number of channels as a ninth free parameter still favors 3D-I,ddp.
When the same six data sets are fit to models with two open states, the most favored model (referred to as COO; shown in Fig. 7) has two open states in a linear arrangement and three desensitized states, one connected to the closed and one connected to each of the two open states. This model is analogous to 3D-I, in that there is one proximal and two distal desensitized states. COO is favored over 3D-I with a median L[LR] of 3.9 and six out of six above 0 (p = 0.016).
Of the 10 kinetic parameters in COO, several have estimates ranging over an order of magnitude and two (both leading away from the second open state) range over more than two orders of magnitude. To determine if this variability is the result of inadequate analysis power, a consensus model is generated using the average of the central four of six values for each parameter (i.e., the highest and lowest values are excluded). This model is then used to generate 10 simulated data sets (200 channels each, 3-s duration, 0.25 ms per point), referred to as COO data (see Table 7 for simulation parameters).
TABLE 7.
GABAR and simulated COO data, parameter estimation
| GABAR
|
COO
|
||||
|---|---|---|---|---|---|
| Average ± SE | Central four Average ± SE | Simulation Parameters | Average ± SE | Central six Average ± SE | |
| N | 200 | 208 ± 18 | 192 ± 5 | ||
| α1 | 299 ± 110 | 267 ± 112 | 183.5 | 266 ± 75 | 209 ± 32 |
| β1 | 5524 ± 979 | 5161 ± 579 | 5202 | 5432 ± 299 | 5561 ± 122 |
| α2 | 87.0 ± 73 | 17.63 ± 9.72 | 9.998 | 31.0 ± 14.4 | 16.0 ± 3.4 |
| β2 | 40.7 ± 16.0 | 32.2 ± 12.7 | 41.6 | 42.4 ± 4.8 | 43.8 ± 2.8 |
| Kf1 | 1026 ± 538 | 652 ± 288 | 864.5 | 910 ± 341 | 606 ± 114 |
| Kr1 | 0.126 ± 0.043 | 0.115 ± 0.031 | 0.1927 | 0.179 ± 0.035 | 0.169 ± 0.021 |
| Kf2 | 129 ± 11 | 133 ± 8 | 140.6 | 159 ± 13 | 152 ± 5 |
| Kr2 | 116 ± 24 | 118 ± 12 | 188.9 | 213 ± 22 | 211 ± 16 |
| Kf3 | 5087 ± 3470 | 2049 ± 488 | 1496 | 1722 ± 179 | 1745 ± 143 |
| Kr3 | 1157 ± 325 | 1154 ± 269 | 799.5 | 749 ± 182 | 605 ± 92 |
| τD1 | 2.84 ms | ||||
| %D1 | 51.2% | ||||
| τD2 | 27.2 ms | ||||
| %D2 | 25.0% | ||||
| τD3 | 725 ms | ||||
| %D3 | 20.3% | ||||
Simulation parameters are used to generate 10 COO data sets, 3 s in duration, 0.25 ms per point, 200 channels per set. For the six GABAR traces and the 10 COO data sets, 200 points are selected along the path of desensitization favoring the earlier phases (tsf = 3). Gaussian noise (σ = 0.564 channels) is added to each point of the COO data sets. All 16 data sets are fit to COO using CVF allowing the number of channels to vary as a free parameter. Central four and Central six averages are the results of excluding the highest and lowest one or two values for each parameter, respectively. Results of fitting GABAR sets are used to create the consensus model shown in Fig. 8. Desensitization parameters are determined by fitting the smooth curve (generated using simulation parameters) to a three-component exponential equation by sum-of-squares minimization.
Initially, 200 points are selected evenly along the path of desensitization from the raw simulated COO data. Gaussian noise is added (σ = 0.564 channels, average of the baseline noise of the six GABAR traces) and all 10 data sets are fit to model COO. There is a comparable variability in the parameter estimates, particularly regarding α2 (the transitions leading from the second open-state back to the first open state). When the two highest and two lowest estimates are excluded, the average of the central six estimates (42 ± 21 s−1) still differs by an unacceptable degree from the simulation parameter (10 s−1). To address this issue, three 100-point data sets are selected from the raw COO data with timescale factor (see Methods) values of 1, 3, and 10 and fit to COO. The resulting averages for the central six estimates of α2 are: 37 ± 5 s−1, 24 ± 4 s−1, and 69 ± 20 s−1, respectively. Because the middle value is closest to the simulation parameter, tsf = 3 is chosen for subsequent data point selection. When 200 points are selected from the raw COO data with tsf = 3, the estimate of α2 based on the central six estimates is within an acceptable range of the true value (16 ± 3 s−1) and nine of the 11 parameter estimates are within two SEs of the true value (Table 7). The above results on COO data suggest that 200 points selected with tsf = 3 is the optimal method of point selection in the analysis of GABAR data. The final analysis of both GABAR and COO data is done using this point-selection method. Unfortunately, a comparable degree of variation in the parameter estimates for GABAR data remained despite this change (Table 7).
Analysis using optimally selected points
Fig. 6 shows a representative GABAR trace before and after selection of 200 points with tsf = 3, as well as the results of fitting the selected data to the COO model. The COO model is heavily favored over 3D-I, and similar results are observed when fitting simulated COO data but not when fitting simulated 3D-I data (Table 2). When comparing COO to a model containing an additional open state connected to the closed state, two of the six GABAR sets had L[LR] of <0.1. Only two of 10 COO sets had L[LR] of <0.1 when making the same comparison. This differs significantly (p = 0.044) from the prediction that half the L[LR]s are <0.1 when comparing a correct model with a model containing an additional desensitized state. The addition of an unnecessary open state may have a greater effect on L[LR] than the addition of an unnecessary desensitized state. When fitting simulated COO data, the total L[LH] is also greater when an unnecessary open state is added than when an unnecessary desensitized state is added (Fig. 7 B).
For both GABAR and simulated COO data, 2D models are heavily disfavored, whereas at least half of the comparisons involving 4D models have L[LR]s <0.1 (Table 2). This includes a model analogous to the one reported by Haas and Macdonald (1999) with two nonconducting states separating the two open states (OCDO). Because COO is not a submodel of OCDO, some L[LR]s are <0 (Table 2).
Fig. 7 shows the sum of L[LH]s that result from fitting both GABAR and simulated COO data to 3D-I and 11 models with at least two open states. Similar results are observed for both GABAR and COO data. Among the models with 10 kinetic parameters tested, COO is slightly favored over a model with the closed state between the two open states (based on total L[LH] alone) and heavily favored over a model analogous to 3D-II with two desensitized states connected to the closed state (Table 3). For GABAR data, the ddp pattern of desensitization is slightly favored over the pdd pattern (based on the total L[LH] alone, p = 0.094), and for COO data, the ddp pattern is heavily favored (p < 0.01).
When analyzing data recorded from a biological system, such as a population of ion channels, there is no way to be certain that a particular model is the correct model. The eventual goal is to obtain a model or models adequate for the purpose of understanding biologically relevant functions and pharmacological modulation. It is, therefore, useful to determine if CVF can extract meaningful information when fitting to models known to be simpler than the correct model. L[LR]s are determined for comparing the arrangement of states and the pattern of desensitization for GABAR and COO data assuming only a single open state. In both cases, fitting to 3D-I is heavily favored over 3D-II (Table 3), and the ddp pattern of desensitization is heavily favored over the pdd pattern (Table 5). Despite using an incorrect model, the number of desensitized states on each side of the gating isomerization and their relationship to the phases of desensitization are discernable.
Comparing the SEs to the means, parameter estimates of the six GABAR traces show a great deal of variability despite the use of optimally selected points. This is particularly true of the two parameters leading away from the second open state (α2 and Kf3; see Table 7). The variability does not appear to be a simple reflection of a shallow likelihood surface. Changing either parameter by as little as 10% from the value associated with the MLE (leaving the other nine parameters at their MLE associated values) decreases the L[LH] by at least a factor of 0.05 for all six GABAR traces. This value is well within the resolution of CVF (see Fig. 5 B).
Properties of the COO consensus model
To determine the properties of the COO model, the averages of the central four parameter estimates from fitting the six GABAR data sets are used to generate a final consensus model (Table 7 and Fig. 8). To allow simulation of deactivation, a single agonist binding step connected to the closed state is included. An on-rate of 107 M−1 s−1 and an off-rate of 500 s−1 are used (Scheller and Forman, 2002), giving an EC50 of ∼20 μM. A series of smooth simulations are done and the results fit to exponential equations by sum-of-squares minimization.
FIGURE 8.
Consensus model for GABAR data. (Top) COO consensus model with addition of an unliganded R state and a single agonist binding step connected to the closed state (C). (Bottom left) Simulated response to 1-s applications of 1 mM GABA. Insets show expanded timescale. (Bottom right) Simulated response to deactivation phase after 1 ms (fastest deactivation), 5 ms (thick line) and 20 ms (slowest deactivation) applications of 1 mM GABA. Plots (1 and 10 ms) are scaled to the 5-ms plot. Scale bars, left, 0.2 probability units, 0.2 and 0.02 s; right, 0.1 probability units, 0.1 s.
Desensitization in response to 1 mM GABA proceeds with three distinct phases having time constants of 3.6 ms (62%), 36 ms (14%), 362 ms (23%). These values are comparable to the average values observed when the decaying phase of the six raw GABAR traces are fit by sum-of-squares minimization to a three-exponential equation: 3.8 ms (56%), 64 ms (20%), 730 ms (19%).
When the deactivation phase after a 1-ms application of 1 mM GABA is fit to a double exponential, the time constants are 5 and 140 ms with the fast phase representing 69% of the total deactivation. These values are comparable to those reported by others studying recombinant (Haas and Macdonald, 1999; Tia et al., 1996) as well as native receptors (Jones and Westbrook, 1995; Mozrzymas et al., 1999; Shen et al., 2000; Zhu and Vicini, 1997). The relative magnitude of the slow component increases as the duration of GABA application increases (Fig. 8) as has been described for native receptors (Jones and Westbrook, 1995).
Recovery from desensitization has been reported to proceed in a biphasic manner with fast time constants ranging between 35 and 150 ms (Bai et al., 1999; Jones and Westbrook, 1995; Shen et al., 2000; Zhu and Vicini, 1997). In its current form, COO does not predict the rapid phase of recovery from desensitization. This is due to accumulation of receptors in the D1 state during deactivation.
First latency analysis applied to recombinant receptors composed of α1β1γ2 subunits favored a 3D-I,pdd model (Burkat et al., 2001). The pdd pattern was chosen because high concentrations of GABA often show first latencies of tens of milliseconds. They suggest that these long first latencies are the result of channels briefly visiting the proximal fast desensitized state before opening. In its current form, the COO model does not predict these first latencies.
The COO model predicts mean open times of 0.49 and 2.5 ms, which agree well with 0.3 and 1.92 ms, the two fastest values reported for single-channel analysis of α1β3γ2L receptors recorded at steady state in the presence of 1 mM GABA (Haas and Macdonald, 1999). The predicted mean closed times of 0.19, 0.87, and 8.5 ms also agree well with the values of 0.2, 1.64, and 8.89 ms reported in the same study.
DISCUSSION
Model discrimination
Use of the LR test to discriminate between kinetic models requires knowledge of the expected distribution of the L[LR]. Application of several statistical methods, including the LR test, to model discrimination in ion channel data has been described in detail (Horn, 1987). This includes the analysis of binned open times collected from steady-state single-channel data. The LR test was used to discriminate between exponential equations with a different number of free parameters, as well as between Markovian and non-Marovian models with the same number of free parameters. In the former case it was assumed that 2 × L[LR] has a χ2-distribution. In the latter case, Monte Carlo analysis was used to determine the expected distribution of the L[LR]. This study applies similar principals to likelihoods identified by fitting macroscopic nonequilibrium data directly to kinetic models.
When comparing fits to a complex model and a correct submodel, the distribution of 2 × L[LR] observed in this study deviates dramatically from that of a χ2-distribution with 2 df. This is most likely due to the restrictions on kinetic parameters. The Akaike information criterion (Akaike, 1974) is often used for comparing models that differ in complexity when the simple model is not a submodel of the complex one. As with the χ2-prediction, this value assumes that parameter estimates are approximately normally distributed around their true values. This requires they be unrestricted in the neighborhood of their true values. When a submodel is correct, the true value of at least one unnecessary parameter of the complex model is either 0 (forward rate constant) or infinite (reverse rate constant). Because kinetic parameters cannot be below 0, this parameter cannot be normally distributed around its true values in either case. This results in a much narrower distribution of L[LR] than would be the case if the unnecessary parameters were unrestricted. In this study, this narrow distribution leads to a useful null hypothesis for ruling out simple models.
In this study, comparisons between simple and complex models are made based on results of fitting to simulated data. For all levels of complexity studied, addition of an unnecessary desensitized state, or an unnecessary transition between states leads to L[LR] distributions with a consistent feature: at least half of the L[LR]s fall below 0.1. Using this feature as a null hypothesis allows the calculation of a p-value for ruling out submodels based on a binomial distribution. An increase in the number of channels and the number of points selected increases the magnitude of L[LR]s when the complex model is correct but has no obvious effect when the submodel is correct (Table 2). From this it appears that when analyzing recorded data, the power of CVF to identify the correct number of desensitized states is primarily limited only by the number of channels in the patch and the number of points selected.
Based on fitting of COO data, the addition of an unnecessary open state may be fundamentally different from the addition of a desensitized state. Only two of 10 L[LR]s are below 0.1 when COO and OCOO are compared. Based on the results of fitting the six GABAR sets to a model with three open states, there is no compelling justification for including a third open state at this time. A third open state, however, is far from being ruled out because only one of the many models with three open states has thus far been tested. In addition, the existence of a third open state is supported by the open time distribution reported from single-channel studies (Macdonald et al., 1989; Weiss and Magleby, 1989).
Comparing models with the same number of states and free parameters is made possible by the use of the full covariance matrix. Fitting by wSS, which only takes into account the magnitude of the current at each point in time, fails to discriminate between differences in the arrangement of states or in the pattern of desensitization. In making such comparisons, a binomial distribution is used to generate p-values based on the null hypothesis that L[LR]s are distributed around 0. Although this is adequate for some comparisons, analysis of simulated data reveals several instances in which models known to be incorrect are not ruled out by the L[LR] distribution, despite having a lower total L[LH] than the correct model. Analysis of COO data, for example, excludes the OCO model based only on the total L[LH], not on the L[LR] distribution. This problem may prove surmountable by using a more accurate L[LR] distribution as the null hypothesis. This would require analyzing simulated data generated using OCO to determine the L[LR] distribution associated with comparing OCO and COO models when the former is correct. This distribution can then be used instead of the binomial distribution as a null hypothesis to rule out OCO.
CVF is very sensitive to changes in the number of desensitized states on each side of the gating isomerization. However, it has been impossible to discriminate between linear and branched arrangements that have the same number of desensitized states on each side of the gating isomerization. This comparison is fundamentally different from others made. There is no difference in the total L[LH] and for each data set, L[LR] is close to zero. This finding is based on the analysis of simulated data in which there is a single perturbation. It remains to be seen if different application paradigms with multiple perturbations (such as those testing deactivation or recovery from desensitization) prove more powerful in discriminating between such models (see below).
Parameter estimation
ML theory predicts that when fitting to the correct model, the observed parameter estimates will be approximately normally distributed around the true values. Because this is an asymptotic theory, its predictions are only observed when the number of determinations is adequate. In this study, simulation parameter values including the number of channels are usually within two SEs of the mean for all single open-state data sets examined.
Both COO and GABAR data show a great deal of variability in parameter estimates when fitting to the COO model, despite adequate curvature of the likelihood surface. This suggests that when fitting to models with 11 free parameters, CVF is close to the limit of its accuracy when studying single perturbation data, with 200 channels and 200 points per set. Reasonable parameter estimates are obtained by excluding the outer four of 10 estimates. In applying CVF to recorded data, it may be necessary to analyze >10 replicates to derive accurate parameter estimates. Added power is also expected by analyzing data recorded during multiple perturbations and by simultaneously fitting multiple data sets recorded from the same patch (see below).
Several factors may contribute to the variability in parameter estimates observed when fitting GABAR data to COO. Agonist binding is assumed in this study to be instantaneous, whereas the reported activation rates for 1 mM GABA are less than those for 10 mM GABA (Li and Pearce, 2000; Lavoie et al., 1997). In addition to lacking the agonist binding step, the COO model is likely to require additional levels of complexity to fully predict the relevant aspects of GABAR function. Finally, the use of a subunit ratio of (1:1:1.2, α1:β2:γ2) HEK cell transfection may have resulted in a heterogeneous mixture of α1β2 and α1β2γ2 receptors (Boileau et al., 2002). By comparing variability within a patch to variability between patches, CVF will be able to address the effect of heterogeneity.
COO consensus model
The main goal of this article is to introduce CVF and report its capabilities and limitations. Application of CVF to GABAR data is primarily done for the purpose of guiding the choice of models to be used for generating simulated data. The consensus model presented here is derived from the results of analyzing only six traces recorded in response to a single perturbation. A more comprehensive model will require a wide range of experimental protocols including deactivation, recovery from desensitization, and application of subsaturating GABA concentrations. Despite this, the COO model reproduces several general features of GABAR function. Because CVF can extract meaningful information from simulated data using models known to be simpler than the correct model, the qualitative features of the COO model are worth discussing briefly.
Although the COO model is derived exclusively from desensitization data, it reproduces the biphasic nature of GABAR deactivation. Failure of the COO model to reproduce the fast phase of recovery from desensitization may be due to the lack of a provision for GABA dissociation from any of the desensitized states. In its present form all activation and deactivation go through the C state, which is connected to the most thermodynamically stable desensitized state. During deactivation, desensitization continues to occur. This can be avoided by allowing GABA to dissociate from the desensitized states, as has been demonstrated for receptors containing the α1β2γ2 subunits (Chang et al., 2002). Failure to reproduce the prolonged first latencies seen for high GABA may be due to the assumption that all receptors start in the activatable state. If a proportion of receptors are in the D2 state at rest, prolonged first latencies could represent recovery from D2 to O1 after agonist binding. This can be tested by allowing the fraction of receptors in the D2 state at rest to vary as a free parameter.
The kinetic parameters of the COO consensus model predict single-channel properties remarkably similar to those reported for receptors containing the α1β3γ2 subunits in the presence of high GABA at steady state (Haas and Macdonald, 1999). This same report includes evidence of a third open state and two nonconducting states separating two open states. When tested here, neither feature is statistically justified or definitively ruled out.
Future directions
Although statistical power increases with the number of points selected, this approach is limited by the computational demands of CVF that increase with the square of the number of points selected. The total number of points fit, however, can be increased by simultaneously fitting two traces from the same patch. As long as the two traces are separated by enough time, their covariance matrices can be calculated separately. The likelihood of observing both traces is simply the product of the likelihood of observing the individual traces. Using traces with different paradigms can emphasize different aspects of a complex model. The same is true for more than two traces and the computational demand only goes up linearly with each added trace.
The CVF method will also be expanded to analyze data sets with more than one perturbation. Each perturbation represents a change in the GABA concentration that is represented by the use of a new Q matrix. The new Q matrix is identical to the first except for the elements corresponding to GABA association. The covariance formula (Eq. 4, Appendix I) can be expanded to calculate the covariance between points on different sides of the second perturbation. Equation 4 will be used as is for all pairs of points on the same side of the second perturbation. This can be used to study deactivation as well as any paradigm that involves changing from one GABA concentration to another. A similar process will be used to study three perturbations that will allow analysis of data studying recovery from desensitization. These added paradigms are expected to emphasize different aspects of receptor function. Parameters poorly estimated using one paradigm might be better estimated using another.
Single-channel analysis has long been the most reliable method for obtaining information on molecular mechanism and discriminating between complex kinetic models. CVF reveals that macroscopic traces contain more information than was previously realized and this study begins to explore its capabilities. In addition to complementing single-channel analysis, CVF has several important advantages. The biological importance of ligand-gated ion channels is their role in mediating fast synaptic potentials. Vital to this end is understanding their response to rapid changes in agonist concentration. CVF is ideally suited for studying ion channel kinetics in response to multiple perturbations. Although this can also be done with single-channel analysis, the same protocol might need to be applied several hundred times to obtain the same statistical power as that of a single macroscopic trace of several hundred channels. Furthermore, CVF does not require correction for missed events. The contribution of brief openings and closings to an ensemble current will largely be preserved. Finally, because it is applied to macroscopic traces, CVF should eventually be directly applicable to the study of synaptic potentials.
By fitting the covariance as well as the magnitude of ion channel current, CVF extracts an enormous amount of information from a limited amount of data. It has proven to be a robust method that can extract useful information even when overly simple models are used to analyze complex data. Although it is very unlikely that a single “correct” model of the GABAR will ever be proven conclusively, CVF will add a great deal of insight to our understanding of basic ion channel function, pharmacological modulation, and the relationship between structural correlates and kinetic parameters.
Acknowledgments
We thank Dr. David H. Farb for the use of laboratory facilities, Scott Downing for assistance with growing HEK cells and DNA transfection, and Drs. Terrel T. Gibbs and Robert A. Pearce for critical review of this manuscript.
This work was supported by National Institute of Mental Health grant RO3 MH59818-01.
APPENDIX I: COVARIANCE AND LIKELIHOOD CALCULATION
Macroscopic ion-channel data recorded in response to a perturbation (such as a change in voltage or agonist concentration) is typically analyzed by fitting to exponential equations using sum-of-squares minimization. This assumes that the value of the noise or variance at different points in time are uniform and independent (Fig. 9 A, top). This is not the case, however, with macroscopic desensitization data. As desensitization proceeds, the value of the current at any time tn will influence the predicted value associated with a subsequent time tn+1 (Fig. 9 A, bottom). Kinetic models are a series of differential equations that predict how a system will change with time. If the current happens to be below the predicted value at tn, it is more likely to be below than above the predicted value at tn+1. This is a reflection of the correlation or covariance between each measurement. In this article, a new method of analysis is described that fits macroscopic currents using maximum likelihood directly to kinetic models taking into account both the magnitude of the current and the covariance between each pair of values.
FIGURE 9.
(A) Illustration of the effects of uncorrelated and correlated noise. The smooth curves in all four panels represent the current predicted by the model in Fig. 2 during desensitization. Solid symbols represent the measured current at one point in time, which, due to random chance, is below the predicted value. (Top panels) Open symbols represent the range of values predicted by the model assuming only uncorrelated Gaussian noise. The current at a subsequent time has an equal chance of being above or below the predicted value. Data points in the top right panel are generated by adding uniform Gaussian noise to the smooth curve. (Bottom panels) Middle arrow is parallel to the curve and represents the change in current predicted by the kinetic model. The top and bottom arrows represent random deviation from this prediction. Open symbols represent the range of values predicted by the model taking into account the correlations. The current at subsequent times has a greater chance of being below than above the predicted value. Data points in the bottom right panel are generated using the model in Fig. 2. (B) Plot of some elements of the covariance matrix (inset) for the model in Fig. 2. The thick line represents the variance (diagonal elements) and the thin lines represent the covariance (rows) for six different time points (3, 20, 30, 60, 90, and 150 ms). All six covariance curves decay biexponentially with time constants equal to the inverse of the eigenvalues of the Q matrix. The time associated with peak variance (18 ms) is the time when 50% of the channels are open.
Although it may be natural to think in terms of the probability that a proposed model is true after the recording of a particular data set (probability of model given observed data), the mathematics of statistical analysis typically functions in reverse. Because a hypothesis can only be true or false, the term likelihood is used rather than probability in describing its plausibility (Nagelkerke, 1992; Sakman and Neher, 1995). The likelihood of a model is defined as the probability that the recorded data would be observed if the data were drawn from the model (probability of observed data given model). The maximum likelihood method (ML) (Nagelkerke, 1992; Press et al., 1992; Rao, 1973; Sakman and Neher, 1995) involves adjusting model parameters until the parameter values associated with the maximum likelihood (the maximum likelihood estimate (MLE)) are found. It can be shown that, when the correct model is used and the number of observed data points is adequate, the parameter estimates identified by the ML method are approximately normally distributed around the true values (Knight, 2000; Rao, 1973). The principal difficulty in applying this method stems from an inability to derive an explicit formula for the relationship between the model parameters and the probability of observing a particular data set.
When making a random selection from a normally distributed population, the probability of observing a value x is given by the formula:
 |
(1) |
where m is the mean and σ the standard deviation of the population. The probability of making two independent observations x1 and x2 is the product of making the individual observations. This is valid because the result of the first observation does not change the values of m or σ associated with the second observation. Regardless of the value of x1, the probability of observing x2 is still given by Eq. 1. The product of the two equations can be expressed in vector notation as:
 |
(2) |
where X is the column vector {x1, x2}, M is the column vector {m, m}, the prime (′) indicates transposition to a row vector, and V is a 2 × 2 diagonal matrix whose elements are σ2. When there is a correlation between the two observations, the value of x1 affects the value expected for x2. Equation 2 can be also be used to describe the probability of making two correlated observations, but V is no longer a diagonal matrix. The two off-diagonal elements reflect the strength and direction of the correlation. Equation 2 is referred to as the general multivariate likelihood function and V is referred to as the covariance matrix (Bevington and Robinson, 1992; Mood et al., 1974; Perlman, 1969; Stevens, 1998). Equation 2 can be expanded to accommodate any arbitrary number of observations.
In the analysis of an electrophysiological recording, each current value is an element of the vector X. When fitting to an exponential equation, the elements of the vector M are generated by evaluating the equation for the times associated with the observations in X. Curve fitting by sum-of-squares minimization is identical to the maximum likelihood method when σ is a constant and the observations are uncorrelated. Under these conditions, V is a diagonal matrix of a single value and maximization of Eq. 2 is accomplished by minimizing (X − M)′(X − M) that is the sum of squares. In fact, neither of these two conditions is met when analyzing macroscopic ion channel data after a perturbation (see Fig. 9 A). There is a correlation between each measurement and so V is not a simple diagonal matrix. The off-diagonal elements of V correspond to the covariance between each pair of points. In addition, the diagonal elements of V, the predicted variance, are not constant but increase as the number of open channels nears 50% of the total. In this study, the Q-matrix method is used to calculate the elements of both M and V.
When a simple two-state molecule (A==B) is perturbed at time 0, it relaxes back to equilibrium according to the equation: At = (A0 − Ass)exp(−kt) + Ass, where A0, At, and Ass are the concentrations of A or probabilities of the molecule being in state A at times 0, t, and infinity, respectively, and k is the sum of the forward and reverse rate constants. When a three-state molecule (A==B==C) is perturbed, its relaxation back to equilibrium is described by an equation of a similar form: pt = p0eQt, where p is a 3 × 1 vector whose elements are the probability of finding the system in each of the three states at various times, and Q is a 3 × 3 matrix whose elements are a specific combination of the four-rate constants (Colquhoun and Hawkes, 1977). Each kinetic model generates a unique Q matrix. A change in the number of states changes the dimensions of the Q matrix and a change in the arrangement of states changes the arrangement of the elements within the Q matrix.
For a population of N ion channels after a perturbation, the total current at time t is given by:
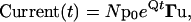 |
(3) |
where p0 is a vector of the initial distribution of states, Γ is a diagonal matrix whose elements reflect the amount of current each states passes, (0 for closed and desensitized states), u is a column vector of 1's that when multiplied by a row vector, adds up the elements giving a single value. Algorithms for raising e to the power of a matrix are given in Sakman and Neher (1995).
In this study, it is assumed that all receptors start in the closed state, so p0 is 0 except for the element corresponding to the closed state. For any time t, the probability of finding the receptor in each state is the product of the initial vector p0 and eQt. Multiplying this by Γ gives a row vector of currents through each state. Multiplying by u adds the currents associated with each state giving the total expected current at time t. The vector M is generated by evaluating Eq. 3 for each time point associated with the data set, X.
At the heart of CVF is the covariance formula (Colquhoun and Hawkes, 1977) that determines the predicted correlation between any two time points, 0 ≤ t1 ≤ t2:
 |
(4) |
The covariance matrix, V, is generated by evaluating Eq. 4 for each pair of time points associated with the data set, X. The diagonal elements of V (t1 = t2) give the variance at each time point. When t1 and t2 are not equal, t2 is the greater of the two times and the result of each evaluation of Eq. 4 is used for two elements of V, ((t1, t2) and (t2, t1)). For a data set of 100 points, 5050 evaluations of Eq. 4 are required to generate a matrix of 10,000 elements. Fig. 9 B is a plot of some of the elements of the covariance matrix for a particular kinetic model.
Using this method, the multivariate normal approximation to the probability of observing any data set, X, can be calculated given a kinetic model and a particular set of parameters. The maximum likelihood method proceeds by adjusting the kinetic parameters, which changes Q and thus changes the likelihood, until the parameters associated with the highest possible likelihood is found, the MLE.
APPENDIX II: GENERATION OF INITIAL VALUES FOR CVF
Initial values for fitting a particular data set to a particular model can be generated from the results of a previous fit to a different model. The following procedure describes how the results of fitting a data set to one model (model A) is used to generate initial values that can be used for fitting the same data set to a different model (model B).
The results of fitting the data set to model A are used to generate a smooth idealized curve.
The same fitting results are also used to generate crude initial values specific for model B (see below).
The smooth curve is fit by sum-of-squares minimization to model B starting with the crude initial values.
The results of fitting the smooth curve to model B are used as the initial values for fitting the original data to model B by CVF.
Analysis of perturbation data begins by fitting the decaying phase to a series of decaying exponential equations by sum-of-squares minimization. These results are then used as described above to generate initial values for kinetic models with a comparable number of desensitized states. Crude starting values are generated from the exponential results by assuming that τ(n) ∼ 1/(XnKf + Kr), where Xn is the fraction of the receptors in the state from which the nth phase of desensitization proceeds (after equilibration with faster states), and that the extent of desensitization is a function of Kf/Kr.
Once real data have been fit to a kinetic model, the results can be used to generate initial values, as described above, for fitting the same data to different kinetic models. Two general methods are used. In some cases, model A and model B have the same number of states but differ in the location of one state. In other cases, model B will have an additional state and thus have two additional free parameters. In the former case, crude initial values are generated by adjusting the forward rate constant of the state that is different. Again assuming τ(n) ∼ 1/(XnKf + Kr), Kf is adjusted to compensate for the difference in Xn between the two models, thus leaving τ(n) unchanged. For example, if model A has a single desensitized state connected to the closed state (D==C==O) and model B has a desensitized state connected to the open state (C==O==D), the crude value for the forward rate constant associated with model B would be given by: Kf* = Kf × (α/β), where Kf, α, and β are the parameters for model A. Because the fraction of receptors in the O states is greater than the fraction in the C state, a much slower forward rate constant is needed in model B to achieve the same τ of desensitization.
When model B has an additional desensitized state, crude starting values are generated by “splitting” one of the existing states into two. The forward rate constants for the two states are given by Kf* = Kf/2, and the reverse rate constants are unchanged. If the two desensitized states are not connected to the same state, the forward rate constant of one is adjusted as above. For example, if model A is (D==C==O) and model B is (D1==C==O==D2), the crude initial value for the forward rate constant for D2 would be given by: Kf2 = Kf × (α/β)/2, where Kf, α, and β are the parameters for model A.
Initial values for a particular data set can also be generated from the results of fitting analogous data sets (replicate data, for example) to the same model. First, each free parameter from the results of fitting the other data sets is averaged. The resulting average parameter set is then used as the origin of a vector space with the number of dimensions equal to the number of parameters. Each individual parameter set is treated as a vector in the space. The likelihood associated with the origin, the individual parameter sets, as well as the sum and average of each vector pair is calculated. The parameter set with the highest likelihood is used as the initial values in a new fit.
References
- Acton, F. S. 1970. Numerical Recipes that Work. Harper and Row Publishers, New York.
- Akaike, H. 1974. A new look at the statistical model identification. IEEE Trans. On Automatic Control. 19:716–723. [Google Scholar]
- Bai, D., P. S. Pennefather, J. F. MacDonald, and B. A. Orser. 1999. The general anesthetic propofol slows deactivation and desensitization of GABA(A) receptors. J. Neurosci. 19:10635–10646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball, F. G., R. McGee, and M. S. P. Sansom. 1989. Analysis of post-perturbation gating kinetics of single ion channels. Proc. R. Soc. Lond. B Biol. Sci. 236:29–52. [DOI] [PubMed] [Google Scholar]
- Ball, F. G., and M. S. P. Sansom. 1989. Ion-channel gating mechanisms: model identification and parameter estimation from single-channel recordings. Proc. R. Soc. Lond. B Biol. Sci. 236:385–416. [DOI] [PubMed] [Google Scholar]
- Bevington, P. R., and D. K. Robinson. 1992. Data Reduction and Error Analysis for the Physical Sciences. WCB/McGraw-Hill, Boston, MA.
- Bishop, Y. M. M., S. E. Fienberg, and P. W. Holland. 1975. Discrete Multivariate Analysis: Theory and Practice. The MIT Press, Cambridge, MA.
- Boileau, A. J., R. Baur, L. M. Sharkey, E. Sigel, and C. Czajkowski. 2002. The relative amount of cRNA coding for γ2 subunits affects stimulation by benzodiazepines in GABAA receptors expressed in Xenopus oocytes. Neuropharmacology. 43:695–700. [DOI] [PubMed] [Google Scholar]
- Burkat, P. M., J. Yang, and K. J. Gingrich. 2001. Dominant gating governing transient GABA(A) receptor activity: a first latency and Po/o analysis. J. Neurosci. 21:7026–7036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang, Y., E. Ghansah, Y. Chen, J. Ye, and D. S. Weiss. 2002. Desensitization mechanism of GABA receptors revealed by single oocyte binding and receptor function. J. Neurosci. 22:7982–7990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, C., and H. Okayama. 1987. High-efficiency transformation of mammalian cells by plasmid DNA. Mol. Cell. Biol. 7:2745–2752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernoff, H. 1954. On the distribution of the likelihood ratio. Ann. Math. Stat. 25:573–586. [Google Scholar]
- Colquhoun, D., C. J. Hatton, and A. G. Hawkes. 2003. The quality of maximum likelihood estimates of ion channel rate constants. J. Physiol. 547:699–728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun, D., and A. G. Hawkes. 1977. Relaxation and fluctuations of membrane currents that flow through drug-operated channels. Proc. R. Soc. Lond. B Biol. Sci. 199:231–262. [DOI] [PubMed] [Google Scholar]
- Colquhoun, D., and A. G. Hawkes. 1987. A note on correlations in single ion channel records. Proc. R. Soc. Lond. B Biol. Sci. 230:15–52. [DOI] [PubMed] [Google Scholar]
- Feder, P. I. 1968. On the distribution of the log likelihood ratio test statistic when the true parameter is “near” the boundaries of the hypothesis regions. Ann. Math. Stat. 39:2044–2055. [Google Scholar]
- Haas, K. F., and R. L. Macdonald. 1999. GABAA receptor subunit γ2 and δ subtypes confer unique kinetic properties on recombinant GABAA receptor currents in mouse fibroblasts. J. Physiol. 514:27–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn, R. 1987. Statistical methods for model discrimination. Biophys. J. 51:255–263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn, R., and K. Lange. 1983. Estimating kinetic constants from single channel data. Biophys. J. 43:207–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones, M. V., and G. L. Westbrook. 1995. Desensitized states prolong GABAA channel responses to brief agonist pulses. Neuron. 15:181–191. [DOI] [PubMed] [Google Scholar]
- Jurman, M. E., L. M. Boland, Y. Liu, and G. Yellen. 1994. Visual identification of individual transfected cells for electrophysiology using antibody-coated beads. Biotechniques. 17:5169–5173. [PubMed] [Google Scholar]
- Knight, K. 2000. Mathematical Statistics. Chapman and Hall, Ontario.
- Kudo, A., and A. Arbor. 1963. A multivariate analogue of the one-sided test. Biometika. 50:403–418. [Google Scholar]
- Lavoie, A. M., J. J. Tingey, N. L. Harrison, D. B. Pritchett, and R. E. Twyman. 1997. Activation and deactivation rates of recombinant GABAA receptor channels are dependent on α-subunit isoform. Biophys. J. 73:2518–2526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, X., and R. A. Pearce. 2000. Effects of halothane on GABAA receptor kinetics: evidence for slowed agonist unbinding. J. Neurosci. 20:899–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macdonald, R. L., C. J. Rogers, and R. Twyman. 1989. Kinetic properties of the GABAA receptor main conductance state of mouse spinal cord neurones in culture. J. Physiol. (Lond.). 410:479–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magleby, K. L., and D. S. Weiss. 1990. Identifying kinetic gating mechanisms for ion channels by using two-dimensional distributions of simulated dwell times. Proc. R. Soc. Lond. B Biol. Sci. 241:220–228. [DOI] [PubMed] [Google Scholar]
- Mood, A. M., F. A. Graybill, and D. C. Boes. 1974. Introduction to the Theory of Statistics. McGraw-Hill Book Company, New York.
- Mozrzymas, J. W., A. Barberis, K. Michalak, and E. Cherubini. 1999. Chlorpromazine inhibits miniature GABAergic currents by reducing the binding and by increasing the unbinding rate of GABAA receptors. J. Neurosci. 19:2474–2488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagelkerke, N. J. D. 1992. Maximum Likelihood Estimation of Functional Relationships. J. Berger, S. Fienberg, J. Gani, K. Krickeberg, I. Olkin, B. Singer, editors. Springer-Verlag, Berlin, Germany.
- Nuesch, P. E. 1965. On the problem of testing location in multivariate populations for restricted alternatives. Ann. Math. Stat. 37:113–119. [Google Scholar]
- Perlman, M. D. 1969. One-sided testing problems in multivariate analysis. Ann. Math. Stat. 40:549–567. [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W., Flannery, B. 1992. Numerical Recipes in C. Cambridge University Press, Cambridge, UK.
- Qin, F., A. Auerbach, and F. Sachs. 1996. Estimating single-channel kinetic parameters from idealized patch-clamp data containing missed events. Biophys. J. 70:264–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin, F., A. Auerbach, and F. Sachs. 1997. Maximum likelihood estimation of aggregated Markov processes. Proc. R. Soc. Lond. B Biol. Sci. 264:375–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin, F., A. Auerbach, and F. Sachs. 2000a. A direct optimization approach to hidden Markov modeling for single-channel kinetics. Biophys. J. 79:1915–1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin, F., A. Auerbach, and F. Sachs. 2000b. Hidden Markov modeling for single-channel kinetics with filtering and correlated noise. Biophys. J. 79:1928–1944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao, C. R. 1973. Linear Statistical Inference and Its Applications. John Wiley and Sons, New York.
- Sakman, B., and E. Neher. 1995. Single-Channel Recording. Plenum Press, New York.
- Scheller, M., and S. A. Forman. 2002. Coupled and uncoupled gating and desensitization effects by pore domain mutations in GABA(A) receptors. J. Neurosci. 22:8411–8421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Self, S. G., and K.-Y. Liang. 1987. Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J. Am. Stat. Assoc. 82:605–610. [Google Scholar]
- Shao, J. 1999. Mathematical Statistics. Springer, New York.
- Shapiro, A. 1985. Asymptotic distribution of test statistics in the analysis of moment structures under inequality constraints. Biometrika. 72:133–144. [Google Scholar]
- Shen, W., S. Mennerick, D. F. Covey, and C. F. Zorumski. 2000. Pregnenolone sulfate modulates inhibitory synaptic transmission by enhancing GABA(A) receptor desensitization. J. Neurosci. 20:3571–3579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigworth, F. J. 1985. Open channel noise. I. Noise in acetylcholine receptor currents suggests conformational fluctuations. Biophys. J. 49:709–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens, C. F. 1998. The Six Core Theories of Modern Physics: A Bradford Book. The MIT Press, Cambridge, MA.
- Tia, S., J. F. Wang, N. Kotchabhakdi, and S. Vicini. 1996. Distinct deactivation and desensitization kinetics of recombinant GABAA receptors. Neuropharmacology. 35:1375–1382. [DOI] [PubMed] [Google Scholar]
- Weiss, D. S., and K. L. Magleby. 1989. Gating scheme for single GABA-activated Cl− channels determined from stability plots, dwell-time distributions, and adjacent-interval durations. J. Neurosci. 9:1314–1324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, W. J., and S. Vicini. 1997. Neurosteroid prolongs GABAA channel deactivation by altering kinetics of desensitized states. J. Neurosci. 17:4022–4031. [DOI] [PMC free article] [PubMed] [Google Scholar]











