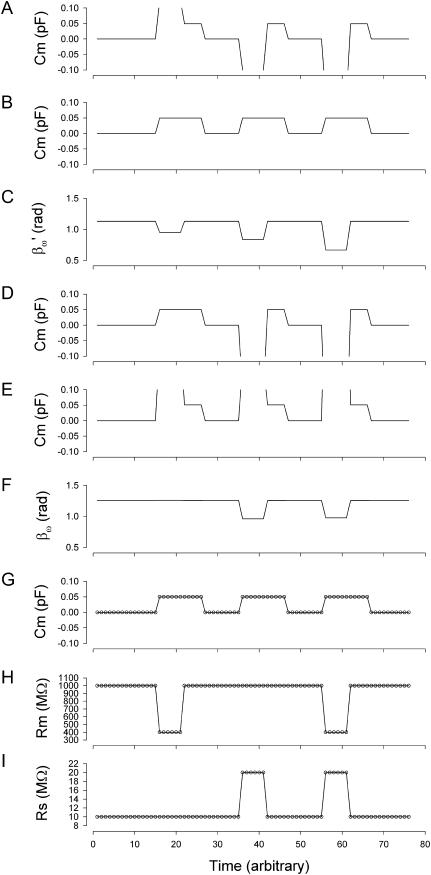
FIGURE 2.

Simulation of capacitance changes in whole-cell mode. The component values of the model (R_s: 10 MΩ, R_m: 1 GΩ, and C_m: 6.5 pF) in Fig. 1 A were modulated out of phase with each other, with a C_m jump of 0.05 pF accompanied by either a 600-MΩ drop in R_m, or a 10-MΩ increase in R_s or all changes occurring simultaneously (see panels G–I). The stimulating frequency f₀ was the same for single-sine and eCm methods, with f₀ at 390.6 Hz and f₁ at twice that. In panels A–C, calculations are based on setting the PSD angle to an estimate (denoted by the prime) of β_ω, the angle of ∂Y/∂G_s − 90°, 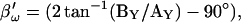to mimic R_s dithering. (A) A true piecewise linear approach was employed using this angle 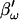in place of β_ω in Eq. 52. Whole-cell capacitance compensation was modeled by connecting and supplying the circuit components R_d and C_d (Fig. 1) with corresponding values of R_s and C_m, but with an overall negative admittance. PSD angle and gain corrections (1/abs(∂Y/∂C_m) were determined from whole-cell conditions at the zero time point and remained fixed throughout. It can be seen that when cell components are changed (G–I) the phase angle changes causing errors in C_m estimation (A). Even though the PSD angle is set to guard against R_s changes, a change from 10 to 20 MΩ (I) is too large to counter; such overpowering effects of parameter changes are well known (Lindau, 1991). However, if capacitance compensation is not employed and point-by-point resetting of new angle and gain factors are made and applied, absolute C_m is obtained without any errors (B). To make point-by-point corrections experimentally, the raw admittance (Y) at each point was taken and the angle of 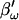was calculated according to Zierler (1992), namely, 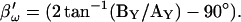The true gain factor, H_c, at each data point was calculated as 1/abs(∂Y/∂C_m). With each new gain and angle, circuit parameters were calculated as in Eq. 52, by extracting the component of Y at that phase angle and multiplying by that gain factor. Each admittance point was so treated to obtain circuit parameters. The reason this procedure works so well is that the value returned by this modified PSD analysis is the imaginary component of Y; thus, this method produces the same results as the eCm method as shown in panel G. This useful single-sine approach, employing the estimate of H_c provided by Gillis (1995), is implemented in jClamp. However, because this is an estimate of the true gain, 1/abs(∂Y/∂C_m), relying on circuit approximations, C_m estimates are not fully immune from circuit parameter changes. In panels D–F, calculations are based on setting the PSD angle to the angle of ∂Y/∂C_m, namely β_ω, to mimic capacitance compensation dithering. (D) The true piecewise linear approach was employed as above in panel A. In this case, using β_ω, the large change in R_m does not affect the phase angle substantially (F), so C_m estimates are accurate and robust. However, R_s changes do interfere with angle and estimate, as expected (Joshi and Fernandez, 1988). Unlike the treatment above (B), panel E shows that applying a point-by-point correction as detailed above to the uncompensated admittance fails to provide error free C_m estimation, because the imaginary component of Y is not returned in this case. Panels G–I show the results of the eCm method, where the calculated absolute values are depicted by the circles. Note an exact correspondence between actual parameter values (solid lines) and calculated estimates (○), with no parameter interactions. Simulation in MatLab.