Abstract
Light-scattering diagrams (phase functions) from single living cells and beads suspended in an optical trap were recorded with 30-ms time resolution. The intensity of the scattered light was recorded over an angular range of 0.5–179.5° using an optical setup based on an elliptical mirror and rotating aperture. Experiments revealed that light-scattering diagrams from biological cells exhibit significant and complex time dependence. We have attributed this dependence to the cell's orientational dynamics within the trap. We have also used experimentally measured phase function information to calculate the time dependence of the optical radiation pressure force on the trapped particle and show how it changes depending on the orientation of the particle. Relevance of these experiments to potential improvement in the sensitivity of label-free flow cytometry is discussed.
INTRODUCTION
When a cell is illuminated, it scatters light in all directions. The spatial distribution of the scattered light intensity is not random. In fact, a complex spatial pattern is formed that is dependent on a cell's size, shape, refraction index, density, and morphology. Because of the emission coherence from the different scattering centers in a cell, elastic light scattering may offer more information on the morphology of the cell compared to incoherent techniques such as, e.g., fluorescence spectroscopy; this is especially true when a label-free approach is sought. Studying the scattered light in appropriate angular ranges enables the determination of morphological information from the cell. This information can be used to discriminate between different cell types or, more importantly between different cell states. This has important potential applications and is in fact already being used in biomedical science for cell analysis and sorting (Shapiro, 1995 and references therein; van de Hulst, 1982). There is a large body of work on cell sorting using flow cytometry systems that detect forward and side-scattered light, primarily for cell size detection. More complex biological applications such as, e.g., label-free detection of small, drug-induced morphological changes inside the cell, have been limited, some of these limitations being due to the experimental difficulties in measuring of the angular distribution of the scattered light intensity, which typically spans 5–8 orders of magnitude. There have been only a few attempts to detect the full 180° or 360° phase function from single biological cells (Salzman et al., 1975; Loken et al., 1976; Bartholdi et al., 1980; Marshall et al., 1976; Doornbos et al., 1996). In the recent past, experiments devised to collect light-scattering diagrams from cells have typically been achieved using low density cell suspensions. These approaches offer statistically averaged information about a cell population, where the fine details of a single cell's phase function are lost due to natural size, shape, orientation, and morphological variations observed over a cell population. Potential applications, however, exist in cytometry, where the analysis is typically done on a single cell at a time. There have been numerous studies that suggest how the nature of a cell affects the angular intensity distribution in the scattering phase function. Forward scattered light in the small angle region (θ ≤ 2°, where θ = 0° corresponds to the direction of incident light) is primarily dependent on the cell's size and refractive index (Mullaney et al., 1969); however, other factors such as, e.g., cell shape and morphology are contributing as well (Kerker et al., 1979). Forward scattered light at larger angles (5–30°) has been suggested to be largely dependent on the nucleus of the cell (nucleus/whole cell volume ratio). Experiments on suspensions of isolated nuclei have yielded similar results to whole cell scattering in this angular region, implying minimal dependence on the cell's smaller internal structures (Brunsting and Mullaney, 1974; Steen and Lindmo, 1985; Kerker et al., 1979). Conversely, light scattered at larger angles (∼50–130°) is highly dependent on the amount of a cell's internal structure (Kerker et al., 1979; Kerker, 1983; Mourant et al., 1998). Organelles such as the mitochondria, peroxisomes, lysosomes, microtubules, etc. serve as scattering sites amid the relatively isotropic refractive index medium of the cytoplasm, contributing to light scattering at large scattering angles (Dubelaar et al., 1987; Dunn and Richards-Kortum, 1996; Beuthan et al., 1996; Barer, 1957; Barer and Joseph, 1954). As an example, the high spatial frequency of refractive index variations of a granulocyte cell causes higher intensity of light scattering at these large angles than does the relatively more isotropic index of a lymphocyte cell. This presents an extremely useful means to discriminate between cells that appear to be similar, yet have different internal structures. Experiments on suspensions of isolated proteins and mitochondria, as well as FDTD models including small internal structures, have validated the claim that cell organelles are primarily responsible for the amount of large angle scattering (Dunn and Richards-Kortum, 1996). Lastly, in the backscatter region (160° < θ < 180°) the cell membrane itself is mainly responsible for the scattered light (Meyer, 1979). It should be noted here that a cell with a damaged membrane scatters much less light in the forward direction than a healthy cell. This property may actually be used to discriminate dead cells from live ones.
In this article, we use a single-beam optical trap geometry (Ashkin et al., 1986; Ashkin, 1970) to isolate a single cell for time-dependent elastic light-scattering studies. We present our findings of a time-dependent phase function due to the orientational dynamics and morphological differences of trapped single cells. We describe an instrument based on a single-beam optical trap which integrates the capability to detect scattered light intensity in 360° with a time resolution of 30 ms. Stable traps were achieved for ∼2 h with actual recording times of up to 30 min. Experiments described in this article entail successful recordings of fresh and fixed A375 cells, lymphocytes, granulocytes, and beads of two different materials (PMMA and Silica) and sizes. Finally we propose methods to improve the sensitivity of light-scattering based flow sorting systems.
EXPERIMENTAL
Apparatus
A single-beam optical trap was used to isolate single cells for scattering measurement. The optical trapping setup is shown in Fig. 1. The trapping beam source is a continuous wave, 1064 nm, Nd:Yag laser (Intelite, Genoa, NV). A power stabilizer (CRI, Woburn, MA) is used for increased trap stability through active laser power control. The beam is spatially filtered and collimated to a diameter of ∼2 mm and subsequently focused using an aspheric lens (NA = 0.68, Thor, Newton, NJ) into a cylindrical cuvette to create a trap for the particle. The aspheric lens is mounted on an XYZ translation stage (460A Series, Newport, Irvine, CA) located below the fixed cuvette. After a cell has been trapped at the bottom of the cuvette, the translation stage is used to manipulate the cell and move it up into the beam of a red laser (40 mW, 658 nm, Crystal Laser, Reno, NV). The working distance of the aspheric lens is 1.6 mm, allowing for sufficient trapping heights (300–800 μm actually demonstrated). Cells were imaged through the bottom of the cuvette using a charge-coupled device sensor with a resolution of ∼2 μm.
FIGURE 1.
Diagram of single-beam optical trap used for levitation of a single particle.
The detection part of the system is designed to record a full 360° light-scatter pattern. Our setup, shown in Fig. 2, is based on an elliptical mirror as described by Gucker et al. (1973). Essentially, it is designed such that a trapped particle within the stationary cuvette is positioned at the focal point of the elliptical mirror. Azimuthally scattered light from the cell passes through the polished cylindrical cuvette walls and is reflected by the elliptical mirror toward its second focal point where the light detector (photomultiplier tube, i.e., PMT, R3896, Hamamatsu, Bridgewater, NJ) is located. A rotating aperture is used to select the angle at which the scattered light intensity is detected. The rotating aperture allows detection of a 360° profile of the scattered light intensity. In the present work, we have chosen to detect the scattered light over half of the possible range (0–180°). It is not possible to detect light scattered at very small angles and in the vicinity of 180° because of the finite divergence of excitation laser beam. In our experiments, light scattering is recorded in the range of 0.5–179.5°. It should be noted that at scattering angles above 160°, the detected light contains significant contribution from internal reflections inside the cylindrical cuvette. This limits accuracy of our data for weakly scattering (small particles) in the angular range of 160–179.5°. Due to the large dynamic range of the scattered light, a circularly graded intensity filter was placed after the rotating aperture such that the back-scattered light was attenuated the least whereas the forward scattered light is attenuated the most. Additionally, an interference filter (646–666 nm) and a condensing lens were placed before the PMT to increase the signal/noise ratio (SNR) of the measurement. A linearly polarized red diode laser source was focused into the cylindrical cuvette to induce light scattering. The intensity variation of the red laser power was measured to be <0.5%. The diameter of the scattering laser beam was evaluated using a beam profiler with 0.2% resolution (Data Ray, Boulder Creek, CA); diameter in the center of the cuvette was 75 or 150 μm, depending on the focusing lens used. The data acquisition system enabled PMT sampling frequencies of up to 200 kHz and the rotation velocity of the rotating aperture could be varied from a few RPM up to 2000 RPM, corresponding to a maximum time resolution of 30 ms (defined as the time interval between the start of one measurement and the start of the next one). Different diameters apertures were used to adjust the angular resolution of the scatter patterns. For the majority of our experiments, the diameter of the rotating aperture was 0.5 mm, yielding an angular resolution of ∼0.17° (distance between the center of the cuvette and the rotating aperture was 163 mm). However, due to diffraction off the aperture, we increased our estimate of the actual angular resolution to ∼0.3°. The complete detecting apparatus is confined in a light-tight box to minimize any source of background noise during experiments.
FIGURE 2.
Schematics of optical setup used to record scattering diagrams from single particles suspended in a optical trap.
Sample preparation
All experimental results in this work were obtained using the following sample preparation method. The density of the buffer used for experiments was increased relative to that of water to achieve stable levitation over long time periods. This was achieved by adding Optiprep (60% Iodoxanolin water solution; density of 1.2 g/ml) to a standard PBS buffer to increase the density of the suspension medium to 1.02–1.05 g/ml. It is important to note that the density of the medium was still slightly below the density of cells so that after a few minutes the cells would still settle naturally at the bottom of the cuvette. The cylindrical, polished glass cuvette (outer diameter of 10 mm) was run under an ionizer to minimize unwanted light scatter and static charge before each experiment. The bottom of cylindrical cuvette was coated with 2% Agarose to prevent the cells from sticking. The cuvette was then filled with 110 μL of the medium described above, resulting in a minimum liquid height of ∼1 mm. The amount of liquid used was optimized to have a small interaction length with the trapping laser and reduce thermal effects, while being large enough to suspend a single cell sufficiently far above any other cells laying on the bottom or other small scattering sources in the solution that could decrease the SNR. The orientation of the cylindrical cuvette inside the elliptical mirror was such that the scattering laser enters and exits normal to the cuvette surface and trapping occurs in the center of the cuvette so that the scattered light will exit normal to the cuvette's surface as well (see Fig. 2). Trapping heights were typically 350–500 μm whereas the trapping laser power was in the range of 15–30 mW. Note that experiments on PMMA and Silica beads (both from Bangs Laboratories, Fishers, IN) were performed in deionized water, and not in the buffer solution described in this section.
Preparation of leukocytes from whole blood
Peripheral blood from healthy donors was collected by venipuncture into glass vials containing sodium heparin as an anticoagulant agent. A preparation of “total leukocytes” was obtained by osmotic lysis of the erythrocytes. Briefly, 1 ml of whole blood was mixed with 14 ml of erythrocyte lysis solution (R&D Systems, Minneapolis, MN) and incubated at room temperature for 5 min. During this time, the ammonium chloride in the buffer causes lysis of erythrocytes while leaving the leukocytes fully intact and viable. The intact cells were then collected by centrifugation at 300 g for 5 min and washed twice in PBS. The cells were then fixed by resuspension of the cell pellet in 500 μl of phosphate-buffered formalin solution (Sigma, St. Louis, MO) for 5 min, washed again in PBS and finally resuspended in 500 μl of PBS. We used fixed cells to eliminate the contributions from any internal cellular dynamics in live cells that might be happening on the timescale of the measurements.
Validation of experimental apparatus
To validate our experimental apparatus, we measured light-scattering diagrams of 5 μm PMMA beads. In Fig. 3, the experimental results are compared to theoretical calculations based on the generalized Lorenz-Mie theory (Gouesbet et al., 1989, 1990). To achieve the best agreement between experimental data and theoretical calculations, the particle radius was varied. The best fit (as shown in Fig. 3) was obtained assuming a particle radius of 2.385 μm which is slightly below the particle size range specified by the bead manufacturer (2.5 ± 0.1 μm). It was actually not possible to achieve a good fit by adjusting the relative refractive index of the bead while keeping the bead radius at 2.5 μm. We believe that this experiment represents the most accurate method of determining the size of homogenous spherical particle compared to other methods (e.g., microscopy, Coulter counter) because, in this case, the large angle scattering (as characterized by peak positions and intensities in the scattering diagram) is an extremely sensitive function of particle size. However, the previous statement does not apply to cells since they are not homogeneous particles. The deviations at small and large angles (see Fig. 3) are only partially caused by extraneous light from the red laser beam reflected by the windows of the cylindrical cuvette. These deviations may also originate from some internal inhomogeneities and shape variations of the bead particle. Thus, the validation of our experimental apparatus in the whole angular range is dependent on the assumption of an ideal, spherical particle.
FIGURE 3.
Comparison between experimental scattering diagram for 5-μm PMMA bead and Lorenz-Mie theory light-scattering calculation. Calculation parameters: relative refraction index nrel = 1.122; particle radius, 2.385 μm; polarization, linear, azimuthal angle, 45° (defined as an angle between the polarization of the laser and detection plane).
RESULTS AND DISCUSSION
To compare the differences in the scattering properties of a cell and a bead we have taken snapshot images of either particle suspended in the optical trap and illuminated by a laser beam. Fig. 4 shows results for a trapped single A375 cell and a single bead recorded in the direction perpendicular to the illuminating laser source at 658 nm. From these images it is apparent that the scattering pattern (image) of the cell is much more irregular than that of the bead. Timed image sequences recorded at 30 frames/s showed that the visual appearance of the scattering pattern (image) of the cell exhibits a very strong time-dependence on the subsecond timescale whereas the scattering pattern of the bead is stable (see Supplementary Material to this article).
FIGURE 4.
Images of a trapped A375 cell and a 6.2-μm Silica bead at two different time points as viewed from the bottom of the cylindrical cuvette. Direction of incident excitation laser light is right to left as shown. The images on the right were recorded ∼3 s later than images on the left. The particles were located in the beam waist of the excitation laser.
Fig. 5 shows a typical phase function (scattering diagram) of a single A375 cell after correction for background signal. The data exhibits a number of oscillations as a function of scattering angle with the major component having a period of ∼10°. A simple Lorenz-Mie theory calculation for a spherical particle (not shown) indicates that the expected period should be ∼2° for a particle of similar size (∼15 μm) and a refractive index of 1.38 (typical average index of a cell). This suggests that the observed oscillations cannot be explained in terms of scattering by a homogeneous spherical particle. Lower angular frequencies are indicative of smaller scattering centers that are most likely small organelles inside the cell. To gain a further understanding of this, we recorded scattering diagrams for a cell as a function of time; Fig. 6 shows the time-dependent scattering diagrams from a single A375 cell for two different timescales. Data shown in Fig. 6 A indicates that the scattering phase function changes dramatically on the timescale from 0 to 4 s: both the scattering intensity and the locations of scattering peaks are varying in the angular spectrum at all scattering angles. Changes in the large angle scattering (side scatter) are more pronounced; however, some changes are also noticeable at smaller scattering angles (forward scatter). Fig. 6 B shows the data from the same experiment on a shorter timescale (0–160 ms). This indicates that the time dependence is significantly reduced at large scattering angles and nearly absent for forward scattered light (<10°).
FIGURE 5.
Scattering diagram of a single A375 cell suspended in a optical trap. The data shown are after subtraction of the background signal.
FIGURE 6.
Time-dependent scattering diagrams from an A375 cell shown for two different timescales. An important feature seen in both plots is that the forward scatter region is much more stable than the side-scatter region. In A, intensity fluctuations are already quite noticeable in the 40-ms time steps, specifically in the 90° region. Note that the intensity is plotted on a log scale, so that small differences are actually quite large. The plot shown in B fluctuates in both peak values and angular position of peaks. Notice the region near 45°, where a peak actually turns into valley, or rather the peak has shifted to the right. This variation in the scatter pattern was evident in all trapped cells.
Most of the applications of light scattering rely on experimental intensity data integrated within a specific range of scattering angles. In other experiments, optical radiation pressure forces are used to analyze the particle (Wang et al., 2003). We have used experimental light-scattering phase functions to calculate the integrated light-scattering signals (see Fig. 7, A and B). Fig. 7 C shows the axial optical force on the particle due to radiation pressure from scattering laser. The optical force on a particle can be calculated from light-scattering data by subtracting the forward momentum of scattered light from the total momentum carried by scattered light (van de Hulst, 1982):
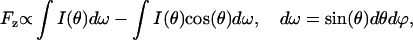 |
where I(θ) is the phase function measured in our experiments, θ is the scattering angle, and ϕ is the azimuth angle. The optical force calculated in this way is only an approximation since it is based on the light-scattering phase function obtained for one azimuth angle ϕ (i.e., light scattering is detected only in one plane). Data presented in Fig. 7 is primarily intended to illustrate the typical timescale of the cell's dynamics when it is released from optical trap and the SNR of the detection system.
FIGURE 7.
Time-dependent integrated light-scattering signals at forward (A) and side (B) scatter angles and axial optical force (C) measured for a A375 cell suspended in optical trap. Cell is released from the trap at time T = 2.5 s.
To elucidate the origin of the observed time dependence we have recorded light-scattering phase functions from a cell and a bead under identical conditions. In Figs. 8 and 9 we present experimental data on integrated light-scattering signals from an A375 cell. Fig. 8 shows the forward scatter and Fig. 9 the side-scatter signals as function of time over a 4-s time period. The signals were obtained from the scattering phase functions by integration over a given scattering angle range. Data on forward scatter indicates that the integrated signal is fluctuating in time with a coefficient of variation (CV) of 3.4% which is significantly larger than the CV of the illuminating laser power (0.5%). Since fluctuations in laser intensity cannot be the source of the observed variation, we have also performed experiments to check how the intensity of scattered light changes if the cell is translated laterally across the beam of illuminating laser. This experiment showed that there is no noticeable change in light-scattering phase function when a particle is translated by up to 4 μm. This is expected since the beam diameter of the red laser at the trapping point was either 75 or 150 μm (both diameters were tested). We have also detected no random lateral movement of the cell within the resolution of our imaging system (<2 μm). This implies that the observed fluctuations must come from a change in some intrinsic scattering ability of the cell. In the case of side scatter (Fig. 9) four successive angular integration ranges were used; this was done to model the detection of side-scattered light by an optical system with different numerical apertures. Notice that the amplitude of the side-scatter fluctuations gradually decreases (from 30% to 8.5%) when the signal is averaged over an increasingly large angular range. To explain the above dynamics of the signal from the cell we decided to perform a similar experiment on a silica bead. Fig. 10 shows the time-dependence profile of integrated light-scattering signals for a 6.2-μm diameter Silica bead. This data clearly shows that the light-scattering signals from the bead are more stable than those of a cell in similar conditions. In particular, the side-scatter signal from the bead is much more stable than that from the cell (4.5 vs. 18%). We have also performed experiments on beads where we have accidentally trapped more than one bead (data not shown). In this case, the fluctuations in the scattering signals increase dramatically and become very similar to those of the cell. The images of multiple beads trapped are time-dependent and more similar to those of the trapped cells (see Fig. 4, top).
FIGURE 8.
Forward scatter and axial optical force from a suspended A375 cell as function of time.
FIGURE 9.
Time-dependent light-scattering signal integrated in four progressively larger angular ranges.
FIGURE 10.
Time-dependent integrated light-scattering signals (at forward and side-scatter angles) and axial optical force measured for a 6.2-μm bead suspended in optical trap.
From all of the information gathered above, we can conclude that a trapped cell is undergoing orientational (rotational) motion in the trap. Most of the cells are not perfect spheres, and therefore a change in orientation leads to a change in the scattering phase function, which in turn gives rise to fluctuations in the integrated scattering signals. It is known from theoretical calculations that even a small amount of ellipticity in a particle can yield significant changes in the angular distribution of scattered light (Latimer et al., 1978). Simulations suggest that larger changes due to ellipticity are expected for large angle scattering (both amplitudes and location of the peaks are expected to change), whereas low angle scatter is affected less. Intuitively this is expected since light scattered at large angles is undergoing multiple reflections inside the particle. Our experimental results seem to correlate with these theoretical findings. Obviously no orientational dependence is expected from spherical beads, which is confirmed by our experiments (the residual fluctuations are likely to be due to imperfections in the bead and/or the measurement system). Ellipticity is not the only factor that can modulate scattering signal during orientational motion. Asymmetrical distribution of organelles in the cell, especially large ones like the nucleus, will also affect scattering function depending on the orientation of the cell. In Fig. 11 we show the time dependence of light-scatter intensity at 45° for a cell and a bead; their respective Fourier transforms are also shown. These spectra indicate that the orientational motion of the cell happens on the timescale of a few seconds; however, they exhibit no distinct frequency components, suggesting that the motion is random.
FIGURE 11.
Time dependence of side-scattering signal for a A375 cell and 6.2-um Silica bead (upper graph) and corresponding Fourier amplitude spectra (lower graph).
Potentially, there are a few reasons why a cell in the trap is undergoing rotational motion. The first cause could be rotational diffusion. However, a calculation of the rotational correlation time due to diffusive motion according to τc = Vη/kT (where V is the volume of the cell and η is viscosity) suggests very long correlation times on the order of ∼400 s, which is not consistent with our experimental observation. Second, the radiation pressure forces from the trapping laser could cause the asymmetric cell to spin. However, this can be excluded for two reasons: 1), there are no well-defined frequency components that would suggest any regular motion (see Fig. 11) and 2), data presented in Fig. 7 indicate that fluctuations in the signal persists for at least a few more seconds after the trapping laser is switched off. In addition, the radiation pressure force from the scattering laser at 658 nm is too weak to be the cause of such behavior because its power density is very low at the trap location (no effect on the cell/particle motion was observed when the trapping laser was switched off). This leads us to conclude that the orientational motion is fueled by the convective currents inside the cuvette. It was possible to directly confirm the existence of these currents in the cuvette by the observation of small dust particles moving along semistraight trajectories (not diffusively) across the illuminating laser beam on the timescale of a few seconds. These currents become progressively stronger when the depth of the liquid in the cuvette is increased. At liquid depths of >2 mm, convective currents were strong enough to actually prevent any stable trapping of the cell.
As an example of the measurement capability of our apparatus, in Fig. 12 we present the full light-scattering phase functions of single granulocyte and monocyte cells. We believe that this kind of data have been recorded for the first time. The differences seen at large scattering angles are consistent with the very well-known observation that integrated light-scattering signals from granulocytes are noticeably stronger than from lymphocytes (monocytes) at large angles (Salzman et al., 1975), whereas the differences at low angles are relatively small (Shapiro, 1995 and references therein). The full light-scattering phase functions shown in Fig. 12 clearly contain more information than the integrated light-scattering signals that are typically used in conventional flow cytometry (Shapiro, 1995). This information could potentially be used for more sensitive and informative label-free cell analysis and sorting. However, a theoretical analysis, based on exact methods (see, e.g., Mishchenko et al., 2002) should be carried out to correlate light-scattering patterns with cell morphology. We believe that the extra information contained in the experimentally measured phase function should allow discrimination between cells based on more subtle morphological differences than currently possible using integrated light-scattering signals.
FIGURE 12.
Light-scattering diagrams of a normal blood lymphocyte and two different granulocytes.
CONCLUSIONS
Our experiments prove that orientation of a cell has a strong affect on the elastic light-scattering signal measured from that cell. Data shows quantitatively that this orientational dependence has a significant contribution to the fluctuations of integrated light-scattering signals in conventional flow cytometry, making cell size measurements less accurate. First, data presented in Fig. 9 suggests that integration of the light-scatter intensity within larger solid angle (using a light collection objective with a higher numerical aperture), would enable reducing the fluctuations of the integrated side-scatter signal. Second, we expect that an optical system with side-scatter detection from multiple directions would further increase the accuracy of light-scatter measurement in flow cytometry. However, complete elimination of the orientational dependence is not possible by only using the enhanced angular integration or multiple detection directions. As long as a single excitation laser is used and the orientation of the cell is constant during the measurement time with respect to the direction of the laser (as is typically the case in flow cytometers where cells flow at high velocities of a few meters/s through an ∼10-μm beam), the orientation of the cell will have an impact on the measured scattering phase function. Thus, the use of multiple lasers to illuminate a cell from different directions will average out the orientational dependence of the cell during the measurement and may help with further increasing the accuracy of light-scattering measurements.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Valeria Liverini and Luis Pestana for early work on the development of the light-scattering apparatus used in this work.
This work was supported in part by Defense Advanced Research Projects Agency contract number DAAH01-03-C-R184.
References
- Ashkin, A. 1970. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 24:156–159. [Google Scholar]
- Ashkin, A., J. M. Dziedzic, J. E. Bjorkholm, and S. Chu. 1986. Observation of a single-beam gradient force optical trap for dielectric particles. Optics Lett. 11:288–290. [DOI] [PubMed] [Google Scholar]
- Barer, R. Refractometry and interferometry of living cells. 1957. J. Opt. Soc. Am. 47:545–556. [DOI] [PubMed] [Google Scholar]
- Barer, R., and S. Joseph. Refractometry of living cells. 1954. Quart. J. Microsc. Sci. 95:399–423. [Google Scholar]
- Bartholdi, M., G. C. Salzman, R. D. Hiebert, and M. Kerker. 1980. Differential light scattering photometer for rapid analysis of single particles in flow. Applied Opt. 19:1573–1581. [DOI] [PubMed] [Google Scholar]
- Beuthan, J., O. Minet, J. Helfman, M. Herrig, and G. Müller. 1996. The spatial variation of the refractive index in biological cells. Phys. Med. Biol. 41:369–382. [DOI] [PubMed] [Google Scholar]
- Brunsting, A., and P. F. Mullaney. 1974. Differential light scattering from spherical mammalian cells. Biophys. J. 14:439–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doornbos, R. M. P., M. Schaeffer, A. G. Hoekstra, P. Sloot, B. de Grooth, and J. Greve. 1996. Elastic light-scattering measurements of single biological cells in an optical trap. Applied Opt. 35:729–734. [DOI] [PubMed] [Google Scholar]
- Dubelaar, G. B. J., J. W. M. Visser, and M. Donze. 1987. Anomalous behaviour of forward and perpendicular light scattering of a cyanobacterium owing to intracellular gas vacuoles. Cytometry. 8:405–412. [DOI] [PubMed] [Google Scholar]
- Dunn, A., and R. Richards-Kortum. 1996. Three-dimensional computation of light scattering from cells. IEEE J. Quantum Electron. 2:898–905. [Google Scholar]
-
Gouesbet, G., G. Gréhan, and B. Maheu. 1989. On the generalized Lorenz-Mie theory: first attempt to design a localized approximation to the computation of the coefficients
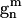 . J. Optics (Paris). 20:31–43. [Google Scholar]
. J. Optics (Paris). 20:31–43. [Google Scholar] -
Gouesbet, G., G. Gréhan, and B. Maheu. 1990. Localized interpretation to compute all the coefficients
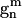 in the generalized Lorenz-Mie theory. J. Opt. Soc. Am. A. 7:998–1007. [Google Scholar]
in the generalized Lorenz-Mie theory. J. Opt. Soc. Am. A. 7:998–1007. [Google Scholar] - Gucker, F. T., J. Tuma, H. M. Lin, C. M. Huang, S. C. Ems, and T. R. Marshall. 1973. Rapid measurement of light-scattering diagrams from single particles in an aerosol stream and determination of latex particle size. Aerosol Sci. 4:389–404. [Google Scholar]
- Kerker, M. 1983. Elastic and inelastic light scattering in flow cytometry (Paul Mullaney Memorial Lecture). Cytometry. 4:1–10. [DOI] [PubMed] [Google Scholar]
- Kerker, M., H. Chew, P. J. McNulty, J. P. Kratohvil, D. D. Cooke, M. Sculley, and M. P. Lee. 1979. Light scattering and fluorescence by small particles having internal structure. J. Histochem. Cytochem. 27:250–263. [DOI] [PubMed] [Google Scholar]
- Latimer, P., A. Brunstig, B. E. Pyle, and C. Moore. 1978. Effects of asphericity on single particle scattering. Applied Opt. 17:3152–3158. [DOI] [PubMed] [Google Scholar]
- Loken, M. R., R. G. Sweet, and L. A. Herzenberg. 1976. Cell discrimination by multiangle light scattering. J. Histochem. Cytochem. 24:284–291. [DOI] [PubMed] [Google Scholar]
- Marshall, T. R., C. S. Parmenter, and M. Seaver. 1976. Characterization of polymer latex aerosols by rapid measurement of 360° light scattering patterns from individual particles. J. Colloid Interface Sci. 55:624–636. [Google Scholar]
- Meyer, R. A. 1979. Light scattering from biological cells: dependence of backscatter radiation on membrane thickness and refractive index. Applied Opt. 18:585–590. [DOI] [PubMed] [Google Scholar]
- Mishchenko, M. I., L. D. Travis, and A. A. Lacis. 2002. Scattering, Absorption, and Emission of Light by Small Particles. Cambridge University Press, Cambridge, UK.
- Mourant, J. R., J. P. Freyer, A. H. Hielscher, A. A. Eick, D. Shen, and T. M. Johnson. 1998. Mechanisms of light scattering from biological cells relevant to noninvasive optical-tissue diagnostics. Appl. Opt. 37:3586–3593. [DOI] [PubMed] [Google Scholar]
- Mullaney, P. F., M. A. Van Dilla, J. R. Coulter, and P. N. Dean. 1969. Cell sizing: a light scattering photometer for rapid volume determination. Rev. Sci. Instrum. 40:1029–1032. [DOI] [PubMed] [Google Scholar]
- Salzman, G. C., J. M. Crowel, J. C. Martin, T. T. Trujillo, A. Romero, P. F. Mullaney, and P. M. LaBauve. 1975. Cell identification by laser light scattering: identification and separation of unstained leukocytes. Acta Cytol. 19:374–377. [PubMed] [Google Scholar]
- Shapiro, H. M. 1995. Practical Flow Cytometry. New York. Wiley-Liss, New York.
- Steen, H. B., and T. Lindmo. 1985. Differential of light-scattering detection in an arc-lamp-based epi-illumination flow cytometer. Cytometry. 6:281–285. [DOI] [PubMed] [Google Scholar]
- van de Hulst, H. C. 1982. Light Scattering by Small Particles. Dover Publications, New York.
- Wang, M. M., C. A. Schnabel, M. Chachisvilis, R. Yang, M. J. Palioti, L. A. Simons, L. McMullin, N. Hagen, K. Lykstad, E. Tu, L. M. Pestana, S. Sur, H. Zhang, W. F. Butler, I. Kariv, and P. J. Marchand. 2003. Optical forces for noninvasive cellular analysis. Applied Opt. 42:5765–5773. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.














