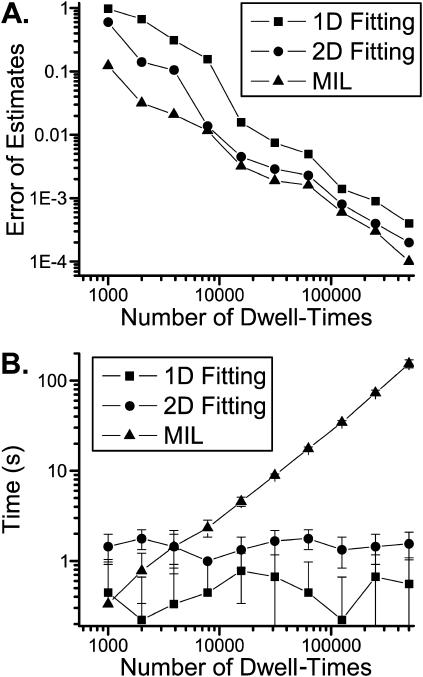
FIGURE 5.

Comparisons of the one-dimensional and two-dimensional histogram fittings with the full likelihood fitting of dwell-time sequences. (A) Mean errors of the estimates of parameters. Increasing data length reduced the estimation variances, and the reduction was approximately inversely proportional to the square-root of the number of events. The full likelihood fitting has the least variances among the three approaches, but the differences become relatively insignificant when the number of dwell-times is large. The mean errors are determined by 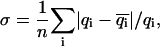where n is the number of rates, q-values are the true values of the rates used in simulation, and 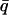-values are the corresponding estimates. (B) Computational times of the fittings. The histogram fittings had a complexity virtually independent of data length, whereas the full likelihood approach increased proportionally. Analysis was based on data simulated from the five-state model for Ca²⁺-activated K⁺ channels in Scheme II. A dead time t_d = 40 μs was used throughout all tests. Results were averaged from 10 independent data sets, which were generated with different random seeds.