Abstract
A high-resolution crystal structure of KvAP, an archeabacterial voltage-gated potassium (Kv) channel, complexed with a monoclonal Fab fragment has been recently determined. Based on this structure, a mechanism for the activation (opening) of Kv channels has been put forward. This mechanism has since been criticized, suggesting that the resolved structure is not representative of the family of voltage-gated potassium channels. Here, we propose a model of the transmembrane domain of Shaker B, a well-characterized Kv channel, built by homology modeling and docking calculations. In this model, the positively charged S4 helices are oriented perpendicular to the membrane and localized in the groove between segments S5 and S6 of adjacent subunits. The structure and the dynamics of the full atomistic model embedded in a hydrated lipid bilayer were investigated by means of two large-scale molecular dynamics simulations under transmembrane-voltage conditions known to induce, respectively, the resting state (closed) and the activation (opening) of voltage-gated channels. Upon activation, the model undergoes conformational changes that lead to an increase of the hydration of the charged S4 helices, correlated with an upward translation and a tilting of the latter, concurrently with movements of the S5 helices and the activation gate. Although small, these conformational changes ultimately result in an alteration of the ion-conduction pathway. Our findings support the transporter model devised by Bezanilla and collaborators, and further underline the crucial role played by internal hydration in the activation of the channel.
INTRODUCTION
Voltage-gated potassium (Kv) channels allow K+ ions to flow through membranes. This remarkable property is of paramount importance for electric signaling in excitable tissues, especially for the regulation of the action potential (Hodgkin and Huxley, 1952). Several human diseases are related to abnormal functions of such proteins, e.g., cardiac diseases (Mandegar and Yuan, 2002). Kv channels control ion conduction by adopting different molecular states in response to variations of the transmembrane (TM) voltage. Three main states, namely resting, activation, and inactivation, have been identified. In contrast with the resting state that occurs at hyperpolarized potentials of the membrane, activation and inactivation are induced by membrane depolarization. Whereas the resting and the inactivated states present low or no level of ion conductance (closed channel), the activated state is related to a high ion conductance (open channel). Transitions between these states are usually treated as a general gating mechanism (Hille, 1992).
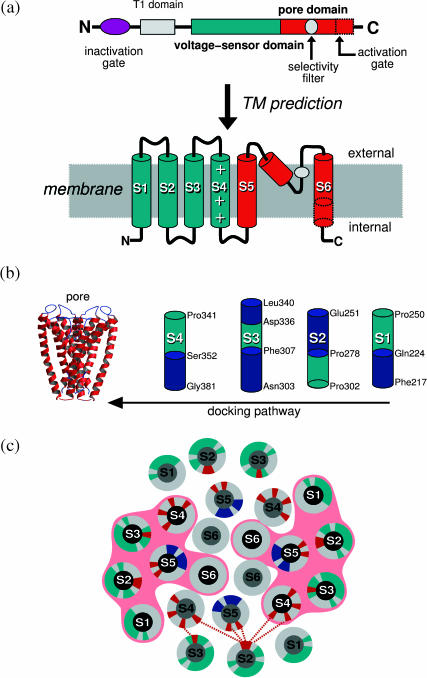
Kv channels are complex quaternary structures, in which the central hydrophilic pore results from an arrangement of four TM domains (Choe, 2002). The primary sequence of each domain is predicted to form six TM helices (S1–S6) and a small pore helical segment buried in the membrane, found between S5 and S6 (Fig. 1). Segments S5–S6 constitute the central pore domain and delineate the hydrophilic pathway for ionic currents. A conserved motif between these segments forms the so-called selectivity filter responsible for ion selectivity. The central pore is surrounded by an arrangement of segments S1–S4, experimentally identified as the voltage-sensor domain (Lu et al., 2001). When the membrane is depolarized, this domain senses the variations of the TM voltage and triggers the conformational changes necessary for channel gating (Horn, 2000). A direct measure of this conformational modification is the gating current believed to derive mainly from the movement of the highly positively charged S4 helix (Bezanilla, 2000, 2002) and to lead to the opening of the channel during activation. The inactivated state involves complex molecular rearrangements hypothesized to result from two mechanisms: a fast inactivation and a slow inactivation. The first involves blocking the inner mouth of the pore with the intracellular N-terminus of the TM domain (Zhou et al., 2001). After prolonged depolarization, the pore domain becomes nonconductive through slow inactivation—a mechanism that is still not well characterized (McCollum et al., 2003).
FIGURE 1.
Homotetrameric Kv channel: (a) Domain organization of the Shaker B. (b) Homology modeling and docking calculations. (Left) Model of the pore domain. (Right) The four helices, each containing a predicted voltage-sensor segment (green). (c) Projection of a 15 Å slab of the TM domain located below the selectivity filter. The representation shows the charged residues (red) involved in the indicated electrostatic network (dashed red lines), residues of S1–S3 found to be tolerant to side-chain replacements (green) and residues of S5 located at the N-terminus of the pore domain, in contact with the central hydrophilic pathway (blue).
In Kv channels, ionic currents are coupled to gating currents (Horn, 2000). This stresses the importance of determining how the motion of the voltage sensor is coupled to that of the pore domain. To do this, not only must the structure of the former be known, but it is also crucial to decipher the coupled conformational changes induced by variations of the TM voltage, which ultimately lead to the opening of the ion-conduction pathway (Yellen, 2002). To this date, only few elements of the puzzle have been well characterized. Among these, the structure of the pore domain, homologous to all Kv channels, has been resolved for the bacterial KcsA channel (Doyle et al., 1998). In recent months, a high resolution x-ray structure of the TM domain of KvAP, an archeabacterial Kv channel from Aeropyrum pernix has been determined (Jiang et al., 2003a,b; Ruta et al., 2003). In the latter, the S4 charged helical segment and portions of S3 are found to form a paddle lying at the periphery of the channel, parallel to the intracellular membrane-water interface. It has been suggested, based on this structure, that activation of the channel during depolarization induces a large, upward movement of the paddle, bringing it from the cytoplasmic region to the extracellular side of the membrane, through the hydrophobic lipid region. The model has since been challenged (Ahern and Horn, 2004; Bell et al., 2004; Broomand et al., 2003; Gandhi et al., 2003; Lainé et al., 2003; Lee et al., 2003; Neale et al., 2003; Starace and Bezanilla, 2004). It was indeed shown that, for eukaryotic Shaker channels in their native membrane environments, S4 is oriented perpendicular to the membrane plane and located in the groove between pore domains from different subunits, as has been suggested previously. Several of these results were based on measurements of binding affinities between specific residues in S4 and in the pore domain. When cysteine mutations are performed on the participating residues, spontaneous disulfide bond formation is observed. It has hence been claimed that the published structure of KvAP is unlikely to correspond to that of a functional channel. Given that the paddle conformation and the opening/closing mechanism proposed by Mackinnon and co-workers also contradicts several earlier reports (Bezanilla, 2000; Choe, 2002; Horn, 2000; Yellen, 2002), one may question how much the complexation of the KvAP channel with a monoclonal Fab fragment and the detergent solubilization necessary to crystallize the protein may have distorted the channel structure. In summary, there is a body of evidence that the paddle model based on the resolved KvAP structure disagrees strongly with a series of recent experiments on Kv channels, and, therefore, may not be appropriate for describing the rearrangements of the voltage-sensor domain taking place during activation of the family of voltage-gated channels.
Modeling techniques in general and molecular dynamics (MD) simulations in particular can, in principle, be used to investigate the stability of the KvAP channel in a simplified lipid bilayer model which mimics a membrane environment, starting from the structure determined by Mackinnon and co-workers. We are pursuing this route, although if one assumes that the structure is not stable, a very long timescale will be required for its relaxation to a conformation where the paddle lies perpendicular to the membrane. The second main issue in this scheme is to propose a reasonable configuration of the channel embedded in a lipid bilayer environment. There is actually no membrane in the KvAP crystal, and probably no bilayer arrangements, but rather an uncharacterized dispersion of detergents and bacterial lipids (Cohen et al., 2003). Modeling results will obviously depend on the initial configuration of the system and, as such may, therefore, be questionable.
Although awaiting further experiments aimed at settling the controversy, we present here the computational results from which a model of the potassium Shaker B channel is proposed, and investigate for the first time its gating mechanism. To reach this goal, a full atomistic TM-domain model of the channel was built using homology modeling and docking calculations. The stability and the dynamics of the TM domain were studied in a lipid membrane by means of MD simulations, considering the influence of applied TM voltages characteristic of the resting state and the activation of the channel. In what follows, we first describe the model of the Shaker B channel built by homology and docking procedures. Next, we present the results of the MD simulations, where conformational changes involving the coupling of the voltage-sensor and the pore domain under the influence of the activating TM voltage were clearly witnessed. Finally, we discuss the overall results in comparison with the three models proposed for the activation of voltage-gated ion channels—conventional, paddle, and transporter models (Blaustein and Miller, 2004).
METHODS
Building the TM domain model
Piecewise decomposition into domains is a necessary approach to understand the molecular function of large TM proteins (Kreusch et al., 1998). For the gating mechanism, the main conformational changes in Kv channels appear to be located within the TM domain, since it was shown that mutants lacking the complete N-terminal extension might be activated (Kobertz and Miler, 1999). In Shaker B, the TM domain is predicted by HMMTOP (Krogh et al., 2001; Tusnády and Simon, 1998) to contain 270 residues (Phe217 to His486). The channel sequence was taken from the Swissprot databank (P08510). Six segments were identified along this extension and have been grouped into voltage-sensor and pore domains (Fig. 1). S5 and S6 segments were inferred from the KcsA channel, whereas the extension of each voltage-sensor segment was predicted from sequence analysis (Krogh et al., 2001; Tusnády and Simon, 1998). In the region of the voltage-sensor domain, the primary sequence contains highly conserved proline residues, as revealed from sequence multiple-alignment (Corpet, 1988). Given that these residues may act as helix breaking points between successive TM segments, four segments featuring proline residues at the tail-ends and containing one of the predicted segments S1–S4 were split along the complete extension of the voltage-sensor domain.
The pore domain was considered to extend from Leu382 to His486 (Fig. 1). The region of Met393 to His486 was modeled by homology from the KcsA structure (PDB 1bl8), considering the same sequence alignment presented and discussed by Ranatunga et al. (2001), in which the residue accessibility in the KcsA structure is correlated with the residue variability in a given position of the multiple alignment of voltage-gated channels. The remaining extension at the N-terminus of the pore domain of Shaker B, not present in KscA, was modeled here as a helical continuation of the S5 segment, in agreement with NMR data (Ohlenschlager et al., 2002).
The complete sequence of the voltage-sensor domain was initially considered as four independent standard helical structures. A docking pathway was employed to search preferential positions of these four segments around the pore domain, considering all helices to be in TM orientations. This strategy is consistent with the two-stage model (Popot and Engelman, 1990) for the folding of membrane proteins, in which blocks of secondary structure are formed before molecular assembly into higher-order tertiary and quaternary structures. 16! (factorial) docking pathways are necessary to sample all the possibilities for a given topology of the voltage-sensor domains (randomly placing 4 × 4 helices around the pore). The number of docking pathways was reduced significantly, considering that: 1), there is evidence of a symmetrical structure of Kv channels (Sokolova et al., 2001); and, 2), specific mutagenesis experiments show that S1 and S2 are highly tolerant to side-chain replacements compared to S3 and especially S4 (Hong and Miller, 2000; Li-Smerin et al., 2000; Monks et al., 1999). This suggests that those amino acids that can be replaced are necessarily involved in lipid-protein rather than protein-protein interactions. S1 and S2 are, therefore, expected to occupy the outer position, closer to the membrane. A symmetry argument was, thus, applied to dock the voltage-sensor helices following four pathways, wherein S3 and S4 were first docked to the pore before S1 and S2.
The specific energy function for TM-helix interactions available in the GRAMM protein-protein docking algorithm (Vakser and Aflalo, 1994) was used for the calculation of the docking pathways. From this procedure, one configuration of the complete TM domain was selected, in which specific orientations of the voltage-sensor segments were chosen to satisfy the following experimental constraints:
Those residues of segments S1–S3 (green shades in Fig. 1 c) found to be tolerant to replacement (Hong and Miller, 2000; Li-Smerin et al., 2000; Monks et al., 1999) are located in the protein-membrane interfacial region.
The contact between tetramer units occurs through an electrostatic network (red dotted lines in Fig. 1 c) involving residues Arg368 and Arg371 of S4 and Asp283 of S2 of the neighboring subunits, in agreement with site-directed mutagenesis experiments (Planells-Cases et al., 1995) and second-site-suppressor analysis (Tiwari-Woodruff et al., 1997). This network is further extended by means of intravoltage-sensor interactions that involve salt-bridges between Glu293 of S2 and Arg377 of S4, and Asp316 of S3 and Lys374 of S4. Mutation experiments have demonstrated that these residues are involved in a well-defined electrostatic network with direct implications in functional protein maturation (Planells-Cases et al., 1995; Tiwari-Woodruff et al., 1997).
The minimized conformation of the TM domain obtained after the docking procedure possesses five well-defined cavities. The central cavity is located below the selectivity filter and four other cavities are located in the voltage-sensor domains. As the latter may correspond to hydrated regions of the protein with direct implications in the function of the channel, the protein was fully hydrated (i.e., 391 water molecules) before placing it in a membrane model. The Kv channel was inserted at the center of the bilayer, optimizing the distance between conserved aromatic side chains (belonging to S1–S3) and the phospholipid headgroups (Tieleman et al., 1998).
Molecular dynamics
The MD simulations were carried out in the NPT ensemble using the program NAMD2 (Kalé et al., 1999). The equations of motion were integrated using a multiple timestep algorithm (Izaguirre et al., 1999). Short- and long-range forces were calculated every two and four timesteps respectively, with a timestep of 1.0 fs. Langevin dynamics and Langevin piston methods were applied to keep the temperature (300 K) and the pressure (1 atm) of the system fixed. Chemical bonds between hydrogen and heavy atoms were constrained to their equilibrium value. Long-range electrostatic forces were taken into account using the particle-mesh Ewald approach (Darden et al., 1993). The water molecules were described using the Tip3p model (Jorgensen et al., 1983). Bond stretching, valence angle deformation, torsional and nonbonded parameters of the protein, and the lipids were extracted from the all-atom CHARMM force field (MacKerell et al., 1998). A united-atom representation was adopted for the alkyl chains of the palmitoyloleylphosphatidylcholine (POPC) lipid molecules forming the bilayer. The complete system contains the Kv channel, 488 lipid units, 391 internal water molecules, 34,463 membrane hydration water molecules, and two potassium ions located in the selectivity filter (a total of ∼158,000 atoms). To ensure the neutrality of the system, 10 sodium counter ions were distributed uniformly in the solvent. The initial dimensions of the simulation cell were 137 × 148 × 100 Å3. Three-dimensional periodic boundary conditions were applied. Execution of NAMD2 was performed in part on 64 R14000 (500 MHz) processors of an Sgi Origin 3800 at the CINES supercomputer center.
External field and the transmembrane potential
In experimental conditions, a voltage difference, ΔV, may be imposed by means of a voltage-clamp or a pulse. In a lipid system formed by a membrane of thickness d and an electrolyte, the voltage applied results in a constant electrical field E = ΔV/d across the membrane and an effective zero field in the bulk (electrolyte) solution. In simulations, due to the small sizes of the systems and the use of periodic boundary conditions, it is impossible to impose a TM voltage by simple addition of explicit ions to the solution at both sides of the bilayer (Roux, 1997; Tieleman et al., 2001). Here, we have adopted the same strategy as in Tieleman et al. (2001), i.e., applied an external electric field, perpendicular to the membrane plane, to maintain a fixed voltage difference across the bilayer. In practice, this is done by adding a force on all the atoms bearing a charge qi, F = qiE, where E is the constant external electric field. Assuming that the field is small enough, so that the linear response approximation holds, the total field in the water phase, roughly E/ɛ (ɛ, dielectric constant ∼80, effectively 91 for Tip3p water model; Tieleman et al., 2001), may be neglected compared to that in the membrane medium (ɛ ∼ 2, effectively 1 in the hydrocarbon region). Recent evidence from calculations of the dielectric permittivity profile from a lipid bilayer simulation (Stern and Feller, 2003) suggests that the width, d, of the low dielectric medium is roughly 25 Å, and that the interfacial region, due to the presence of the lipid polar headgroups, possesses a higher permittivity than water. The electric field, therefore, induces a voltage difference, ΔV = Ed, across the membrane, and may be neglected in the solvent on account of the polarization of the water.
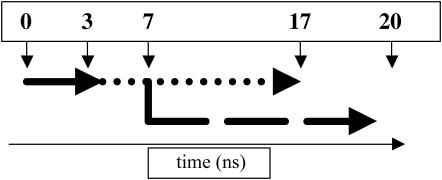
For Shaker B, the resting state, as determined by electrophysiological experiments (Hille, 1992), is obtained under a TM voltage of ∼−100 mV (negative at the intracellular side of the membrane). Assuming a typical membrane thickness of 25 Å (Stern and Feller, 2003; Tieleman et al., 2001), the resting field trajectory was generated by applying an external field of ∼4 mV/Å, pointing from the outer side of the membrane to the inner side (defined by the orientation of the channel, i.e., from top to bottom in Fig. 3). Inversion of the external field produces a TM potential of ∼+100 mV that promotes the activation of the channel (Hille, 1992). Estimates from Hille suggest that the timescale for activation is within milliseconds. A lower bound for opening and closing the channel, within microseconds, has been proposed recently for the fast component of the gating current (Sigg et al., 2003). Investigating such dynamics evidently remains beyond the current capabilities of MD simulations. We have consequently chosen to apply an electrical field approximately five-times-larger than that of experimental conditions (e.g., corresponding to a TM-voltage difference of +500 mV), to promote a faster response of the system. The TM voltages involved in both the resting-field and the activating-field trajectories are shown not to produce any unrealistic effects such as a destabilization of the channel model, specifically in the region of the selectivity filter, nor a denaturation of the helical TM segments. See Diagram 1, MD Simulations, below.
FIGURE 3.
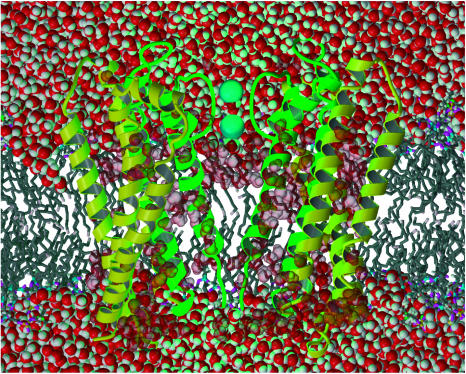
Representation of the Shaker B model embedded in the POPC lipid bilayer. The configuration is representative of the resting-field trajectory. For clarity, only two subunits of the channel are displayed as ribbons (pore domain, S5–S6: green; voltage-sensor domain, S1–S4: yellow). The two potassium ions (cyan) are located in the selectivity filter. Water molecules are represented by their van der Waals radii (O, red; H, white). For clarity, the lipid acyl chains (dark shaded) are represented as sticks.
DIAGRAM 1.
Equilibration (solid line); resting-field trajectory (dotted); and activating-field trajectory (dashed).
Covariance analysis
Essential dynamics analysis is a well-suited method for filtering out locally confined fluctuations in a large macromolecule from global structural anharmonic motions. This is based on the analysis of a covariance displacement matrix (C) evaluated from the MD trajectory (Amadei et al., 1993; Horiuchi and Go, 1991; Ichiye and Karplus, 1991),
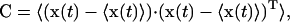 |
(1) |
where 〈 〉 denotes an average over time. x(t) is the 3N-dimensional vector of atomic coordinates at time t, after elimination of the overall translation and rotation of the molecule.
The diagonalization of the covariance matrix (Eq. 2) results in a set of eigenvectors describing a direction in the high configurational space and eigenvalues, λi, representing the mean-square fluctuations of the total displacements along the eigenvectors (Eq. 3):
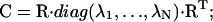 |
(2) |
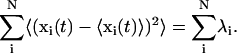 |
(3) |
In many proteins, there are only a few essential eigenvectors that describe protein dynamics. Motions along these eigenvectors are mainly large anharmonic fluctuations that can generally be related to the protein biological function. Eigenvalues at higher indices represent harmonic fluctuations (thermal fluctuations) that have narrow Gaussian distributions in the displacement space and do not contribute significantly to the positional fluctuations. For a long enough simulation, the first few modes usually describe collective motions along the so-called principal components. These are evaluated from the projection of the trajectory onto the corresponding eigenvectors (Eq. 4):
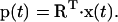 |
(4) |
Random diffusion is known to produce patterns that resemble collective behavior. Hess, however, showed that for random diffusion in a flat energy surface, principal components of the major modes are cosines with the number of periods equal to half of the principal component index (Hess, 2002). The cosine content (ci), a measure of the similarity to random diffusion, may be used to estimate how much of the major modes are likely to describe functional motions: it is equal to unity for a perfect cosine, and zero in the absence of similarity. It may be evaluated from a covariance analysis as
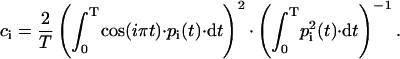 |
(5) |
Finally, it is possible to investigate how much of space sampled by one trajectory overlaps with another (Hess, 2002). This can be estimated by calculating the overlap (o) between the covariance matrices of two simulations parts of a trajectory, or that of two independent trajectories (A and B),
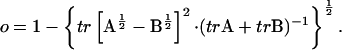 |
(6) |
If sampling is identical for the two trajectories, the overlap is 1, otherwise, i.e., for orthogonal spaces, the overlap is 0.
RESULTS
In the initial configuration of the Shaker B model the pore domain is closed. The KcsA structure used to model part of this domain corresponds, indeed, to a closed conformation (Perozo et al., 1999). The remaining N-terminal region of this domain, modeled as a helical continuation of S5, is in contact with the ion-conduction pathway. In particular, residues Leu385, Thr388, Ser392, Glu395, and Leu396 (blue shades in Fig. 1 c) are accessible to this pathway. Their side chains have been recognized to be part of the binding site of the N-terminal region of the protein (Isacoff et al., 1991) that works as an inactivation particle by binding the inner mouth of the pore in the inactivated state (Zhou et al., 2001). Some of these side chains alter ionic currents (Isacoff et al., 1991), therefore, highlighting a reasonable close contact with the ion-conduction pathway.
In the overall topology of the model, segments S4 occupy the groove formed between segments S5 and S6 of adjacent subunits and are oriented perpendicular to the membrane. This agrees with recent experiments indicating atomic proximity of S4 and pore-domain segments (Broomand et al., 2003; Lainé et al., 2003; Neale et al., 2003), as well as with the molecular model obtained independently by Lainé et al. (2003). S4 helices occupy central positions in the voltage-sensor domain and are protected from the membrane by segments S1–S3. The estimates of the hydrophobic moments and hydrophobicities (Fig. 2 a) of the voltage-sensor segments suggest that S4 participate in protein-protein interactions more than S1, S2, and S3. A hydrophobic moment higher than hydrophobicity characterizes, indeed, buried transmembrane helical segments, compared to peripheral or solvent-exposed segments (Eisenberg et al., 1984). Last, segments from different subunits are in close contact, in agreement with fluorescence measurements revealing that voltage-sensor domains from different subunits are coupled. This is based on the measured cooperativity movement of segments S4 during activation (Mannuzzu and Isacoff, 2000).
FIGURE 2.
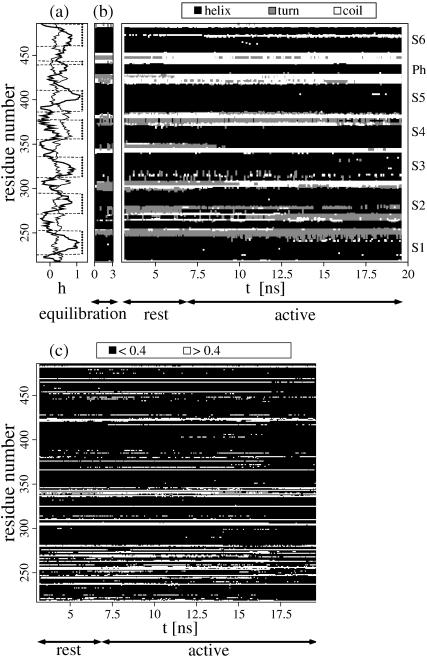
Microscopic properties. (a) Sequence analysis of the Kv channel. Hydrophobicity (solid lines, Eisenberg scale) and hydrophobic moment (Eisenberg et al., 1984) (thin lines) calculated along the Shaker B sequence and limits of the hydrophobic membrane domains from the MD simulation (dashed squares). (b) Secondary structure analysis (Frishman and Argos, 1995). This property is shown for the equilibration run, the initial part of the resting-field trajectory and for the activating-field trajectory. Note the disruption of the secondary structure in the N-terminal region of S3 and the formation of the coil around the PVP motif in S6. (c) Solvent-accessibility analysis (Flower, 1997) of a given subunit during the simulation. Residues were considered buried (solid symbols) for relative accessibilities <0.4 and accessible (open symbols) otherwise. Similar results were observed for all subunits.
The obtained model of the Shaker B channel was embedded in an equilibrated POPC bilayer. The hydrophobic regions of the segments S1–S6 overlap with the membrane hydrophobic core (Fig. 2 a). As far as the amphipathy of the sequence is concerned, large hydrophobic moments are witnessed at the tail-ends of the helical segments rather than along their buried TM extension, which is consistent with the location of these regions near the membrane-water interface.
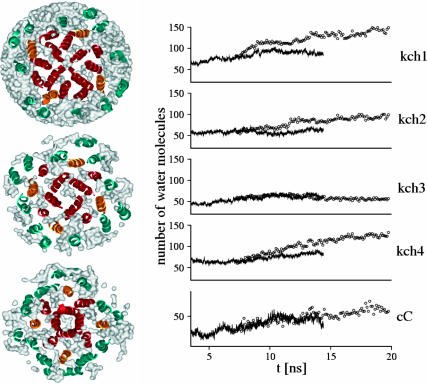
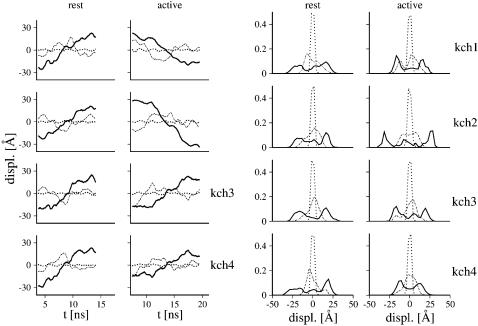
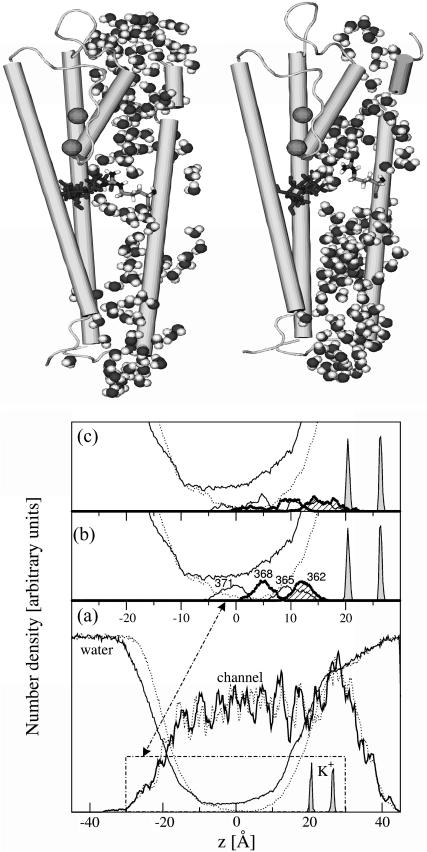
All well-defined helical segments remain conserved during both resting and activating-field trajectories (Fig. 2 b). Due to helix-break points containing proline residues, helices S3 and S6 show mild disruption of their secondary structure (see below). One remarkable change in the Shaker B model between the resting and activating-field trajectories lies in the hydration of the TM region. For the former, equilibration has led to the formation of two disconnected hydrated regions located at the upper and the lower parts of the TM domain (Fig. 3). The voltage-sensor domain is hydrated by means of cytoplasmic opened cavities centered on S4 and communicating with other hydration regions of the channel (Fig. 4). In particular, water molecules participating in the hydration of S4 communicate with the bulk aqueous medium and with the central cavity in the pore domain region. For instance, for a selected 2-ns time frame, up to half of the 365 ± 10 water molecules located in the TM domain migrated from bulk.
FIGURE 4.
Hydration of the Kv channel model. (Left panel) Water densities (white) around the TM segments (ribbons) from the resting-field trajectory estimated for transverse slabs of 15 Å each. From top to bottom, slabs located around the selectivity filter, the central cavity, and the activation gate. Note the hydration of S4 (orange) and the water communication through the cavities in the voltage-sensor and the pore domains (red). (Right panel) Hydration changes of S4 during the MD simulation for both the resting (solid lines) and the activating-field (open circles) trajectories. The number of water molecules hydrating S4, of each subunit (kch1–kch4), was calculated considering a cutoff of 15 Å from the geometrical center of the helix, localized at the middle of the TM region. Only the trace of S4 was used for determination of the geometrical center. For comparison, the number of water molecules in the region of the central cavity (Cc) is also shown (bottom plot). A cutoff of 15 Å was also considered here even though this cutoff is slightly larger than the diameter of the central cavity.
For all but one subunit (Kch3), the number of water molecules inside the voltage-sensor domain has converged for the resting-field trajectory, and increased under the influence of the activating field, specifically around S4 (Fig. 4). These hydration changes are not due to a destabilization of the model under inversion of the field, such as an opening of large pores through the protein. The solvent accessibility of the helices shows that, indeed, the TM domain remains a compact structure during the activating-field trajectory (Fig. 2 c). Only minor and localized variations of this microscopic property, especially in the C-terminus region of S4, altered the hydration. Overall, this is consistent with the picture emerging from the 20 Å resolution structure of a related, voltage-gated sodium channel (Sato et al., 2001), showing a TM region with several cavities. Hydration of the voltage-sensor domain in the presence of the resting field is also consistent with the accessibility of several side chains of S4 from the internal side of the membrane (Bezanilla, 2000). In addition, several experiments have indicated that this accessibility changes upon variation of the TM voltage (Starace et al., 1997).
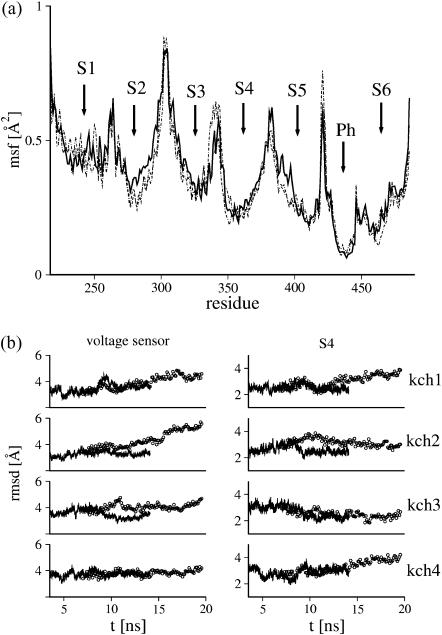
External segments of the voltage-sensor domain are shown to be more mobile than the inner ones for both trajectories (Fig. 5). The pore helical segment exhibited the lowest fluctuations, in agreement with the small mobility of spin labels attached to this region, as determined by EPR measurements (Perozo et al., 1999). The conformational changes of the Shaker B model have been determined through the analysis of the root mean-squared deviations (RMSDs) with respect to the initial structure (Fig. 5). Although these quantities appear to have converged throughout the resting-field trajectory, larger deviations are witnessed when the system is under the activating field. This is suggestive that the resting and activating fields act differently on the overall structure of the channel. When looking specifically at S4, conformational changes of the helices are, for all but Kch3, correlated with the increase of hydration during activation.
FIGURE 5.
Mobility of the TM domain. (a) Mean-square fluctuation (msf) of the backbone atoms averaged for time blocks of 250 ps along the MD simulation are plotted as a function of residue number for both the resting (dashed line) and a selected activating-field (solid line) trajectory. The mean-square fluctuations were calculated after elimination of overall translation and rotation. Small arrows indicate the location of the TM helices (S1–S6) and the small pore helical segment (Ph). Note for S6, the largest mobility is localized at its C terminus. (b) Root mean-square deviations (rmsd) of the voltage sensor domain (left) and of S4 (right) from their structure at the beginning of the equilibration run, for the resting (solid lines) and the activating-field (open circles) trajectories. Root mean-square deviations were calculated after elimination of overall translation and rotation. Only the traces of the voltage-sensor domain and of S4 of each subunit were considered.
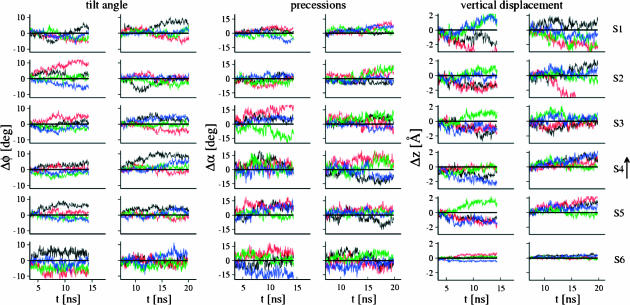
Conservation of most helical segments (Fig. 2 b) indicates that the observed conformational changes correspond to rigid-body movements. These motions were analyzed, for each helix, considering their upward translation, tilt angle with respect to n (the normal to the bilayer), and precession around n (Fig. 6). The results highlight clearly an inversion of most movements after varying the TM voltage. In particular, under the influence of the activating field, S4 undergoes an upward translation and a tilt. This shows again, that S4 helices respond to the applied external field, in agreement with gating charge measurements demonstrating that S4 movements contribute mostly to the gating current (Seoh et al., 1996).
FIGURE 6.
Rigid-body movements of the TM domain segments during the resting field (left) and activating field (right) trajectories. Three movements are considered for each helical segment: its tilt angle Δφ with respect to n, the normal to the bilayer; its precession Δα around n; and its upward translation Δz. These were calculated as follows: Δφi = φi(t)−φi(0), Δαi = αi(t)−αi(0), and Δzi = zi(t)−zi(0), where φi(0), αi(0), and zi(0) are the tilt, precession, and translations at the beginning of the respective trajectory. φi(t), αi(t), and zi(t) were determined after elimination of overall translation and rotation by fitting to the pore helices in the tetramer, at the beginning of the respective trajectory. For S6, only the region below the PVP motif was considered. Movements of helical segments from different subunits are colored as follows: kch1 (black), kch2 (red), kch3 (green), and kch4 (blue).
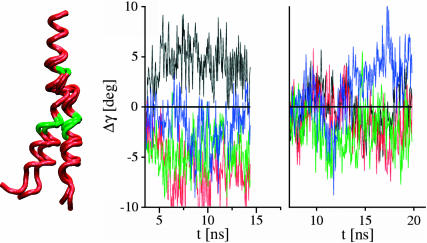
Translation and tilt of S4 segments have a direct consequence on the motions of S5, which, in turn, influence segment S6. The mean-squared deviation of the pore domain between the conformations at the end of the resting and the end of the activating-field trajectories amounts to 2.5 Å. Rigid-body movements in S5 and S6 helices account for most of the deviation, in agreement with EPR measurements (Perozo et al., 1999). Motions of S5 are mainly dominated by an upward translation, just like for S4, and by a precession around n. Motions of S6 are, on the other hand, more complex. This is due to the existence of two hinge points that increase its internal flexibility. The first corresponds to a conserved glycine residue, shown to work as a hinge in the opened conformation of MthK channel (Jiang et al., 2002). The second is the well-known Pro-Val-Pro (PVP) motif, not conserved in all K+ channels, but present in Shaker B (Bright et al., 2002). The secondary structure analysis of S6 in the present model reveals a kinked helix around this motif (Fig. 2 b).
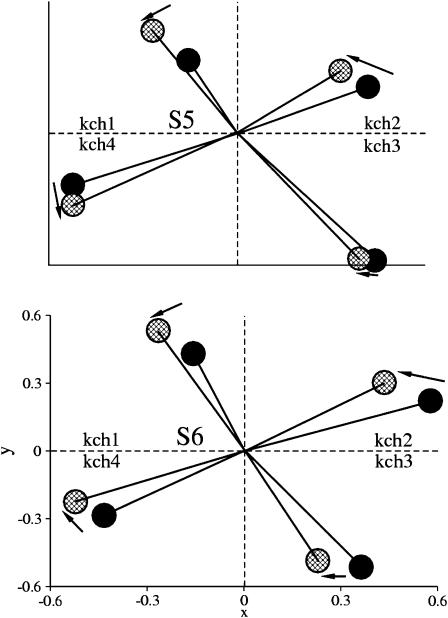
The region below the PVP motif is known to work as an activation gate that opens and closes the inner mouth of the pore (Bright et al., 2002; del Camino et al., 2000; Perozo et al., 1999). This region, under the activating field, undergoes a tilt and a precession, as shown in Fig. 6. The internal motions of S6, on the other hand, were investigated by monitoring the bending angle between the helical regions above and below the PVP motif. Although this bending persists in both trajectories, S6 adopts a less extended structure under the influence of the activating field (right panel of Fig. 7). Finally, the activating field induces an overall precession of S5 and S6, resulting in a collective anticlockwise motion, although not too pronounced for subunit 3 (compare to Fig. 8).
FIGURE 7.
Internal motion of S6 segments. (Left) Kinked helical structure of S6. The average structure from the resting-field trajectory is shown for each subunit. Hinge points are shown in green. (Right) Internal motions of S6 during the simulation runs. A bending movement, corresponding to the angle Δγ between the helical regions before and after the Pro-Val-Pro motif is considered for both the resting field (left) and the activating field (right) trajectories. It was calculated as Δγi = γi(t) − γi(0), where γi(0) is the angle value at the beginning of the respective trajectory. The value γi(t) was determined after elimination of overall translation and rotation of the tetramer. Movements of helical segments from different subunits are colored as follows: kch1 (black), kch2 (red), kch3 (green), and kch4 (blue).
FIGURE 8.
Precession movements of segments S5 and S6. The solid and shaded points correspond to plane projections of the overall tilt of these segments at the end of resting and the activating-field trajectories, respectively. Differences between the final conformations symbolically represented by the arrows indicate a near anticlockwise motion of the helices. In the case of S6, the activation gate located bellow the Pro-Val-Pro motif is considered.
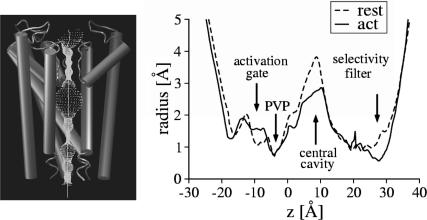
A direct consequence of the conformational changes of the pore domains is the alteration of the ion-conduction pathway. This pathway can be investigated by analyzing the profile of the pore radius (Fig. 9) and shows clear differences between the resting and the activating-field trajectories. Changes around the selectivity filter region result from the high flexibility of the structure, as has been observed for the inward rectifier (Kir) potassium channel (Capener and Sansom, 2002). In the present case, this flexibility has not led to translocation of the potassium ions during the simulation. The structural alterations of S6 have also led to an increase of the pore volume in the region of the activation gate although maintaining it constricted at the PVP motif. However, the discrete increase of the radius observed near the activation gate is not enough to affect the number of water molecules present in the central cavity (right panel of Fig. 4).
FIGURE 9.
Pore radius profile (Smart et al., 1993). (Left) Pore volume (point density) along the ion-conduction pathway. For clarity, only three channel subunits are shown. (Right) Pore radius profile calculated along the Z direction, normal to the channel for both the resting and the activating-field trajectories, corresponding to an average over a window time of 1.5 ns at the end of each trajectory. The regions of the selective filter, central cavity, PVP motif, and activation gate are indicated.
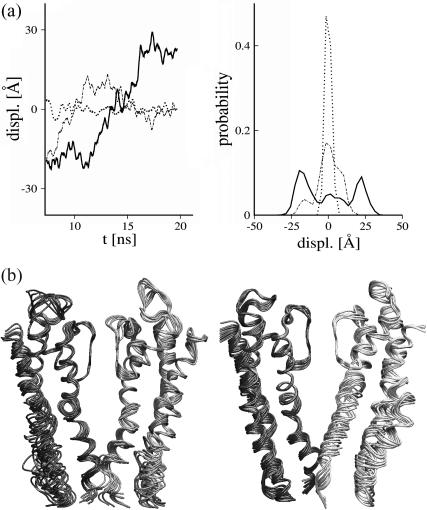
Two questions remain to be addressed. Are the motions of the voltage-sensor domain coupled to those of the pore domain? Are the previously identified movements occurring during the activating-field trajectory merely diffusive-like, or are they relevant collective motions leading to the opening of the pore? To address this, the MD trajectories were analyzed using essential dynamics techniques (Amadei et al., 1993). Collective motions were determined by covariance analysis (Amadei et al., 1993; de Groot et al., 1996; Horiuchi and Go, 1991; Ichiye and Karplus, 1991; Merlino et al., 2002; Tieleman et al., 2002). In both trajectories, the first nonharmonic mode was identified for each subunit as having larger amplitudes than the following ones combined. Movements along this mode account for ∼60% of the total atomic mean-squared displacement of the subunit (Fig. 10). Estimates of the cosine contents reveal that this mode does not correspond to random diffusion, and, therefore, is expected to be functional (see Methods).
FIGURE 10.
Collective motions in the TM domain model. (Left panel) Motions along selected essential modes are depicted for both the resting (left) and activating-field (right) trajectories for each tetramer subunit. Only the protein trace was considered for the covariance analysis (see Methods). Displacements were calculated from the projection of internal movements along the 1th (solid lines), 2nd (long dashed lines), and 15th (dotted lines) modes (classified according to their amplitudes). (Right panel) Probability distribution of the selected motions along the modes. Note the highly non-Gaussian amplitude of motion along the 1th mode compared to motions along the high frequency mode (15th).
For the resting-field trajectory, motions of each subunit, projected onto their first essential mode, show only small movements involving S4 and the pore domain segments (motions are delocalized over the whole subunit) (Fig. 11). In contrast, the same analysis performed for the activating-field trajectory highlights movements with larger amplitudes in the S4–S6 region, in particular, an upward translation of S4, and complex motions of both S5 and the cytoplasmic region of S6. The motions sampled by the essential modes are clearly different for the two trajectories. This has been confirmed by the analysis of the overlap of the covariance matrices (Table 1), indicating that the two trajectories occupy different regions of the conformational space.
FIGURE 11.
Collective motions of the tetramer subunits. Superposition of frames (snapshots for time windows of 2 ns) obtained from the projection of motion onto the first essential mode. For clarity, only S4 (shaded) and pore domain segments (solid) are shown and the amplitudes of the motion are rescaled by a factor of 0.1. Motions of subunits kch1–kch4 (from left to right) are depicted for the resting-field trajectory (top panels) and the activating-field trajectory (lower panels).
TABLE 1.
Overlap (see Methods for overlap determination) among the subunits for both resting and activating-field trajectories
| Kch1 | Kch2 | Kch3 | Kch4 | |
|---|---|---|---|---|
| Kch1 | 0.30 | 0.20 | 0.24 | 0.26 |
| Kch2 | 0.24 | 0.24 | 0.22 | 0.24 |
| Kch3 | 0.23 | 0.20 | 0.33 | 0.26 |
| Kch4 | 0.21 | 0.21 | 0.25 | 0.32 |
Further analysis show that the overall response of the Shaker B model to the activating field results from collective modes involving all subunits. The first nonharmonic mode extracted from the essential dynamics analysis of the tetramer is found again to possess an amplitude larger than all other modes combined and accounts for ∼65% of the total motion in the essential space. This mode encompasses upward motions of most S4 helices and motions localized at the cytoplasmic region of the pore (Fig. 12).
FIGURE 12.
Collective motions of the tetramer for the activating-field trajectory. (a) Motion along selected essential modes determined from the covariance analysis. (Left) displacements calculated from the projection of internal movements along the 1th, 2nd, and 15th modes (eigenvector). (Right) Corresponding probability distributions of the displacement along the modes. (b) Superposition of frames (time windows of 2 ns) obtained from the projection of the motion onto the first essential mode. For clarity, only S4 and pore domain segments are shown for subunits kch1 and kch3 (left) and kch2 and kch4 (right). The amplitudes of the motion are rescaled by a factor of 0.2.
It is important to remind the reader for completeness, that, along the activating-field trajectory, the most important essential modes are different for each subunit (Fig. 11). This implies that the monomers occupy different regions of the conformational space. This is confirmed by the small values of the overlap between the subunit trajectories (Table 2). This further suggests the existence of several substates on the road toward activation, where each subunit undergoes different transitions between canonical conformations of the resting and the activated states (Schoppa and Sigworth, 1998).
TABLE 2.
Overlap (see Methods for overlap determination) among the subunits for the activating-field trajectory
| Kch1 | Kch2 | Kch3 | Kch4 | |
|---|---|---|---|---|
| Kch1 | 1.00 | 0.20 | 0.24 | 0.27 |
| Kch2 | 0.20 | 1.00 | 0.20 | 0.22 |
| Kch3 | 0.24 | 0.20 | 1.00 | 0.30 |
| Kch4 | 0.27 | 0.22 | 0.30 | 1.00 |
DISCUSSION
In the present investigation, we have studied the stability and the activation of a TM-domain model of the voltage-gated potassium Shaker B channel obtained by homology modeling and docking techniques. A significant effort has been invested in recent years to model the conduction states of the pore domain of voltage-gated channels (Åqvist and Luzhkov, 2000; Beckstein et al., 2003; Bernèche and Roux, 2000, 2003; Chung and Kuyucak, 2002; Domene and Sansom, 2003; Domene et al., 2003; Luzhkov et al., 2003; Roux, 2002). So far, computational studies have been restricted mainly to the investigation of the pore domain using the KcsA and MthK structures for respectively modeling the closed and opened states. Here, just like in previous studies, KcsA was used to model part of the pore domain of Shaker B. This domain is a homologous structure in potassium channels (Jiang et al., 2002) derived from a common ancient gene (Jan and Jan, 1997, 1994; Milkman, 1994). The crystal structure of the bacterial KscA channel and comparative structural studies on eukaryotic potassium channels indicate that the pore architecture of potassium transporters is remarkably conserved from bacteria, yeast, and plants to animals (Koprowski and Kubalski, 2001). In particular, the crystal structures of KcsA, MthK, and KvAP reveal a similar fold of the pore domain, even though the sequence identity between them is small. The remaining extension at the N-terminus of the pore domain of the Shaker B, not present in KscA, was modeled here as a helical continuation of the S5 segment, in agreement with NMR data (Ohlenschlager et al., 2002).
An additional effort was made to model the voltage-sensor domain. Despite the low-resolution quality of our docking procedure, one configuration of the channel was selected in which: S4 helices adopt TM orientations; are packed against the pore domain near the interface between adjacent units; and are protected from the membrane by segments S1–S3. The TM domain is organized in a right-handed quaternary structure, in which the voltage-sensor domains of neighboring subunits interdigitate. The main difference between this topology and that proposed recently by Lainé et al. (2003) resides in the localization of segments S1 and S2. In their model, obtained by MD simulated annealing and experimental constraints, using the MthK structure for the pore, the TM domain is arranged in a left-handed quaternary structure and the four subunits of the tetramer are well separated.
The initial conformation of our model is probably not a unique solution of the docking procedure that satisfies the ensemble of available experimental constraints. As more specific features emerge from experiment, the model could be improved by optimizing, for instance, the atomic proximity of S4 to the pore, or the arrangement of external segments S1–S3. Several such studies have been recently carried out, and those focused on potassium channels in the closed state may be confronted directly by our model. For instance, in the HERG K+ channel, second-site-suppressor analyses show that the terminal ends of S4 (Asp540) and S6 (Arg665) are in close proximity at hyperpolarized membrane potentials (Tristani-Firouzi et al., 2002). In the Shaker B model, the Cβ atoms of the corresponding Arg377 and Tyr483 residues are on average distant by 11 Å during the resting-field trajectory. This distance is ∼3 Å larger than that of a typical electrostatic interaction. In another recent study (Neale et al., 2003), a disulphide bridge has been shown to form spontaneously in the closed state of the Shaker B channel, between Ser357 and Glu418 located respectively at the extracellular ends of S4 and S5. The corresponding Cβ atoms of these residues are separated by 15 Å on average, i.e., 7 Å away to enable spontaneous disulphide bridge formation. Comparison to similar experiments for the open state (Broomand et al., 2003; Gandhi et al., 2003; Lainé et al., 2003) shows that further rotation and translation of S4 is necessary to reconcile our final configuration of the activating-field trajectory with experiment. This underlines that, as expected, the complete response of the model to activation has not been reached in the present calculation. Interestingly enough, although the modeling techniques—in particular, the set of constraints considered in deriving the tridimensional model of Shaker B in both Lainé et al. and ours—are not exactly the same, the obtained configurations share many key structural features that are shown here to play a significant role in the activation process. In particular, S4 is oriented perpendicular to the membrane plane and localized in the groove formed between segments S5 and S6 of adjacent subunits and protected from the membrane by segments S1–S3.
Although the MD trajectories are undoubtedly dependent upon the initial molecular model, the conformational changes resulting from the depolarization of the membrane are relevant for rationalizing the activation mechanism of the Shaker B channel. The initial structure was relaxed in a realistic membrane environment to investigate the structural modifications of the model when the system is subjected to TM voltages corresponding to depolarization and hyperpolarization of the bilayer. The voltage-sensor S4 segments were found to be hydrated. This remarkable property may correspond to a structural stabilizing requisite to maintain the positively charged S4 segments inside the protein core, even in the resting state (Green, 2002). Hydration properties were significantly affected upon variations of the TM voltage, with direct consequences on the structure of the voltage-sensor domain. Concomitant conformational changes in this domain, triggering the motion of the segments of the pore, underline the correlation between the hydration of S4 and the opening of the channel. Internal TM hydration of Kv channels may, therefore, constitute a crucial property necessary for the conformational transitions occurring during the activation gating mechanism. This hydration of the voltage-sensor domain, and especially that of S4, is consistent with the model proposed by Islas and Sigworth (2001) to rationalize the observed electrostatic effects on the gating currents in Shaker B channels. It is also in agreement with Yang et al. (1996), who propose that S4 is located in a water-filled cavity referred to as the gating pore in sodium channels.
Hydration of the voltage-sensor domain has been suggested to explain the results of accessibility measurements of several residues of S4 in Shaker B channels (Starace and Bezanilla, 2001). Histidine scanning mutagenesis experiments show that the charged residues 365, 368, and 371 of S4 contribute to the gating current. These results provide evidence that, in both the resting and the activated states, the charged residues reside in aqueous crevices surrounded by anions of the bulk solution. In particular, it is suggested that external aqueous crevices that give access to residue 368 in the hyperpolarized state may extend down to expose residue 371 (located in the middle of the S4 segment) when depolarized. Similarly, the internal crevice that extends up to residue 365 in the hyperpolarized state may also expose residue 371 in the depolarized state. This picture is in agreement with our findings, as clearly demonstrated in the equilibrium configuration of the model under the resting field.
Solvent-connected pathways penetrating the hydrophobic region around S4 are believed to become narrower and restricted, and converge on a space confined enough to confer selectivity to proton passage. Very recent experiments show, indeed, that for Shaker B channels in the closed state, mutation of Arg362 by histidine promotes proton conductance with a high turnover rate (Starace and Bezanilla, 2004). This proton conduction implies that residue 362 has to be simultaneously accessible through water crevices from both sides of the membrane and be in a conformation compatible with the formation of a gate between those water columns. This is consistent with our current findings, as can be seen in Fig. 13, highlighting selected configurations from the resting-field and the activating-field trajectories for subunit kch4 (a similar behavior was observed for all but subunit kch1). As suggested by Bezanilla and co-workers (Bezanilla, 2000; Starace et al., 1997; Starace and Bezanilla, 2001, 2004), the solvent region is very constricted around the charged S4 residues in the resting-field trajectory (Fig. 13 b). Further analysis shows that when the model is activated, there are several other water pathways, not involving this specific gate, that connect the intra- and the extracellular sides. Interestingly enough, activation induces upward charge movements in S4 in the order of 2–6 Å. This suggests clearly that the gating current (charge movements) in the Shaker B model may be achieved by rather small conformational changes of S4 (Bezanilla, 2002; Cha et al., 1999).
FIGURE 13.
Hydration properties of the Shaker B model. (Top) Selected conformations for the S4–S6 segments and S4 hydration shell of subunit kch4 from the resting (left panel) and the activating-field trajectories (right panel). Note the gate formed by Arg362 of S4 (side chain in light shading) and nearby channel residues (side chain in dark shading) that opens under activation of the model. (Bottom) Density profiles of the channel and the water along the normal to the membrane (z = 0 being the center of the bilayer) averaged over 750 ps from the MD simulations of the resting (dotted lines) and activated (solid lines) states. Also displayed are the density profiles of the two potassium ions and of the charged Arg362, Arg365, Arg368, and Arg371 of S4. Note the location of the charged residues with respect to the water density at the resting state (b) and their displacement toward the extracellular side under activation (c).
Conformational changes of the Shaker B model under activating field were shown to be part of collective motions and not only random fluctuations. The structural variations of the channel during the activating-field trajectory (13 ns) are not very large, yet differ clearly from those of the resting-field trajectory (14 ns). The upward motion of S4 segments appears to be communicated to S5 and to propagate further into the activation gate in S6. A bending motion in S6, around the PVP motif, leads to an increase in the pore volume below this motif. The pore remains, however, constricted around the PVP motif during activation. Previous computational studies restricted to the pore domain of the Shaker B channel (starting from the KcsA structure) have also reproduced the kink in S6 (Beckstein et al., 2003; Domene et al., 2003; Domene and Sansom, 2003; Luzhkov et al., 2003) and have underlined the possible role that the PVP motif might play in the opening of the pore. Here, by considering the complete TM domain, modifications of the ion conduction pathway under activation, owing to the presence of the voltage sensor domain, have reproduced a consistent picture with experiment. Indeed, the movements around the activation gate obtained from the present study are in agreement with the results by Yellen and collaborators (Webster et al., 2004) derived from high-affinity metal binding experiments on Shaker channels. Put together, these results suggest that the gating mechanism in voltage-gated channels containing the PVP motif results mainly from a bending of S6 at this motif. The gating transition would swivel, thereby blocking residues from the ion pathway, and result in an increased volume of the pore below that point, without widening of the pore at the PVP motif. This mechanism is different from that proposed, based on the x-ray structure of the opened MthK channel which does not contain the PVP motif. When MthK is activated, the glycine-conserved hinge enables a large, outward swing of S6 that opens a wide internal vestibule (Jiang et al., 2002).
Until now, three classes of competing models have been proposed for the activation of voltage-gated potassium channels, named conventional, paddle, and transporter models (Blaustein and Miller, 2004). The Shaker B model investigated here is clearly different from the x-ray structure of the KvAP channel (Jiang et al., 2003a). We remind the reader that in the KvAP structure, parts of S3 segment and S4 are oriented parallel to the membrane water interface, forming a voltage-sensor paddle. In the resting state, the paddle is localized at the periphery of the channel, near the cytoplasmic face of the membrane. It is believed to undergo a large, upward movement under depolarization (Jiang et al., 2003b). This corresponds to a model in drastic rupture with several experimental data accumulated so far on eukaryotic channels (Ahern and Horn, 2004; Bell et al., 2004; Bezanilla, 2000; Broomand et al., 2003; Choe, 2002; Gandhi et al., 2003; Horn, 2000; Lainé et al., 2003; Lee et al., 2003; Neale et al., 2003; Starace and Bezanilla, 2004; Yellen, 2002). Sequence homology between KvAP and eukaryotic channels such as Shaker B is limited. The most obvious differences between the two corresponding sequences are localized in the S1–S2 and the S3–S4 loops, and it is not clear whether the voltage-sensor paddle sequence is conserved in voltage-gated potassium channels (see also Cohen et al., 2003). Whether the KvAP structure and the proposed activation mechanism are specific to this channel from hyperthermophilic archeabacteria remains a matter of debate and further experimental and simulations studies are necessary to shed new light on this issue. In the two other models, S4 is buried in the protein, and adopts a transmembrane orientation. In the conventional model, S4 slides within its own protein-lined pathway or “gating pore” formed by the other voltage-sensor segments and the pore domain (Horn, 2000; Larsson et al., 1996; Yang et al., 1996). The piston-like movement of S4 is characterized by large up-and-down displacements. In the transporter-like model proposed by Bezanilla and co-workers, S4 is also protected from the membrane by the voltage-sensor segments. However, a specific hydration of S4 shapes the electric field in the TM domain region. Depolarization of the membrane produces rather small conformational changes of S4 to account for the activation mechanism (Bezanilla, 2002, 2000; Starace and Bezanilla, 2004; Starace et al., 1997).
The dynamical processes taking place at least to some extent during the in silico activation indicate that S4 moves upward and tilts, triggering the necessary conformational changes that are required for the opening of the channel. Movements of the tetramer are shown to be collective essential modes rather than mere independent fluctuations. The main motion of S4, in contrast with what has been proposed in the conventional model, is rather small and correlated with an increase of the hydration of the channel by water molecules migrating from both extra- and intracellular regions of the membrane. This is believed to constitute a crucial structural modification of the channel, necessary for its opening, thus rationalizing the activation model of voltage-gated potassium channels proposed by Bezanilla and co-workers (Starace and Bezanilla, 2001, 2004).
Acknowledgments
The authors thank the Centre National de la Recherche Scientifique for the Action Thématique Anticipée sur Programme (ATIP) grant of M. T. and the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) for the fellowship of W.T. The Centre Informatique National de l'Enseignement Supérieur (CINES), Montpellier, France, is gratefully acknowledged for provision of generous amounts of CPU time on the Sgi Origin 3800.
References
- Ahern, C. A., and R. Horn. 2004. Specificity of charge-carrying residues in the voltage sensor of potassium channels. J. Gen. Physiol. 123:205–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amadei, A., A. B. M. Linssen, and H. J. C. Berendsen. 1993. Essential dynamics of proteins. Proteins Struct. Funct. Genet. 17:412–425. [DOI] [PubMed] [Google Scholar]
- Åqvist, J., and V. Luzhkov. 2000. Ion permeation mechanism of the potassium channel. Nature. 404:881–884. [DOI] [PubMed] [Google Scholar]
- Beckstein, O., P. C. Biggin, P. Bond, J. N. Bright, C. Domene, A. Grottesi, J. Holyoake, and M. S. P. Sansom. 2003. Ion channel gating: insights via molecular dynamics. FEBS Lett. 555:85–90. [DOI] [PubMed] [Google Scholar]
- Bell, D., H. Yao, R. Saenger, J. Riley, and S. Sielgelbaum. 2004. Changes in local S4 environment provide a voltage-sensing mechanism for mammalian hyperpolarization-activated HCN channels. J. Gen. Physiol. 123:5–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernèche, S., and B. Roux. 2000. Molecular dynamics of KcsA K+ channel in a bilayer membrane. Biophys. J. 78:2900–2917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernèche, S., and B. Roux. 2003. A microscopic view of ion conduction through the potassium channel. Proc. Natl. Acad. Sci. USA. 100:8644–8648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla, F. 2000. The voltage sensor in voltage-dependent ion channels. Physiol. Rev. 80:555–592. [DOI] [PubMed] [Google Scholar]
- Bezanilla, F. 2002. Voltage-sensor movements. J. Gen. Physiol. 120:465–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaustein, R. O., and C. Miller. 2004. Shake, rattle or roll. Nature. 427:499–500. [DOI] [PubMed] [Google Scholar]
- Bright, J. N., I. H. Shrivastava, F. S. Cordes, and M. S. P. Sansom. 2002. Conformational dynamics of helix S6 from Shaker potassium channel: simulation studies. Biopolymers. 64:303–313. [DOI] [PubMed] [Google Scholar]
- Broomand, A., R. Männikkö, P. Larsson, and F. Elinder. 2003. Molecular movement of the voltage sensor in a K channel. J. Gen. Physiol. 122:741–748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capener, C. E., and M. S. P. Sansom. 2002. Molecular dynamics simulations of a K+ channel model: sensitivity to changes in ions, waters, and membrane environment. J. Phys. Chem. 106:4543–4551. [Google Scholar]
- Cha, A., P. C. Ruben, A. L. George, E. Fujimoto, and F. Bezanilla. 1999. Atomic scale movement of the voltage-sensing region in a potassium channel measured via spectroscopy. Nature. 402:813–817. [DOI] [PubMed] [Google Scholar]
- Choe, S. 2002. Potassium channel structures. Nat. Rev. Neurosci. 3:115–121. [DOI] [PubMed] [Google Scholar]
- Chung, S. H., and S. Kuyucak. 2002. Recent advances in ion channel research. Biochim. Biophys. Acta. 1565:267–286. [DOI] [PubMed] [Google Scholar]
- Cohen, B. E., M. Grabe, and L. Y. Jan. 2003. Answers and questions from the KvAP structures. Neuron. 39:395–400. [DOI] [PubMed] [Google Scholar]
- Corpet, F. 1988. Multiple sequence alignment with hierarchical clustering. Nucleic Acids Res. 16:10881–10890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald—an Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- de Groot, B. L., A. Amadei, R. M. Scheek, N. A. J. van Nuland, and H. J. C. Berendsen. 1996. An extended sampling of the configurational space of HPr from E. coli. Proteins Struct. Funct. Genet. 26:314–322. [DOI] [PubMed] [Google Scholar]
- del Camino, D., M. Holmgren, Y. Liu, and G. Yellen. 2000. Blocker protection in the pore of a voltage-gated K+ channel and its structural implications. Nature. 403:321–325. [DOI] [PubMed] [Google Scholar]
- Domene, C., S. Haider, and M. S. P. Sansom. 2003. Ion channel structures: a review of recent progress. Curr. Opin. Drug Discov. Dev. 6:611–619. [PubMed] [Google Scholar]
- Domene, C., and M. S. Sansom. 2003. Potassium channel, ions, and water: simulation studies based on the high resolution x-ray structure of KcsA. Biophys. J. 85:2787–2800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doyle, D. A., J. M. Cabral, R. A. Pfuetzner, A. Kuo, J. M. Gulbis, S. L. Cohen, B. T. Chait, and R. MacKinnon. 1998. The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science. 280:69–77. [DOI] [PubMed] [Google Scholar]
- Eisenberg, D., E. Schwarz, M. Komaromy, and R. Wall. 1984. Analysis of membrane and protein sequences with the hydrophobic moment plot. J. Mol. Biol. 179:125–142. [DOI] [PubMed] [Google Scholar]
- Flower, D. R. 1997. SERF: a program for accessible surface area calculations. J. Mol. Graph. Model. 15:238–244. [DOI] [PubMed] [Google Scholar]
- Frishman, D., and P. Argos. 1995. Knowledge-based protein secondary structure assignment. Proteins. 23:566–579. [DOI] [PubMed] [Google Scholar]
- Gandhi, C., E. Clark, E. Loots, A. Pralle, and E. Isacoff. 2003. The orientation and molecular movement of a potassium channel voltage-sensing domain. Neuron. 40:515–525. [DOI] [PubMed] [Google Scholar]
- Green, M. E. 2002. Water as a structural element in a channel: gating in the KcsA channel, and implications for voltage-gated ion channels. J. Biomol. Struct. Dyn. 19:725–730. [DOI] [PubMed] [Google Scholar]
- Hess, B. 2002. Convergence of sampling in protein simulations. Phys. Rev. E. 65:1–10. [DOI] [PubMed] [Google Scholar]
- Hille, B. 1992. Ionic Channels of Excitable Membranes. Sinauer, Sunderland, MA.
- Hodgkin, A. L., and A. F. Huxley. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (Lond.). 117:500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong, K. H., and C. Miller. 2000. The lipid-protein interface of a Shaker K+ channel. J. Gen. Physiol. 115:51–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horiuchi, T., and N. Go. 1991. Projection of Monte Carlo and molecular dynamics trajectories onto normal mode axes: human lysozyme. Proteins. 10:106–116. [DOI] [PubMed] [Google Scholar]
- Horn, R. 2000. Conversation between voltage sensors and gates of ion channels. Biochemistry. 39:15653–15658. [DOI] [PubMed] [Google Scholar]
- Ichiye, T., and M. Karplus. 1991. Collective motions in proteins: a covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulation. Proteins. 11:205–217. [DOI] [PubMed] [Google Scholar]
- Isacoff, E. Y., Y. N. Jan, and L. Y. Jan. 1991. Putative receptor for the cytoplasmic inactivation gate in the Shaker K+ channel. Nature. 353:86–90. [DOI] [PubMed] [Google Scholar]
- Islas, L. D., and F. J. Sigworth. 2001. Electrostatics and the gating pore of Shaker potassium channels. J. Gen. Physiol. 117:69–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izaguirre, J. A., S. Reich, and R. D. Skeel. 1999. Longer timesteps for molecular dynamics. J. Chem. Phys. 110:9853–9864. [Google Scholar]
- Jan, L. Y., and Y. N. Jan. 1994. Potassium channels and their evolving gates. Nature. 371:119–122. [DOI] [PubMed] [Google Scholar]
- Jan, L. Y., and Y. N. Jan. 1997. Cloned potassium channels from eukaryotes and prokaryotes. Annu. Rev. Neurosci. 20:91–123. [DOI] [PubMed] [Google Scholar]
- Jiang, Y., A. Lee, J. Chen, M. Cadene, B. T. Chalt, and R. Mackinnon. 2002. The open pore conformation of potassium channels. Nature. 417:523–526. [DOI] [PubMed] [Google Scholar]
- Jiang, Y., A. Lee, J. Chen, V. Ruta, M. Cadene, B. T. Chait, and R. MacKinnon. 2003a. X-ray structure of a voltage-dependent K+ channel. Nature. 423:33–41. [DOI] [PubMed] [Google Scholar]
- Jiang, Y., V. Ruta, J. Chen, A. Lee, and R. MacKinnon. 2003b. The principle of gating charge movement in a voltage-dependent K+ channel. Nature. 423:42–48. [DOI] [PubMed] [Google Scholar]
- Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- Kalé, L., R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten. 1999. NAMD2: greater scalability for parallel molecular dynamics. J. Comput. Phys. 151:283–312. [Google Scholar]
- Kobertz, W. R., and C. Miler. 1999. K+ channels lacking the “tetramerization” domain: implications for pore structure. Nat. Struct. Biol. 6:1122–1125. [DOI] [PubMed] [Google Scholar]
- Koprowski, P., and A. Kubalski. 2001. Bacterial ion channels and their eukariotic homologues. Bioessays. 23:1148–1158. [DOI] [PubMed] [Google Scholar]
- Kreusch, A., P. J. Pfaffinger, C. F. Stevens, and S. Choe. 1998. Crystal structure of the tetramerization domain of the Shaker potassium channel. Nature. 392:945–948. [DOI] [PubMed] [Google Scholar]
- Krogh, A., B. Larsson, G. von Heijne, and E. L. L. Sonnhammer. 2001. Predicting transmembrane protein topology with a hidden Markov model: application to complete genomes. J. Mol. Biol. 305:567–580. [DOI] [PubMed] [Google Scholar]
- Lainé, M., M. A. Lin, J. P. A. Bannister, W. R. Silverman, A. F. Mock, B. Roux, and D. M. Papazian. 2003. Atomic proximity between S4 segment and pore domain in Shaker potassium channels. Neuron. 39:467–481. [DOI] [PubMed] [Google Scholar]
- Larsson, H. P., O. S. Baker, D. S. Dhillon, and E. Y. Isacoff. 1996. Transmembrane movement of the Shaker K+ channel S4. Neuron. 16:387–397. [DOI] [PubMed] [Google Scholar]
- Lee, H. C., J. M. Wang, and K. J. Swartz. 2003. Interaction between extracellular hanatoxin and the resting conformation of the voltage-sensor paddle in Kv channels. Neuron. 40:527–536. [DOI] [PubMed] [Google Scholar]
- Li-Smerin, Y., D. H. Hackos, and K. J. Swartz. 2000. Alpha-helical structural elements within the voltage-sensing domains of a K+ channel. J. Gen. Physiol. 115:33–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu, Z., A. M. Klem, and Y. Ramu. 2001. Ion conduction pore is conserved among potassium channels. Nature. 413:809–813. [DOI] [PubMed] [Google Scholar]
- Luzhkov, V., J. Nilsson, P. Arhem, and J. Åqvist. 2003. Computational modelling of the open-state Kv 1.5 ion channel block by bupivacaine. Biochim. Biophys. Acta. 1652:35–51. [DOI] [PubMed] [Google Scholar]
- MacKerell, A. D., Jr., D. Bashford, M. Bellott, R. L. Dunbrack, Jr., J. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- Mandegar, M., and J. X. J. Yuan. 2002. Role of K+ channels in pulmonary hypertension. Vasc. Pharmacol. 38:25–33. [DOI] [PubMed] [Google Scholar]
- Mannuzzu, L. M., and E. Y. Isacoff. 2000. Independence and cooperativity in rearrangements of a potassium channel voltage sensor revealed by single subunit fluorescence. J. Gen. Physiol. 115:257–268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCollum, I. L., Y. Y. Vilin, E. Spackman, E. Fujimoto, and P. C. Ruben. 2003. Negatively charged residues adjacent to IFM motif in the DIII-DIV linker of hNa(V)1.4 differentially affect slow inactivation. FEBS Lett. 552:163–169. [DOI] [PubMed] [Google Scholar]
- Merlino, A., L. Vitagliano, M. A. Ceruso, A. Di Nola, and L. Mazzarela. 2002. Global and local motions in ribonuclease A: a molecular dynamics study. Biopolymers. 65:274–283. [DOI] [PubMed] [Google Scholar]
- Milkman, R. 1994. An Escherichia coli homologue of eukaryotic potassium channel proteins. Proc. Natl. Acad. Sci. USA. 91:3510–3514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monks, S. A., D. J. Needleman, and C. Miller. 1999. Helical structure and packing orientation of the S2 segment in the Shaker K+ channel. J. Gen. Physiol. 113:415–423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale, E. J., D. J. S. Elliott, M. Hunter, and A. Sivaprasadarao. 2003. Evidence for intersubunit interactions between S4 and S5 transmembrane segments of the Shaker potassium channel. J. Biol. Chem. 278:29079–29085. [DOI] [PubMed] [Google Scholar]
- Ohlenschlager, O., H. Hojo, R. Ramachandran, M. Gorlach, and P. I. Haris. 2002. Three-dimensional structure of the S4–S5 segment of the Shaker potassium channel. Biophys. J. 82:2995–3002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perozo, E., D. M. Cortes, and L. G. Cuello. 1999. Structural rearrangements underlying K+ channel activation gating. Science. 285:73–78. [DOI] [PubMed] [Google Scholar]
- Planells-Cases, R., A. V. Ferrer-Montiel, C. D. Patten, and M. Montal. 1995. Mutation of conserved negatively charged residues in the S2 and S3 transmembrane segments of a mammalian K+ channel selectively modulates channel gating. Proc. Natl. Acad. Sci. USA. 92:9422–9426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popot, J.-L., and D. M. Engelman. 1990. Membrane protein folding and oligomerization: the two-stage model. Biochemistry. 2721:4031–4037. [DOI] [PubMed] [Google Scholar]
- Ranatunga, K. M., R. J. Law, G. R. Smith, and M. S. Sansom. 2001. Electrostatics studies and molecular dynamics simulations of a homology model of the Shaker K+ channel pore. Eur. Biophys. J. 30:295–303. [DOI] [PubMed] [Google Scholar]
- Roux, B. 1997. Influence of the membrane potential on the free energy of an intrinsic protein. Biophys. J. 73:2980–2989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux, B. 2002. Theoretical and computational models of ion channels. Curr. Opin. Struct. Biol. 12:182–189. [DOI] [PubMed] [Google Scholar]
- Ruta, V., Y. Jiang, A. Lee, J. Chen, and R. MacKinnon. 2003. Functional analysis of an archeabacterial voltage-dependent K+ channel. Nature. 422:180–185. [DOI] [PubMed] [Google Scholar]
- Sato, C., Y. Ueno, K. Asal, K. Takahashi, M. Sato, A. Engel, and Y. Fujiyoshi. 2001. The voltage-sensitive sodium channel is a bell-shaped molecule with several cavities. Nature. 409:1047–1051. [DOI] [PubMed] [Google Scholar]
- Schoppa, N. E., and F. J. Sigworth. 1998. Activation of Shaker potassium channels. III. An activation gating model for wild-type and V2 mutant channel. J. Gen. Physiol. 111:313–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seoh, S. A., D. Sigg, D. M. Papazian, and F. Bezanilla. 1996. Voltage-sensing residues in the S2 and S4 segments of the Shaker K+ channel. Neuron. 16:1159–1167. [DOI] [PubMed] [Google Scholar]
- Sigg, D., F. Bezanilla, and E. Stefani. 2003. Fast gating in the Shaker K+ channel and the energy landscape of activation. Proc. Natl. Acad. Sci. USA. 100:7611–7615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smart, O. S., J. M. Goodfellow, and B. A. Wallace. 1993. The pore dimensions of gramicidin A. Biophys. J. 72:1109–1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokolova, O., L. Kolmakova-Partensky, and N. Grigorieff. 2001. Three-dimensional structure of a voltage-gated potassium channel at 2.5 nm resolution. Structure (Camb.). 9:215–220. [DOI] [PubMed]
- Starace, D. M., and F. Bezanilla. 2001. Histidine scanning mutagenesis of basic residues of the S4 segment of the Shaker potassium channel. J. Gen. Physiol. 117:469–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starace, D. M., and F. Bezanilla. 2004. A proton pore in a potassium channel voltage sensor reveals a focused electric field. Nature. 427:548–553. [DOI] [PubMed] [Google Scholar]
- Starace, D. M., E. Stefani, and F. Bezanilla. 1997. Voltage-dependent proton transport by the voltage sensor of the Shaker K+ channel. Neuron. 19:1319–1327. [DOI] [PubMed] [Google Scholar]
- Stern, H. A., and S. E. Feller. 2003. Calculation of the dielectric permittivity profile for a nonuniform system: application to a lipid bilayer simulation. J. Chem. Phys. 118:3401–3412. [Google Scholar]
- Tieleman, D. P., J. H. C. Berendsen, and M. S. P. Sansom. 2001. Voltage-dependent insertion of alamethicin at phospholipid/water and octane water interfaces. Biophys. J. 80:331–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tieleman, D. P., L. R. Forrest, M. S. P. Sansom, and H. J. C. Berendsen. 1998. Lipid properties and the orientation of aromatic residues in OmpF, Influenza M2 and alamethicin systems: molecular dynamics simulations. Biochemistry. 37:17544–17561. [DOI] [PubMed] [Google Scholar]
- Tieleman, D. P., B. Hess, and M. S. P. Sansom. 2002. Analysis and evaluation of channel models: simulations of alamethicin. Biophys. J. 83:2393–2407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiwari-Woodruff, S. K., C. T. Schulteis, A. F. Mock, and D. M. Papazian. 1997. Electrostatic interactions between transmembrane segments mediate folding of Shaker K+ channel subunits. Biophys. J. 72:1489–1500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tristani-Firouzi, M., J. Chen, and M. Sanguinetti. 2002. Interactions between S4–S5 linker and S6 transmembrane domain modulate gating of HERG potassium channels. J. Biol. Chem. 277:18994–19000. [DOI] [PubMed] [Google Scholar]
- Tusnády, G. E., and I. Simon. 1998. Principles governing amino acid composition of integral membrane proteins: application to topology prediction. J. Mol. Biol. 283:489–506. [DOI] [PubMed] [Google Scholar]
- Vakser, A., and C. Aflalo. 1994. Hydrophobic docking: a proposed enhancement to molecular recognition techniques. Proteins. 20:320–329. [DOI] [PubMed] [Google Scholar]
- Webster, S. M., D. del Camino, J. P. Dekker, and G. Yellen. 2004. Intracellular gate opening in Shaker K1 channels defined by high-affinity metal bridges. Nature. 428:864–868. [DOI] [PubMed] [Google Scholar]
- Yang, N., A. L. J. George, and R. Horn. 1996. Molecular basis of charge movement in voltage-gated sodium channels. Neuron. 16:113–122. [DOI] [PubMed] [Google Scholar]
- Yellen, G. 2002. The voltage-gated potassium channels and their relatives. Nature. 419:35–42. [DOI] [PubMed] [Google Scholar]
- Zhou, M., J. H. Morais-Cabral, S. Mann, and R. MacKinnon. 2001. Potassium channel receptor site for the inactivation gate and quaternary amine inhibitors. Nature. 411:657–661. [DOI] [PubMed] [Google Scholar]